Estimation of Shear-Wave Velocity Structures in Taichung, Taiwan, Using Array Measurements of Microtremors
Abstracts
1. Introduction
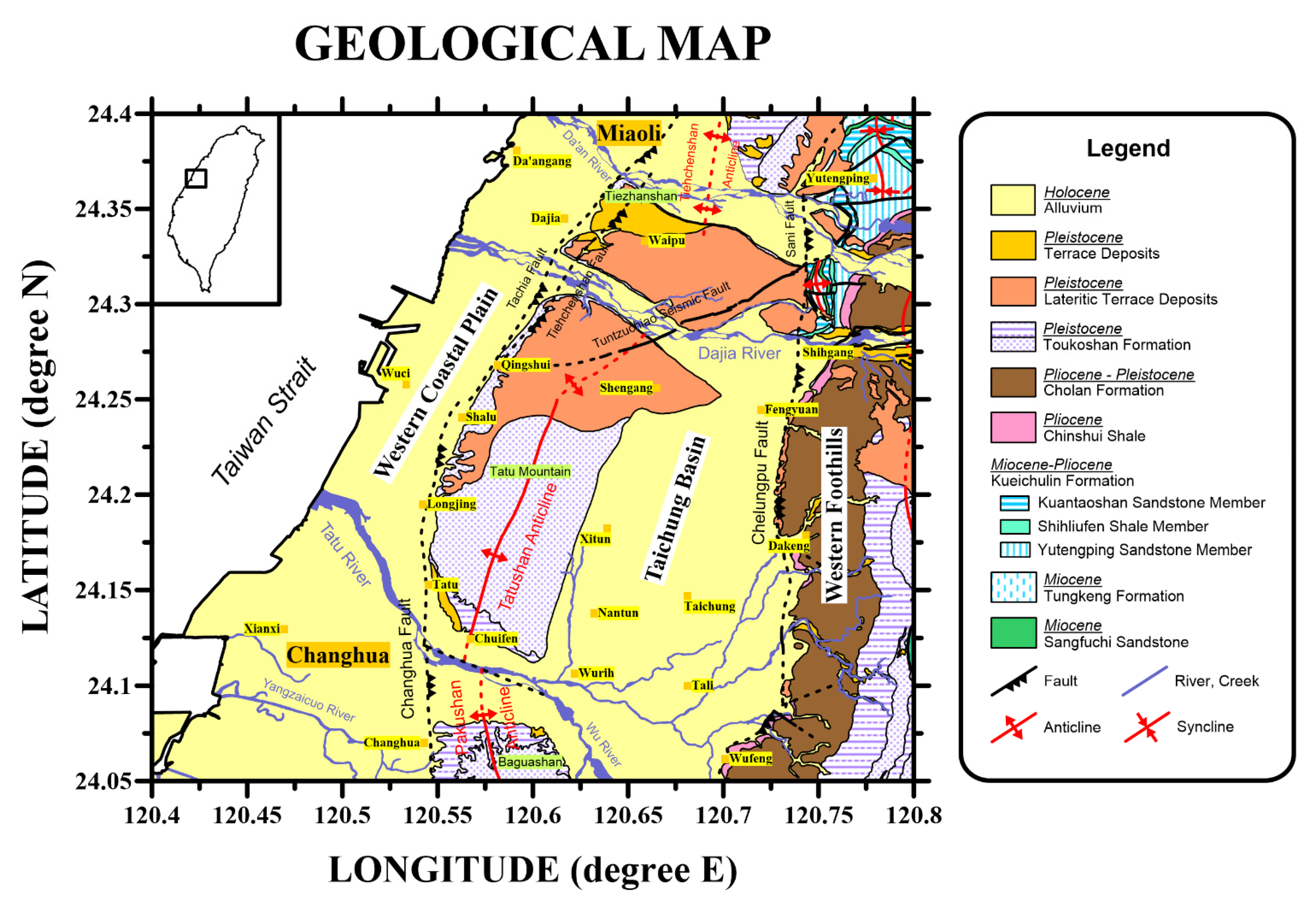
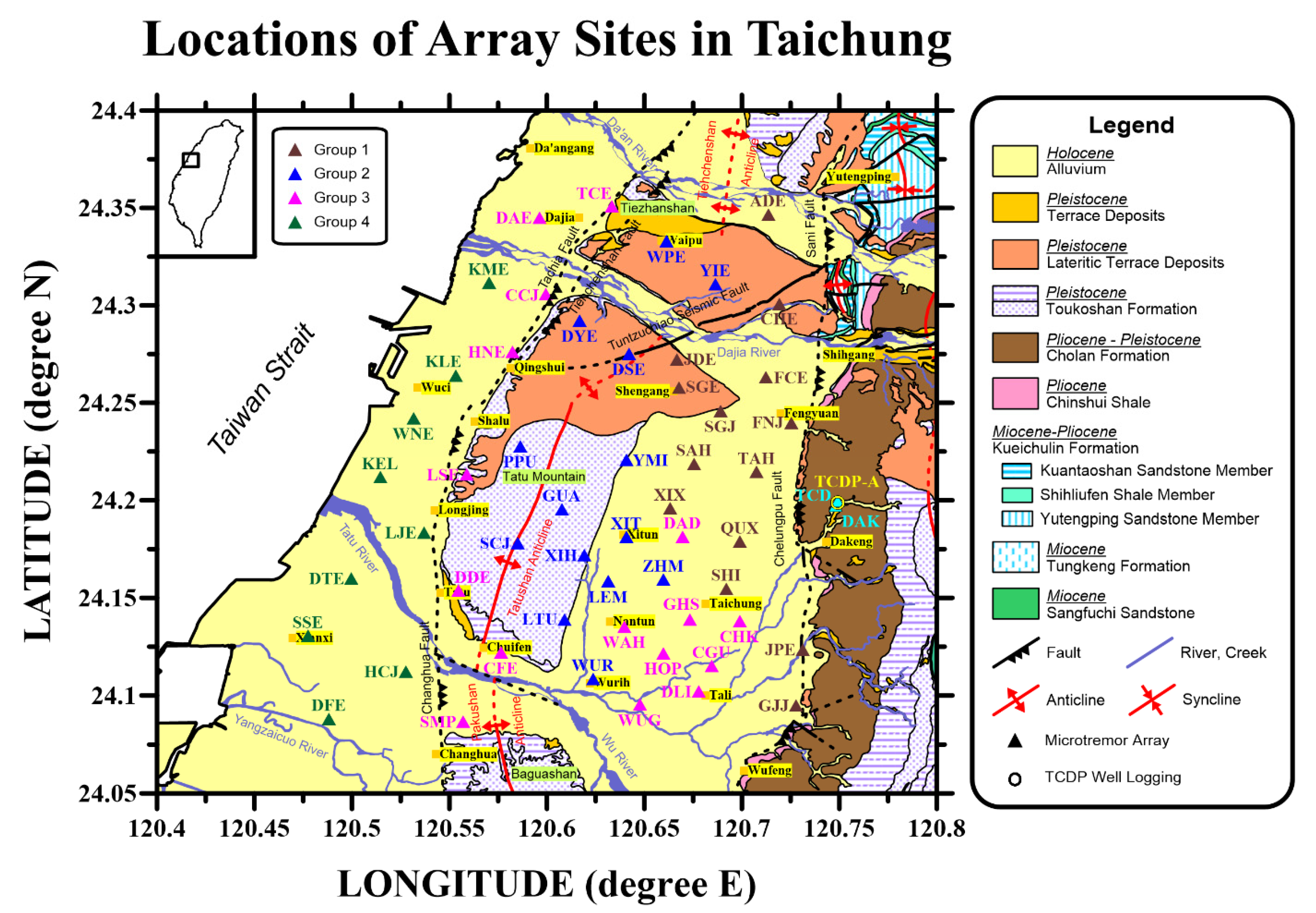
2. Sites and Data
3. Methodology
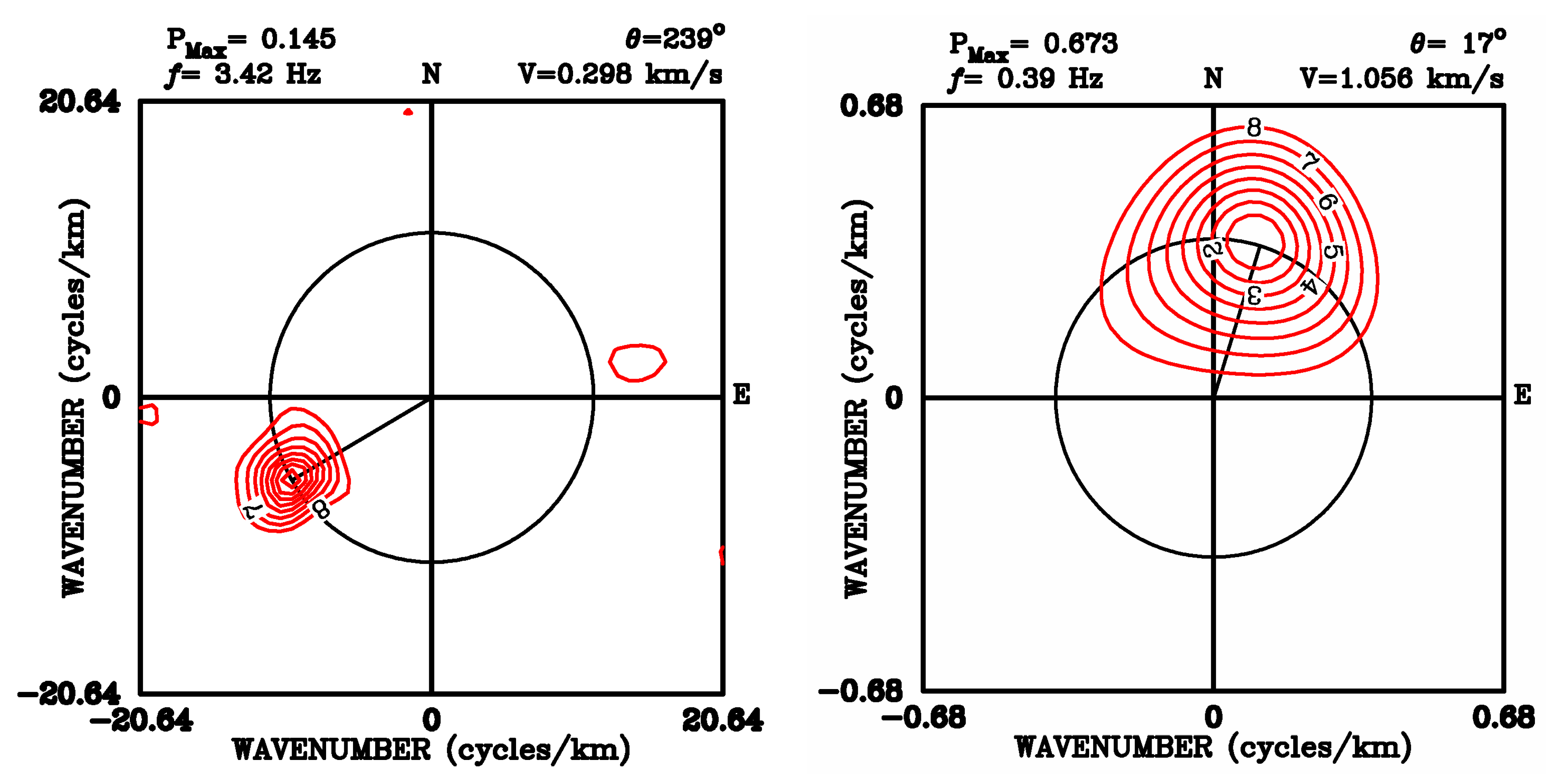
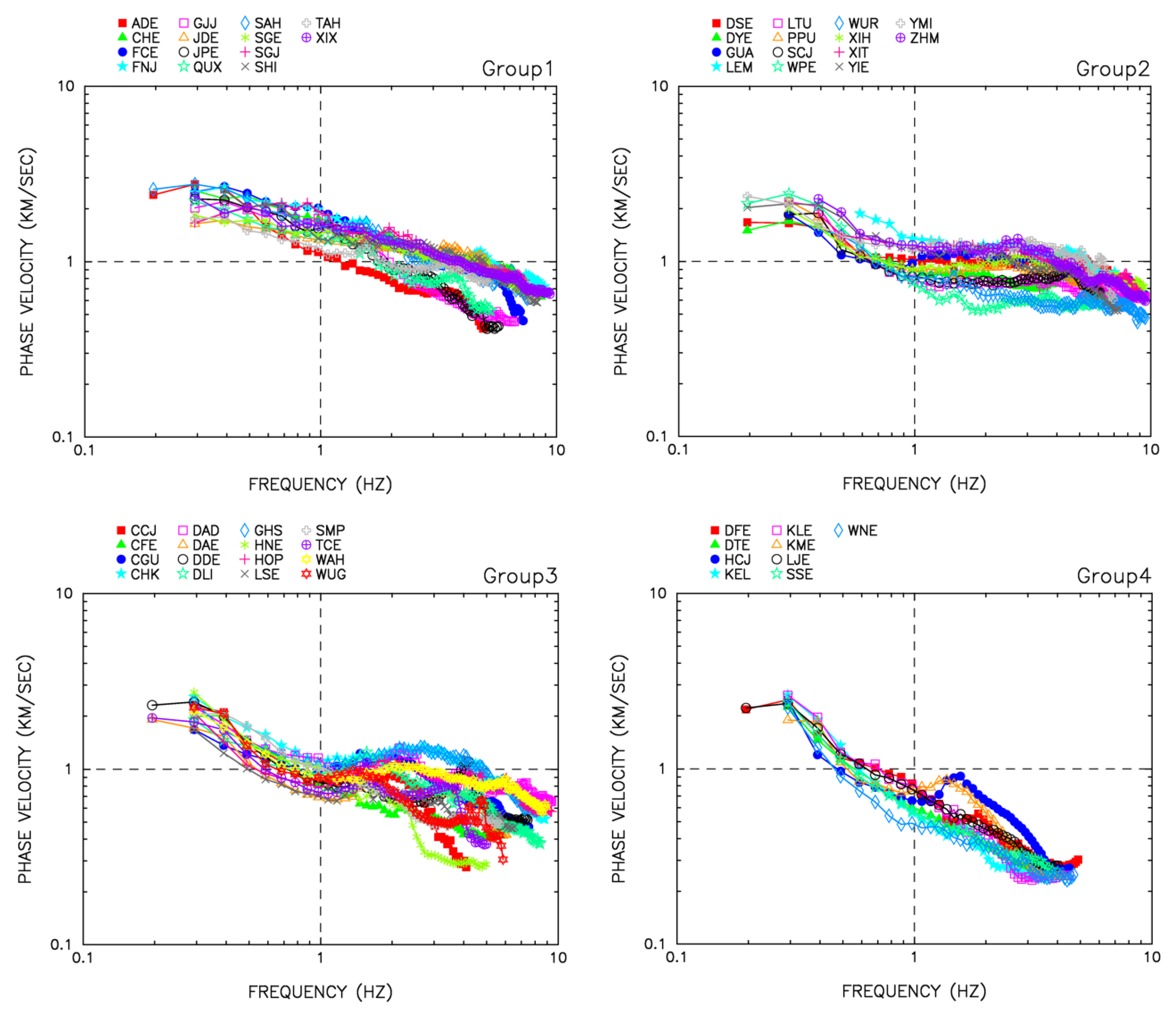
3.1. Frequency–Wavenumber Spectral Analysis Method
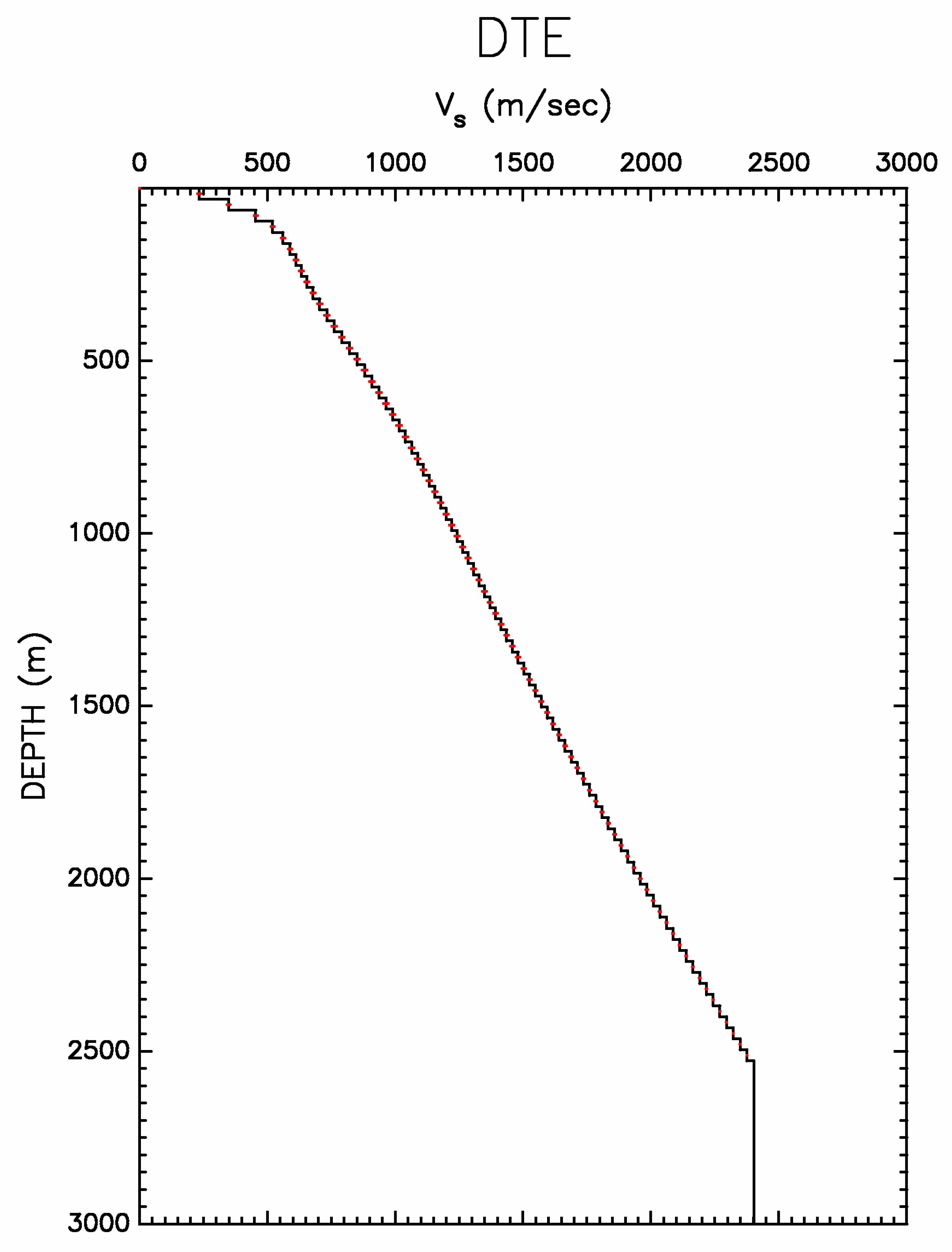
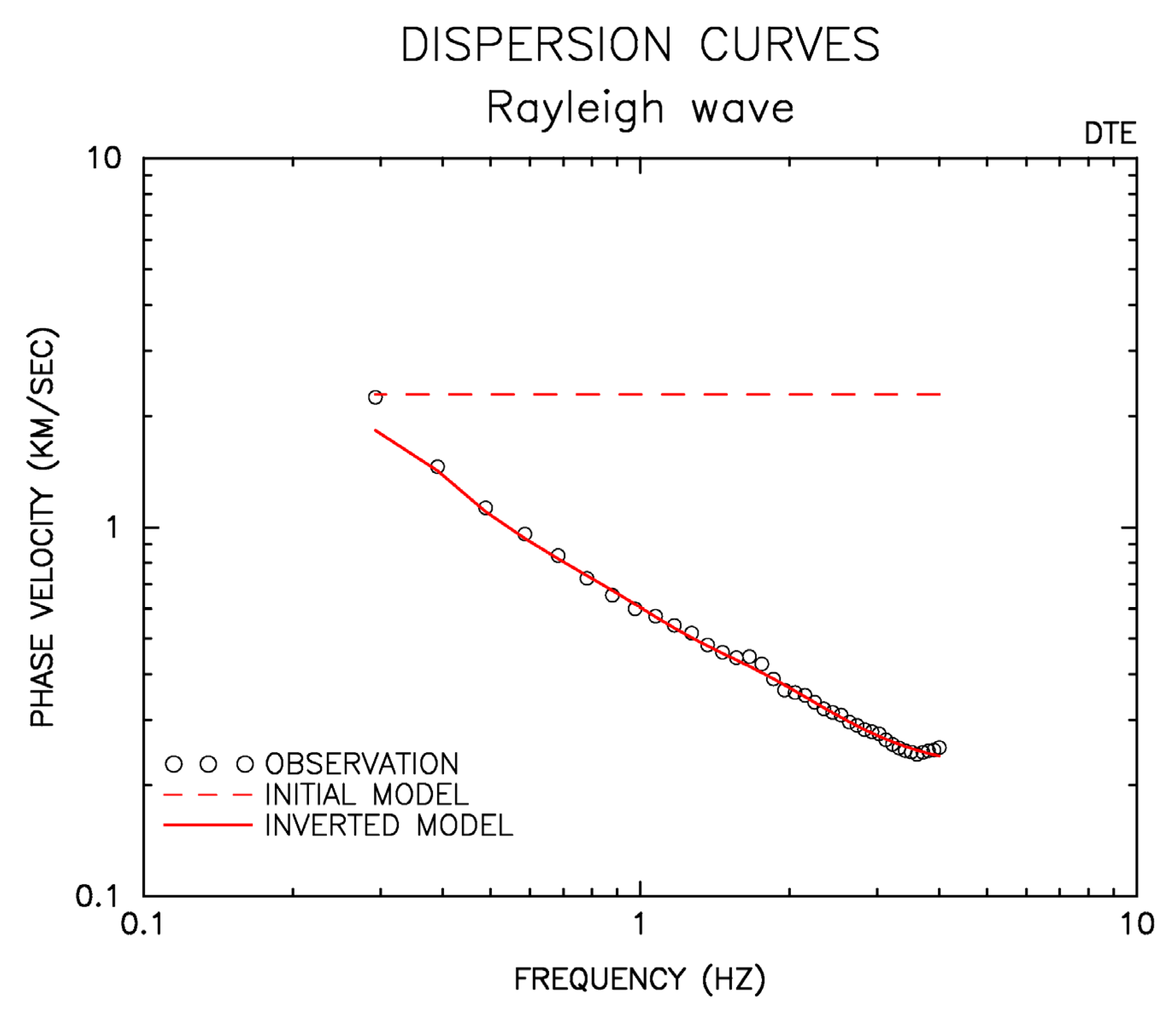
3.2. Inversion of the S-Wave Velocity Structure
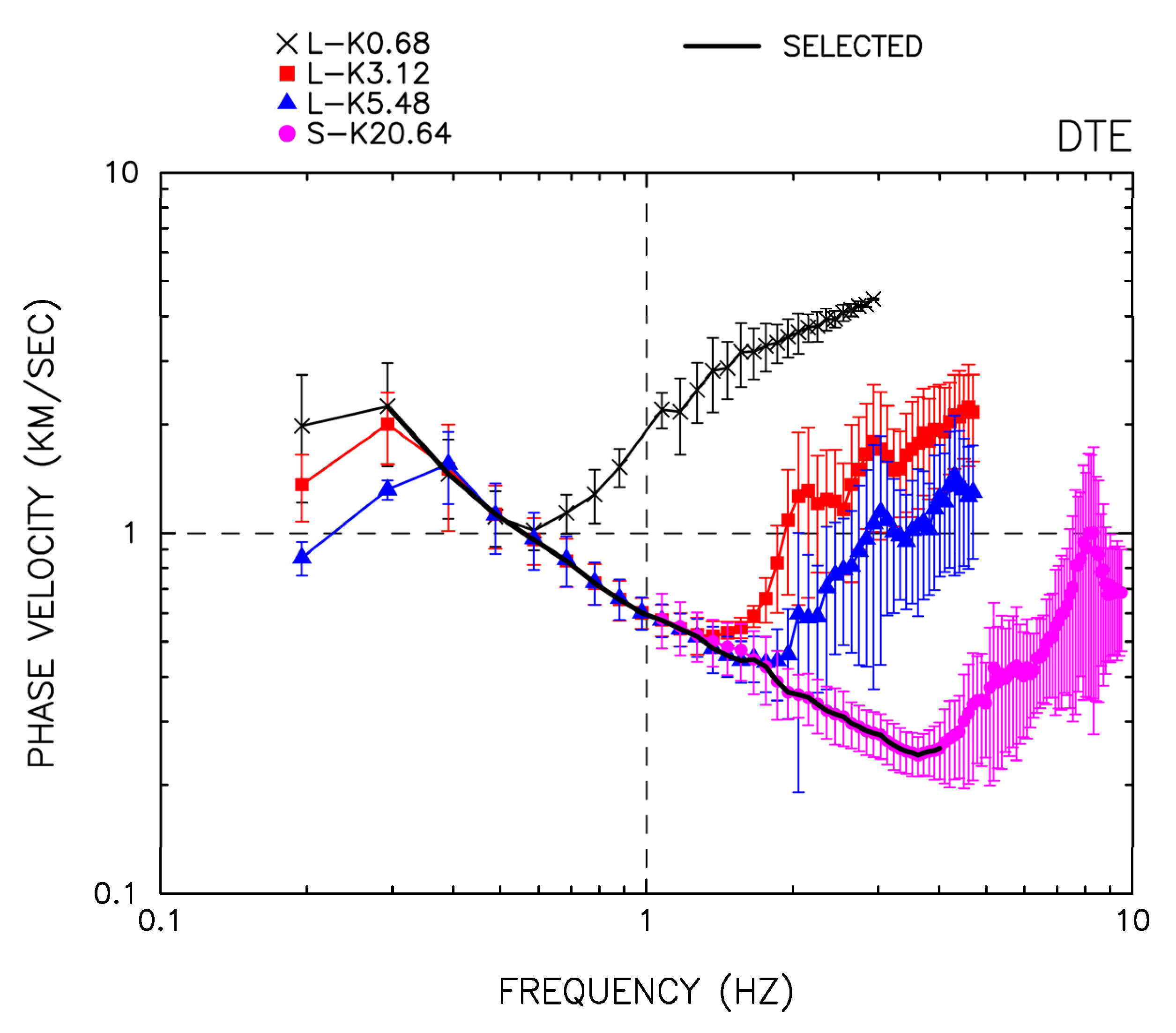
3.3. Examination of Analysis Methods
4. Results and Discussion
4.1. F-K Analysis of the Microtremor Array Data
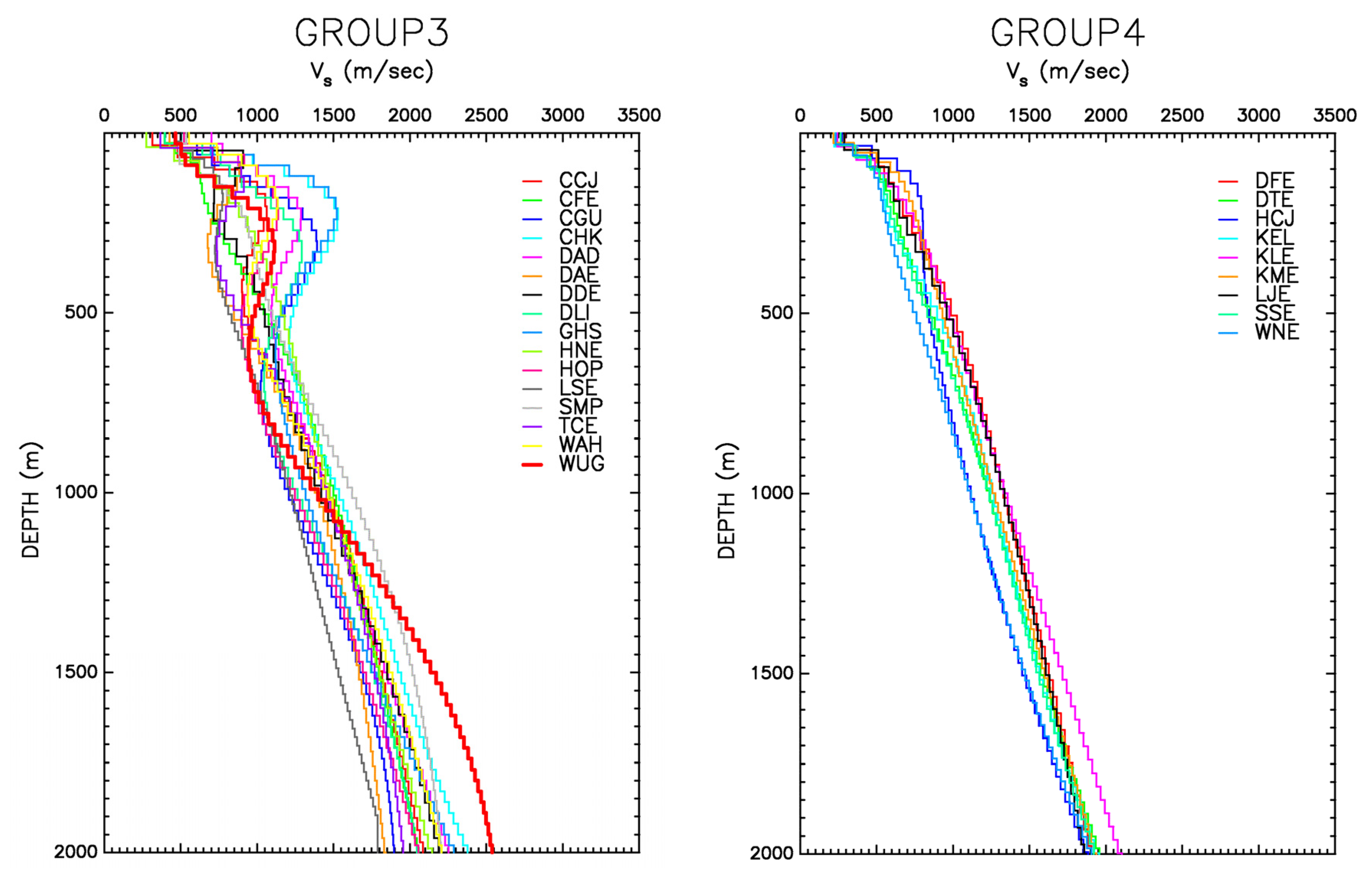
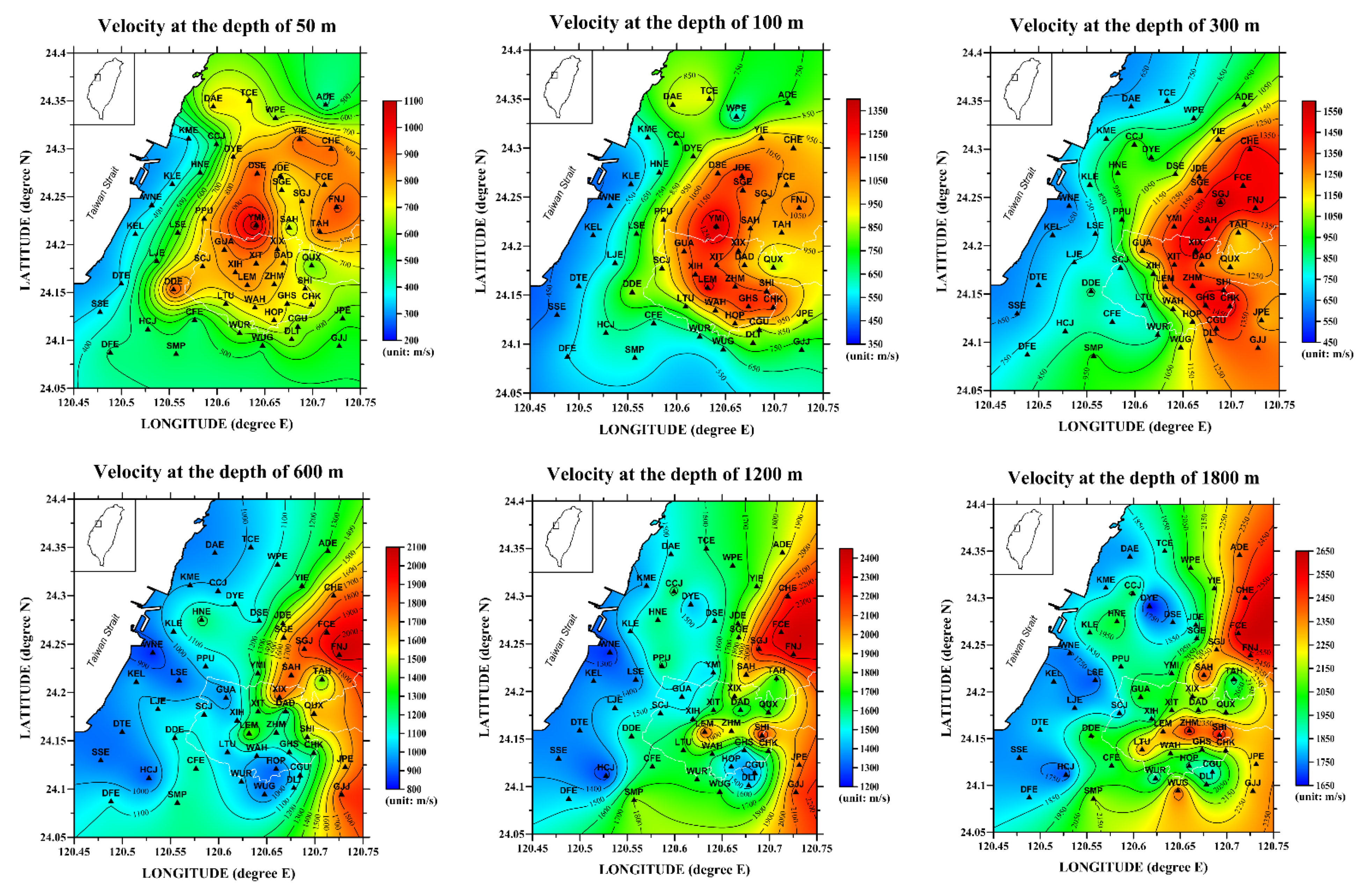
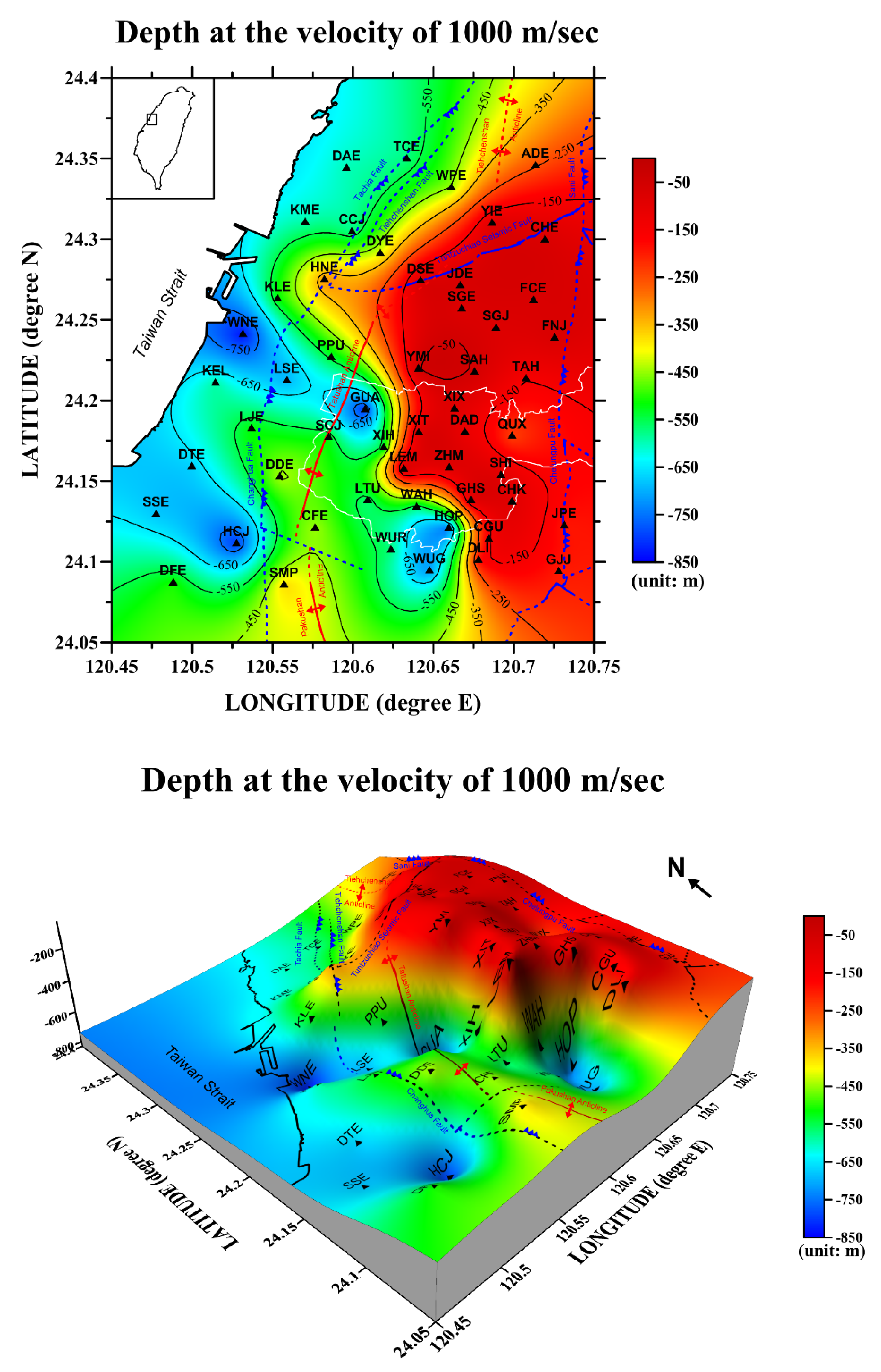
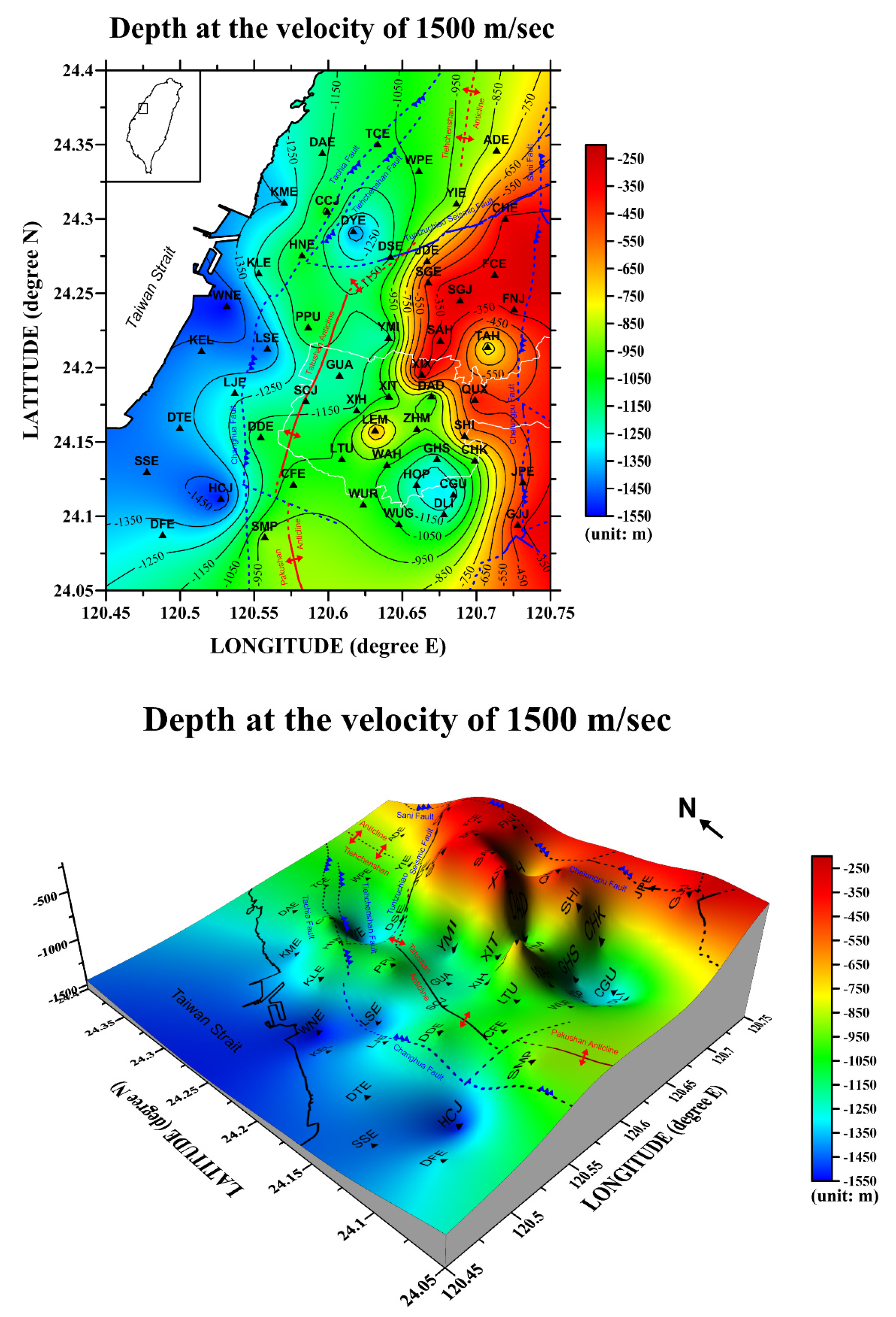
4.2. Inversion of the S-Wave Velocity Structure
- (1)
- Depths of 50–300 m: The highest velocities appear at the central part (YMI), whereas the lowest velocities appear at the western part (WNE). The area with the highest S-wave velocities gradually shifts from the central part (YMI) to the northeastern part (SGJ) as depth increases.
- (2)
- Depths of 300–600 m: The area with the highest S-wave velocities gradually shifts from the central part (SGJ) to the eastern part (FNJ), which is near the Chelungpu Fault, as depth increases. The lower velocities still appear at the western part (WNE).
- (3)
- Depths of 600–1200 m: The highest velocities appear at the eastern part (FNJ, FCE), whereas the lower velocities appear at the western (WNE) and southwestern (HCJ) parts.
- (4)
- Depths of 1200–1800 m: The highest velocities remain at the eastern part (FNJ, FCE). The second highest velocity zone appears at the area near sites SHI and ZHM. Similarly, the western part (WNE, HCJ) still exhibits the lowest velocities.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horike, M. Inversion of phase velocity of long-period microtremors to the S-wave-velocity structure down to the basement in urbanized area. J. Phys. Earth 1985, 33, 59–96. [Google Scholar] [CrossRef] [Green Version]
- Central Geology Survey (2019) National Geological Data Warehouse, Central Geology Survey, the Ministry of Economic Affairs, Taipei, Taiwan. Available online: https://gis3.moeacgs.gov.tw/gwh/gsb97-1/sys8/t3/index1.cfm (accessed on 31 March 2020).
- Matsushima, T.; Okada, H. Determination of deep geological structures under urban areas using long-period microtremors. Butsuri-Tansa 1990, 43, 21–33. [Google Scholar]
- Kawase, H.; Satoh, T.; Iwata, T.; Irikura, K. S-wave velocity structures in the San Fernando and Santa Monica areas. In Proceedings of the 2nd International Symposium on Effects of Surface Geology on Seismic Motions, Yokohama, Japan, 1–3 December 1998; Volume 2, pp. 733–740. [Google Scholar]
- Satoh, T.; Kawase, H.; Iwata, T.; Higashi, S.; Sato, T.; Irikura, K.; Huang, H.C. Estimation of S-wave velocity structures in and around the Sendai basin, Japan, using array records of microtremors. Bull. Seism. Soc. Am. 2001, 91, 206–218. [Google Scholar] [CrossRef]
- Satoh, T.; Kawase, H.; Iwata, T.; Higashi, S.; Sato, T.; Irikura, K.; Huang, H.C. S-wave velocity structure of the Taichung basin, Taiwan, estimated from array and single-station records of microtremors. Bull. Seism. Soc. Am. 2001, 91, 1267–1282. [Google Scholar] [CrossRef]
- Huang, H.C.; Wu, C.F. Estimation of S-wave velocity structures in the Chia-Yi City, Taiwan using array records of microtremors. Earth Planets Space 2006, 58, 1455–1462. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.M.; Chang, T.M.; Huang, Y.C.; Chiang, H.J.; Kuo, C.H.; Wen, K.L. Shallow S-wave velocity structures in the Western Coastal Plain of Taiwan. Terr. Atmos. Ocean Sci. 2009, 20, 299–308. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.F.; Huang, H.C. Estimation of shallow S-wave velocity structure in the Puli basin, Taiwan, using array measurements of microtremors. Earth Planets Space 2012, 64, 389–403. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.F.; Huang, H.C. Near-surface shear-wave velocity structure of the Chiayi area, Taiwan. Bull. Seism. Soc. 2013, 103, 1154–1164. [Google Scholar] [CrossRef]
- Wu, C.F.; Huang, H.C. S-Wave Velocity Structure of the Taiwan Chelungpu-Fault Drilling Project (TCDP) Site Using Microtremor Array Measurements. Pure Appl. Geophys. 2015, 172, 2545–2556. [Google Scholar] [CrossRef]
- Wu, C.F.; Huang, H.C. Detection of a Fracture Zone Using Microtremor Array Measurement. Geophysics 2019, 84, B33–B40. [Google Scholar] [CrossRef]
- Huang, H.C.; Wu, C.F.; Lee, F.M.; Hwang, R.D. S-Wave Velocity Structures of the Taipei Basin, Taiwan, Using Microtremor Array Measurements. J. Asian Earth Sci. 2015, 101, 1–13. [Google Scholar] [CrossRef]
- Kuo, C.H.; Chen, C.T.; Lin, C.M.; Wen, K.L.; Huang, J.Y.; Chang, S.C. S-wave velocity structure and site effect parameters derived from microtremor arrays in the Western Plain of Taiwan. J. Asian Earth Sci. 2016, 128, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.P.; Shukla, A.; Kumar, M.R.; Thakkar, M.G. Characterizing surface geology, liquefaction potential, and maximum intensity in the Kachchh Seismic Zone, Western India, through microtremor analysis. Bull. Seism. Soc. Am. 2017, 107, 1277–1292. [Google Scholar] [CrossRef]
- Özmen, Ö.T.; Yamanaka, H.; Alkan, M.A.; Çeken, U.; Öztürk, T.; Sezen, A. Microtremor array measurements for shallow S-wave profiles at strong-motion stations in Hatay and Kahramanmaras Provinces, Southern Turkey. Bull. Seism. Soc. Am. 2017, 107, 445–455. [Google Scholar] [CrossRef]
- Ridwan, M.; Cummins, P.R.; Widiyantoro, S.; Irsyam, M. Site characterization using microtremor array and seismic hazard assessment for Jakarta, Indonesia. Bull. Seism. Soc. Am. 2019, 109, 2644–2657. [Google Scholar] [CrossRef]
- Ku, T.; Palanidoss, S.; Zhang, Y.; Moona, S.W.; Wei, X.; Huang, E.S.; Kumarasamy, J.; Goh, K.H. Practical configured microtremor array measurements (MAMs) for the geological investigation of underground space. Undergr. Space 2021, 6, 240–251. [Google Scholar] [CrossRef]
- Satoh, T.; Kawase, H.; Iwata, T.; Higashi, S.; Sato, T.; Huang, H.C. S-wave velocity structures of sediments estimated from array microtremor records and site responses in the near-fault Region of the 1999 Chi-Chi, Taiwan earthquake. J. Seismol. 2004, 8, 545–558. [Google Scholar]
- Ho, H.C.; Chen, M.M. Explanation Text of the Geological Map of Taiwan (Taichung, Scale 1:50,000, Sheet 24); Central Geological Survey, the Ministry of Economic Affairs: Taipei, Taiwan, 2000; p. 65, (In Chinese with English Summary). [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectral analysis. Proc. IEEE 1969, 57, 1408–1419. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, R.B. Computer Program in Seismology, Volume IV: Surface Wave Inversion; University of St. Louis: St. Louis, MO, USA, 1991; p. 58. [Google Scholar]
- Wu, H.Y.; Ma, K.F.; Zoback, M.; Boness, N.; Ito, H.; Hung, J.H.; Hickman, S. Stress orientations of Taiwan Chelungpu-Fault Drilling Project (TCDP) hole-A as observed from geophysical logs. Geophys. Res. Lett. 2007, 34, L01303. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.H.; Hung, J.H.; Dong, J.J. Seismic velocities, density, porosity, and permeability measured at a deep hole penetrating the Chelungpu fault in central Taiwan. J. Asian Earth Sci. 2009, 36, 135–145. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.-C.; Shih, T.-H.; Hsu, C.-T.; Wu, C.-F. Estimation of Shear-Wave Velocity Structures in Taichung, Taiwan, Using Array Measurements of Microtremors. Appl. Sci. 2022, 12, 170. https://doi.org/10.3390/app12010170
Huang H-C, Shih T-H, Hsu C-T, Wu C-F. Estimation of Shear-Wave Velocity Structures in Taichung, Taiwan, Using Array Measurements of Microtremors. Applied Sciences. 2022; 12(1):170. https://doi.org/10.3390/app12010170
Chicago/Turabian StyleHuang, Huey-Chu, Tien-Han Shih, Cheng-Ta Hsu, and Cheng-Feng Wu. 2022. "Estimation of Shear-Wave Velocity Structures in Taichung, Taiwan, Using Array Measurements of Microtremors" Applied Sciences 12, no. 1: 170. https://doi.org/10.3390/app12010170
APA StyleHuang, H.-C., Shih, T.-H., Hsu, C.-T., & Wu, C.-F. (2022). Estimation of Shear-Wave Velocity Structures in Taichung, Taiwan, Using Array Measurements of Microtremors. Applied Sciences, 12(1), 170. https://doi.org/10.3390/app12010170





