Monitoring of Liquid Viscosity for Viscous Dampers through a Wireless Impedance Measurement System
Abstract
:1. Introduction
2. Monitoring Method of Damper Fluid Viscosity
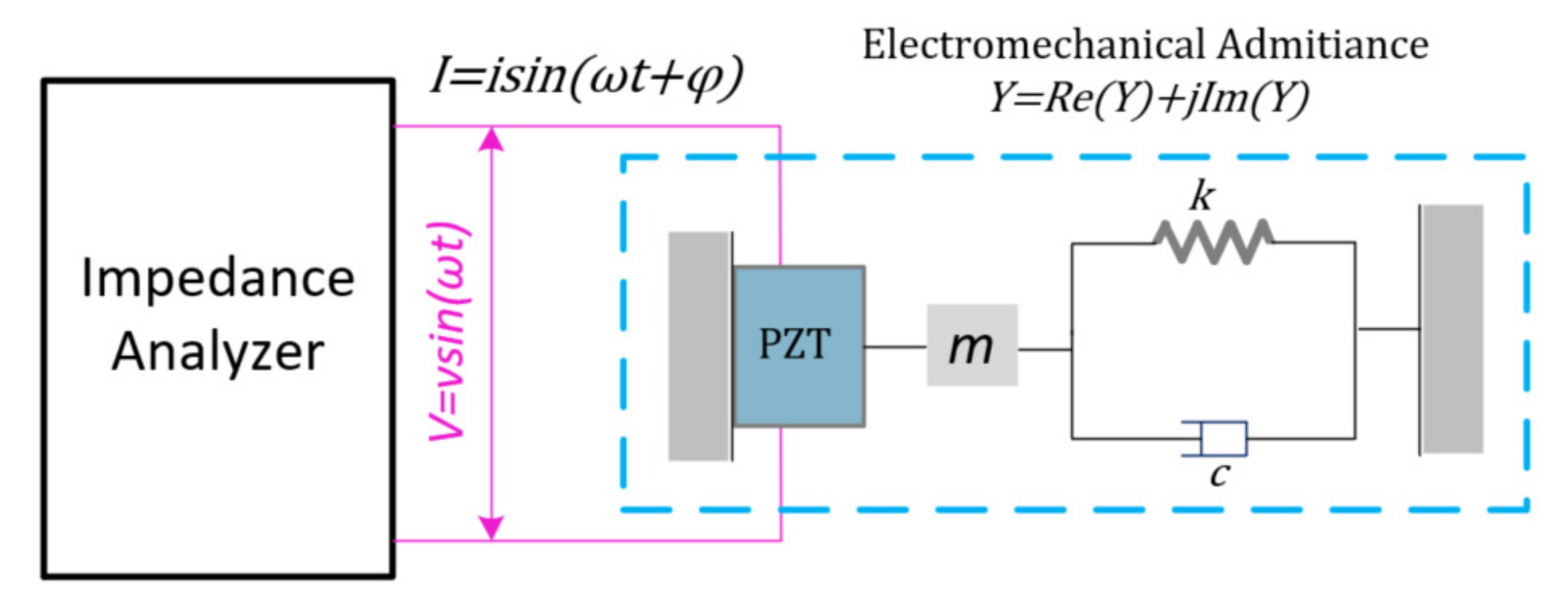
2.1. The Principle of the EMI Method
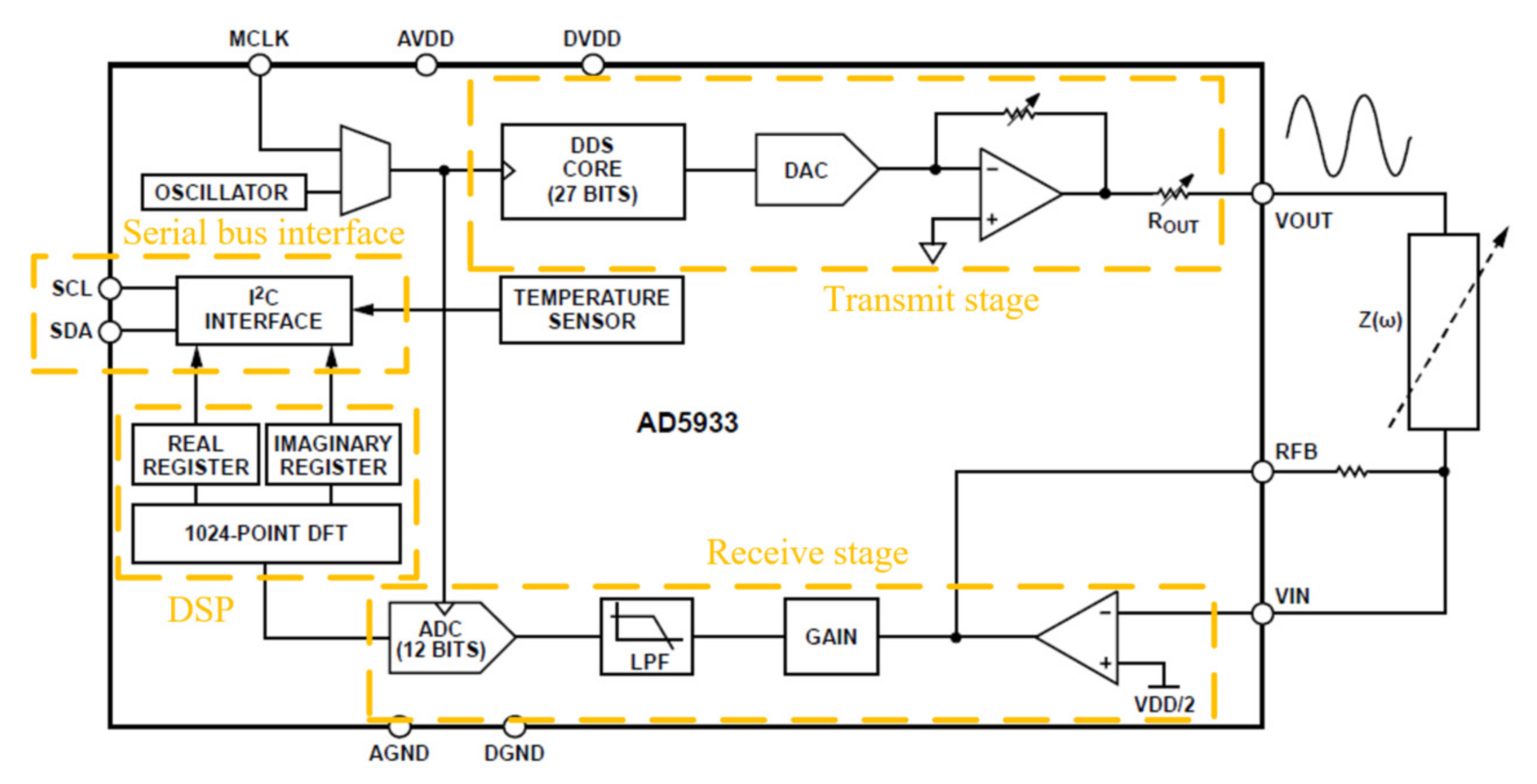
2.2. Design of Wireless Impedance Measurement System
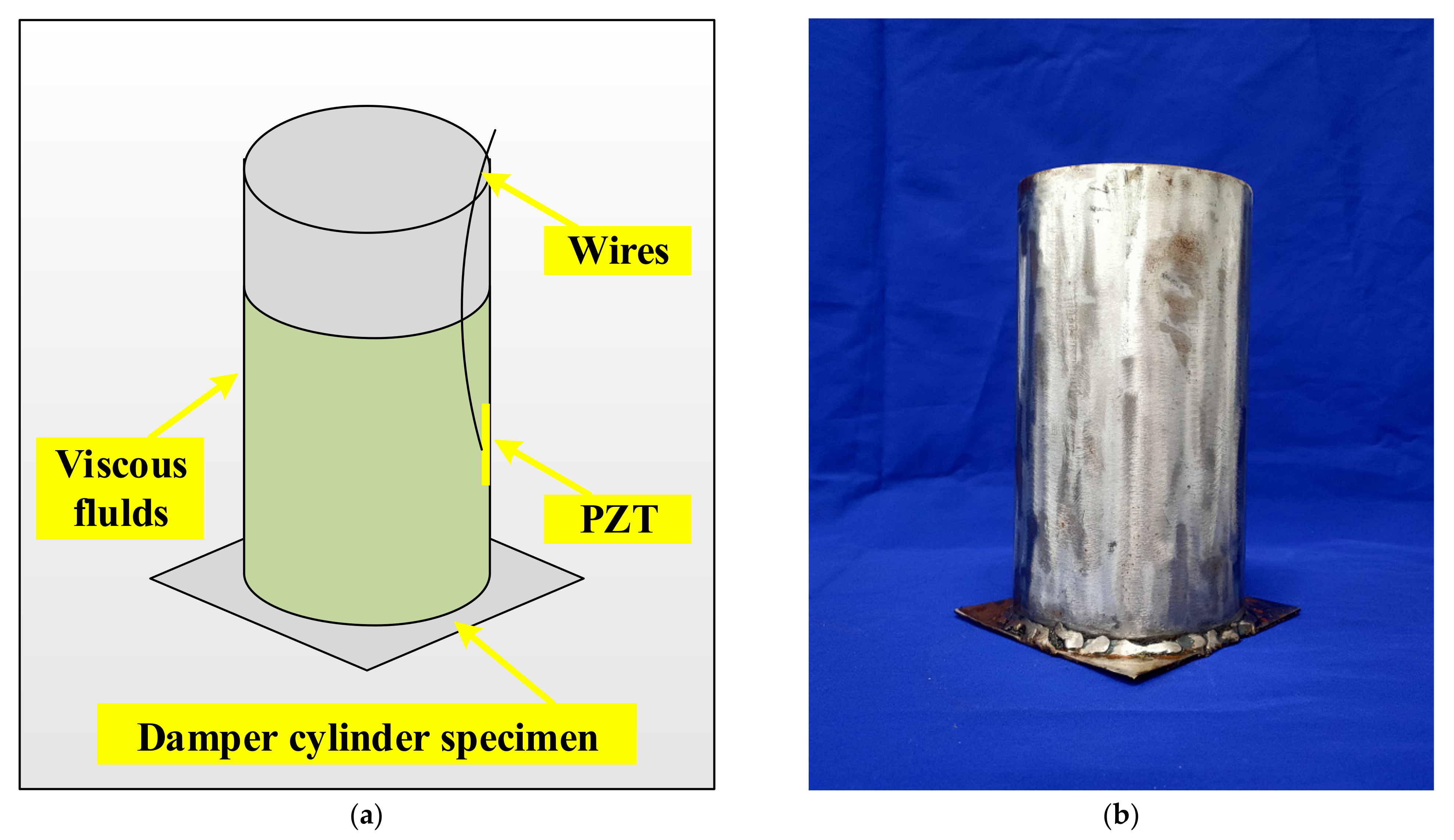
3. Experimental Set Up
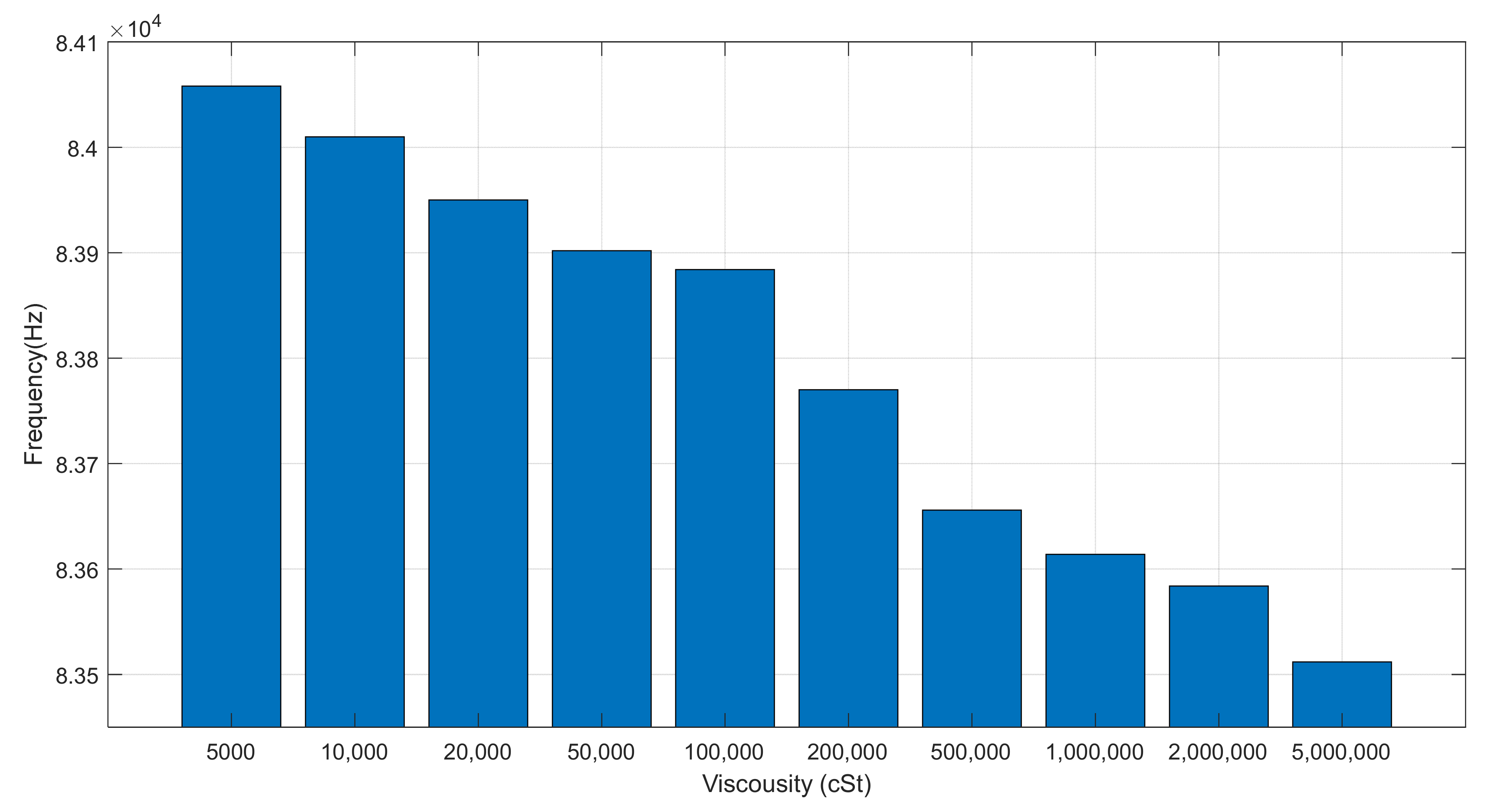
4. Experimental Results
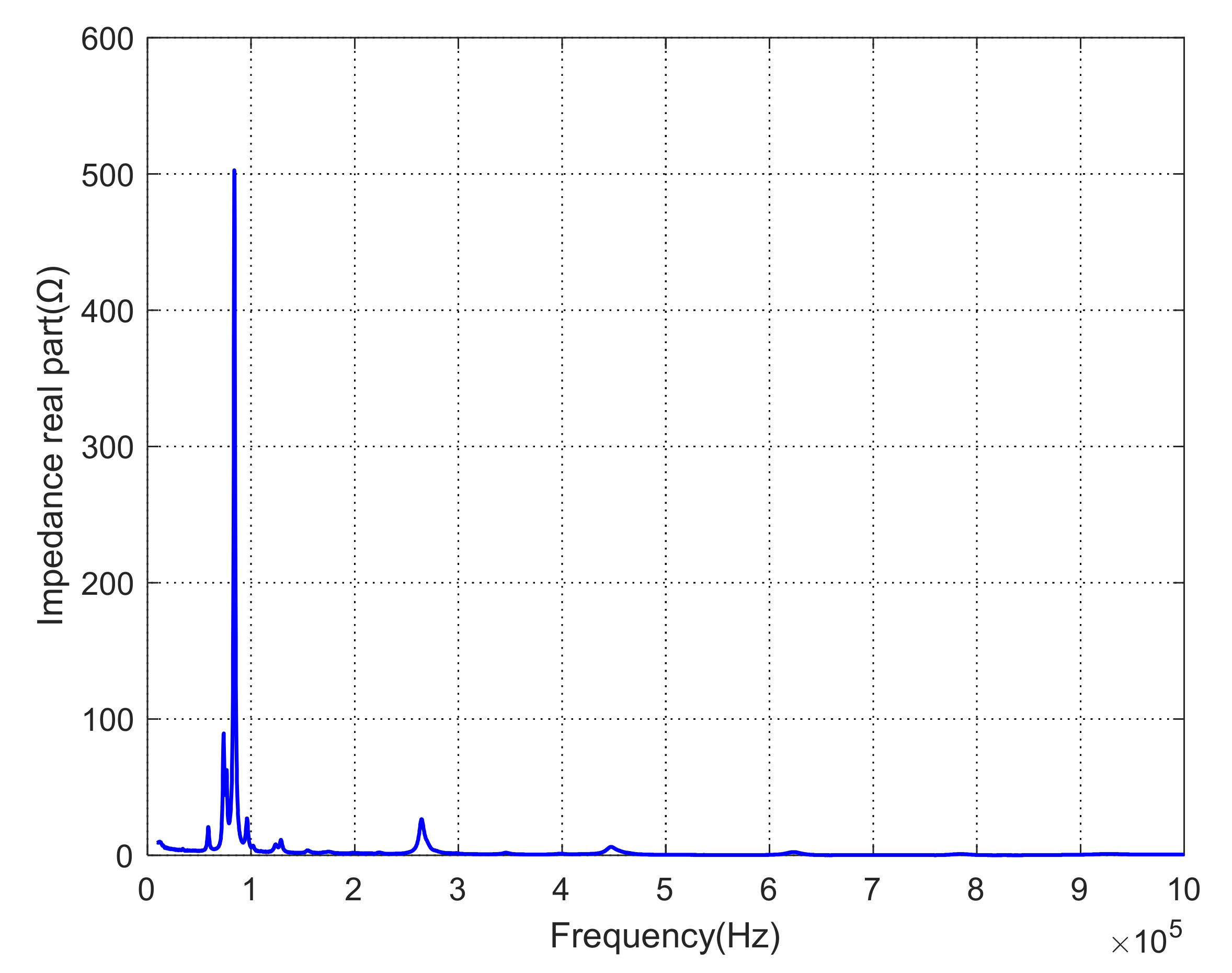
4.1. Results and Analysis
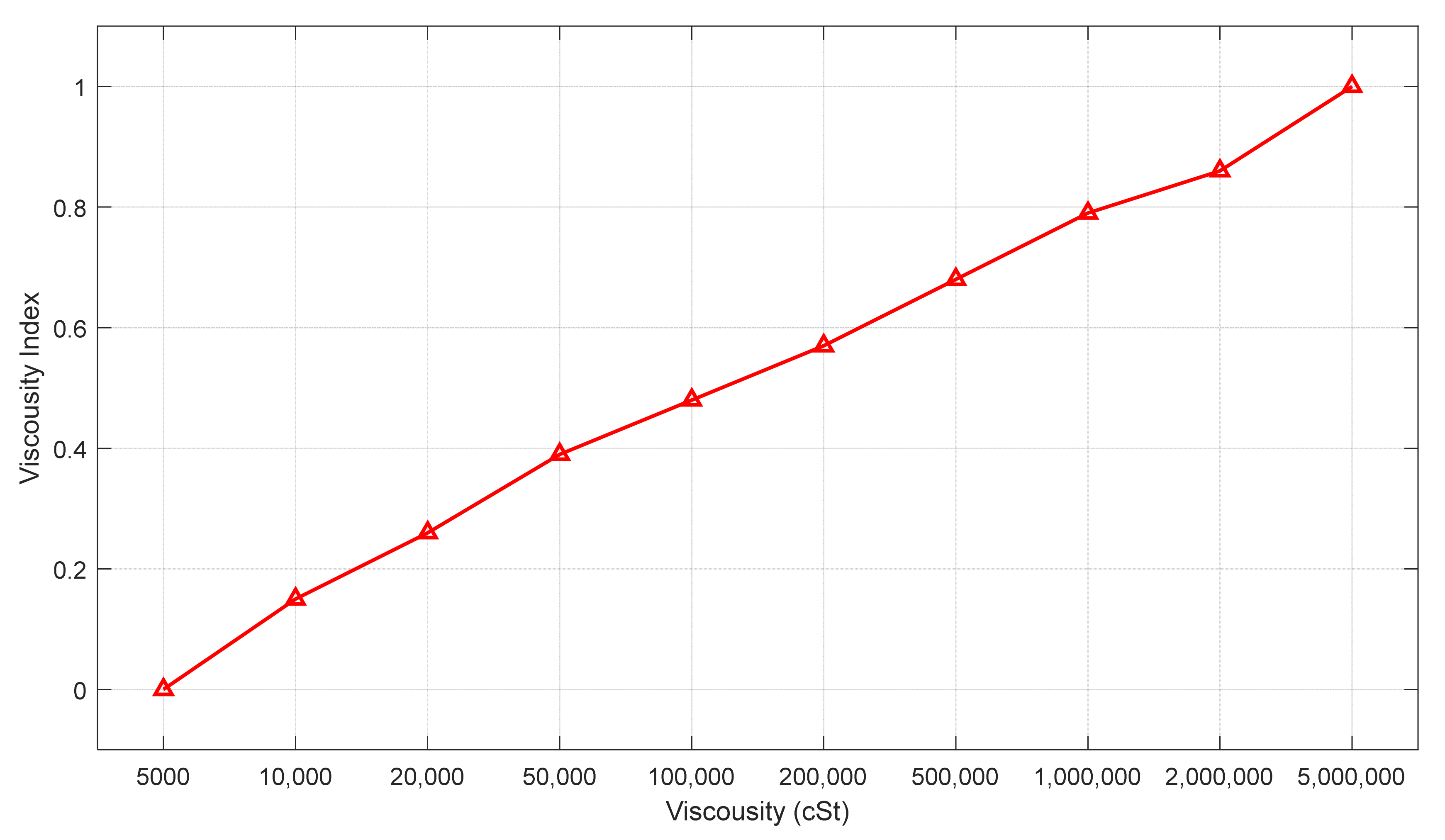
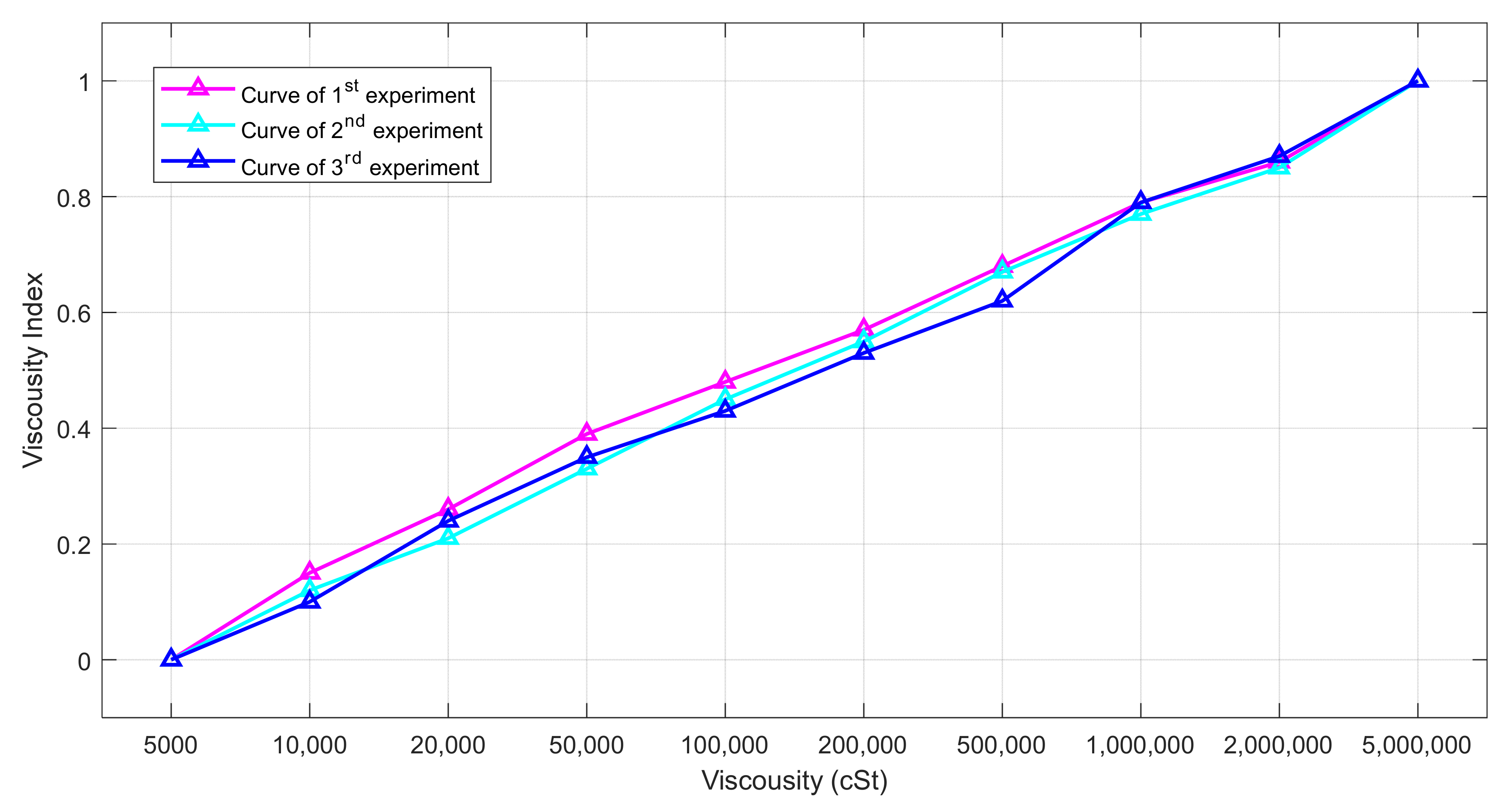
4.2. Viscous Damper Viscosity Index (VI) Based on RMSD
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, D.; Taylor, D.P. Viscous damper development and future trends. Struct. Des. Tall Build. 2001, 10, 311–320. [Google Scholar] [CrossRef]
- Huang, H.C. Efficiency of the motion amplification device with viscous dampers and its application in high-rise buildings. Earthq. Eng. Eng. Vib. 2010, 8, 521–536. [Google Scholar] [CrossRef]
- Sonda, D.; Cigada, A.; Ciccaldo, G.; Goppion, A.; Pollini, A.V. Seismic and vibration protection of the statue Pietà Rondanini by Michelangelo. In Proceedings of the Atti del XVII Convegno ANIDIS L’Ingegneria Sismica, Pistoia, Italy, 17–21 September 2017; PISA University Press: Paris, France, 2017; pp. 287–296. [Google Scholar]
- Xu, Y.L.; Ko, H. Dynamic response of damper-connected adjacent buildings under earthquake excitation. Eng. Struct. 1999, 21, 135–148. [Google Scholar] [CrossRef]
- Giresini, L.; Puppio, M.; Laccone, F.; Froli, M. Experimental and numerical investigation on a passive control system for the mitigation of vibrations on SDOF and MDOF Structures: Mini Tribological ROCKing Seismic Isolation Device (miniTROCKSISD). J. Earthq. Eng. 2021, 1–19. [Google Scholar] [CrossRef]
- Madhekar, S.N.; Jangid, R.S. Variable dampers for earthquake protection of benchmark highway bridges. Smart Mater. Struct. 2009, 18, 115011. [Google Scholar] [CrossRef]
- Froli, M.; Giresini, L.; Laccone, F. Dynamics of a new seismic isolation device based on tribological smooth rocking (TROCKSISD). Eng. Struct. 2019, 193, 154–169. [Google Scholar] [CrossRef]
- Guo, A.; Xu, Y.L.; Wu, B. Seismic reliability analysis of hysteretic structure with viscoelastic dampers. Eng. Struct. 2002, 24, 373–383. [Google Scholar] [CrossRef]
- Ceravolo, R.; Pecorelli, M.L.; Fragonara, L.Z. Semi-active control of the rocking motion of monolithic art objects. J. Sound Vib. 2016, 374, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, H.K.; Gilani, A.S.J.; Wada, A.; Ariyaratana, C. Limit states and failure mechanisms of viscous dampers and the implications for large earthquakes. Earthq. Eng. Struct. Dyn. 2010, 39, 1279–1297. [Google Scholar] [CrossRef]
- Kandemir, E.C.; Mazda, T.; Nurui, H.; Miyamoto, H. Seismic Retrofit of an Existing Steel Arch Bridge Using Viscous Damper. Procedia Eng. 2011, 14, 2301–2306. [Google Scholar] [CrossRef] [Green Version]
- De Canio, G. Marble devices for the Base isolation of the two Bronzes of Riace: A proposal for the David of Michelangelo. In Proceedings of the XV World Conference on Earthquake Engineering-WCEE, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Baggio, S.; Berto, L.; Favaretto, T.; Saetta, A.; Vitaliani, R. Seismic isolation technique of marble sculptures at the Accademia Gallery in Florence: Numerical calibration and simulation modelling. Bull. Earthq. Eng. 2015, 13, 2719–2744. [Google Scholar] [CrossRef]
- Radestroem, S.; Uelker-Kaustell, M.; Andersson, A.; Tell, V.; Karoumi, R. Application of fluid viscous dampers to mitigate vibrations of high-speed railway bridges. Int. J. Rail Transp. 2017, 5, 47–62. [Google Scholar] [CrossRef]
- Wei, M.; Lin, K.; Liu, H. Experimental investigation on hysteretic behavior of a shear thickening fluid damper. Struct. Control Health Monit. 2019, 26, e2389. [Google Scholar] [CrossRef]
- Lavan, O. On the efficiency of viscous dampers in reducing various seismic responses of wall structures. Earthq. Eng. Struct. Dyn. 2012, 41, 1673–1692. [Google Scholar] [CrossRef]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Marano, G.C.; Trentadue, F.; Greco, R. Stochastic optimum design criterion for linear damper devices for seismic protection of buildings. Struct. Multidiscip. Optim. 2007, 33, 441–455. [Google Scholar] [CrossRef]
- Chen, C.; Chen, G. Shake table tests of a quarter-scale three-storey building model with piezoelectric friction dampers. Struct. Control Health Monit. 2004, 11, 239–257. [Google Scholar] [CrossRef]
- Lin, S.; Tian, H. Study on the sandwich piezoelectric ceramic ultrasonic transducer in thickness vibration. Smart Mater. Struct. 2008, 17, 015034. [Google Scholar] [CrossRef]
- Ihn, J.-B.; Chang, F.-K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network: I. Diagnostics. Smart Mater. Struct. 2004, 13, 609–620. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K. Structural health monitoring by piezo-impedance transducers. II: Applications. J. Aerosp. Eng. 2004, 17, 166–175. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K. Structural Health Monitoring by Piezo-Impedance Transducers. I: Modeling. J. Aerosp. Eng. 2004, 17, 154–165. [Google Scholar] [CrossRef]
- Gyuhae, P.; Hoon, S.; Farrar, C.R.; Inman, D.J. Overview of piezoelectric impedance-based health monitoring and path forward. Shock Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]
- Gong, P.; Luo, M.; Zhou, L.; Jiang, L.; Chen, X. An image processing method for extraction of the stress wave reflection period. Appl. Sci. 2020, 10, 3486. [Google Scholar] [CrossRef]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959–968. [Google Scholar] [CrossRef] [Green Version]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Wang, B.; Huo, L.; Chen, D.; Li, W.; Song, G. Impedance-based pre-stress monitoring of rock bolts using a piezoceramic-based smart washer—A feasibility study. Sensors 2017, 17, 250. [Google Scholar] [CrossRef]
- Zhao, N.; Huo, L.; Song, G. A nonlinear ultrasonic method for real-time bolt looseness monitoring using PZT transducer–enabled vibro-acoustic modulation. J. Intell. Mater. Syst. Struct. 2019, 31, 364–376. [Google Scholar] [CrossRef]
- Luo, Z.; Deng, H.; Li, L.; Luo, M. A simple PZT transducer design for electromechanical impedance (EMI)-based multi-sensing interrogation. J. Civ. Struct. Health Monit. 2021, 11, 235–249. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Ding, F.; Zhang, W. Effect of piezoelectric ceramic particles size gradation on piezoelectric properties of 0–3 cement-based piezoelectric composites. Smart Mater. Struct. 2018, 27, 085029. [Google Scholar] [CrossRef]
- Lin, S.; Hu, J.; Fu, Z. Electromechanical characteristics of piezoelectric ceramic transformers in radial vibration composed of concentric piezoelectric ceramic disk and ring. Smart Mater. Struct. 2013, 22, 045018. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Yang, Y. Practical implementation of piezo-impedance sensors in monitoring of excavation support structures. Struct. Control Health Monit. 2012, 19, 231–245. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef]
- Chen, D.; Huo, L.; Song, G. EMI based multi-bolt looseness detection using series/parallel multi-sensing technique. Smart Struct. Syst. 2020, 25, 423–432. [Google Scholar]
- Huo, L.; Chen, D.; Kong, Q.; Li, H.; Song, G. Smart washer—A piezoceramic-based transducer to monitor looseness of bolted connection. Smart Mater. Struct. 2017, 26, 025033. [Google Scholar] [CrossRef]
- Huo, L.; Chen, D.; Liang, Y.; Li, H.; Feng, X.; Song, G. Impedance based bolt pre-load monitoring using piezoceramic smart washer. Smart Mater. Struct. 2017, 26, 057004. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Gao, S.; Luo, M.; Wang, J.; Wu, J. An electromechanical impedance-instrumented corrosion-measuring probe. J. Intell. Mater. Syst. Struct. 2019, 30, 2135–2146. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Zou, D.; Wang, J.; Yi, T.-H. PZT based smart corrosion coupon using electromechanical impedance. Mech. Syst. Signal Process. 2019, 129, 455–469. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Wang, J.; Zou, D.; Gao, S. Finite-element analysis of an electromechanical impedance–based corrosion sensor with experimental verification. J. Aerosp. Eng. 2019, 32, 04019012. [Google Scholar] [CrossRef]
- Shi, Y.; Luo, M.; Li, W.; Song, G. Grout compactness monitoring of concrete-filled fiber-reinforced polymer tube using electromechanical impedance. Smart Mater. Struct. 2018, 27, 055008. [Google Scholar] [CrossRef]
- Abdulkareem, A.; Erturun, U.; Mossi, K. Non-destructive evaluation device for monitoring fluid viscosity. Sensors 2020, 20, 1657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Chen, D.; Fan, S.; Huo, L.; Song, G. Monitoring of viscous damper fluid viscosity using piezoceramic transducers—A feasibility study. Smart Mater. Struct. 2021, 30, 025034. [Google Scholar] [CrossRef]








| Test No. | Viocousity (cSt) | Test No. | Viscousity (cSt) |
|---|---|---|---|
| 1 | 5000 | 6 | 200,000 |
| 2 | 10,000 | 7 | 500,000 |
| 3 | 20,000 | 8 | 1,000,000 |
| 4 | 50,000 | 9 | 2,000,000 |
| 5 | 100,000 | 10 | 5,000,000 |
| Viscosity of Damping Fluid (cSt) | RMSD | Viscosity of Damping Fluid (cSt) | RMSD |
|---|---|---|---|
| 5000 | 0.0958 | 200,000 | 0.0412 |
| 10,000 | 0.0814 | 500,000 | 0.0307 |
| 20,000 | 0.0709 | 1,000,000 | 0.0201 |
| 50,000 | 0.0584 | 2,000,000 | 0.0134 |
| 100,000 | 0.0498 | 5,000,000 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Luo, M. Monitoring of Liquid Viscosity for Viscous Dampers through a Wireless Impedance Measurement System. Appl. Sci. 2022, 12, 189. https://doi.org/10.3390/app12010189
Jia S, Luo M. Monitoring of Liquid Viscosity for Viscous Dampers through a Wireless Impedance Measurement System. Applied Sciences. 2022; 12(1):189. https://doi.org/10.3390/app12010189
Chicago/Turabian StyleJia, Sihui, and Mingzhang Luo. 2022. "Monitoring of Liquid Viscosity for Viscous Dampers through a Wireless Impedance Measurement System" Applied Sciences 12, no. 1: 189. https://doi.org/10.3390/app12010189
APA StyleJia, S., & Luo, M. (2022). Monitoring of Liquid Viscosity for Viscous Dampers through a Wireless Impedance Measurement System. Applied Sciences, 12(1), 189. https://doi.org/10.3390/app12010189





