Reliability Assessment of RC Bridges Subjected to Seismic Loadings
Abstract
:1. Introduction
2. Reliability Approach
3. Demand Hazard Assessment
4. Example of Application
4.1. Expected Structural Properties of Materials, Loads, and Structural Sections
4.2. Nonlinear Dynamic Procedure
4.3. Ground Motions
4.4. Structural Capacity Estimation
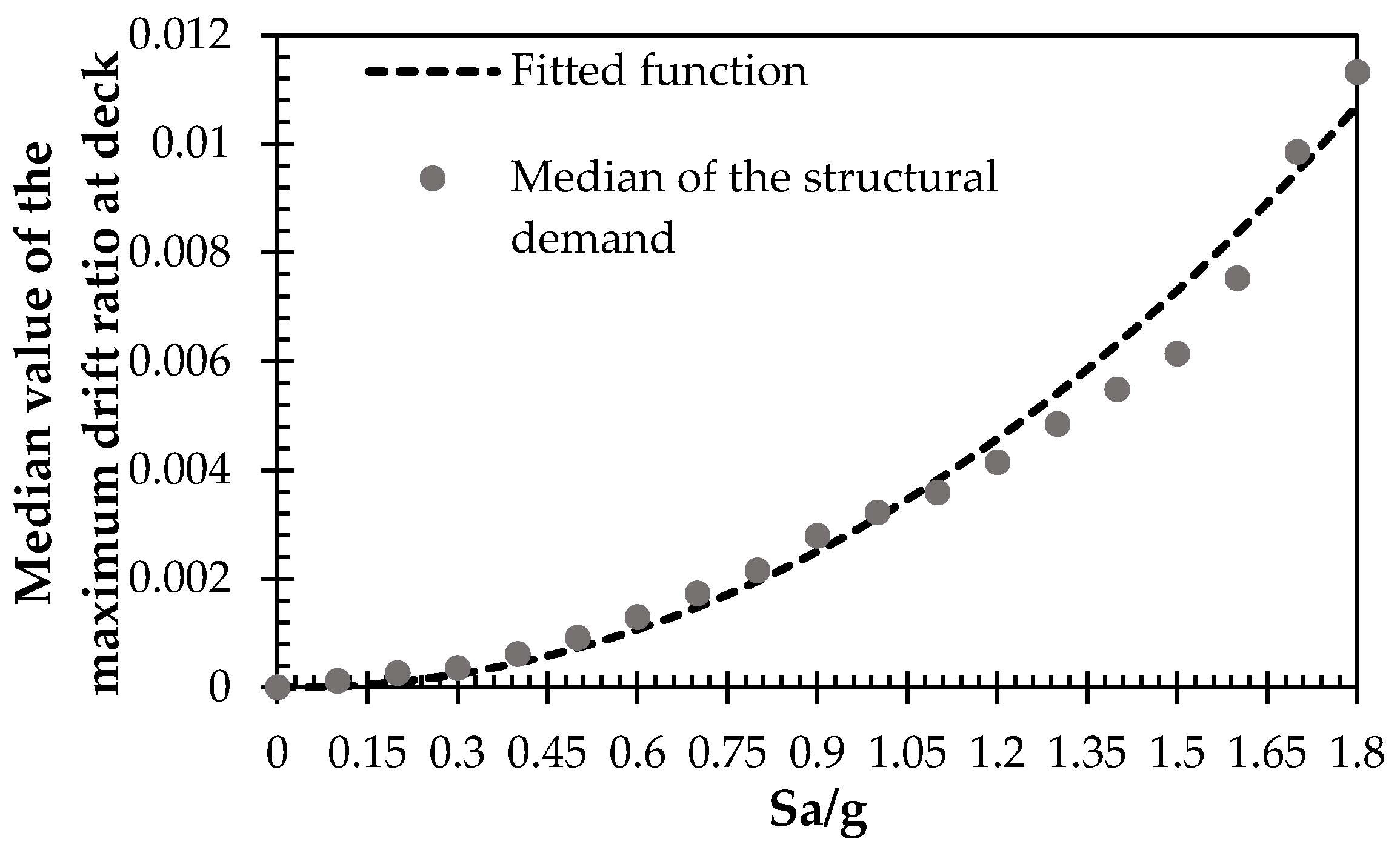
4.5. Structural Demand Assessment
| “Acapulco Centro Cultural”, ACAC | “Acapulco Diana”, ACAD | ||||||
|---|---|---|---|---|---|---|---|
| CN | ID | Date | Magnitude | CN | ID | Date | Magnitude |
| 1 | 9509-141/N00E | 09/14/95 | 6.4 | 21 | 1112-111/N00E | 12/11/11 | 6.5 |
| 2 | 9509-141/N90E | 09/14/95 | 6.4 | 22 | 1112-111/N90E | 12/11/11 | 6.5 |
| 3 | 0205-281/N90E | 05/28/02 | 4.9 | 23 | 9509-141/N00E | 09/14/95 | 6.4 |
| 4 | 0205-281/N00E | 05/28/02 | 4.9 | 24 | 9509-141/N90E | 09/14/95 | 6.4 |
| 5 | 0206-191/N90E | 06/19/02 | 5.5 | 25 | 9701-111/N00E | 01/11/97 | 6.9 |
| 6 | 0206-191/N00E | 06/19/02 | 5.5 | 26 | 9701-111/N90E | 01/11/97 | 6.9 |
| 7 | 0209-251/N90E | 09/25/02 | 4.7 | 27 | 9906-151/N00E | 06/15/99 | 6.4 |
| 8 | 0301-221/N90E | 01/22/03 | 5.6 | 28 | 9906-151/N90E | 06/15/99 | 6.4 |
| 9 | 0401-011/N00E | 01/01/04 | 5.7 | 29 | 9909-301/N00E | 09/30/99 | 7.5 |
| 10 | 0401-012/N90E | 01/01/04 | 5.8 | 30 | 9909-301/N90E | 09/30/99 | 7.5 |
| 11 | 0401-012/N00E | 01/01/04 | 5.8 | 31 | 0007-211/N90E | 07/21/00 | 5.1 |
| 12 | 0401-131/N00E | 01/13/04 | 5.1 | 32 | 0401-011/N90E | 01/01/04 | 5.7 |
| 13 | 0406-141/N00E | 06/14/04 | 5.6 | 33 | 0608-111/N90E | 08/11/06 | 5.9 |
| 14 | 0411-151/N00E | 11/15/04 | 4.7 | 34 | 1105-051/N90E | 05/05/11 | 5.5 |
| 15 | 0508-141/N00E | 08/14/05 | 4.8 | 35 | 1105-051/N00E | 05/05/11 | 5.5 |
| 16 | 0608-111/N00E | 08/11/06 | 5.9 | 36 | 1112-111/N90E | 12/11/11 | 6 |
| 17 | 0905-221/N90E | 05/22/09 | 5.7 | 37 | 1112-111/N00E | 12/11/11 | 6 |
| 18 | 1005-251/N00E | 05/25/10 | 5 | 38 | 1306-271/N90E | 06/27/13 | 4 |
| 19 | 1006-301/N90E | 06/30/10 | 6 | 39 | 1308-161/N90E | 08/16/13 | 5.1 |
| 20 | 1306-161/N90E | 06/16/13 | 5.8 | 40 | 1308-161/N00E | 08/16/13 | 5.1 |
4.6. Spectral Acceleration Hazard
4.7. Probability of Exceeding a Certain Drift Threshold
4.8. Mean Annual Demand Exceedance Rate
4.9. Reliability Index
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Echard, B.; Gayton, N.; Lemaire, M.; Relun, N. A combined Importance Sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliab. Eng. Syst. Saf. 2013, 111, 232–240. [Google Scholar] [CrossRef]
- Huang, X.; Chen, J.; Zhu, H. Assessing small failure probabilities by AK-SS: An active learning method combining Kriging and Subset Simulation. Struct. Saf. 2016, 59, 86–95. [Google Scholar] [CrossRef]
- Decò, A.; Frangopol, D.M. Risk assessment of highway bridges under multiple hazards. J. Risk Res. 2011, 14, 1057–1089. [Google Scholar] [CrossRef]
- Lokuge, W.; Wilson, M.; Tran, H.; Setunge, S. Predicting the probability of failure of timber bridges using fault tree analysis. Struct. Infrastruct. Eng. 2019, 15, 783–797. [Google Scholar] [CrossRef]
- Hirzinger, B.; Adam, C.; Oberguggenberger, M.; Salcher, P. Approaches for predicting the probability of failure of bridges subjected to high-speed trains. Probabilistic Eng. Mech. 2020, 59, 103021. [Google Scholar] [CrossRef]
- Wang, R.; Leander, J.; Karoumi, R. Fatigue reliability assessment of steel bridges considering spatial correlation in system evaluation. Struct. Infrastruct. Eng. 2021, 6, 1–15. [Google Scholar] [CrossRef]
- Xia, H.W.; Ni, Y.Q.; Wong, K.Y.; Ko, J.M. Reliability-based condition assessment of in-service bridges using mixture distribution models. Comput. Struct. 2012, 106–107, 204–213. [Google Scholar] [CrossRef]
- Lü, Q.; Chan, C.L.; Low, B.K. System reliability assessment for a rock tunnel with multiple failure modes. Rock Mech. Rock Eng. 2013, 46, 821–833. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimisation and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Yuhua, D.; Datao, Y. Estimation of failure probability of oil and gas transmission pipelines by fuzzy fault tree analysis. J. Loss Prev. Process Ind. 2005, 18, 83–88. [Google Scholar] [CrossRef]
- Celarec, D.; Vamvatsikos, D.; Dolšek, M. Simplified estimation of seismic risk for reinforced concrete buildings with consideration of corrosion over time. Bull. Earthq. Eng. 2011, 9, 1137–1155. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Dolšek, M. Equivalent constant rates for performance-based seismic assessment of ageing structures. Struct. Saf. 2011, 33, 8–18. [Google Scholar] [CrossRef]
- Tolentino, D.; Ruiz, S.E.; Torres, M.A. Simplified closed-form expressions for the mean failure rate of structures considering structural deterioration. Struct. Infrastruct. Eng. 2012, 8, 483–496. [Google Scholar] [CrossRef]
- Tolentino, D.; Ruiz, S.E. Time-dependent confidence factor for structures with cumulative damage. Earthq. Spectra 2015, 31, 441–461. [Google Scholar] [CrossRef]
- Mackie, K.; Stojadinović, B. Probabilistic seismic demand model for California highway bridges. J. Bridg. Eng. 2001, 6, 468–481. [Google Scholar] [CrossRef] [Green Version]
- Dall’asta, A.; Tubaldi, E.; Ragni, L. Influence of the nonlinear behavior of viscous dampers on the seismic demand hazard of building frames. Earthq. Eng. Struct. Dyn. 2016, 45, 149–169. [Google Scholar] [CrossRef]
- Liu, X.X.; Wu, Z.Y.; Liang, F. Multidimensional performance limit state for probabilistic seismic demand analysis. Bull. Earthq. Eng. 2016, 14, 3389–3408. [Google Scholar] [CrossRef]
- Fanaie, N.; Sadegh Kolbadi, M.; Afsar Dizaj, E. Probabilistic Seismic Demand Assessment of Steel Moment Resisting Frames Isolated by LRB. Numer. Methods Civ. Eng. J. 2017, 2, 52–62. Available online: http://nmce.kntu.ac.ir/article-1-127-en.html (accessed on 1 September 2021). [CrossRef]
- Yee, E. Use of the t-Distribution to Construct Seismic Hazard Curves for Seismic Probabilistic Safety Assessments. Nucl. Eng. Technol. 2017, 49, 373–379. [Google Scholar] [CrossRef]
- Gavabar, S.G.; Alembagheri, M. Structural demand hazard analysis of jointed gravity dam in view of earthquake uncertainty. KSCE J. Civ. Eng. 2018, 22, 3972–3979. [Google Scholar] [CrossRef]
- Deylami, A.; Mahdavipour, M.A. Probabilistic seismic demand assessment of residual drift for Buckling-Restrained Braced Frames as a dual system. Struct. Saf. 2016, 58, 31–39. [Google Scholar] [CrossRef]
- Afsar Dizaj, E.; Fanaie, N.; Zarifpour, A. Probabilistic seismic demand assessment of steel frames braced with reduced yielding segment buckling restrained braces. Adv. Struct. Eng. 2018, 21, 1002–1020. [Google Scholar] [CrossRef]
- Maleki, M.; Ahmady Jazany, R.; Ghobadi, M.S. Probabilistic seismic assessment of SMFs with drilled flange connections subjected to near-field ground motions. Int. J. Steel Struct. 2019, 19, 224–240. [Google Scholar] [CrossRef]
- Zaker Esteghamati, M.; Farzampour, A. Probabilistic seismic performance and loss evaluation of a multi-story steel building equipped with butterfly-shaped fuses. J. Constr. Steel Res. 2020, 172, 106–187. [Google Scholar] [CrossRef]
- Yang, S.I.; Frangopol, D.M.; Neves, L.C. Service life prediction of structural systems using lifetime functions with emphasis on bridges. Reliab. Eng. Syst. Saf. 2004, 86, 39–51. [Google Scholar] [CrossRef]
- Yang, S.I.; Frangopol, D.M.; Kawakami, Y.; Neves, L.C. The use of lifetime functions in the optimization of interventions on existing bridges considering maintenance and failure costs. Reliab. Eng. Syst. Saf. 2006, 91, 698–705. [Google Scholar] [CrossRef]
- Tobias, P.; Trindade, D. Applied Reliability, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2011. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic Basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Rosenblueth, E.; Esteva, L. Reliability Basis for Some Mexican Codes. Spec. Publ. 1972, 31, 1–42. [Google Scholar]
- Nowak, A.S.; Rakoczy, A.M.; Szeliga, E.K. Revised Statistical Resistance Models for R/C Structural Components; American Concrete Institute: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Rodríguez, M.; Botero, J. Comportamiento sísmico de estructuras considerando propiedades mecánicas de aceros de refuerzo mexicanos. Rev. Ing. Sísmica 1995, 1, 39–50. Available online: https://www.smis.mx/index.php/RIS/article/view/268 (accessed on 2 August 2021). [CrossRef]
- Ellinwood, B.; Galambos, T.V.; McGregor, J.G.; Cornell, C.A. Development of a Probability Based Load Criterion for American National Standard A58 Building Code Requirements for Minimum Design Loads in Buildings and Other Structures; NBS SPECIAL PUBLICATION 577; U.S. Department of Commerce: Washington, DC, USA, 1980.
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Otani, S. Inelastic Analysis of R/C Frame Structures. J. Struct. Div. 1974, 100, 1433–1449. [Google Scholar] [CrossRef]
- Carr, A.J. RUAUMOKO 3D Volume 3: User Manual for the 3-Dimensional Version; University of Canterbury: Christchurch, New Zealand, 2003; Volume 3, p. 152. [Google Scholar]
- Tolentino, D.; Márquez-Domínguez, S.; Gaxiola-Camacho, J.R. Fragility assessment of bridges considering cumulative damage caused by seismic loading. KSCE J. Civ. Eng. 2020, 24, 551–560. [Google Scholar] [CrossRef]
- NTC. Normas Técnicas Complementarias del Reglamento de Construcciones del Distrito Federal. Gaceta Oficial, Mexico City (in Spanish), 6th ed.; Trillas: Ciudad de Mexico, Mexico, 2004. [Google Scholar]
- Bradley, B.A.; Dhakal, R.P.; Cubrinovski, M.; Mander, J.B.; MacRae, G.A. Improved seismic hazard model with application to probabilistic seismic demand analysis. Earthq. Eng. Struct. Dyn. 2007, 36, 2211–2225. [Google Scholar] [CrossRef] [Green Version]
- AASHTO. Standard Specifications for Highway Bridges; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012. [Google Scholar]








| Bias Factor | Coefficient of Variation | |
|---|---|---|
| 27.60 | 1.24 | 0.15 |
| 31.00 | 1.21 | 0.14 |
| 41.40 | 1.15 | 0.125 |
| Mean | 440.02 | 0.0066 | 713.92 | 0.11 |
| Standard deviation | 16.57 | 0.0022 | 16.28 | 0.012 |
| Bias Factor | Coefficient of Variation | |
|---|---|---|
| Factory items | 1.03 | 0.08 |
| Site elements | 1.05 | 0.10 |
| Asphalt | 1.00 | 0.25 |
| Non–structural elements | 1.03–1.05 | 0.08–0.01 |
| Mean (m) | Standard Deviation (m) | |
|---|---|---|
| Slab width | 7.62 × 10−4 | 6.60 × 10−3 |
| Beam height | −5.33 × 10−3 | 6.35 × 10−3 |
| Beam width | 2.54 × 10−3 | 3.81 × 10−3 |
| Columns dimensions | 1.52 × 10−3 | 6.35 × 10−3 |
| Cover | 8.13 × 10−3 | 4.32 × 10−3 |
| With epistemic uncertainties | 1.531 × 10−3 | 1.529 × 10−3 | 2.96 |
| Without epistemic uncertainties | 1.318 × 10−3 | 1.317 × 10−3 | 3.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrera, D.; Varela, G.; Tolentino, D. Reliability Assessment of RC Bridges Subjected to Seismic Loadings. Appl. Sci. 2022, 12, 206. https://doi.org/10.3390/app12010206
Herrera D, Varela G, Tolentino D. Reliability Assessment of RC Bridges Subjected to Seismic Loadings. Applied Sciences. 2022; 12(1):206. https://doi.org/10.3390/app12010206
Chicago/Turabian StyleHerrera, Daniel, Gerardo Varela, and Dante Tolentino. 2022. "Reliability Assessment of RC Bridges Subjected to Seismic Loadings" Applied Sciences 12, no. 1: 206. https://doi.org/10.3390/app12010206
APA StyleHerrera, D., Varela, G., & Tolentino, D. (2022). Reliability Assessment of RC Bridges Subjected to Seismic Loadings. Applied Sciences, 12(1), 206. https://doi.org/10.3390/app12010206






