Field Test for a Base Isolation Structure on Condition of Horizontal and Initial Displacement
Abstract
:1. Introduction
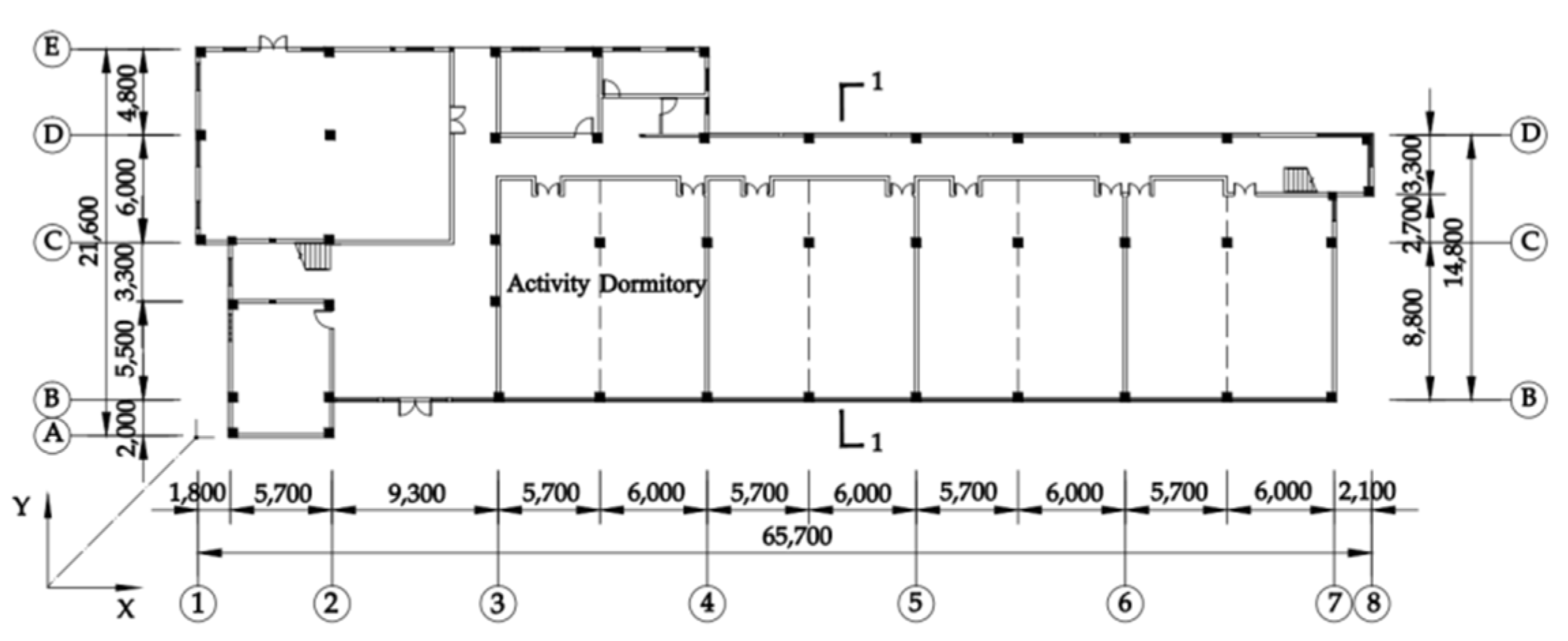
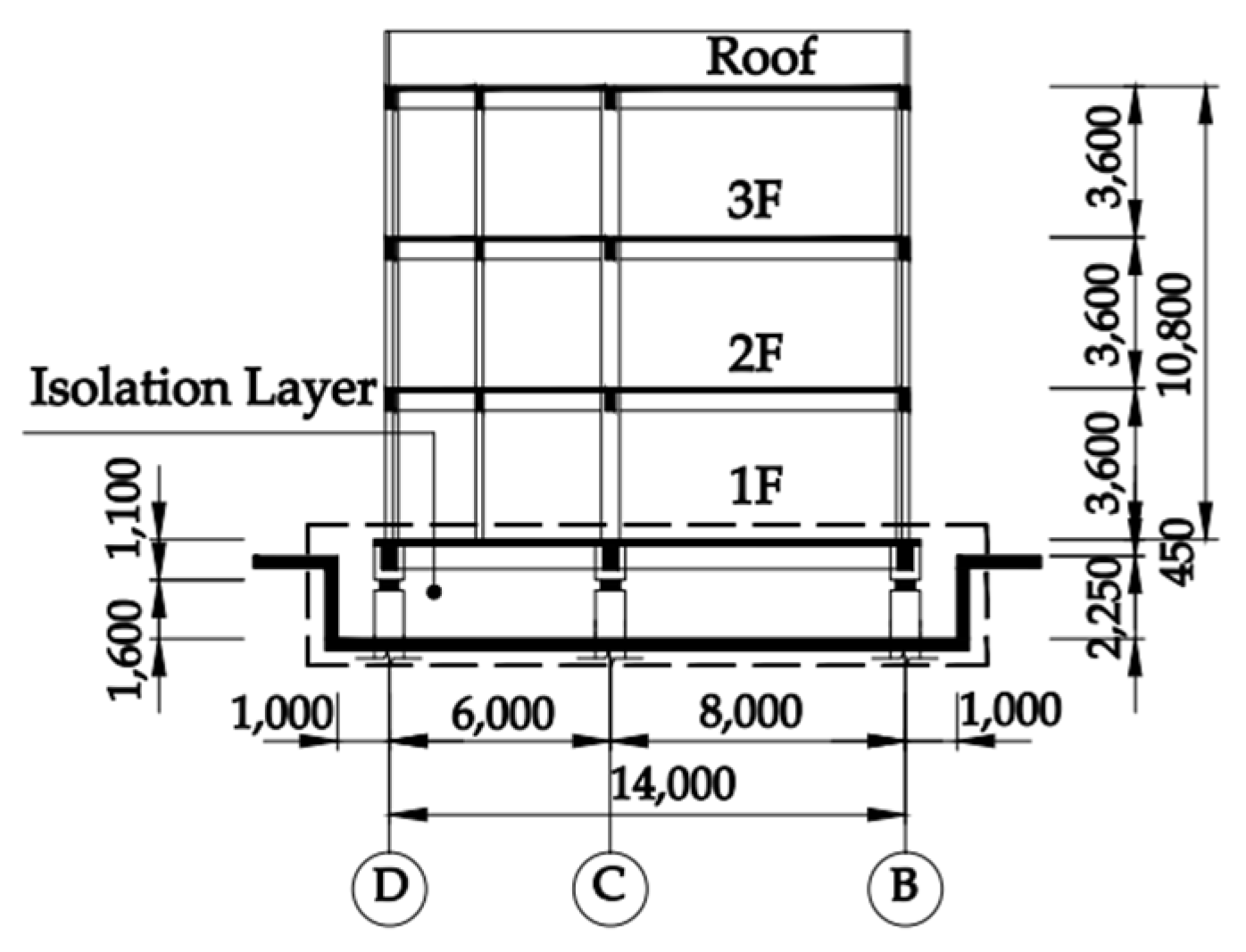
2. Overview of Test Project
3. Devices Setup and Field Test
3.1. Field Test Instruments and Related Equipment
3.2. Sensors Arrangement
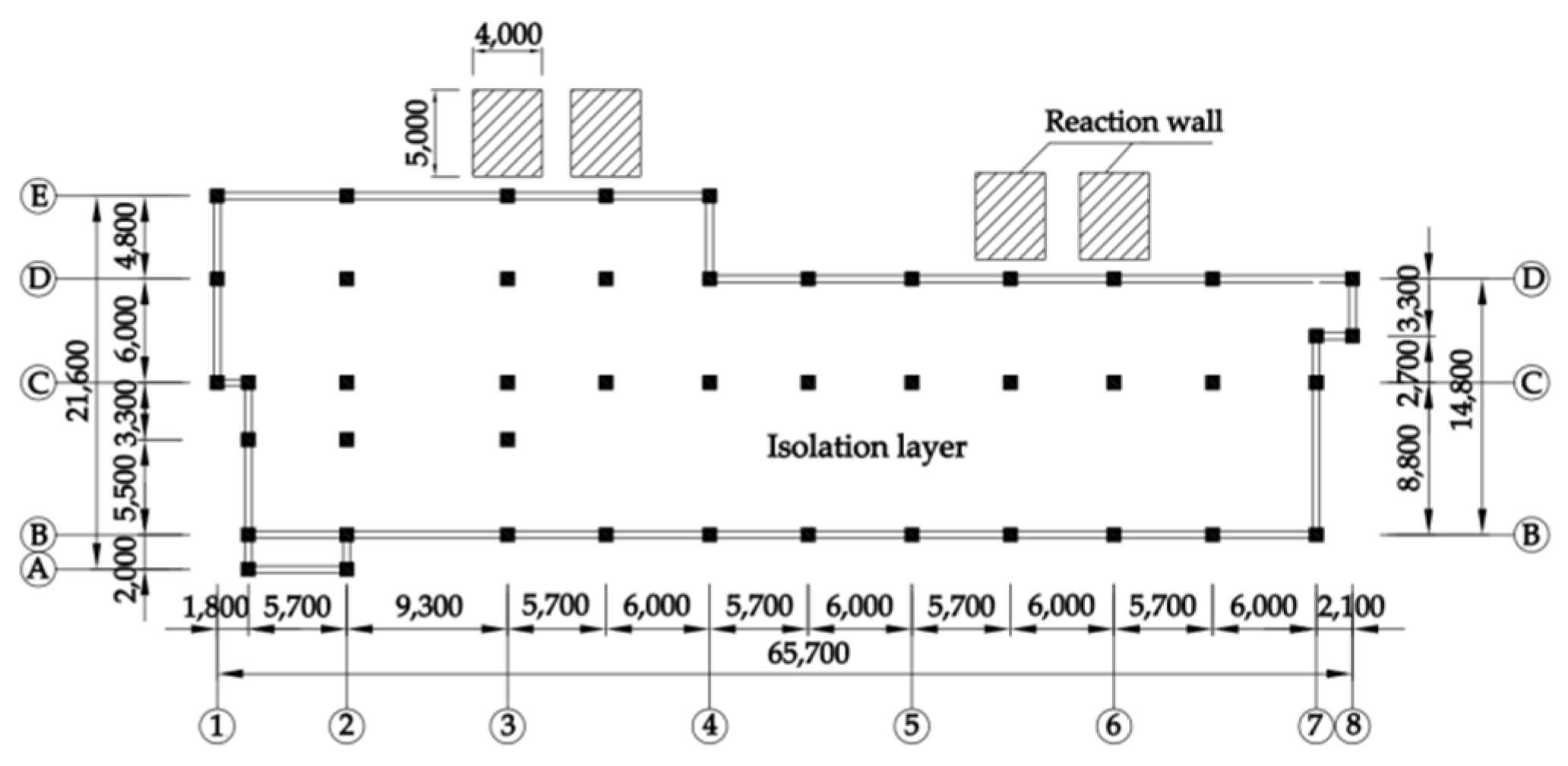
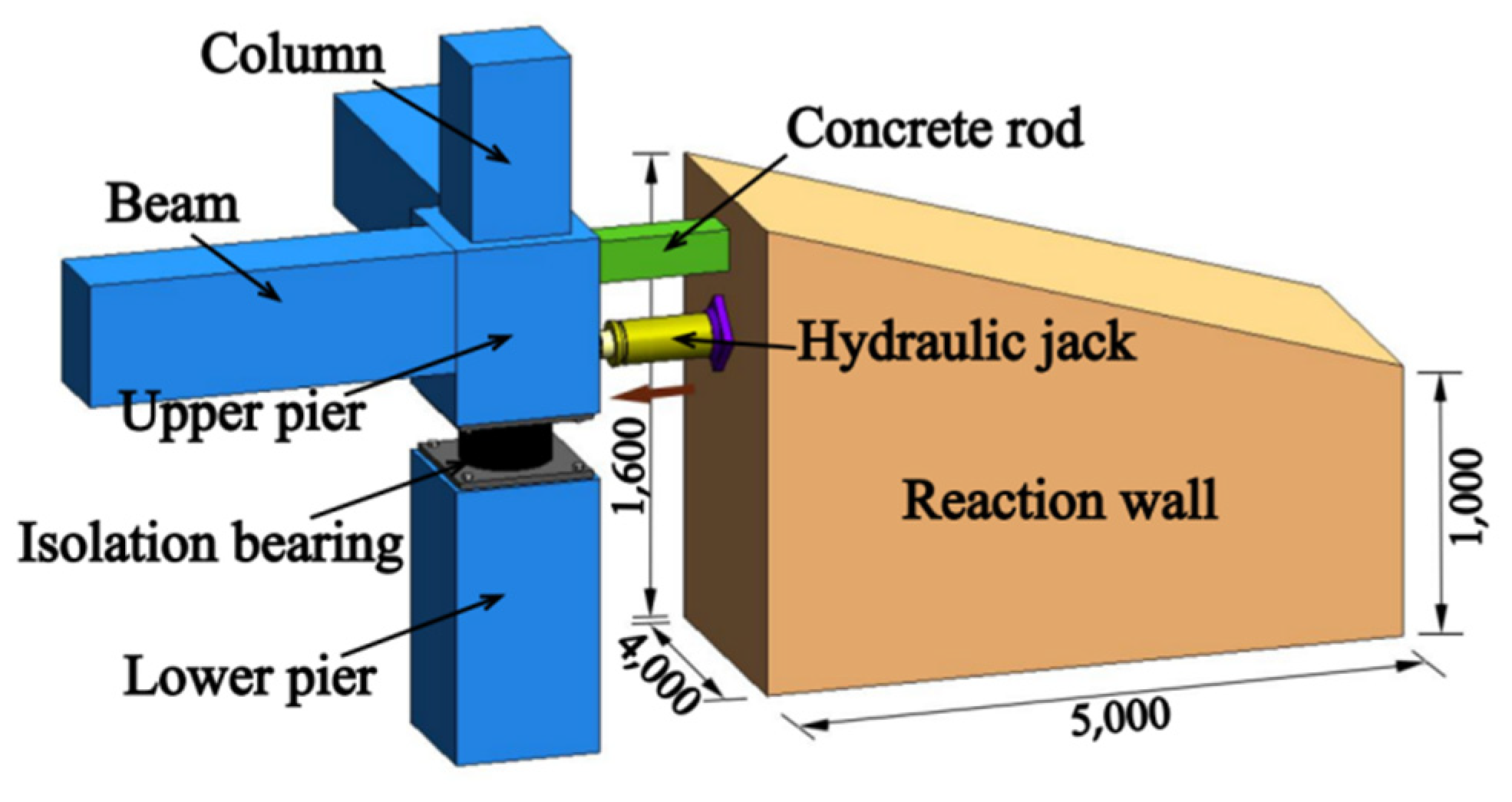
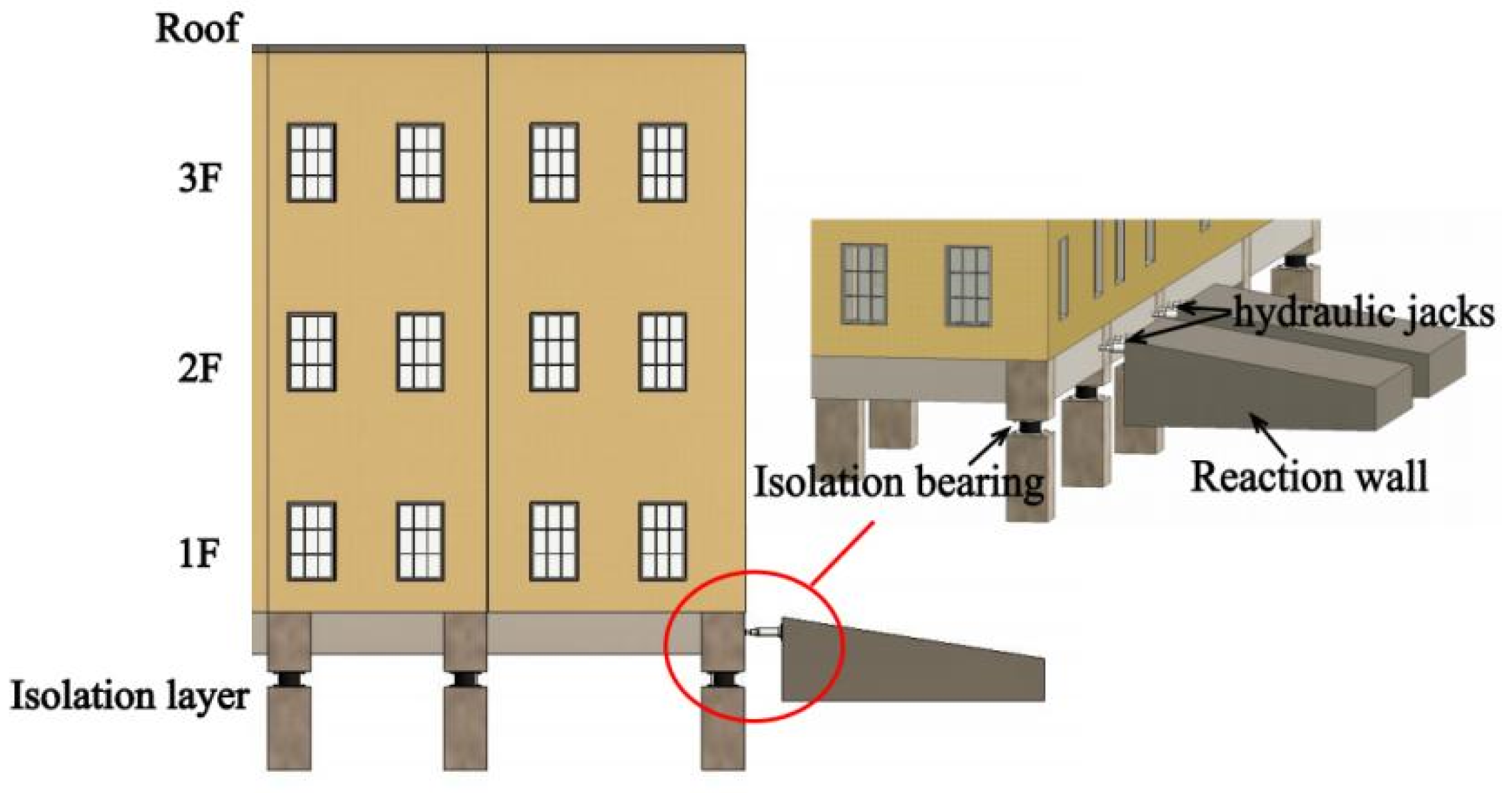
3.3. Design and Test of Horizontal Displacement Loading and Unloading Device
3.4. Data Acquisition and Analysis
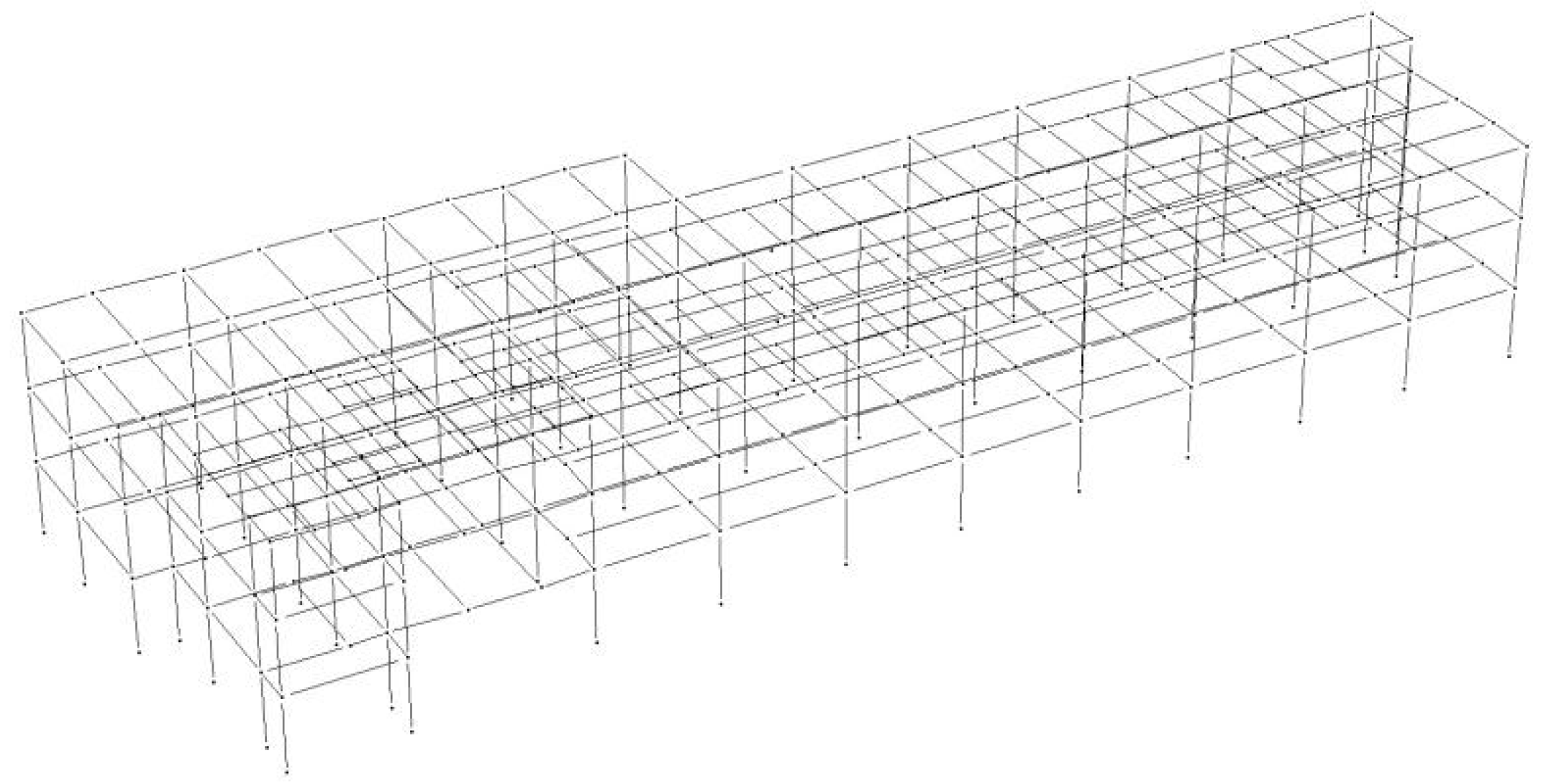
3.5. Establishment of Structure Numerical Model
4. Test Results and Analysis
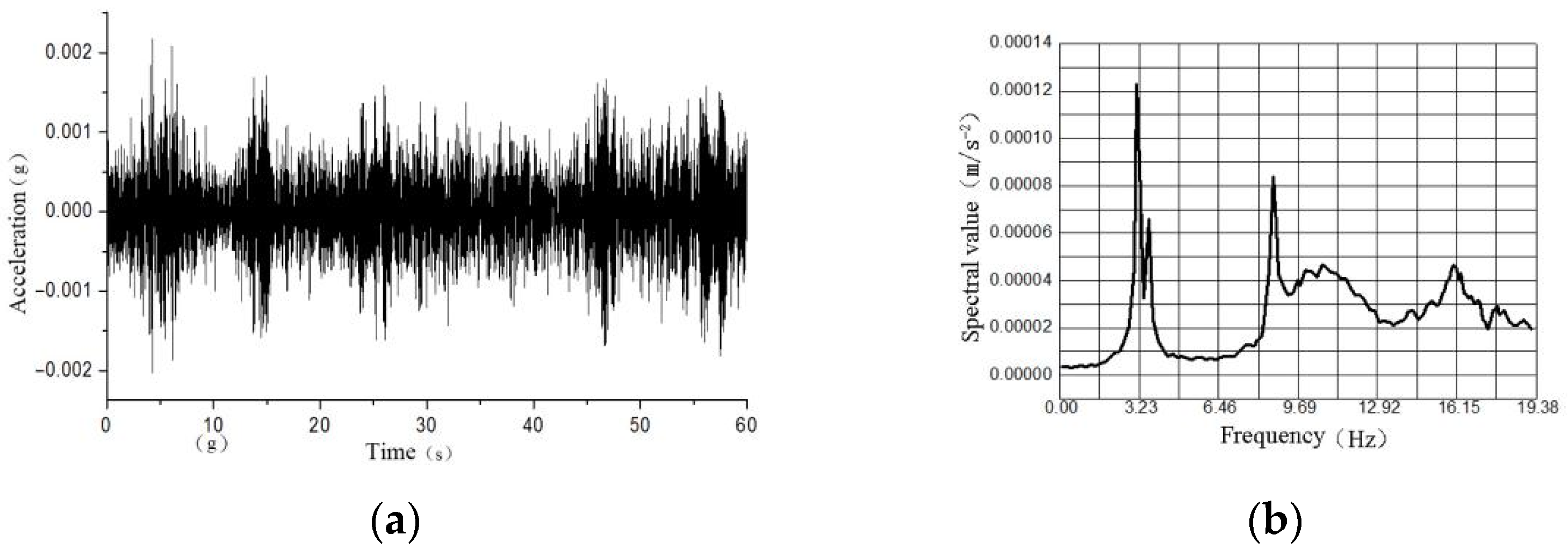
4.1. Analysis of Results under Ambient Excitation
4.2. Test Results and Analysis of Horizontal Initial Displacement
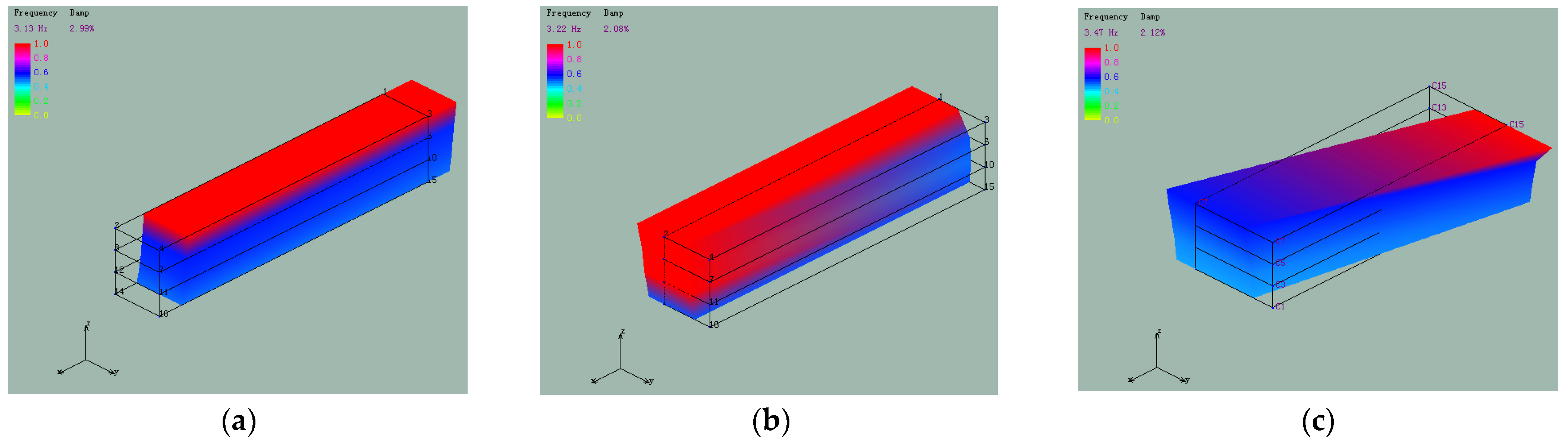
4.2.1. Self-Vibration Characteristics of the Structure
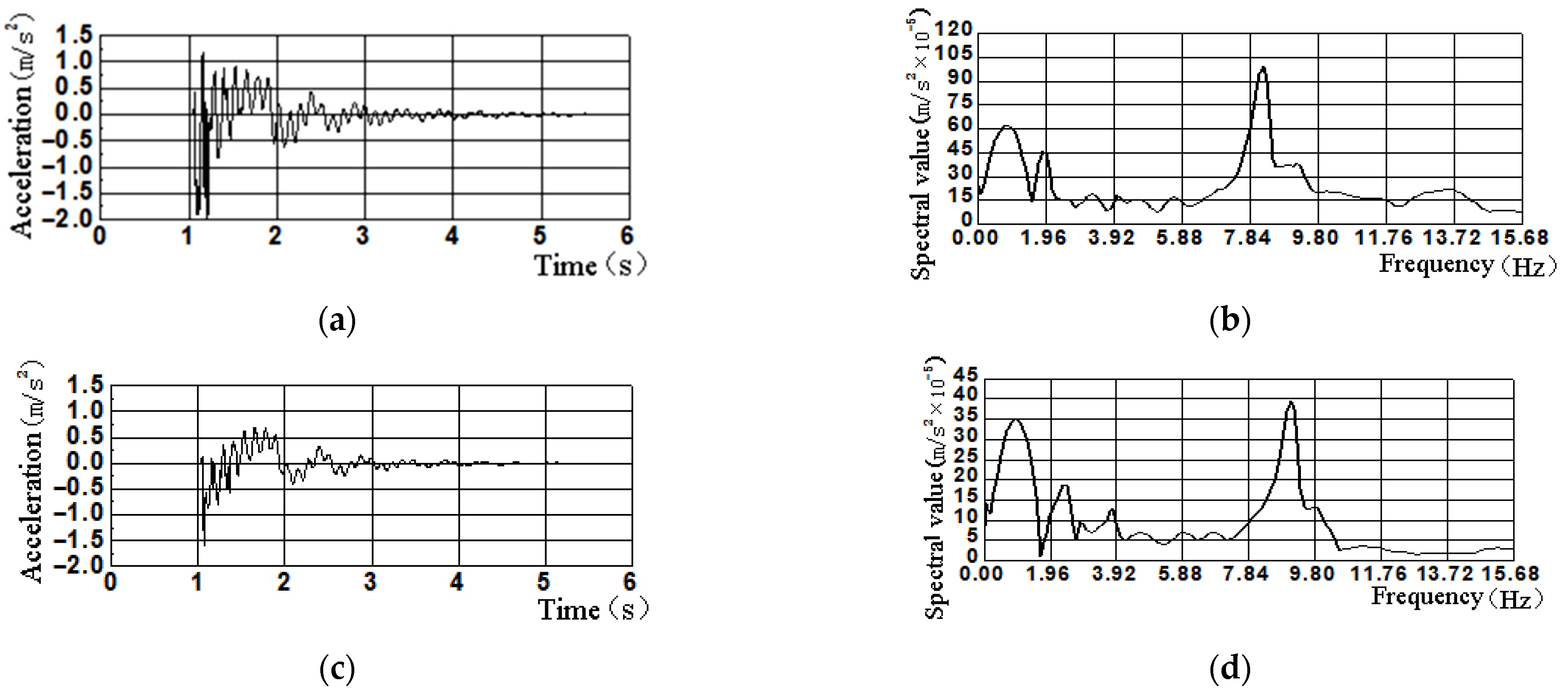
4.2.2. Floor Acceleration Response
4.3. Reset Performance of Isolation Layer
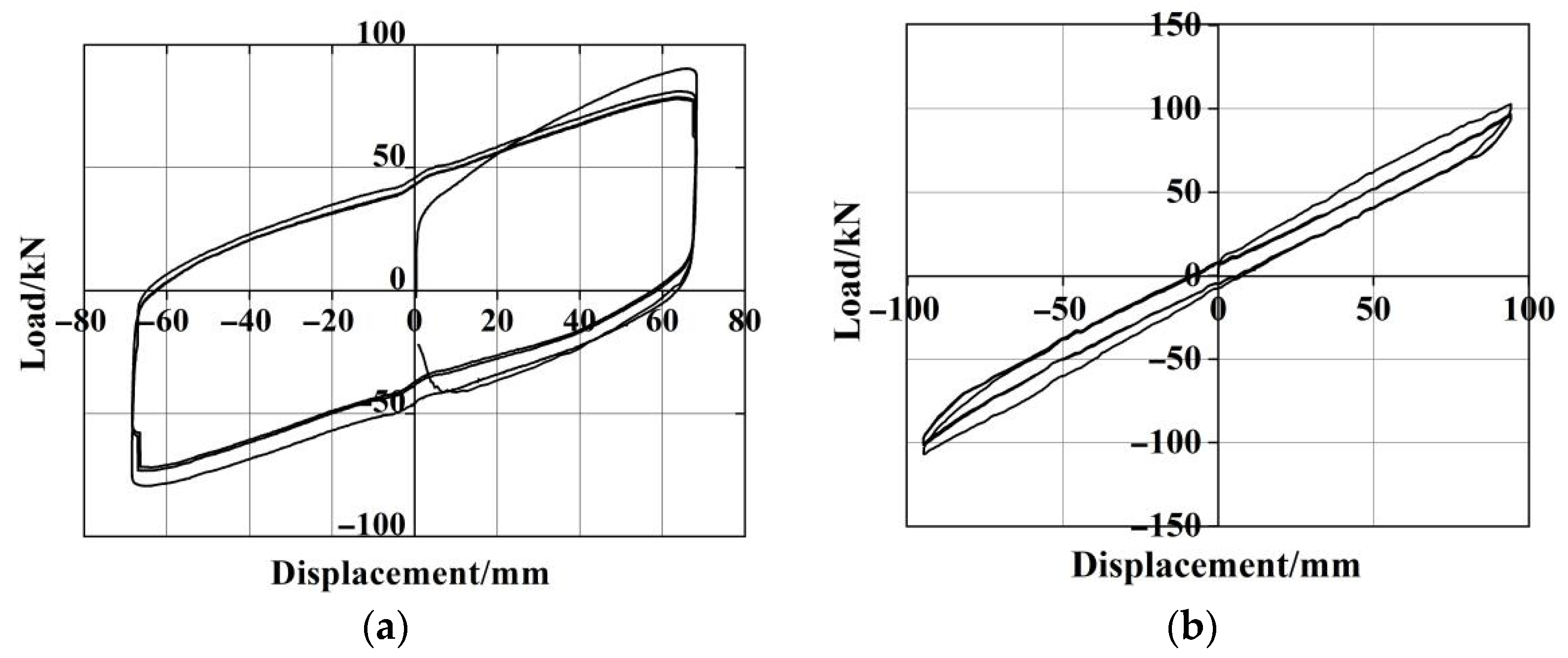
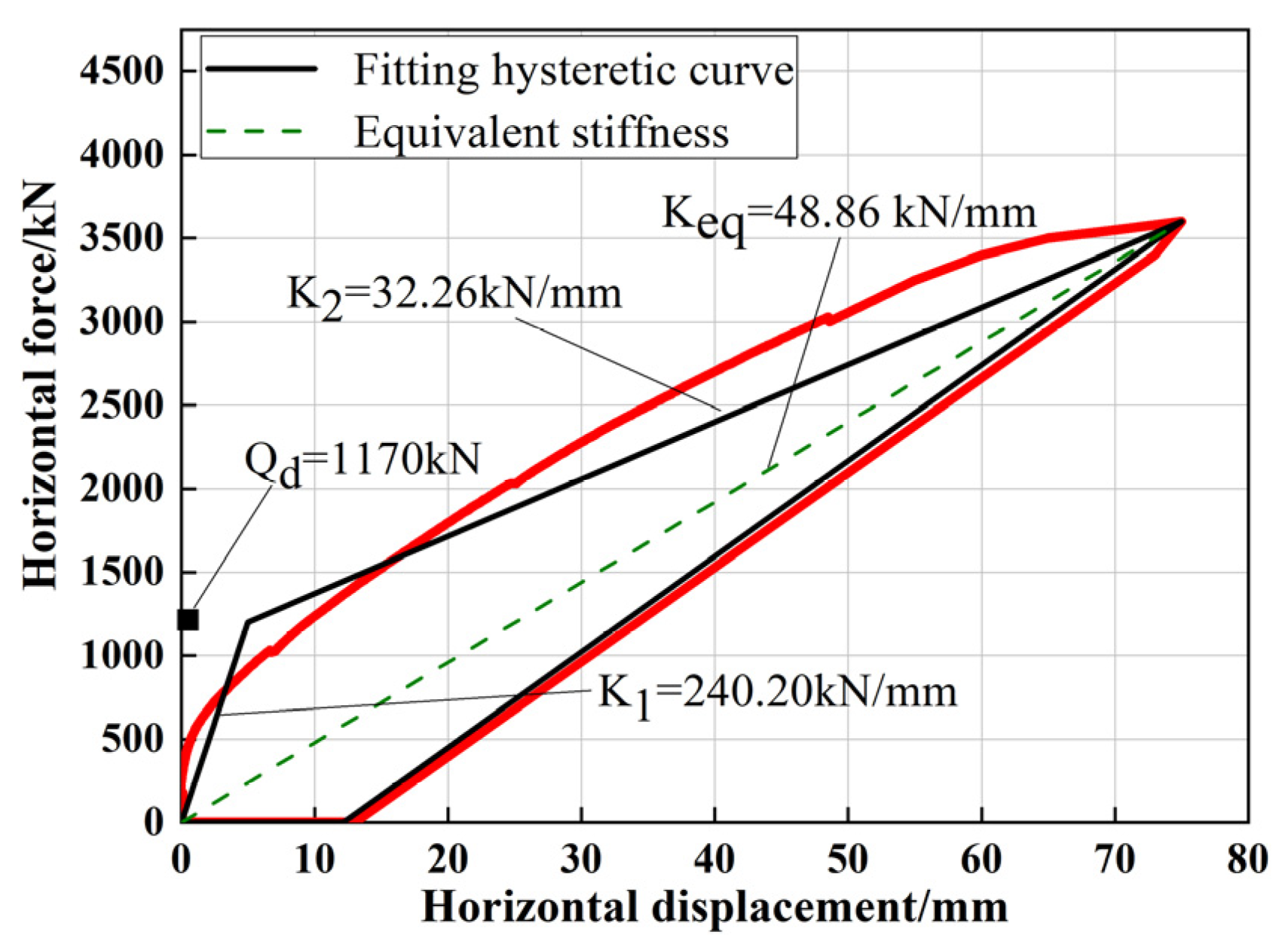
4.4. Hysteretic Curve of Isolation Layer
5. Discussion and Suggestions
- (1)
- This paper presents a one-time and one-way horizontal push and release test on the building, which is not representative of the building’s reciprocating horizontal displacement during an earthquake. As a result, the parameters such as dynamic response obtained during the test are utilized as a benchmark for evaluating the performance of isolated structures.
- (2)
- The isolation layer can be reset almost instantly after the load is released. It can be inferred that when an earthquake occurs, the isolation layer will exhibit free attenuation movement and will promptly return to its initial position. This conclusion dispels any questions about the isolation bearing’s ability to be swiftly reset.
- (3)
- Edge and corner isolation bearings exhibit greater horizontal deformation than center bearings during the initial displacement. Therefore, while designing structural members, the displacement amplification factor of edge and corner isolation bearings should be considered, or the displacement of the least unfavorable isolation bearing should be used as the design value.
- (4)
- The building has been put into service, and the reserved reaction wall will be kept for later isolation structure tests, as well as the natural aging and degradation performance of the isolation bearing.
6. Conclusions
- (1)
- The natural vibration characteristics of isolated and seismic structure are similar in the presence of environmental excitation. Under regular use conditions, the isolated structure is sufficiently stable, which is consistent with the research conclusions of relevant literature.
- (2)
- Under the condition of 75 mm horizontal initial displacement, the isolated structure’s natural vibration period is significantly longer than that of the seismic structure, and the first-order period ratio is 2.82 times, indicating that the isolation layer achieves the goal of prolonging the isolated structural period. The damping ratio of the first order is 22.39%, indicating that the isolation layer has achieved the goal of further reducing the horizontal seismic action.
- (3)
- The acceleration of an isolated structure increases slightly as the floor height increases, and it typically exhibits translational motion characteristics. This demonstrates that the isolation structure has an excellent level of control over each floor’s seismic reaction, and the acceleration dampening effect is rather impressive. However, the roof layer has an amplification effect, and its amplification value of 1.27 is noteworthy.
- (4)
- After releasing horizontal initial displacement, the isolation layer is basically instantaneously reset, indicating that the isolation layer has a high degree of reset performance.
- (5)
- The horizontal initial displacement test shows that the isolation layer’s force-displacement relationship curve is a plump hysteretic loop, demonstrating its superior energy dissipation capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nagarajaiah, S.; Sun, X.H. Seismic perfomance od base isolated buildings in the 1994 northridge earthquake. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 1–6 August 1996; Paper No. 598; Pergamon: Oxford, UK, 1996. [Google Scholar]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolation Structure: From Theory to Practice; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fu, J.H. Design Method for Seismic and Isolation Structures in Japan; China Architecture & Building Press: Beijing, China, 2011. [Google Scholar]
- The Japan Society of Seicmic Isolation. Introduction to Isolation Structures; Ohmsha Press: Tokyo, Japan, 1995. [Google Scholar]
- Han, J.P.; Wang, H.T.; Liu, Y.S.; Du, Y.F.; Li, H. Investigation on main dynamic characteristics of base-isolated structures under ambient excitation. J. Vib. Shock 2011, 30, 266–271. [Google Scholar]
- Architectural Institute of Japan. Structural Design Concepts for Seismically Isolated Buildings against Extreme Ground Motions; Architectural Institute of Japan: Tokyo, Japan, 2020. [Google Scholar]
- Liu, W.D.; Lan, Z.J.; Liu, W.Q.; Liu, D.P. Vibration test of a high-rise building and seismic performance analysis. World Inform. Earthq. Eng. 2010, 26, 169–174. [Google Scholar]
- Bettinali, F.; Forni, M.; Indirli, M. In-situ dynamic tests of a large seismically isolated building. In Proceedings of the Interntional Meeting on Earthquake Protection of Buildings, Ancona, Italy, 22 April 1991. [Google Scholar]
- Forni, M.; Martelli, A.; Spadoni, B. Dynamic tests on seismically isolated structure mock-ups and validation of numerical models. In Proceedings of the International Meeting on Earthquake Protection of Buildings, Ancona, Italy, 22 April 1991. [Google Scholar]
- Braga, F.; Laterza, M.; Gigliotti, R. Seismic isolation using slide and rubber bearings: Large amplitude free vibration tests on the Rapolla residence building. In Proceedings of the 7th International Seminar on Seismic Isolation, Assisi, Italy, 2–5 October 2001; Passive Energy Dissipation and Active Control of Vibrations of Structures: Assisi, Italy, 2001; pp. 121–152. [Google Scholar]
- Bixio, A.R.; Dolce, M.; Nigro, D.; Ponzo, F.C.; Braga, F.; Ncoletti, M. Repeatable dynamic release tests on a base-isolated building. J. Earthq. Eng. 2001, 5, 369–393. [Google Scholar] [CrossRef]
- Braga, F.; Laterza, M. Field testing of low-rise base isolated building. Eng. Struct. 2004, 26, 1599–1610. [Google Scholar] [CrossRef]
- Wei, L.S.; Zhou, F.L.; Chen, J.Q.; Ren, M.; Xia, C. Study on test of dynamic characteristics for avibration isolation building. J. Vib. Shock 2007, 26, 150–152. [Google Scholar]
- He, Y.M. Dynamic Field Test for A Base-Isolated High-Rise Steel Building Structure. Master’s Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, June 2013. [Google Scholar]
- GB 50011-2010. Code for Seismic Design of Buildings; China Architecture & Building Press: Beijing, China, 2016. [Google Scholar]
- Pianese, G.; Milani, G.; Cerchiaro, R.; Milani, F. Optimal vulcanization of unbonded fiber reinforced elastomeric isolator devices. Chem. Eng. Trans. 2021, 86, 1321–1326. [Google Scholar]
- Milani, G.; Milani, F. Optimal vulcanization of tires: Experimentation on idealized NRPB natural and poly-butadiene rubber blends, phenomenological smoothed numerical kinetic model and FE implementation. Polym. Test. 2018, 72, 63–85. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.C.; Tang, Y.G.; Deng, X.S. Analysis of optimal placement of rubber isolated bearins in District E of the Guangdong Science Center. Earthq. Eng. Eng. Dyn. 2009, 29, 183–191. [Google Scholar]
- Chieffo, N.; Mosoarca, M.; Formisano, A.; Lourenço, P.B.; Milani, G. The effect of ground motion vertical component on the seismic response of historical masonry buildings: The case study of the Banloc Castle in Romania. Eng. Struct. 2021, 249, 113346. [Google Scholar] [CrossRef]
- GB 20688.3-2006. Rubber Bearings-Part 3: Elastomeric Seismic-Protection Isolators for Buildings; Standards Press of China: Beijing, China, 2006. [Google Scholar]
- Li, T.; Pan, Y.X.; Tong, K.T.; Ventura, C.E.; de Silva, C.W. A multi-scale attention neural network for sensor location selection and nonlinear structural seismic response prediction. Comput. Struct. 2021, 248, 106507. [Google Scholar] [CrossRef]
- Robinson, W.H. Lead-rubber hysteretic bearing suitable for protecting structures during earthquake. Earthq. Eng. Struct. Dyn. 1982, 10, 359–604. [Google Scholar] [CrossRef]
- Derivendt, C.; Guillaume, P. Operational modal analysis in the presence of unknown arbitrary loads using transmissibility measurements. In Proceedings of the 13th International Congress on Sound and Vibration, Viennal, Austria, 2–6 July 2006; International Institute of Acoustics and Vibrations: Auburn, AL, USA, 2006. [Google Scholar]
- Li, X.Z.; Yue, X.B.; Huang, W.; Dong, X.J.; Peng, J.K. Vibration response transmissibility and operationalmodal analysis methods: A review and comparative study. J. Vib. Shock 2019, 38, 24–34. [Google Scholar]
- Xie, L.L.; Lu, X.Z.; Guan, H. Experimental study and numerical model calibration for earthquake-induced collapse of RC frames with emphasis on key columns, joints and the overall structure. J. Earthq. Eng. 2015, 19, 1320–1344. [Google Scholar] [CrossRef]
- Al Mamuna, A.; Saatcioglu, M. Analytical modeling of moderately ductile RC frame structures for seismic performance evaluation using PERFORM-3D. Earthq. Spectr. 2019, 35, 635–652. [Google Scholar] [CrossRef]
- Computer and Structures, Inc. PERFORM-3D Nonlinear Analysis and Performance Assessment for 3D Structures USER GUIDE, 4rd ed.; University of California: Berkeley, CA, USA, 2006. [Google Scholar]
- The Japan Society of Seismic Isolation. Guidelines for the Wind-resistant Design of Seismically Based-isolated Buildings; The Japan Society of Seismic Isolation: Tokyo, Japan, 2012. [Google Scholar]
- Ventura, C.E.; Finn, W.D.L.; Lord, J.F.; Fujita, N. Dynamic characteristics of a base isolated building from ambient vibration measurements and low level earthquake shaking. Soil Dyn. Earthq. Eng. 2003, 23, 313–322. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, D.C.; Zhang, J.C.; Zhan, X.Y.; Qian, T. Seismic velocity changes in the eqicentral region of the 2013 Lushan earthquake measured from ambient seismic noise. Chin. J. Geophys. 2020, 63, 517–531. [Google Scholar]
- Takeuchi, T.; Wada, A. Buckling-Restrained Braces and Applications; The Japan Society of Seismic Isolation: Tokyo, Japan, 2017. [Google Scholar]
- The Japan Society of Seismic Isolation. Design Guidelines for Joints of Base Isolated Members, 3rd ed.; The Japan Society of Seismic Isolation: Tokyo, Japan, 2020. [Google Scholar]










| Bearing Type | Total Thickness of Internal Rubber Layer/mm | Pre-Yield Stiffness/kN·mm−1 | Post-Yield Stiffness Kd/kN·mm−1 | Horizontal Equivalent Stiffness Kh/kN·mm−1 | Equivalent Damping Ratio | Yield Force Qd/kN | |||
|---|---|---|---|---|---|---|---|---|---|
| γ = 100% | γ = 250% | γ = 100% | γ = 250% | γ = 100% | γ = 250% | ||||
| LRB 400 | 68.60 | 10.44 | 0.870 | 0.699 | 1.435 | 1.019 | 0.26 | 0.18 | 45 |
| LNR 500 | 96 | / | / | / | 0.937 | 0.890 | 0.05 | 0.05 | / |
| Sensor Type | Floor Location | |||||||
|---|---|---|---|---|---|---|---|---|
| 1st Floor Westward | 2nd Floor Westward | 3rd Floor Westward | Roof Floor Westward | 1st Floor Eastward | 2nd Floor Eastward | 3rd Floor Eastward | Roof Floor Eastward | |
| Speed sensor | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 |
| Acceleration sensor | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| Mode Order | Natural Vibration Period/s | Damping Ratio/% | Mode Description | |||
|---|---|---|---|---|---|---|
| Isolation Structure | Seismic Structure | Isolation Structure | Seismic Structure | Isolation Structure | Seismic Structure | |
| First order | 0.320 | 0.416 | 2.99 | 5.00 | horizontal movement | horizontal movement |
| Second order | 0.311 | 0.408 | 2.08 | 5.00 | horizontal movement | horizontal movement |
| Third order | 0.288 | 0.382 | 2.12 | 5.00 | torsional movement | torsional movement |
| Mode Order | Natural Vibration Period/s | Damping Ratio/% | ||
|---|---|---|---|---|
| Seismic Structure | Horizontal Movement | Seismic Structure | Horizontal Movement | |
| First order | 0.416 | 1.173 | 5.00 | 22.39 |
| Second order | 0.221 | 0.386 | 5.00 | 10.86 |
| Third order | 0.115 | 0.176 | 5.00 | 3.72 |
| Floor | Seismic Structure/gal | Isolation Structure/gal | Seismic-Reduction Rate/% |
|---|---|---|---|
| Roof floor | 351 | 195 | 45.80 |
| 3 | 254 | 173 | 31.89 |
| 2 | 207 | 169 | 18.36 |
| 1 | 154 | 154 | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-X.; Dong, X.-J.; Lin, Y.-Q.; Cheng, H.-D. Field Test for a Base Isolation Structure on Condition of Horizontal and Initial Displacement. Appl. Sci. 2022, 12, 232. https://doi.org/10.3390/app12010232
Wu Y-X, Dong X-J, Lin Y-Q, Cheng H-D. Field Test for a Base Isolation Structure on Condition of Horizontal and Initial Displacement. Applied Sciences. 2022; 12(1):232. https://doi.org/10.3390/app12010232
Chicago/Turabian StyleWu, Ying-Xiong, Xin-Jun Dong, You-Qin Lin, and Hao-De Cheng. 2022. "Field Test for a Base Isolation Structure on Condition of Horizontal and Initial Displacement" Applied Sciences 12, no. 1: 232. https://doi.org/10.3390/app12010232
APA StyleWu, Y. -X., Dong, X. -J., Lin, Y. -Q., & Cheng, H. -D. (2022). Field Test for a Base Isolation Structure on Condition of Horizontal and Initial Displacement. Applied Sciences, 12(1), 232. https://doi.org/10.3390/app12010232






