Dynamics Investigation on Axial-Groove Gas Bearing-Rotor System with Rod-Fastened Structure
Abstract
:1. Introduction
2. Kinematic Model and Mathematical Method of Three-Axial-Groove Gas Bearing
2.1. Kinematic Model
- The gas film pressures at the both ends of bearing: P (φ, Bb/2Rb) = P (φ, −Bb/2Rb) = 1;
- The gas film pressures at the leading edge (φi1) and trailing edge (φi2) of single pad in the axial direction: P (φ1, λ) = P (φ2, λ) = 1.
2.2. Mathematical Method of Nonlinear Gas Film Force
3. Dynamic Model and Method of the Rod-Fastened Rotor-Gas Bearing System
3.1. Dynamic Motion of the Rod-Fastened Rotor-Gas Bearing System
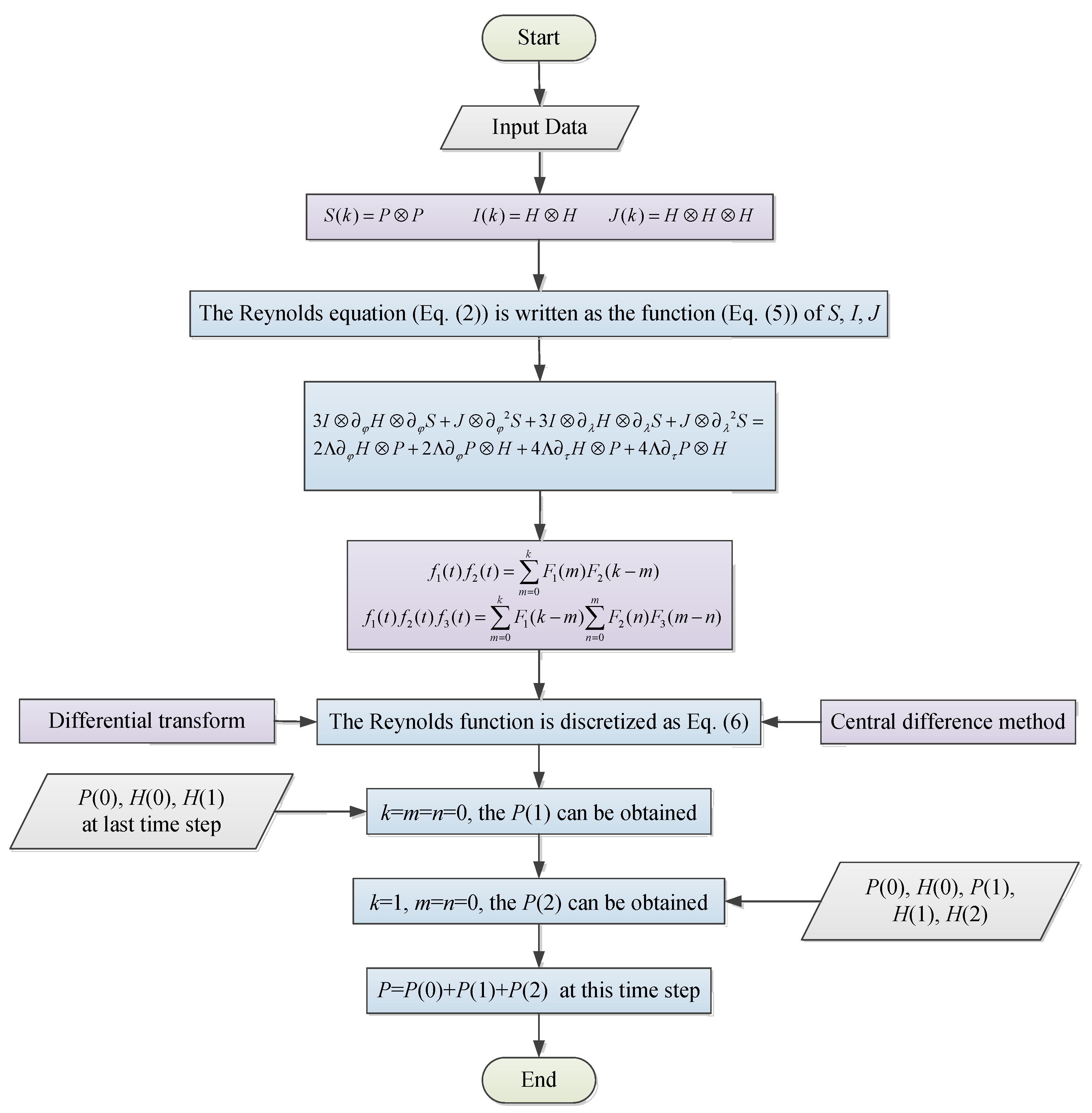
3.2. Newmark-β Method Based on Disturbance Compensation
4. Results and Discussions
4.1. Comparison of the Rod-Fastened Rotor and Continuous Integral Rotor
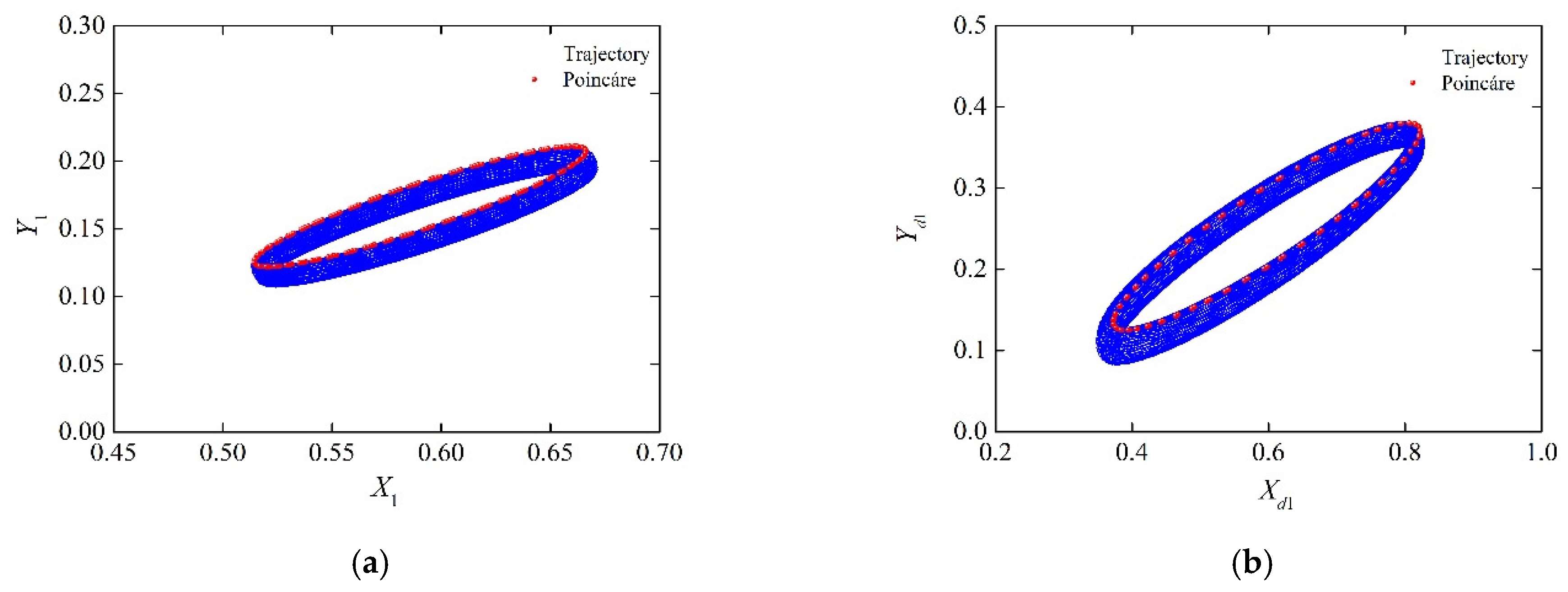
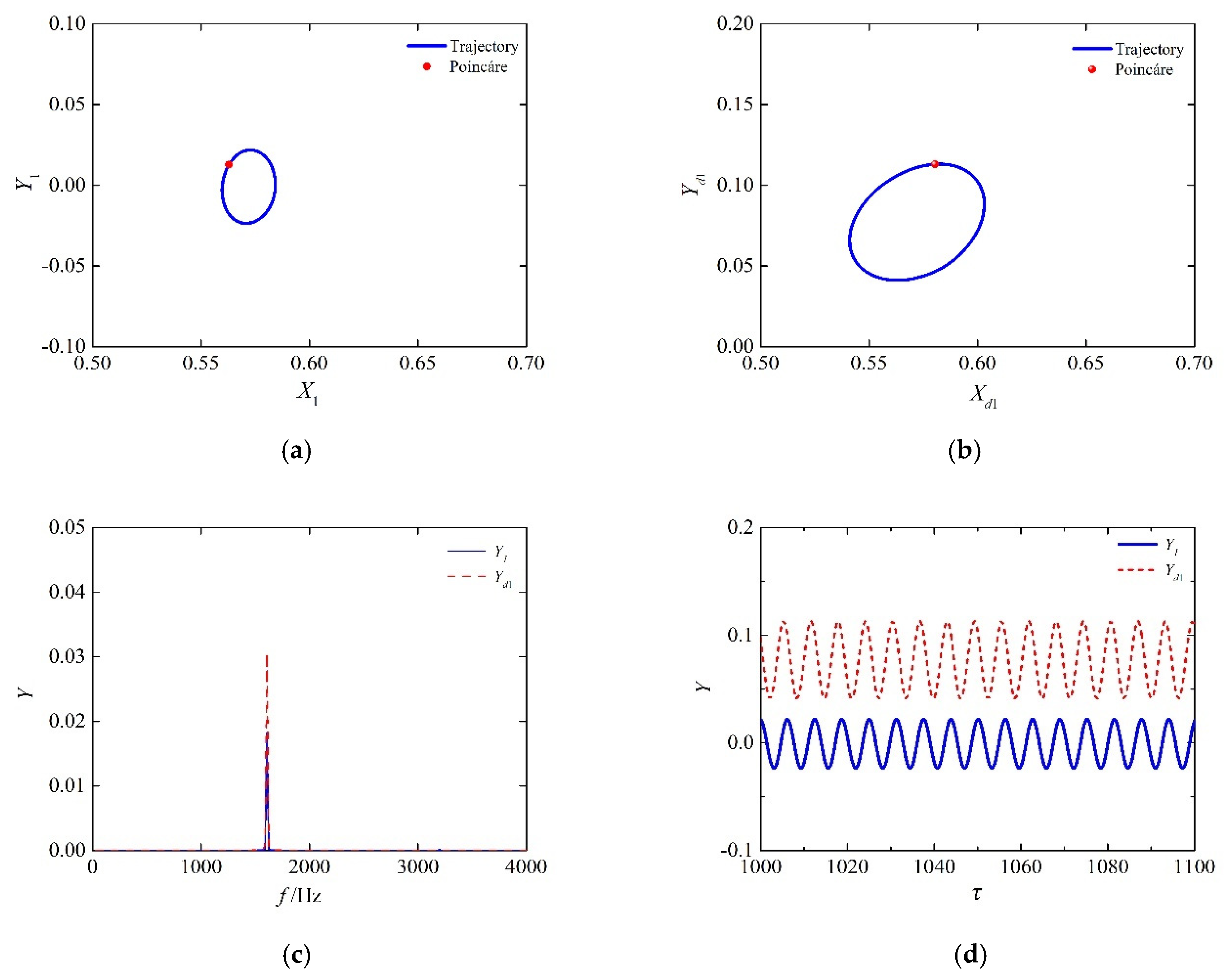
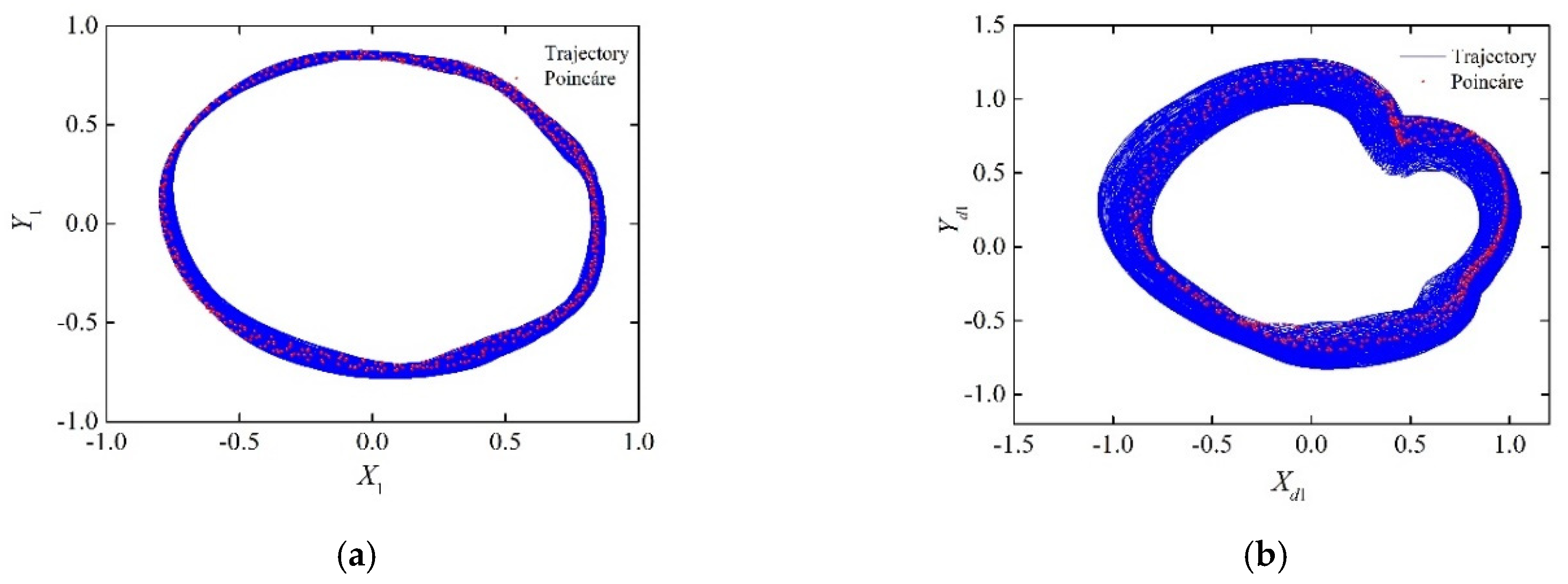
4.2. Bifurcation Characteristics
4.3. Unbalance Responses Versus Rotating Speed ω
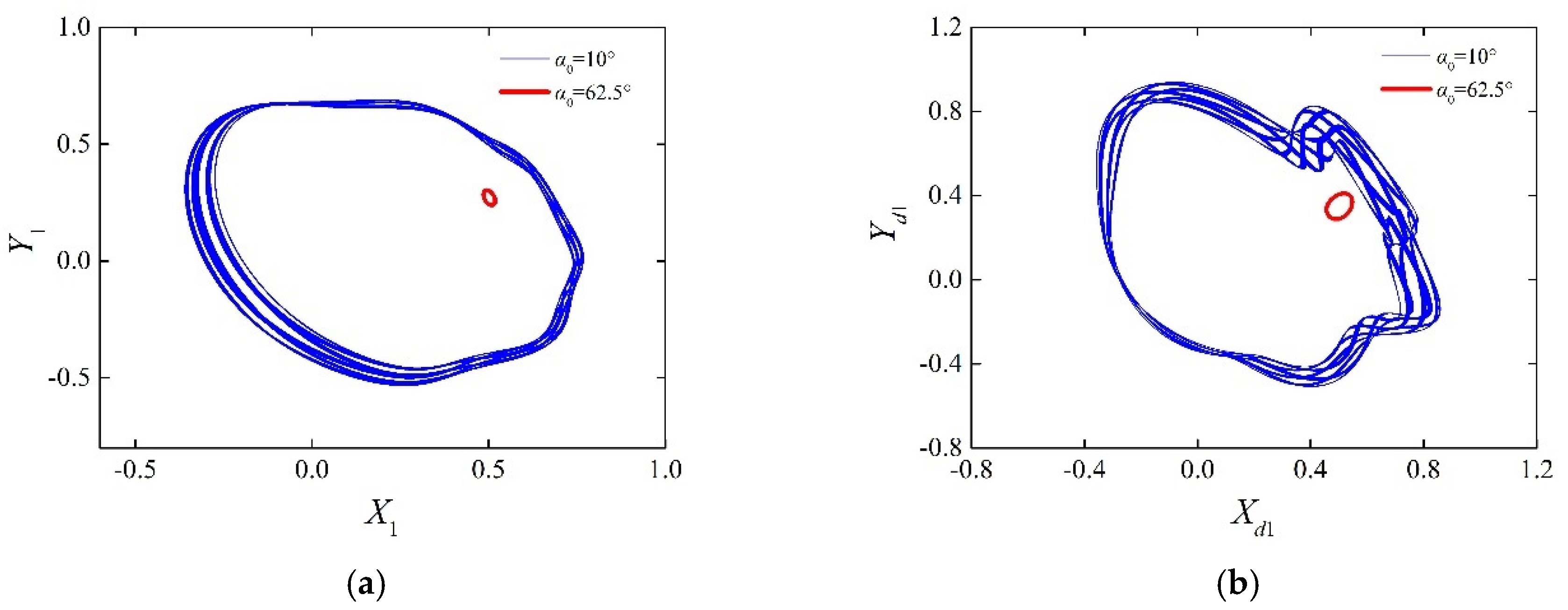
4.4. Effects of the Position Angle of Pad α0
4.5. Comparison of Three-Axial-Grooved and Two-Axial-Grooved Gas Bearings
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.T.; Li, R.R.; Ye, Y.L.; Li, X.L.; Chen, Y. Numerical analysis on the performance characteristics of a new gas journal bearing by using finite difference method. Adv. Mech. Eng. 2021, 13, 16878140211028056. [Google Scholar] [CrossRef]
- Hao, L.; Han, D.J.; Zhao, W.; Zhao, Q.J.; Yang, J.F. Numerical and experimental investigation on axial rub impact dynamic characteristics of flexible rotor supported by hybrid gas bearings. J. Low Freq. Noise Vib. Act. Control. 2021, 40, 1252–1270. [Google Scholar] [CrossRef]
- Shi, M.H.; Liu, X.J.; Feng, K.; Zhang, K.; Huang, M. Running performance of a squeeze film air bearing with flexure pivot tilting pad. Tribol. T. 2020, 63, 704–717. [Google Scholar] [CrossRef]
- Gharanjik, A.; Mohammadi, A.K. Effect of temperature on the nonlinear dynamic behavior of two-lobe non-circular gas-lubricated micro-bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2316–2334. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.Q.; Li, X.M.; Li, Q. Effects of surface waviness on the nonlinear vibration of gas lubricated bearing-rotor system. Shock Vib. 2018, 2018, 8269384. [Google Scholar] [CrossRef]
- Wang, C.C.; Lee, R.M.; Lin, C.J.; Huang, C.Y.; Lee, S.E. Research on the nonlinear dynamic characteristics of opposed high-speed gas bearing systems. J. Low Freq. Noise Vib. Act. Control. 2019, 39, 502–522. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Liu, Y.L.; Zhang, H.J. Unbalance response of micro gas bearing-rotor system considering rarefaction effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 230, 281–288. [Google Scholar] [CrossRef]
- Wang, C.C.; Lee, R.M.; Yau, H.T.; Lee, T.E. Nonlinear analysis and simulation of active hybrid aerodynamic and aerostatic bearing system. J. Low Freq. Noise Vib. Act. Control. 2018, 38, 1404–1421. [Google Scholar] [CrossRef] [Green Version]
- Feng, K.; Li, W.J.; Wu, S.B.; Liu, W.H. Thermohydrodynamic analysis of micro spherical spiral groove gas bearings under slip flow and surface roughness coupling effect. Microsyst. Technol. 2017, 23, 1779–1792. [Google Scholar] [CrossRef]
- Zhang, C.W.; Gu, L.; Wang, J.Y. Effect of air rarefaction on the contact behaviors of air lubricated spiral-groove thrust micro-bearings. Tribol. Int. 2017, 111, 167–175. [Google Scholar] [CrossRef]
- Jia, C.H.; Pang, H.J.; Ma, W.S.; Qiu, M. Dynamic Stability Prediction of Spherical Spiral Groove Hybrid Gas Bearings Rotor System. ASME J. Tribol. 2017, 139, 021701. [Google Scholar] [CrossRef]
- Jia, C.H.; Zhang, H.J.; Guo, S.J.; Qiu, M.; Ma, W.S.; Zhang, Z.Y. Study on dynamic characteristics of gas films of spherical spiral groove hybrid gas bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1169–1181. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.H.; Bättig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear study on a rigid rotor supported by herringbone grooved gas bearings: Theory and validation. Mech. Syst. Signal. 2021, 146, 106983. [Google Scholar] [CrossRef]
- Du, J.J.; Yang, G.W.; Ge, W.P.; Liu, T. Nonlinear dynamic analysis of a rigid rotor supported by a spiral-grooved opposed-hemisphere gas bearing. STLE Tribol. Trans. 2016, 59, 781–800. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Zhang, S.; Liu, F.X.; Zhou, C.; Lu, Y.J.; Müller, N. Motion analysis of a rotor supported by self-acting axial groove gas bearing system with double time delays. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2014, 228, 2888–2899. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Hei, D.; Lu, Y.J.; Wang, Q.D.; Müller, N. Bifurcation and chaos analysis of nonlinear rotor system with axial-grooved gas-lubricated journal bearing support. Chin. J. Mech. Eng. 2014, 27, 58–368. [Google Scholar] [CrossRef]
- Li, Y.Q.; Luo, Z.; Liu, J.X.; Ma, H. Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint. Mech. Syst. Signal. 2021, 158, 107778. [Google Scholar] [CrossRef]
- Lu, Y.J.; Zhang, Y.F.; Dai, R.; Liu, H.; Yu, L.; Hei, D.; Wang, Y. Non-linear analysis of a flexible rotor system with multi-span bearing supports. Proc. Inst. Mech. Eng. J. Heir. Eng. Tribol. 2008, 222, 87–95. [Google Scholar] [CrossRef]
- Chasalevris, A.C.; Papadopoulos, C.A. A novel semi-analytical method for the dynamics of nonlinear rotor-bearing systems. Mech. Mach. Theory 2014, 72, 39–59. [Google Scholar] [CrossRef]
- Yang, L.H.; Sun, Y.H.; Yu, L. Active control of unbalance response of rotor systems supported by tilting-pad gas bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 87–98. [Google Scholar]
- Liu, Y.; Liu, H.; Yi, J.; Jing, M.Q. Investigation on the stability and bifurcation of a rod-fastening rotor bearing system. J. Vib. Control 2015, 21, 2866–2880. [Google Scholar] [CrossRef]
- Wu, X.L.; Jiao, Y.H.; Chen, Z.B.; Ma, W.S. Establishment of a contact stiffness matrix and its effect on the dynamic behavior of rod-fastening rotor bearing system. Arch. Appl. Mech. 2021, 91, 3247–3271. [Google Scholar] [CrossRef]
- Li, J.Q.; Li, Y.; Zhang, F.; Feng, Y.L. Nonlinear Analysis of Rod Fastened Rotor under Nonuniform Contact Stiffness. Shock Vib. 2020, 2020, 8851996. [Google Scholar] [CrossRef]
- Wang, L.K.; Wang, A.L.; Jin, M.; Yin, Y.J.; Heng, X.; Ma, P.W. Nonlinear dynamic response and stability of a rod fastening rotor with internal damping effect. Arch. Appl. Mech. 2021, 91, 3851–3867. [Google Scholar] [CrossRef]
- Hei, D.; Lu, Y.J.; Zhang, Y.F.; Lu, Z.Y.; Gupta, P.; Müller, N. Nonlinear dynamic behaviors of a rod fastening rotor supported by fixed–tilting pad journal bearings. Chaos Solitons Fractals 2014, 69, 129–150. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Y.B.; Teng, W.; Zhou, C. Nonlinear Coupled Dynamics of a Rod Fastening Rotor under Rub-Impact and Initial Permanent Deflection. Energies 2016, 9, 883. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Liu, Y.B.; Zhao, L.; Zhou, C. Nonlinear dynamic response of a rub-impact rod fastening rotor considering nonlinear contact characteristic. Arch. Appl. Mech. 2016, 86, 1869–1886. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Hashemian, M. Modified differential transformation method for solving nonlinear dynamic problems. Appl. Math. Model. 2017, 47, 76–95. [Google Scholar] [CrossRef]
- Zhao, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. (In Chinese) [Google Scholar]











| Parameters | Value or Formula |
|---|---|
| α | 0.25 |
| δ, δ = 2α | 0.5 |
| a0 | 1/ατ2 |
| a1 | δ/ατ2 |
| a2 | 1/ατ |
| a3 | 1/2α − 1 |
| a4 | δ/α − 1 |
| a5 | (1/2α − 1) |
| a6 | (1 − δ)τ |
| a7 | δτ |
| Parameter | Value | Unit |
|---|---|---|
| Structure parameters parameter values of the three-axial-groove gas bearing | ||
| Radius of bearing, Rb | 0.005 | m |
| Bearing width, Bb | 0.01 | m |
| Width-to-diameter ratio, Bb/2Rb | 1 | |
| Radial clearance, c | 5 × 10−6 | m |
| Position angle of pad, α0 | 10 | deg |
| Groove width angle, α | 5 | deg |
| Arc bushing angle, β | 115 | deg |
| Structure parameters parameter values of the rod-fastened rotor | ||
| Radius of shaft, R | 0.005 | m |
| Length of the left and right segments, l1 = l2 | 0.2 | m |
| Radius of disk, Rd | 0.01 | m |
| Width of disk, Bd | 0.02 | m |
| Mass eccentricities of the disk, ed1 = ed2 | 1 × 10−6 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Lu, Y.; Zhang, Y.; Hei, D.; Zhao, X. Dynamics Investigation on Axial-Groove Gas Bearing-Rotor System with Rod-Fastened Structure. Appl. Sci. 2022, 12, 250. https://doi.org/10.3390/app12010250
Li S, Lu Y, Zhang Y, Hei D, Zhao X. Dynamics Investigation on Axial-Groove Gas Bearing-Rotor System with Rod-Fastened Structure. Applied Sciences. 2022; 12(1):250. https://doi.org/10.3390/app12010250
Chicago/Turabian StyleLi, Sha, Yanjun Lu, Yongfang Zhang, Di Hei, and Xiaowei Zhao. 2022. "Dynamics Investigation on Axial-Groove Gas Bearing-Rotor System with Rod-Fastened Structure" Applied Sciences 12, no. 1: 250. https://doi.org/10.3390/app12010250






