Aerodynamics of a Train and Flat Closed-Box Bridge System with Train Model Mounted on the Upstream Track
Abstract
:1. Introduction
2. Configurations of Wind Tunnel Setup
2.1. Wind Tunnels and Models
2.2. Testing Points and Instruments
3. Aerodynamic Interactions
3.1. Train Model
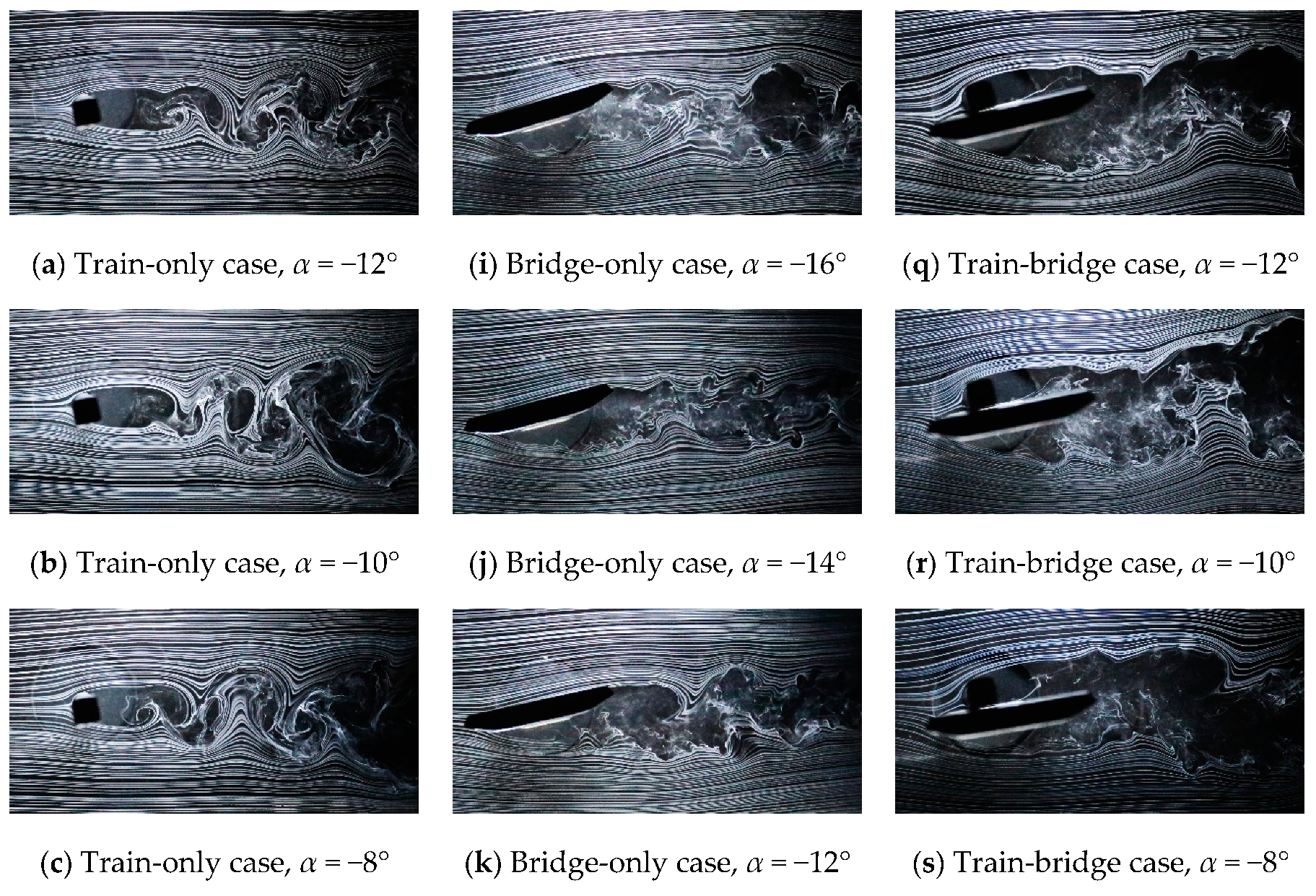
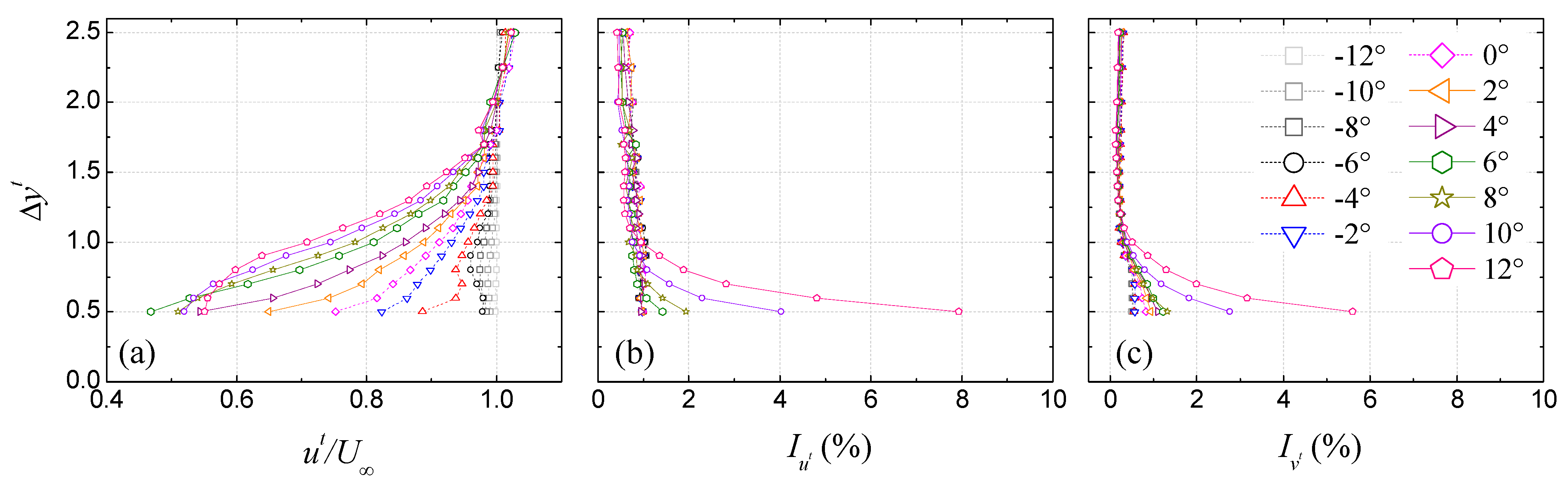
3.1.1. Underbody Flow Restraining Effect
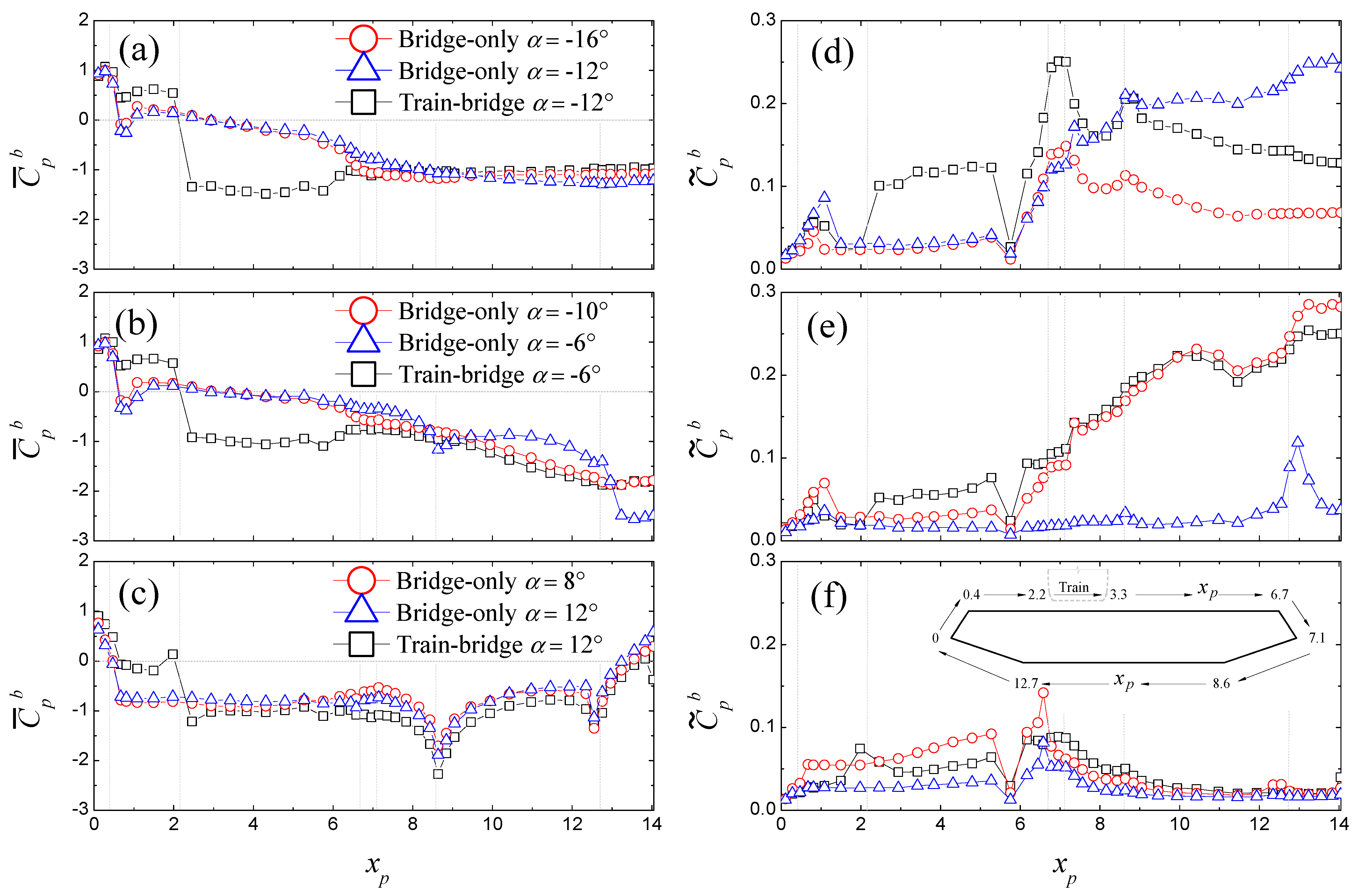
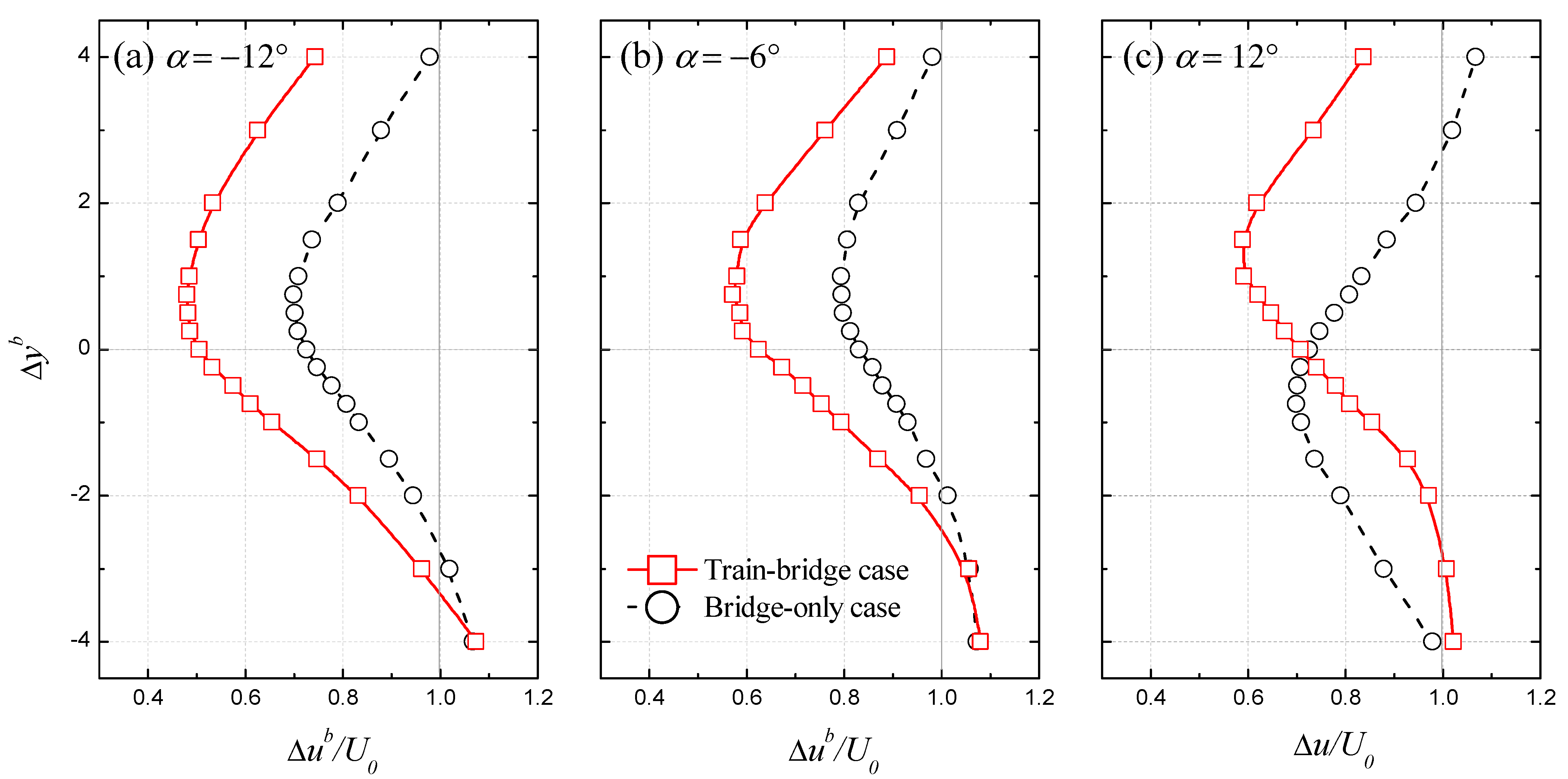
3.1.2. Bridge Deck Shielding Effect
3.2. Bridge-Deck Model
3.2.1. Flow Transition Promoting Effect
3.2.2. Flow Separation Intensifying Effect
4. Aerodynamic Characteristics
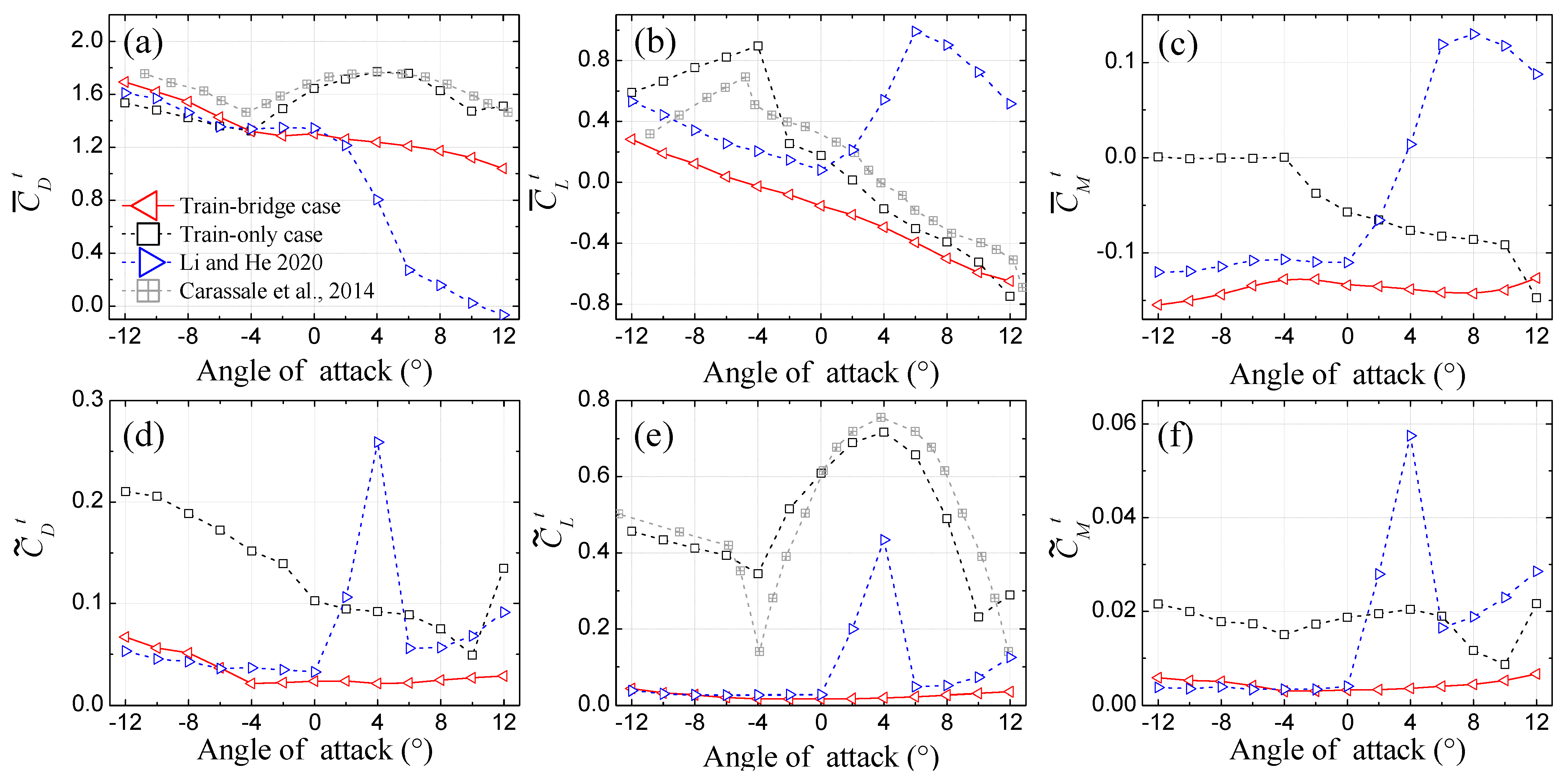
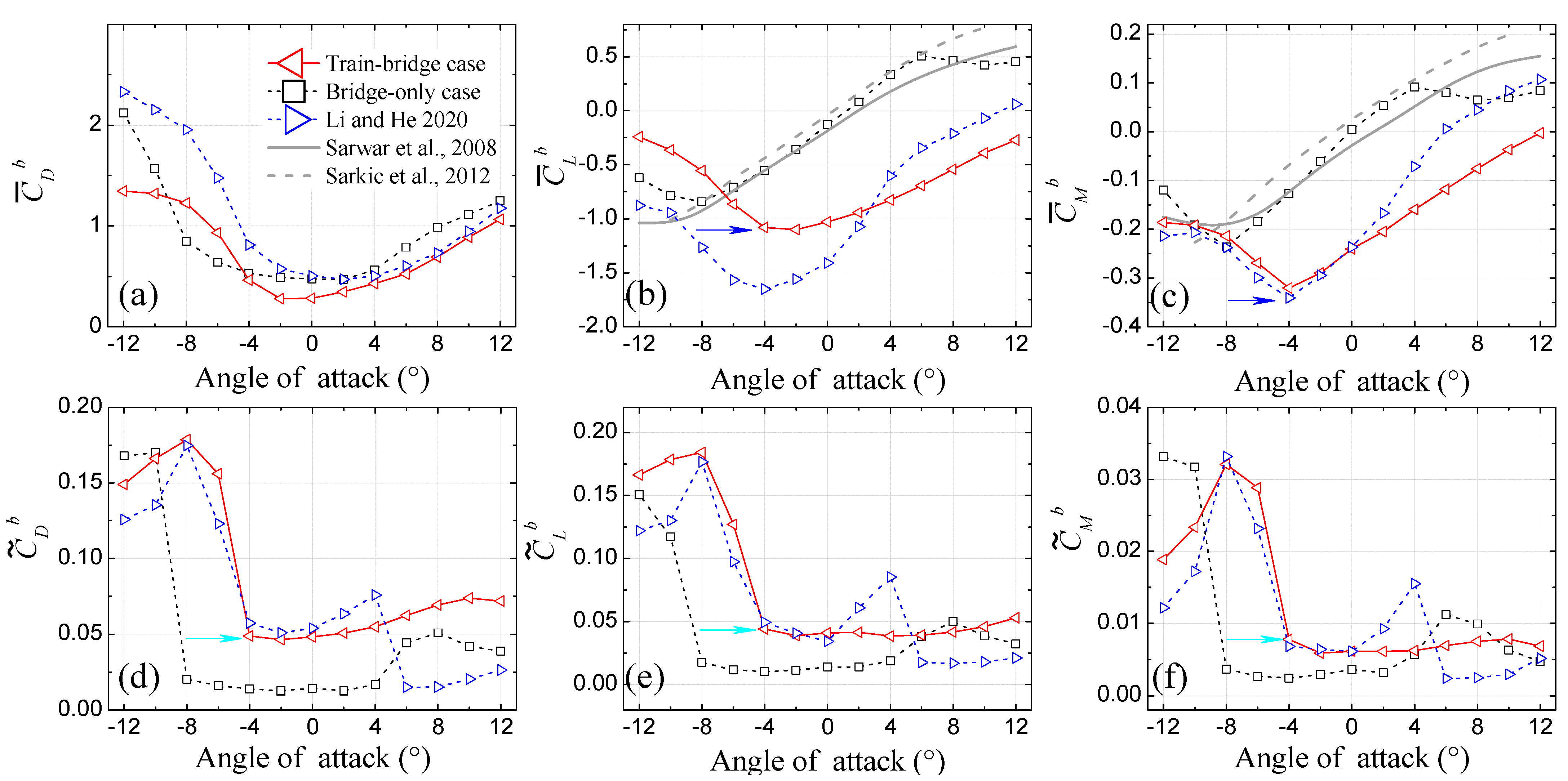
4.1. Aerodynamic Force Coefficients
- (a)
- In α = [0°, 12°], no abrupt changes, i.e., drag crisis (Figure 8a), jumping and recovering of lift, moment, and three fluctuating force coefficients (Figure 8b–f), can be observed in the present study. As concluded in Section 3, these differences shall be chiefly caused by the disappearance of the quasi-Reynolds number effect.
- (a)
- In α = [−12°, 0°], the , , and in the two cases with train model mounted on the upstream and downstream tracks share almost the similar behaviors, as described in Figure 8a–c. However, the in the present study is reduced by 0.23 in the range of α = [−12°, 0°].
- (a)
- In α = [0°, 12°], no abrupt changes, i.e., jumping and recovering of , , , , and can be observed in the present study relative to those of [34]. Obviously, this difference shall also be caused by the disappearance of the quasi-Reynolds number effect as concluded in Section 3.1.2.
- (b)
- In α = [−12°, 0°], , , , and in the two cases with train model mounted on the upstream and downstream tracks display similar behaviors, while the values of || and || in the present study are much smaller than those of [34].
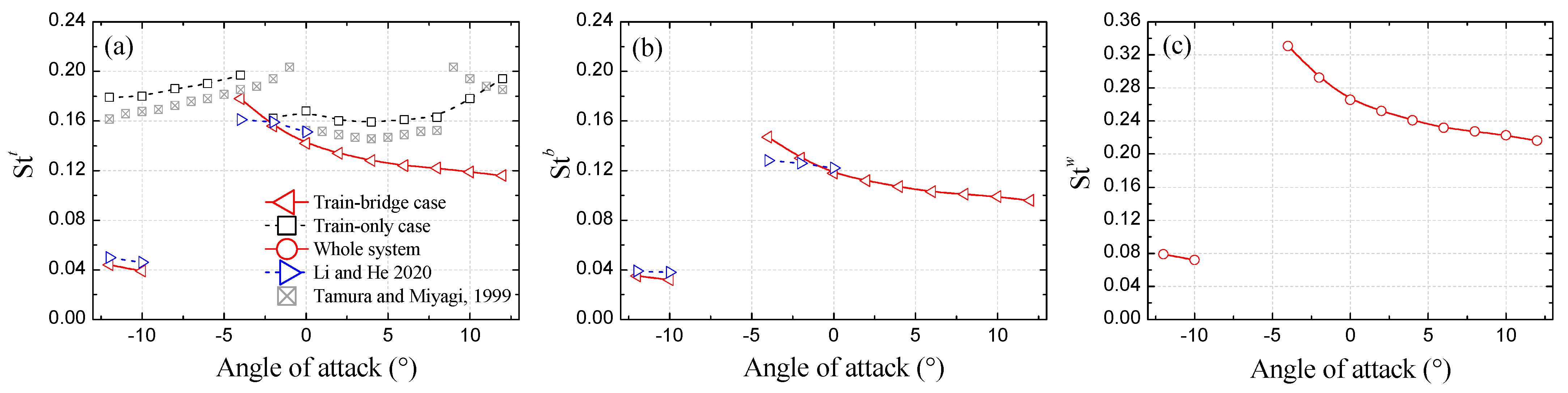
4.2. Strouhal Numbers
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; Wu, T.; Zou, Y.; Chen, Y.F.; Guo, H.; Yu, Z. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Baker, C. The flow around high speed trains. J. Wind Eng. Ind. Aerodyn. 2010, 98, 277–298. [Google Scholar] [CrossRef]
- Baker, C.; Johnson, T.; Flynn, D.; Hemida, H.; Quinn, A.; Soper, D.; Sterling, M. Train Aerodynamics: Fundamentals and Applications; Butterworth-Heinemann: Cambridge, MA, USA, 2019. [Google Scholar]
- Li, Y.; Qiang, S.; Liao, H.; Xu, Y.L. Dynamics of wind–rail vehicle–bridge systems. J. Wind Eng. Ind. Aerodyn. 2005, 93, 483–507. [Google Scholar] [CrossRef]
- Baker, C. A review of train aerodynamics Part 1–Fundamentals. Aeronaut. J. 2014, 118, 201–228. [Google Scholar] [CrossRef]
- Olmos, J.M.; Astiz, M.A. Improvement of the lateral dynamic response of a high pier viaduct under turbulent wind during the high-speed train travel. Eng. Struct. 2018, 165, 368–385. [Google Scholar] [CrossRef]
- Olmos, J.M.; Astiz, M.A. Non-linear vehicle-bridge-wind interaction model for running safety assessment of high-speed trains over a high-pier viaduct. J. Sound Vib. 2018, 419, 63–89. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; Guo, W.W. Analysis of resonance mechanism and conditions of train-bridge system. J. Sound Vib. 2006, 297, 810–822. [Google Scholar] [CrossRef]
- Xu, Y.L.; Ding, Q.S. Interaction of railway vehicles with track in cross-winds. JFS 2006, 22, 295–314. [Google Scholar] [CrossRef]
- Xu, Y.L.; Zhang, N.; Xia, H. Vibration of coupled train and cable-stayed bridge systems in cross winds. Eng. Struct. 2004, 26, 1389–1406. [Google Scholar] [CrossRef]
- CEN. Railway Applications-Aerodynamics-Part 6: Requirements and Test Procedures for Cross Wind Assessment. 2010, 14067-6. Available online: https://standards.iteh.ai/catalog/standards/cen/a9acedac-3968-4b8c-a6cc-5a035c91e9b3/en-14067-6-2018 (accessed on 24 December 2021).
- Cheli, F.; Ripamonti, F.; Rocchi, D.; Tomasini, G. Aerodynamic behaviour investigation of the new EMUV250 train to cross wind. J. Wind Eng. Ind. Aerodyn. 2010, 98, 189–201. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.; Eloy, C.; Li, H. Multi-mode responses, rivulet dynamics, flow structures and mechanism of rain-wind induced vibrations of a flexible cable. J. Fluids Struct. 2018, 82, 154–172. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.-L.; Zhang, R.-T.; Huang, Y.-W.; Li, H. Multi-modal vortex- and rain–wind-induced vibrations of an inclined flexible cable. Mech. Syst. Signal Processing 2019, 118, 245–258. [Google Scholar] [CrossRef]
- Gao, D.; Deng, Z.; Yang, W.; Chen, W. Review of the excitation mechanism and aerodynamic flow control of vortex-induced vibration of the main girder for long-span bridges: A vortex-dynamics approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]
- He, X.H.; Li, H. Review of aerodynamics of high-speed train-bridge system in crosswinds. J. Cent. South Univ. 2020, 27, 1054–1073. [Google Scholar] [CrossRef]
- Li, H.; He, X.H.; Wang, H.F.; Kareem, A. Aerodynamics of a scale model of a high-speed train on a streamlined deck in cross winds. J. Fluids Struct. 2019, 91, 102717. [Google Scholar] [CrossRef]
- Li, X.-Z.; Wang, M.; Xiao, J.; Zou, Q.-Y.; Liu, D.-J. Experimental study on aerodynamic characteristics of high-speed train on a truss bridge: A moving model test. J. Wind Eng. Ind. Aerodyn. 2018, 179, 26–38. [Google Scholar] [CrossRef]
- Baker, C. The determination of topographical exposure factors for railway embankments. J. Wind Eng. Ind. Aerodyn. 1985, 21, 89–99. [Google Scholar] [CrossRef]
- Barcala, M.A.; Meseguer, J. Visualization study of the influence of parapets on the flow around a train vehicle under cross winds. WIT Trans. Built Environ. 2008, 103, 797–806. [Google Scholar] [CrossRef] [Green Version]
- Barcala, M.A.; Meseguer, J. An experimental study of the influence of parapets on the aerodynamic loads under cross wind on a two-dimensional model of a railway vehicle on a bridge. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 487–494. [Google Scholar] [CrossRef]
- Bocciolone, M.; Cheli, F.; Corradi, R.; Muggiasca, S.; Tomasini, G. Crosswind action on rail vehicles: Wind tunnel experimental analyses. J. Wind Eng. Ind. Aerodyn. 2008, 96, 584–610. [Google Scholar] [CrossRef]
- Guo, W.; Xia, H.; Karoumi, R.; Zhang, T.; Li, X. Aerodynamic effect of wind barriers and running safety of trains on high-speed railway bridges under cross winds. Wind Struct. 2015, 20, 213–236. [Google Scholar] [CrossRef]
- He, X.H.; Li, H.; Hu, L.; Wang, H.F.; Kareem, A. Crosswind aerodynamic characteristics of a stationary interior railway carriage through a long-span truss-girder bridge. Eng. Struct. 2020, 210. [Google Scholar] [CrossRef]
- Ogueta-Gutiérrez, M.; Franchini, S.; Alonso, G. Effects of bird protection barriers on the aerodynamic and aeroelastic behaviour of high speed train bridges. Eng. Struct. 2014, 81, 22–34. [Google Scholar] [CrossRef]
- Suzuki, M.; Tanemoto, K.; Maeda, T. Aerodynamic characteristics of train/vehicles under cross winds. J. Wind Eng. Ind. Aerodyn. 2003, 91, 209–218. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.-Z.; Xiao, J.; Zou, Q.-Y.; Sha, H.-Q. An experimental analysis of the aerodynamic characteristics of a high-speed train on a bridge under crosswinds. J. Wind Eng. Ind. Aerodyn. 2018, 177, 92–100. [Google Scholar] [CrossRef]
- Xiang, H.; Li, Y.; Chen, S.; Li, C. A wind tunnel test method on aerodynamic characteristics of moving vehicles under crosswinds. J. Wind Eng. Ind. Aerodyn. 2017, 163, 15–23. [Google Scholar] [CrossRef]
- Xiang, H.; Li, Y.; Liao, H.; Li, C. An adaptive surrogate model based on support vector regression and its application to the optimization of railway wind barriers. Struct. Multidiscip. Optim. 2016, 55, 701–713. [Google Scholar] [CrossRef]
- Gao, D.-L.; Chen, W.-L.; Li, H.; Hu, H. Flow around a circular cylinder with slit. Exp. Therm. Fluid Sci. 2017, 82, 287–301. [Google Scholar] [CrossRef]
- Naudascher, E.; Wang, Y. Flow-Induced Vibrations of Prismatic Bodies and Grids of Prisms. J. Fluids Struct. 1993, 7, 341–373. [Google Scholar] [CrossRef]
- Zhou, Y.; Alam, M.M. Wake of two interacting circular cylinders: A review. Int. J. Heat Fluid Flow 2016, 62, 510–537. [Google Scholar] [CrossRef]
- Ma, C.; Duan, Q.; Li, Q.; Chen, K.; Liao, H. Buffeting Forces on Static Trains on a Truss Girder in Turbulent Crosswinds. J. Bridge Eng. 2018, 23, 04018086. [Google Scholar] [CrossRef]
- Li, H.; He, X.H. Lateral aerodynamic interference between an interior train and a flat box bridge-deck. Exp. Therm. Fluid Sci. 2020, 117, 110115. [Google Scholar] [CrossRef]
- Deniz, S.; Staubli, T. Oscillating Rectangular and Octagonal Profiles: Interaction of Leading- and Trailing-Edge Vortex Formation. J. Fluids Struct. 1997, 11, 3–31. [Google Scholar] [CrossRef]
- Païdoussis, M.P.; Price, S.J.; De Langre, E. Fluid-Structure Interactions: Cross-Flow-Induced Instabilities; Cambridge University Press: Near York, NY, USA, 2010. [Google Scholar]
- Carassale, L.; Freda, A.; Marre-Brunenghi, M. Experimental investigation on the aerodynamic behavior of square cylinders with rounded corners. J. Fluids Struct. 2014, 44, 195–204. [Google Scholar] [CrossRef]
- Sarwar, M.W.; Ishihara, T.; Shimada, K.; Yamasaki, Y.; Ikeda, T. Prediction of aerodynamic characteristics of a box girder bridge section using the LES turbulence model. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1895–1911. [Google Scholar] [CrossRef]
- Šarkić, A.; Fisch, R.; Höffer, R.; Bletzinger, K.-U. Bridge flutter derivatives based on computed, validated pressure fields. J. Wind Eng. Ind. Aerodyn. 2012, 104-106, 141–151. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
- Nakamura, Y.; Ohya, Y.; Tsuruta, H. Experiments on vortex shedding from flat plates with square leading and trailing edges. J. Fluid Mech. 1991, 222, 437–447. [Google Scholar] [CrossRef]
- Norberg, C.; Sunden, B. Turbulence and reynolds number effects on the flow and fluid forces on a single cylinder in cross flow. J. Fluids Struct. 1987, 1, 337–357. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, H.; He, X. Aerodynamics of a Train and Flat Closed-Box Bridge System with Train Model Mounted on the Upstream Track. Appl. Sci. 2022, 12, 276. https://doi.org/10.3390/app12010276
Wang H, Li H, He X. Aerodynamics of a Train and Flat Closed-Box Bridge System with Train Model Mounted on the Upstream Track. Applied Sciences. 2022; 12(1):276. https://doi.org/10.3390/app12010276
Chicago/Turabian StyleWang, Hui, Huan Li, and Xuhui He. 2022. "Aerodynamics of a Train and Flat Closed-Box Bridge System with Train Model Mounted on the Upstream Track" Applied Sciences 12, no. 1: 276. https://doi.org/10.3390/app12010276
APA StyleWang, H., Li, H., & He, X. (2022). Aerodynamics of a Train and Flat Closed-Box Bridge System with Train Model Mounted on the Upstream Track. Applied Sciences, 12(1), 276. https://doi.org/10.3390/app12010276





