Experimental Study on Flow and Heat Transfer Characteristics in the Circular-Arc-Shaped Flow Channel
Abstract
:1. Introduction
2. Experimental Method
2.1. Samples
2.2. Wind Tunnel Tests
2.3. Data Reduction
3. Results and Discussion
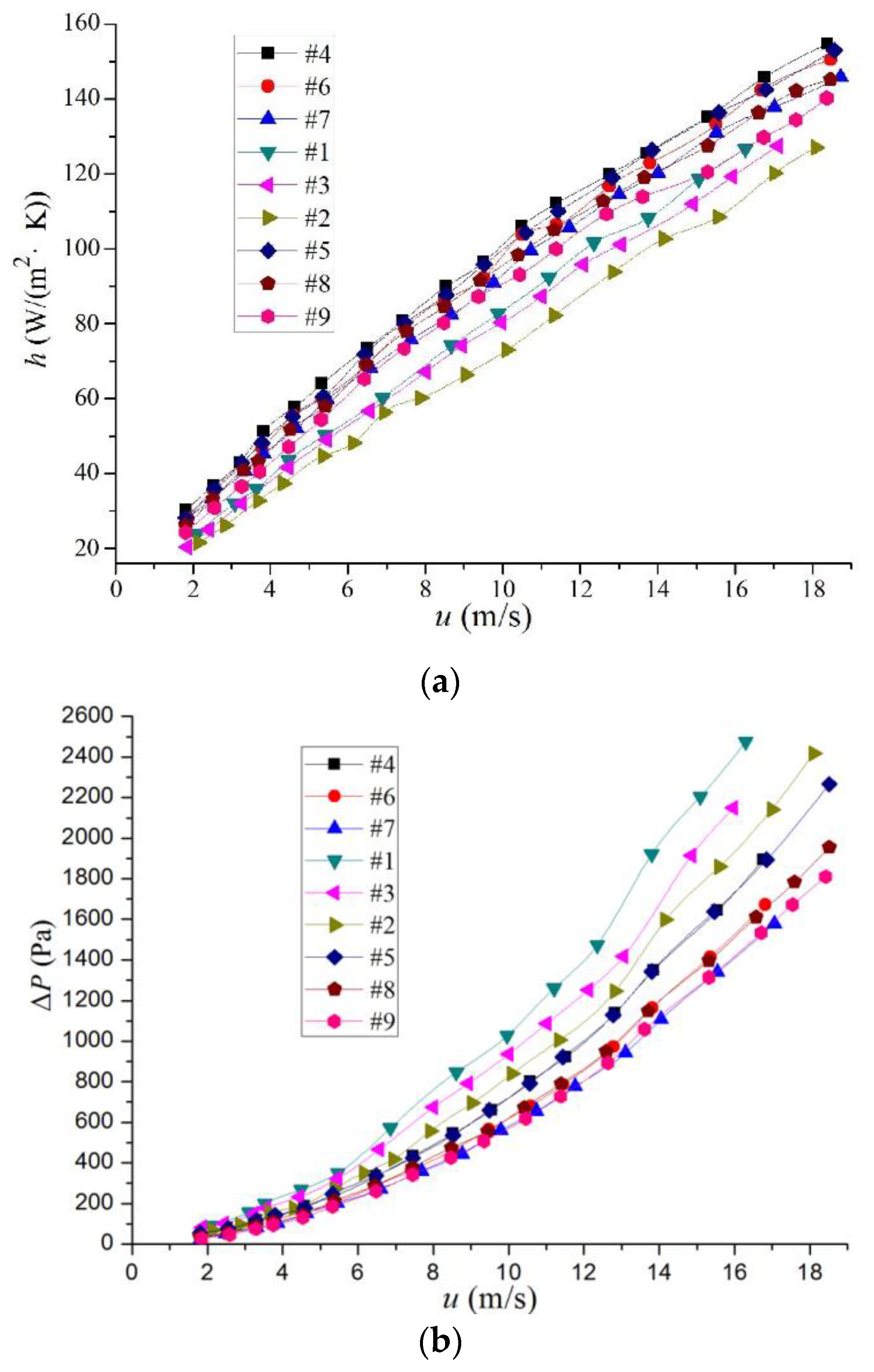
3.1. Overall Heat Transfer Performance for Different Flow Channels
3.2. Performance of Heat Transfer and Flow Characteristics in Different Circular-Arc-Shaped Flow Channels
3.2.1. Heat Transfer and Flow Performance with Different Structural Parameters
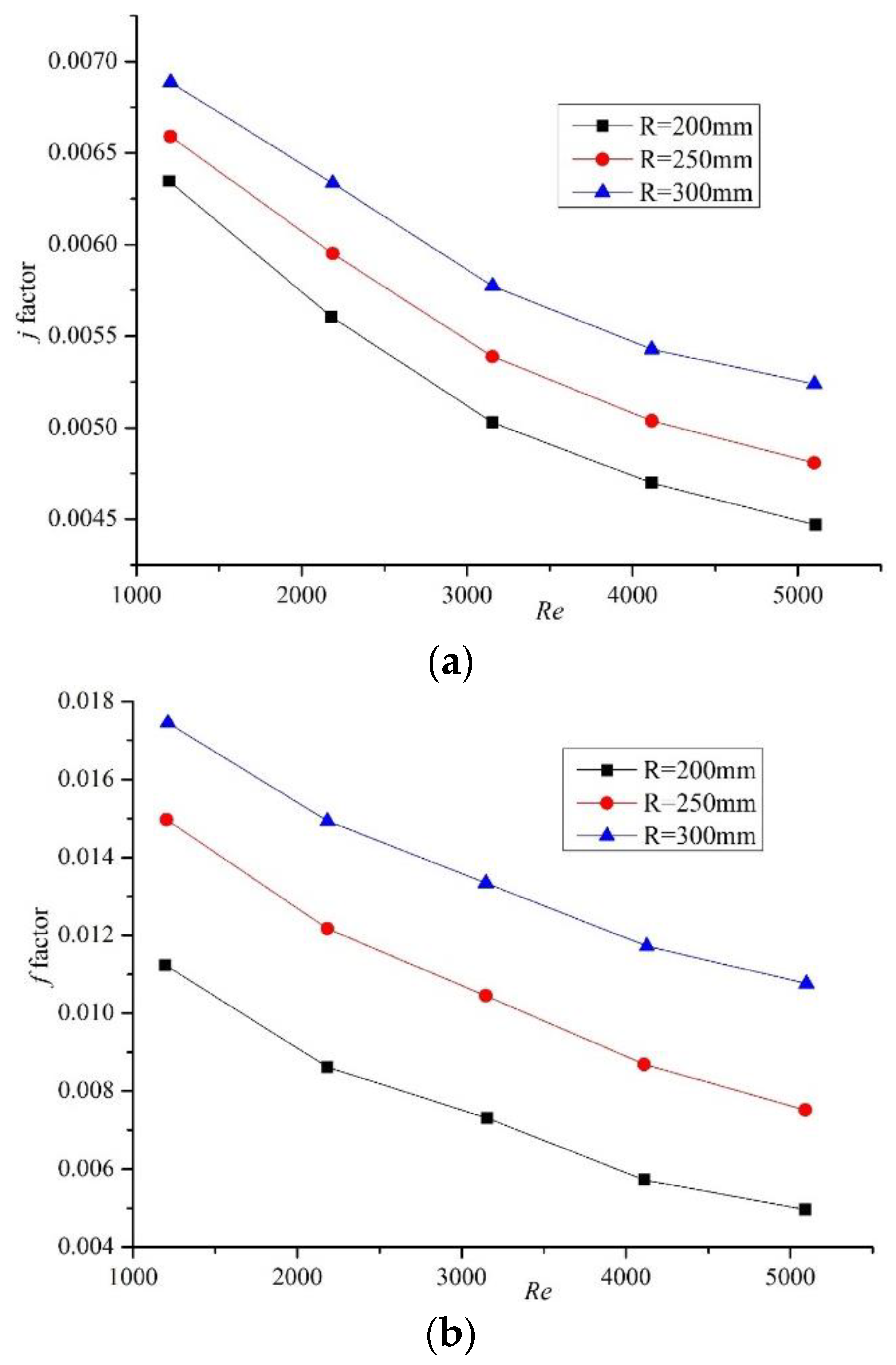
3.2.2. Performance Analysis with Different Circular Radii
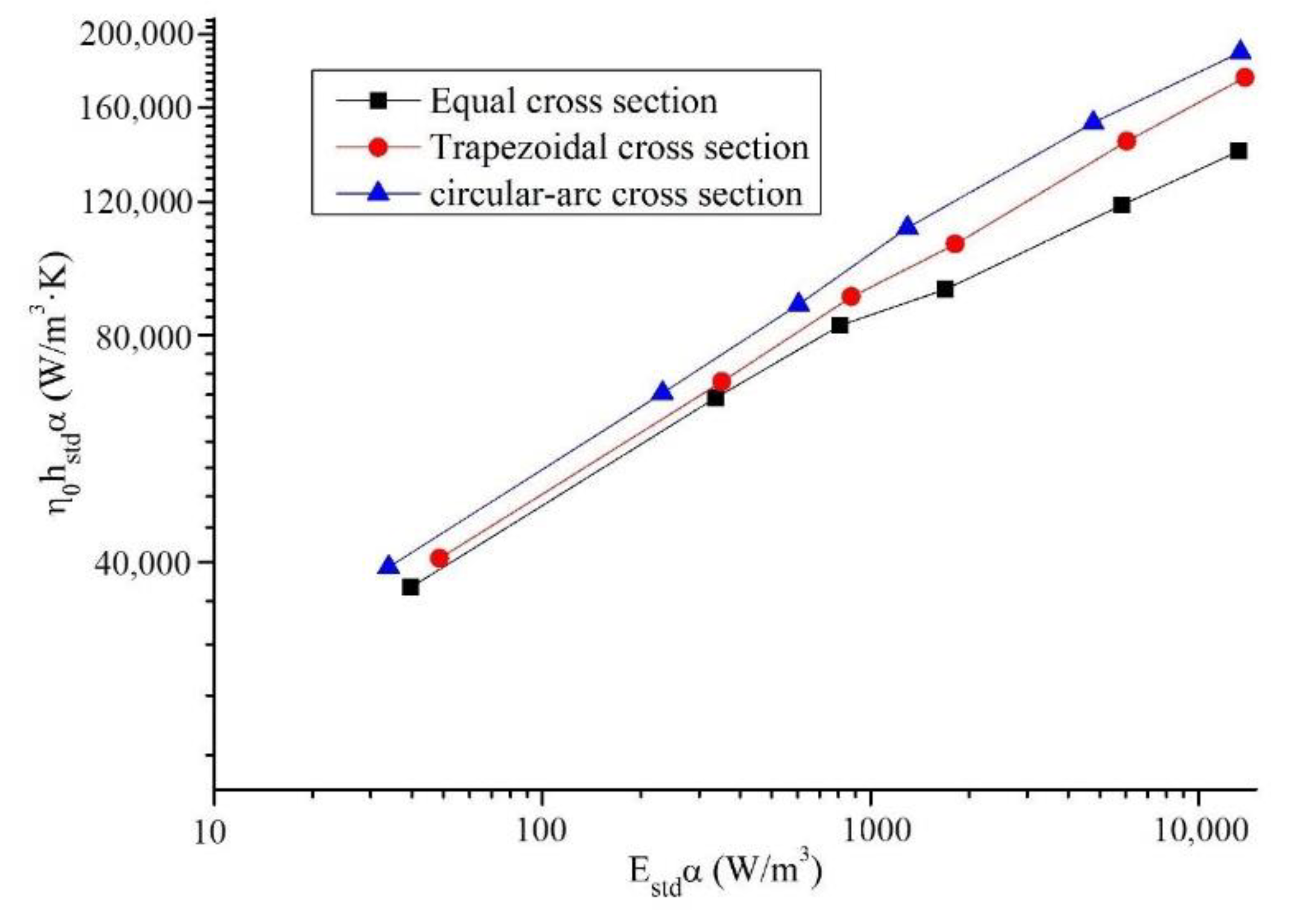
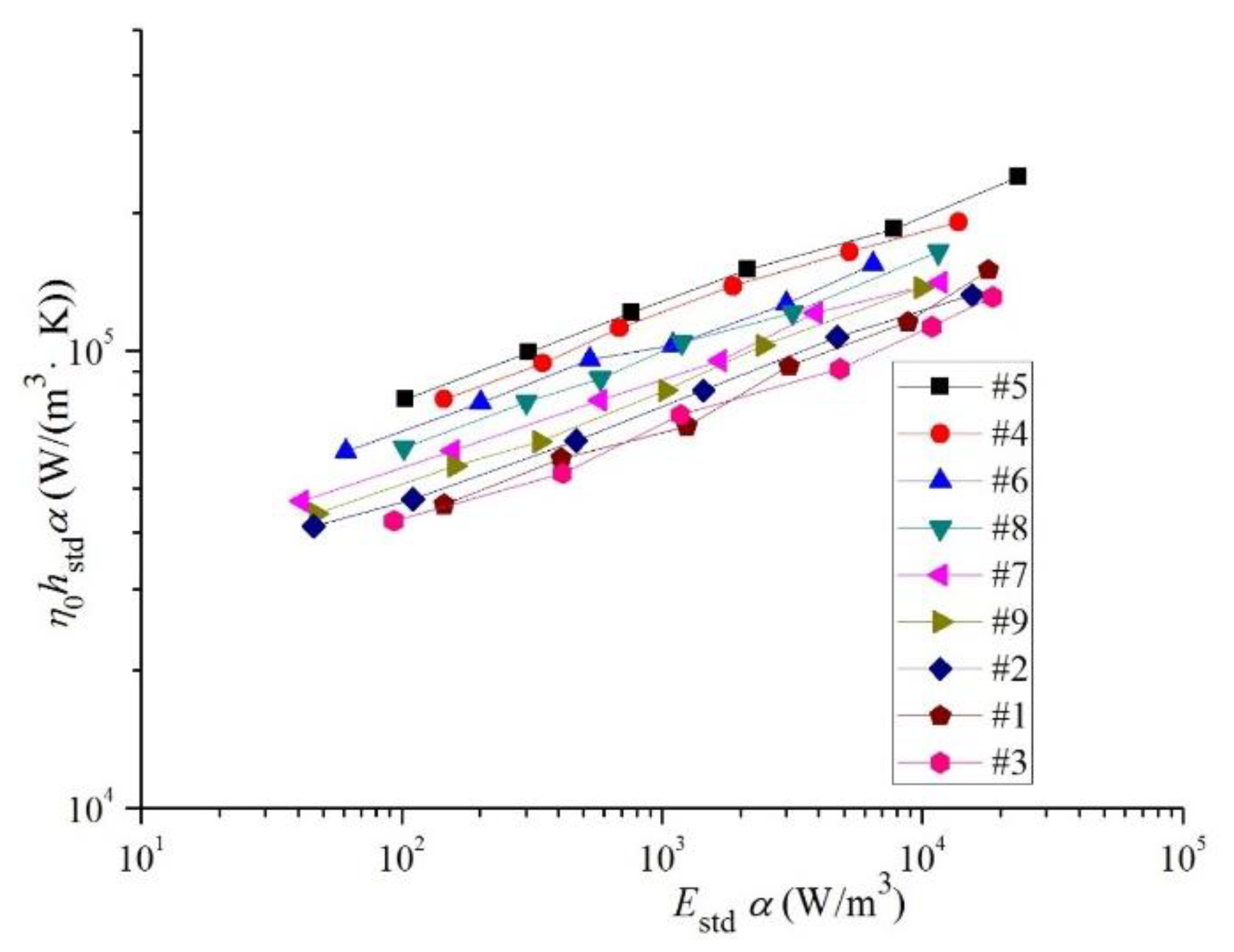
3.2.3. Overall Heat Transfer Performance
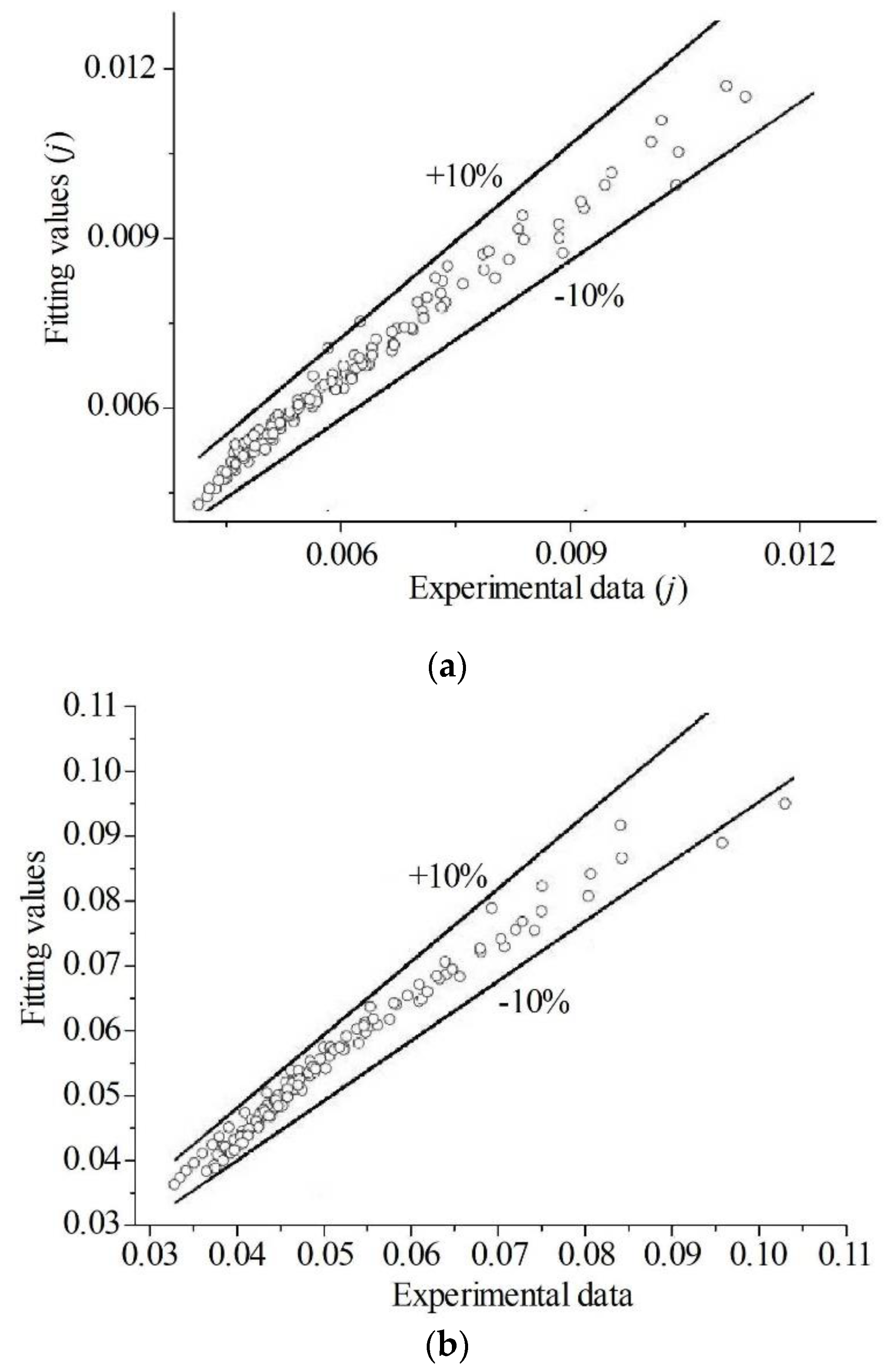
3.3. Empirical Formulas for Heat Transfer and Flow Performance of Circular-Arc-Shaped Flow Channels with Different Structures
4. Conclusions
- With the increase in the circular radius, both the j and f factors increase, and the highest overall heat transfer performance is obtained at R = 300 mm.
- Comparing the three kinds of flow channels by using the core volume goodness factor shows that the overall heat transfer performance ranks from the circular-arc-shaped flow channel, trapezoidal flow channel to equal cross-section flow channel from best to worst. The overall heat transfer performance of the circular-arc-shaped flow channel is 26.2% (maximum value) larger than that of the equal cross-section channel. The divergent structure has better thermal hydraulic performance than the tapered and straight structures.
- With the decrease in the inlet height (Fh), h in the flow channels increases gradually. The pressure drop in different flow channels increases with the increase in flow velocity in the form of a parabola.
- The empirical formulas for heat transfer and flow performance of different circular-arcs were fitted by multiple regression analysis and F significance test. The empirical formula of the j and f factors can achieve 90% accurate prediction and the error range is controlled within 10%. When processing experimental data, the maximum mean deviation and maximum absolute deviation of the j factor were 1.05% and 3.77%, respectively. The maximum mean deviation and maximum absolute deviation of the f factor were 2.8% and 4.91%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vitillo, F.; Cachon, L.; Reulet, F.; Millan, P. Flow analysis of an innovative compact heat exchanger channel geometry. Int. J. Heat Fluid Flow 2016, 58, 30–39. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhang, Y.L. Experimental study on enhanced heat transfer and flow performance of magnetic nanofluids under alternating magnetic field. Int. J. Therm. Sci. 2021, 164, 106897. [Google Scholar] [CrossRef]
- Khoshvaght, A.M.; Zanganeh, A.; Akbari, M.H.; Eskandari, M. Experimental investigation on thermal-hydraulic characteristics of a tube equipped with modified vortex-generator inserts. Exp. Heat Transf. 2017, 30, 11–24. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhang, Y.L. Heat transfer and flow characteristics of Fe3O4-water nanofluids under magnetic excitation. Int. J. Therm. Sci. 2021, 163, 106826. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Liu, Z.; Liu, J. Analysis of heat transfer and flow characteristics in typical cambered ducts. Int. J. Therm. Sci. 2020, 150, 106226. [Google Scholar] [CrossRef]
- Falkner, V.M.; Skan, S.W. Some approximate solutions of the boundary layer equations. Philos. Mag. 1931, 12, 865–896. [Google Scholar] [CrossRef]
- Hartree, D.R. On an equation occurring in Falkner and Skan’s approximate treatment of the equation of the boundary layer. Math. Proc. Camb. Philos. Soc. 1937, 33, 223–239. [Google Scholar] [CrossRef]
- Stewartson, K. Further solution of the Falkner-Skan equation. Math. Proc. Camb. Philos. Soc. 1954, 50, 454–465. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Farhanieh, B.; Sunden, B. Three-dimensional laminar flow and heat transfer in the entrance region of trapezoidal ducts. Int. J. Numer. Methods Fluids 1991, 13, 537–559. [Google Scholar] [CrossRef]
- Ghosh, S.; Pratihar, D.K.; Maiti, B.; Das, P.K. An evolutionary optimization of diffuser shapes based on CFD simulations. Int. J. Numer. Methods Fluids 2010, 63, 1147–1166. [Google Scholar] [CrossRef]
- Chen, W.X.; Chong, D.T.; Yan, J.J.; Liu, L.P. Numerical optimization on the geometrical factors of natural gas ejectors. Int. J. Therm. Sci. 2011, 50, 1554–1561. [Google Scholar] [CrossRef]
- Cur, N.O.; Anselmino, J.J. Evaporator for Home Refrigerator. U.S. Patent No. 5157941, 27 October 1992. [Google Scholar]
- Waltrich, P.J.; Barbosa, J.R.; Melo, C.; Hermes, C.L. Air-side heat transfer and pressure drop in accelerated flow evaporators. Int. Refrig. Air Cond. Conf. 2008, 7, 2311–2319. [Google Scholar] [CrossRef]
- Waltrich, P.J.; Barbosa, J.R.; Hermes, C.L.; Melo, C. Air-side heat transfer and pressure drop characteristics of accelerated flow evaporators. Int. J. Refrig. 2011, 34, 484–497. [Google Scholar] [CrossRef]
- Matsubara, K.; Miura, T. Spatially advancing turbulent flow and heat transfer in a curved channel at friction-velocity-based Reynolds number 550. Int. J. Heat Mass Transf. 2017, 108, 2433. [Google Scholar] [CrossRef]
- Bahaidarah, H.M. Entropy generation during fluid flow in sharp edge wavy channels with horizontal pitch. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, M.; Paramane, S.B.; Sharma, A. Periodically fully developed heat and fluid flow characteristics in furrowed wavy channel. Heat Transf. Eng. 2016, 38, 278–288. [Google Scholar] [CrossRef]
- Ho, J.Y.; Leong, K.C.; Wong, T.N. Filmwise condensation of steam on sinusoidal pin fin arrays: Effects of fin height and fin pitch. Int. J. Heat Mass Transf. 2019, 130, 1004–1015. [Google Scholar] [CrossRef]
- Wen, J.; Li, K.; Wang, C.; Zhang, X.; Wang, S. Optimization investigation on configuration parameters of sine wavy fin in plate-fin heat exchanger based on fluid structure interaction analysis. Int. J. Heat Mass Transf. 2019, 131, 385–402. [Google Scholar] [CrossRef]
- Vidal, A.; Nagib, H.; Schlatter, P.; Vinuesa, R. Secondary flow in spanwise-periodic in-phase sinusoidal channels. J. Fluid Mech. 2018, 851, 288–316. [Google Scholar] [CrossRef]
- Marin, O.; Vinuesa, R.; Obabko, A.V.; Schlatter, P. Characterization of the secondary flow in hexagonal ducts. Phys. Fluids 2016, 28, 125101. [Google Scholar] [CrossRef]
- ASHRAE. Handbook Fundamental S1 Edition; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 1993; Chapter 13; pp. 14–15. [Google Scholar]
- Wan, R.; Wang, Y.; Kavtaradze, R.; Ji, H.; He, X. Research on the air-side thermal hydraulic performance of louvered fin and flat tube heat exchangers under low-pressure environment. Exp. Heat Transf. 2020, 33, 81–99. [Google Scholar] [CrossRef]
- Manglik, R.M.; Bergles, A.E. Heat transfer and pressure drop correlations for the rectangular offset strip fin compact heat exchanger. Exp. Therm. Fluid Sci. 1995, 10, 171–180. [Google Scholar] [CrossRef]
- Mofft, R.J. Describing the uncertainties in experiment results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wang, Y.; Li, M.; Wang, S.; Li, X. Improved flow and heat transfer characteristics for heat exchanger by using a new humped wavy fin. Appl. Therm. Eng. 2017, 124, 510–520. [Google Scholar] [CrossRef]
- Yakut, K.; Alemdaroglu, N.; Kotcioglu, I.; Celik, C. Experimental investigation of thermal resistance of a heat sink with hexagonal fins. Appl. Therm. Eng. 2006, 26, 2262–2271. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Zhang, Y.; Zhang, X.; Li, M.; Liu, Z. Research on heat transfer enhancement and flow characteristic of heat exchange surface in cosine style runner. Heat Mass Transf. 2019, 55, 3117–3131. [Google Scholar] [CrossRef]
- ARI Standard 410; Standard for Forced Circulation Air-Cooling and Air-Heating Coils. Air-Conditioning and Refrigeration Institute: Arlington, VA, USA, 1981.

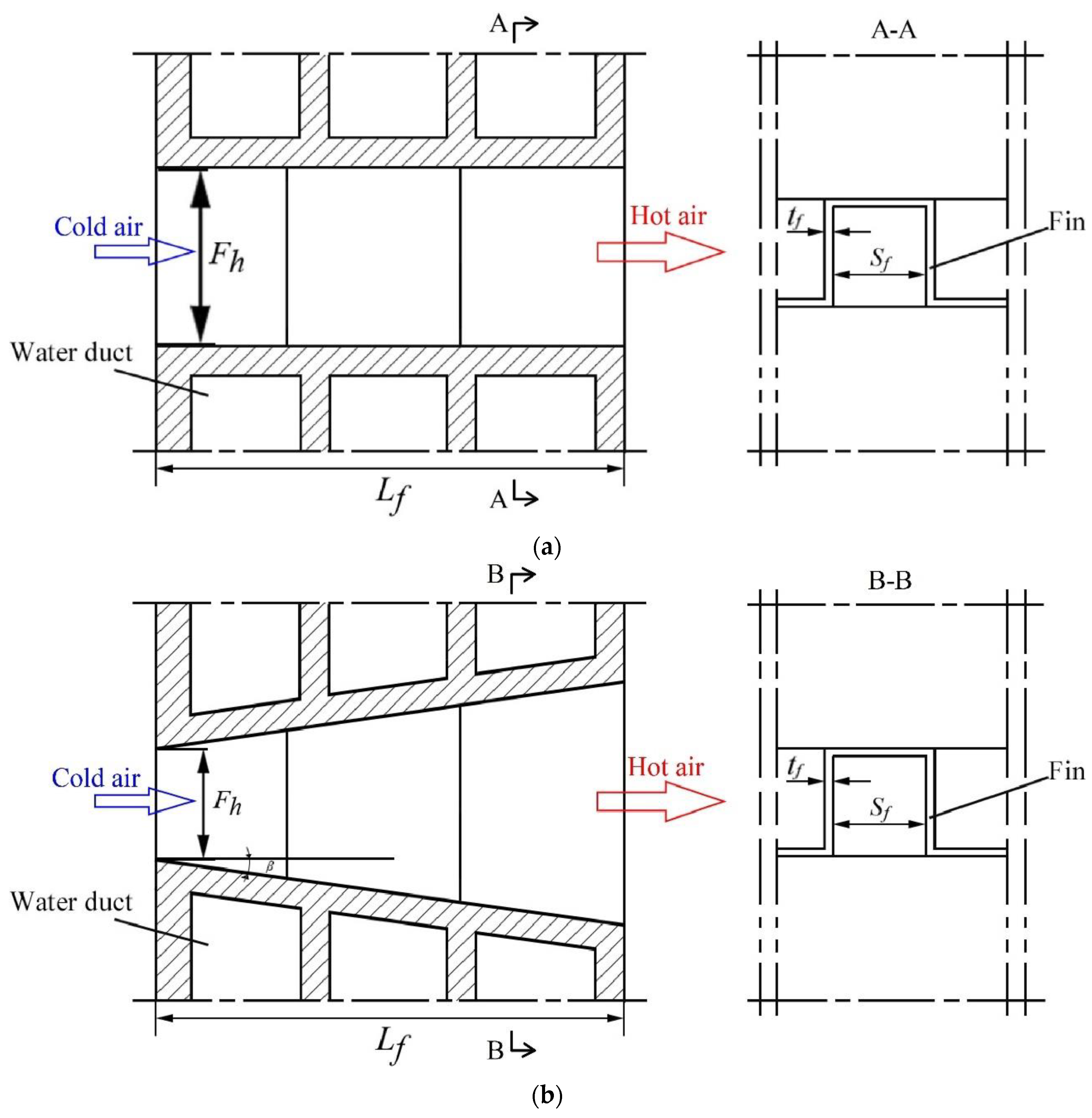
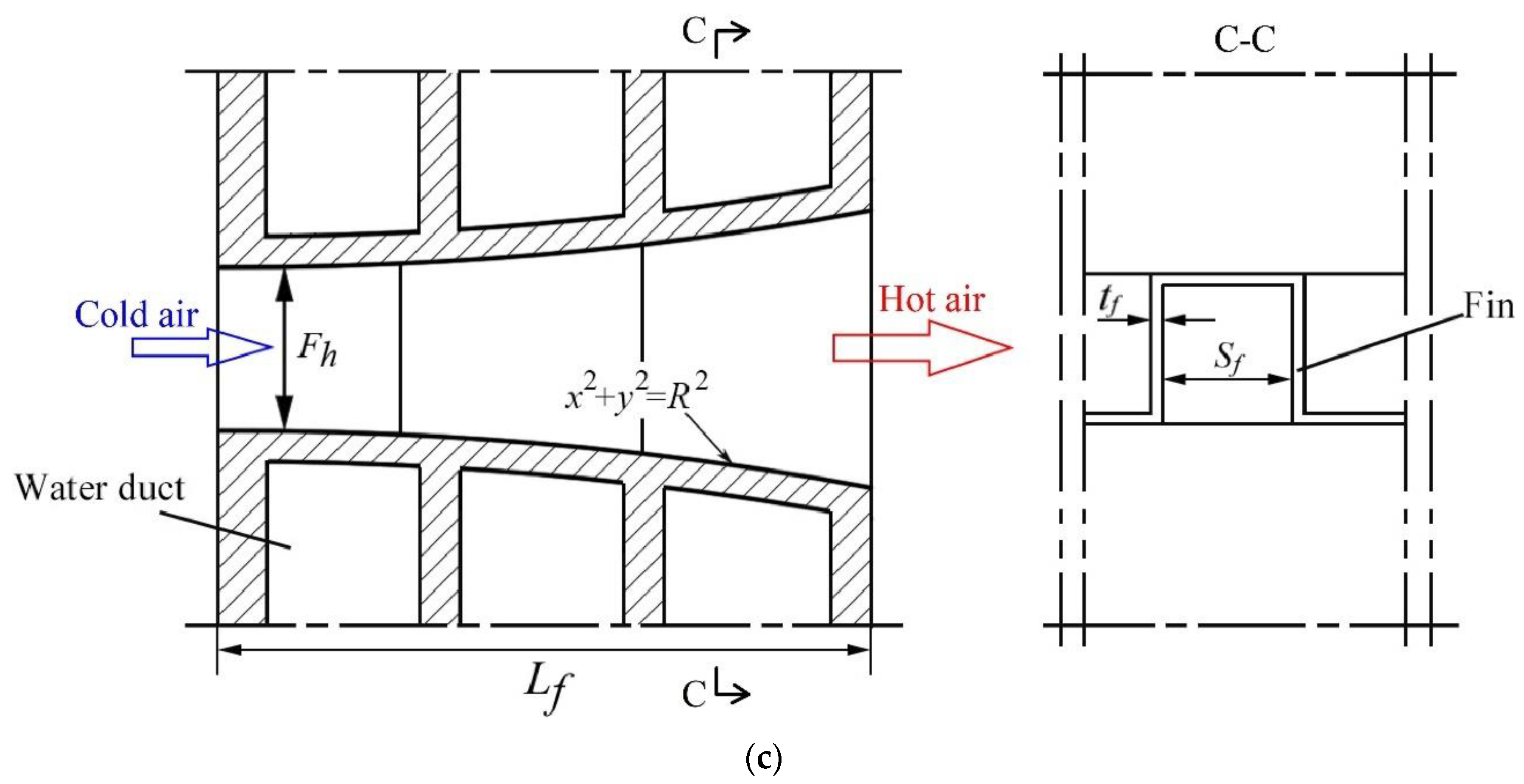
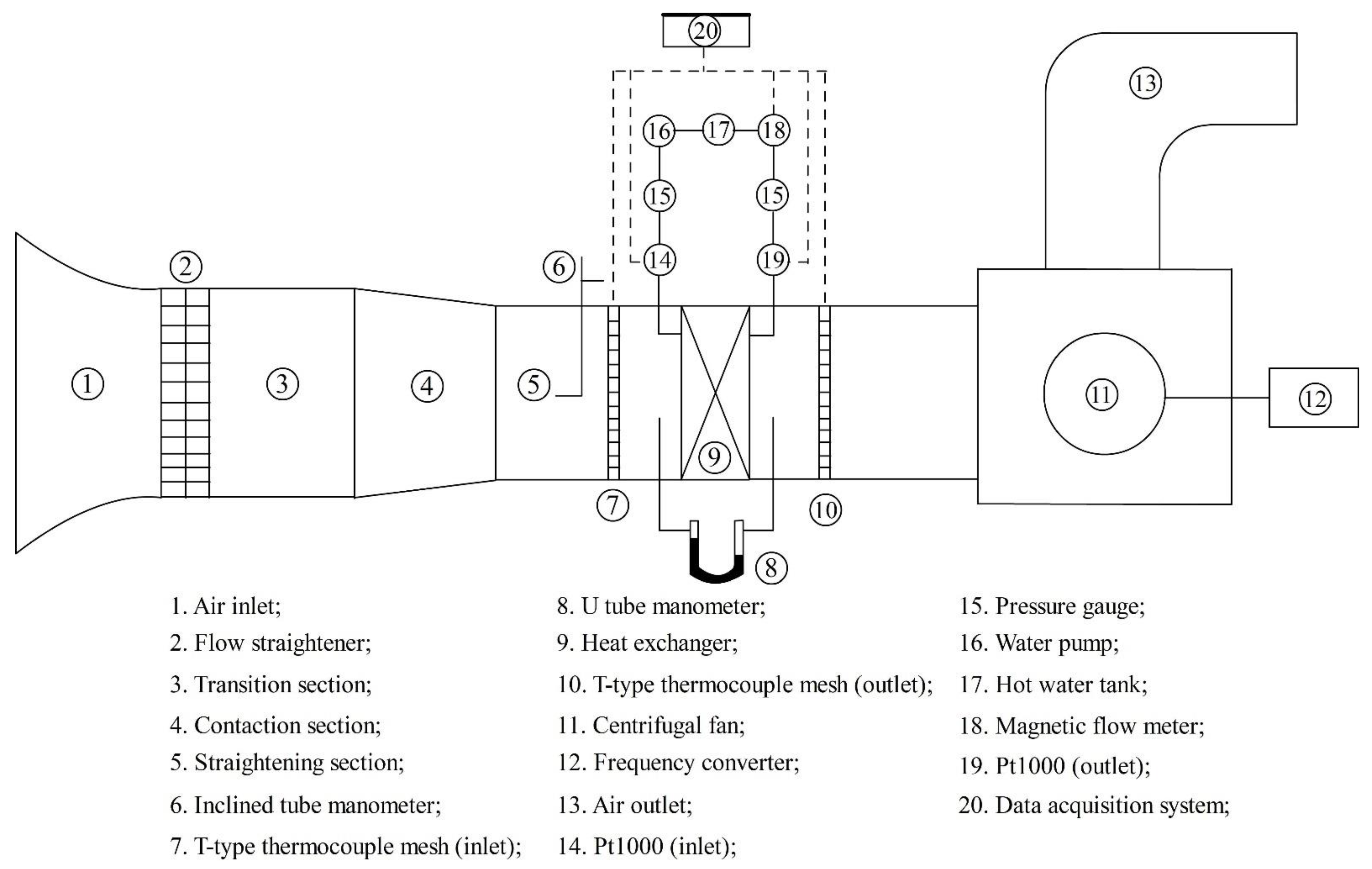

| NO. | Lf/mm | Sf/mm | Fh/mm | tf/mm |
|---|---|---|---|---|
| 1 | 60 | 3.0 | 9.0 | 0.4 |
| 2 | 60 | 3.5 | 9.0 | 0.4 |
| 3 | 60 | 4.0 | 9.0 | 0.4 |
| 4 | 55 | 3.0 | 9.0 | 0.4 |
| 5 | 55 | 3.5 | 9.0 | 0.4 |
| 6 | 55 | 4.0 | 9.0 | 0.4 |
| 7 | 45 | 3.0 | 8.0 | 0.3 |
| 8 | 45 | 3.5 | 8.0 | 0.3 |
| 9 | 45 | 4.0 | 8.0 | 0.3 |
| 10 | 45 | 3.0 | 9.0 | 0.3 |
| 11 | 45 | 3.0 | 11.0 | 0.3 |
| NO. | Fh/mm | β/° | Sf/mm | Lf/mm | tf/mm |
|---|---|---|---|---|---|
| 1 | 9.5 | 20 | 4.0 | 60 | 0.4 |
| 2 | 10.5 | 20 | 4.0 | 60 | 0.4 |
| 3 | 11.5 | 20 | 4.0 | 60 | 0.4 |
| 4 | 9.5 | 30 | 4.0 | 60 | 0.4 |
| 5 | 10.5 | 30 | 4.0 | 60 | 0.4 |
| 6 | 11.5 | 30 | 4.0 | 60 | 0.4 |
| 7 | 9.5 | 40 | 4.0 | 60 | 0.4 |
| 8 | 10.5 | 40 | 4.0 | 60 | 0.4 |
| 9 | 11.5 | 40 | 4.0 | 60 | 0.4 |
| NO. | Fh/mm | R/mm | Sf/mm | Lf/mm | tf/mm |
|---|---|---|---|---|---|
| 1 | 9.5 | 200 | 4.0 | 60 | 0.4 |
| 2 | 10.5 | 200 | 4.0 | 60 | 0.4 |
| 3 | 11.5 | 200 | 4.0 | 60 | 0.4 |
| 4 | 9.5 | 250 | 4.0 | 60 | 0.4 |
| 5 | 10.5 | 250 | 4.0 | 60 | 0.4 |
| 6 | 11.5 | 250 | 4.0 | 60 | 0.4 |
| 7 | 9.5 | 300 | 4.0 | 60 | 0.4 |
| 8 | 10.5 | 300 | 4.0 | 60 | 0.4 |
| 9 | 11.5 | 300 | 4.0 | 60 | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Fan, S.; Qu, D. Experimental Study on Flow and Heat Transfer Characteristics in the Circular-Arc-Shaped Flow Channel. Appl. Sci. 2022, 12, 376. https://doi.org/10.3390/app12010376
Song H, Fan S, Qu D. Experimental Study on Flow and Heat Transfer Characteristics in the Circular-Arc-Shaped Flow Channel. Applied Sciences. 2022; 12(1):376. https://doi.org/10.3390/app12010376
Chicago/Turabian StyleSong, Hui, Shuangxiu Fan, and Dayi Qu. 2022. "Experimental Study on Flow and Heat Transfer Characteristics in the Circular-Arc-Shaped Flow Channel" Applied Sciences 12, no. 1: 376. https://doi.org/10.3390/app12010376
APA StyleSong, H., Fan, S., & Qu, D. (2022). Experimental Study on Flow and Heat Transfer Characteristics in the Circular-Arc-Shaped Flow Channel. Applied Sciences, 12(1), 376. https://doi.org/10.3390/app12010376





