Analysis of Influence of Different Parameters on Numerical Simulation of NACA0012 Incompressible External Flow Field under High Reynolds Numbers
Abstract
:1. Introduction
2. Simulation Basics
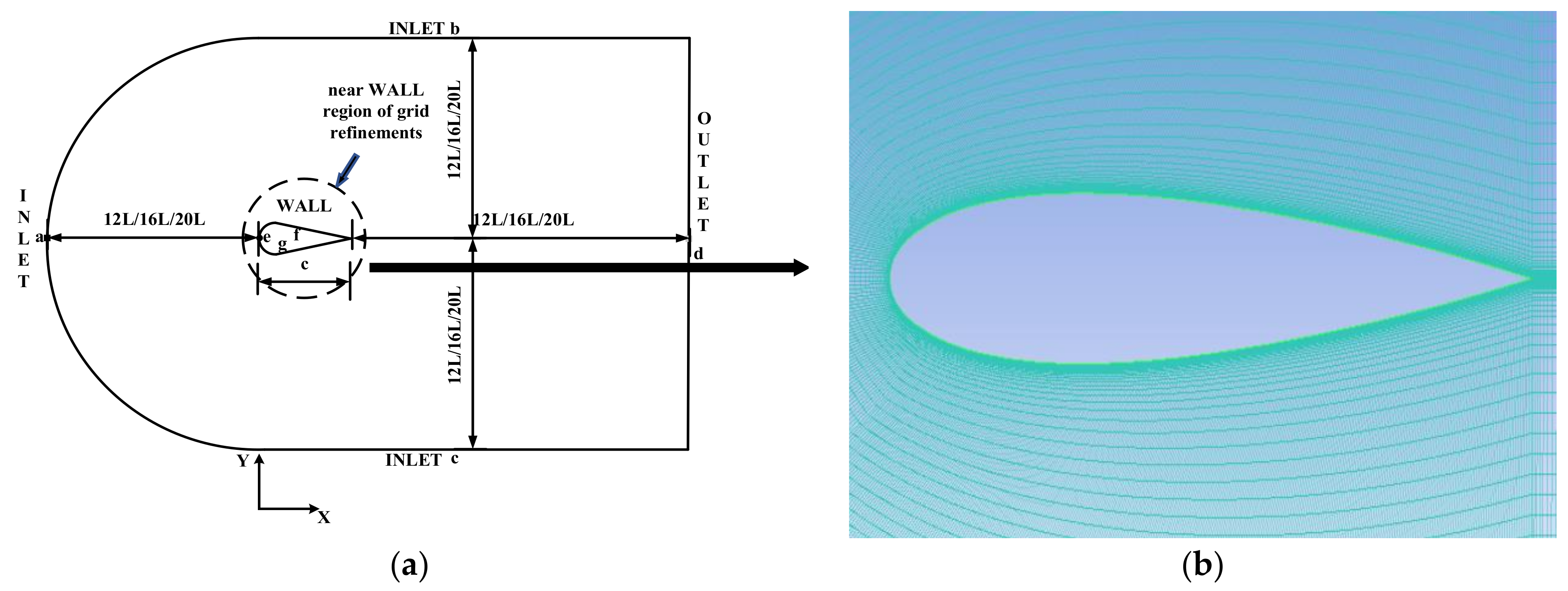
2.1. NACA0012 Models
2.2. Meshing
2.3. Turbulence
2.4. Numerical Procedure
3. Numerical Simulations
3.1. Grid Strategy
3.2. Numerical Method
3.3. Numerical Results
4. Results and Discussion
4.1. Results of NACA0012 Models
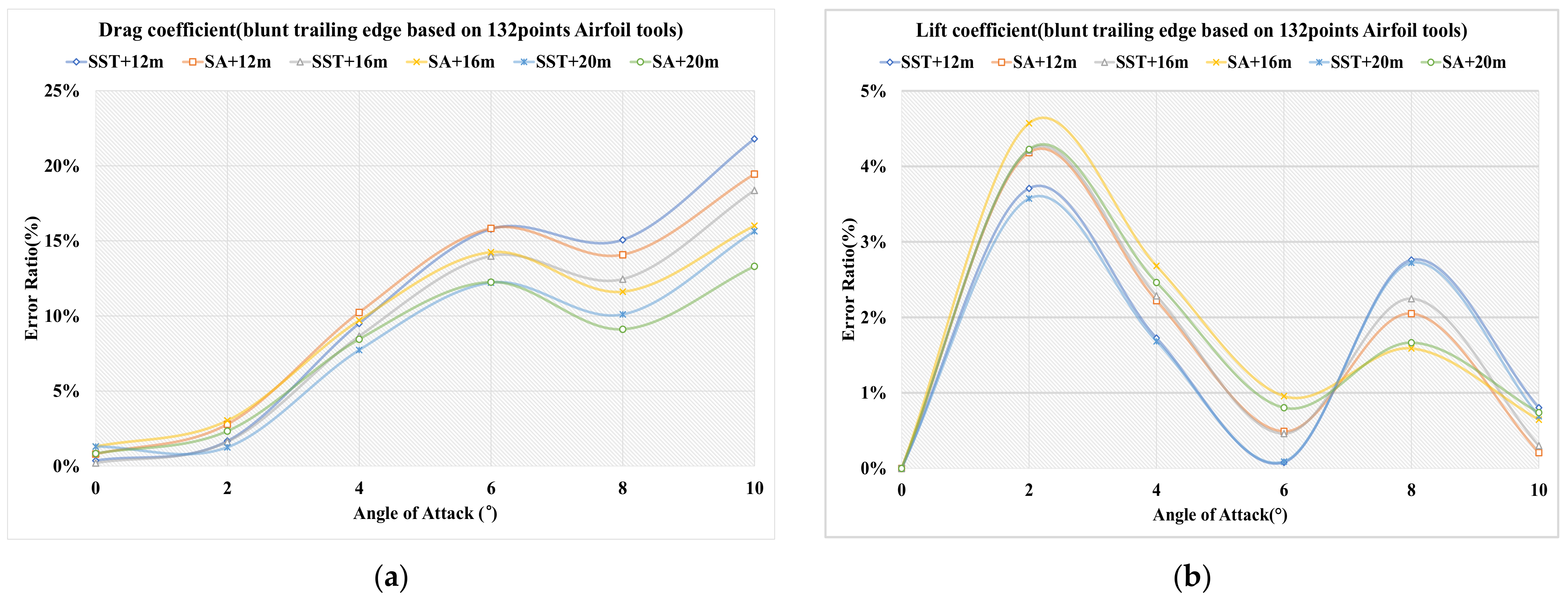
4.1.1. Blunt Trailing Edge
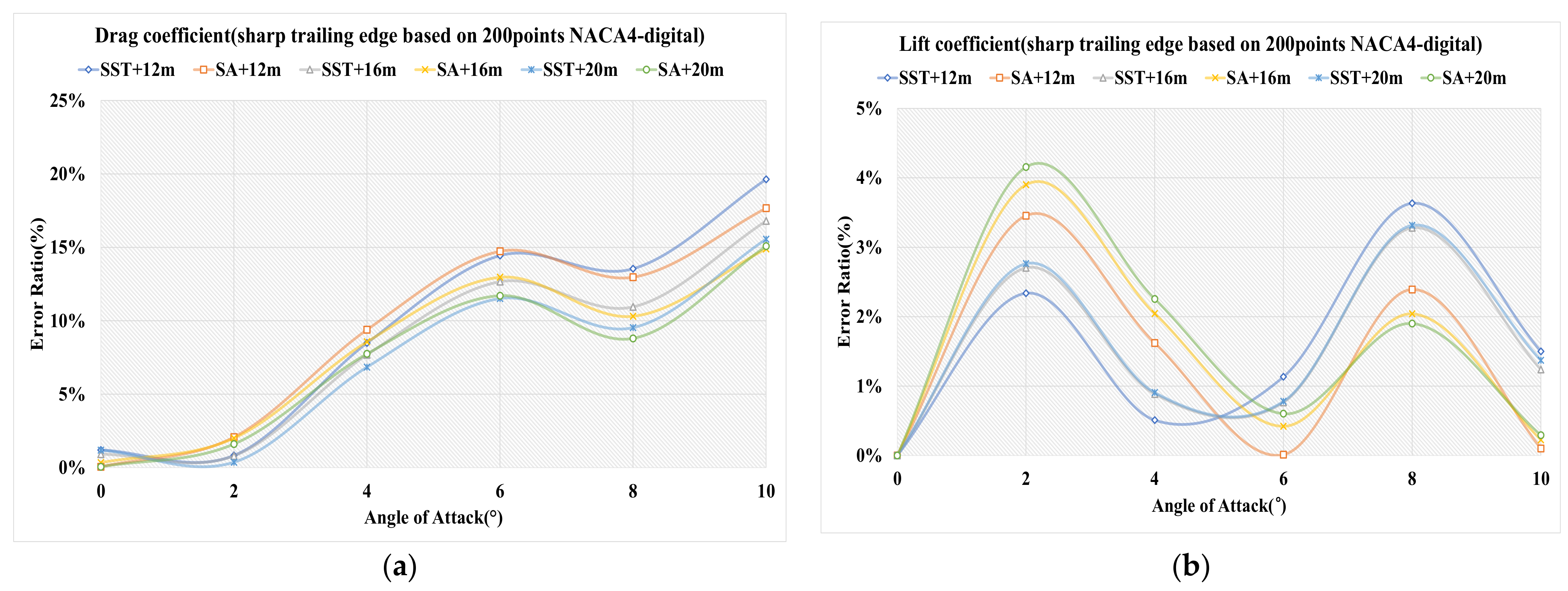
4.1.2. Sharp Trailing Edge Based on NACA4-Digital Generator
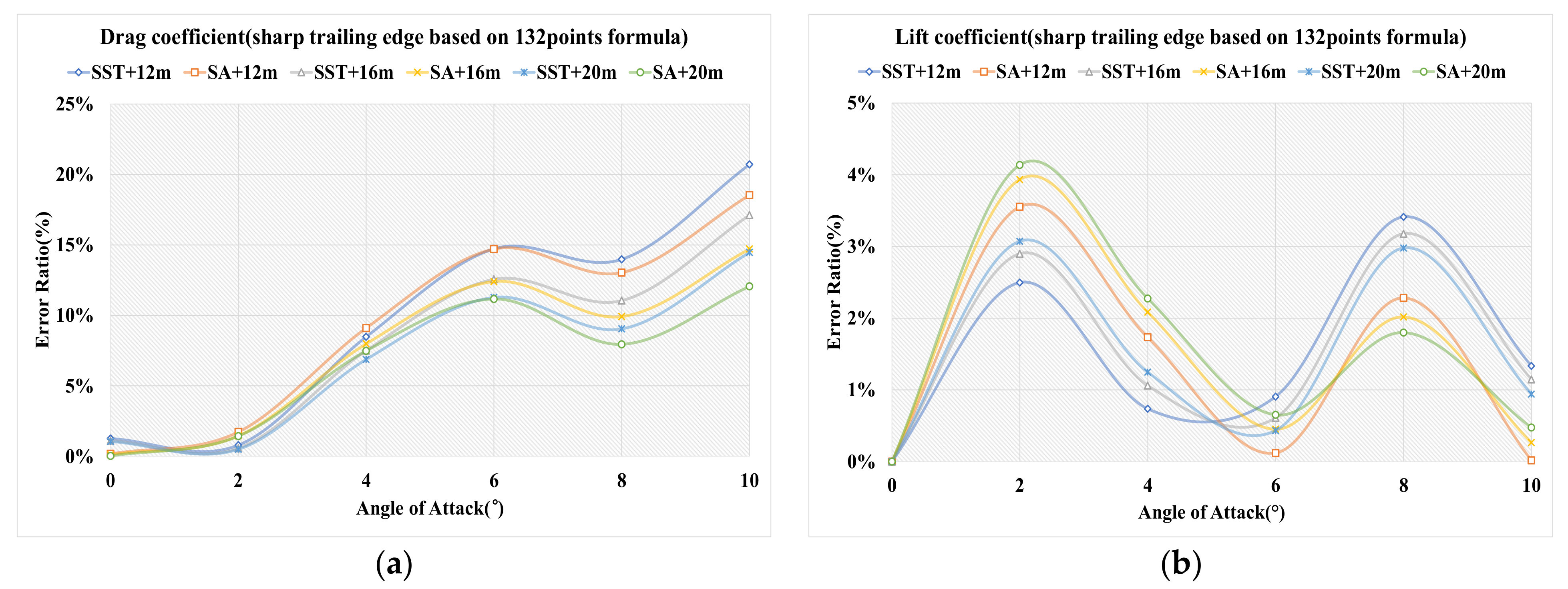
4.1.3. Sharp Trailing Edge Based on Definition Formula Applying 132 Points
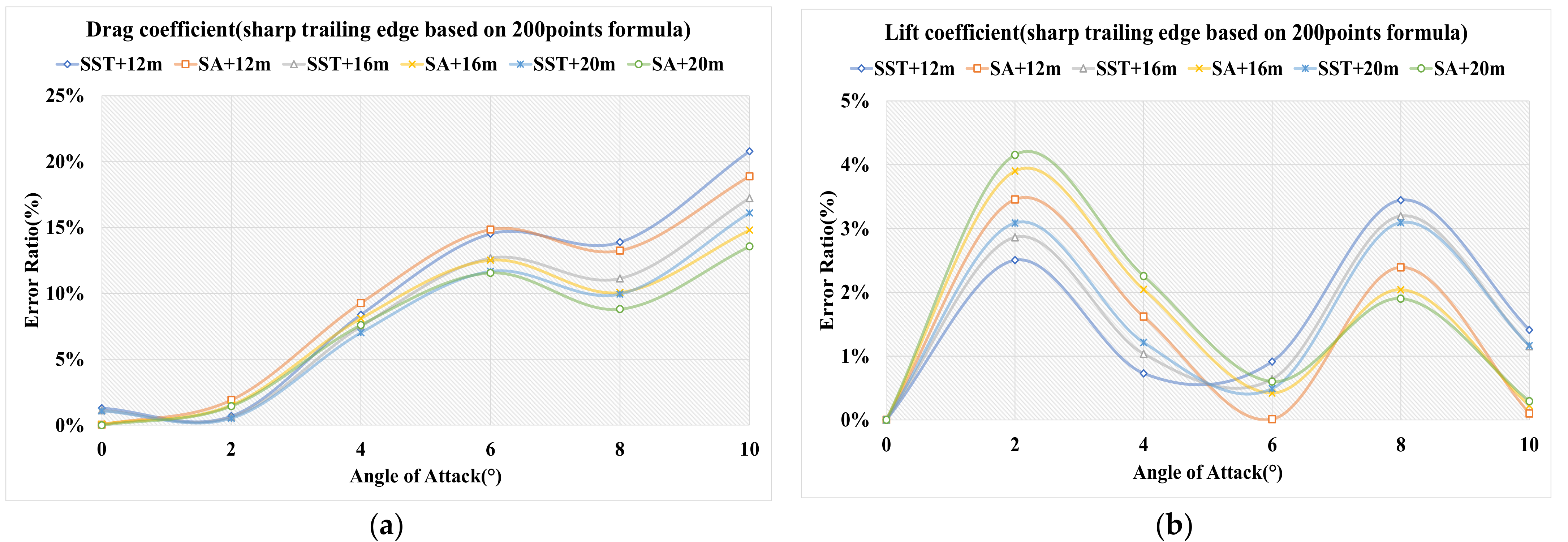
4.1.4. Sharp Trailing Edge Based on Definition Formula Applying 200 Points
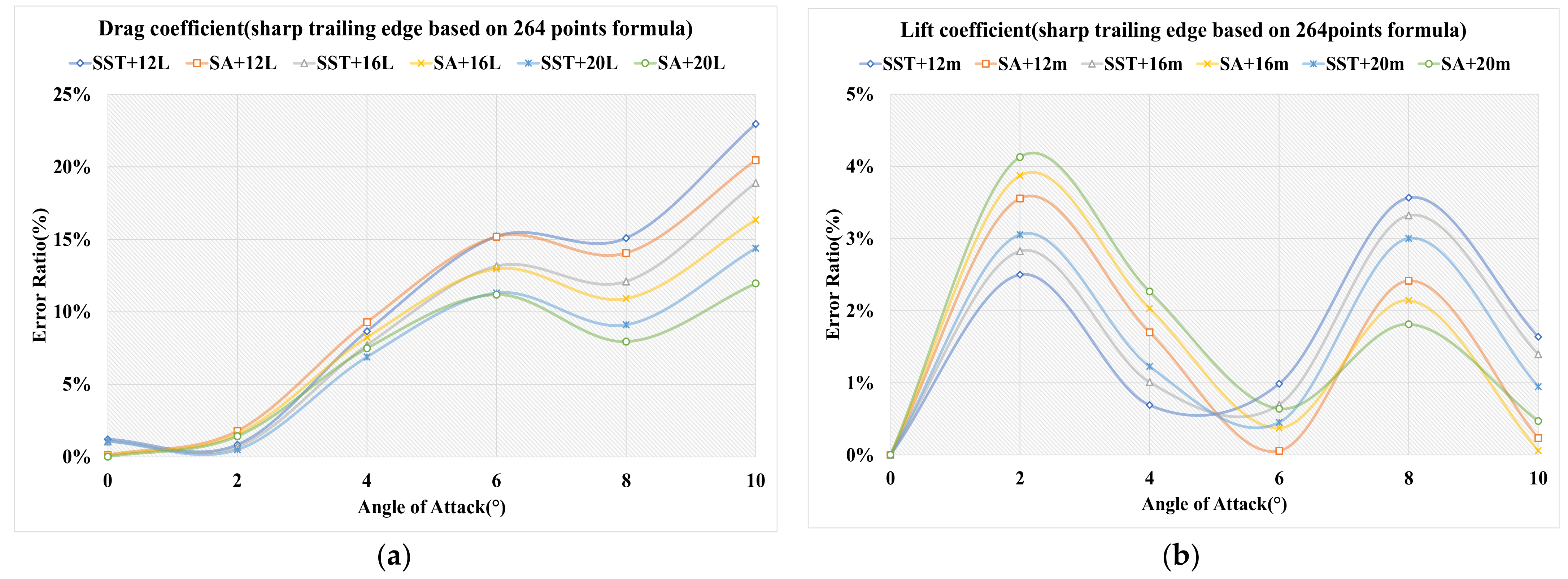
4.1.5. Sharp Trailing Edge Based on Definition Formula Applying 264 Points
4.1.6. Sharp Trailing Edge Based on Definition Formula Applying 400 Points
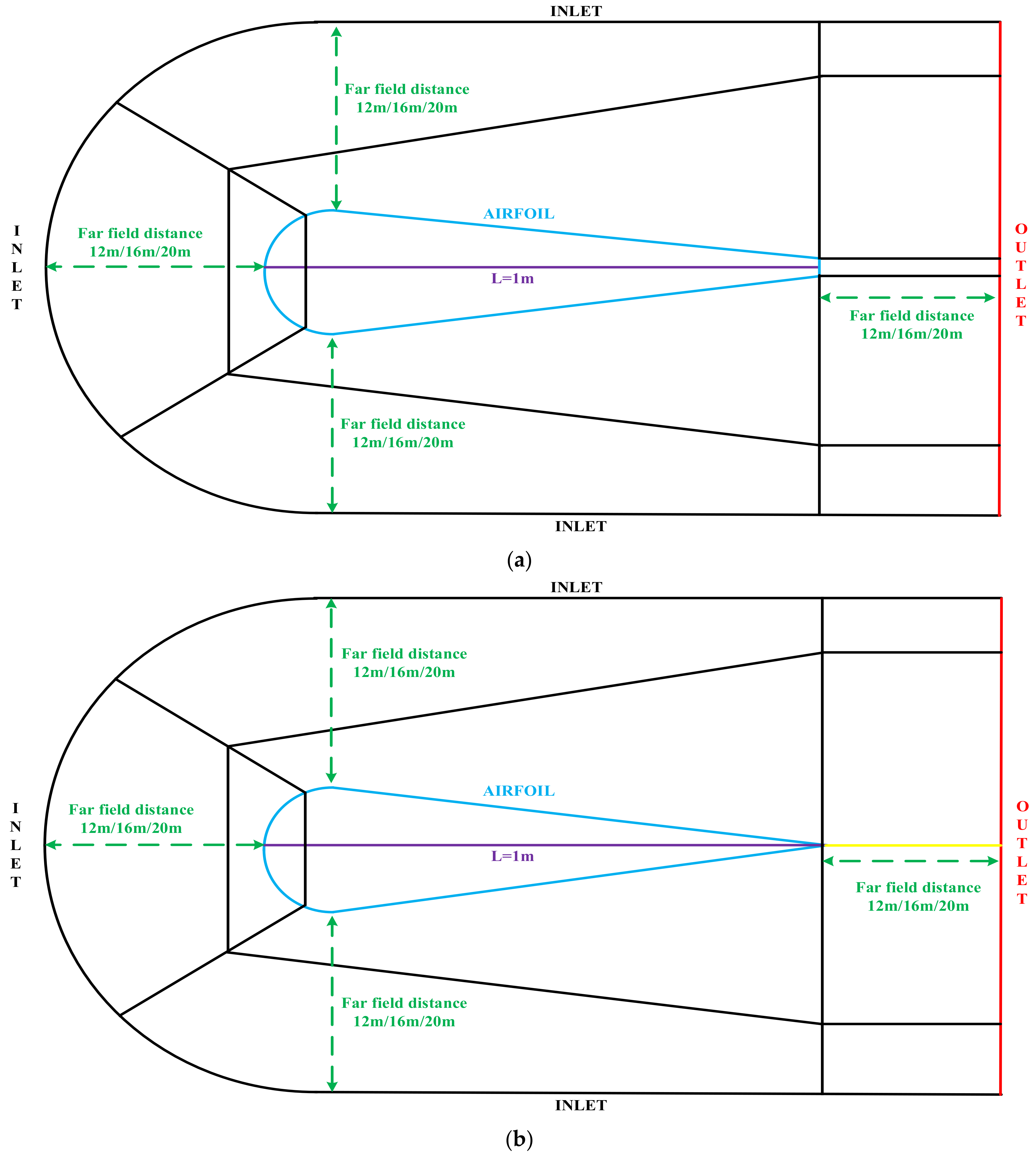
4.2. Results of Far-Field Distances
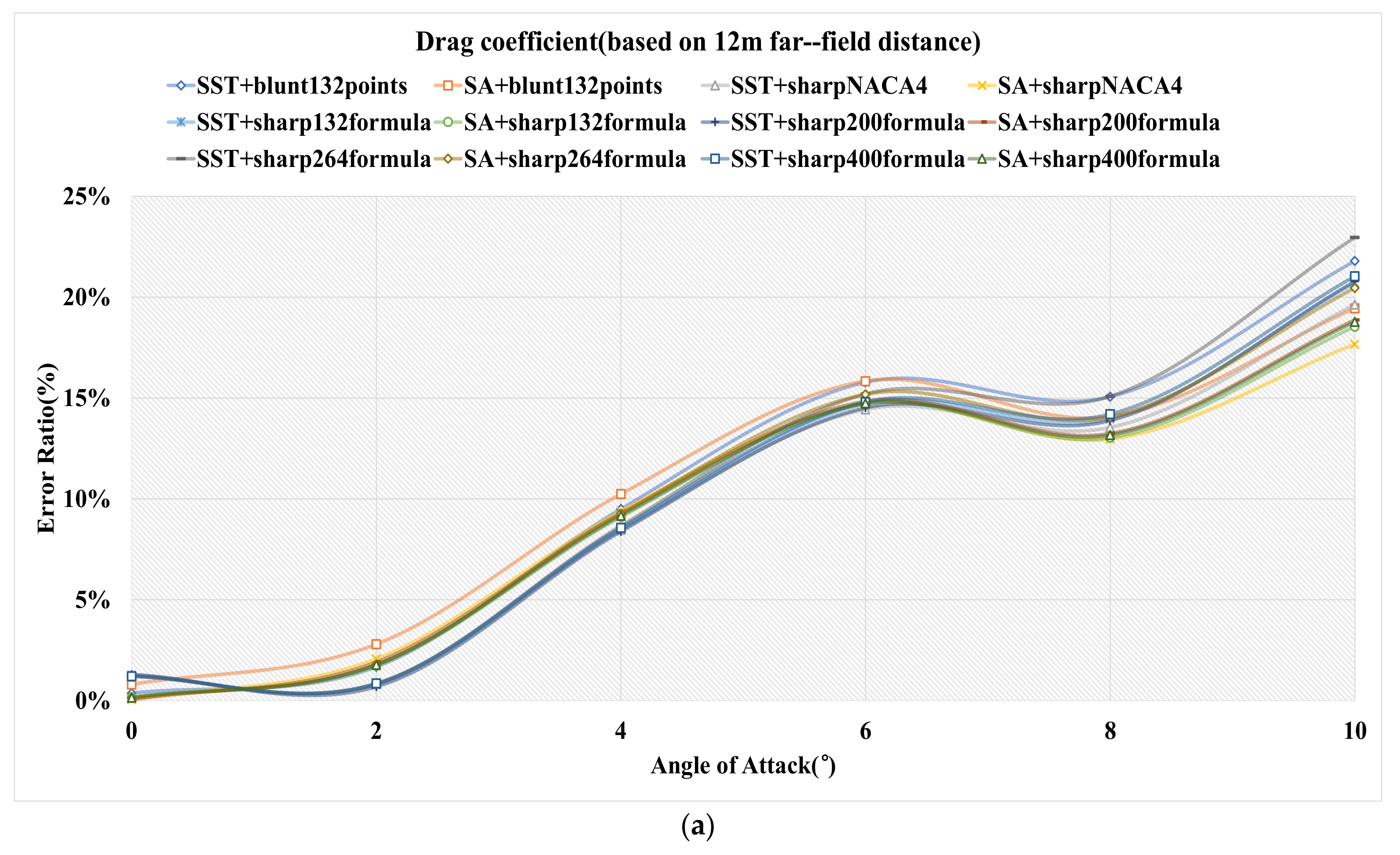
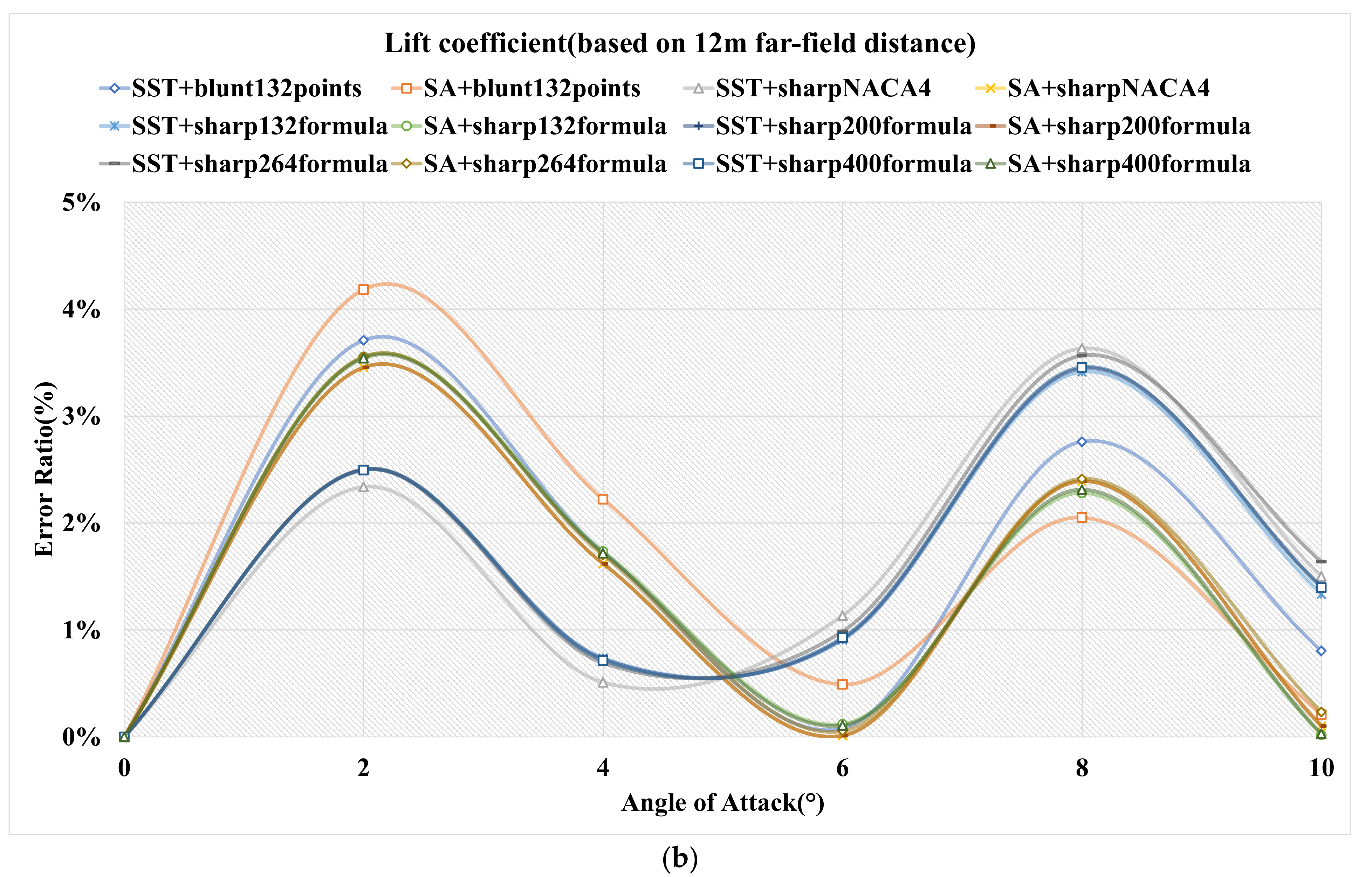
4.2.1. 12 m Far-Field Distance
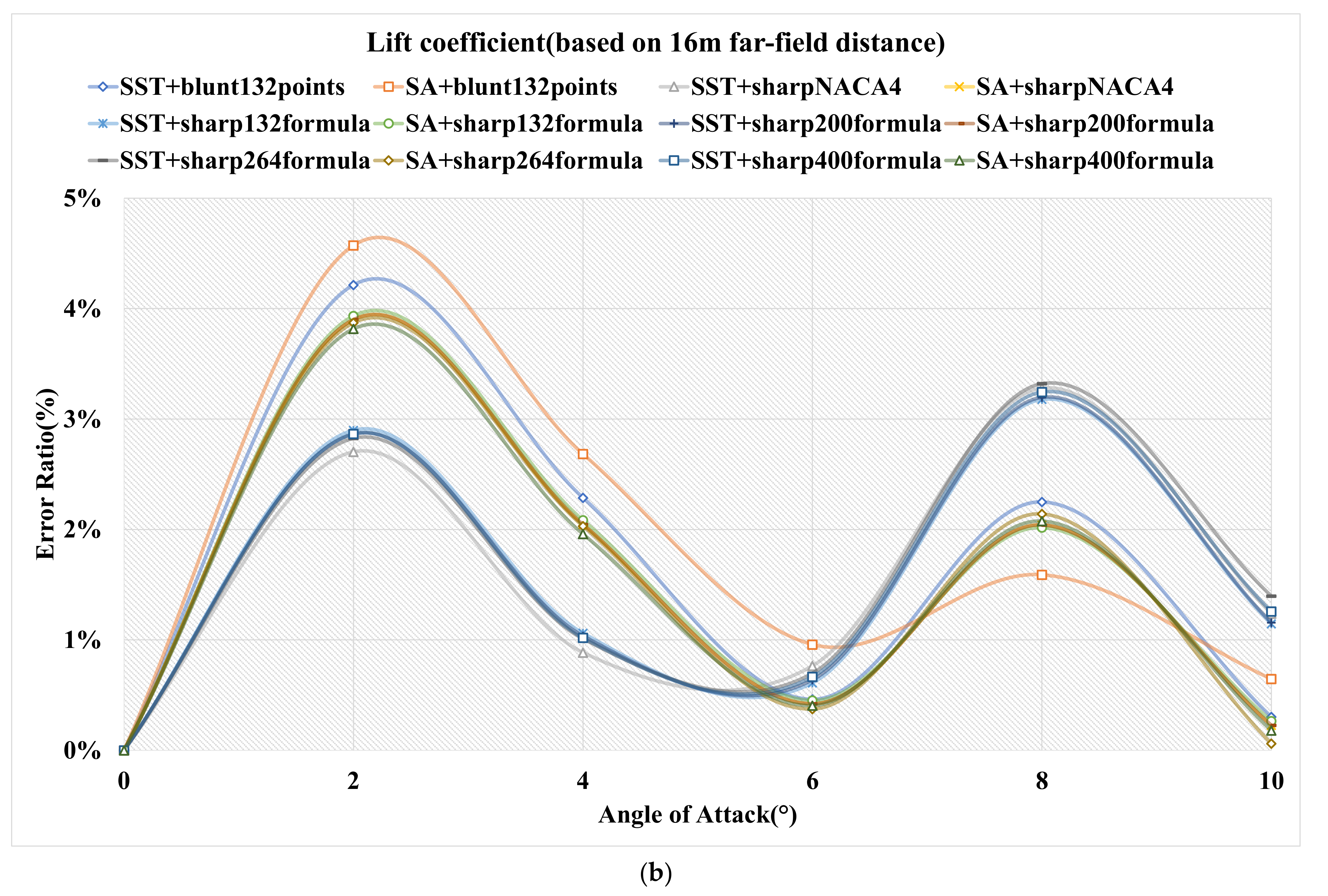
4.2.2. 16 m Far-Field Distance
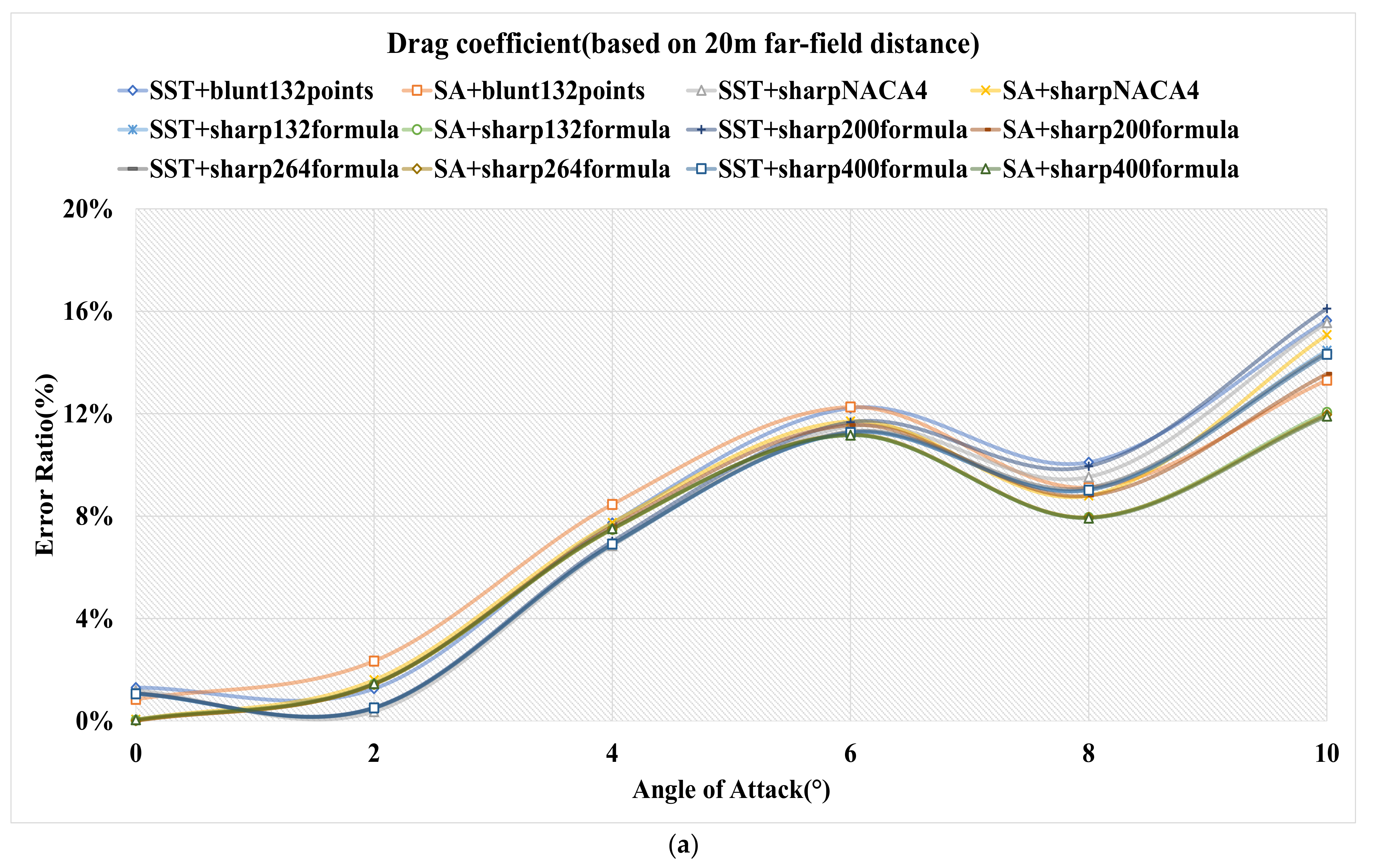
4.2.3. 20 m Far-Field Distance
4.3. Results of Turbulence Models
4.3.1. SST k-Omega
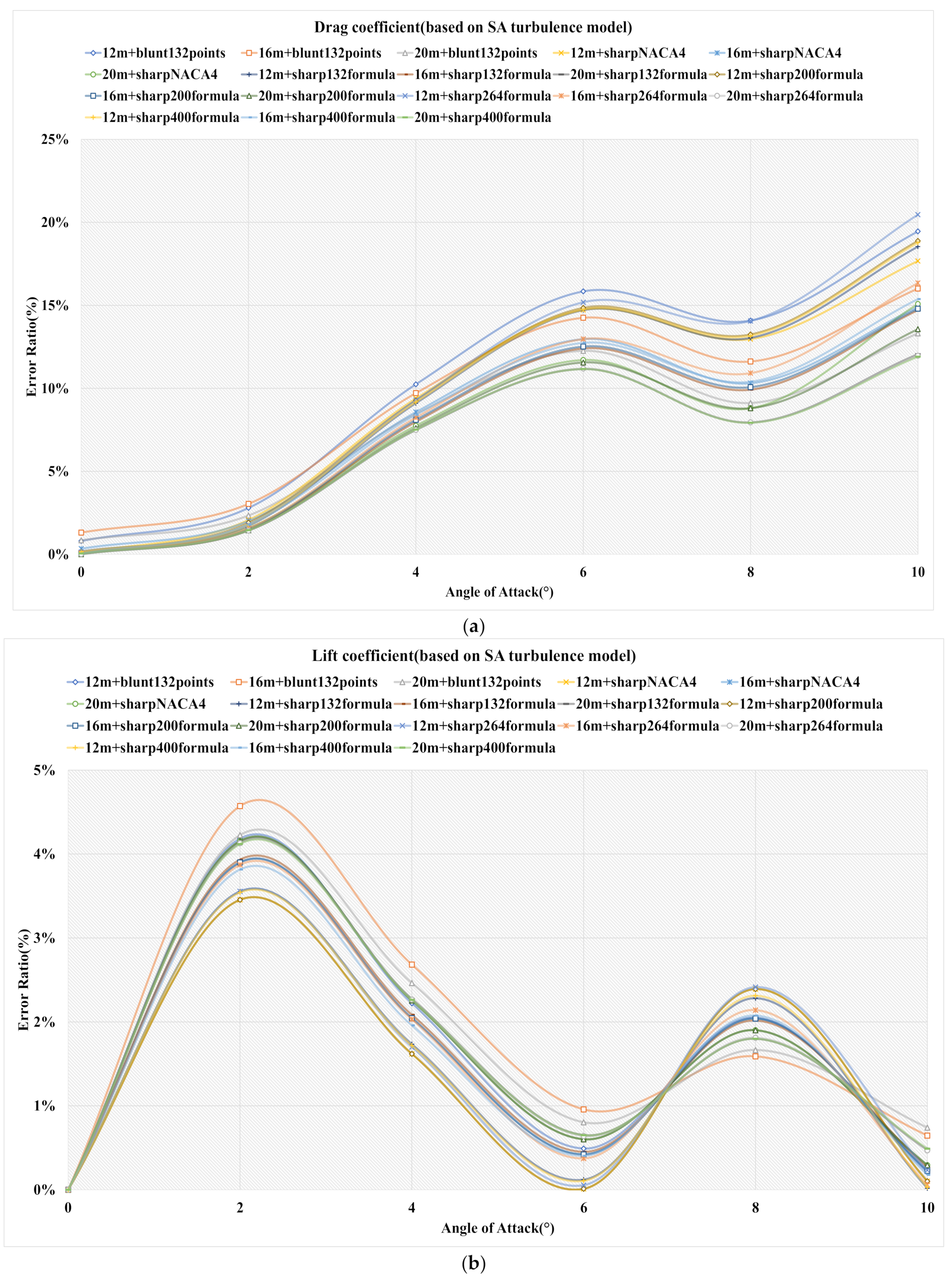
4.3.2. Spalart–Allmaras
4.4. Discussion
5. Conclusions
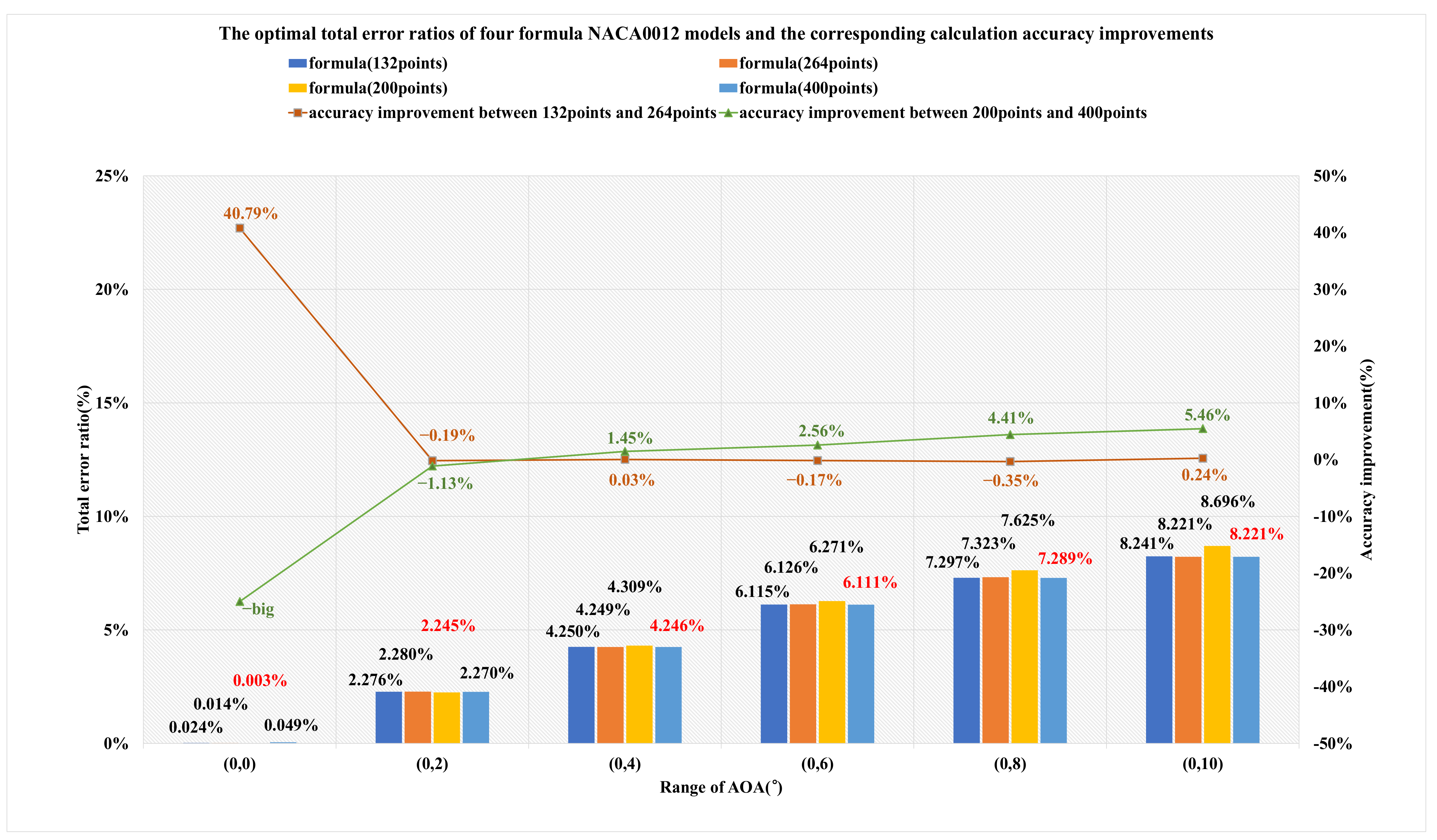
- nlike the choice of the trailing edge shape depending on the value of AOA under a lower Reynolds number, we should prioritize adopting the sharp trailing edge under a high Reynolds number. Therefore, the corresponding methods of NACA4 generator and the definition formula are suggested. The definition formula is preferred if the studied ranges are (0°, 0°), (0°, 8°), and (0°, 10°). If this is not the case, the NACA4 generator is preferred. It should be noted that a greater number of data points adopted into the definition formula does not neccesarily imply better performance. On the one hand, this may reqiore more computing resources. On the other hand, as described in Section 4.4, the improvement in calculation accuracy is limited, and accuracy may even be reduced.
- When plotting the computational domain of the airfoil external flow field, on the premise of sufficient computer resources, a far-field distance of 20 L is preferred. Although the increase of the far-field distance leads to the rise of the aspect ratio of the mesh quality, as long as it can be controlled within a reasonable range, which in this paper is smaller than 5000, the maximum far-field distance can bring the minimum simulation error ratio.
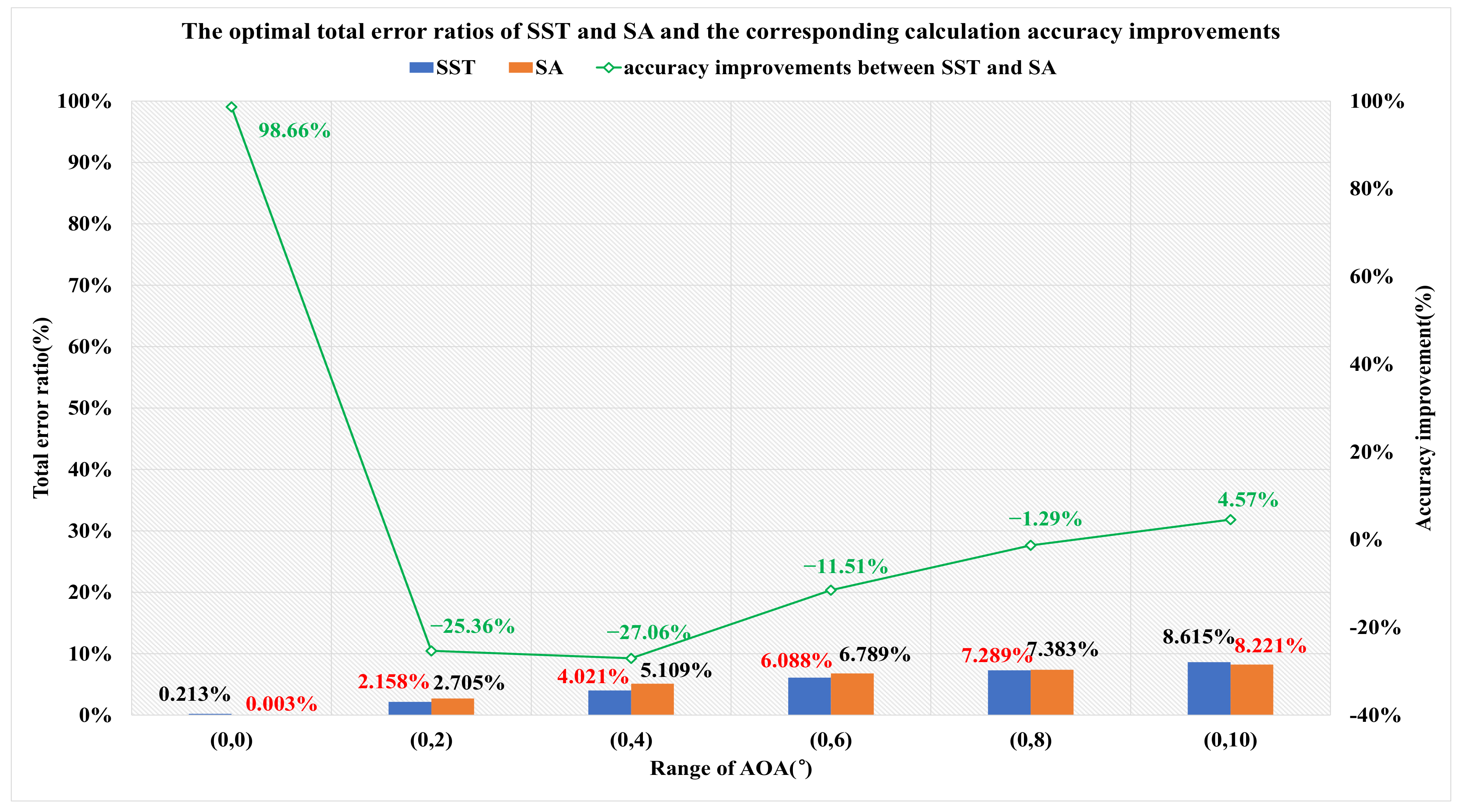
- The confirmation of the turbulence model depends on the AOA range with which one is concerned. The Spalart–Allmaras turbulence model performs better at AOA ranges of (0°, 0°) and (0°, 10°), while the SST k-omega performs better at AOA ranges of (0°, 2°), (0°, 4°), (0°, 6°), and (0°, 8°).
- In this paper, under the studied AOA ranges, the recommended simulation configurations are sharp trailing edge + 20 L far-field distance + SA/SST/SST/SST/SA, respectively, and the corresponding optimal results are (0.00%, 0.00%), (0.78%, 1.38%), (2.80%, 1.22%), (4.98%, 1.11%), (5.75%, 1.54%), and (6.67%, 1.55%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, F.; Liu, H.; Zhang, S. Time-adaptive loosely coupled analysis on fluid–thermal–structural behaviors of hypersonic wing structures under sustained aeroheating. Aerosp. Sci. Technol. 2018, 78, 620–636. [Google Scholar] [CrossRef]
- Qu, F.; Kong, W.; Sun, D.; Bai, J. Shock-stable flux scheme for predicting aerodynamic heating load of hypersonic airliners. Sci. China Ser. G: Phys. Mech. Astron. 2019, 62, 984711. [Google Scholar] [CrossRef]
- Lu, Y.; Guangming, Z. An Effective Simulation Scheme for Predicting the Aerodynamic Heat of a Scramjet-Propelled Vehicle. Appl. Sci. 2021, 11, 9344. [Google Scholar] [CrossRef]
- 2D NACA 0012 Airfoil Validation Case. Available online: https://turbmodels.larc.nasa.gov/naca0012_val.html (accessed on 16 April 2021).
- Qu, F.; Sun, D.; Bai, J.; Zuo, G.; Yan, C. Numerical investigation of blunt body’s heating load reduction with combination of spike and opposing jet. Int. J. Heat Mass Transf. 2018, 127, 7–15. [Google Scholar] [CrossRef]
- Qu, F.; Chen, J.; Sun, D.; Bai, J.; Yan, C. A new all-speed flux scheme for the Euler equations. Comput. Math. Appl. 2019, 77, 1216–1231. [Google Scholar] [CrossRef]
- Cook, C.; Balachandar, S.; Chung, J.; Vu-Quoc, L. A generalized Characteristic-Based Split projection method for Navier-Stokes with real fluids. Int. J. Heat Mass Transf. 2018, 124, 1045–1058. [Google Scholar] [CrossRef]
- Sadikin, A.; Yunus, N.A.M.; Abd Hamid, S.A.; Ismail, A.; Salleh, S.; Ahmad, S.; Rahman, M.N.A.; Mahzan, S.; Ayop, S.S. A comparative study of turbulence models on aerodynamics characteristics of a NACA0012 airfoil. Int. J. Integr. Eng. 2018, 10, 134–137. [Google Scholar] [CrossRef] [Green Version]
- Vassberg, J.C.; Jameson, A. In pursuit of grid convergence for two-dimensional Euler solutions. J. Aircr. 2010, 47, 1152–1166. [Google Scholar] [CrossRef] [Green Version]
- Diskin, B.; Thomas, J.L.; Rumsey, C.L.; Schwoppe, A. Grid-convergence of Reynolds-averaged Navier-stokes solutions for benchmark flows in two dimensions. AIAA J. 2016, 54, 2563–2588. [Google Scholar] [CrossRef]
- Lam, K.; Lin, Y.F.; Liu, Y.; Zou, L. Numerical Investigation of Flow Past a Wavy Airfoil. In Proceedings of the 2nd Interna-tional Conference on Mechanical and Aerospace Engineering (ICMAE 2011), Bangkok, Thailand, 29–31 July 2011; pp. 110–116. [Google Scholar]
- Lin, Y.F.; Lam, K.; Zou, L.; Liu, Y. Numerical study of flows past airfoils with wavy surfaces. J. Fluids Struct. 2013, 36, 136–148. [Google Scholar] [CrossRef]
- Matin, R.K.; Ghassemi, H.; Arzideh, M.H. Numerical study of the effect of geometrical changes on the aerodynamic performance. Int. J. Fluid Mech. Res. 2016, 43, 28–38. [Google Scholar] [CrossRef]
- Devi, P.B.; Paulson, V.; Madhanraj, V.; Shah, D.A. Heat transfer and temperature effects on a dimpled NACA0012 airfoil with various angles of attack. Int. J. Ambient. Energy 2018, 39, 783–786. [Google Scholar] [CrossRef]
- Li, Y.C.; Wang, J.J.; Zhang, P.F. Effects of Gurney flaps on a NACA0012 airfoil. Flow Turbul. Combust. 2002, 68, 27–39. [Google Scholar] [CrossRef]
- Chao, D.D.; van Dam, C.P. Computational aerodynamic analysis of a blunt trailing-edge airfoil modification to the NREL phase VI rotor. Wind. Energy 2007, 10, 529–550. [Google Scholar] [CrossRef]
- Grebert, A.; Bodart, J.; Joly, L. Investigation of wall-pressure fluctuations characteristics on a naca0012 airfoil with blunt trailing edge. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Prigent, S.L.; Buxton, O.R.H.; Bruce, P.J.K. Wake of a lifting wing with cut-in sinusoidal trailing edges. AIAA J. 2017, 55, 1590–1601. [Google Scholar] [CrossRef]
- Juntao, Z.; Zhongxi, H.; Zheng, G. Aerodynamic performance of configurations of two-dimension inflatable wings under high Reynolds number. J. Aerosp. Power 2017, 32, 657–665. (In Chinese) [Google Scholar]
- Jha, S.K.; Gautam, U.; Pawar, P.; Narayanan, S. Investigations of Flow Phenomena Over a Flat Plate and NACA0012 Airfoil at High Angles of Attack. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 985–996. [Google Scholar] [CrossRef]
- Arini, N.R.; Turnock, S.R.; Tan, M. A study of modified vertical axis tidal turbine to improve lift performance. Int. J. Electr. Energy 2016, 4, 37–41. [Google Scholar] [CrossRef] [Green Version]
- Perrin, R.; Rattanasiri, P.; Lamballais, E.; Yooyen, S. Influence of the trailing edge shape on the aerodynamic characteristics of an airfoil at low Re number using RANS. IOP Conf. Ser. Mater. Sci. Eng. 2020, 886, 012021. [Google Scholar] [CrossRef]
- Thomareis, N.; Papadakis, G. Effect of trailing edge shape on the separated flow characteristics around an airfoil at low Reynolds number: A numerical study. Phys. Fluids 2017, 29, 014101. [Google Scholar] [CrossRef] [Green Version]
- Ansys, Inc. Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA; p. 15317.
- Smirnov, N.N.; Penyazkov, O.G.; Sevrouk, K.L.; Nikitin, V.F.; Stamov, L.I.; Tyurenkova, V.V. Tyurenkova, Detonation onset following shock wave focusing. Acta Astronaut. 2017, 135, 114–130. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical Solution of the Euler Equations by Finite Volume Methods Using Runge-Kutta Time-Stepping Schemes. Technical Report AIAA-81-1259. In Proceedings of the AIAA 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA, 23–25 June 1981. [Google Scholar]
- Abbott, I.H.; von Doenhoff, A.E. Theory of Wing Sections; Dover Publications: New York, NY, USA, 1959. [Google Scholar]
- Gregory, N.; O’Reilly, C.L. Low-Speed Aerodynamic Characteristics of NACA 0012 Aerofoil Sections, including the Effects of Upper-Surface Roughness Simulation Hoar Frost. Aerodynamic Division, N.P.L. Reports and Memoranda No. 3726 January, 1970. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.227.696&rep=rep1&type=pdf (accessed on 1 December 2021).
- Ladson, C.L. Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section. NASA TM: Washington, DC, USA, 1988; p. 4074. [Google Scholar]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745. [Google Scholar] [CrossRef]
- Barth, T.J.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the AIAA 27th Aerospace Sciences Meeting, Reno, Nevada, 9–12 January 1989. Technical Report AIAA-89-0366. [Google Scholar]








| Mesh (Cells) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 2° | 4° | 6° | 8° | 10° | |||||||
| 0.00809 | 0 | 0.00816 | 0.2125 | 0.00823 | 0.4316 | 0.00885 | 0.6546 | 0.0105 | 0.8873 | 0.01201 | 1.0707 | |
| 400,000 | 0.00791 | Approx. 0 | 0.00836 | 0.21990 | 0.00911 | 0.43983 | 0.01044 | 0.64020 | 0.01243 | 0.84399 | 0.01529 | 1.03809 |
| 2.28% | / | 2.42% | 3.48% | 10.63% | 1.91% | 17.95% | 2.20% | 18.37% | 4.88% | 27.29% | 3.05% | |
| 590,000 | 0.00799 | Approx. 0 | 0.00823 | 0.21747 | 0.00893 | 0.43380 | 0.01013 | 0.64718 | 0.01192 | 0.85506 | 0.01437 | 1.05464 |
| 1.19% | / | 0.82% | 2.34% | 8.48% | 0.51% | 14.44% | 1.13% | 13.54% | 3.63% | 19.36% | 1.50% | |
| 840,000 | 0.00801 | Approx. 0 | 0.00831 | 0.21750 | 0.00904 | 0.43375 | 0.01034 | 0.64685 | 0.01231 | 0.85387 | 0.01515 | 1.04991 |
| 0.29% | / | 1.80% | 2.35% | 9.83% | 0.50% | 16.78% | 1.18% | 17.20% | 1.50% | 26.11% | 1.94% | |
| Mesh (Cells) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 2° | 4° | 6° | 8° | 10° | |||||||
| 0.00809 | 0 | 0.00816 | 0.2125 | 0.00823 | 0.4316 | 0.00885 | 0.6546 | 0.0105 | 0.8873 | 0.01201 | 1.0707 | |
| 400,000 | 0.00792 | Approx. 0 | 0.00799 | 0.22065 | 0.00895 | 0.43996 | 0.01009 | 0.64220 | 0.01191 | 0.84574 | 0.01448 | 1.04173 |
| 2.16% | / | 1.99% | 3.83% | 8.80% | 1.94% | 14.01% | 1.89% | 13.38% | 4.68% | 20.52% | 2.71% | |
| 590,000 | 0.00802 | Approx. 0 | 0.00822 | 0.21824 | 0.00886 | 0.43542 | 0.00997 | 0.64960 | 0.01165 | 0.85820 | 0.01403 | 1.05745 |
| 0.91% | / | 0.79% | 2.70% | 7.68% | 0.89% | 12.66% | 0.76% | 10.95% | 3.28% | 16.80% | 1.24% | |
| 840,000 | 0.00801 | Approx. 0 | 0.00823 | 0.21810 | 0.00887 | 0.43504 | 0.01003 | 0.64861 | 0.01180 | 0.85591 | 0.01436 | 1.05249 |
| 0.96% | / | 0.82% | 2.64% | 7.81% | 0.80% | 13.29% | 0.91% | 12.40% | 3.54% | 19.60% | 1.70% | |
| Far-Field Distance | Type of Upwind Order | ||||||
|---|---|---|---|---|---|---|---|
| 0° | 2° | 4° | |||||
| 0.00809 | 0 | 0.00816 | 0.2125 | 0.00823 | 0.4316 | ||
| 12 m | First-order | 0.00809427 | Approx. 0 | 0.00832899 | 0.21984088 | 0.00900243 | 0.43858932 |
| 0.05% | / | 2.07% | 3.45% | 9.39% | 1.62% | ||
| Second-order | 0.00810023 | Approx. 0 | 0.00833216 | 0.21977944 | 0.00900414 | 0.43871334 | |
| 0.13% | / | 2.11% | 3.43% | 9.41% | 1.65% | ||
| 16 m | First-order | 0.00811742 | Approx. 0 | 0.00832344 | 0.22078817 | 0.00893481 | 0.44042730 |
| 0.34% | / | 2.00% | 3.90% | 8.56% | 2.05% | ||
| Second-order | 0.0081189 | Approx. 0 | 0.008322422 | 0.22087445 | 0.00892964 | 0.44054850 | |
| 0.36% | / | 2.01% | 3.94% | 8.50% | 2.07% | ||
| Validation Parameters | ||
|---|---|---|
| Solver | Pressure-based with coupled algorithm | Pressure-based with coupled algorithm |
| Turbulence Models | SST k-omega | Spalart–Allmaras |
| Materials | Density (kg/m3): 1.225 Viscosity (Pa × s): 1.0474 × 10−5 | Density (kg/m3): 1.225 Viscosity (Pa × s): 1.0474 × 10−5 |
| Initial conditions | Mach number: 0.15 | Mach number: 0.15 |
| Static temperature: 300 K | Static temperature: 300 K | |
| Boundary conditions | INLET: velocity-inlet | INLET: velocity-inlet |
| OUTLET: pressure outlet | OUTLET: pressure outlet | |
| AIRFOIL: no-slip, adiabatic | AIRFOIL: no-slip, adiabatic | |
| Spatial discretization | Gradient: least-squares cell-based | Gradient: least-squares cell-based |
| Pressure: second-order | Pressure: second-order | |
| Momentum: second-order upwind | Momentum: second-order upwind | |
| Turbulent kinetic energy: second-order upwind | Modified turbulent viscosity: first-order upwind | |
| Specific dissipation rate: second-order upwind |
| Type of NACA0012 Model | Angle of Attack (°) and Experiment data of and (Numerical Data of and with Error Ratios) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 m (SST k-omega) | 16 m (SST k-omega) | ||||||||||||
| 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | ||
| 0 | 0.2125 | 0.4316 | 0 | 0.2125 | 0.4316 | ||||||||
| Blunt trailing edge (Airfoil Tools 132 points) | 0.00806 | 0.37% | 0.00830 | 1.67% | 0.00901 | 9.50% | 0.00807 | 0.21% | 0.00829 | 1.62% | 0.00894 | 8.66% | |
| Approx. 0 | 0.00% | 0.2204 | 3.71% | 0.4391 | 1.73% | Approx. 0 | 0.00% | 0.2215 | 4.21% | 0.4415 | 2.29% | ||
| Sharp trailing edge (NACA4 200 points) | 0.00799 | 1.19% | 0.00823 | 0.82% | 0.00893 | 8.48% | 0.00802 | 0.91% | 0.00822 | 0.79% | 0.01437 | 19.63% | |
| Approx. 0 | 0.00% | 0.2175 | 2.34% | 0.4338 | 0.51% | Approx. 0 | 0.00% | 0.2182 | 2.70% | 1.0546 | 1.50% | ||
| Sharp trailing edge (Formula adopts 132 points) | 0.00799 | 1.26% | 0.00822 | 0.79% | 0.00893 | 8.48% | 0.00800 | 1.11% | 0.00821 | 0.57% | 0.01450 | 20.71% | |
| Approx. 0 | 0.00% | 0.2178 | 2.50% | 0.4348 | 0.74% | Approx. 0 | 0.00% | 0.2187 | 2.90% | 1.0564 | 1.33% | ||
| Sharp trailing edge (Formula adopts 200 points) | 0.00799 | 1.30% | 0.00822 | 0.69% | 0.00892 | 8.38% | 0.00800 | 1.12% | 0.00821 | 0.61% | 0.01451 | 20.78% | |
| Approx. 0 | 0.00% | 0.2178 | 2.50% | 0.4347 | 0.73% | Approx. 0 | 0.00% | 0.2186 | 2.86% | 1.0556 | 1.41% | ||
| Sharp trailing edge (Formula adopts 264 points) | 0.00799 | 1.21% | 0.00823 | 0.84% | 0.00894 | 8.66% | 0.00800 | 1.06% | 0.00822 | 0.70% | 0.01477 | 22.96% | |
| Approx. 0 | 0.00% | 0.2178 | 2.50% | 0.4346 | 0.69% | Approx. 0 | 0.00% | 0.2185 | 2.83% | 1.0532 | 1.64% | ||
| Sharp trailing edge (Formula adopts 400 points) | 0.00799 | 1.21% | 0.00823 | 0.85% | 0.00894 | 8.57% | 0.00801 | 1.04% | 0.00821 | 0.64% | 0.01454 | 21.04% | |
| Approx. 0 | 0.00% | 0.2178 | 2.50% | 0.4347 | 0.72% | Approx. 0 | 0.00% | 0.2186 | 2.86% | 1.0558 | 1.40% | ||
| Type of NACA0012 Model | Angle of Attack (°) and Experiment Data of and (Numerical Data of and with Error Ratios) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 m (SST k-omega) | 12 m (Spalart–Allmaras) | ||||||||||||
| 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | ||
| 0 | 0.2125 | 0.4316 | 0 | 0.2125 | 0.4316 | ||||||||
| Blunt trailing edge (Airfoil Tools 132 points) | 0.00820 | 1.30% | 0.00826 | 1.26% | 0.00887 | 7.73% | 0.00816 | 0.80% | 0.00839 | 2.79% | 0.00907 | 10.24% | |
| Approx. 0 | 0.00% | 0.2201 | 3.57% | 0.4389 | 1.68% | Approx. 0 | 0.00% | 0.2214 | 4.18% | 0.4412 | 2.22% | ||
| Sharp trailing edge (NACA4 200 points) | 0.00799 | 1.19% | 0.00819 | 0.36% | 0.00879 | 6.84% | 0.00809 | 0.05% | 0.00833 | 2.07% | 0.01388 | 15.56% | |
| Approx. 0 | 0.00% | 0.2184 | 2.76% | 0.4355 | 0.91% | Approx. 0 | 0.00% | 0.2198 | 3.45% | 1.0560 | 1.37% | ||
| Sharp trailing edge (Formula adopts 132 points) | 0.00800 | 1.05% | 0.00820 | 0.50% | 0.00880 | 6.88% | 0.00808 | 0.18% | 0.00830 | 1.73% | 0.01375 | 14.47% | |
| Approx. 0 | 0.00% | 0.2190 | 3.07% | 0.4370 | 1.25% | Approx. 0 | 0.00% | 0.2201 | 3.55% | 1.0606 | 0.94% | ||
| Sharp trailing edge (Formula adopts 200 points) | 0.00800 | 1.08% | 0.00820 | 0.53% | 0.00881 | 7.02% | 0.00809 | 0.04% | 0.00832 | 1.91% | 0.01394 | 16.11% | |
| Approx. 0 | 0.00% | 0.2191 | 3.09% | 0.4368 | 1.21% | Approx. 0 | 0.00% | 0.2198 | 3.45% | 1.0583 | 1.16% | ||
| Sharp trailing edge (Formula adopts 264 points) | 0.00800 | 1.07% | 0.00820 | 0.50% | 0.00880 | 6.89% | 0.00808 | 0.13% | 0.00831 | 1.79% | 0.01374 | 14.39% | |
| Approx. 0 | 0.00% | 0.2190 | 3.05% | 0.4369 | 1.23% | Approx. 0 | 0.00% | 0.2201 | 3.56% | 1.0606 | 0.95% | ||
| Sharp trailing edge (Formula adopts 400 points) | 0.00800 | 1.06% | 0.00820 | 0.51% | 0.00880 | 6.91% | 0.00808 | 0.15% | 0.00830 | 1.77% | 0.01373 | 14.32% | |
| Approx. 0 | 0.00% | 0.2190 | 3.04% | 0.4369 | 1.22% | Approx. 0 | 0.00% | 0.2200 | 3.54% | 1.0608 | 0.92% | ||
| Type of NACA0012 Model | Angle of Attack (°) and Experiment Data of
and
(Numerical Data of and with Error Ratios) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 m (Spalart–Allmaras) | 20 m (Spalart–Allmaras) | ||||||||||||
| 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | 0° | 0.00809 | 2° | 0.00816 | 4° | 0.00823 | ||
| 0 | 0.2125 | 0.4316 | 0 | 0.2125 | 0.4316 | ||||||||
| Blunt trailing edge (Airfoil Tools 132 points) | 0.00820 | 1.31% | 0.00841 | 3.04% | 0.00903 | 9.71% | 0.00816 | 0.84% | 0.00835 | 2.34% | 0.00893 | 8.46% | |
| Approx. 0 | 0.00% | 0.2222 | 4.57% | 0.4432 | 2.68% | Approx. 0 | 0.00% | 0.2215 | 4.23% | 0.4422 | 2.46% | ||
| Sharp trailing edge (NACA4 200 points) | 0.00812 | 0.34% | 0.00832 | 2.00% | 0.00893 | 8.56% | 0.00809 | 0.06% | 0.00829 | 1.60% | 0.01380 | 14.90% | |
| Approx. 0 | 0.00% | 0.2208 | 3.90% | 0.4404 | 2.05% | Approx. 0 | 0.00% | 0.2213 | 4.15% | 1.0731 | 0.23% | ||
| Sharp trailing edge (Formula adopts 132 points) | 0.00808 | 0.11% | 0.00828 | 1.45% | 0.00889 | 7.98% | 0.00809 | 0.02% | 0.00828 | 1.43% | 0.01378 | 14.71% | |
| Approx. 0 | 0.00% | 0.2209 | 3.93% | 0.4406 | 2.08% | Approx. 0 | 0.00% | 0.2213 | 4.14% | 1.0735 | 0.27% | ||
| Sharp trailing edge (Formula adopts 200 points) | 0.00808 | 0.08% | 0.00828 | 1.52% | 0.00890 | 8.10% | 0.00809 | 0.00% | 0.00828 | 1.45% | 0.01379 | 14.79% | |
| Approx. 0 | 0.00% | 0.2208 | 3.90% | 0.4404 | 2.05% | Approx. 0 | 0.00% | 0.2213 | 4.15% | 1.0731 | 0.23% | ||
| Sharp trailing edge (Formula adopts 264 points) | 0.00808 | 0.09% | 0.00829 | 1.57% | 0.00891 | 8.24% | 0.00809 | 0.01% | 0.00828 | 1.43% | 0.01397 | 16.34% | |
| Approx. 0 | 0.00% | 0.2207 | 3.87% | 0.4404 | 2.03% | Approx. 0 | 0.00% | 0.2213 | 4.13% | 1.0713 | 0.06% | ||
| Sharp trailing edge (Formula adopts 400 points) | 0.00809 | 0.05% | 0.00831 | 1.79% | 0.00892 | 8.41% | 0.00809 | 0.05% | 0.00828 | 1.46% | 0.01386 | 15.38% | |
| Approx. 0 | 0.00% | 0.2206 | 3.82% | 0.4401 | 1.96% | Approx. 0 | 0.00% | 0.2213 | 4.12% | 1.0726 | 0.18% | ||
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (0.37%, 0.00%) | (1.02%, 1.85%) | (3.85%, 1.81%) | (6.83%, 1.38%) | (8.48%, 1.66%) | (10.70%, 1.51%) |
| SST+16 m | (0.21%, 0.00%) | (0.92%, 2.11%) | (3.50%, 2.17%) | (6.12%, 1.74%) | (7.39%, 1.84%) | (9.22%, 1.59%) |
| SST+20 m | (1.30%, 0.00%) | (1.28%, 1.79%) | (3.43%, 1.75%) | (5.63%, 1.34%) | (6.52%, 1.61%) | (8.04%, 1.46%) |
| SA+12 m | (0.80%, 0.00%) | (1.80%, 2.09%) | (4.61%, 2.14%) | (7.42%, 1.72%) | (8.75%, 1.79%) | (10.54%, 1.53%) |
| SA+16 m | (1.31%, 0.00%) | (2.17%, 2.29%) | (4.69%, 2.42%) | (7.08%, 2.05%) | (7.98%, 1.96%) | (9.32%, 1.74%) |
| SA+20 m | (0.84%, 0.00%) | (1.59%, 2.11%) | (3.88%, 2.23%) | (5.97%, 1.87%) | (6.60%, 1.83%) | (7.72%, 1.65%) |
| Simulation Configurations | Range of AOA (°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (1.19%, 0.00%) | (1.01%, 1.17%) | (3.50%, 0.95%) | (6.23%, 1.00%) | (7.69%, 1.52%) | (9.68%, 1.52%) |
| SST+16 m | (0.91%, 0.00%) | (0.85%, 1.35%) | (3.13%, 1.20%) | (5.51%, 1.09%) | (6.60%, 1.53%) | (8.30%, 1.48%) |
| SST+20 m | (1.19%, 0.00%) | (0.78%, 1.38%) | (2.80%, 1.22%) | (4.98%, 1.11%) | (5.89%, 1.55%) | (7.50%, 1.52%) |
| SA+12 m | (0.05%, 0.00%) | (1.06%, 1.73%) | (3.84%, 1.69%) | (6.56%, 1.27%) | (7.84%, 1.50%) | (9.48%, 1.26%) |
| SA+16 m | (0.34%, 0.00%) | (1.17%, 1.95%) | (3.64%, 1.98%) | (5.97%, 1.59%) | (6.84%, 1.68%) | (8.18%, 1.44%) |
| SA+20 m | (0.06%, 0.00%) | (0.83%, 2.08%) | (3.13%, 2.14%) | (5.28%, 1.75%) | (5.98%, 1.78%) | (7.50%, 1.53%) |
| Simulation Configurations | Range of AOA (°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (1.26%, 0.00%) | (1.03%, 1.25%) | (3.51%, 1.08%) | (6.31%, 1.04%) | (7.85%, 1.51%) | (9.99%, 1.48%) |
| SST+16 m | (1.11%, 0.00%) | (0.84%, 1.45%) | (3.06%, 1.32%) | (5.43%, 1.14%) | (6.56%, 1.55%) | (8.32%, 1.48%) |
| SST+20 m | (1.05%, 0.00%) | (0.78%, 1.54%) | (2.81%, 1.44%) | (4.93%, 1.19%) | (5.75%, 1.55%) | (7.20%, 1.45%) |
| SA+12 m | (0.18%, 0.00%) | (0.95%, 1.78%) | (3.67%, 1.76%) | (6.43%, 1.35%) | (7.75%, 1.54%) | (9.55%, 1.28%) |
| SA+16 m | (0.11%, 0.00%) | (0.78%, 1.97%) | (3.18%, 2.01%) | (5.49%, 1.62%) | (6.37%, 1.70%) | (7.76%, 1.46%) |
| SA+20 m | (0.02%, 0.00%) | (0.73%, 2.07%) | (2.98%, 2.14%) | (5.03%, 1.77%) | (5.61%, 1.77%) | (6.68%, 1.56%) |
| Simulation Configurations | Range of AOA (°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (1.30%, 0.00%) | (0.99%, 1.25%) | (3.46%, 1.08%) | (6.22%, 1.04%) | (7.75%, 1.52%) | (9.93%, 1.50%) |
| SST+16 m | (1.12%, 0.00%) | (0.87%, 1.43%) | (3.08%, 1.30%) | (5.48%, 1.13%) | (6.61%, 1.55%) | (8.37%, 1.48%) |
| SST+20 m | (1.08%, 0.00%) | (0.81%, 1.54%) | (2.88%, 1.43%) | (5.07%, 1.20%) | (6.05%, 1.58%) | (7.73%, 1.51%) |
| SA+12 m | (0.04%, 0.00%) | (0.98%, 1.73%) | (3.74%, 1.69%) | (6.52%, 1.27%) | (7.86%, 1.50%) | (9.70%, 1.26%) |
| SA+16 m | (0.08%, 0.00%) | (0.80%, 1.95%) | (3.23%, 1.98%) | (5.55%, 1.59%) | (6.46%, 1.68%) | (7.85%, 1.44%) |
| SA+20 m | (0.00%, 0.00%) | (0.72%, 2.08%) | (3.02%, 2.14%) | (5.15%, 1.75%) | (5.88%, 1.78%) | (7.16%, 1.53%) |
| Simulation Configurations | Range of AOA (°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (1.21%, 0.00%) | (1.03%, 1.25%) | (3.57%, 1.06%) | (6.48%, 1.04%) | (8.20%, 1.55%) | (10.66%, 1.56%) |
| SST+16 m | (1.06%, 0.00%) | (0.88%, 1.41%) | (3.15%, 1.28%) | (5.65%, 1.13%) | (6.94%, 1.57%) | (8.93%, 1.54%) |
| SST+20 m | (1.07%, 0.00%) | (0.79%, 1.53%) | (2.82%, 1.43%) | (4.94%, 1.18%) | (5.78%, 1.55%) | (7.21%, 1.45%) |
| SA+12 m | (0.13%, 0.00%) | (0.96%, 1.78%) | (3.73%, 1.75%) | (6.60%, 1.33%) | (8.09%, 1.54%) | (10.15%, 1.33%) |
| SA+16 m | (0.09%, 0.00%) | (0.83%, 1.94%) | (3.30%, 1.97%) | (5.72%, 1.57%) | (6.76%, 1.68%) | (8.35%, 1.41%) |
| SA+20 m | (0.01%, 0.00%) | (0.72%, 2.06%) | (2.98%, 2.13%) | (5.03%, 1.76%) | (5.61%, 1.77%) | (6.67%, 1.55%) |
| Simulation Configurations | Range of AOA (°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+12 m | (1.21%, 0.00%) | (1.02%, 1.25%) | (3.54%, 1.07%) | (6.36%, 1.03%) | (7.93%, 1.52%) | (10.11%, 1.50%) |
| SST+16 m | (1.04%, 0.00%) | (0.84%, 1.43%) | (3.12%, 1.29%) | (5.57%, 1.14%) | (6.76%, 1.56%) | (8.61%, 1.51%) |
| SST+20 m | (1.06%, 0.00%) | (0.79%, 1.52%) | (2.83%, 1.42%) | (4.94%, 1.18%) | (5.75%, 1.54%) | (7.18%, 1.43%) |
| SA+12 m | (0.15%, 0.00%) | (0.96%, 1.77%) | (3.70%, 1.75%) | (6.46%, 1.34%) | (7.80%, 1.54%) | (9.63%, 1.28%) |
| SA+16 m | (0.05%, 0.00%) | (0.92%, 1.91%) | (3.42%, 1.92%) | (5.75%, 1.54%) | (6.68%, 1.65%) | (8.13%, 1.41%) |
| SA+20 m | (0.05%, 0.00%) | (0.75%, 2.06%) | (3.01%, 2.13%) | (5.05%, 1.76%) | (5.62%, 1.77%) | (6.67%, 1.55%) |
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+blunt | (0.37%, 0.00%) | (1.02%, 1.85%) | (3.85%, 1.81%) | (6.83%, 1.38%) | (8.48%, 1.66%) | (10.70%, 1.51%) |
| SST+NACA4 | (1.19%, 0.00%) | (1.01%, 1.17%) | (3.50%, 0.95%) | (6.23%, 1.00%) | (7.69%, 1.52%) | (9.68%, 1.52%) |
| SST+132formula | (1.26%, 0.00%) | (1.03%, 1.25%) | (3.51%, 1.08%) | (6.31%, 1.04%) | (7.85%, 1.51%) | (9.99%, 1.48%) |
| SST+200formula | (1.30%, 0.00%) | (0.99%, 1.25%) | (3.46%, 1.08%) | (6.22%, 1.04%) | (7.75%, 1.52%) | (9.93%, 1.50%) |
| SST+264formula | (1.21%, 0.00%) | (1.02%, 1.25%) | (3.57%, 1.06%) | (6.48%, 1.04%) | (8.20%, 1.55%) | (10.66%, 1.56%) |
| SST+400formula | (1.21%, 0.00%) | (1.03%, 1.25%) | (3.54%, 1.07%) | (6.36%, 1.03%) | (7.93%, 1.52%) | (10.11%, 1.50%) |
| SA+blunt | (0.80%, 0.00%) | (1.80%, 2.09%) | (4.61%, 2.14%) | (7.42%, 1.72%) | (8.75%, 1.79%) | (10.54%, 1.53%) |
| SA+NACA4 | (0.05%, 0.00%) | (1.06%, 1.73%) | (3.84%, 1.69%) | (6.56%, 1.27%) | (7.84%, 1.50%) | (9.48%, 1.26%) |
| SA+132formula | (0.18%, 0.00%) | (0.95%, 1.78%) | (3.67%, 1.76%) | (6.43%, 1.35%) | (7.75%, 1.54%) | (9.55%, 1.28%) |
| SA+200formula | (0.04%, 0.00%) | (0.98%, 1.73%) | (3.74%, 1.69%) | (6.52%, 1.27%) | (7.86%, 1.50%) | (9.70%, 1.26%) |
| SA+264formula | (0.13%, 0.00%) | (0.96%, 1.78%) | (3.73%, 1.75%) | (6.60%, 1.33%) | (8.09%, 1.54%) | (10.15%, 1.33%) |
| SA+400formula | (0.15%, 0.00%) | (0.96%, 1.77%) | (3.70%, 1.75%) | (6.46%, 1.34%) | (7.80%, 1.54%) | (9.63%, 1.28%) |
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+blunt | (0.21%, 0.00%) | (0.92%, 2.11%) | (3.50%, 2.17%) | (6.12%, 1.74%) | (7.39%, 1.84%) | (9.22%, 1.59%) |
| SST+NACA4 | (0.91%, 0.00%) | (0.85%, 1.35%) | (3.13%, 1.20%) | (5.51%, 1.09%) | (6.60%, 1.53%) | (8.30%, 1.48%) |
| SST+132formula | (1.11%, 0.00%) | (0.84%, 1.45%) | (3.06%, 1.32%) | (5.43%, 1.14%) | (6.56%, 1.55%) | (8.32%, 1.48%) |
| SST+200formula | (1.12%, 0.00%) | (0.87%, 1.43%) | (3.08%, 1.30%) | (5.48%, 1.13%) | (6.61%, 1.55%) | (8.37%, 1.48%) |
| SST+264formula | (1.06%, 0.00%) | (0.83%, 1.94%) | (3.15%, 1.28%) | (5.65%, 1.13%) | (6.94%, 1.57%) | (8.93%, 1.54%) |
| SST+400formula | (1.04%, 0.00%) | (2.17%, 2.29%) | (3.12%, 1.29%) | (5.57%, 1.14%) | (6.76%, 1.56%) | (8.61%, 1.51%) |
| SA+blunt | (1.31%, 0.00%) | (1.17%, 1.95%) | (4.69%, 2.42%) | (7.08%, 2.05%) | (7.98%, 1.96%) | (9.32%, 1.74%) |
| SA+NACA4 | (0.34%, 0.00%) | (0.78%, 1.97%) | (3.64%, 1.98%) | (5.97%, 1.59%) | (6.84%, 1.68%) | (8.18%, 1.44%) |
| SA+132formula | (0.11%, 0.00%) | (0.80%, 1.95%) | (3.18%, 2.01%) | (5.49%, 1.62%) | (6.37%, 1.70%) | (7.76%, 1.46%) |
| SA+200formula | (0.08%, 0.00%) | (0.92%, 1.91%) | (3.23%, 1.98%) | (5.55%, 1.59%) | (6.46%, 1.68%) | (7.85%, 1.44%) |
| SA+264formula | (0.09%, 0.00%) | (0.96%, 1.78%) | (3.30%, 1.97%) | (5.72%, 1.57%) | (6.76%, 1.68%) | (8.35%, 1.41%) |
| SA+400formula | (0.05%, 0.00%) | (0.88%, 1.41%) | (3.42%, 1.92%) | (5.75%, 1.54%) | (6.68%, 1.65%) | (8.13%, 1.41%) |
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| SST+blunt | (1.31%, 0.00%) | (1.28%, 1.79%) | (3.43%, 1.75%) | (5.63%, 1.34%) | (6.52%, 1.61%) | (8.04%, 1.46%) |
| SST+NACA4 | (1.19%, 0.00%) | (0.78%, 1.38%) | (2.80%, 1.22%) | (4.98%, 1.11%) | (5.89%, 1.55%) | (7.50%, 1.52%) |
| SST+132formula | (1.05%, 0.00%) | (0.78%, 1.54%) | (2.81%, 1.44%) | (4.93%, 1.19%) | (5.75%, 1.55%) | (7.20%, 1.45%) |
| SST+200formula | (1.08%, 0.00%) | (0.81%, 1.54%) | (2.88%, 1.43%) | (5.07%, 1.20%) | (6.05%, 1.58%) | (7.73%, 1.51%) |
| SST+264formula | (1.07%, 0.00%) | (0.79%, 1.53%) | (2.82%, 1.43%) | (4.94%, 1.18%) | (5.78%, 1.55%) | (7.21%, 1.45%) |
| SST+400formula | (1.06%, 0.00%) | (0.79%, 1.52%) | (2.83%, 1.42%) | (4.94%, 1.18%) | (5.75%, 1.54%) | (7.18%, 1.43%) |
| SA+blunt | (0.84%, 0.00%) | (1.59%, 2.11%) | (3.88%, 2.23%) | (5.97%, 1.87%) | (6.60%, 1.83%) | (7.72%, 1.65%) |
| SA+NACA4 | (0.06%, 0.00%) | (0.83%, 2.08%) | (3.13%, 2.14%) | (5.28%, 1.75%) | (5.98%, 1.78%) | (7.50%, 1.53%) |
| SA+132formula | (0.02%, 0.00%) | (0.73%, 2.07%) | (2.98%, 2.14%) | (5.03%, 1.77%) | (5.61%, 1.77%) | (6.68%, 1.56%) |
| SA+200formula | (0.00%, 0.00%) | (0.72%, 2.08%) | (3.02%, 2.14%) | (5.15%, 1.75%) | (5.88%, 1.78%) | (7.16%, 1.53%) |
| SA+264formula | (0.01%, 0.00%) | (0.72%, 2.06%) | (2.98%, 2.13%) | (5.03%, 1.76%) | (5.61%, 1.77%) | (6.67%, 1.55%) |
| SA+400formula | (0.05%, 0.00%) | (0.75%, 2.06%) | (3.01%, 2.13%) | (5.05%, 1.76%) | (5.62%, 1.77%) | (6.67%, 1.55%) |
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| 12 m+blunt | (0.37%, 0.00%) | (1.02%, 1.85%) | (3.85%, 1.81%) | (6.83%, 1.38%) | (8.48%, 1.66%) | (10.70%, 1.51%) |
| 12 m+NACA4 | (1.19%, 0.00%) | (1.01%, 1.17%) | (3.50%, 0.95%) | (6.23%, 1.00%) | (7.69%, 1.52%) | (9.68%, 1.52%) |
| 12 m+132formula | (1.26%, 0.00%) | (1.03%, 1.25%) | (3.51%, 1.08%) | (6.31%, 1.04%) | (7.85%, 1.51%) | (9.99%, 1.48%) |
| 12 m+200formula | (1.30%, 0.00%) | (0.99%, 1.25%) | (3.46%, 1.08%) | (6.22%, 1.04%) | (7.75%, 1.52%) | (9.93%, 1.50%) |
| 12 m+264formula | (1.21%, 0.00%) | (1.02%, 1.25%) | (3.57%, 1.06%) | (6.48%, 1.04%) | (8.20%, 1.55%) | (10.66%, 1.56%) |
| 12 m+400formula | (1.21%, 0.00%) | (1.03%, 1.25%) | (3.54%, 1.07%) | (6.36%, 1.03%) | (7.93%, 1.52%) | (10.11%, 1.50%) |
| 16 m+blunt | (0.21%, 0.00%) | (0.92%, 2.11%) | (3.50%, 2.17%) | (6.12%, 1.74%) | (7.39%, 1.84%) | (9.22%, 1.59%) |
| 16 m+NACA4 | (0.91%, 0.00%) | (0.85%, 1.35%) | (3.13%, 1.20%) | (5.51%, 1.09%) | (6.60%, 1.53%) | (8.30%, 1.48%) |
| 16 m+132formula | (1.11%, 0.00%) | (0.84%, 1.45%) | (3.06%, 1.32%) | (5.43%, 1.14%) | (6.56%, 1.55%) | (8.32%, 1.48%) |
| 16 m+200formula | (1.12%, 0.00%) | (0.87%, 1.43%) | (3.08%, 1.30%) | (5.48%, 1.13%) | (6.61%, 1.55%) | (8.37%, 1.48%) |
| 16 m+264formula | (1.06%, 0.00%) | (0.88%, 1.41%) | (3.15%, 1.28%) | (5.65%, 1.13%) | (6.94%, 1.57%) | (8.93%, 1.54%) |
| 16 m+400formula | (1.04%, 0.00%) | (0.84%, 1.43%) | (3.12%, 1.29%) | (5.57%, 1.14%) | (6.76%, 1.56%) | (8.61%, 1.51%) |
| 20 m+blunt | (1.30%, 0.00%) | (1.28%, 1.79%) | (3.43%, 1.75%) | (5.63%, 1.34%) | (6.52%, 1.61%) | (8.04%, 1.46%) |
| 20 m+NACA4 | (1.19%, 0.00%) | (0.78%, 1.38%) | (2.80%, 1.22%) | (4.98%, 1.11%) | (5.89%, 1.55%) | (7.50%, 1.52%) |
| 20 m+132formula | (1.05%, 0.00%) | (0.78%, 1.54%) | (2.81%, 1.44%) | (4.93%, 1.19%) | (5.75%, 1.55%) | (7.20%, 1.45%) |
| 20 m+200formula | (1.08%, 0.00%) | (0.81%, 1.54%) | (2.88%, 1.43%) | (5.07%, 1.20%) | (6.05%, 1.58%) | (7.73%, 1.51%) |
| 20 m+264formula | (1.07%, 0.00%) | (0.79%, 1.53%) | (2.82%, 1.43%) | (4.94%, 1.18%) | (5.78%, 1.55%) | (7.21%, 1.45%) |
| 20 m+400formula | (1.06%, 0.00%) | (0.79%, 1.52%) | (2.83%, 1.42%) | (4.94%, 1.18%) | (5.75%, 1.54%) | (7.18%, 1.43%) |
| Simulation Configurations | Range of AOA(°) | |||||
|---|---|---|---|---|---|---|
| (0°, 0°) | (0°, 2°) | (0°, 4°) | (0°, 6°) | (0°, 8°) | (0°, 10°) | |
| 12 m+blunt | (0.80%, 0.00%) | (1.80%, 2.09%) | (4.61%, 2.14%) | (7.42%, 1.72%) | (8.75%, 1.79%) | (10.54%, 1.53%) |
| 12 m+NACA4 | (0.05%, 0.00%) | (1.06%, 1.73%) | (3.84%, 1.69%) | (6.56%, 1.27%) | (7.84%, 1.50%) | (9.48%, 1.26%) |
| 12 m+132formula | (0.18%, 0.00%) | (0.95%, 1.78%) | (3.67%, 1.76%) | (6.43%, 1.35%) | (7.75%, 1.54%) | (9.55%, 1.28%) |
| 12 m+200formula | (0.04%, 0.00%) | (0.98%, 1.73%) | (3.74%, 1.69%) | (6.52%, 1.27%) | (7.86%, 1.50%) | (9.70%, 1.26%) |
| 12 m+264formula | (0.13%, 0.00%) | (0.96%, 1.78%) | (3.73%, 1.75%) | (6.60%, 1.33%) | (8.09%, 1.54%) | (10.15%, 1.33%) |
| 12 m+400formula | (0.15%, 0.00%) | (0.96%, 1.77%) | (3.70%, 1.75%) | (6.46%, 1.34%) | (7.80%, 1.54%) | (9.63%, 1.28%) |
| 16 m+blunt | (1.31%, 0.00%) | (2.17%, 2.29%) | (4.69%, 2.42%) | (7.08%, 2.05%) | (7.98%, 1.96%) | (9.32%, 1.74%) |
| 16 m+NACA4 | (0.34%, 0.00%) | (1.17%, 1.95%) | (3.64%, 1.98%) | (5.97%, 1.59%) | (6.84%, 1.68%) | (8.18%, 1.44%) |
| 16 m+132formula | (0.11%, 0.00%) | (0.78%, 1.97%) | (3.18%, 2.01%) | (5.49%, 1.62%) | (6.37%, 1.70%) | (7.76%, 1.46%) |
| 16 m+200formula | (0.08%, 0.00%) | (0.80%, 1.95%) | (3.23%, 1.98%) | (5.55%, 1.59%) | (6.46%, 1.68%) | (7.85%, 1.44%) |
| 16 m+264formula | (0.09%, 0.00%) | (0.83%, 1.94%) | (3.30%, 1.97%) | (5.72%, 1.57%) | (6.76%, 1.68%) | (8.35%, 1.41%) |
| 16 m+400formula | (0.05%, 0.00%) | (0.92%, 1.91%) | (3.42%, 1.92%) | (5.75%, 1.54%) | (6.68%, 1.65%) | (8.13%, 1.41%) |
| 20 m+blunt | (0.84%, 0.00%) | (1.59%, 2.11%) | (3.88%, 2.23%) | (5.97%, 1.87%) | (6.60%, 1.83%) | (7.72%, 1.65%) |
| 20 m+NACA4 | (0.06%, 0.00%) | (0.83%, 2.08%) | (3.13%, 2.14%) | (5.28%, 1.75%) | (5.98%, 1.78%) | (7.50%, 1.53%) |
| 20 m+132formula | (0.02%, 0.00%) | (0.73%, 2.07%) | (2.98%, 2.14%) | (5.03%, 1.77%) | (5.61%, 1.77%) | (6.68%, 1.56%) |
| 20 m+200formula | (0.00%, 0.00%) | (0.72%, 2.08%) | (3.02%, 2.14%) | (5.15%, 1.75%) | (5.88%, 1.78%) | (7.16%, 1.53%) |
| 20 m+264formula | (0.01%, 0.00%) | (0.72%, 2.06%) | (2.98%, 2.13%) | (5.03%, 1.76%) | (5.61%, 1.77%) | (6.67%, 1.55%) |
| 20 m+400formula | (0.05%, 0.00%) | (0.75%, 2.06%) | (3.01%, 2.13%) | (5.05%, 1.76%) | (5.62%, 1.77%) | (6.67%, 1.55%) |
| Range of AOA(°) | Type of NACA0012 Model | |||||
|---|---|---|---|---|---|---|
| Blunt Trailing Edge | Sharp Trailing Edge | |||||
| NACA4 | Formula (132 Points) | Formula (200 Points) | Formula (264 Points) | Formula (400 Points) | ||
| (0°, 0°) | (0.21%, 0.00%) | (0.05%, 0.00%) | (0.02%, 0.00%) | (0.00%, 0.00%) | (0.01%, 0.00%) | (0.05%, 0.00%) |
| SST+16 m | SA+12 m | SA+20 m | SA+20 m | SA+20 m | SA+16 m | |
| (0°, 2°) | (1.02%, 1.85%) | (0.78%, 1.38%) | (1.03%, 1.25%) | (0.99%, 1.25%) | (1.03%, 1.25%) | (1.02%, 1.25%) |
| SST+12 m | SST+20 m | SST+12 m | SST+12 m | SST+12 m | SST+12 m | |
| (0°, 4°) | (3.43%, 1.75%) | (2.80%, 1.22%) | (2.81%, 1.44%) | (2.88%, 1.43%) | (2.82%, 1.43%) | (2.83%, 1.42%) |
| SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | |
| (0°, 6°) | (5.63%, 1.34%) | (4.98%, 1.11%) | (4.93%, 1.19%) | (5.07%, 1.20%) | (4.94%, 1.18%) | (4.94%, 1.18%) |
| SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | |
| (0°, 8°) | (6.52%, 1.61%) | (5.89%, 1.55%) | (5.75%, 1.55%) | (6.05%, 1.58%) | (5.78%, 1.55%) | (5.75%, 1.54%) |
| SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | SST+20 m | |
| (0°, 10°) | (7.72%, 1.65%) | (7.50%, 1.53%) | (6.68%, 1.56%) | (7.16%, 1.53%) | (6.67%, 1.55%) | (6.67%, 1.55%) |
| SA+20 m | SA+20 m | SA+20 m | SA+20 m | SA+20 m | SA+20 m | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhang, G. Analysis of Influence of Different Parameters on Numerical Simulation of NACA0012 Incompressible External Flow Field under High Reynolds Numbers. Appl. Sci. 2022, 12, 416. https://doi.org/10.3390/app12010416
Yang L, Zhang G. Analysis of Influence of Different Parameters on Numerical Simulation of NACA0012 Incompressible External Flow Field under High Reynolds Numbers. Applied Sciences. 2022; 12(1):416. https://doi.org/10.3390/app12010416
Chicago/Turabian StyleYang, Lu, and Guangming Zhang. 2022. "Analysis of Influence of Different Parameters on Numerical Simulation of NACA0012 Incompressible External Flow Field under High Reynolds Numbers" Applied Sciences 12, no. 1: 416. https://doi.org/10.3390/app12010416
APA StyleYang, L., & Zhang, G. (2022). Analysis of Influence of Different Parameters on Numerical Simulation of NACA0012 Incompressible External Flow Field under High Reynolds Numbers. Applied Sciences, 12(1), 416. https://doi.org/10.3390/app12010416






