Negotiating Uneven Terrain by a Simple Teleoperated Tracked Vehicle with Internally Movable Center of Gravity
Abstract
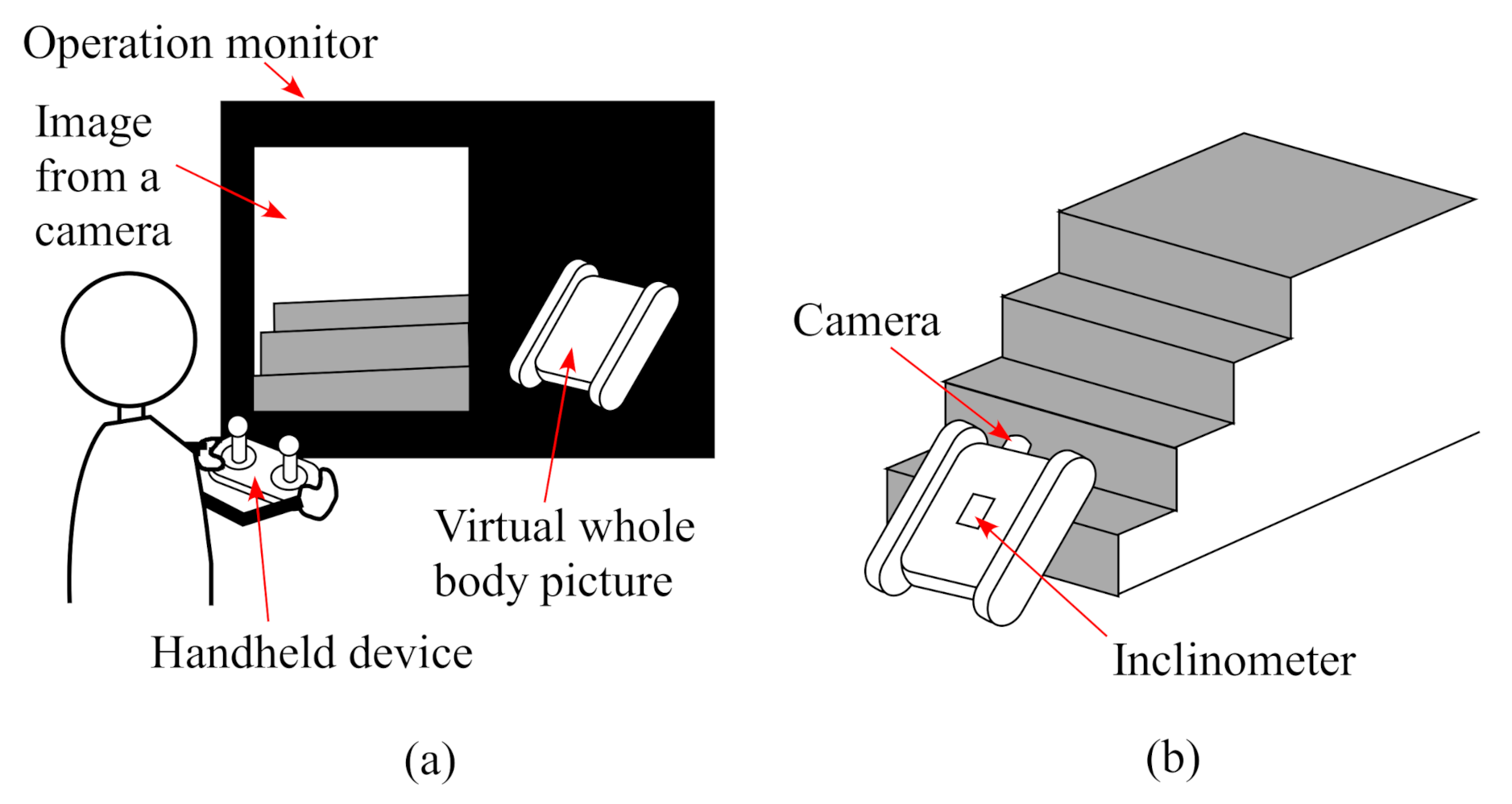
:1. Introduction
2. Tracked Vehicle “Dyjob” with Internally Movable COG
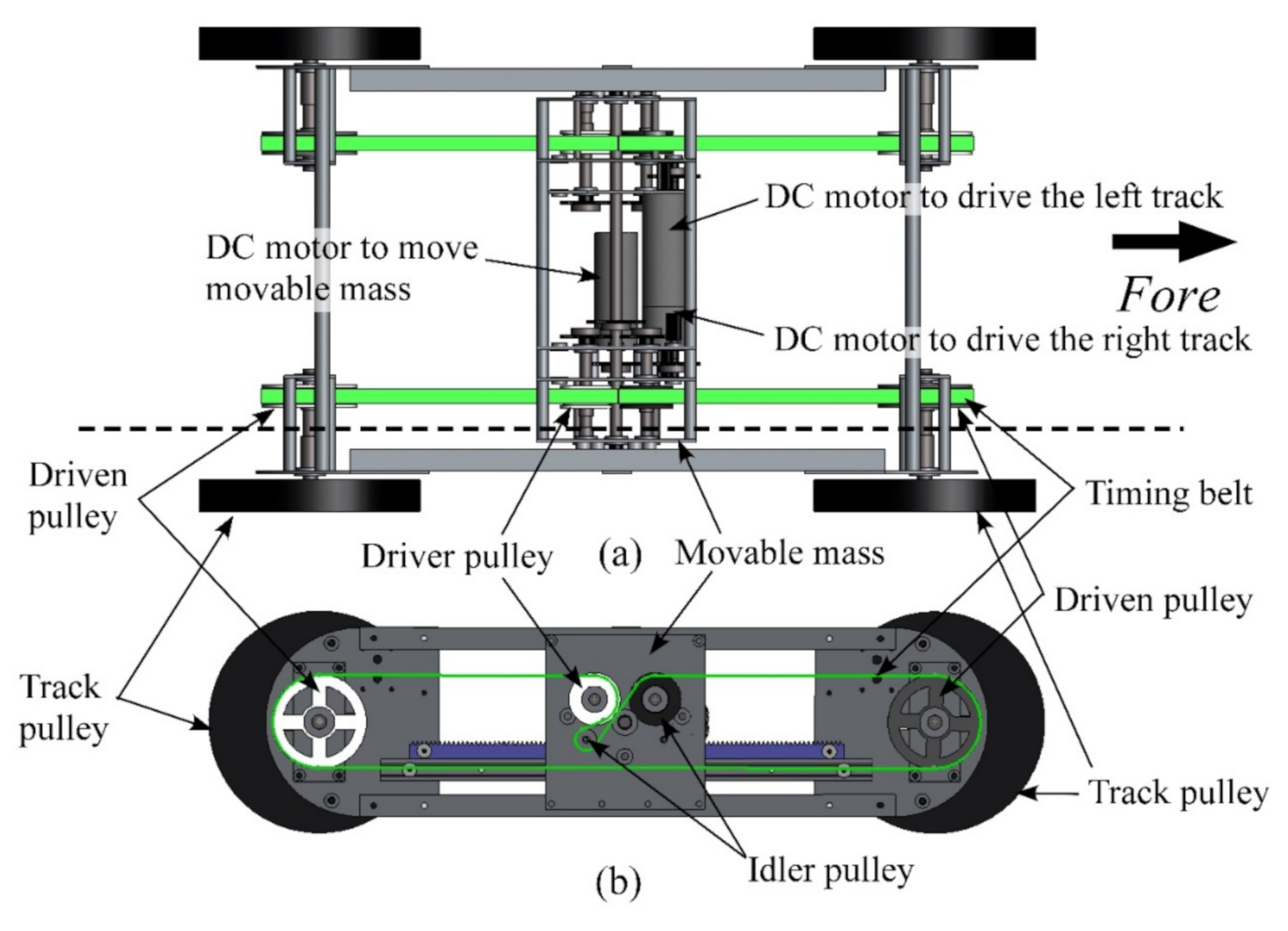
2.1. Prototype Tracked Vehicle “Dyjob”
2.2. Mechanism to Drive the Movable Mass and Each Rubber Track
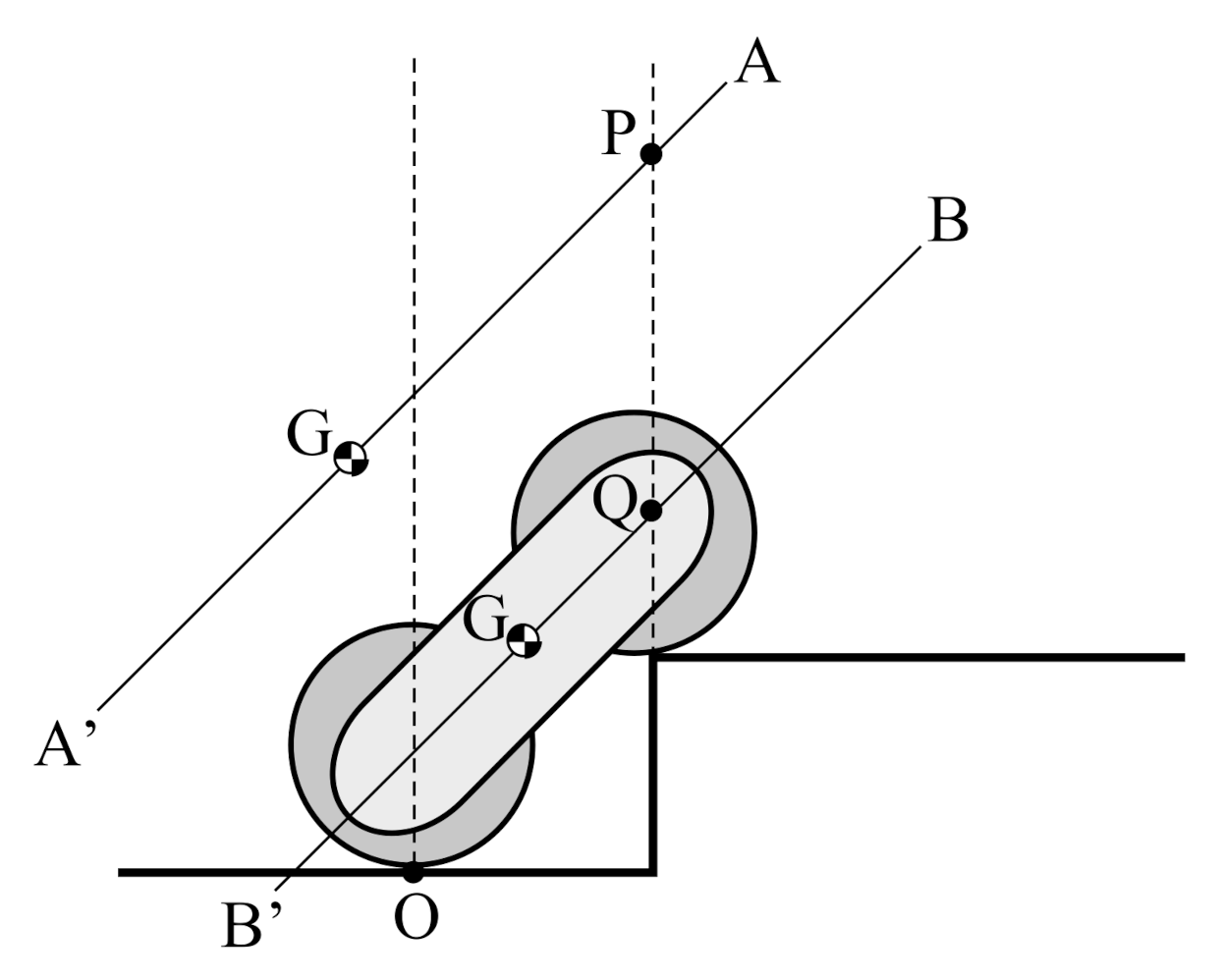
3. Analysis of Movement over a Step
3.1. Strategy
- Step (1)
- The front end of the vehicle climbs onto the step.
- Step (2)
- The rear end of the vehicle climbs onto the step.
- Step (3)
- The vehicle lands on the ground without turning over forward.
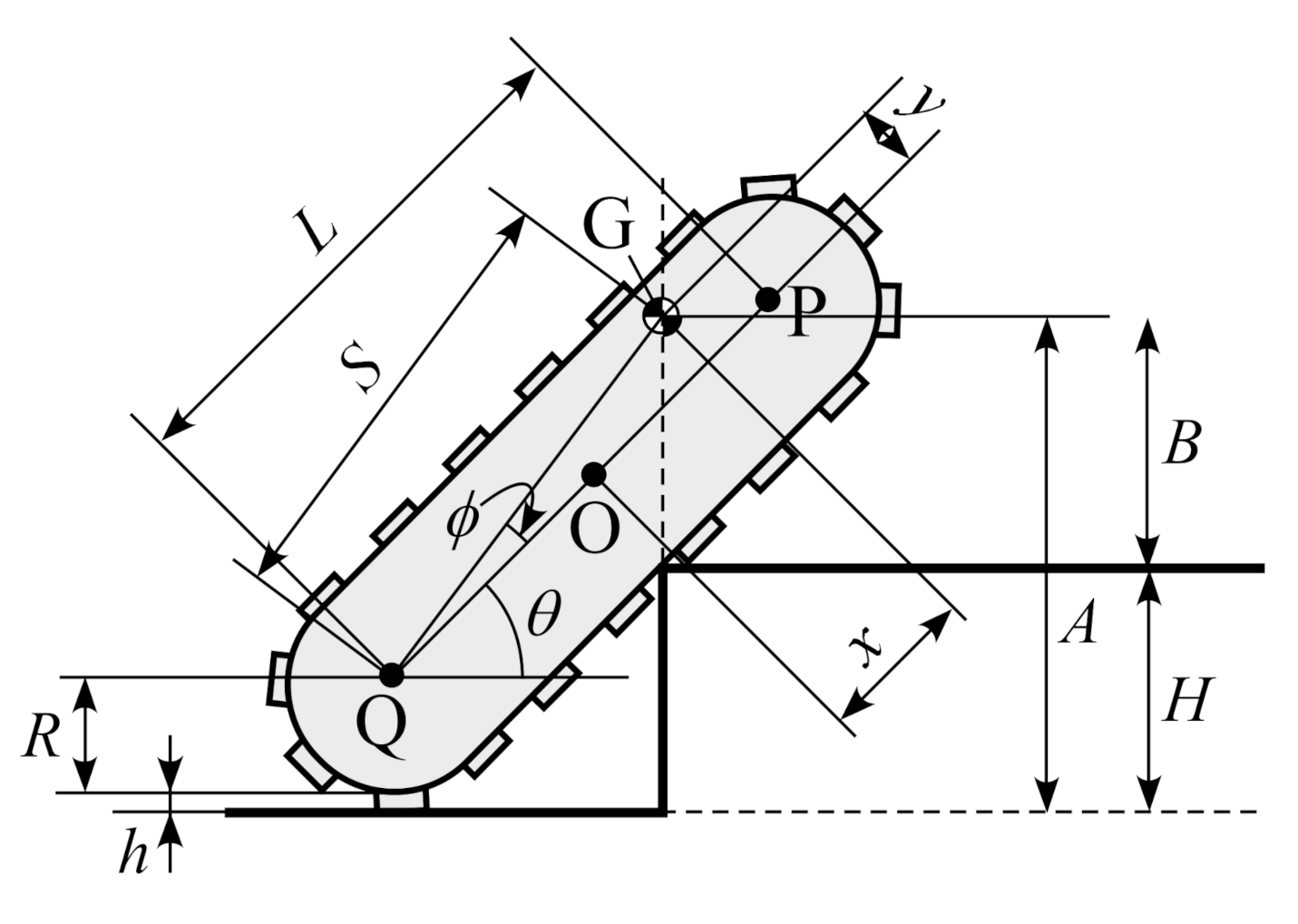
3.2. Geometric Analysis of Effect of Adjustment of COG Position on Rear End of the Vehicle Climbing a Step
4. Experimental Results
4.1. Experiments with “Dyjob” Moving over a Step
4.2. Experiments with “Dyjob” Climbing up Stairs
4.3. Experiments with “Dyjob” Moving over a Gap
4.4. Experiments with “Dyjob” Climbing a Slope
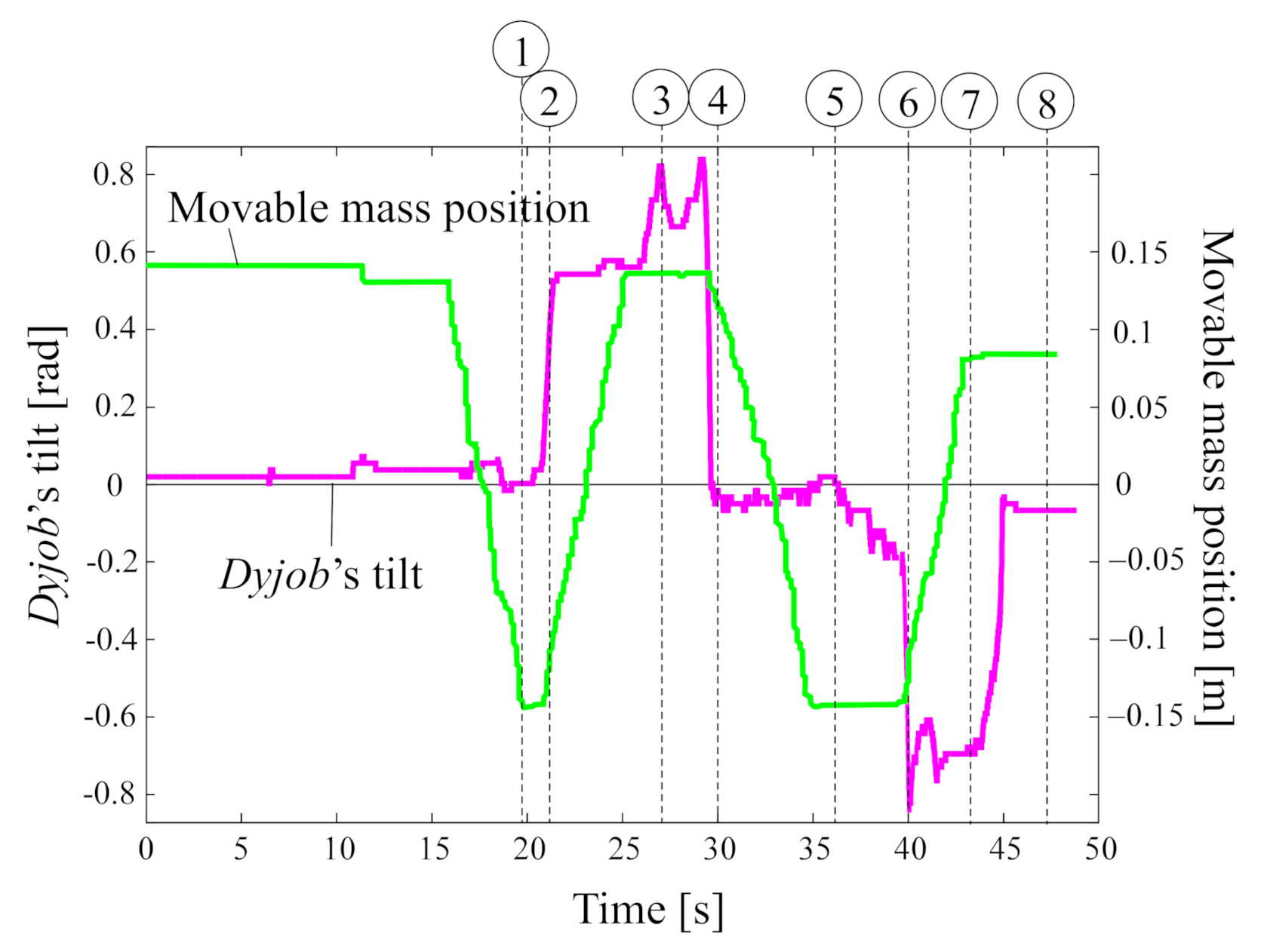
5. Discussion on Operation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boston Dynamics. Available online: https://www.bostondynamics.com/ (accessed on 29 December 2021).
- Kim, S.; Clark, J.E.; Cutkosky, M.R. iSprawl: Design and Tuning for High-speed Autonomous Open-loop Running. Int. J. Robot. Res. 2006, 25, 903–912. [Google Scholar] [CrossRef]
- Murphy, M.P.; Saunders, A.; Moreira, C.; Rizzi, A.A.; Raibert, M. The LittleDog robot. Int. J. Robot. Res. 2011, 30, 145–149. [Google Scholar] [CrossRef]
- Semini, C.; Barasuol, V.; Boaventura, T.; Frigerio, M.; Focchi, M.; Caldwell, D.G.; Buchli, J. Towards versatile legged robots through active impedance control. Int. J. Robot. Res. 2015, 34, 1003–1020. [Google Scholar] [CrossRef]
- Bjelonic, M.; Kottege, N.; Beckerle, P. Proprioceptive control of an over-actuated hexapod robot in unstructured terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2016), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Fukui, T.; Fujisawa, H.; Otaka, K.; Fukuoka, Y. Autonomous gait transition and galloping over unperceived obstacles of a quadruped robot with CPG modulated by vestibular feedback. Robot. Auton. Syst. 2019, 111, 1–19. [Google Scholar] [CrossRef]
- Xin, G.-Y.; Wolfslag, W.; Lin, H.-C.; Tiseo, C.; Mistry, M. An Optimization-Based Locomotion Controller for Quadruped Robots Leveraging Cartesian Impedance Control. Front. Robot. AI 2020, 7, 48. [Google Scholar] [CrossRef] [Green Version]
- Daltorio, K.A.; Wei, T.E.; Horchler, A.D.; Southard, L.; Wile, G.D.; Quinn, R.D.; Gorb, S.N.; Ritzmann, R.E. Mini-Whegs TM Climbs Steep Surfaces Using Insect-inspired Attachment Mechanisms. Int. J. Robot. Res. 2009, 28, 285–302. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, W.; Ma, L.; Wang, Z. Biologically inspired jumping robots: A comprehensive review. Robot. Auton. Syst. 2020, 124, 103362. [Google Scholar] [CrossRef]
- Collins, S.; Ruina, A.; Tedrake, R.; Wisse, M. Efficient Bipedal Robots Based on Passive-Dynamic Walkers. Science 2005, 307, 1082–1085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saranli, U.; Buehler, M.; Koditschek, D.E. RHex: A Simple and Highly Mobile Hexapod Robot. Int. J. Robot. Res. 2001, 20, 616–631. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-S.; Jung, G.-P.; Kim, H.; Cho, K.-J.; Chu, C.-N. Wheel Transformer: A Wheel-Leg Hybrid Robot with Passive Transformable Wheels. IEEE Trans. Robot. 2014, 30, 1487–1498. [Google Scholar] [CrossRef]
- Laumond, J.; Benallegue, M.; Carpentier, J.; Berthoz, A. The Yoyo-Man. Int. J. Robot. Res. 2017, 36, 1508–1520. [Google Scholar] [CrossRef] [Green Version]
- Eich, M.; Grimminger, F.; Kirchner, F. Proprioceptive control of a hybrid legged-wheeled robot. In Proceedings of the 2008 IEEE International Conference on Robotics and Biomimetics, Bangkok, Thailand, 22–25 February 2009. [Google Scholar]
- Breckwoldt, W.; Bachmann, R.; Leibach, R.; Quinn, R. Speedy whegs climbs obstacles slowly and runs at 44 km/hour. In Proceedings of the Conference on Biomimetic and Biohybrid Systems, Living Machines 2019: Biomimetic and Biohybrid Systems, Nara, Japan, 9–12 July 2019; pp. 27–37. [Google Scholar]
- Dalvand, M.M.; Moghadam, M.M. Stair Climber Smart Mobile Robot (MSRox). Auton. Robot. 2006, 20, 3–14. [Google Scholar] [CrossRef]
- Quaglia, G.; Nisi, M. Design and construction of a new version of the Epi.q UGV for monitoring and surveillance tasks. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Endo, G.; Hirose, S. Study on Roller-Walker—Improvement of Locomotive Efficiency of Quadruped Robots by Passive Wheels. Adv. Robot. 2012, 26, 969–988. [Google Scholar] [CrossRef] [Green Version]
- Du, W.; Fnadi, M.; Benamar, F. Rolling based locomotion on rough terrain for a wheeled quadruped using centroidal dynamics. Mech. Mach. Theory 2020, 153, 103984. [Google Scholar] [CrossRef]
- Du, W.; Amar, F. A compact form dynamics controller for a high-DOF tetrapod-on-wheel robot with one manipulator via null space based convex optimization and compatible impedance controllers. Multibody Syst. Dyn. 2020, 49, 447–463. [Google Scholar] [CrossRef]
- Estier, T.; Piguet, R.; Eichhorn, R.; Siegwart, R. Shrimp, a rover architecture for long range martian mission. In Proceedings of the Sixth ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA’2000), Noordwijk, The Netherlands, 5–7 December 2000. [Google Scholar]
- Cordes, F.; Kirchner, F.; Babu, A. Design and field testing of a rover with an actively articulated suspension system in a Mars analog terrain. J. Field Robot. 2018, 35, 1149–1181. [Google Scholar] [CrossRef]
- Harrington, B.D.; Voorhees, C. The challenges of designing the rocker-bogie suspension for the Mars Exploration Rover. In Proceedings of the of the 37th Aerospace Mechanisms Symposium, Galveston, TX, USA, 19–21 May 2004. [Google Scholar]
- Nayar, H.; Kim, J.; Chamberlain-Simon, B.; Carpenter, K.; Hans, M.; Boettcher, A.; Meirion-Griffith, G.; Wilcox, B.; Bittner, B. Design optimization of a lightweight rocker–bogie rover for ocean worlds applications. Int. J. Adv. Robot. Syst. 2019, 16, 1–10. [Google Scholar] [CrossRef]
- Takamori, T.; Kobayashi, S.; Ohira, T.; Takashima, M.; Ikeuchi, A.; Takashima, S. Development of UMRS (Utility Mobile Robot for Search) and searching system for sufferers with cellphone. In Proceedings of the First International Symposium on System & Human Science—For Safety, Security, and Dependability, Osaka, Japan, 19–20 November 2003; pp. 47–52. [Google Scholar]
- Yamauchi, B.M. PackBot: A versatile platform for military robotics. In Proceedings of the SPIE 5422, Unmanned Ground Vehicle Technology VI, Orlando, FL, USA, 13–15 April 2004. [Google Scholar]
- Kamimura, A.; Kurokawa, H. High-step climbing by a crawler robot DIR-2—Realization of automatic climbing motion. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009. [Google Scholar]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Emergency response to the nuclear accident at the Fukushima Daiichi Nuclear Power Plants using mobile rescue robots. J. Field Robot. 2013, 30, 44–63. [Google Scholar] [CrossRef]
- Nakamura, K.; Tohashi, K.; Funayama, Y.; Harasawa, H.; Ogawa, J. Dual-arm robot teleoperation support with the virtual world. Artif. Life Robot. 2020, 25, 286–293. [Google Scholar] [CrossRef]
- Sim, B.-S.; Kim, K.-J.; Yu, K.-H. Development of body rotational wheeled robot and its verification of effectiveness. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10405–10411. [Google Scholar]
- Falcone, E.; Gockley, R.; Porter, E.; Nourbakhsh, I. The Personal Rover Project: The comprehensive design of a domestic personal robot. Robot. Auton. Syst. 2003, 42, 245–258. [Google Scholar] [CrossRef]
- Nishio, N.; Nishida, S.-I.; Nakatani, S. Study of a Planetary Exploration Rover with a Hinge-type Center-of-gravity Shift Mechanism. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2021, 19, 469–476. [Google Scholar] [CrossRef]
- Nakamura, S.; Faragalli, M.; Mizukami, N.; Nakatani, I.; Kunii, Y.; Kubota, T. Wheeled robot with movable center of mass for traversing over rough terrain. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Diego, CA, USA, 29 October–2 November 2007; pp. 1228–1233. [Google Scholar]
- Yokoyama, M.; Matsuhasi, Y.; Sano, A.; Ko, M.T. Slip control of a wheeled mobile robot with a movable auxiliary mass. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015; pp. 1008–1013. [Google Scholar]
- Onozuka, Y.; Tomokuni, N.; Murata, G.; Shino, M. Dynamic stability control of inverted-pendulum-type robotic wheelchair for going up and down stairs. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 4114–4119. [Google Scholar]
- Iagnemma, K.D.; Dubowsky, S. Terrain estimation for high-speed rough-terrain autonomous vehicle navigation. In Proceedings of the SPIE 4715, Unmanned Ground Vehicle Technology IV, Orland, FL, USA, 1–5 April 2002. [Google Scholar]
- Fnadi, M.; Plumet, F.; Benamar, F. Nonlinear tire cornering stiffness observer for a double steering off-road mobile robot. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Fnadi, M.; Du, W.; Plumet, F.; Benamar, F. Constrained Model Predictive Control for dynamic path tracking of a bi-steerable rover on slippery grounds. Control Eng. Pract. 2020, 107, 104693. [Google Scholar] [CrossRef]
- Delmerico, J.; Mintchev, S.; Giusti, A.; Gromov, B.; Melo, K.; Horvat, T.; Cadena, C.; Hutter, M.; Ijspeert, A.; Floreano, D.; et al. The current state and future outlook of rescue robotics. J. Field Robot. 2019, 36, 1171–1191. [Google Scholar] [CrossRef]
- Hebert, M.H.; Thorpe, C.; Stentz, A. Intelligent Unmanned Ground Vehicles. In The Springer International Series in Engineering and Computer Science; Springer: New York, NY, USA, 1997. [Google Scholar]
- Casper, J.; Murphy, R.R. Human-robot interactions during the robot-assisted urban search and rescue response at the World Trade Center. IEEE Trans. Syst. Man, Cybern. Part B (Cybern.) 2003, 33, 367–385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture point: A step toward humanoid push recovery. In Proceedings of the 2006 IEEE/RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006. [Google Scholar]










| Physical Feature and Device | Specification |
|---|---|
| Length | 600 mm |
| Width | 360 mm |
| Height | 180 mm excluding the protruding part of the movable mass |
| Whole weight | 8.5 kg |
| Weight of the movable mass | 3.5 kg |
| Coefficient of friction between the rubber track and an indoor hard ground | 0.82 |
| Coefficient of friction between the rubber track and a block as an obstacle | 1.13 |
| Coefficient of friction between the rubber track and a slope | 1.12 |
| Moving range of the movable mass | 0.142 m from the center of Dyjob |
| Moment of inertia about the axis O in Figure 2 when the movable mass is placed in the center | 0.275 kgm2 |
| Moment of inertia about the axis O in Figure 2 when the movable mass is placed most forward/backward | 0.345 kgm2 |
| Actuator for each track | 60 W DC motor (RE30 by Maxon) with reduction ratios of 36:1 |
| Actuator for the movable mass | 60 W DC motor (RE30 by Maxon) with reduction ratios of 25:1 |
| Motor driver | 1Axis DC Power Module by Hibot Co. |
| Encoder to detect the rotation angle of the track pulley and the movable mass’s position | MR Type L by Maxon |
| Inclinometer to detect the body tilt | SCA61T-FA1H1G by VTI Technologies Co. |
| On-board computer | HRP-3P-CN and MCN by General Robotics Inc. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fukuoka, Y.; Oshino, K.; Ibrahim, A.N. Negotiating Uneven Terrain by a Simple Teleoperated Tracked Vehicle with Internally Movable Center of Gravity. Appl. Sci. 2022, 12, 525. https://doi.org/10.3390/app12010525
Fukuoka Y, Oshino K, Ibrahim AN. Negotiating Uneven Terrain by a Simple Teleoperated Tracked Vehicle with Internally Movable Center of Gravity. Applied Sciences. 2022; 12(1):525. https://doi.org/10.3390/app12010525
Chicago/Turabian StyleFukuoka, Yasuhiro, Kazuyuki Oshino, and Ahmad Najmuddin Ibrahim. 2022. "Negotiating Uneven Terrain by a Simple Teleoperated Tracked Vehicle with Internally Movable Center of Gravity" Applied Sciences 12, no. 1: 525. https://doi.org/10.3390/app12010525
APA StyleFukuoka, Y., Oshino, K., & Ibrahim, A. N. (2022). Negotiating Uneven Terrain by a Simple Teleoperated Tracked Vehicle with Internally Movable Center of Gravity. Applied Sciences, 12(1), 525. https://doi.org/10.3390/app12010525






