A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior
Abstract
:1. Introduction
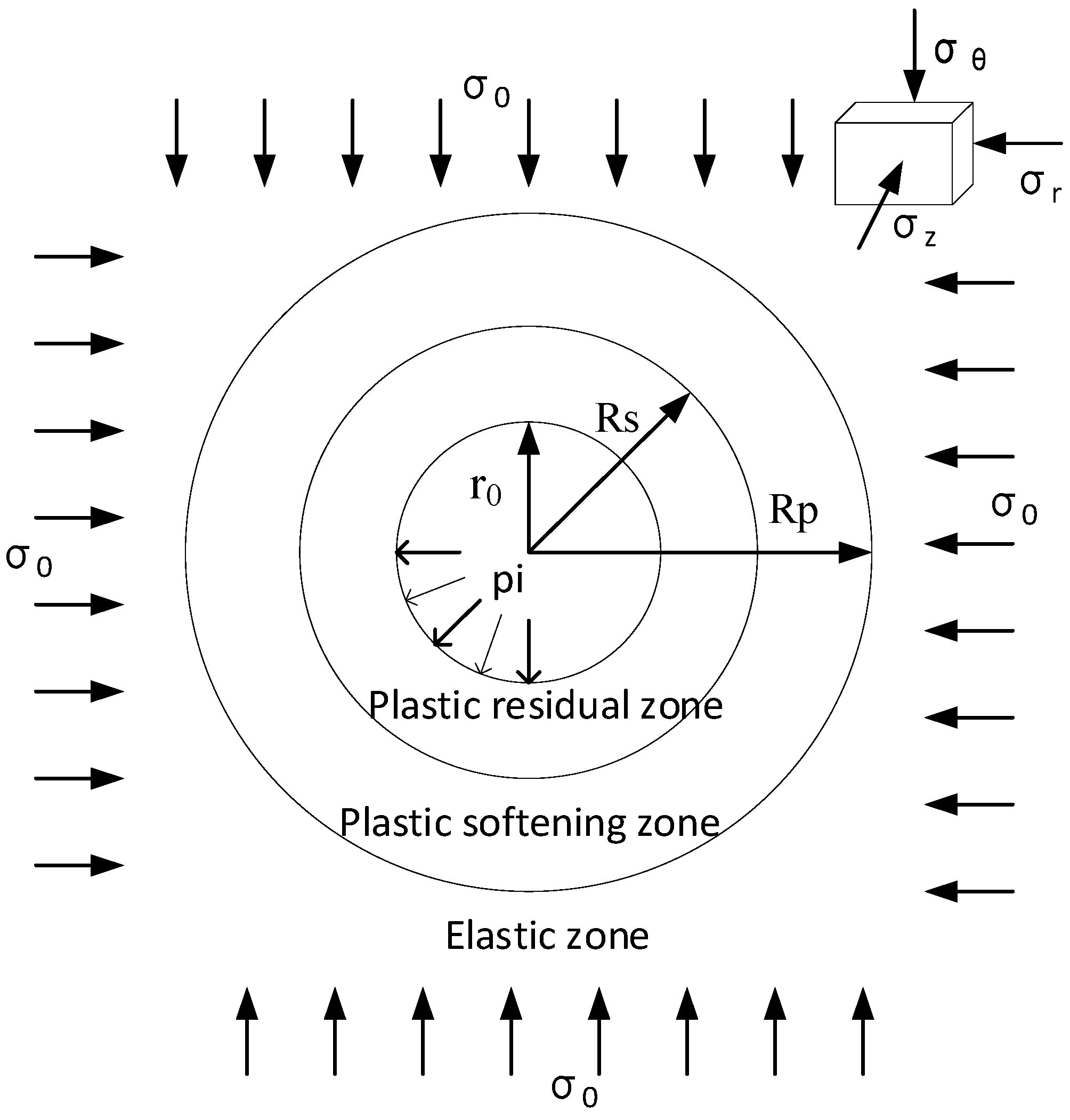
2. Description of the Problem
2.1. Theoretical Representation of a Tunnel Surrounded by Rock Mass
2.2. D–P Criterion Yield Function
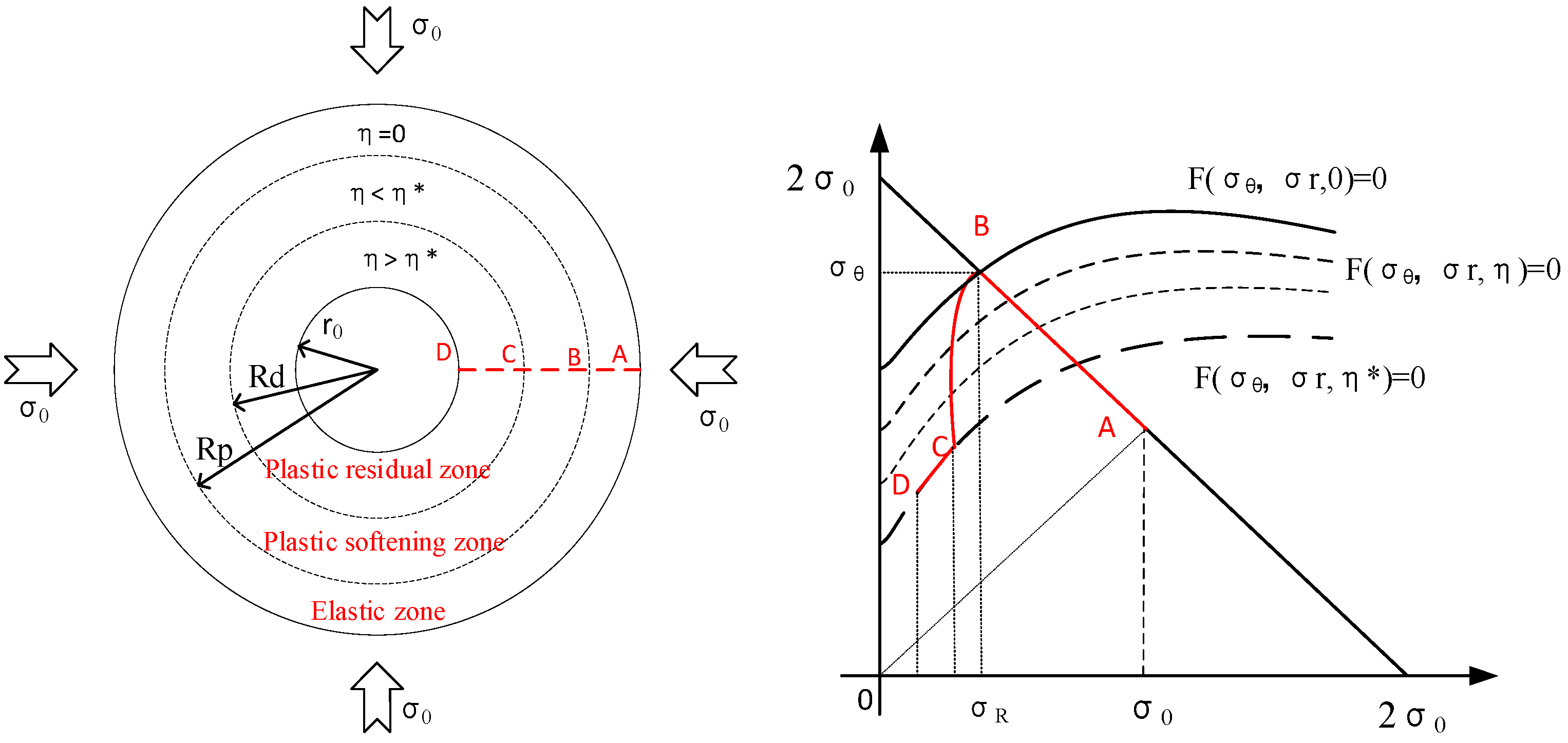
2.3. Strain-Softening Model
3. Calculation of Stress and Displacement in the Elastic–Plastic Zone
3.1. Basic Equation
3.2. Calculation of Rock Mass Deformation in the Elastic Region
3.3. Calculation of Yield Deformation of the Rock Mass in the Plastic Zone
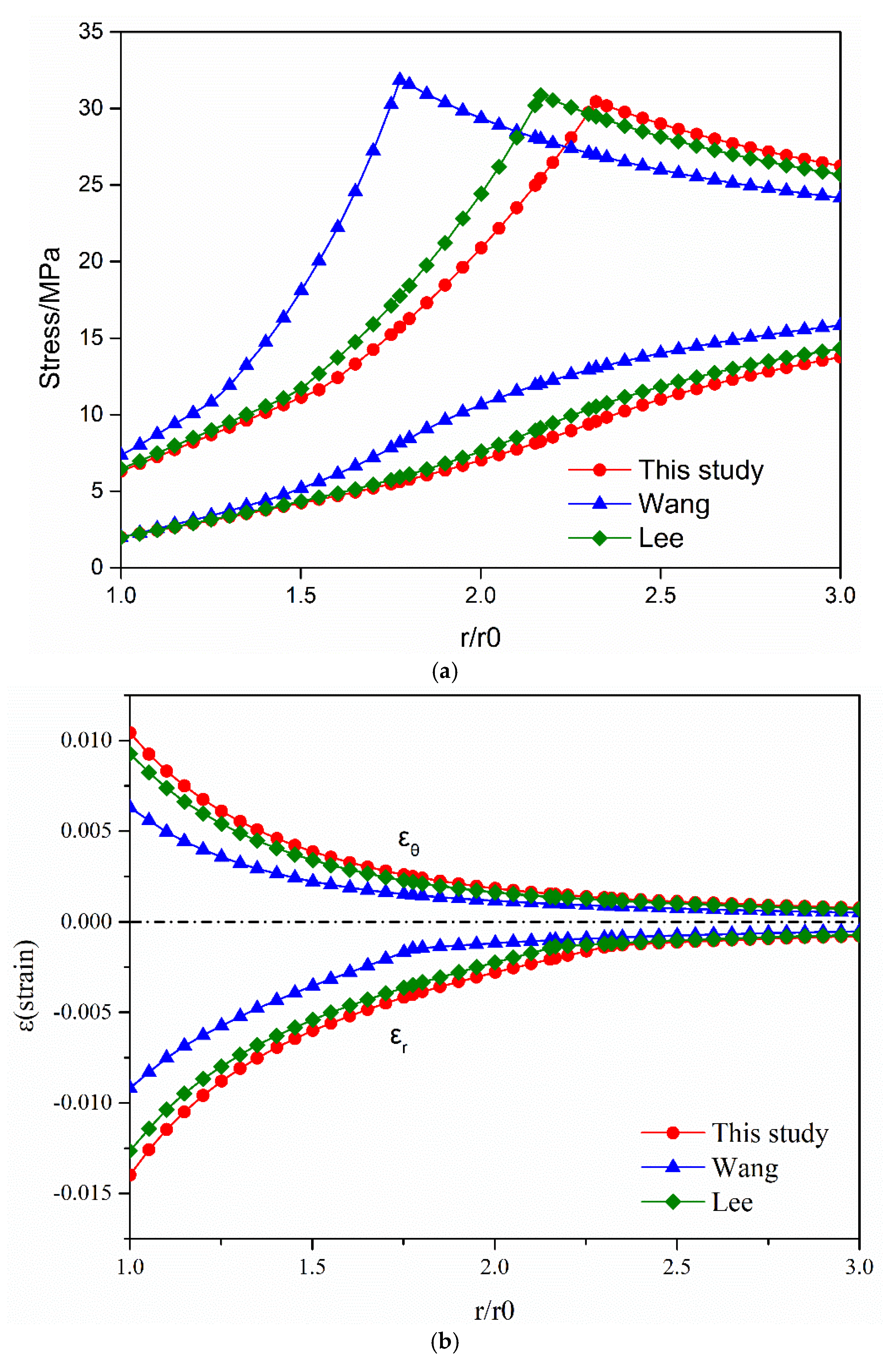
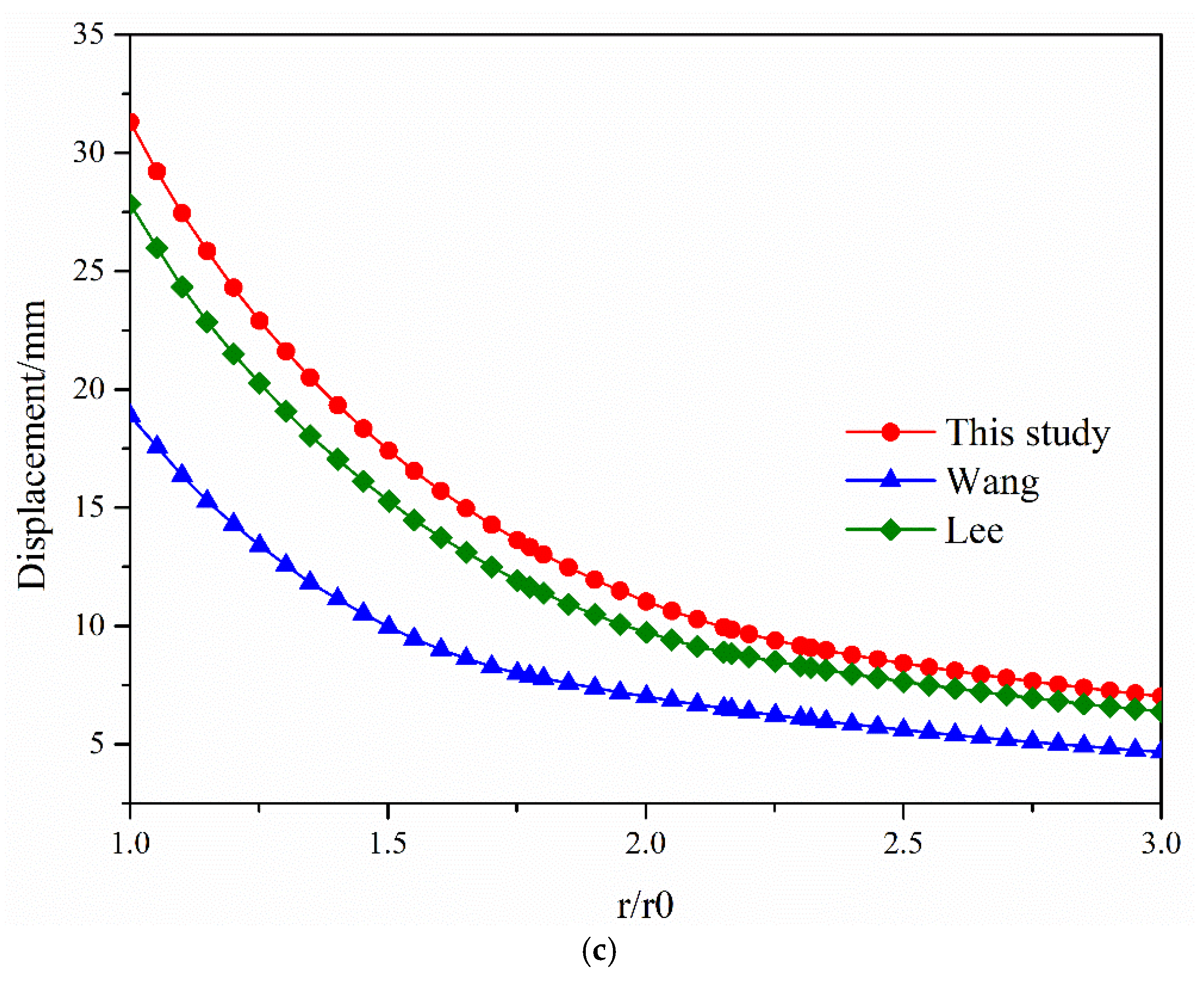
4. Verification of the Proposed Algorithm
5. Discussion
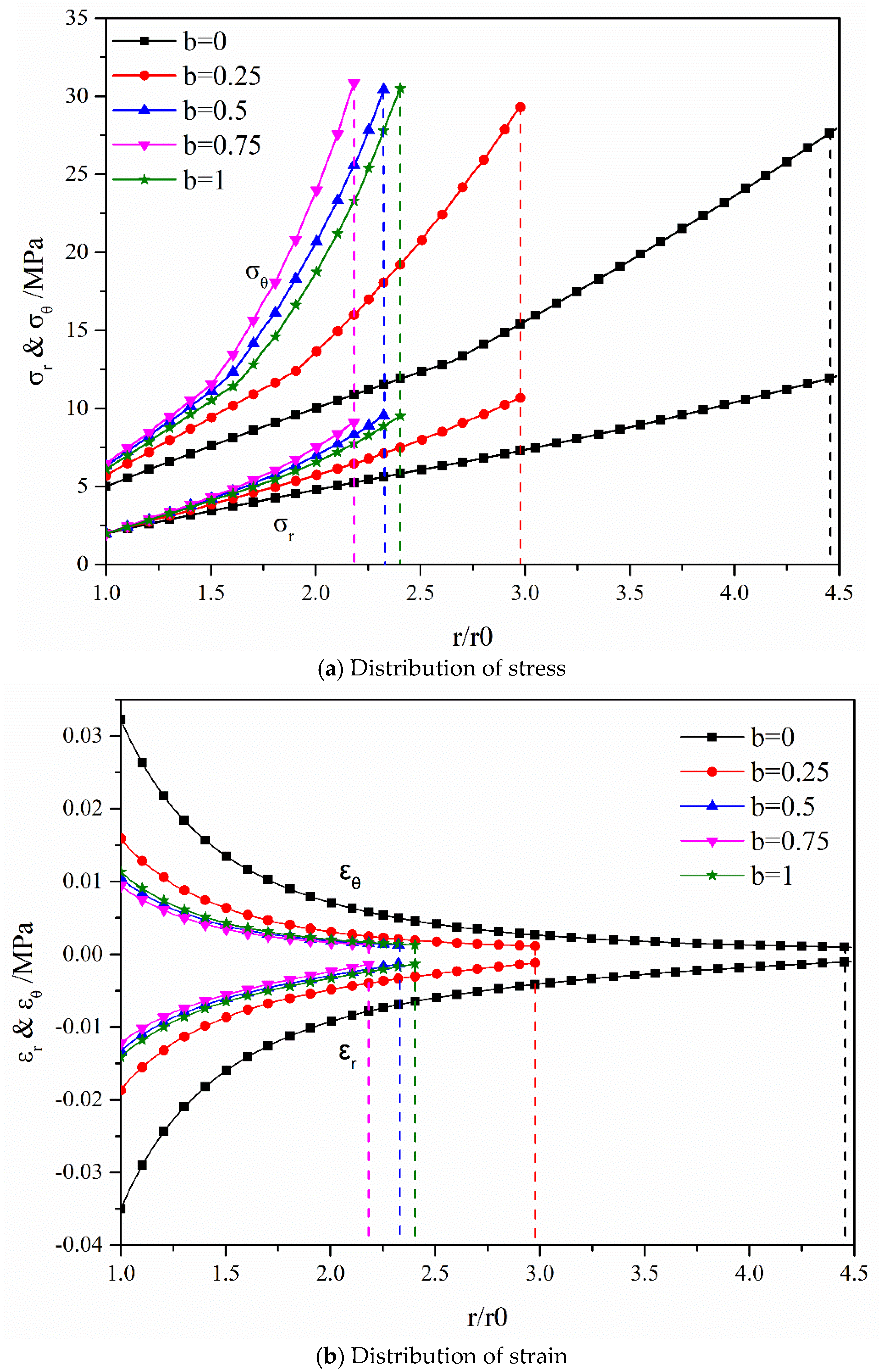
5.1. The Effect of Intermediate Principal Stress on the Distribution of Stress and Strain of Surrounding Rock
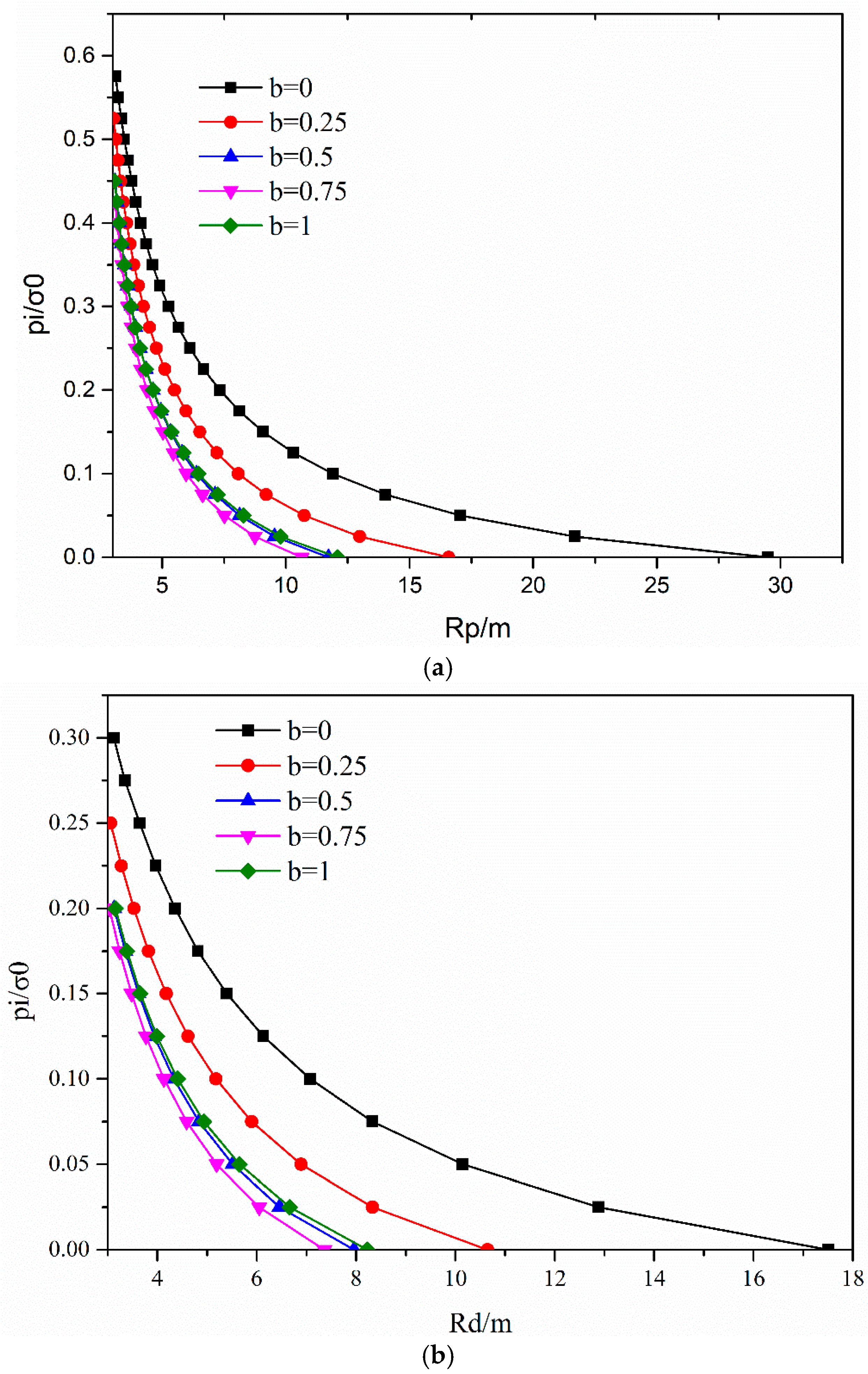
5.2. The Effect of Intermediate Principal Stress on the Development of the Plastic Range
5.3. Influence of Support Pressure pi on Dilatancy Coefficient
5.4. Influence of Intermediate Principal Stress on the Dilatancy of Surrounding Rock
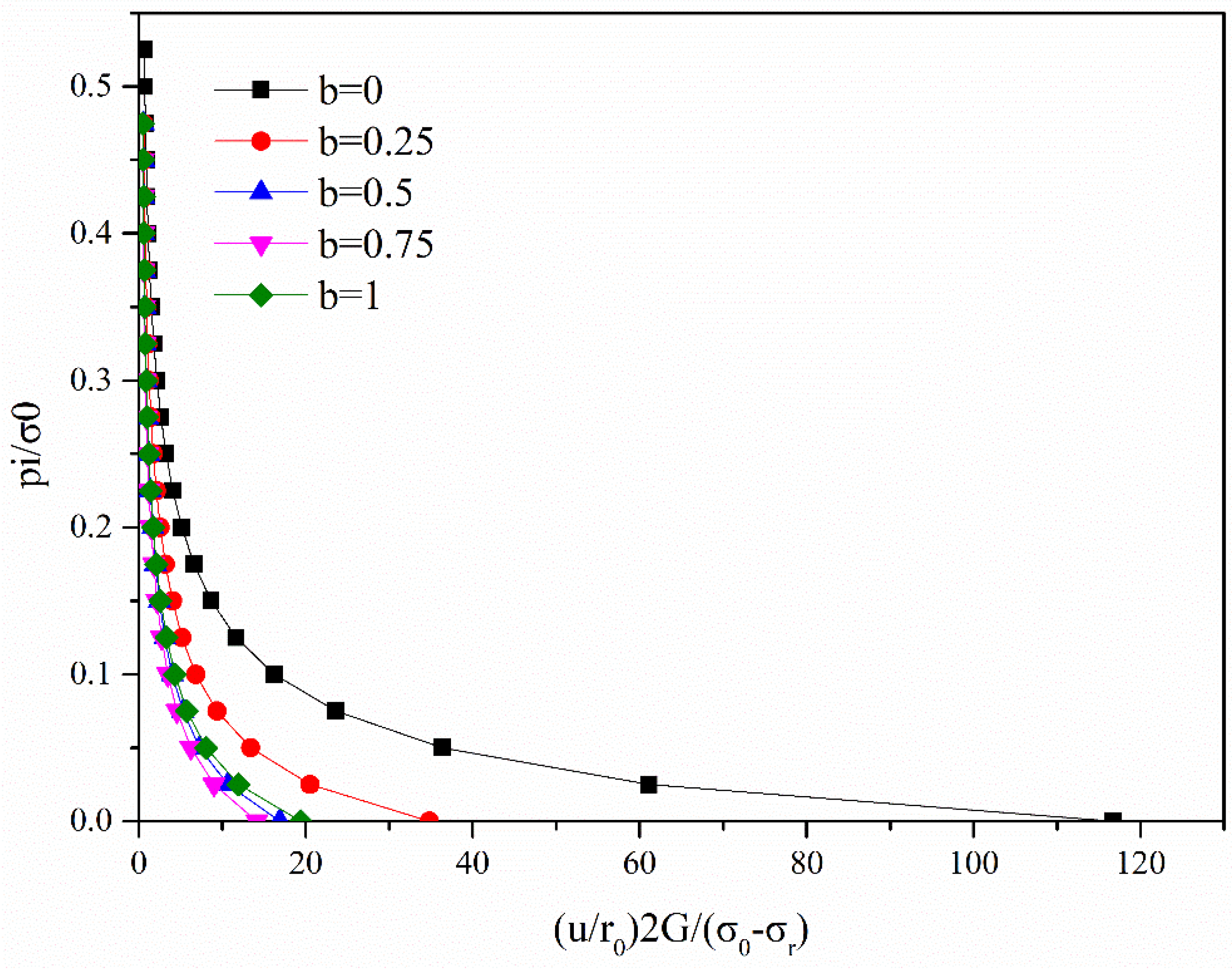
5.5. The Effect of Intermediate Principal Stress on the Ground Response Curve (GRC)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.C.; Hu, C.; Li, L.P.; Song, S.G.; Zhou, Y.; Shi, S.S. Bidirectional construction process mechanics for tunnels in dipping layered formation. Tunn. Undergr. Space Technol. 2013, 36, 57–65. [Google Scholar] [CrossRef]
- Huang, H.W.; Gong, W.P.; Khoshnevisan, S.; Juang, C.H.; Zhang, D.M.; Wang, L. Simplified procedure for finite element analysis of the longitudinal performance of shield tunnels considering spatial soil variability in longitudinal direction. Comput. Geotech. 2015, 64, 132–145. [Google Scholar] [CrossRef]
- Detournay, E. Elastoplastic model of a deep tunnel for a rock with variable dilatancy. Rock Mech. Rock Eng. 1986, 19, 99–108. [Google Scholar] [CrossRef]
- Ogawa, T.; Lo, K.Y. Effects of dilatancy and yield criteria on displacements around tunnels. Can. Geotech. J. 1987, 24, 100–113. [Google Scholar] [CrossRef]
- Brown, E.T.; Bray, J.W.; Ladanyi, B.; Hoek, E. Ground Response Curves for Rock Tunnels. J. Geotech. Eng. 1983, 109, 15–39. [Google Scholar] [CrossRef]
- Fama, M. Numerical Modeling of Yield Zones in Weak Rock. Anal. Des. Methods 1993, 49–75. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C.T. Application of the Convergence-Confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Ghorbani, A.; Hasanzadehshooiili, H. A comprehensive solution for the calculation of ground reaction curve in the crown and sidewalls of circular tunnels in the elastic-plastic-EDZ rock mass considering strain softening. Tunn. Undergr. Space Technol. 2019, 84, 413–431. [Google Scholar] [CrossRef]
- Alejano, L.R.; Alonso, E.; Rodríguez-Dono, A.; Fernández-Manín, G. Application of the convergence-confinement method to tunnels in rock masses exhibiting Hoek–Brown strain-softening behaviour. Int. J. Rock Mech. Min. 2010, 47, 150–160. [Google Scholar] [CrossRef]
- Alejano, L.R.; Rodriguez-Dono, A.; Alonso, E.; Manin, G.F. Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behaviour. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2009, 24, 689–705. [Google Scholar] [CrossRef]
- Song, F.; Rodriguez-Dono, A.; Olivella, S. Hydro-mechanical modelling and analysis of multi-stage tunnel excavations using a smoothed excavation method. Comput. Geotech. 2021, 135, 104150. [Google Scholar] [CrossRef]
- Azadi, M.; Hosseini, S. Analyses of the effect of seismic behavior of shallow tunnels in liquefiable grounds. Tunn. Undergr. Space Technol. 2010, 25, 543–552. [Google Scholar] [CrossRef]
- Alejano, L.R.; Alonso, E. Considerations of the dilatancy angle in rocks and rock masses. Int. J. Rock Mech. Min. 2005, 42, 481–507. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, J.; Zhou, A.; Luo, T.; Wang, N. Unified strength criterion for soils, gravels, rocks, and concretes. Acta Geotech. 2015, 10, 749–759. [Google Scholar] [CrossRef]
- Singh, A.; Rao, K.S.; Ayothiraman, R. An analytical solution to wellbore stability using Mogi-Coulomb failure criterion. J. Rock Mech. Geotech. Eng. 2019, 11, 1211–1230. [Google Scholar] [CrossRef]
- Al-Ajmi, A.M.; Zimmerman, R.W. Relation between the Mogi and the Coulomb failure criteria. Int. J. Rock Mech. Min. Sci. 2005, 42, 431–439. [Google Scholar] [CrossRef]
- Yu, M.H.; He, L.N. A New Model and Theory on Yield and Failure of Materials under the Complex Stress State. In Mechanical Behaviour of Materials-VI, Proceedings of the Sixth International Conference, Kyoto, Japan, 29 July–2 August 1991; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1–4, pp. C841–C846. [Google Scholar]
- Xu, S.Q.; Yu, M.H. The effect of the intermediate principal stress on the ground response of circular openings in rock mass. Rock Mech. Rock Eng. 2006, 39, 169–181. [Google Scholar] [CrossRef]
- Hou, G.Y.; Niu, X.S. Perfect elastoplastic solution of axisymmetric circular openings in rock mass based on Levy-Mises constitutive relation and D-P yield criterion. Rock Soil Mech. 2009, 30, 1555–1562. [Google Scholar]
- Zhang, Q.; Wang, H.Y.; Wang, S.L.; Ge, X.R.; Shao, G. Deterioration elasto-plastic analysis of cracked surrounding rocks based on unified strength theory. Mtan Xuebao/J. China Coal Soc. 2010, 35, 381–386. [Google Scholar]
- Wang, F.; Qian, D. Elasto-analysis for a deep tunnel considering intermediate stress and strain-softening behavior. J. China Coal Soc. 2018, 43, 3329–3337. [Google Scholar]
- Singh, A.; Rao, K.S.; Ayothiraman, R. Effect of Intermediate Principal Stress on Cylindrical Tunnel in an Elasto-plastic Rock Mass. Procedia Eng. 2017, 173, 1056–1063. [Google Scholar] [CrossRef]
- Alonso, E.; Alejano, L.R.; Varas, F.; Fdez-Manin, G.; Carranza-Torres, C. Ground response curves for rock masses exhibiting strain-softening behaviour. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 1153–1185. [Google Scholar] [CrossRef]
- Lee, Y.K.; Pietruszczak, S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass. Tunn. Undergr. Space Technol. 2008, 23, 588–599. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, J.J.; Zhang, R.J.; Dong, Y.K. Elasto-plastic analysis of a circular opening in rock mass with confining stress-dependent strain-softening behaviour. Tunn. Undergr. Space Technol. 2015, 50, 94–108. [Google Scholar] [CrossRef]
- Zhao, X.G.; Cai, M. A mobilized dilation angle model for rocks. Int. J. Rock Mech. Min. 2010, 47, 368–384. [Google Scholar] [CrossRef]
- Khoiri, M.; Ou, C.Y. Evaluation of deformation parameter for deep excavation in sand through case histories. Comput. Geotech. 2013, 47, 57–67. [Google Scholar] [CrossRef]
- Kaliszky, S.; Lógó, J.; Havady, T. Optimal design of elasto-plastic structures under various loading conditions and displacement constraints. Arch. Immunol. Et Ther. Exp. 1989, 20, 169–173. [Google Scholar]
- Medhurst, T.P. Estimation of the In Situ Strength and Deformability of Coal for Engineering Design. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 1997. [Google Scholar]
- Zhang, Q.; Wang, H.-Y.; Jiang, Y.-J.; Lu, M.-M.; Jiang, B.-S. A numerical large strain solution for circular tunnels excavated in strain-softening rock masses. Comput. Geotech. 2019, 114, 103142. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, C.; Guo, Q.; Min, M.; Wang, Y.; Jiang, B. A simple approach to the elasto-plastic coupling analyses of circular tunnels in confining pressure-dependent strain-softening rock masses. Geosystem Eng. 2017, 20, 261–270. [Google Scholar] [CrossRef]
- Wang, F.; Qian, D. Difference solution for a circular tunnel excavated in strain-softening rock mass considering decayed confinement. Tunn. Undergr. Space Technol. 2018, 82, 66–81. [Google Scholar] [CrossRef]
- Wang, S.L.; Yin, X.T.; Tang, H.; Ge, X.R. A new approach for analyzing circular tunnel in strain-softening rock masses. Int. J. Rock Mech. Min. 2010, 47, 170–178. [Google Scholar] [CrossRef]



| Intermediate Principal Stress Coefficient b | ||||
|---|---|---|---|---|
| 0 | 0 | 29.49273 | 17.51012 | 0.5937 |
| 0.25 | 0 | 16.57937 | 10.64699 | 0.6422 |
| 0.5 | 0 | 11.71721 | 7.95609 | 0.6790 |
| 0.75 | 0 | 10.64056 | 7.36186 | 0.6919 |
| 1 | 0 | 12.08821 | 8.22679 | 0.6806 |
| b | 0 | 0.25 | 0.5 | 0.75 | 1.0 |
|---|---|---|---|---|---|
| 1.1805 | 1.2061 | 1.2312 | 1.2404 | 1.2330 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; He, X.; Shen, C.; Zheng, X. A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior. Appl. Sci. 2022, 12, 85. https://doi.org/10.3390/app12010085
Li J, He X, Shen C, Zheng X. A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior. Applied Sciences. 2022; 12(1):85. https://doi.org/10.3390/app12010085
Chicago/Turabian StyleLi, Jinwang, Xiufeng He, Caihua Shen, and Xiangtian Zheng. 2022. "A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior" Applied Sciences 12, no. 1: 85. https://doi.org/10.3390/app12010085
APA StyleLi, J., He, X., Shen, C., & Zheng, X. (2022). A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior. Applied Sciences, 12(1), 85. https://doi.org/10.3390/app12010085






