Abstract
The active jet noise control received significant attention due to the little influence it has on the engine performance. The active jet noise control is a multivariable problem because it needs to achieve the simultaneous closed-loop control of jet noise and engine performance. Model predictive control (MPC) has great application potentials in the field of multivariable control of aero-engines, but the real-time performance of MPC is intractable. This paper proposed an active jet noise controller of a turbofan engine, based on explicit model predictive control (EMPC). An integrated model of turbofan engine and jet noise, which calculates the engine parameters and jet noise in real time, was established. The online computational burden of MPC was transferred to offline computation using multi-parametric quadratic programming (MPQP). To improve the efficiency of the online positioning algorithm, the sequence search method was replaced by a binary search tree. Step simulations were performed to test the effectiveness of the proposed controller. The results show that the proposed EMPC controller not only achieves the simultaneous control of jet noise and the turbofan engine, but also improve the real-time performance greatly.
1. Introduction
Jet noise is the main noise source of jet aircraft. It is caused by the strong turbulent pulsation formed by the rapid mixing of the high-speed air jet from the nozzle and the surrounding medium. Relevant government agencies documents of various countries, such as the Federal Aviation Regulations of the United States [1], aircraft type and airworthiness noise certification regulations of the CAAC [2], aircraft noise environment standards around airports of the State Environmental Protection Administration and so on, have made detailed restrictions on aircraft noise [3]. Aircraft noise reduction, especially jet noise reduction technology, has become an important competitive bargaining chip for the development of large passenger aircraft in various countries [4].
At present, most of the jet noise reduction technologies used in aero-engines are passive noise control technologies, which are mainly achieved by increasing the bypass ratio, and adopting optimized nozzles with special shapes (such as lobe-shaped and saw-tooth-shaped nozzles). Due to the limitation of the engine installation size, the bypass ratio lacks the room for improvement, and the noise reduction potential is limited. When leaving the design point, the noise reduction effect is reduced, and there is a negative impact on the engine’s thrust and other performance parameters. In recent years, some progress was made in the active control of jet noise [5]. Micro jet technology reduces jet noise by injecting air or water into the tail jet flow field. In 1958, Rask et al. [6] in the Langley Research Center in the United States carried out a water jet noise reduction test. Harrison et al. [7] carry out micro-jet noise reduction for core and bypass nozzles at the same time. The overall noise level is reduced by 1.6 dB, and the perceived sound pressure level is reduced by 1.0 dB. Kopiev et al. [8] conduct part of a jet noise control experiment using the model test method. The guide blade technology changes the condition of the bypass jet flow field, shields the strong noise generated by the central gas in a specific direction, and reduces the noise radiation in that direction. This method was first proposed in 2004. Papamoschou et al. [9] verify its effectiveness with experiments, which reduce the peak overall sound pressure level by 8 dB. However, all the above methods actively control jet noise, but also affect the thrust and stability performance of the engine. Therefore, it is necessary to comprehensively consider the noise reduction and performance requirements, and carry out multivariable control for the practical application.
The active jet noise control needs to solve a multivariable control problem [10]. In the closed-loop control structure, the relationship between the speed control loop and the jet noise control loop is strongly coupled, and many constraints need to be considered during the control process. Model predictive control (MPC) is an optimal control method that treats constraints in an efficient way [11]. It has the advantages of prediction and constraint handling, where prediction allows the future dynamics of the system to be considered, and constraint handling capabilities make the output smoother. MPC was successfully applied in the control of an aero-engine. Brunell et al. [12] investigate the feasibility of constrained nonlinear MPC with state estimation, and test this output feedback controller on a high-fidelity turbojet aircraft engine model. Zheng et al. [13] propose a novel nonlinear MPC method for aero-engine direct thrust control. The deep neural network is designed as a predictive model, which improves the control accuracy. Xiao et al. [14] combine a hybrid grey wolf optimizer with a nonlinear MPC method to deal with control constraints and the performance optimization requirements in aircraft engines. Yu et al. [15] propose a wide-range model predictive controller that controls the engine over a wide range within the flight envelope. However, the MPC method needs to compute optimal control online at each step, which means it is computationally expensive [16,17]. This is also verified in the above literature. The real-time performance of the MPC method cannot be guaranteed in practice, especially when the hardware resource is poor. To deal with this drawback, the explicit MPC method is proposed to resolve the multiparametric programming problem corresponding to MPC.
The EMPC method expresses the optimal solution as a piecewise affine (PWA) equation of the state space of the system, and divides the state space of the system convexly to obtain different regions, which are called state partitions by offline calculation [16]. Online calculation only needs to determine the PWA equation in the state partition according to the current system state, and calculate the corresponding feedback control rate solution through the PWA equation, which is called the location problem [17]. Therefore, online optimization is replaced with offline calculation and online parameter positioning, which improves the real-time performance of MPC and expands its application range. Johansen et al. [18] show the digital hardware architecture design results for that explicit MPC solutions, which means it can be implemented in a standard field programmable gate array, or an application specific integrated circuit. However, the regions for storing the explicit solution increases exponentially as the number of constraints increase. The larger the number of regions, the longer it takes to locate the parameters [19].
In order to deal with location problem, many algorithms were proposed. Most of them focus on new data structures and data searching methods, which are introduced to balance online location time and storage requirements. Johansen et al. [20] impose an orthogonal search tree structure on the partition to determine an approximate explicit PWA state feedback solution. The number of the regions for storing the explicit solution is reduced significantly, and the control error is bounded and small. Tøndel et al. [21] firstly use a binary search tree (BST) to evaluate the PWA solution. Through the optimization of a location algorithm, the number of the regions for storing the explicit solution is within the acceptable range, even if the prediction horizon is large. Bayat et al. [22] utilize the hash tables and the associated hash functions to an aggregated point location problem that overcomes prohibitive complexity growth with the number of polyhedral regions, and propose scaling parameters to reduce the storage complexities. Considering the limits of embedded control systems, Bayat et al. [23] deal with a wider class of problems for which the BST method becomes prohibitive in terms of preprocessing time or memory requirements, by combining an orthogonal truncated binary search tree and lattice representation for PWA functions in a unified structure. The above studies show that the real-time performance of an explicit MPC controller is greatly improved. However, it has not been discussed how to apply a binary search tree to an explicit MPC method for aero-engine real-time control, especially for active jet noise control.
Based on the above discussion, this paper designed an active jet noise controller based on explicit model predictive control. The main contributions of this paper can be summarized as follows:
1. To calculate the engine parameters and jet noise in real time, an integrated model of turbofan engine and jet noise was established. The integrated model used the semi-empirical model to calculate the jet noise, and used the component level model of the turbofan engine to calculate the performance parameters. The relationship of parameter transmission between two models was determined.
2. Based on the integrated model of the turbofan engine and jet noise, the explicit MPC controller of active jet noise control was proposed. To improve the search efficiency and the real-time performance of explicit MPC, a binary search tree was adopted as the online positioning algorithm.
3. Comparison experiments were conducted to determine the optimal prediction horizon of the explicit MPC. Moreover, comparison analysis was systematically conducted between the MPC controller, the explicit MPC controller based on a sequential search, and the explicit MPC controller based on a binary search tree, in order to clarify the tracking performance and real-time performance.
The rest of the paper is organized as follows. The integrated model of turbofan engine and jet noise is introduced in Section 2. The explicit MPC controller based on a binary search tree is proposed in Section 3. Several simulation experiments are conducted in Section 4. Conclusions are given in Section 5.
2. Integrated Model of Turbofan Engine and Jet Noise
2.1. Semi-Empirical Model of Jet Noise
A real-time model of the jet noise of turbofan engines with a separate exhaust is the basis of active jet noise control. To meet the real-time requirements of active noise control, a semi-empirical model was chosen for the calculation of the jet noise. There are three main semi-empirical calculation methods: STNJET, ST2JET, and SAE. STNJET and ST2JET are suitable for far-field noise, and SAE is suitable for calculating near-field noise. As the measurable jet noise is far-field noise, SAE cannot ensure good calculation accuracy for the jet noise of turbofan engines. The application ranges between STNJET and ST2JET are different. The subjects of STNJET are usually single or coaxial double flow nozzles, which are limited by the fact that jet speed in the inner duct is faster than that in the outer duct. Compared with STNJET, the application ranges of ST2JET include convergent or convergent-expanding nozzles, and single or coaxial double flow nozzles; the nozzle of turbofan engines is convergent or convergent-expanding. Besides, ST2JET has higher calculation accuracy, especially for high bypass turbofan engines [24]. Therefore, this paper selected ST2JET to build a semi-empirical model of the jet noise of turbofan engines.
The magnitude of noise is usually described by sound power , sound intensity , and sound pressure . The sound power reflects the total sound energy radiated by the sound source per unit time. The square of sound pressure is proportional to sound intensity . The sensitivity of the auditory nerve to sound pressure is directly proportional to its logarithm. Therefore, sound pressure level is usually used to measure the size of sound pressure , which is defined as:
where is the threshold of sound pressure, which can be recognized by the human ear, and .
The noise source of jet noise of aero-engines is a small area centered on the nozzle. The type of jet noise is a quadrupole noise source. For the sound field generated by the turbulent vortex, the sound pressure at the far-field receiving point is:
where is the position vector of the receiving point, is the position vector of the turbulent vortex, is the average density of gas in the turbulent region of the jet, is the volume of the turbulent vortex, is the local speed of sound, is the pulsation speed of the vortex, and is the time variable.
There is no correlation between the pulsations of different vortices. The mean square value of sound pressure at the receiving point in the far-field is the linear superposition of the mean square value of sound pressure generated by each vortex, namely:
where is the number of vortices. The sound intensity is:
The turbulent pulsation of jet flow field is monochromatic. The frequency is assumed as . Then, the following proportional relationship can be obtained:
According to [25], it can be known that:
where is the outlet velocity of jet and is the longitudinal spatial scale of turbulent vortex. The above proportional relationship of unit volume can be simplified as:
The sound power of unit volume is proportional to:
For the jet flow field of turbofan engines, the volume of a ring sheet in the flow field is
where is the equivalent diameter of nozzle area and is the distance from the nozzle. Considering that is positively correlated with , the sound power of a ring sheet is proportional to:
The length of the mixing zone of the jet is about , so the total sound power of the jet is proportional to:
When the distance between the receiving point and sound source is , the sound pressure is proportional to:
Then, the sound pressure level generated by the jet flow at the far-field can be simplified as:
where are constants, is the velocity of jet flow, represents the average density in the turbulent region, is the outlet area, is the distance between the sound source and receiving point, and is calculated by local density and sonic speed .
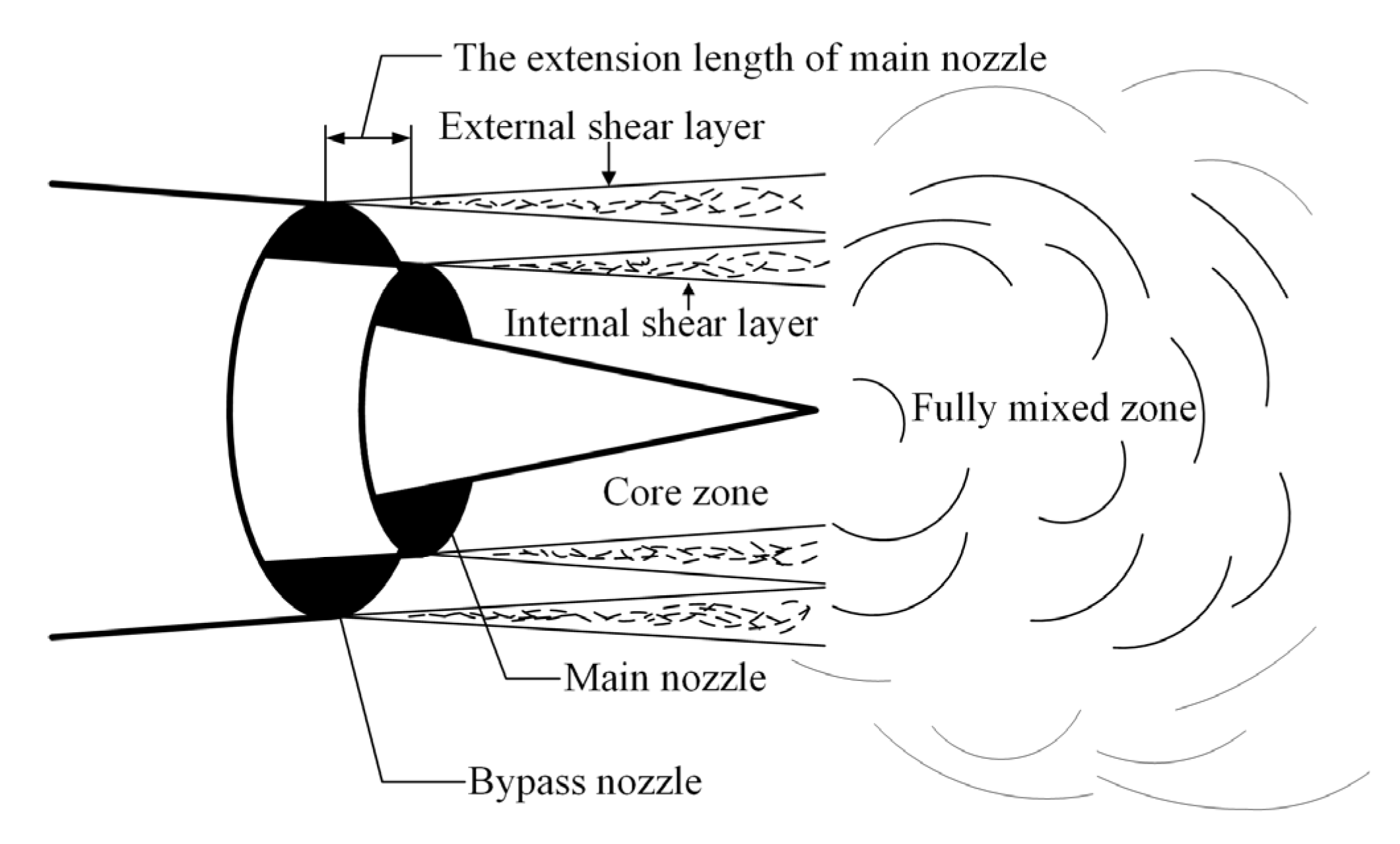
According to the different flow field characteristics, the jet flow field of a turbofan engine with a separate exhaust is divided into several zones for analysis and calculation, which is shown in Figure 1. There are four main zones in the figure, namely, the jet core zone, full mixing zone, external shear layer, and internal shear layer. Therefore, the sound pressure level of four zones is calculated by Equation (13), and the total sound pressure level is obtained through the logarithmic superposition of sound pressure level of four parts, which is shown in Equation (14).
where is the total sound pressure level, is the sound pressure level of external shear layer, is the sound pressure level of internal shear layer, and is the sound pressure level of the jet core zone.
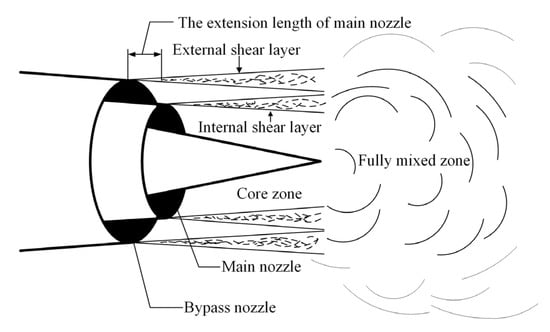
Figure 1.
The structure of jet flow of turbofan engines with separate exhaust.
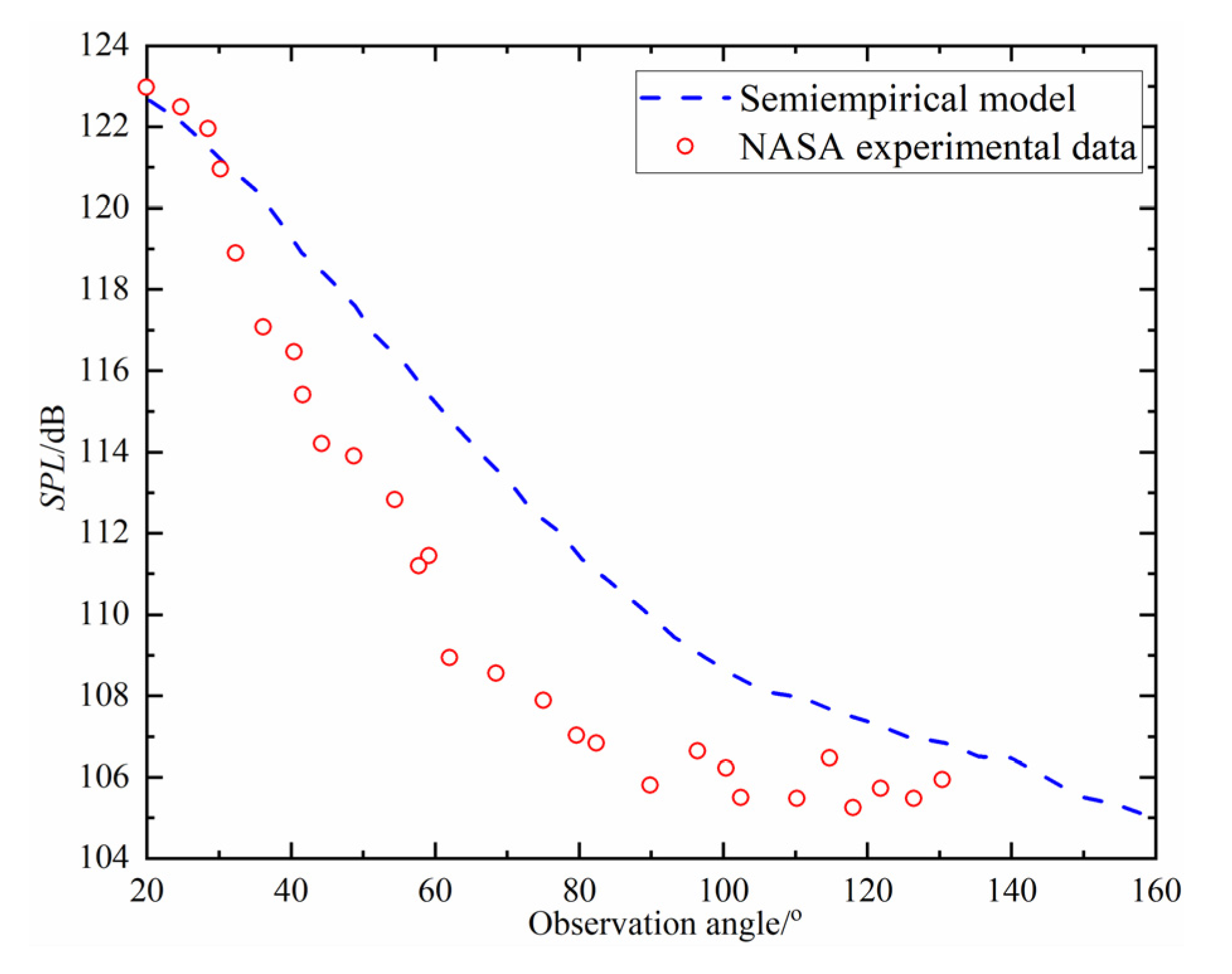
According to Ref [26], NASA carried out a full-size jet noise measurement experiment on a separate exhaust nozzle, with an inner diameter of 0.7 m and an outer diameter of 1.37 m. The experimental object is similar to the object studied in this paper. The experimental data can be used to verify the jet noise model in this paper. Therefore, a simulation test was carried out to verify the calculation accuracy of the semi-empirical model. By regulating the Mach number in the mixed zone, the simulation conditions were similar to the experiment conditions. The measuring radius of the sound field is 50 m. The comparison results between the simulation and experiment are shown in Figure 2. The difference between the simulation and experiment at each observation angle is within the range of 5 dB, and the change trend is basically consistent. The results show that the semi-empirical model in this paper has good accuracy in noise prediction, and can be used to conduct the design of the controller.
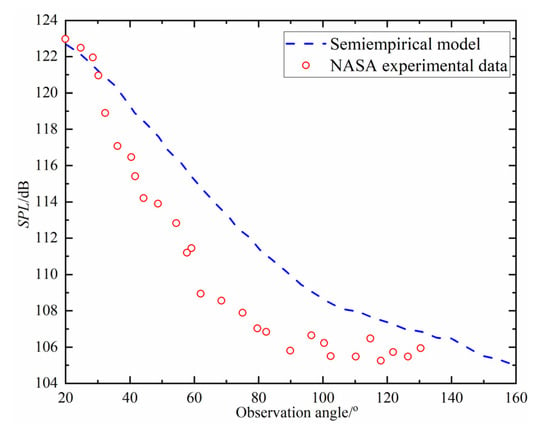
Figure 2.
Comparison results between simulation and experiment data.
2.2. Component Level Model of Turbofan Engine with Separate Exhaust
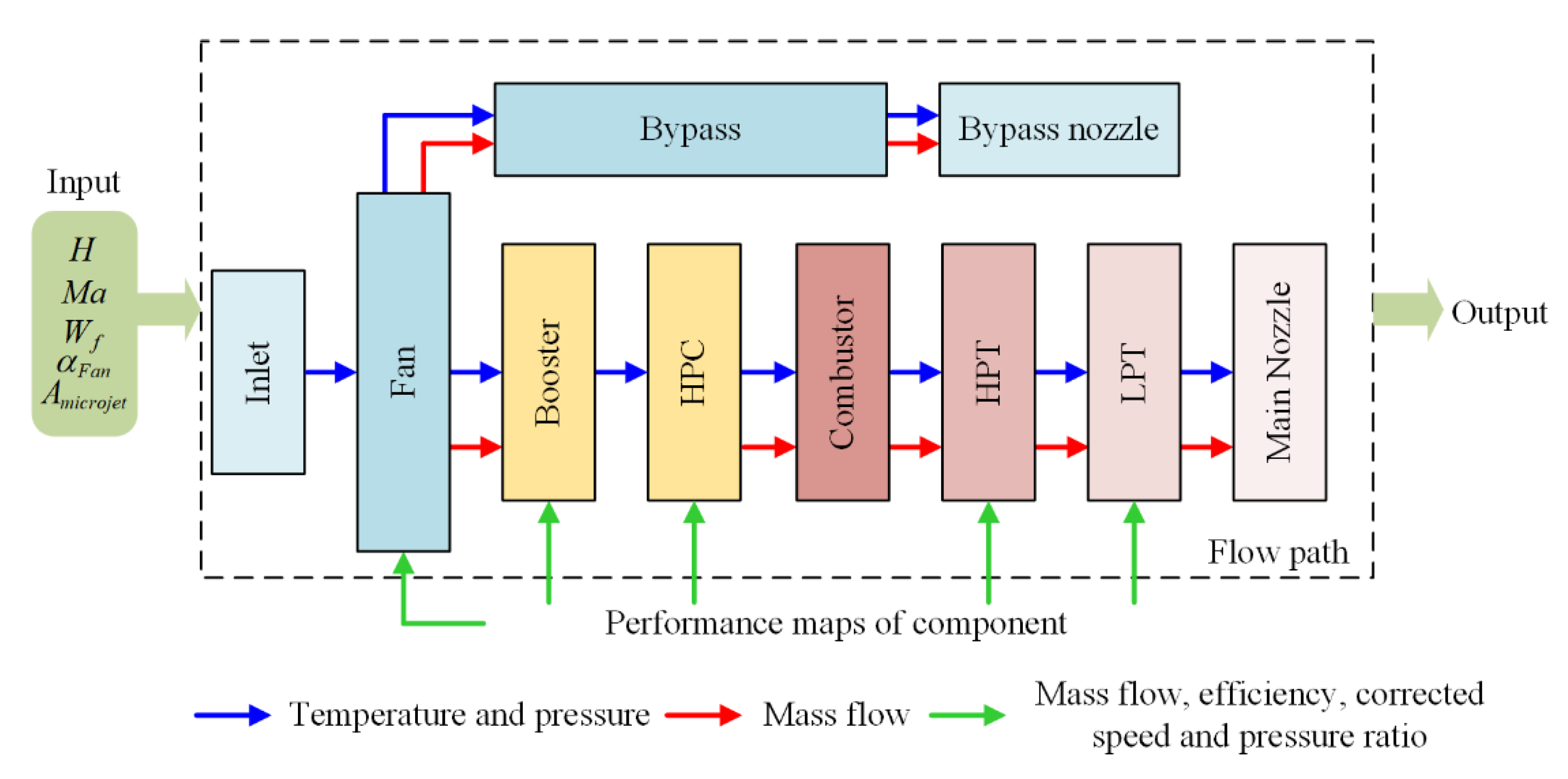
The structure of the turbofan engine with separate exhaust includes ten components, namely, inlet, fan, booster, high pressure compressor (HPC), combustor, high pressure turbine (HPT), low pressure turbine (LPT), main nozzle, bypass, and bypass nozzle. The component level model (CLM) of the turbofan engine is used most extensively as a performance model. For model construction, each component of the engine is modelled based on dynamic aerothermodynamics principles, rotor dynamics, etc. Then, the operation relationship among components is established by the co-operating equations, including the flow continuity equations, pressure balance equations, and power balance equations or shaft dynamics equations [27]. The Newton–Raphson method is usually used to solve the formulated nonlinear co-operation equations, and the performance parameters, which are the outputs of the CLM, derived.
A detailed description of CLM is found to in [28], and Figure 3 gives the computation flowchart of the CLM. denotes the flight height; denotes the flight Mach number; represents the fuel flow of combustor; is the inlet guide blade angle of fan; and is the area of micronozzle throat. and can adjust the running state of the engine. The role of micronozzle is to mix a small fraction of gas in the booster with the outlet airflow of the main nozzle. In this paper, the active jet noise control was realized by controlling the flow of the micronozzle, and regulating the inlet guide blade angle of the fan.
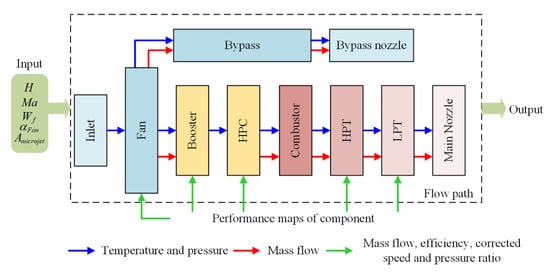
Figure 3.
Schematic diagram of computational interaction of turbofan engine model.
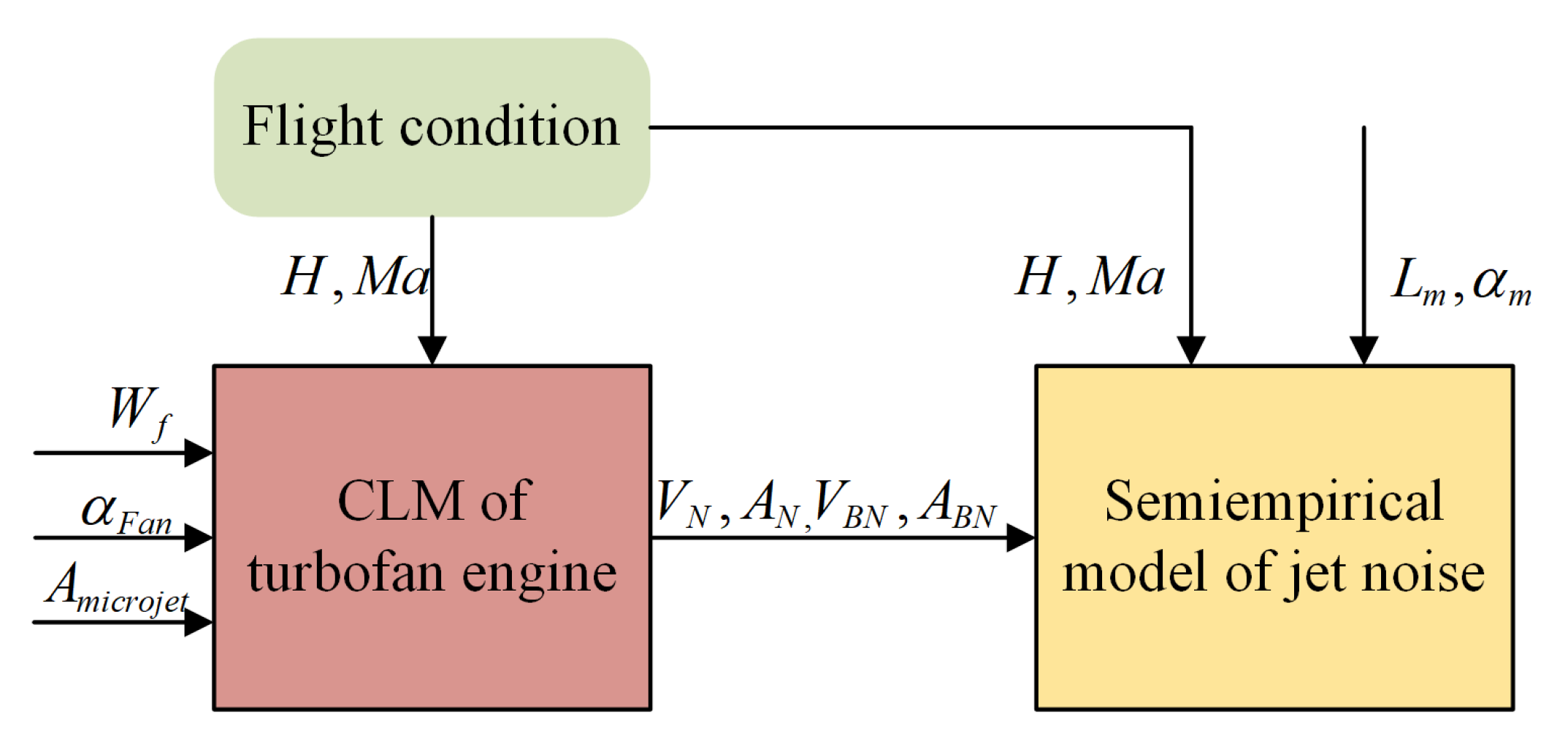
2.3. Integrated Model of Turbofan Engine and Jet Noise
The role of the integrated model of the turbofan engine and jet noise is to calculate real-time performance parameters and noise, which is the basis of active jet noise control. The relationship of the parameter delivery between the semi-empirical model of jet noise and the CLM of the turbofan engine with separate exhaust is illustrated in Figure 4. The flight conditions, namely height and Mach number , are both the input of CLM and the semi-empirical model. The semi-empirical model calculates noise according to the parameters of the CLM, which are the velocity of main nozzle , the area of main nozzle throat , the velocity of bypass nozzle , and the area of bypass nozzle throat . The distance and angle between the noise source and receiving point are also the input of the semi-empirical model.
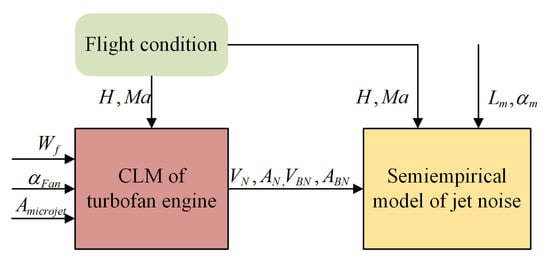
Figure 4.
The structure of integrated model of turbofan engine and jet noise.
3. Explicit MPC Controller Design
3.1. Control Structure of Active Jet Noise Control of Turbofan Engine
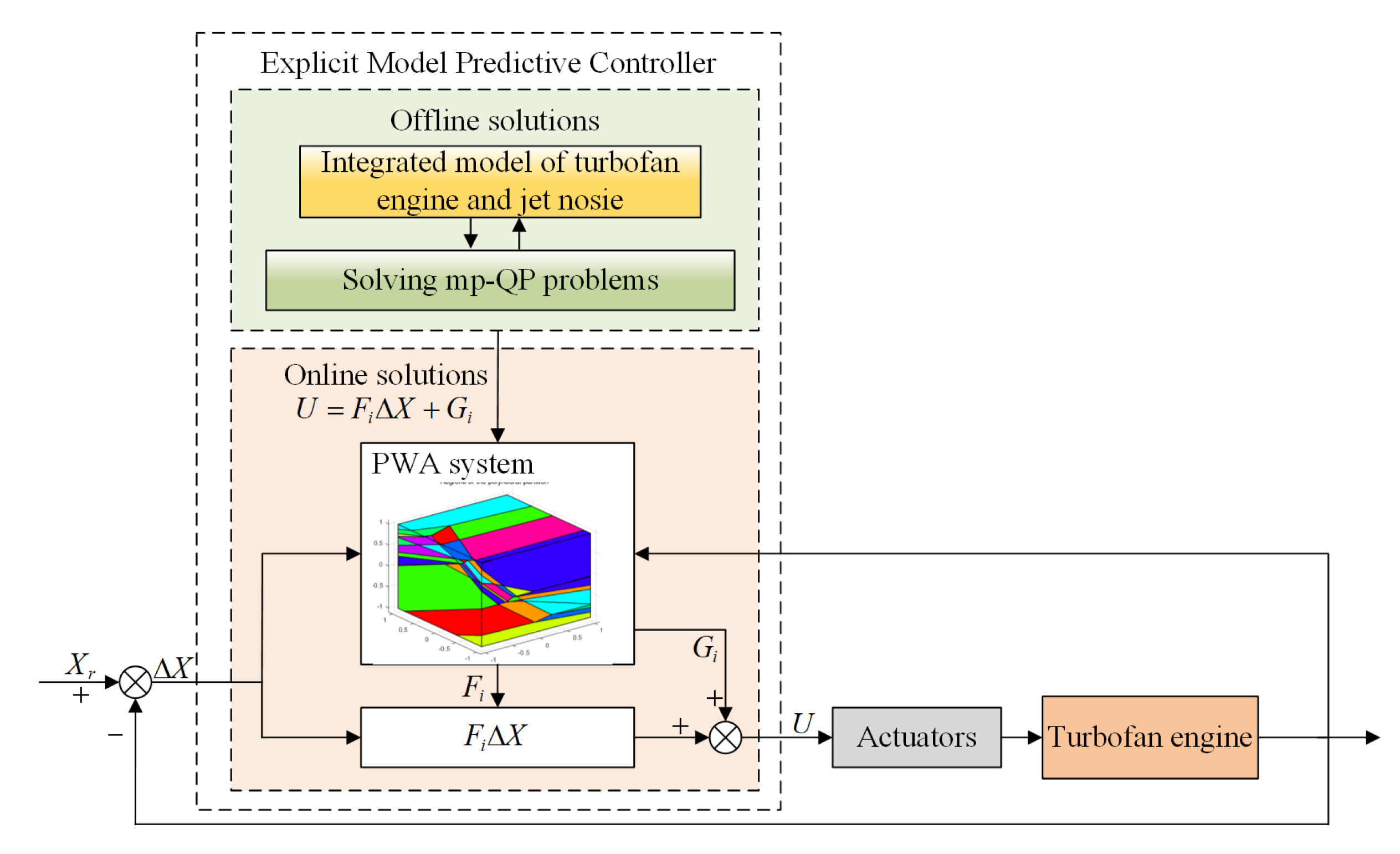
The structure diagram of an active jet noise controller based on the explicit model prediction is shown in Figure 5. The explicit model controller is divided into two parts: offline solution and online solution. Offline solving introduces multi-parameter programming to solve the constrained quadratic programming problem; that is, to solve the multi-parametric quadratic programming (MPQP) problem about jet noise. The state feedback explicit control rate is calculated, that is, the piecewise affine system (PWA) between the optimal control amount of the engine and the current state amount in a specific flight state, and the optimal control variable is expressed as:
where is the difference between the system state quantity and the command, namely , which are the engine high and low pressure speed and the sound pressure value of the jet noise at the measurement point, respectively, and is the obtained optimal control quantity, namely . and are constant matrices, and the subscript i corresponds to the i-th partition area of the PWA system. The size of the two constant matrices depends on the current system state quantity and the controller input . The online solution of the explicit MPC needs to search for the corresponding partition and constant matrix according to the current state quantity and command, and calculate the optimal control quantity at the current moment, according to the explicit solution of the control rate on the partition. This solution does not require repeated online rolling optimization calculations, and the calculation time is greatly reduced, and it is easy to realize the project of the online real-time model predictive control.
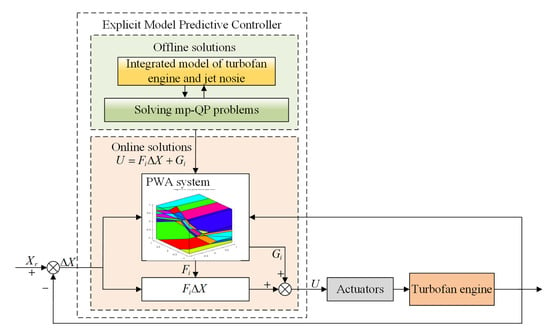
Figure 5.
Active jet noise reduction controller structure based on explicit model prediction method.
3.2. Construction of Explicit MPC Model
For a specific flight stage, the state space model is established at different low pressure shaft speeds, by linearizing the integrated model of the turbofan engine and jet noise. The state space model and equilibrium parameters corresponding to other values are obtained by using values as interpolation variables, so as to establish the variable parameter linear model within the whole range of variation in the flight state. Under a certain value of , the discrete state space model of the system can be written as:
Among them, state , and input . represents the difference relative to the corresponding value of the balance point at the speed, that is, if the balance point corresponding to a certain is , then . The discrete state space model is used as the prediction model to calculate the output of the system corresponding to the input at multiple times in the future.
Assuming a finite control horizon and prediction horizon , the control increment sequence is , and the state increment sequence is Each term in the state increment sequence can be expanded with Equation (16), as follows:
The output increment sequence is . With matrix multiplication, can be expressed as follows:
where
The track performance of the controller is determined by the output errors. The smaller their absolute value, the better the track performance. In addition, the variation of control sequence must be limited. At the time , the track performance cost is defined as:
where , are the weight matrices, and is the target command.
The total performance cost is the sum of in a finite horizon. It can be calculated as follows:
where
;
.
Considering Equation (18), Equation (21) can be simplified into the following form:
where , and . is the optimization variable, while the term has nothing to do with the optimization variable. So the term is removed. As and are constant, is replaced with . The updated cost is as follows:
where . There are many constraints on the control sequence and the state sequence. For the sake of description, the constraints can be written as the following uniform form:
where are determined according to the constraint conditions, then the problem is transformed into solving the following multi-parameter quadratic programming (MPQP) problem:
To simplify the MPQP problem, a new optimization variable is defined. The final MPQP optimization problem is as follows:
where .
The next goals are: within the parameter limit, find the expressions of the value function and the optimal value function corresponding to the parameter , and prove that the optimal value function is a continuous PWA function on .
3.3. Offline Solution of Explicit MPC Model
For the above MPQP problem, because is a convex set, the solution , under the Karush–Kuhn–Tucker (KKT) conditions, is the global minimum. At this time, the corresponding KKT condition is:
In the formula, represents the ith row, is the Lagrangian operator, and is the number of constraints, which can be solved:
The above formula can be combined as . This formula is valid for all . is called the critical region for the current state value . For this critical region, it can be obtained by the following method:
Lagrange multipliers are non-negative, so:
So the critical region is:
That is, according to the current engine system state , the corresponding critical region can be found, and the current optimal control parameters can be obtained by solving the linear function of the critical region . As the control quantity is a single-valued function of , a further simplification can be written as:
This is a piecewise affine explicit relationship, where is the i-th state partition, and are the control variable constant matrix corresponding to the partition. Then the optimal control quantity of the system at this time is:
The optimal control problem of the system is transformed into a calculation of the PWA function with the system state as the independent variable, and the optimal control input as the dependent variable.
3.4. Online Solution of Explicit MPC Model
The core of the online solution is to determine the position in the state partition, according to the state value of the current system. The calculating speed of this part directly affects the real-time performance of the control system. The general online solution is a sequential search. This method determines the position through traversing each polyhedron, which is shown in Algorithm 1 below. However, if the number of polyhedral regions is large, the traverse takes too much time. In this paper, the efficient binary search tree (BST) method was employed. A binary tree storing polyhedrons and corresponding solutions was constructed offline in advance.
| Algorithm 1 Sequential search algorithm |
| 1: Input 2: Initialize 3: While 4: if break; 5: ; 6: end while 7: if the problem is unfeasible, otherwise 8: 9: Output: |
The polyhedral regions are divided into the set . Each polyhedral region is determined by a limited number of hyperplanes. The total hyperplane set is . is the total number of hyperplanes. The positional relationship between a hyperplane and a polyhedron can be determined based on signs of , where . The minimum of is . The maximum of is . If and , is on the negative side of . If
and , is on the positive side of . If , is on the both sides of . The polyhedron regions set on the negative side is , and on the positive side is (polyhedrons on both sides belong to and at the same time). and can be further divided with new hyperplanes. The binary search tree is formed by following this rule recursively.
The main idea of the BST method is to construct a BST tree, and select the best boundary hyperplane as the partition hyperplane, so that the number of PWA control functions is minimized from the current node of the tree to the child nodes of the next layer. The size of a node represents how many polyhedron regions the node contains, so a method that reduces the size of a node is adapted by solving the problem below:
where and are the sizes of sets , . The hyperplane corresponding to index is selected as the split hyperplane. A node in the binary tree, consists of the polyhedron regions set and the split hyperplane.
After the construction of the binary search tree, the binary tree search algorithm is proposed. is the highest node in a binary tree, and the explored node is initialized by firstly. By calculating the distance between the split hyperplane and , is updated to the child node. Until the size of the explored node is 1, the search process is completed. The detailed binary tree search algorithm is shown in Algorithm 2, as follows
| Algorithm 2 Binary tree search algorithm |
| 1: Input and a binary tree 2: let , is the explored node; 3: while : 4: calculate is the split hyperplane; 5: if update to its left children node; 6: else update to its right children node; 7: end while 8: Calculate according to the unique element in set 9: Output: |
4. Simulation Results and Analysis
To verify the performance of the proposed explicit MPC controller, several experiments are simulated on the Simulink platform. The simulation hardware is Intel Core i7 9700K, 3.6 GHz CPU, and 16 GB RAM. All the algorithms are programmed in MATLAB R2019b.
4.1. Predictive Model of Explicit MPC
The explicit MPC is based on the state space model. Therefore, the integrated model of the turbofan engine and jet noise is linearized at steady-state points. Select as the input of the state space model, as the state of the state space model, and as the output of the state space model, where is the speed of high pressure rotor, is the speed of the low pressure rotor, is the total sound pressure level of jet noise, is the thrust of the turbofan engine, and is the inlet temperature of the high pressure turbine of the turbofan engine. In this paper, the climb phase of an aircraft is used an example. At this phase, Ma = 0.2 and the flying altitude is about sea level. When is 100% rotation speed, the continuous state space equation of the integrated model is obtained by the small deviation method, and the following normalized system matrix is obtained:
The state weighting matrix and the input weighting matrix for the explicit MPC controller are, respectively:
4.2. Step Simulation with Different Prediction Horizons
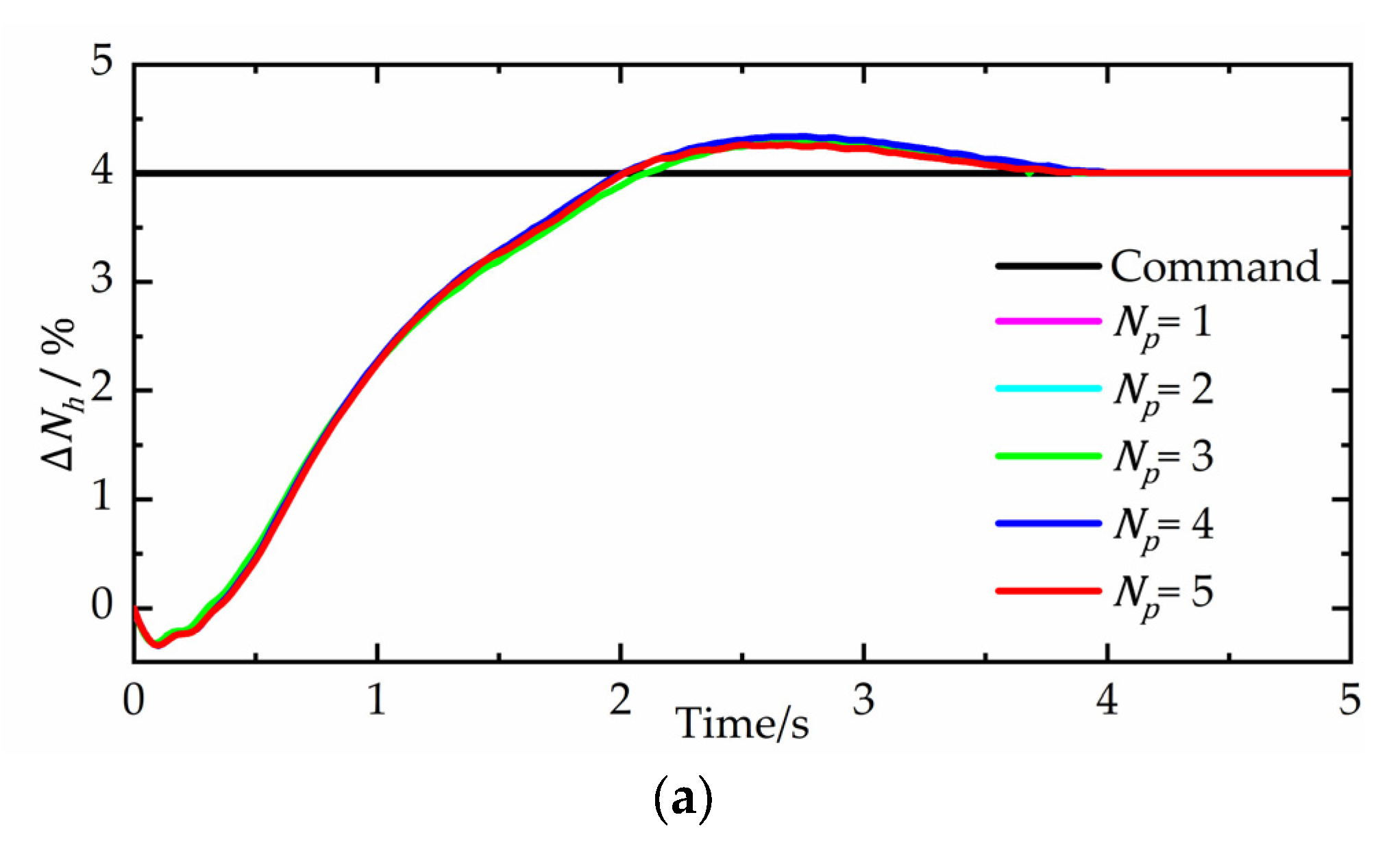
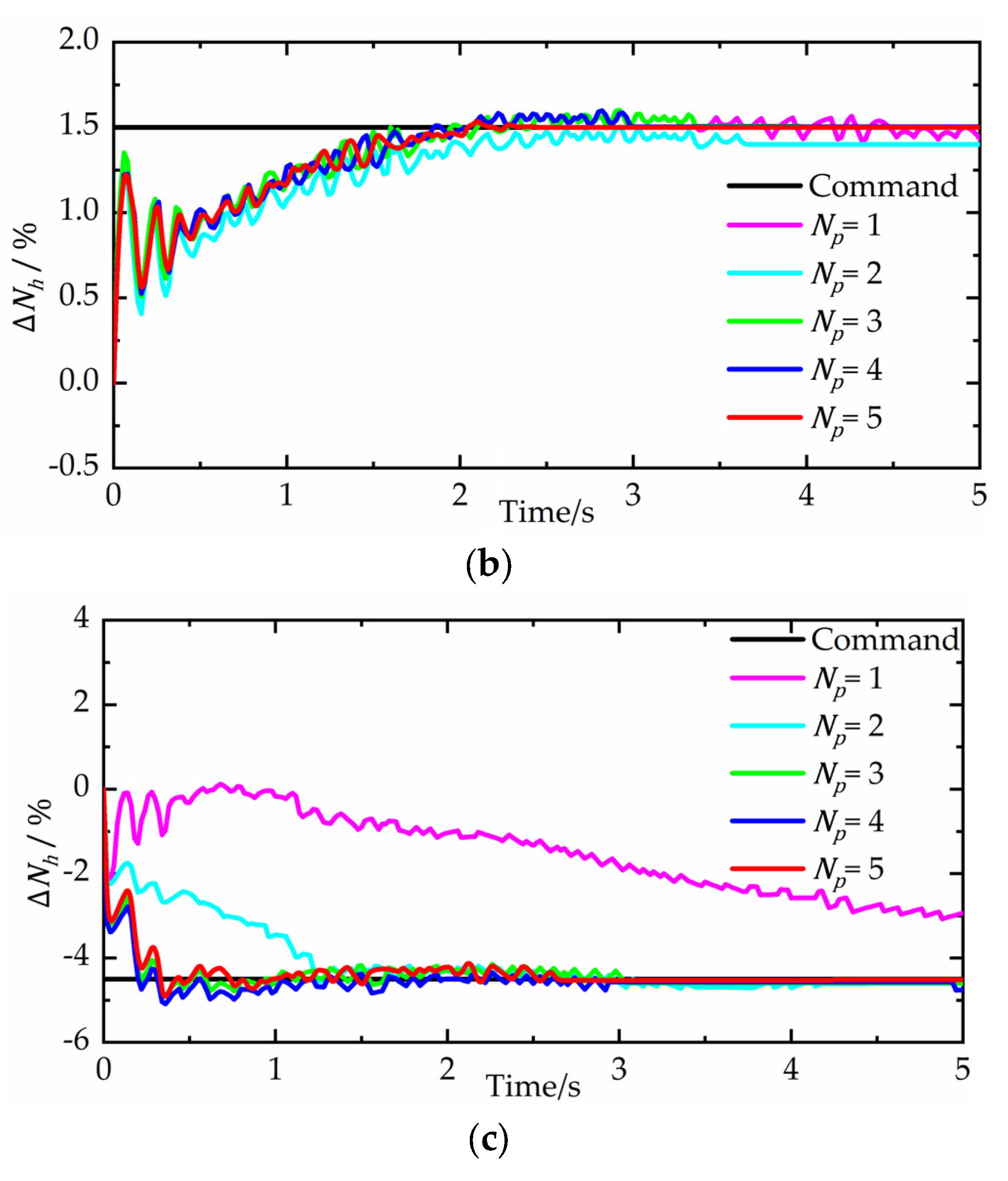
To determine the best prediction horizon of the explicit MPC controller, a step simulation experiment is carried out. The command changes 4%, command changes 1.5%, and command changes −4.5%. The simulation results are shown in Figure 6. It is noticed that the prediction horizon and control horizon are always equal in this paper. The range of the prediction horizon is from 1 to 5.
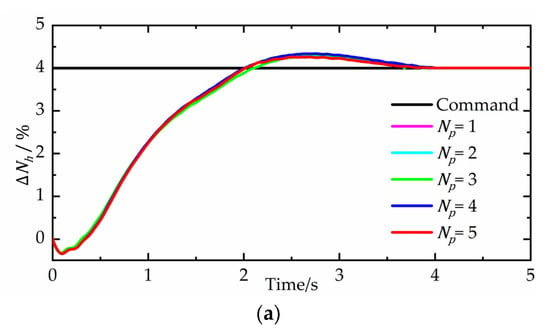
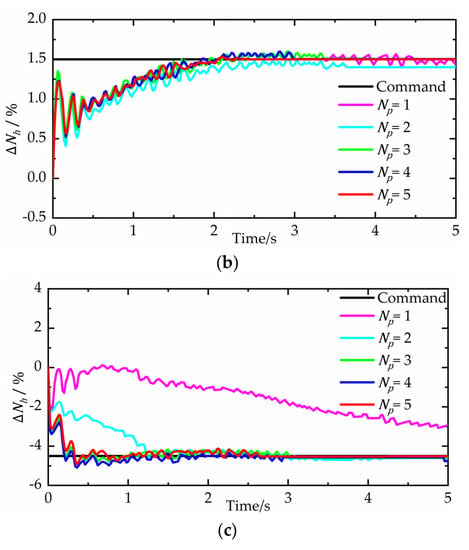
Figure 6.
Step responses at different prediction horizons. (a) Variation of speed of high pressure rotor. (b) Variation of speed of low pressure rotor. (c) Variation of total sound pressure level of jet noise.
From Figure 6a, the control effect of is similar at different prediction horizons. The settling times are all less than 4 s. When the prediction horizon is 5, the step response has the smallest overshoot. However, all the settling processes of have different degrees of oscillation in Figure 6b. When the prediction horizon is 5, the settling time is 2.43 s, while the others are more than 4 s.
As the explicit MPC controller is a three-variable controller, there are strong interactions between different control loops. The control effect of , especially when is 1, is terrible. The step response cannot follow the command. From Figure 6c, it can be seen that the control effect gradually becomes better with the increasing of the prediction horizon.
To show the control effect more intuitively, the root mean square errors (RMSE) between the step responses and commands are calculated by
where is the number of sampling time points, is the command value, and is the step response.
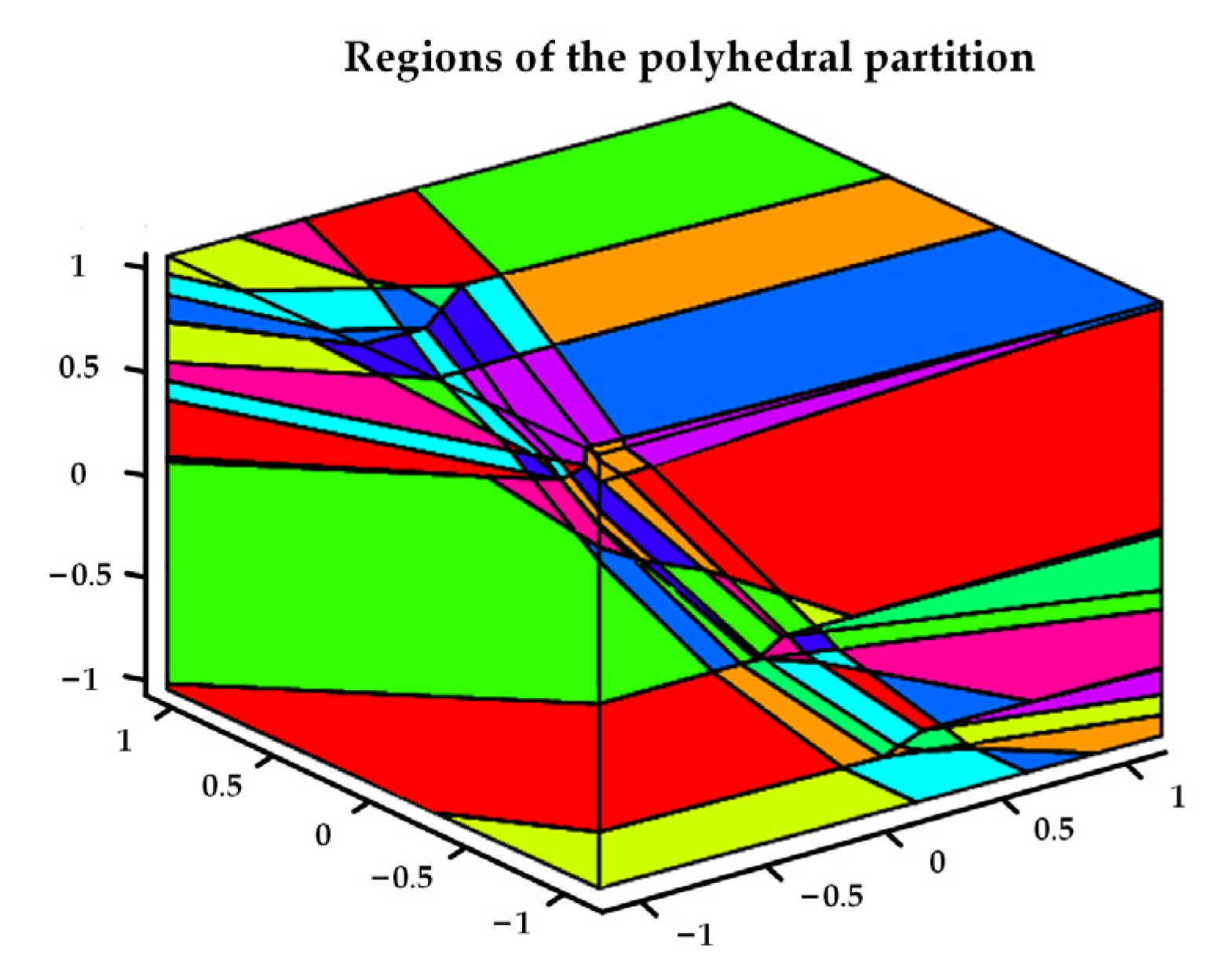
Table 1 gives the comparison of the control error at different prediction horizons. The prediction horizon 4 has the smallest RMSE of , and the prediction horizon 5 has the smallest RMSE of and . The difference of between the prediction horizon 4 and 5 is only 0.063%, which can be neglected. There is no doubt that the prediction horizon 5 is the best choice. When the prediction horizon is more than 5, the computation burden increases significantly, and the computing accuracy improves a little. So, the prediction horizon is chosen as 5 in this paper. The regions of the polyhedral partition at the prediction horizon 5 are shown in Figure 7.

Table 1.
Control errors at different prediction horizons.
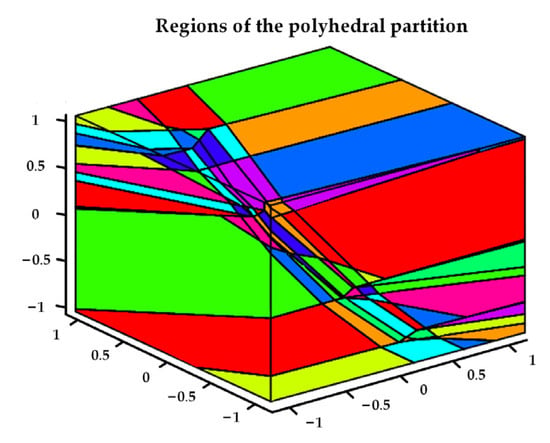
Figure 7.
Regions of the polyhedral partition at the prediction horizon 5.
4.3. Continuous Step Simulation
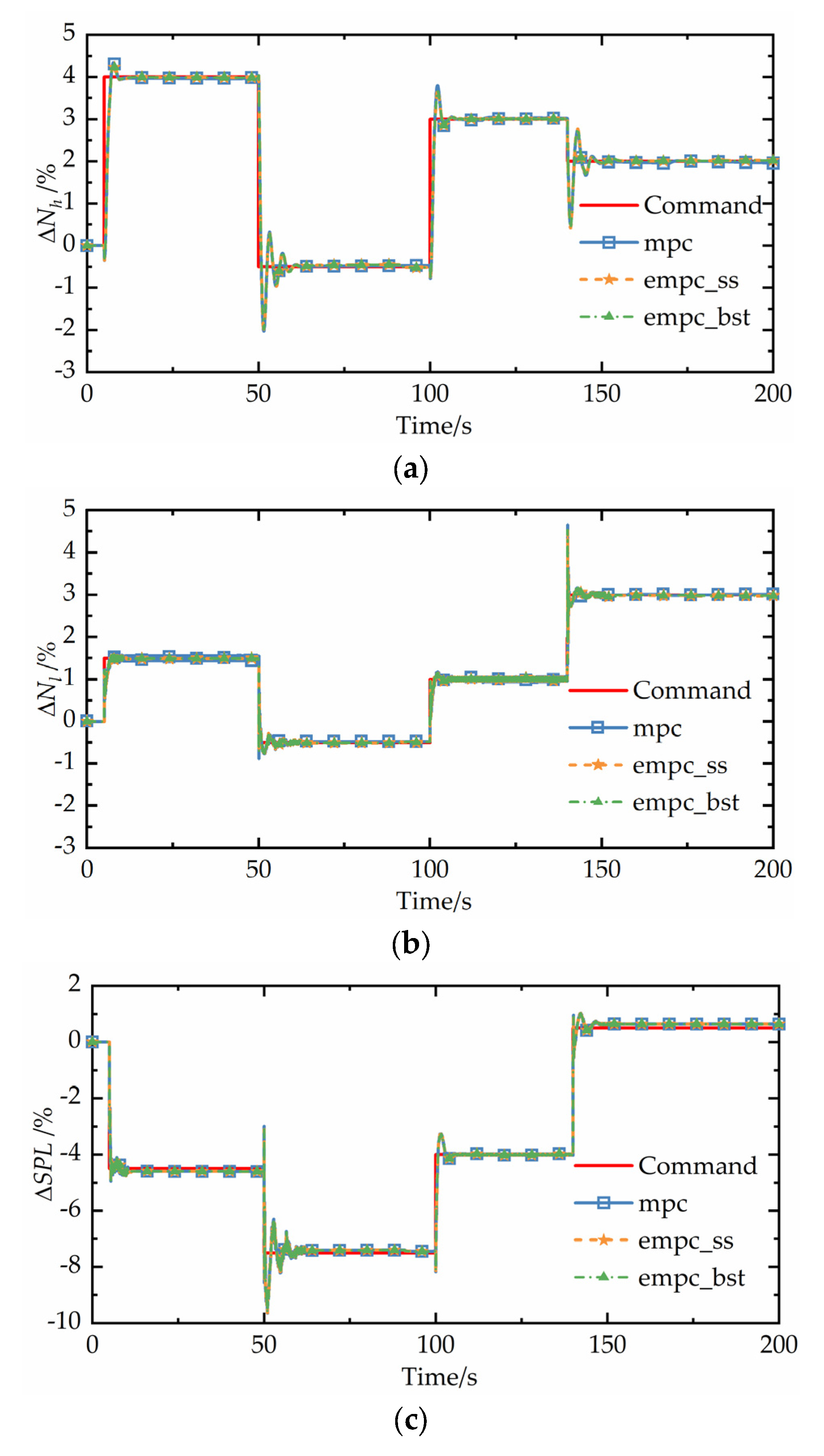
To highlight the performance of the proposed explicit MPC controller with a binary search, continuous step simulation experiments are carried out. The control performance is compared with original MPC and explicit MPC based on a sequence search. In the figure below, the ‘‘explicit MPC based on binary search tree’’ method, the ‘‘explicit MPC based on sequence search’’ method, and original MPC are notated as ‘‘empc_bst,’’ ‘‘empc_ss,’’ and ‘‘mpc’’, respectively.
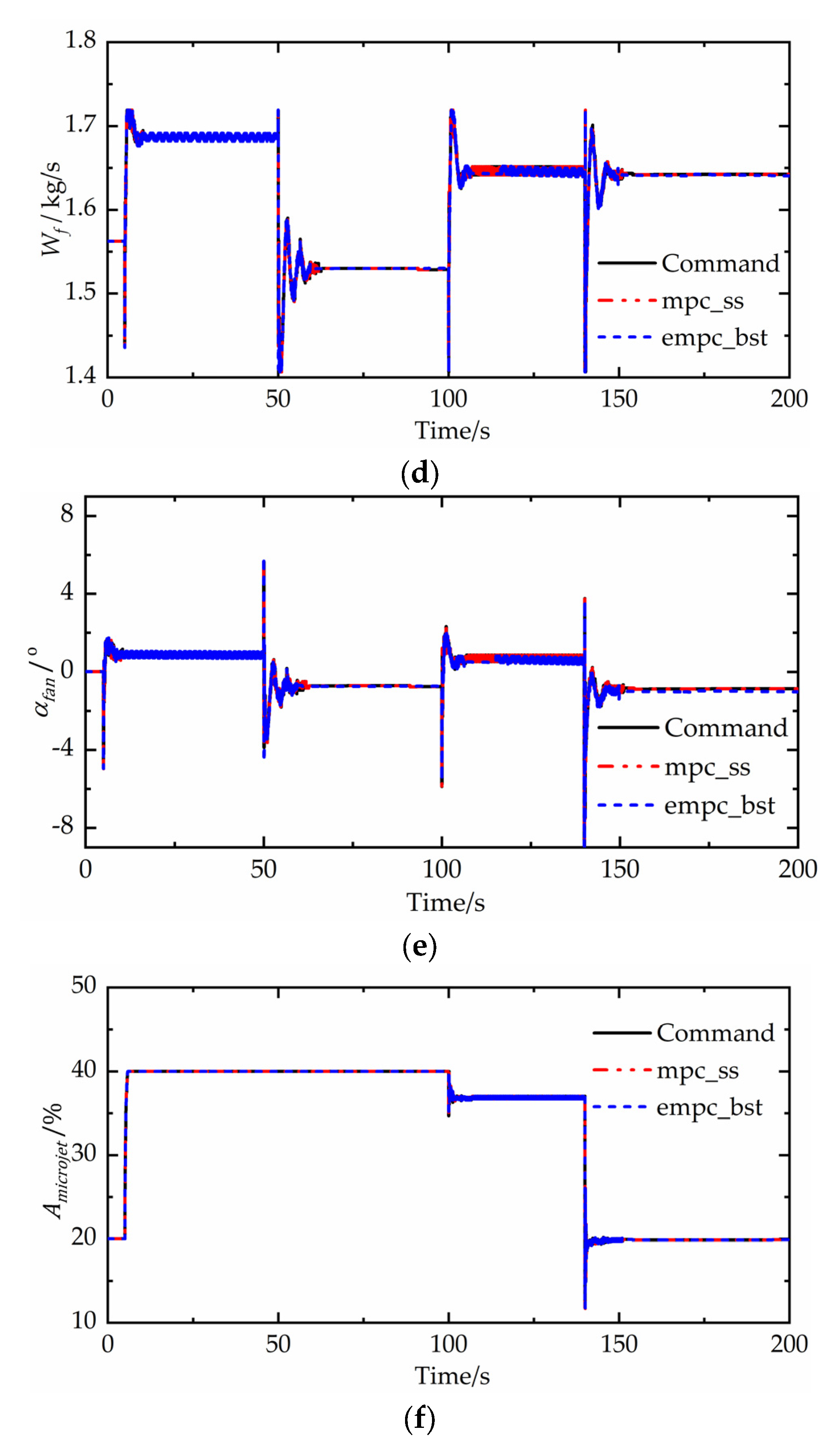
Table 2 gives the control commands at different time. Figure 8 shows the continuous step response results between different controllers. It is found that the absolute values of and are both less than 5%, satisfying constraints. When the control command of changes from 4% to −0.5%, the response oscillates, and the maximum of overshoot is 1.571%. When the control command of changes from 1% to 3%, the response oscillates significantly, and the maximum of overshoot is 1.534%. When the control command of changes from −4.5% to −7.5%, the response oscillates considerably, and the maximum of overshoot is 2.365%. The reason for the existence of oscillation when the commands change is the strong interactions between the three control loops, which is a big challenge for multivariable controllers. The control effect of the three controlled variables are similar between different controllers, as seen in Figure 8a–c. The difference of the control effect between different controllers is less than 0.4%. The premise of designing an explicit MPC controller is to achieve a traditional MPC controller, while sequence search and binary search are different online search solutions, which mainly affect the running time. So the simulation results show that compared with the MPC controller, the explicit MPC controller hardly reduces the control accuracy. Figure 8d–f shows the values of control parameters.

Table 2.
The range of control command.
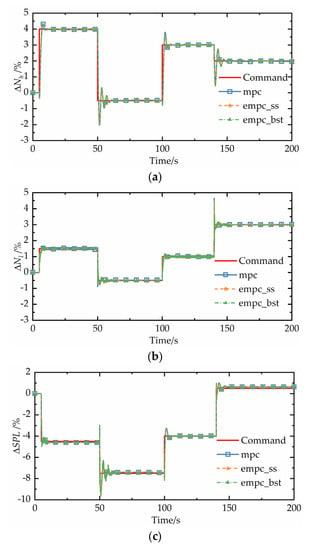
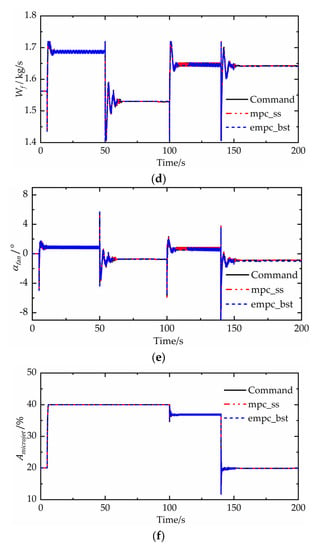
Figure 8.
Continuous step responses between different controllers. (a) Variation of speed of high pressure rotor. (b) Variation of speed of low pressure rotor. (c) Variation of total sound pressure level of jet noise. (d) Variation of fuel flow. (e) Variation of inlet guide blade angle of fan. (f) Variation of area of micronozzle throat.
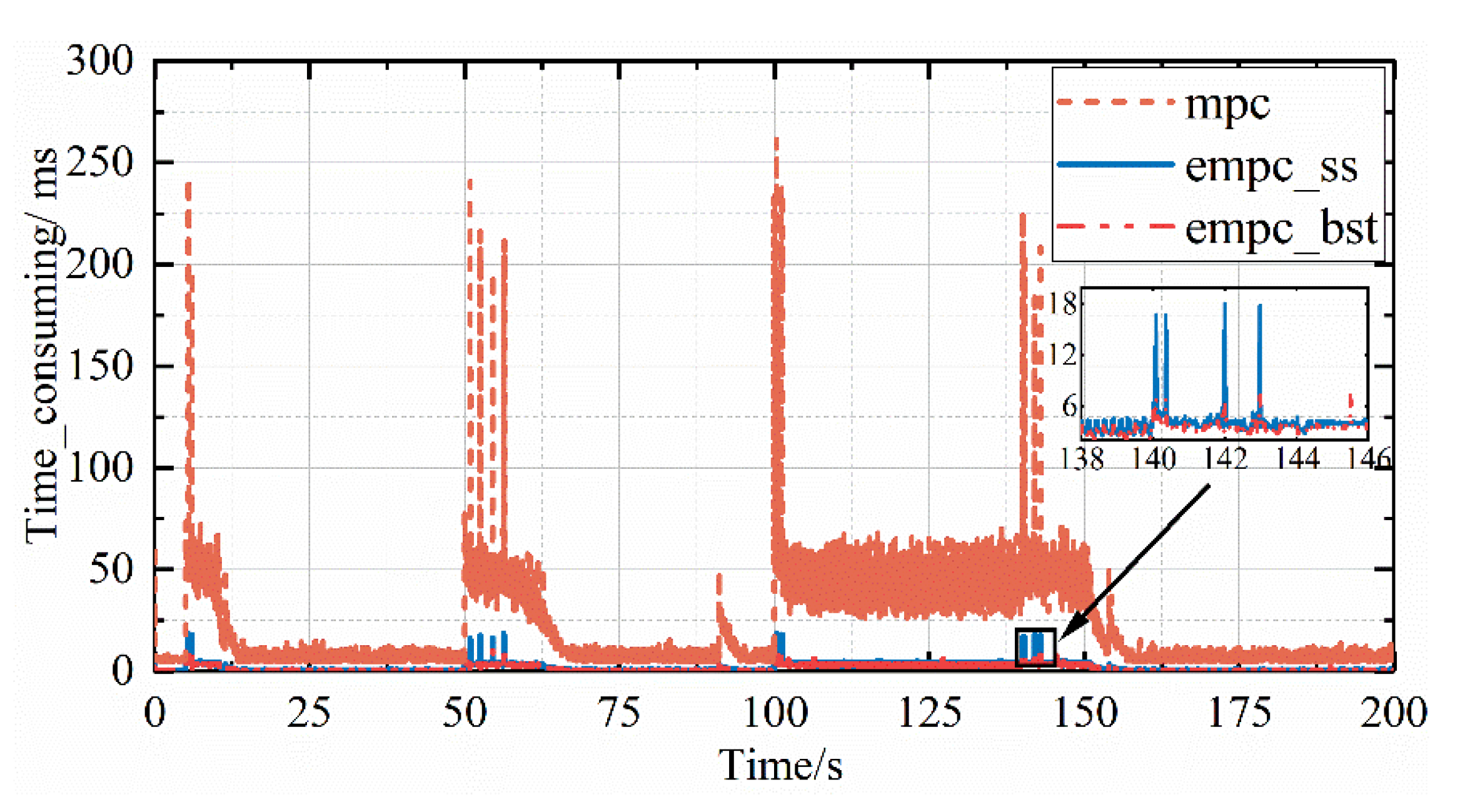
Compared with the traditional MPC controller, the goal of the explicit MPC controller is to improve the real-time performance. Different online solutions for the location problem also affect the real-time performance further. Figure 9 shows the time consumed in each step between the different controllers. Obviously, the explicit MPC based on a sequence search, and the explicit MPC based on a binary search tree, both reduce the time in each step to less than 20 ms, while the maximum consumption of the MPC is more than 250 ms. For hardware platforms with limited computation resources, the real-time performance of the MPC controller is unacceptable.
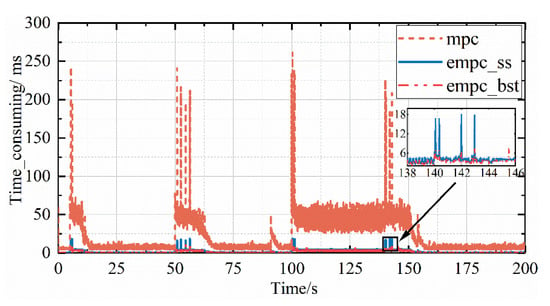
Figure 9.
Comparison of time consumed between different controllers.
Table 3 shows the statistical characteristics of calculate time consumption in each step. For the MPC controller, the mean of all steps is 20.916 ms, the mean for the explicit MPC controller based on a sequence search is 1.671 ms, and the mean for the explicit MPC controller based on a binary search tree is 1.389 ms. The real-time performance of the explicit MPC controller based on a binary search tree is the best. Moreover, compared with the explicit MPC based on a sequential search, the maximum of all steps and the minimum of all steps decrease 25.6% and 65.8%, respectively, for the explicit MPC controller based on a binary search tree. At each iteration, the method based on a binary search tree needs to complete a comparation, judging where holds, while an iteration implies many comparations for the sequence search. holds when each inequation corresponding to each row holds. This is why the explicit MPC controller based on a binary search tree consumes less time. Through the comparison experiments, choosing the explicit MPC controller based on a binary search as the active jet noise controller is feasible.

Table 3.
Statistical characteristics of calculated time consumption in each step.
5. Conclusions
This paper designed an active jet noise controller based on an explicit model predictive control. Firstly, an integrated model of a turbofan engine and jet noise was established to calculate the engine parameters and jet noise in real time. The semi-empirical model of jet noise and the component level model of the turbofan engine were adopted. Secondly, the explicit MPC controller of active jet noise control was designed, based on explicit MPC theory. Thirdly, to improve the search efficiency and the real-time performance of the explicit MPC, a binary search tree was adopted as the online search algorithm to solve the location problem. Several conclusions can be drawn.
- (1)
- The integrated model proposed in this paper reflects the characteristics of the turbofan engine. It can be used to calculate the engine parameters and jet noise in real time simultaneously.
- (2)
- The prediction horizon 5 is the best choice. The explicit MPC controller with the prediction horizon 5 balances the computation burden and control accuracy. If the prediction horizon is less than 5, the control effect is worse, and if the prediction horizon is more than 5, the computation burden is large.
- (3)
- From Table 3, the explicit MPC controller based on a binary search tree has better real-time performance than the MPC controller with the same parameters for the studied system, with little loss of track performance. Compared with the explicit MPC controller based on a sequential search, the mean of time consumed at all steps decreases 16.87%.
Author Contributions
Conceptualization, R.J.; Data curation, R.J.; Formal analysis, X.H.; Investigation, X.Z.; Methodology, R.J.; Resources, X.H.; Writing—original draft, R.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 51976089 and 51576097.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this paper are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| MPC | model predictive control |
| MPQP | multi-parametric quadratic programming |
| PWA | piecewise affine |
| BST | binary search tree |
| CLM | component level model |
| RMSE | root mean square error. |
References
- Florio, F.D. Airworthiness: An Introduction to Aircraft Certification and Operations; Butterworth-Heinemann: Oxford, UK, 2016; ISBN 978-0-08-100940-6. [Google Scholar]
- Kun, Y.; Cunxi, L. Comparison on the Ways of Airworthiness Management of Civil Aircraft Design Organization. Procedia Eng. 2011, 17, 388–395. [Google Scholar] [CrossRef][Green Version]
- Xie, H.; Li, H.; Kang, J. The Characteristics and Control Strategies of Aircraft Noise in China. Appl. Acoust. 2014, 84, 47–57. [Google Scholar] [CrossRef]
- Zhao, K.; Okolo, P.; Neri, E.; Chen, P.; Kennedy, J.; Bennett, G.J. Noise Reduction Technologies for Aircraft Landing Gear-A Bibliographic Review. Prog. Aerosp. Sci. 2020, 112, 100589. [Google Scholar] [CrossRef]
- Henderson, B. Fifty Years of Fluidic Injection for Jet Noise Reduction. Int. J. Aeroacoustics 2010, 9, 91–122. [Google Scholar] [CrossRef]
- Rask, O.; Harrison, S.; Munday, D.; Harris, C.; Mihaescu, M.; Gutmark, E. Jet Aircraft Propulsion Noise Reduction Research at University of Cincinnati. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8 July 2007. [Google Scholar]
- Harrison, S.; Gutmark, E.; Martens, S. Jet Noise Reduction by Fluidic Injection on a Separate Flow Exhaust System. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8 January 2007. [Google Scholar]
- Kopiev, V.F.; Bityurin, V.A.; Belyaev, I.V.; Godin, S.M.; Zaitsev, M.Y.; Klimov, A.I.; Kopiev, V.A.; Moralev, I.A.; Ostrikov, N.N. Jet Noise Control Using the Dielectric Barrier Discharge Plasma Actuators. Acoust. Phys. 2012, 58, 434–441. [Google Scholar] [CrossRef]
- Papamoschou, D. Engine Cycle and Exhaust Configuration for Quiet Supersonic Propulsion. J. Propuls. Power 2004, 20, 255–262. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active Noise Control: A Tutorial Review. Proc. IEEE 1999, 87, 943–973. [Google Scholar] [CrossRef]
- Rawlings, J.B. Tutorial Overview of Model Predictive Control. IEEE Control Syst. Mag. 2000, 20, 38–52. [Google Scholar] [CrossRef]
- Brunell, B.J.; Bitmead, R.R.; Connolly, A.J. Nonlinear Model Predictive Control of an Aircraft Gas Turbine Engine. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 4, pp. 4649–4651. [Google Scholar]
- Zheng, Q.; Pang, S.; Zhang, H.; Hu, Z. A Study on Aero-Engine Direct Thrust Control with Nonlinear Model Predictive Control Based on Deep Neural Network. Int. J. Aeronaut. Space Sci. 2019, 20, 933–939. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, M.; Chen, Y.; Chen, Y. Hybrid Grey Wolf Optimization Nonlinear Model Predictive Control for Aircraft Engines Based on an Elastic BP Neural Network. Appl. Sci. 2019, 9, 1254. [Google Scholar] [CrossRef]
- Yu, B.; Li, Z.; Ke, H.; Zhang, T. Wide-Range Model Predictive Control for Aero-Engine Transient State. Chin. J. Aeronaut. 2021, in press. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The Explicit Linear Quadratic Regulator for Constrained Systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Tøndel, P.; Johansen, T.A.; Bemporad, A. An Algorithm for Multi-Parametric Quadratic Programming and Explicit MPC Solutions. Automatica 2003, 39, 489–497. [Google Scholar] [CrossRef]
- Johansen, T.A.; Jackson, W.; Schreiber, R.; Tondel, P. Hardware Architecture Design for Explicit Model Predictive Control. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Alessio, A.; Bemporad, A. A Survey on Explicit Model Predictive Control. In Nonlinear Model Predictive Control: Towards New Challenging Applications; Magni, L., Raimondo, D.M., Allgöwer, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 345–369. ISBN 978-3-642-01094-1. [Google Scholar]
- Johansen, T.A.; Grancharova, A. Approximate explicit model predictive control implemented via orthogonal search tree partitioning. IFAC Proc. Vol. 2002, 35, 195–200. [Google Scholar] [CrossRef]
- Tøndel, P.; Johansen, T.A.; Bemporad, A. Evaluation of Piecewise Affine Control via Binary Search Tree. Automatica 2003, 39, 945–950. [Google Scholar] [CrossRef]
- Bayat, F.; Johansen, T.A.; Jalali, A.A. Using Hash Tables to Manage the Time-Storage Complexity in a Point Location Problem: Application to Explicit Model Predictive Control. Automatica 2011, 47, 571–577. [Google Scholar] [CrossRef]
- Bayat, F.; Johansen, T.A.; Jalali, A.A. Flexible Piecewise Function Evaluation Methods Based on Truncated Binary Search Trees and Lattice Representation in Explicit MPC. IEEE Trans. Control Syst. Technol. 2012, 20, 632–640. [Google Scholar] [CrossRef]
- Stone, J.R.; Krejsa, E.A.; Clark, B.J. Jet Noise Modeling for Coannular Nozzles Including the Effects of Chevrons; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2003. [Google Scholar]
- Lighthill, M.J. On Sound Generated Aerodynamically II. Turbulence as a Source of Sound. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1954, 222, 1–32. [Google Scholar] [CrossRef]
- Stone, J.R.; Krejsa, E.A.; Clark, B.J. Jet Noise Modeling for Supersonic Business Jet Application; NASA CR-2004-212984; NASA: Washington, DC, USA, 2004. [Google Scholar]
- Ma, Y.-H.; Du, X.; Sun, X.-M. Adaptive Modification of the Turbofan Engine Nonlinear Model Based on LSTM Neural Networks and Hybrid Optimization Method. Chin. J. Aeronaut. 2021. [Google Scholar] [CrossRef]
- Pang, S.; Li, Q.; Feng, H.; Zhang, H. Joint Steady State and Transient Performance Adaptation for Aero Engine Mathematical Model. IEEE Access 2019, 7, 36772–36787. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).