Parameter Observer Useable for the Condition Monitoring of a Capacitor
Abstract
:1. Introduction
2. Materials and Methods
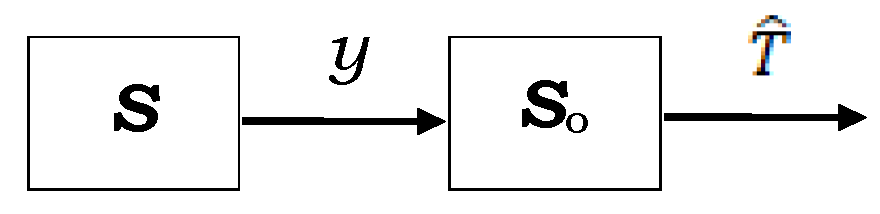
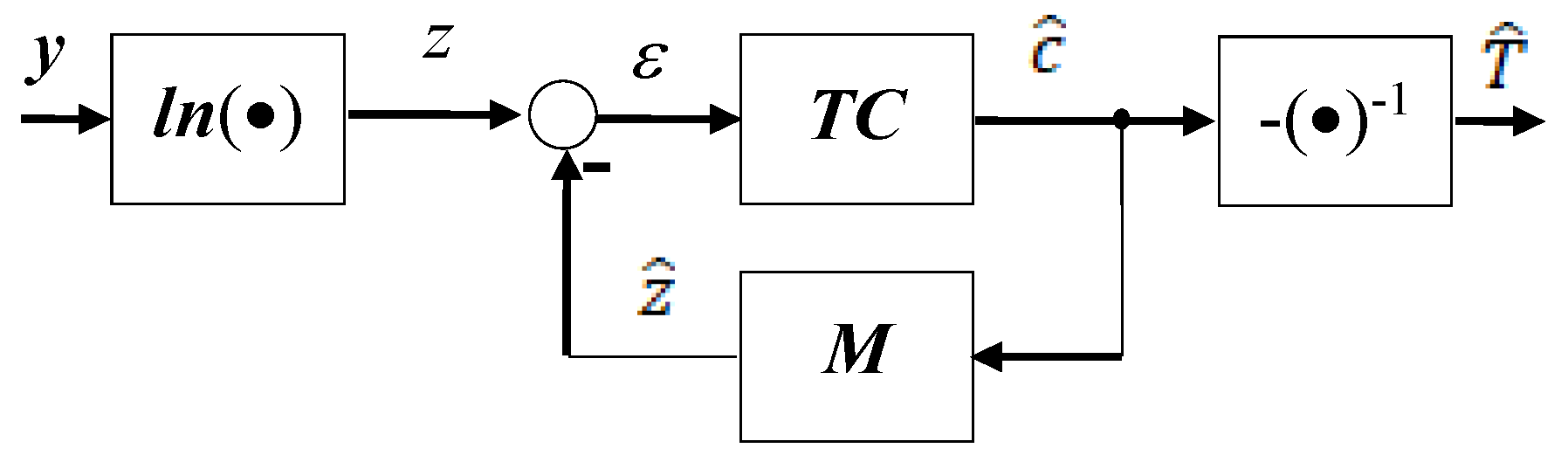
2.1. Continuous-Time Observer for Determining the Variation of the Parameters of a First-Order Continuous-Time System from Its Non-Sampled Free Response
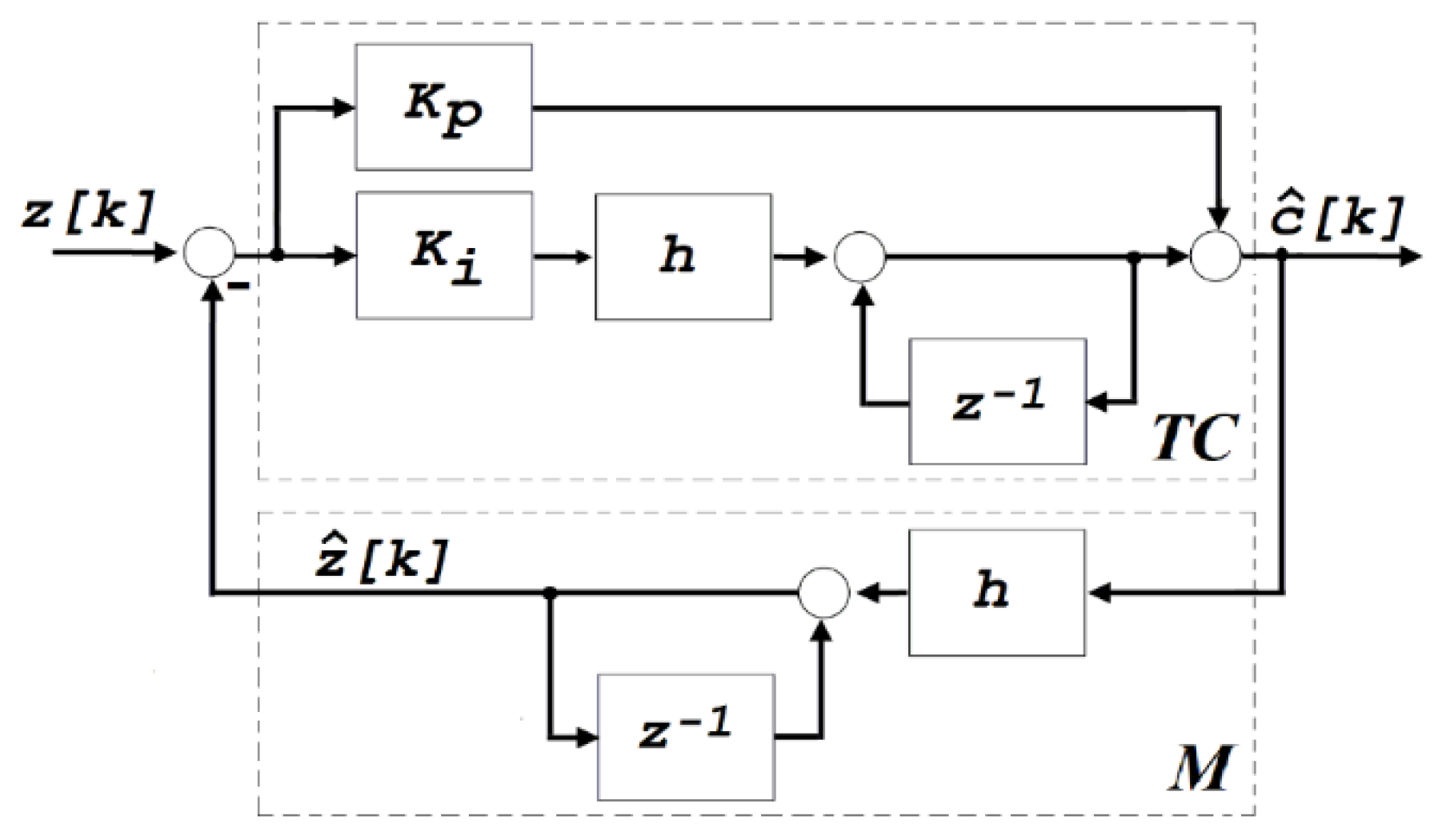
2.2. Discrete-Time Observer for Determining the Variation in the Parameters of a First-Order Continuous-Time System from Its Sampled Free Regime
- Interpolation of the signal (21) followed by the processing of the interpolated signal with the PO from Figure 2
- Replacing the continuous-time PO with a homologous PO in discrete-time.
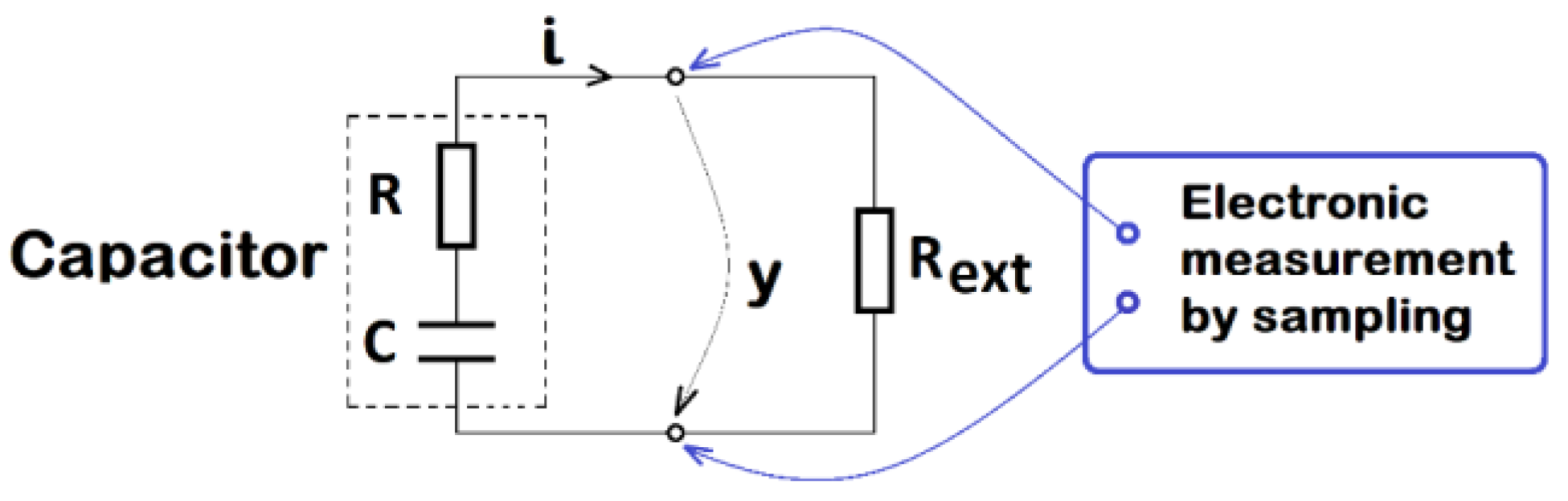
2.3. Method for Estimating the Parameters of a Capacitor
2.4. Bisector Method
3. Results
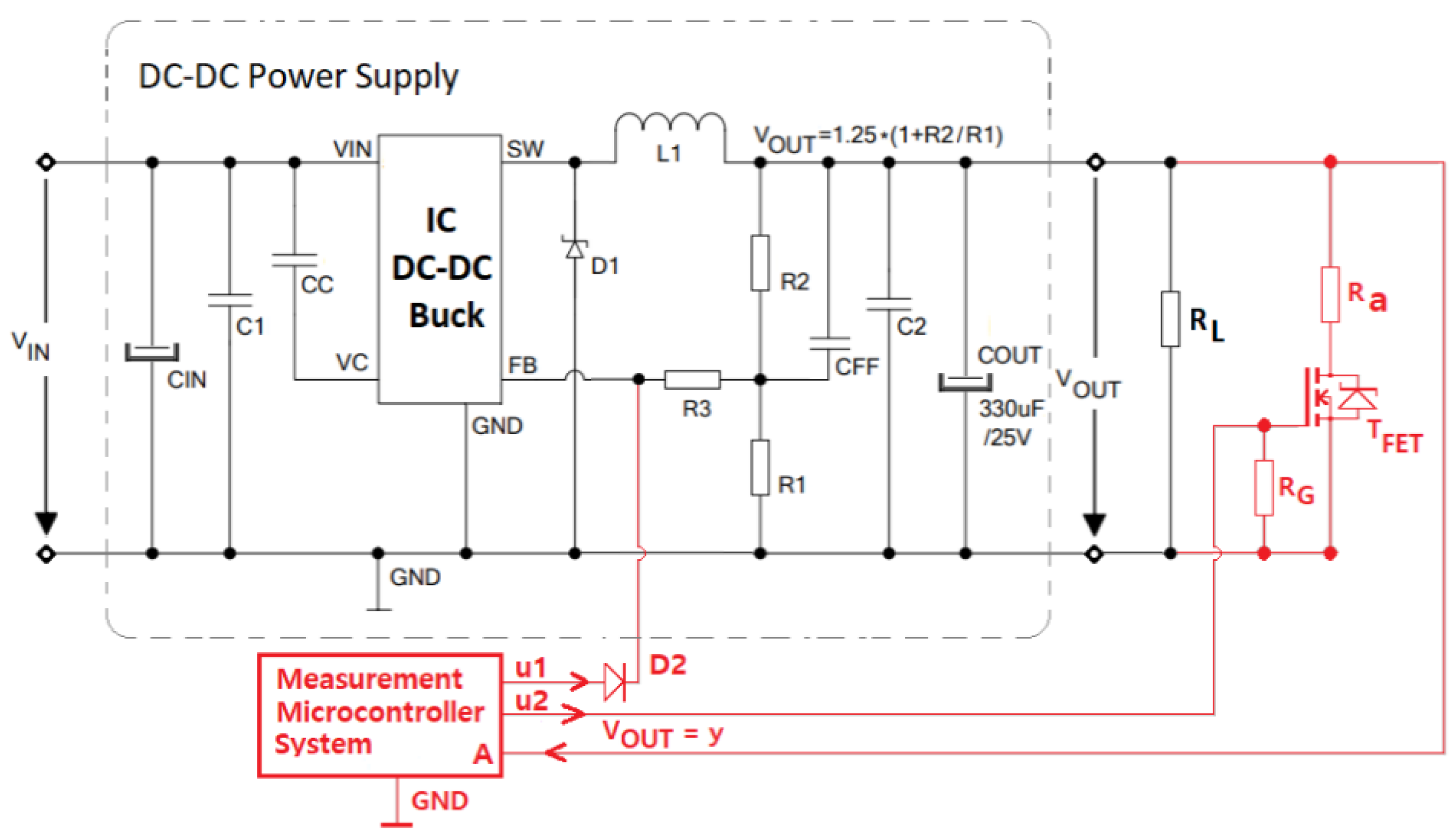
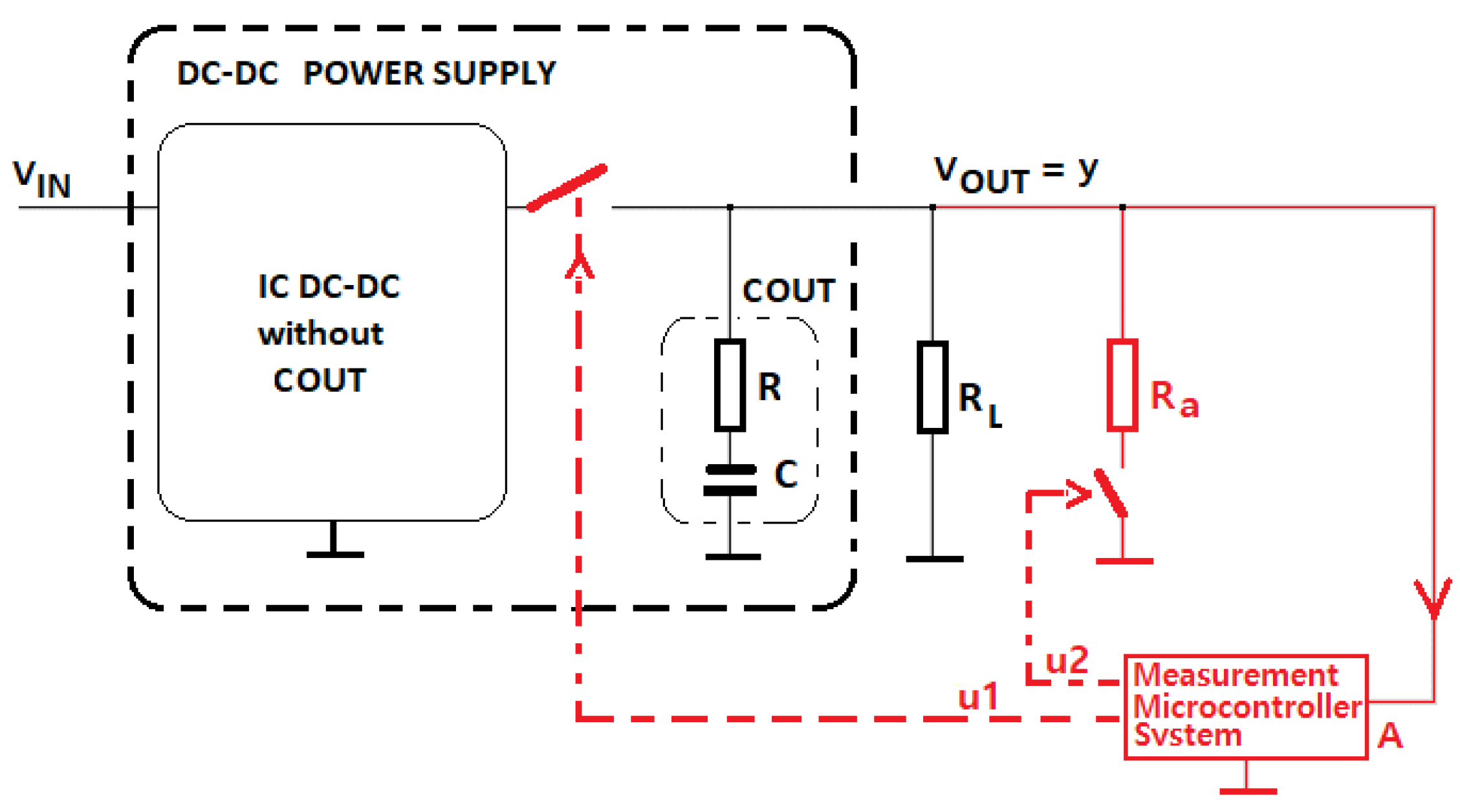
3.1. The Circuit Used to Estimate the Parameters of the Output Capacitor of a DC–DC Buck Converter
3.2. Experimental Results
4. Discussion
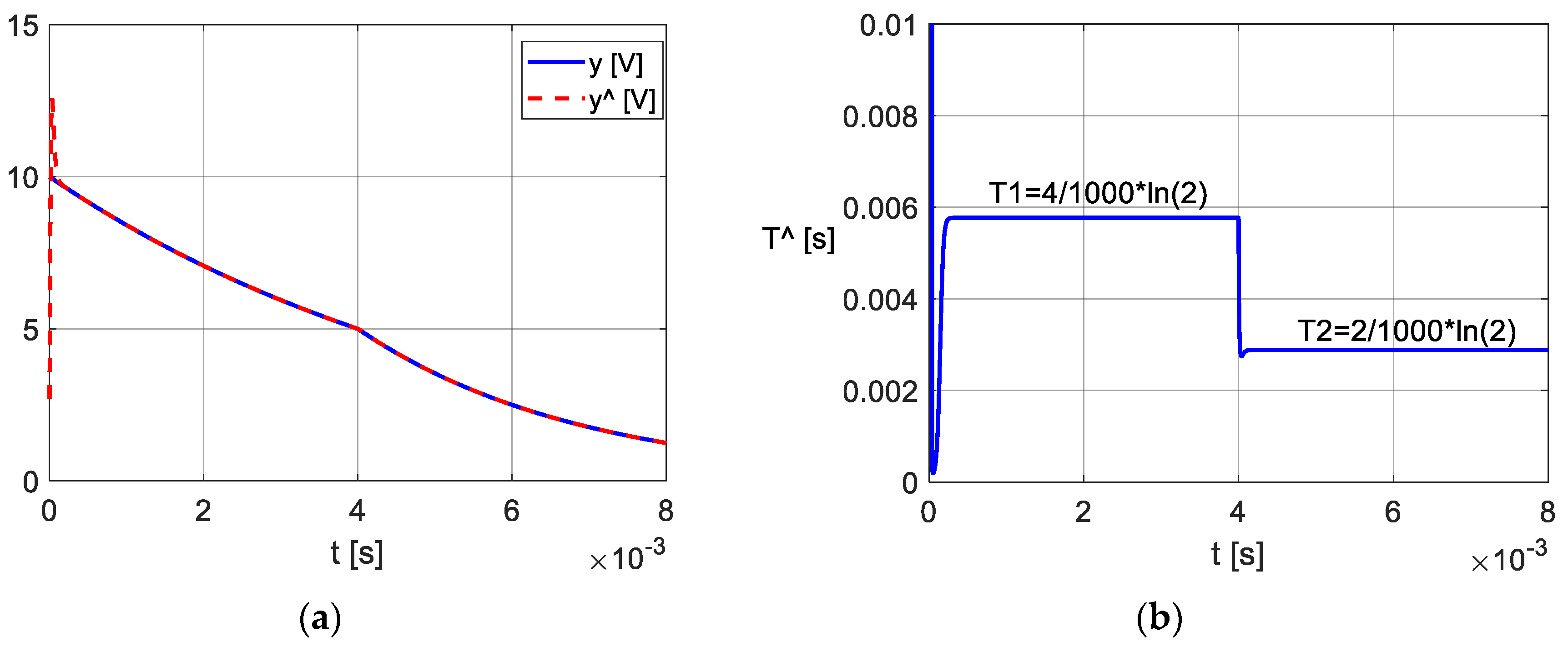
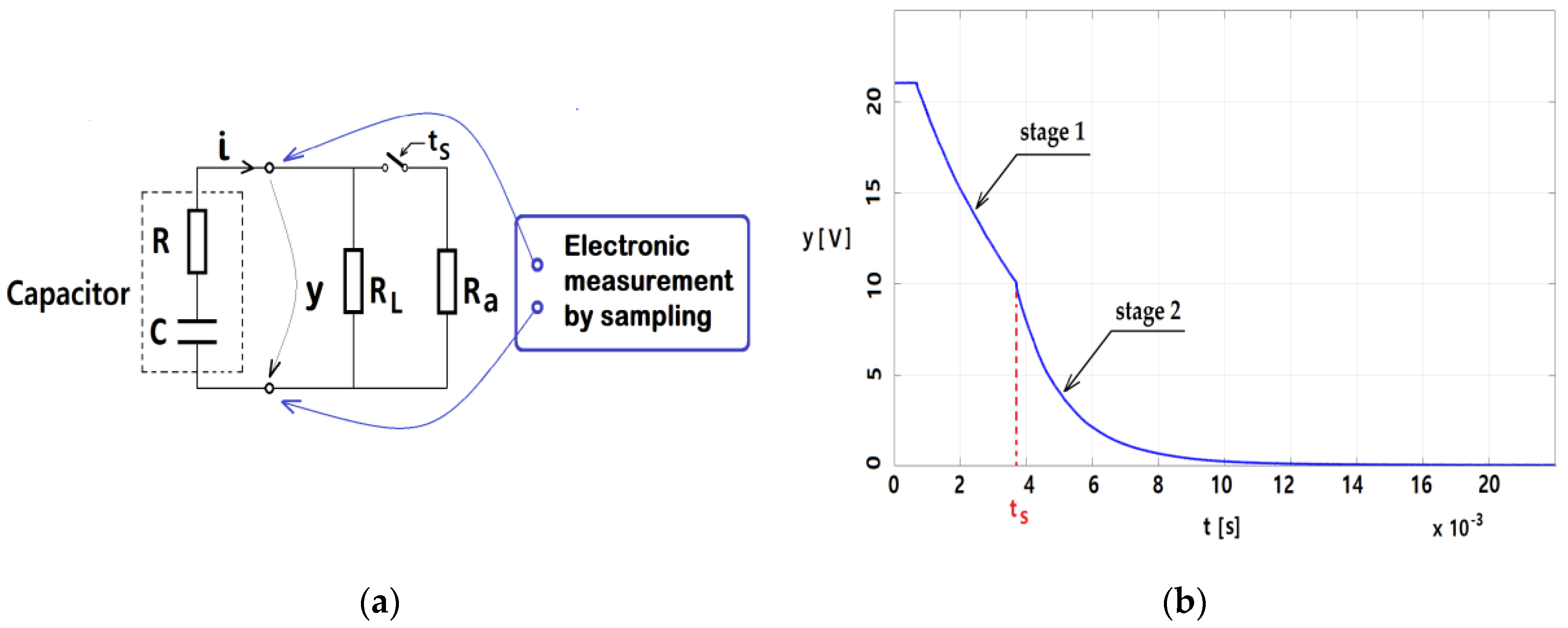
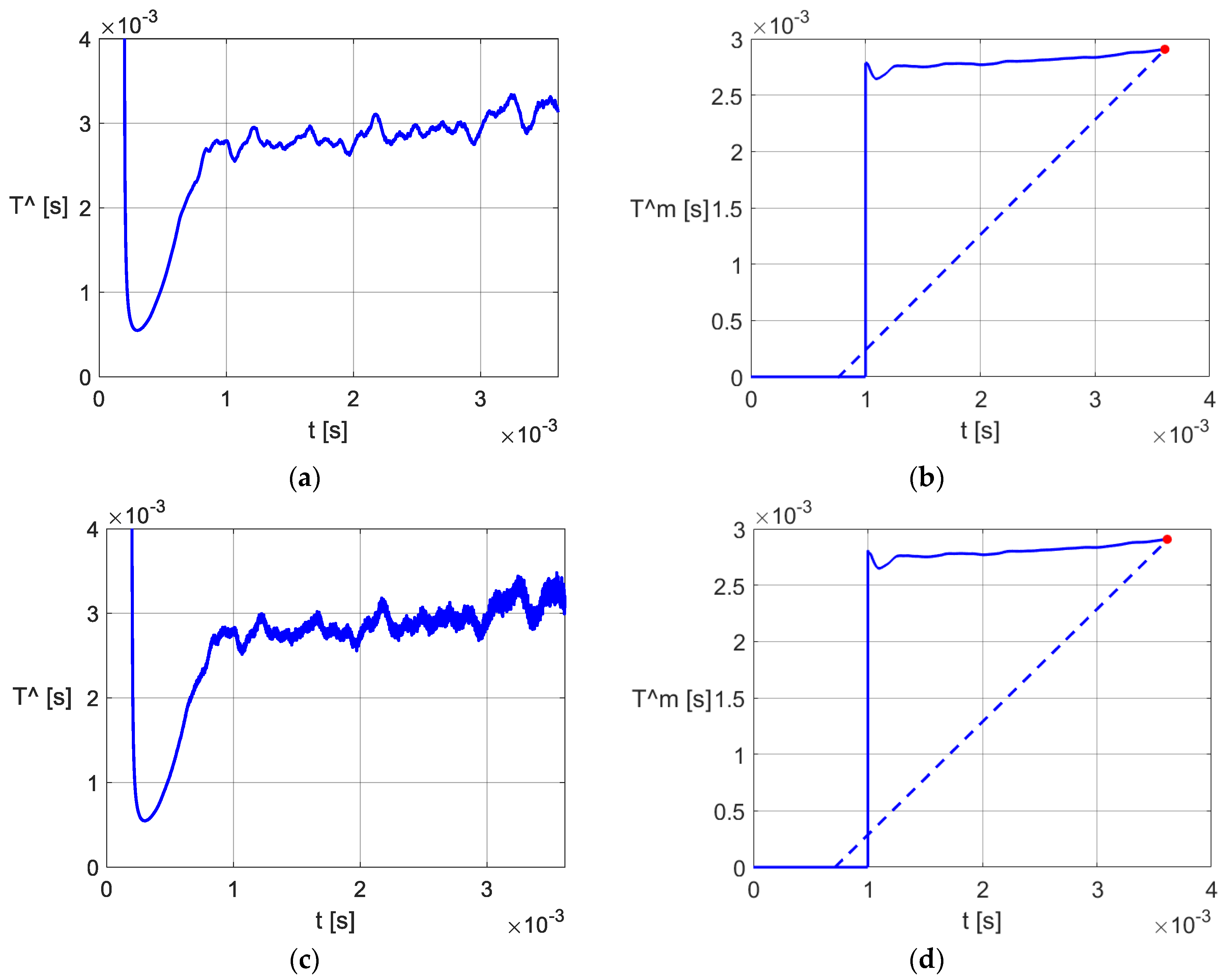
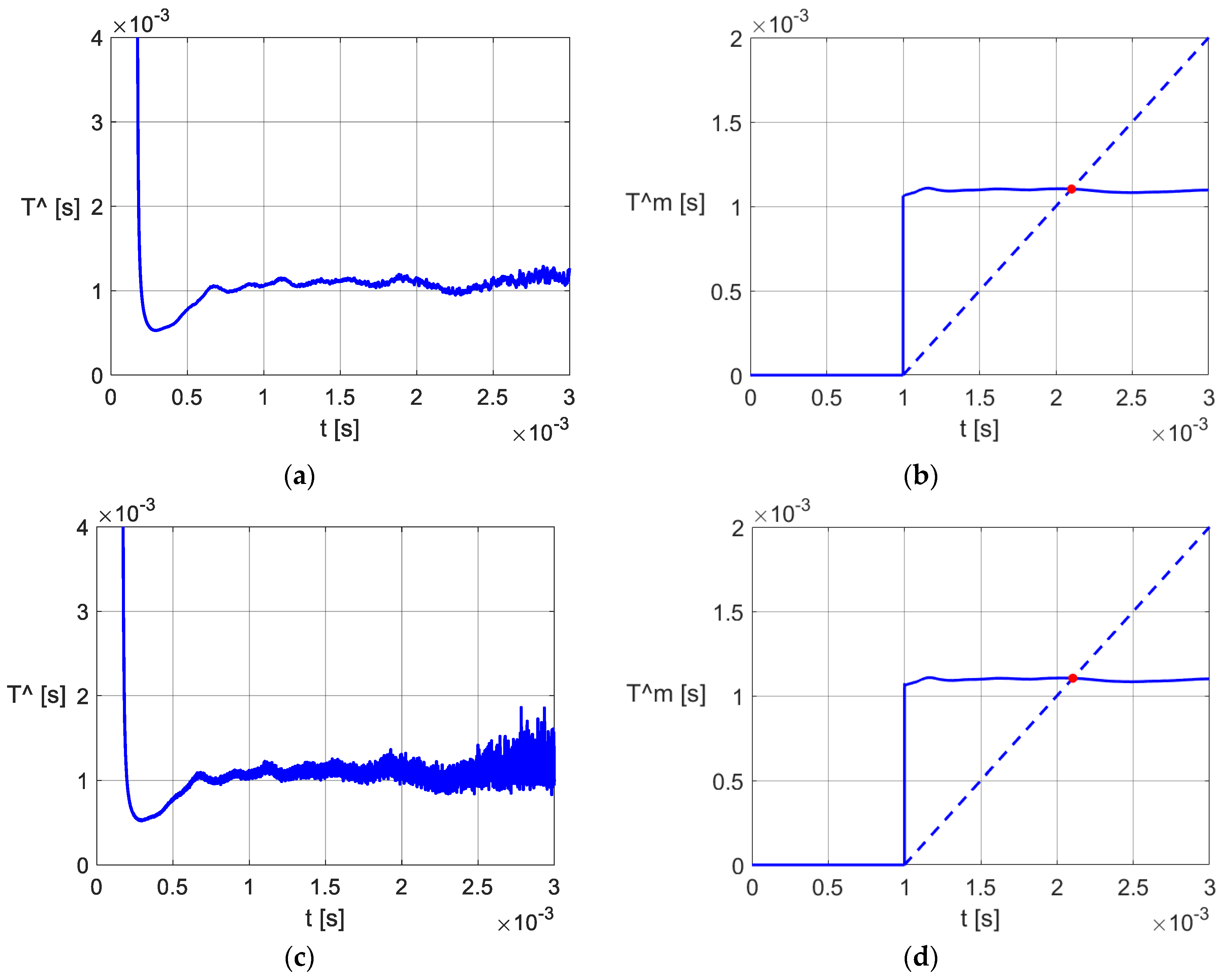
- During the capacitor’s discharging process, the parameter T of the circuit, currently called the time constant, varies (Figure 15a,c and Figure 16a,c). According to [19], the variation in the estimated value reflects that both C and ESR vary in time. From a practical perspective, this conclusion implies the defining of equivalent values: To determine the equivalent value of T(t), the variation in the average value was calculated using the discrete-time PO, and was extracted by the “bisector method” (Figure 11, Figure 15b,d and Figure 16b,d).
- Obtaining the values requires two discharging experiments. To maintain, as far as possible, the same discharging regime, according to the method presented in [6] a two-stage discharge was used (Figure 10). For each capacitor, the two stages were treated separately (Figure 15 and Figure 16). As the time required for the two discharge steps is much longer than the ripple’s discharge time, the method can be applied as in [6], only when the converter is stopped. Unlike [6], where the capacitor discharge process exceeds 10 s, in our paper the discharge time is less than 0.02 s. As a result, the necessary stop time of the converter is quite short. The difference is due to the inertia of the discharging electrical circuits to which the capacitors belong.
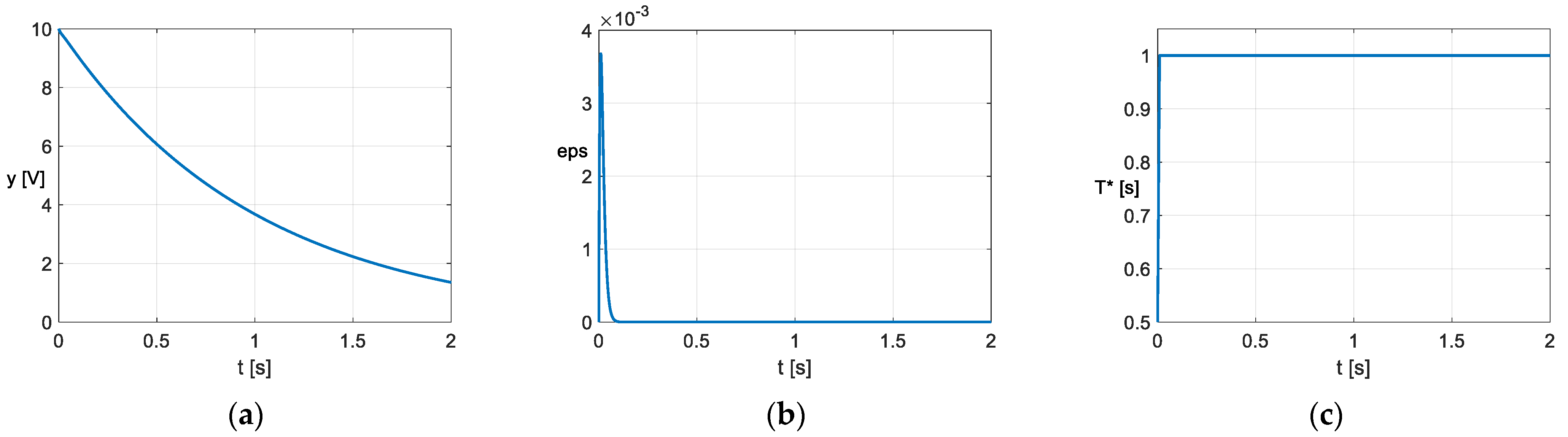
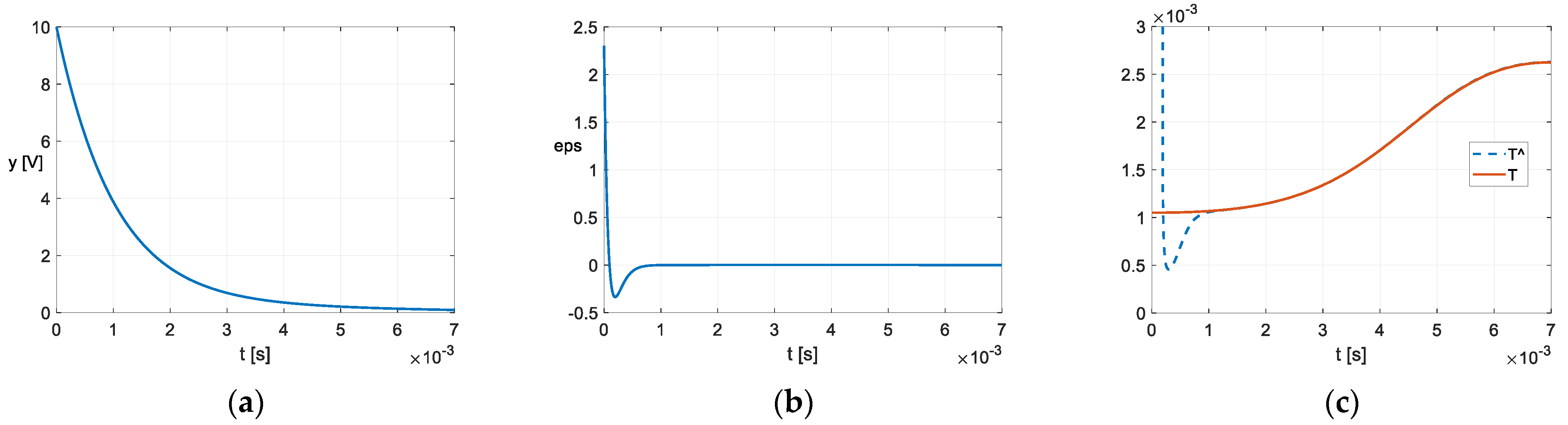
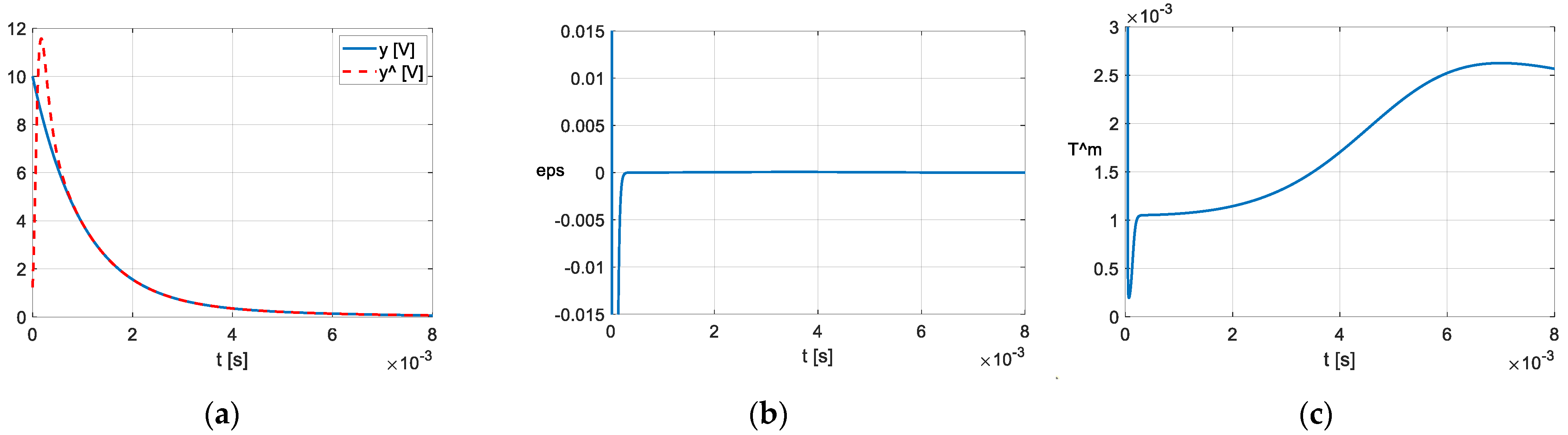
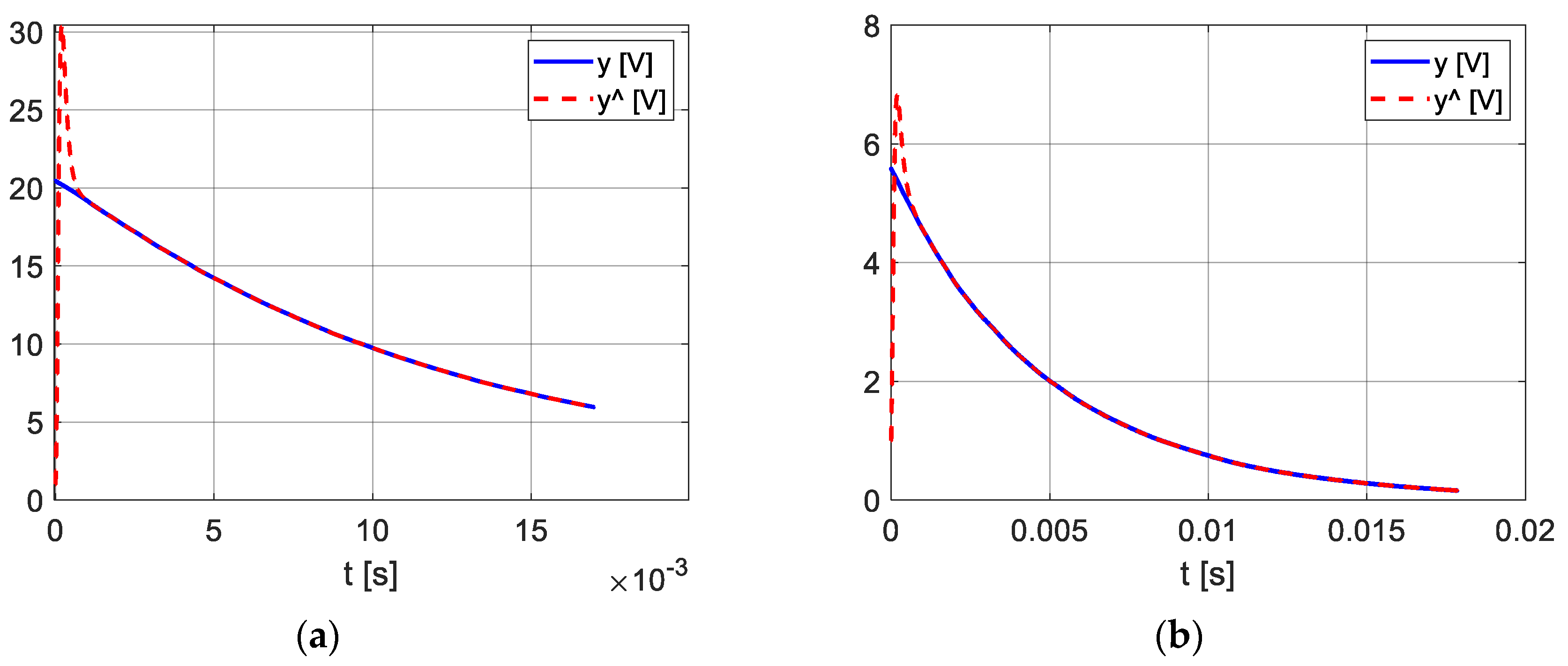
- The estimation of the T parameter with both proposed POs is affected at the beginning by a short transient regime caused by the inconsistency between the initial state variables of the PO with the observer’s input. The duration of the transient may be shortened by appropriately adopting the parameters of the observer. As the transient cannot be eliminated, it was avoided in the calculation of by choosing the moment t0. The attenuation time of the estimation error of the PO used for the experimental data is a maximum of 10−3 s (Figure 14 et seq.), and so is smaller than the attenuation of approx. 5·10−3 s that occurred in [3], and much smaller than that of approx. 50·10−3 s that occurred in [27,28].
- The study of the influence of noise filtering on , applied for 100 μF, does not show favorable noticeable consequences on the equivalent value (Figure 16b,d).
- In the theoretical examples, for which the values of T(t) can be verified analytically, the PO ensures the correct estimation of T after the attenuation of the transient regime (Figure 3, Figure 4, Figure 7 and Figure 8). Since a theoretical verification of T(t) is impossible in the practical case of the two capacitors, we analysed the equivalent values (40) and (41). Both values of are in the range of 20 Hz–25 kHz of the measured frequency characteristics C(f), while the values of are below 20 Hz. It should be also noted that the calculated values of with Formula (36) are very sensitive in relation to the values of , RL and Ra, while the values of are less sensitive.
- The recording resolution, as shown in Figure 14, Figure 15 and Figure 17, in relation to the dynamics of the capacitor’s discharge process, should not lead to the conclusion that the use of PO requires a high sampling frequency or oversampling. Indeed, the calculated values of have undergone non-essential changes using a set of measured sequences , corresponding to a sampling period of 20 μs from the discharge curves in Figure 16. This result, in conjunction with the simplicity of the PO algorithm, expands the potential of the POs for real-time implementation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESR | Equivalent serial resistance |
| PO | Parameter observer |
References
- Wang, H.; Blaabjerg, F. Reliability of capacitors for DC-link applications in power electronic converters—An overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Ma, K.; Blaabjerg, F. Design for reliability of power electronic systems. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 33–34. [Google Scholar]
- Cen, Z.; Stewart, P. Condition parameter estimation for photovoltaic buck converters based on adaptive model observers. IEEE Trans. Reliab. 2017, 66, 148–160. [Google Scholar] [CrossRef]
- Laadjal, K.; Bento, F.; Jlassi, I.; Cardoso, A.J.M. Online Condition Monitoring of Electrolytic Capacitors in DC-DC Interleaved Boost Converters, Adopting a Model-Free Predictive Controller. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021. [Google Scholar]
- Khandebharad, A.R.; Dhumale, R.B.; Lokhande, S.S.; Lokhande, S.D. Real time remaining useful life prediction of the electrolytic capacitor. In Proceedings of the 2015 International Conference on Information Processing (ICIP), Pune, India, 16–19 December 2015; pp. 631–633. [Google Scholar]
- Wu, Y.; Du, X. A VEN Condition Monitoring Method of DC-Link Capacitors for Power Converters. IEEE Trans. Ind. Electron. 2019, 66, 1296–1306. [Google Scholar] [CrossRef]
- Zhao, Z.; Davari, P.; Lu, W.; Wang, H.; Blaabjerg, F. An Overview of Condition Monitoring Techniques for Capacitors in DC-Link Applications. IEEE Trans. Power Electron. 2021, 36, 3692–3716. [Google Scholar] [CrossRef]
- Zhao, Z.; Lu, W.; Davari, P.; Du, X.; Iu, H.H.C.; Blaabjerg, F. An Online Parameters Monitoring Method for Output Capacitor of Buck Converter Based on Large-Signal Load Transient Trajectory Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4004–4015. [Google Scholar] [CrossRef]
- Gupta, Y.; Ahmad, M.W.; Narale, S.; Anand, S. Health Estimation of Individual Capacitors in a Bank with Reduced Sensor Requirements. IEEE Trans. Ind. Electron. 2019, 66, 7250–7259. [Google Scholar] [CrossRef]
- Corti, F.; Reatti, A.; Patrizi, G.; Ciani, L.; Catelani, M.; Kazimierczuk, M.K. Probabilistic evaluation of power converters as support in their design. IET Power Electron. 2020, 13, 4542–4550. [Google Scholar] [CrossRef]
- Yao, B.; Chen, H.; Hi, X.-Q.; Xiao, Q.-Z.; Kuang, X.-J. Reliability and failure analysis of DC/DC converter and case studies. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 1133–1135. [Google Scholar]
- Bindi, M.; Corti, F.; Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.-C.; Reatti, A. Failure prevention in DC-DC converters: Theoretical approach and experimental application on a Zeta converter. In IEEE Transactions on Industrial Electronics (Early Access); IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Duan, X.; Zou, J.; Li, B.; Wu, Z.; Lei, D. An Online Monitoring Scheme of Output Capacitor’s Equivalent Series Resistance for Buck Converters without Current Sensors. IEEE Trans. Ind. Electron. 2021, 68, 10107–10117. [Google Scholar] [CrossRef]
- Ren, L.; Gong, C.; Zhao, Y. An Online ESR Estimation Method for Output Capacitor of Boost Converter. IEEE Trans. Power Electron. 2019, 34, 10153–10165. [Google Scholar] [CrossRef]
- Gasperi, M.L. Life prediction modeling of bus capacitors in AC variable frequency drives. In Proceedings of the IEEE Conference Record of Annual Pulp and Paper Industry Technical Conference, Jacksonville, FL, USA, 20–23 June 2005; pp. 141–146. [Google Scholar]
- Plazas-Rosas, R.A.; Orozco-Gutierrez, M.L.; Spagnuolo, G.; Franco-Mejía, É.; Petrone, G. DC-Link Capacitor Diagnosis in a Single-Phase Grid-Connected PV System. Energies 2021, 14, 6754. [Google Scholar] [CrossRef]
- Ahmeid, M.; Armstrong, M.; Gadoue, S.; Al-Greer, M.; Missailidis, P. Real-time parameter estimation of DC-DC converters using a self-tuned kalman filter. IEEE Trans. Power Electron. 2017, 32, 5666–5674. [Google Scholar] [CrossRef] [Green Version]
- Soliman, H.; Wang, H.; Blaabjerg, F. A Review of the Condition Monitoring of Capacitors in Power Electronic Converters. IEEE Trans. Ind. Appl. 2016, 52, 4976–4989. [Google Scholar] [CrossRef]
- Barbulescu, C.; Dragomir, T.-L. Parameter estimation for a simplified model of an electrolytic capacitor in transient regimes. J. Phys. Conf. Ser. 2021, 2090, 012143. [Google Scholar] [CrossRef]
- Li, L.; Yao, K.; Guan, C.; Wu, C.; Fang, B.; Zhang, Z.; Ma, C.; Chen, J.; Zhang, J. A quasi-online monitoring method of output capacitor and boost inductor for DCM boost converter. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2205–2211. [Google Scholar]
- Luenberger, D. Introduction to Dynamic Systems. In Theory, Models, and Applications; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Setoodeh, P.; Habibi, S.; Haykin, S. Nonlinear Filters: Theory and Applications; John Wiley & Sons: New York, NY, USA, 2022. [Google Scholar]
- Radke, A.; Gao, Z. A survey of state and disturbance observers for practitioners. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; Volume 2006, pp. 5183–5188. [Google Scholar]
- Gonzalez-Fonseca, N.; de Leon-Morales, J.; Leyva-Ramos, J. Observer-based controller for switch-mode dc-dc converters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 4773–4778. [Google Scholar]
- Levin, K.T.; Hope, E.M.; Domínguez-Garcíay, A.D. Observer-based fault diagnosis of power electronics systems. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 4434–4440. [Google Scholar]
- Chowdhury, N.R.; Belikov, J.; Baimel, D.; Levron, Y. Observer-based detection and identification of sensor attacks in networked CPSs. Automatica 2020, 121, 109166. [Google Scholar] [CrossRef]
- Jain, P.; Poon, J.; Jian, L.; Spanos, C.; Sanders, S.R.; Xu, J.X.; Panda, S.K. An improved robust adaptive parameter identifier for DC-DC converters using H-infinity design. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2922–2926. [Google Scholar]
- Meng, J.L.; Chen, E.X.; Ge, S.J. Online E-cap condition monitoring method based on state observer. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Szidarovszky, F.; Bahill, A.T. Linear Systems Theory, 2nd ed.; Routledge: London, UK, 2018. [Google Scholar]
- James, G. Advanced Modern Engineering Mathematics; Pearson Education Limited: London, UK, 2004. [Google Scholar]
- Datasheet 5 A 180 KHz 36 V Buck DC to DC Converter XL4015. Available online: www.xlsemi.com (accessed on 26 April 2022).
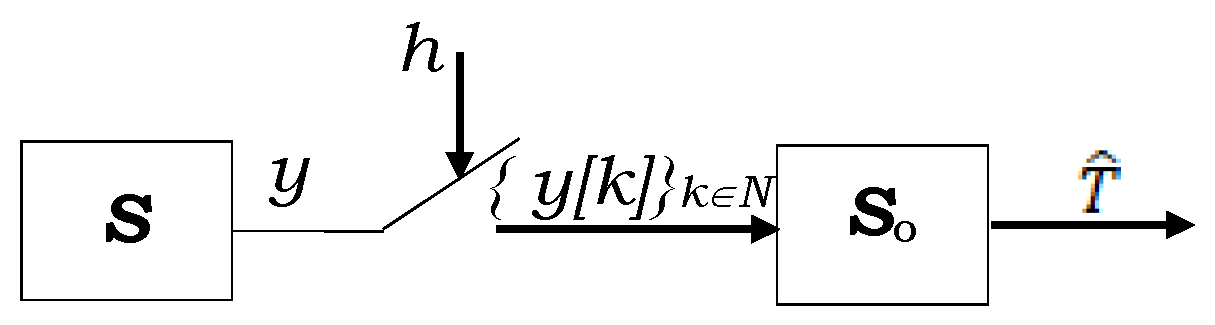


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bărbulescu, C.; Căiman, D.-V.; Dragomir, T.-L. Parameter Observer Useable for the Condition Monitoring of a Capacitor. Appl. Sci. 2022, 12, 4891. https://doi.org/10.3390/app12104891
Bărbulescu C, Căiman D-V, Dragomir T-L. Parameter Observer Useable for the Condition Monitoring of a Capacitor. Applied Sciences. 2022; 12(10):4891. https://doi.org/10.3390/app12104891
Chicago/Turabian StyleBărbulescu, Corneliu, Dadiana-Valeria Căiman, and Toma-Leonida Dragomir. 2022. "Parameter Observer Useable for the Condition Monitoring of a Capacitor" Applied Sciences 12, no. 10: 4891. https://doi.org/10.3390/app12104891





