CFD Investigations of Cyclone Separators with Different Cone Heights and Shapes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Continuous Phase Equations
Reynolds Stress Model (RSM)
2.2. Solid-Phase Transport
2.3. Details of the Analyzed Geometric Variants and the Adopted Assumptions of CFD Study
2.3.1. Details of the Cyclone Models
2.3.2. Mesh Generation and Solver Settings
2.3.3. Materials and Boundary Conditions
2.4. Validation
3. Results and Discussion
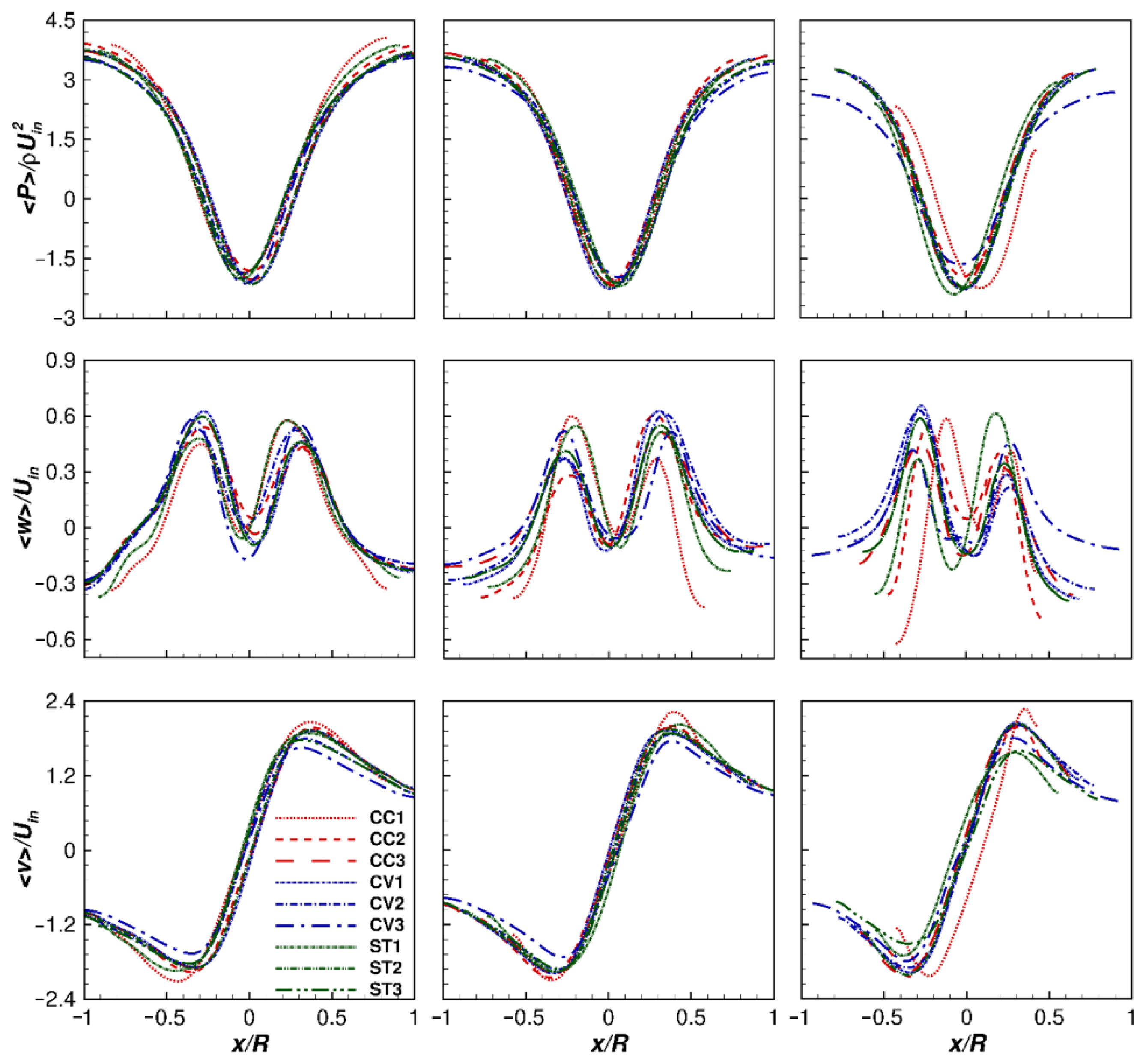
3.1. Continuous Phase
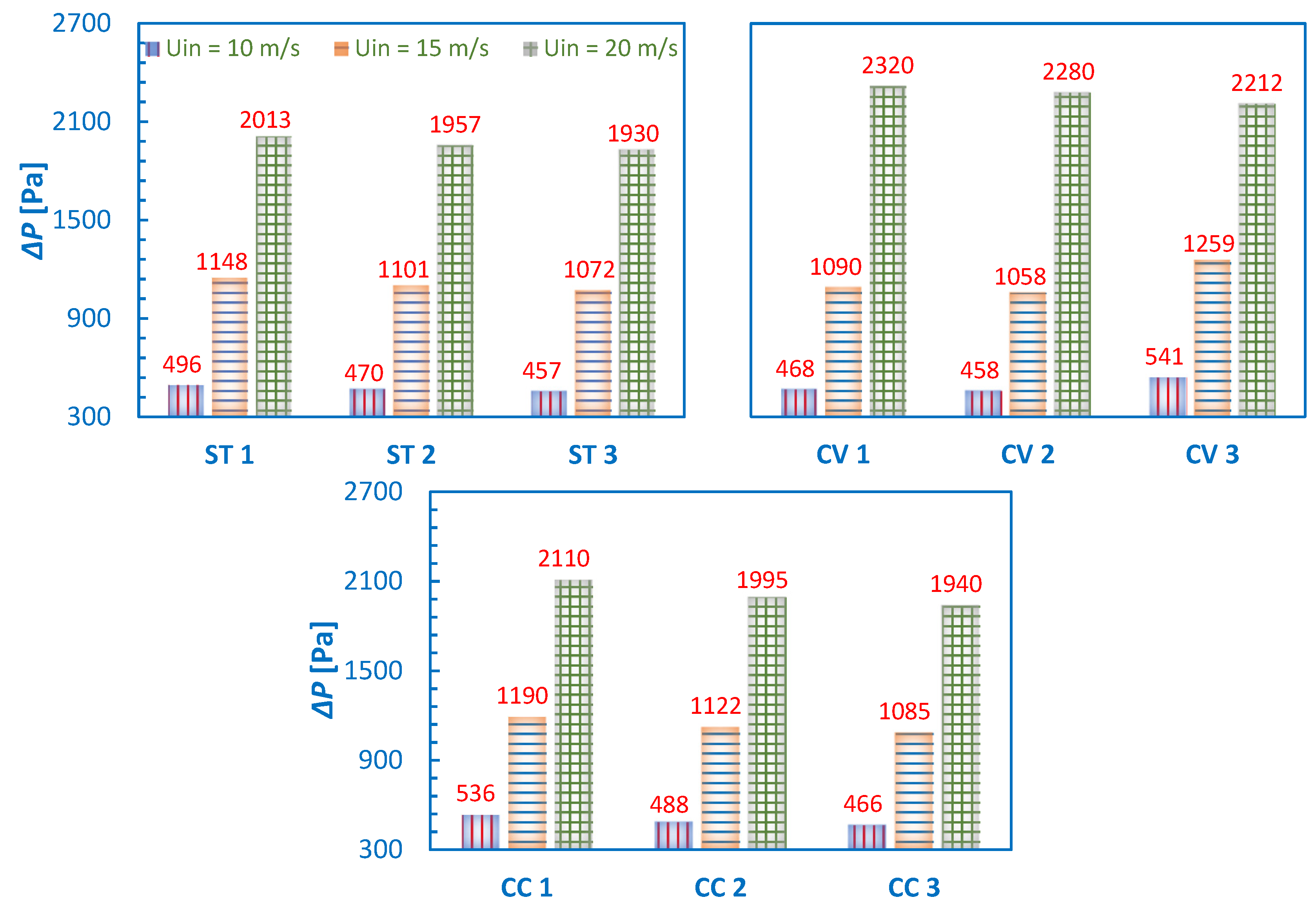
3.2. Pressure Drop
3.3. Analysis of the Separation Efficiency
4. Conclusions
- With the increase in inlet velocity:
- Pressure drop increased significantly in all cyclone variants.
- Cut-off particle size reduced tremendously.
- Collection efficiency increased by a large amount.
- With an increase in the length of the cylindrical section:
- Pressure drop was reduced in all the cyclone variants.
- Cut-off particle size increased mildly.
- Collection efficiency reduced by a marginal amount.
- With wall profile:
- Pressure drop was the lowest in models 1 and 2 of the CV, particularly at Uin = 10 m/s, and 15 m/s. At Uin = 20 m/s, pressure drop was the largest in CV variants, and at Uin = 10 m/s, and 15 m/s, as compared with the ST variant, the variations were moderate.
- Cut-off particle size showed a mild variation at a given Uin. The cut-off size was largest in CV variants, whereas this size was comparable in ST and CC variants.
- Collection efficiency increased by a marginal amount in the CC variant and was minimum in the CV variant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brar, L.S.; Derksen, J.J. Revealing the details of vortex core precession in cyclones by means of large-eddy simulation. Chem. Eng. Res. Des. 2020, 159, 339–352. [Google Scholar] [CrossRef]
- Faulkner, W.B.; Shaw, B.W. Efficiency and pressure drop of cyclones across a range of inlet velocities. Appl. Eng. Agric. 2006, 22, 155–161. [Google Scholar] [CrossRef] [Green Version]
- Safikhani, H.; Akhavan-Behabadi, M.A.; Shams, M.; Rahimyan, M.H. Numerical simulation of flow field in three types of standard cyclone separators. Adv. Powder Technol. 2010, 21, 435–442. [Google Scholar] [CrossRef]
- Hoffman, A.C.; Stein, L.E. Gas Cyclones and Swirl Tubes: Principles, Design and Operation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P.; Dwivedi, R. Effect of vortex finder diameter on flow field and collection efficiency of cyclone separators. Part. Sci. Technol. 2014, 33, 34–40. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S. Optimization of the geometry of cyclone separators used in clinker burning process: A case study. Powder Technol. 2017, 313, 293–302. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Experimental and numerical investigation on the performance of square cyclones with different vortex finder configurations. Sep. Purif. Technol. 2020, 239, 1–20. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of cyclone vortex finder dimensions on the flow pattern and performance using LES. Comput. Fluids 2013, 71, 224–239. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. Impacts of the vortex finder eccentricity on the flow pattern and performance of a gas cyclone. Sep. Purif. Technol. 2017, 187, 1–13. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of cyclone separators with eccentric vortex finders using large eddy simulation and artificial neural network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Pei, B.; Yang, L.; Dong, K.; Jiang, Y.; Du, X.; Wang, B. The effect of cross-shaped vortex finder on the performance of cyclone separator. Powder Technol. 2017, 313, 135–144. [Google Scholar] [CrossRef]
- Misiulia, D.; Antonyuk, S.; Andersson, A.G.; Lundström, T.S. Effects of deswirler position and its centre body shape as well as vortex finder extension downstream on cyclone performance. Powder Technol. 2018, 336, 45–56. [Google Scholar] [CrossRef]
- Kumar, V.; Jha, K. Multi-objective shape optimization of vortex finders in cyclone separators using response surface methodology and genetic algorithms. Sep. Purif. Technol. 2019, 215, 25–31. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P. Effect of varying diameter on the performance of industrial scale gas cyclone dust separators. Mater. Today Proc. 2015, 4, 3230–3237. [Google Scholar] [CrossRef]
- Brar, L.S. Application of response surface methodology to optimize the performance of cyclone separator using mathematical models and CFD simulations. Mater. Today Proc. 2018, 5, 20426–20436. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P.; Elsayed, K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 2015, 286, 668–677. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of cyclone inlet dimensions on the flow pattern and performance. Appl. Math. Model. 2011, 35, 1952–1968. [Google Scholar] [CrossRef] [Green Version]
- Wasilewski, M.; Brar, L.S. Effect of the inlet duct angle on the performance of cyclone separators. Sep. Purif. Technol. 2019, 213, 19–33. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of multi-inlet gas cyclones using large eddy simulation and artificial neural network. Powder Technol. 2017, 311, 465–483. [Google Scholar] [CrossRef]
- Misiulia, D.; Andersson, A.G.; Lundström, T.S. Effects of the inlet angle on the collection efficiency of a cyclone with helical-roof inlet. Powder Technol. 2017, 305, 48–55. [Google Scholar] [CrossRef]
- Piemjaiswang, R.; Ratanathammapan, K.; Kunchonthara, P.; Piumsomboon, P.; Chalermsinsuwan, B. CFD study of cyclone performance: Effect of inlet section angle and particle size distribution. J. Teknol. 2016, 78, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Huang, W.; Wu, Y.; Zhang, Y.; Zhang, M.; Yang, H.; Lyu, J. Effects of the inlet duct length on the flow field and performance of a cyclone separator with a contracted inlet duct. Powder Technol. 2021, 393, 12–22. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G.; Jiao, Y. Experimental study of large-scale single and double inlet cyclone separators with two types of vortex finder. Chem. Eng. Process.-Process Intensif. 2020, 158, 108188. [Google Scholar] [CrossRef]
- Qiang, L.; Qinggong, W.; Weiwei, X.; Zilin, Z.; Konghao, Z. Experimental and computational analysis of a cyclone separator with a novel vortex finder. Powder Technol. 2020, 360, 398–410. [Google Scholar] [CrossRef]
- Le, D.K.; Yoon, J.Y. Numerical investigation on the performance and flow pattern of two novel innovative designs of four-inlet cyclone separator. Chem. Eng. Process.-Process Intensif. 2020, 150, 107867. [Google Scholar] [CrossRef]
- Noh, S.Y.; Heo, J.E.; Woo, S.H.; Kim, S.J.; Ock, M.H.; Kim, Y.J.; Yook, S.J. Performance improvement of a cyclone separator using multiple subsidiary cyclones. Powder Technol. 2018, 338, 145–152. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Effect of the central rod dimensions on the performance of cyclone separators-optimization study. Sep. Purif. Technol. 2021, 274, 119020. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Elsayed, K.; Ahmadi, G. Influence of the dipleg shape on the performance of gas cyclones. Sep. Purif. Technol. 2020, 233, 116000. [Google Scholar] [CrossRef]
- Xu, M.; Yang, L.; Sun, X.; Wang, J.; Gong, L. Numerical analysis of flow resistance reduction methods in cyclone separator. J. Taiwan Inst. Chem. Eng. 2019, 96, 419–430. [Google Scholar] [CrossRef]
- Qiang, L.; Jianjun, W.; Weiwei, X.; Meng, Z. Investigation on separation performance and structural optimization of a two-stage series cyclone using CPFD and RSM. Adv. Powder Technol. 2020, 31, 3706–3714. [Google Scholar] [CrossRef]
- Galletti, C.; Rum, A.; Turchi, V.; Nicolella, C. Numerical analysis of flow field and particle motion in a dynamic cyclonic selector. Adv. Powder Technol. 2020, 31, 1264–1273. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, L.; Liu, Q.; Yu, X. Effect of the particle injection position on the performance of a cyclonic gas solids classifier. Adv. Powder Technol. 2020, 31, 227–233. [Google Scholar] [CrossRef]
- Fu, S.; Zhou, F.; Sun, G.; Yuan, H.; Zhu, J. Performance evaluation of industrial large-scale cyclone separator with novel vortex finder. Adv. Powder Technol. 2021, 32, 931–939. [Google Scholar] [CrossRef]
- Mofarrah, M.; Hojjat, Y.; Mashayekh, S.; Liu, Z.; Yan, K. Introduction and simulation of a small electro cyclone for collecting indoor pollen particles. Adv. Powder Technol. 2021, 33, 103384. [Google Scholar] [CrossRef]
- An, I.H.; Lee, C.H.; Lim, J.H.; Lee, H.Y.; Yook, S.J. Development of a miniature cyclone separator operating at low Reynolds numbers as a pre-separator for portable black carbon monitors. Adv. Powder Technol. 2021, 32, 4779–4787. [Google Scholar] [CrossRef]
- Gimbun, J.; Chuah, T.G.; Choong, T.S.Y.; Fakhru’l-Razi, A. Prediction of the effects of cone tip diameter on the cyclone performance. Aerosol Sci. 2005, 36, 1056–1065. [Google Scholar] [CrossRef]
- Xiang, R.; Park, S.H.; Lee, K.W. Effects of cone dimension on cyclone performance. J. Aerosol Sci. 2001, 32, 549–561. [Google Scholar] [CrossRef]
- Stern, A.; Caplan, K.; Bush, P. Cyclone Dust Collectors; American Petroleum Institute: New York, NY, USA, 1955. [Google Scholar]
- Shastri, R.; Brar, L.S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation. Sep. Purif. Technol. 2020, 249, 1–17. [Google Scholar] [CrossRef]
- Shastri, R.; Sharma, R.P.; Brar, L.S. Numerical investigations of cyclone separators with different cylinder-to-cone ratios. Part. Sci. Technol. 2021, 40, 337–345. [Google Scholar] [CrossRef]
- Ghodrat, M.; Kuang, S.B.; Yu, A.B.; Vince, A.; Barnett, G.D.; Barnett, P.J. Numerical analysis of hydrocyclones with different conical section designs. Miner. Eng. 2014, 62, 74–84. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: La Cañada Flintridge, CA, USA, 1994. [Google Scholar]
- Fluent Theory Guide; Fluent Inc.: Canonsburg, PA, USA, 2016.
- Morsi, A.J.; Alexander, S.A. An Investigation of Particle Trajectories in Two-Phase Flow System. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Shukla, S.K.; Shukla, P.; Ghosh, P. Evaluation of Numerical Schemes for Dispersed Phase Modeling of Cyclone Separators. Eng. Appl. Comp. F Mech. 2010, 5, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Stairmand, C.J. The design and performance of cyclone separators. Ind. Eng. Chem. 1951, 29, 356–383. [Google Scholar]
- Wasilewski, M. Analysis of the effects of temperature and the share of solid and gas phases on the process of separation in a cyclone suspension preheater. Sep. Purif. Technol. 2016, 168, 114–123. [Google Scholar] [CrossRef]
- Wasilewski, M. Analysis of the effect of counter-cone location on cyclone separator efficiency. Sep. Purif. Technol. 2017, 179, 236–247. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S. Investigations of the flow field inside a square cyclone separator using DPIV and CFD. E3S Web Conf. 2019, 100, 1–8. [Google Scholar] [CrossRef]
- Venkatesh, S.; Kumar, R.S.; Sivapirakasam, S.P.; Sakthivel, M.; Venkatesh, D.; Arafath, S.Y. Multi-objective optimization, experimental and CFD approach for performance analysis in a square cyclone separator. Powder Technol. 2020, 371, 115–129. [Google Scholar] [CrossRef]
- Wasilewski, M.; Duda, J. Multicriteria optimisation of first-stage cyclones in the clinker burning system by means of numerical modelling and experimental research. Powder Technol. 2016, 289, 143–158. [Google Scholar] [CrossRef]
- Stachnik, M.; Jakubowski, M. Multiphase model of flow and separation phases in a whirlpool: Advanced simulation and phenomena visualization approach. J. Food Eng. 2020, 274, 109846. [Google Scholar] [CrossRef]
- Jakubowski, M.; Sterczyska, M.; Matysko, R.; Poreda, A. Simulation and experimental research on the flow inside a whirlpool separator. J. Food Eng. 2014, 133, 9–15. [Google Scholar] [CrossRef]
- Slack, M.D.; Prasad, R.O.; Bakker, A.; Boysan, F.M. Advances in Cyclone Modelling Using Unstructured Grids. Chem. Eng. Res. Des. 2000, 78, 1098–1104. [Google Scholar] [CrossRef]
- Demir, S.; Karadeniz, A.; Aksel, M. Effects of cylindrical and conical heights on pressure and velocity fields in cyclones. Powder Technol. 2016, 295, 209–217. [Google Scholar] [CrossRef]
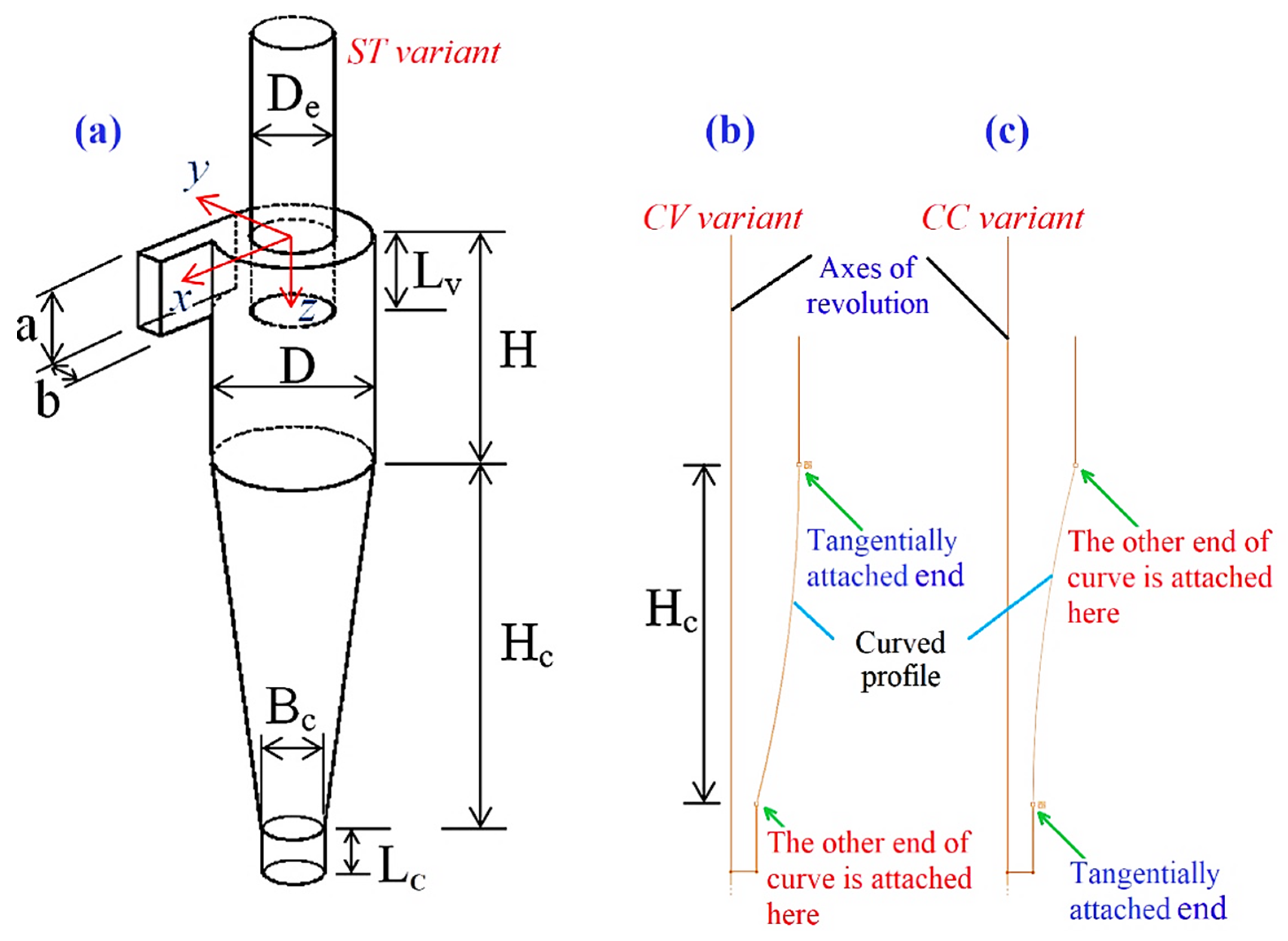
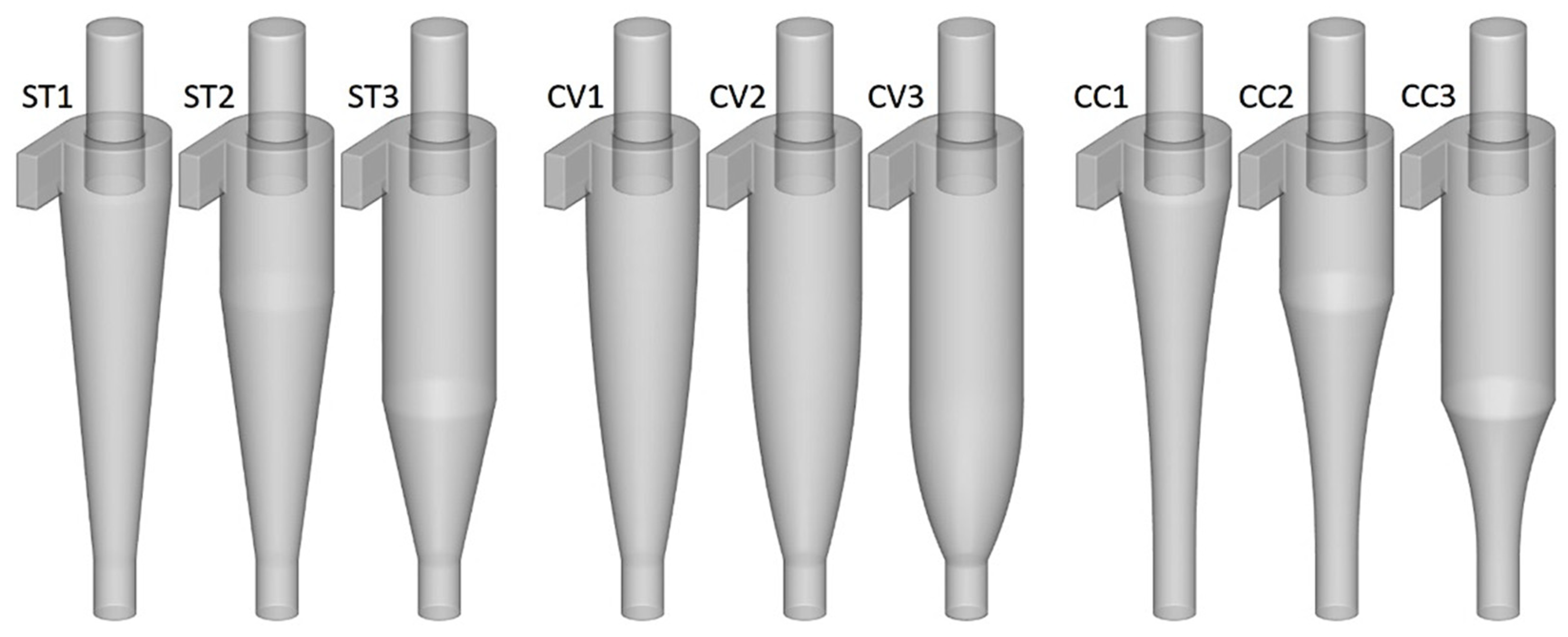






| Cyclone Variants | Cyclones Models | Symbol | Dimensionless Ratio (Dimension)/D |
|---|---|---|---|
| De | 0.5 | ||
| a | 0.5 | ||
| b | 0.2 | ||
| Lv | 0.5 | ||
| Lc | 0.5 | ||
| Bc | 0.375 | ||
| ST | ST1 | H | 0.5 |
| ST2 * | 1.5 | ||
| ST3 | 2.5 | ||
| CV | CV1 | 0.5 | |
| CV2 | 1.5 | ||
| CV3 | 2.5 | ||
| CC | CC1 | 0.5 | |
| CC2 | 1.5 | ||
| CC3 | 2.5 | ||
| ST | ST1 | Hc | 3.5 |
| ST2 | 2.5 | ||
| ST3 | 1.5 | ||
| CV | CV1 | 3.5 | |
| CV2 | 2.5 | ||
| CV3 | 1.5 | ||
| CC | CC1 | 3.5 | |
| CC2 | 2.5 | ||
| CC3 | 1.5 |
| Cyclone Variants | Cyclone Models | % Change in Pressure Drop * | ||
|---|---|---|---|---|
| Uin = 10 m/s | Uin = 15 m/s | Uin = 20 m/s | ||
| ST | ST1 | 5.53 | 4.27 | 2.86 |
| ST2 | – | – | – | |
| ST3 | −2.77 | −2.63 | −1.38 | |
| CV | CV1 | −0.425 | −1.00 | 18.55 |
| CV2 | −2.55 | −3.91 | 16.51 | |
| CV3 | 15.11 | 14.35 | 22.12 | |
| CC | CC1 | 14.04 | 8.08 | 7.82 |
| CC2 | 3.83 | 1.91 | 1.94 | |
| CC3 | −0.85 | −1.45 | −0.87 | |
| Cyclone Variants | Cyclone Models | % Change in Overall Separation Efficiency * | % Change in Cut-Off Diameter * | ||||
|---|---|---|---|---|---|---|---|
| Uin = 10 m/s | Uin = 15 m/s | Uin = 20 m/s | Uin = 10 m/s | Uin = 15 m/s | Uin = 20 m/s | ||
| ST | ST1 | 0.73 | 2.36 | 2.45 | −2.16 | −2.95 | −2.14 |
| ST2 | – | – | – | – | – | – | |
| ST3 | −2.37 | −2.17 | −2.66 | 3.30 | 1.91 | 1.77 | |
| CV | CV1 | −0.31 | 5.19 | −1.78 | 0.36 | −2.31 | 3.35 |
| CV2 | −1.69 | 3.16 | −1.74 | 1.26 | 4.55 | 8.93 | |
| CV3 | 1.55 | 6.77 | −0.24 | 1.98 | 6.54 | 13.67 | |
| CC | CC1 | 0.89 | 5.98 | 4.13 | −7.02 | −4.47 | 1.30 |
| CC2 | −1.25 | 3.40 | 1.10 | −1.74 | 0.56 | 5.21 | |
| CC3 | −0.52 | 3.60 | −3.55 | 1.92 | 6.38 | 10.88 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, S.; Saha, I.; Prakash, O.; Mukherjee, T.; Iqbal, J.; Roy, A.K.; Wasilewski, M.; Brar, L.S. CFD Investigations of Cyclone Separators with Different Cone Heights and Shapes. Appl. Sci. 2022, 12, 4904. https://doi.org/10.3390/app12104904
Pandey S, Saha I, Prakash O, Mukherjee T, Iqbal J, Roy AK, Wasilewski M, Brar LS. CFD Investigations of Cyclone Separators with Different Cone Heights and Shapes. Applied Sciences. 2022; 12(10):4904. https://doi.org/10.3390/app12104904
Chicago/Turabian StylePandey, Satyanand, Indrashis Saha, Om Prakash, Tathagata Mukherjee, Jawed Iqbal, Amit Kumar Roy, Marek Wasilewski, and Lakhbir Singh Brar. 2022. "CFD Investigations of Cyclone Separators with Different Cone Heights and Shapes" Applied Sciences 12, no. 10: 4904. https://doi.org/10.3390/app12104904






