Rod–Airfoil Interaction Noise Reduction Using Gradient Distributed Porous Leading Edges

Abstract

Rod–airfoil interaction noise is a major concern in several practical industrial and aeronautical applications. In this study, we constructed bio-inspired gradient distributed porous leading edges to reduce rod–airfoil interaction noise. Noise radiations by NACA 0012 airfoils with nonporous aluminum and porous leading edges were experimentally compared in an anechoic wind tunnel by changing the streamwise gap between the upstream rod and the downstream airfoil, as well as the angle of attack of the airfoil. The results of detailed acoustic tests showed that the proposed gradient distributed porous leading edges can significantly reduce noise radiation around and above the peak frequency of the baseline rod–airfoil interaction. Parametric studies on the piecewise porous characteristics showed that rod–airfoil interaction noise reduction is sensitive to the coverage percentage, position, and arrangement order of the porous materials. Porous leading edges with lower pores per inch, larger coverage, and gradually sparse distributed pores better reduced noise. Moreover, the position of the porous material affected the frequency band of noise reduction, and the noise reduction performance was better when it was located in the downstream strips of the porous leading edge.

1. Introduction

Noise radiated from a rod–airfoil configuration, i.e., rod–airfoil interaction noise, has recently attracted extensive research interest [1,2,3,4] because it is a benchmark well-suited for studying the noise generation mechanisms encountered in several practical industrial and aeronautical applications. Examples of such mechanisms include blade–vortex interaction noise in helicopter rotors and the rotor–stator interaction noise between the rotor wake and the leading edges of the downstream stator blades in turbo-engines. Furthermore, rod–airfoil interaction noise is a simple but relevant test case for theoretical and numerical broadband noise modeling [5].

Jacob et al. [5] performed a rod–airfoil experiment in the large anechoic room of the Ecole Centrale de Lyon. In their benchmark experiment, a symmetric airfoil with a NACA-0012 profile (chord length c = 100 mm) was placed at a distance of 10 times the rod diameter (d = 10 mm, $d/c$ = 0.1) downstream of the rod to avoid feedback of the downstream airfoil onto the vortex shedding of the upstream rod. The results of far-field acoustic measurements and near-field particle image velocimetry (PIV), single hot-wire, and wall pressure coherence measurements of the rod–airfoil configuration at a zero angle of attack of the airfoil provided a detailed database about the main flow statistics and sound pressure spectra of the rod–airfoil interaction noise. These benchmark data were then used to validate the ability of several combined CFD solvers and aeroacoustic models to predict broadband noise, such as RANS + FW-H computations [1,5], LES + FW-H computations [5,6,7], and DES + FW-H computations [8,9].

Following Jacob et al. [5], parametric studies of the rod–airfoil interaction noise were further conducted by experimental methods. Siller et al. [10] used a single far-field microphone to measure the sound pressure level (SPL) of the rod–airfoil configuration under several rod diameters ranging from d = 4 to 16 mm. The airfoil was also placed 10 times the rod diameter downstream of the cylindrical rod in their experiments. The results showed that the Strouhal frequency is lower and the sound pressure levels are higher in the low frequencies below and around the Strouhal frequency for larger rod diameters. In addition to different rod diameters, Giesler and Sarradj [11] performed microphone array measurements to investigate rod–airfoil interaction noise characteristics for different types of airfoils and different streamwise gaps between the rod and the airfoil. They found that the rod/wake noise and the trailing edge noise of the airfoil are nearly identical, whereas the leading edge noise of the airfoil is considerably less for a bigger and blunter leading airfoil edge. They also found that the emitted rod–airfoil interaction noise depends more on the rod diameter than on the streamwise gap. Li et al. [12] performed phased microphone array tests on the noise characteristics of a rod–airfoil configuration by changing four parameters: rod type (cylindrical or square), rod diameter, cross-stream position of the rod, and streamwise gap between the airfoil leading edge and the rod. Their acoustic results revealed that the interaction noise at the leading airfoil edge significantly increases as the rod diameter increases. They also found that the intensity and corresponding peak SPL of the rod–airfoil interaction first increase and then decrease as the streamwise gap increases from 30 to 170 mm (rod diameter d = 15 mm). The intensity and overall SPL gradually decrease as the cross-stream position of the rod increases. Li et al. [12] further used a planar PIV system to acquire the instantaneous spanwise vorticity for different rod–airfoil configurations and then to explain the underlying physical mechanisms responsible for the observed noise characteristics. They found that the size of the upstream shed vortices increases with increasing rod diameter, and the rod shed vortices gradually miss the airfoil leading edge as the cross-stream position increases. Munekata et al. [13] investigated the effects of the attack angle of the downstream airfoil on the characteristics of aerodynamic noise and the wake structure of the rod–airfoil configuration. They reported that both the peak SPL and peak frequency of the rod–airfoil interaction noise decrease with increasing attack angle of the downstream airfoil due to the larger vortex scale but weaker vortex entrainment, which is caused by the blocking effect produced by the downstream airfoil.

To reduce rod–airfoil interaction noise, researchers have proposed several noise control methods. Siller et al. [10] applied boundary layer suction or blowing near the leading edge on both sides of the downstream airfoil to control rod–airfoil interaction noise. They found that the peak SPL in the far field could be significantly reduced by blowing (up to 7.2 dB), whereas it is slightly increased by the application of suction (about 2.7 dB). Both a soft-vane leading edge on the downstream airfoil and the air blowing out of the sides of the upstream rod were investigated by Li et al. [12] to reduce rod–airfoil interaction noise. Their comparison of sound pressure spectra showed that both concepts can be applied to effectively attenuate the broadband noise around the peak frequency (up to 6 dB). A hybrid computational aeroacoustics model (2D URANS + FW-H equation) was introduced by Siozos-Rousoulis et al. [14] to prove the potential of a rotating cylinder as a noise reduction technique. The numerical simulation results illustrated that a cylinder with rotational frequencies higher than the vortex shedding frequency of the nonrotating case can notably reduce noise.

In recent years, inspired by the three special feather adaptations of the silent flying owl (i.e., leading edge serrations, trailing edge fringes, and soft downy coating surface), researchers have developed a number of innovative bio-inspired noise reduction solutions [4] to reduce rod–airfoil interaction noise. LES and FW-H acoustic analogy methods were applied by Chen et al. [15] to investigate the effect of leading edge serrations on rod–airfoil interaction noise. Their numerical results showed that leading edge serrations in the form of sinusoidal profiles achieve a noise reduction of about 2.4 dB at the vortex shedding frequency and a significant noise attenuation (up to 10 dB) over a quite wide frequency range above the vortex shedding frequency. Subsequently, Chen et al. [2] experimentally investigated the effect of the amplitude and wavelength of the leading edge serrations on rod–airfoil interaction noise. Their experimental results demonstrated that the noise reduction effects increase with increasing amplitude and decreasing wavelength, and the nondimensional amplitude-to-wavelength ratio is a key parameter for reducing rod–airfoil interaction noise.

Porous leading edges have also been used to reduce turbulence-interaction noise in the past few years. Three-dimensional third-octave band sound maps by Geyer et al. [16] showed that the noise produced by the leading edge of the porous airfoils that interacts with the grid-generated turbulence is below than that produced by the nonporous leading edges. Moreover, turbulence-interaction noise reduction increases with the (on average) larger pores of the porous leading edges. Roger et al. [17] demonstrated that a porous airfoil (a thin, rigid, flat-plate core covered with metallic porous materials and a wiremesh skin) reduces turbulence-interaction noise, but less efficiently than the airfoil with tubercle-like serrations at the leading edge. Chaitanya et al. [18] found that a single row of pores downstream of the leading edge significantly reduces turbulence-interaction noise, and a source cutoff radiation effect was proposed to explain the observed behavior. A lattice Boltzmann method was employed by Teruna et al. [19] to numerically study the aeroacoustics and aerodynamics of airfoils equipped with porous leading edges. They found that the porous leading edges reduce interaction noise by dampening surface pressure fluctuations, but may result in lift reduction and drag increase.

Although porous materials have been used to reduce interaction noise, they have dominantly been applied to verify the feasibility and effectiveness of the concept, and the porous parameters have not been optimized [17]. The porous materials used in the current bio-inspired noise reduction concept generally have homogenous pore properties, such as porosity and pores per inch (ppi). The effect of nonhomogenous porous materials with gradient-distributed properties [20,21] on the rod–airfoil interaction noise reduction is not well-understood. These two aspects motivated our experimental study, in which we aimed to advance the field by using piecewise gradient distributed porous leading edges to reduce rod–airfoil interaction noise. The detailed acoustic measurements in an open jet wind tunnel indicated that the proposed porous leading edges reduce the peak SPL of the rod–airfoil configuration, and can significantly reduce the medium- to high-frequency noise above the peak frequency. Moreover, parametric tests on the porous properties (coverage, position, and arrangement order) provided the relevant design criteria for the gradient distributed treatments, i.e., larger porous coverage and reasonable arrangement order.

2. Experimental Set-Up and Data Processing

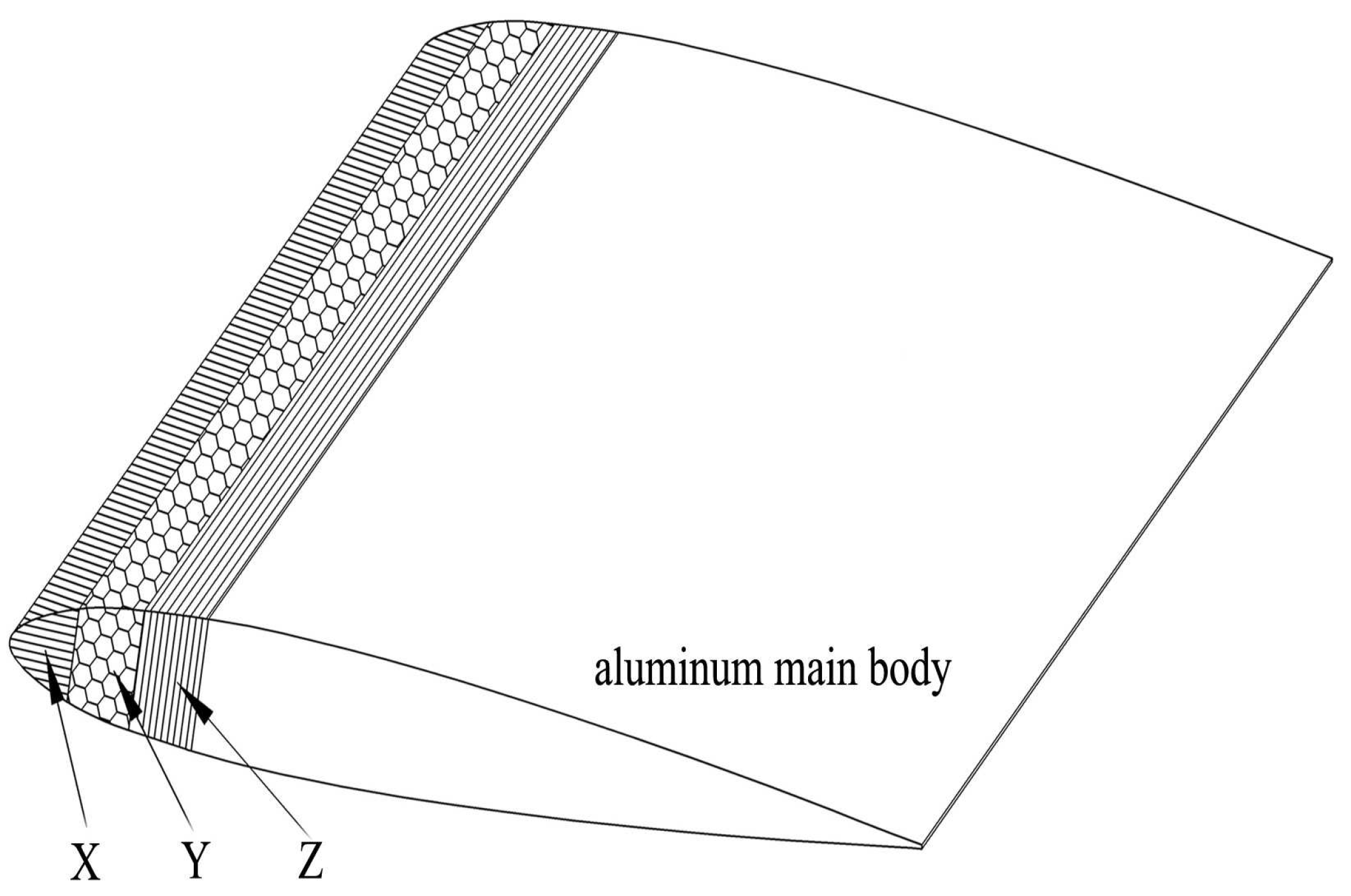
2.1. Test Facility and Model

The acoustic tests of the rod–airfoil system were conducted in a small anechoic wind tunnel at the China Aerodynamics Research and Development Center (CARDC), i.e., in a 0.55 m × 0.4 m aeroacoustic wind tunnel. The rectangular nozzle exit of this wind tunnel is 0.4 m high and 0.55 m wide. All six walls of the anechoic chamber are covered with fibreglass wedges, yielding a background noise level of less than 76 dB(A) for a flow velocity of 80 m/s (measured at a distance of 2 m perpendicular to the center of the nozzle). The maximum flow velocity is 100 m/s, and the incoming turbulence level is less than 0.2% at the centerline.

A sketch of the experimental set-up is illustrated in Figure 1. A symmetric NACA 0012 airfoil was located downstream of a cylindrical rod. The rod diameter was d = 20 mm, while the airfoil chord length was c = 200 mm; thus, the dimensionless quantity $d/c$ = 0.1 was the same as the benchmark set-up in Jacob et al. [5]. The rod–airfoil system was vertically installed between two parallel side plates that were flush-mounted with the nozzle exit. The downstream airfoil was placed at angles of attack ranging from $\alpha =0^{\circ }$ to ${20}^{\circ }$, with its fixed rotating axis located at a 30% chord length (i.e., 60 mm, the same as in [21]). In our experiments, the positions of the upstream rod were also changeable to enable adjustment of the streamwise gap L between the trailing edge point of the rod and the leading edge point of the airfoil at the angle of attack $\alpha =0^{\circ }$. Three different gaps were set, i.e., L = 100, 140, and 200 mm. The last one produced $L/d$ = 10, which is the same as the benchmark set-up in Jacob et al. [5]. Smaller gaps were not used as the downstream airfoil would have acted as a splitter plate, which would have prevented the formation of Kármán vortices from the upstream rod and thus would have drastically reduced the noise radiation of the rod–airfoil configuration [12,22,23]. The range of the flow velocities under investigation was between $V_{\infty }$ = 20 and 80 m/s, corresponding to Reynolds numbers based on a rod diameter and airfoil chord of $R{e}_d=2.67\times {10}^4$− $1.07\times {10}^5$ and $R{e}_c=2.67\times {10}^5$−$1.07\times {10}^6$, respectively.

As shown in Figure 2, the tested airfoil was composed of an aluminum main body and three interchangeable leading edge strips (denoted as X, Y, and Z) with equal lengths in the chordwise direction (i.e., 10 mm or 5% of c). We used porous metallic foams (copper or iron-nickel) with a wide range of ppi values (20 to 120 ppi) and nonporous aluminum, whose ppi value was taken as 0, to manufacture the interchangeable strips. At present, we are unable to provide the detailed information of the porosity and the static permeability of the porous media, because neither we nor the material supplier had the dedicated devices to measure these parameters. In our tests, we used X**Y**Z** to label each leading edge configuration of the airfoil. For example, X80Y60Z40 corresponded to the configuration whose three strips were composed of 80, 60, and 40 ppi metallic foams from upstream to downstream.

2.2. Data Acquisition and Processing

As shown in Figure 1, far-field noise was measured by a single microphone at a polar angle of 90${}^{\circ }$ and a distance of 1 m away from the jet-flow centerline, in the mid-span plane of the airfoil. Sound pressure data were acquired at a sampling rate of 51.2 kHz with a sampling duration of 30 s. The SPL of the far-field sound pressure (reference pressure $p_{ref}=2\times {10}^{-5}$ Pa) was computed using a Hanning window with a block size of 8192 samples and an overlap of 50%, yielding a spectral resolution of 6.25 Hz. The overall sound pressure level (OASPL) of the noise radiation was computed by integrating the SPL between 100 Hz (cutoff frequency of the anechoic chamber) and 25.6 kHz (Nyquist frequency).

In the acoustic measurements, the noise data at the three angles of attack of the airfoil (i.e., $\alpha =0^{\circ }$, ${10}^{\circ }$, and ${20}^{\circ }$) and three streamwise gaps (i.e., L = 100, 140, and 200 mm) were measured for the baseline rod–airfoil configuration, in which the main body of the downstream airfoil was equipped with three aluminum leading edge strips. We recorded the acoustic time signals under three typical operating conditions (i.e., $\alpha =0^{\circ }$ at L = 100 and 200 mm, and $\alpha ={10}^{\circ }$ at L = 200 mm) for the porous leading edges due to the limited time of the wind tunnel was available. The noise levels of the isolated rod at L = 100 and 200 mm were also measured to check the contribution of the airfoil to the rod–airfoil interaction noise.

3. Results

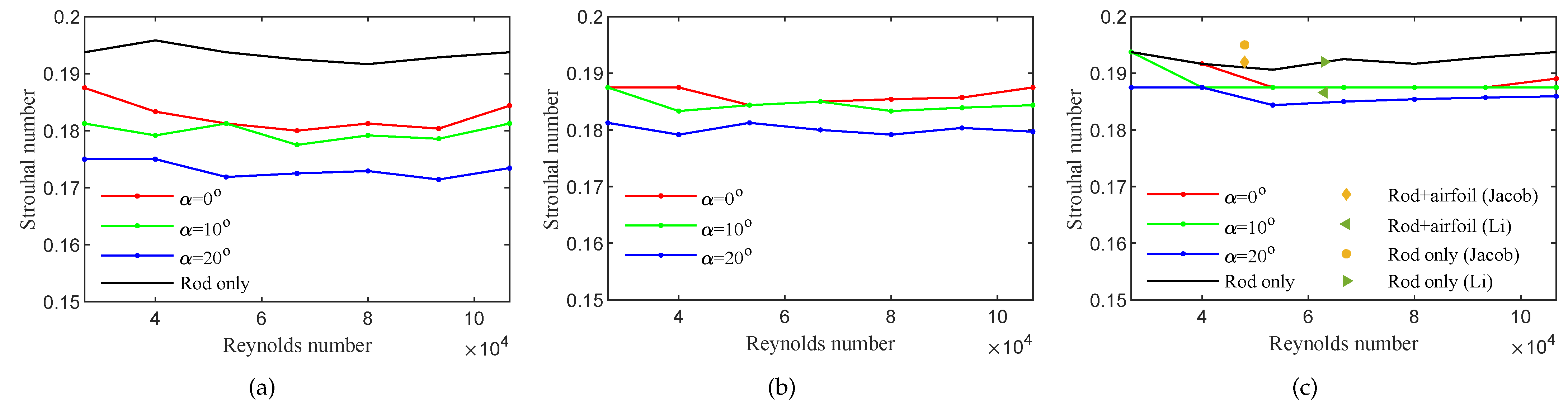
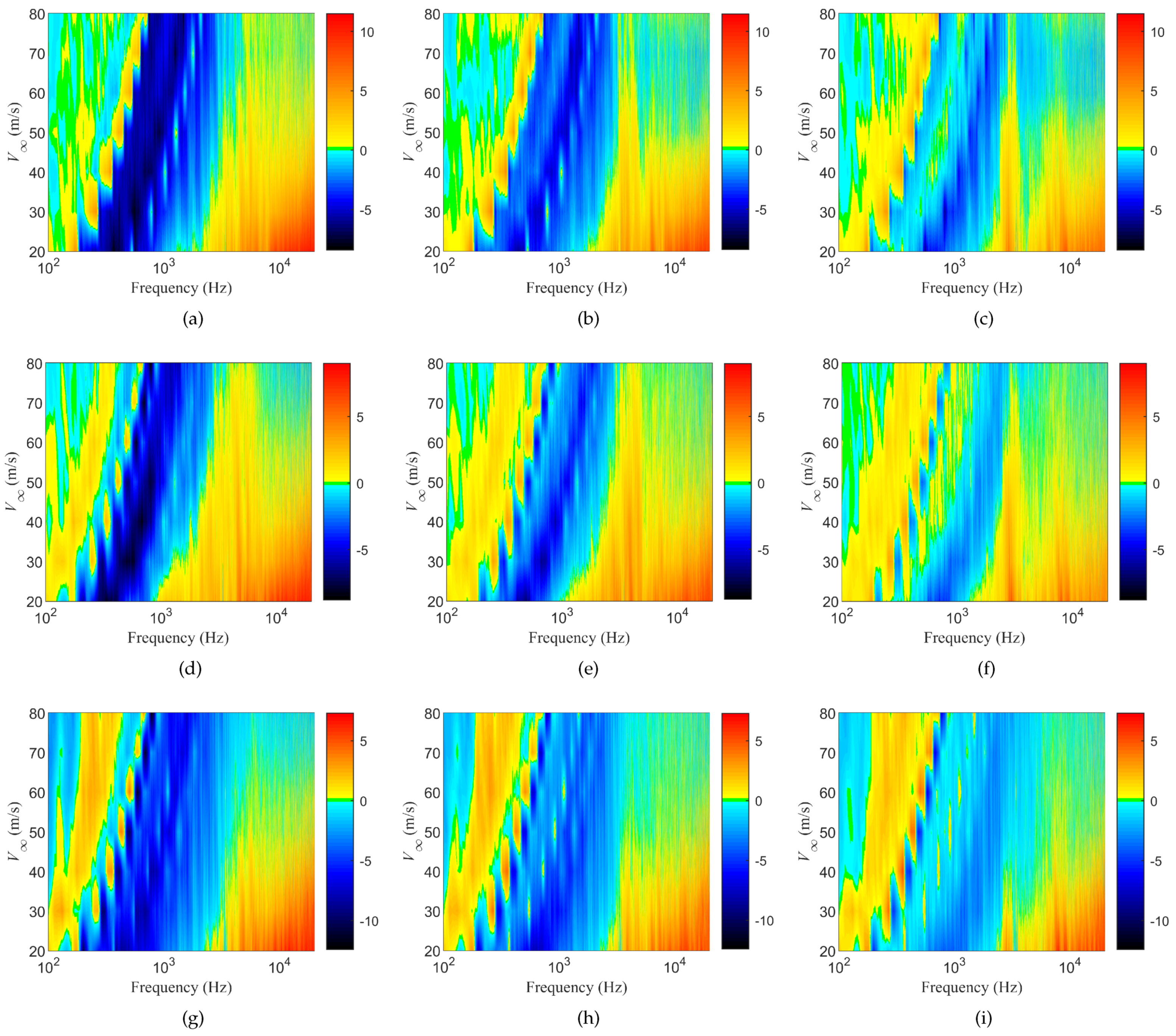
3.1. Noise Characteristics of the Baseline Case

Figure 3 shows the typical noise spectra generated by the baseline rod–airfoil case (i.e., all the three leading edge strips were made of aluminum) at different airfoil attack angles. The noise spectra of the isolated rod and the flow only are plotted in Figure 3. As trends were similar for all flow velocities, only the values for $V_{\infty }$ = 50 m/s are presented. Figure 4 and Figure 5 compare the magnitude of the main peak (i.e., peak SPL) and the corresponding Strouhal number of the peak frequency based on the rod diameter. Because the validation and comparison of the presented experimental results with data from the literature are compulsory steps before performing any parametric study, Figure 5c also provides the Strouhal numbers of the rod–airfoil configuration and the rod-only configuration obtained by Jacob et al. [5] and Li et al. [12] for the benchmark case ($d/c$ = 0.1, $L/d$ = 10 and $\alpha =0^{\circ }$).

Several interesting points were drawn from these figures: (1) The measured spectra for the isolated d= 20 mm rod featured a strong tonal component and a substantial broadband part around the main peak, corresponding to the frequency of Kármán vortices shed by the rod (the Strouhal number was about 0.195). The presence of the airfoil embedded in the wake of the isolated rod increased the level of emission peak of about 10 dB and the broadband spectra around the main peak, which we attributed to the impingement of the periodic shedding vortices onto the airfoil leading edge, as proved in [12,13]. The spectra for frequencies above 8–9 kHz were dominated by rod noise, which implied that the noise in these frequency bands may have been caused by small-scale turbulent vortices, which do not strongly interact with the leading airfoil edge. (2) As the streamwise gap increased, the peak SPL of the rod–airfoil configuration generally reduced, in good with prior experimental findings of various rotor–stator configurations [24] where the tonal noise levels reduced with larger rotor–stator spacing. The phenomenon can be understood because the energy of the shedding vortices and the corresponding impingement intensity onto the airfoil gradually weakened as the shed vortices moved and dissipated downstream. (3) The main peak somewhat shifted to a lower frequency in the presence of the downstream airfoil, which could be ascribed to a possible weak hydrodynamic–acoustic feedback of the airfoil onto the vortex shedding of the rod, as suggested by Casalino et al. [1], Jacob et al. [5], and Lorenzoni et al. [25]. Moreover, the shifting became more obvious as the streamwise gap decreased, which may have occurred due to the enhancement in the aforementioned hydrodynamic–acoustic feedback because the spacing between the rod and the airfoil reduced. Additional evidence of this conclusion is that splitter plates close to the rod could completely suppress vortex shedding and tonal noise, as experimentally demonstrated by You et al. [22] and Spiteri et al. [23]. (4) The sound pressure level of the main peak slightly reduced as the angle of attack of the downstream airfoil increased, which is similar to the experimental observations of Munekata et al. [13], whose flow visualization tests proved that it is due to the weaker vortex entrainment. On the contrary, the broadband part of the spectrum far away from the main peak (both the low- and mid-to-high-frequency range) substantially increased as the angle of attack increased. Moreover, the frequency corresponding to the main peak further reduced with increasing downstream airfoil attack angle, which we attributed to the increased vortex–airfoil interaction area and the enhanced hydrodynamic–acoustic feedback. With decreasing streamwise gap, the frequency shifting of the main peak under different angles of attack increased and the Strouhal number generally reduced (similar to [12]), which indicated that the hydrodynamic–acoustic feedback was strengthened in this situation.

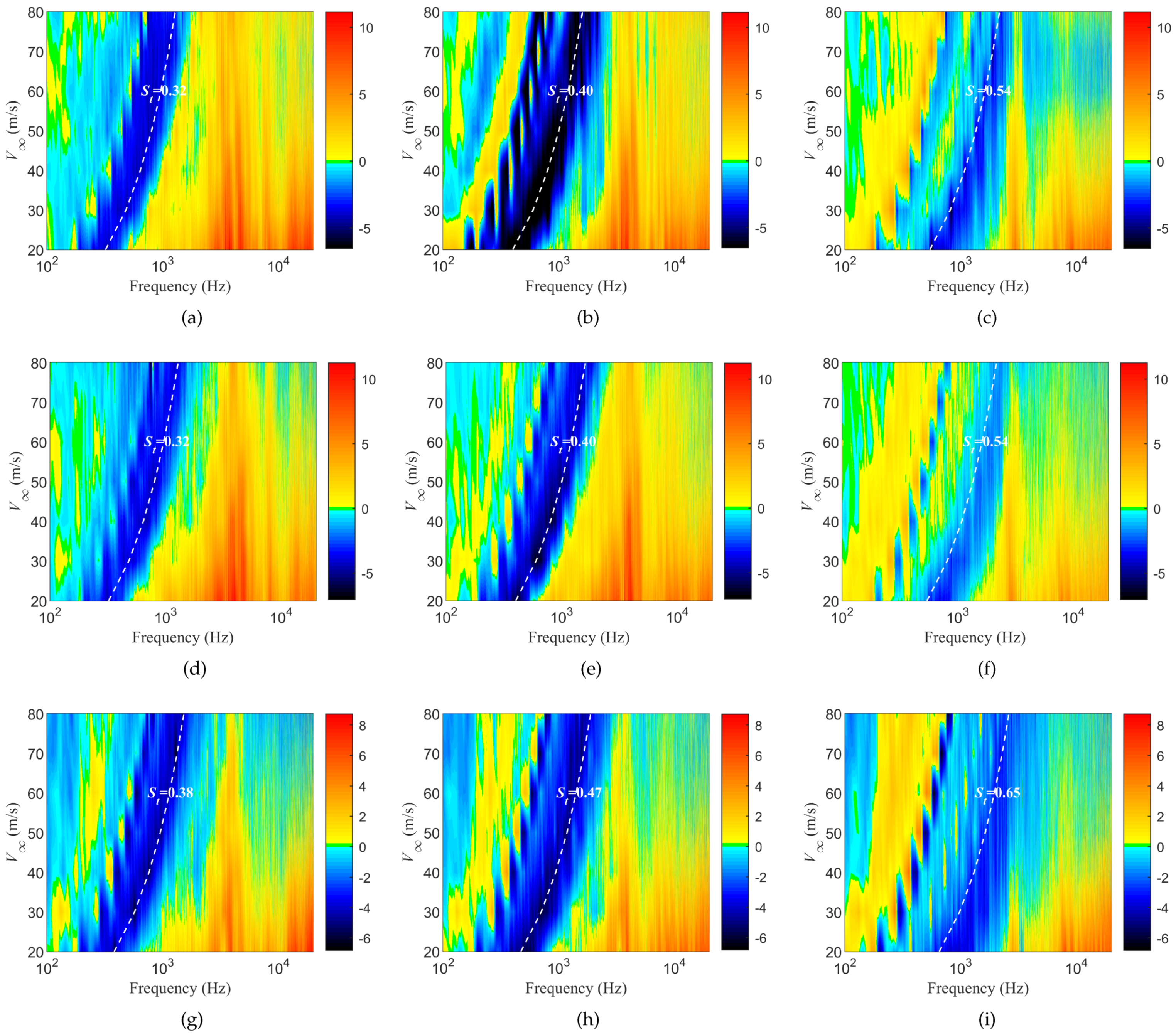
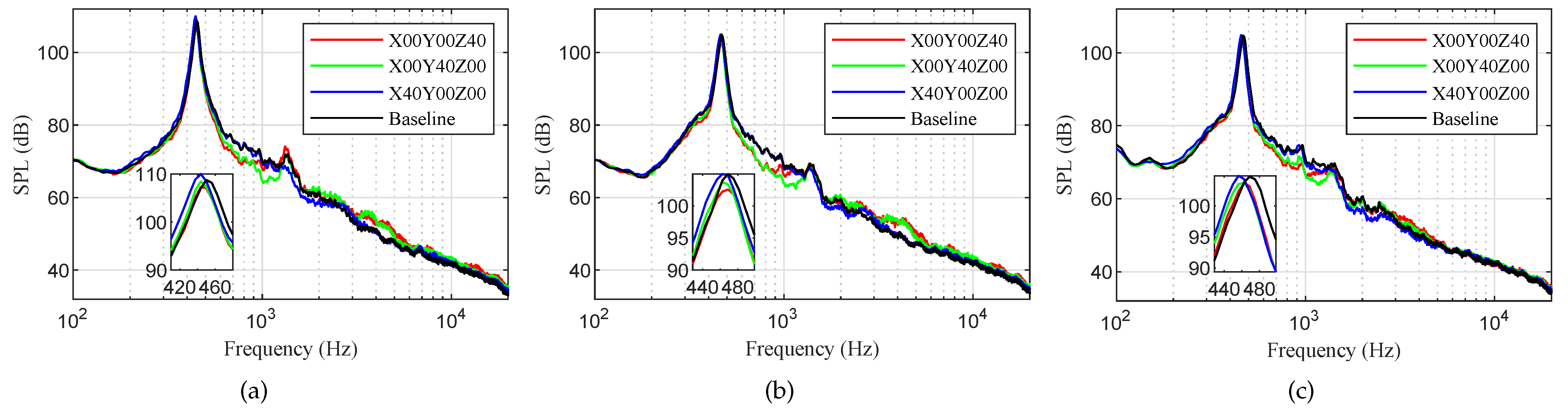
3.2. Noise Characteristics of Porous Leading Edges

A comparison of the sound pressure reduction level ($\Delta$SPL = SPL${}_p$− SPL${}_b$) versus the frequency and flow velocity between the porous leading edge SPL${}_p$ and the baseline case SPL${}_b$ is shown in Figure 6 for different airfoil attack angles and in Figure 7 for different streamwise gaps. Positive and negative values in $\Delta$SPL represent a noise amplification and noise reduction effects, respectively. Comparisons of the noise spectra at a typical flow velocity of $V_{\infty }$ = 50 m/s are plotted in Figure 8.

These figures reveal several characteristic features associated with rod–airfoil interaction noise reduced by the porous leading edges: (1) Porous leading edges can reduce rod–airfoil interaction noise around the peak frequency and substantially suppress the mid-to-high frequency broadband noise above the peak frequency. The maximum noise reduction is 20.71 dB at L = 200 mm and $\alpha ={20}^{\circ }$. However, low-frequency noise below the peak frequency generally increases due to the shifting of the main peak (Figure 8). Moreover, high-frequency noise above 2000 Hz also increases, and this noise amplification effect increases with the decrease in the ppi value of the porous materials. This phenomenon is consistent with published experimental observations and can be attributed to the surface roughness of porous materials [21,26,27]: lower ppi values indicate higher surface roughness noise, which is usually noticeable at high frequencies. (2) With the increase in the airfoil attack angle, the noise reduction effect becomes more considerable and the frequency range with $\Delta$SPL < 0 widens. For example, the upper limit increases from about 2000 Hz in Figure 8b to about 3000 Hz in Figure 8c. This phenomenon may be due to the enhanced flow communication across the pressure and suction sides of the porous airfoil and thus the decreased intensity of the impingement of the vortices onto the solid leading edge because of the increased pressure difference between the two sides of the downstream airfoil at a high attack angle. (3) With the increase in the streamwise gap, the frequency range with noise reduction capability (i.e., $\Delta$SPL < 0) is basically unchanged, and the variation in noise attenuation for different streamwise gaps is not as large as that at different attack angles of the downstream airfoil. (4) With the decrease in the ppi value of the porous materials, the noise reduction ability is enhanced and the peak frequency decreases. The reason for this is that lower-ppi materials have relatively bigger pores, which allows the shedding vortices and the impinging turbulence to permeate into the porous leading edge and thus reduces the intensity of the surface pressure fluctuations. This is in agreement with previous findings [19], because surface pressure fluctuations mitigation reduces sound source intensity; the latter is one of the mechanisms through which noise is attenuated.

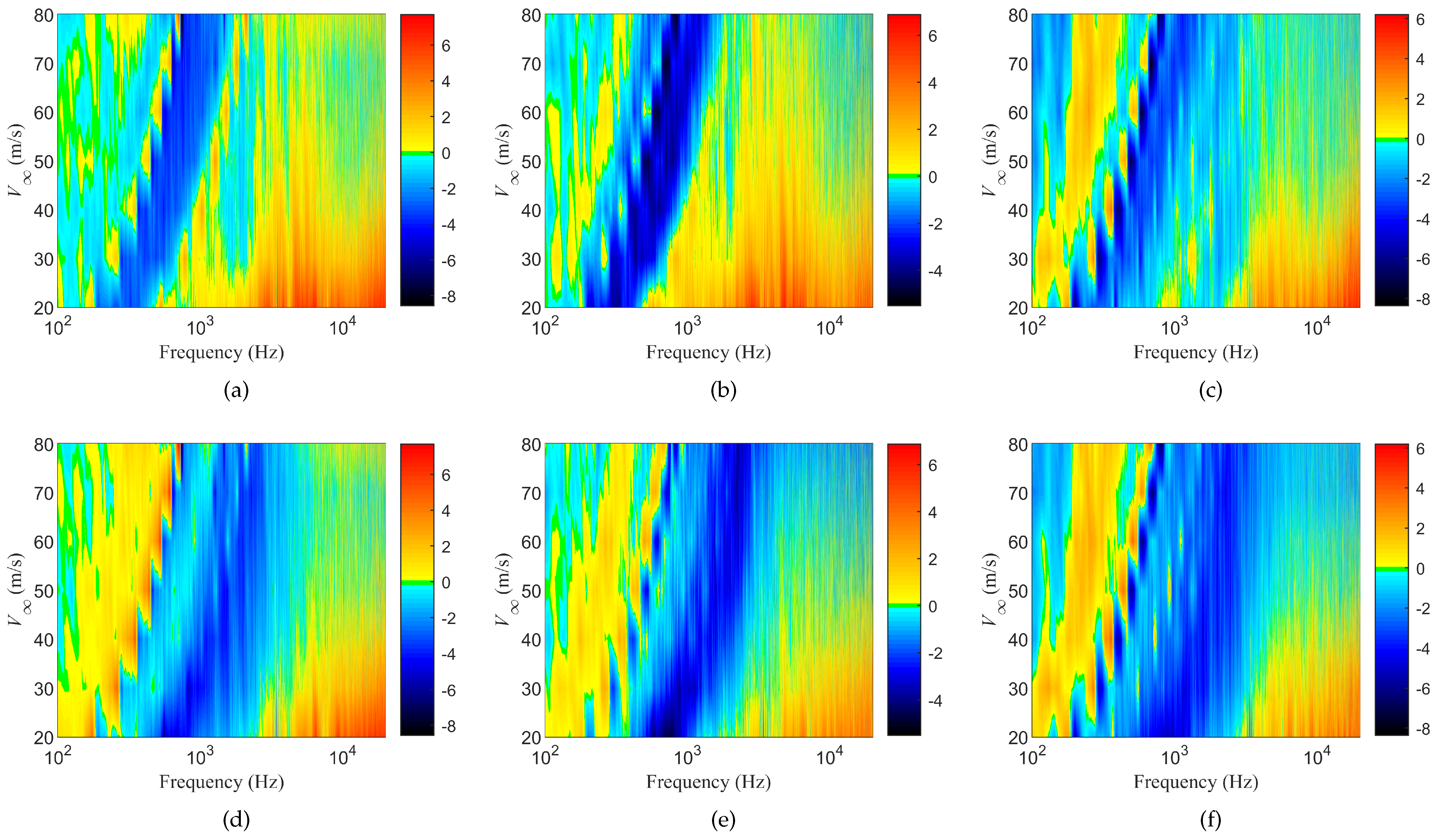
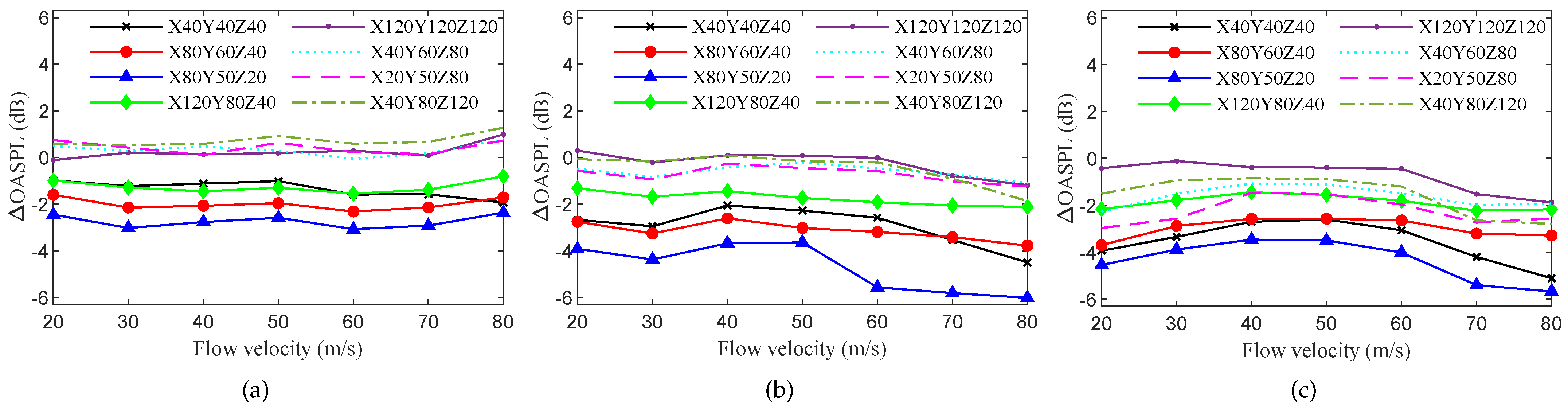
3.3. Effect of Gradient Properties on Noise Reduction

Figure 9 compares the $\Delta$SPL values for different coverage percentages of the porous treatments for three typical operating conditions (i.e., $\alpha =0^{\circ }$ at L = 100 mm and L = 200 mm, and $\alpha ={10}^{\circ }$ at L = 200 mm). From left to right in Figure 9, all three interchangeable leading edge strips or only part of them were composed of 40 ppi porous material. These figures show that both the maximum noise attenuation and the range of noise attenuation at mid-to-high frequency decreased with decreasing porous coverage. The reason for this finding may be that a large porous coverage increases the flow penetrating into the porous media, which thus reduces the rod–airfoil interaction noise. Figure 9 shows that the noise-increasing effect at high frequencies slightly decreases with a lower porous coverage, which is consistent with the smaller porous surface.

Figure 10 compares the $\Delta$SPL values when the upstream, middle, or downstream of the three interchangeable leading edge strip was composed of porous material. Figure 11 illustrates the typical noise spectra at a flow velocity of $V_{\infty }$ = 50 m/s. From these figures, we can see that the position of the porous material had different effects on the noise attenuation, though the porous coverage was basically the same when the pores were located in different strips. Generally, the pores located on the middle strip (i.e., X00Y40Z00) produced the best noise attenuation, whereas the minimum noise reduction was achieved using the X40Y00Z00 configuration. This finding is relevant for applications in which the mean lift coefficient of the wing profile must be preserved. As proved [19], porous treatment of the airfoil can reduce lift and increase drag, which finding implies that we can substantially attenuate interaction noise with a lower aerodynamic penalty by introducing porous holes only a small chordwise area downstream of the leading airfoil edge. The Strouhal number corresponding to the maximum reduction in the mid- to high-frequency band increased with the upstream movement of the porous position. For example, the Strouhal number increased from $S_t$ = 0.38 for X00Y00Z40 (Figure 10g) to $S_t$ = 0.65 for X40Y00Z00 (Figure 10i) at the operating conditions of L = 200 mm and $\alpha ={10}^{\circ }$. The underlying mechanism for these observations is not clear at this stage, but may be related to the characteristics of the shedding vortices (such as vortex intensity or vortex size) at different leading edge positions, which will be revealed by our ongoing work involving flow-field measurements and numerical simulations.

Figure 12, Figure 13 and Figure 14 show the effect of arrangement order of the porous leading edges on the rod–airfoil interaction noise reduction. In these figures, the porous leading edges represented in the upper rows were composed of gradually sparser porous materials (i.e., lower ppi value or larger pores, such as X80Y60Z40 and X80Y50Z20) from the upstream strip to the downstream strip, whereas the leading edges represented in the lower rows were composed of gradually denser porous materials. Figure 15 summarizes the difference in OASPL (i.e., $\Delta$OASPL = OASPL${}_p$− OASPL${}_b$, where OASPL${}_p$ and OASPL${}_b$ denote the OASPL of the porous leading edge and the baseline leading edge, respectively). The $\Delta$OASPL of two homogeneous porous leading edges (X40Y40Z40 and X120Y120Z120) are also presented in Figure 15. Several observations were obtained from these figures. First, the noise reduced (whether $\Delta$SPL around and above the peak frequency or $\Delta$OASPL) by the gradually more sparsely distributed porous leading edges were generally larger than those of the corresponding gradually denser counterparts, though the denser ones had a slightly wider frequency range of $\Delta$SPL < 0. Second, the gradient-distributed porous leading edge could attenuate more noise than the homogeneous-distributed porous leading edge. For example, X80Y60Z40 and X80Y50Z20 generally performed better than X40Y40Z40, as shown in Figure 15a. However, a larger gradient difference does not mean increased noise reduction: X80Y50Z20 (gradient difference of 30 ppi from upstream strip to downstream strip) rather than X120Y80Z40 reduced the most noise. Overall sound pressure level reductions of up to 3.07, 6.02, and 5.67 dB were obtained by X80Y50Z20 for the operating conditions of L = 100 mm with $\alpha =0^{\circ }$, L = 200 mm with $\alpha =0^{\circ }$, and L = 200 mm with $\alpha ={10}^{\circ }$, respectively. We attributed these findings to two candidate factors: (1) Secondary vortex–structure interaction may form when the airflows or shedding vortices pass across the upstream sparse porous area and then encounter the downstream dense porous area. This interaction increases noise emission because vortex–structure interaction increases the noise spectra around the main peak, as shown in Section 3.1. (2) As demonstrated in Figure 6, Figure 7 and Figure 8, Figure 10 and Figure 11, the porous leading edge with a lower-ppi material reduces more noise and the use of an upstream porous strip results in the smallest noise reduction. Therefore, the gradually more sparsely distributed porous leading edges, which have lower-ppi porous materials in the last two downstream strips, reduced more noise.

4. Conclusions

In this study, the acoustic radiation characteristics of piecewise gradient distributed porous leading edges were experimentally investigated and compared with the baseline nonporous leading edge. The experimental results showed that the proposed modifications can substantially reduce rod–airfoil interaction noise around and above the peak frequency of the rod–airfoil configuration. The findings of systematically parametric studies showed that the noise reduction effects are sensitive to the properties of the porous materials. In general, higher noise reduction is achieved with higher vortex–porous interactions through larger pores, porous coverage, and higher downstream airfoil attack angle. Moreover, we found that the rod–airfoil interaction noise reduction effects are related to the characteristics of the incoming shedding vortex to a certain extent: pores located in downstream positions or gradually more sparsely distributed pores can achieve greater noise reduction. The underlying mechanisms of these findings will revealed through numerical simulations and flow-field measurements in our future work. Moreover, we did not consider the effect of gradient distributed porous leading edges on aerodynamics with changes in lift and drag in this experimental study, due to the lack of suitable measuring equipment (such as balance and its support), which is another future research direction.