Accounting for Patient Engagement in Randomized Controlled Trials Evaluating Digital Cognitive Behavioral Therapies
Abstract
:1. Introduction
- What is the proper approach to the statistical analysis of such a trial?
- How do we compare treatment effects accounting for different levels of engagement?
- How should we perform a sample size planning for such a trial given that engagement patterns are unknown upfront?
2. Statistical Modeling and Some Theoretical Results
- (I)
- The difference , which is the contrast between the novel CBT alone and the control intervention.
- (II)
- The difference , which is the contrast between the novel CBT + dCBT engaged at the level and the control intervention.
- If both and are significantly different from zero, then the novel CBT is deemed efficacious, and its effect can be magnified or decreased by the individual engagement with the dCBT.
- If is significantly different from zero but is not, then the novel CBT is deemed efficacious but the engagement with the dCBT is not helpful for synergizing this effect.
- If is significantly different from zero, then a combination of the novel CBT with the dCBT engaged at the average level observed in the trial is more efficacious than the control condition.
2.1. Analysis of Covariance (ANCOVA)
- Inference on
- Inference on the linear slope
- Inference on
2.2. Two-Sample t-Test
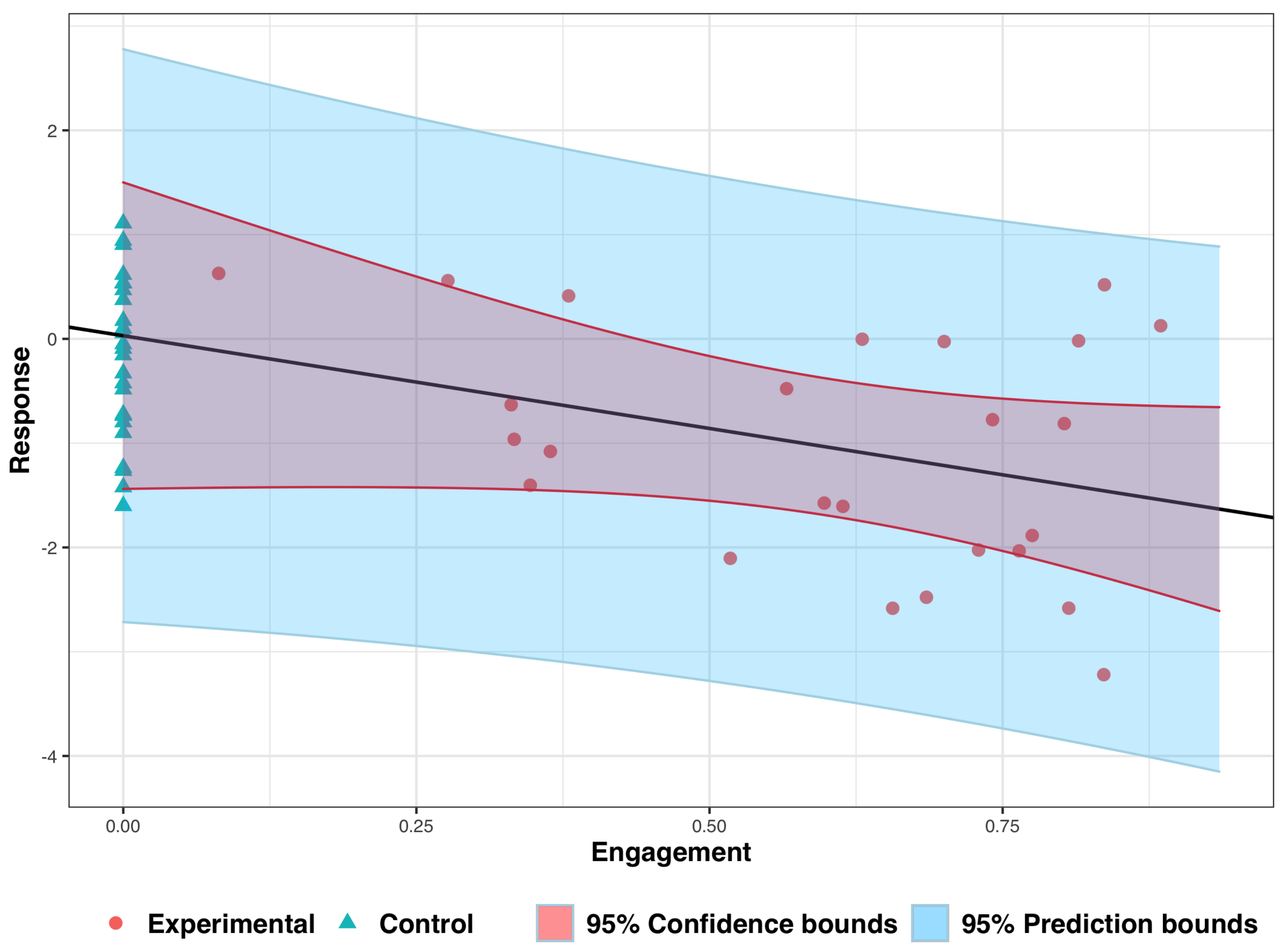
3. Analyzing Experimental Data: An Illustrative Example
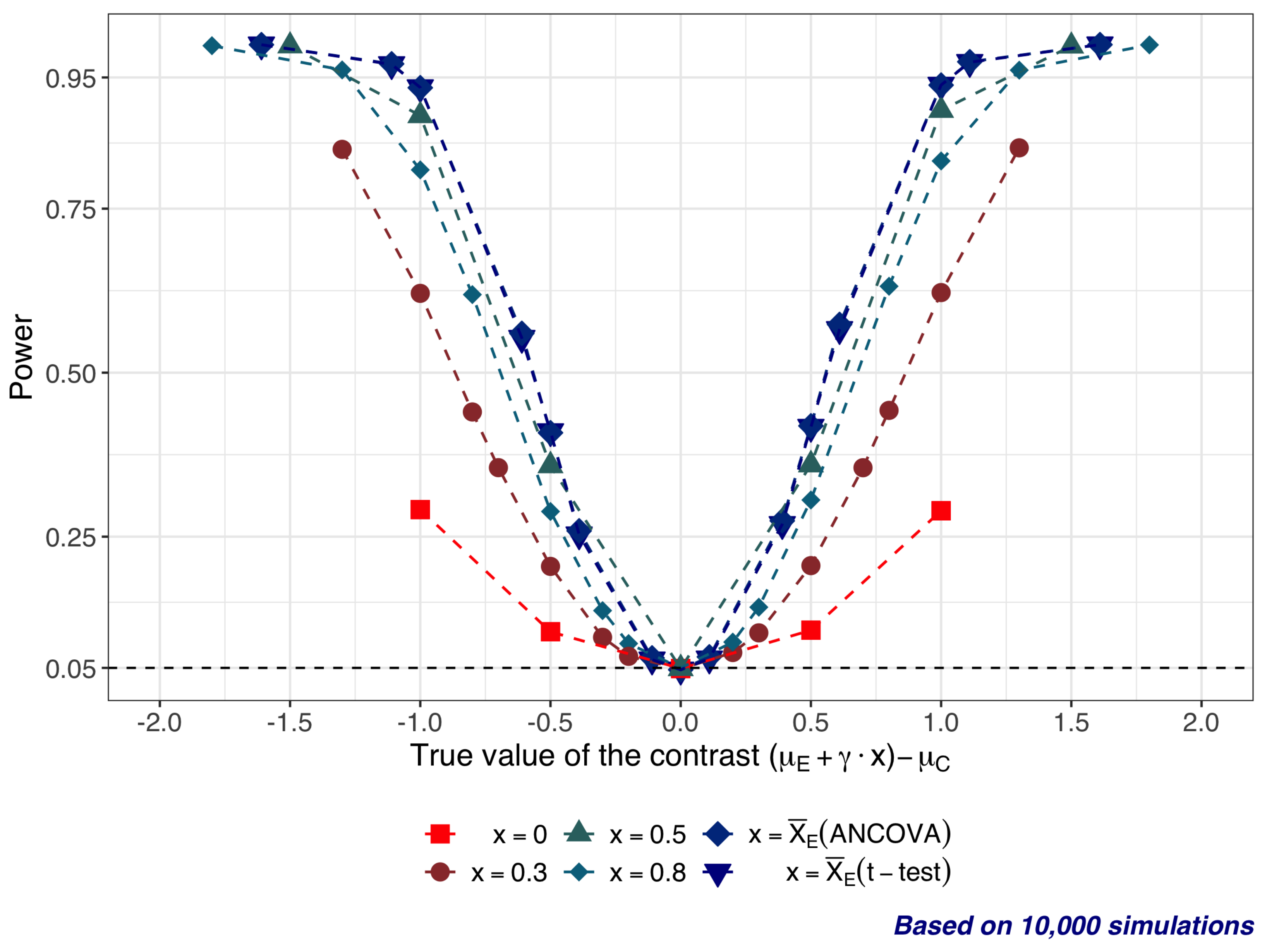
4. Statistical Properties of Significance Tests: A Simulation Study
- and is in the range from −1 to 1; therefore .
- (slope) is in the range from −1 to 1 ().
- .
- (25 subjects per arm).
- All tests are 2-sided, with significance level .
5. Design Aspects
5.1. Optimality of Equal Allocation
5.2. Sample Size Considerations
- = chance of a false positive result;
- = chance of a false negative result;
- the “clinically relevant” mean treatment difference that we would not like to miss;
- the presumed standard deviation of the primary outcome.
- Step 1: Sample size for a given set of engagement measurements
- Step 2: Distribution of the requisite sample size
- (i)
- , which has and ;
- (ii)
- , which has and ;
- (iii)
- with and ; and
- (iv)
- with and .
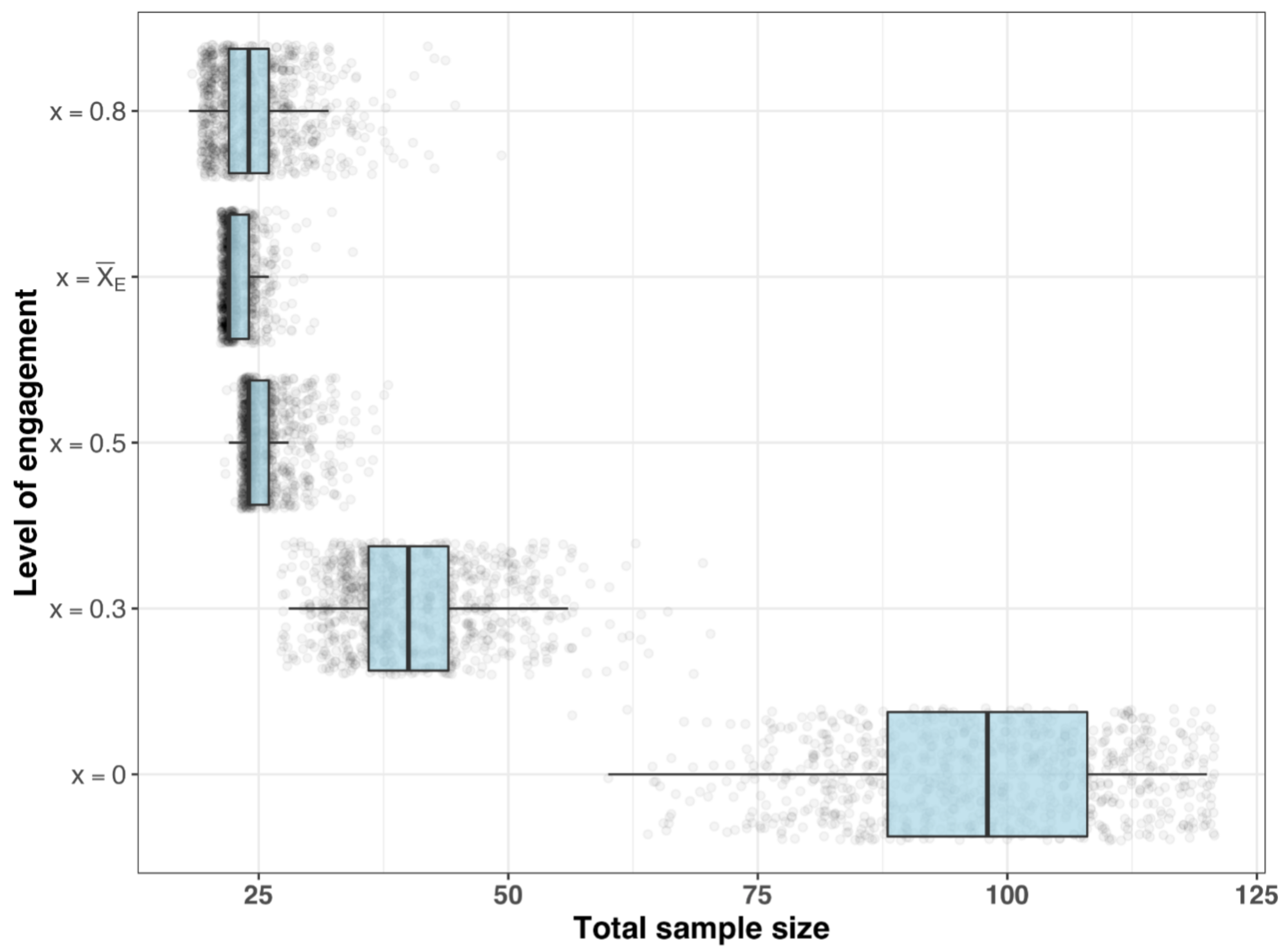
- Sample size requirements for different estimands
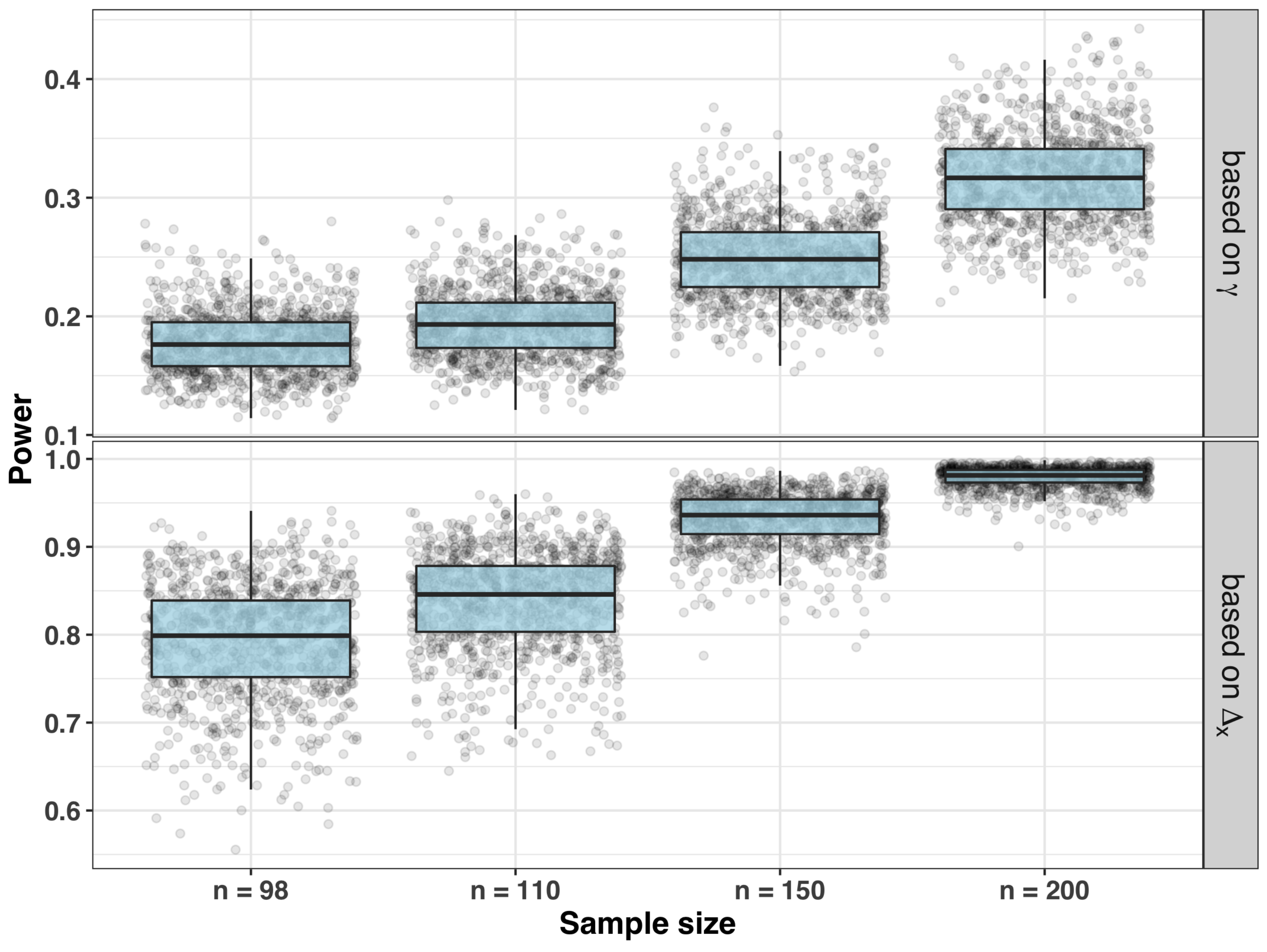
- Sample size and power for testing significance of the slope
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marsch, L.A. Sector perspective: Digital therapeutics in behavioral health. In Digital Therapeutics: Scientific, Statistical, Clinical and Regulatory Development Aspects, 1st ed.; Sverdlov, O., vam Dam, J., Eds.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Sverdlov, O.; van Dam, J.; Hannesdottir, K.; Thornton-Wells, T. Digital Therapeutics: An Integral Component of Digital Innovation in Drug Development. Clin. Pharmacol. Ther. 2018, 104, 72–80. [Google Scholar] [CrossRef] [PubMed]
- Espie, C.A.; Henry, A.L. Designing and delivering a DTx clinical research program: No need to re-invent the wheel. In Digital Therapeutics: Scientific, Statistical, Clinical and Regulatory Development Aspects, 1st ed.; Sverdlov, O., van Dam, J., Eds.; CRC Press: Boca Raton, FL, USA, 2022; Chapter 4. [Google Scholar]
- Chung, J.Y. Digital therapeutics and clinical pharmacology. Transl. Clin. Pharmacol. 2019, 27, 6–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yardley, L.; Spring, B.J.; Riper, H.; Morrison, L.G.; Crane, D.H.; Curtis, K.; Merchant, G.C.; Naughton, F.; Blandford, A. Understanding and Promoting Effective Engagement With Digital Behavior Change Interventions. Am. J. Prev. Med. 2016, 51, 833–842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghaemi, S.N.; Sverdlov, O.; van Dam, J.; Campellone, T.; Gerwien, R. A Smartphone-Based Intervention as an Adjunct to Standard-of-Care Treatment for Schizophrenia: Randomized Controlled Trial. JMIR Form. Res. 2022, 6, e29154. [Google Scholar] [CrossRef] [PubMed]
- Truzoli, R.; Reed, P.; Osborne, L.A. Patient expectations of assigned treatments impact strength of randomised control trials. Front. Med. 2021, 8, 648403. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, S.A.; Åsberg, M. A New Depression Scale Designed to be Sensitive to Change. Br. J. Psychiatry 1979, 134, 382–389. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Guo, Y.; Li, L.; Hong, Y.A.; Li, Y.; Zhu, M.; Zeng, C.; Zhang, H.; Cai, W.; Liu, C.; et al. Relationship Between Patient Engagement and Depressive Symptoms Among People Living with HIV in a Mobile Health Intervention: Secondary Analysis of a Randomized Controlled Trial. JMIR mHealth uHealth 2020, 8, e20847. [Google Scholar] [CrossRef] [PubMed]
- Palmier-Claus, J.E.; Ainsworth, J.; Machin, M.; Barrowclough, C.; Dunn, G.; Barkus, E.; Rogers, A.; Wykes, T.; Kapur, S.; Buchan, I.; et al. The feasibility and validity of ambulatory self-report of psychotic symptoms using a smartphone software application. BMC Psychiatry 2012, 12, 172. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kreyenbuhl, J.; Record, E.J.; Himelhoch, S.; Charlotte, M.; Palmer-Bacon, J.; Dixon, L.B.; Medoff, D.R.; Li, L. Development and Feasibility Testing of a Smartphone Intervention to Improve Adherence to Antipsychotic Medications. Clin. Schizophr. Relat. Psychoses 2019, 12, 152–167. [Google Scholar] [CrossRef] [PubMed]
- Bucci, S.; Barrowclough, C.; Ainsworth, J.; Machin, M.; Morris, R.; Berry, K.; Emsley, R.; Lewis, S.; Edge, D.; Buchan, I.; et al. Actissist: Proof-of-concept trial of a theory-driven digital intervention for psychosis. Schizophr. Bull. 2018, 44, 1070–1080. [Google Scholar] [CrossRef] [PubMed]
- Myers, R.H. Classical and Modern Regression with Applications, 2nd ed.; Duxbury Press: London, UK, 1990. [Google Scholar]
- European Medicines Agency (EMA). Guideline on Adjustment for Baseline Covariates in Clinical Trials; EMA/CHMP/295050/2013, 26 February 2015. Available online: https://www.fda.gov/media/148910/download (accessed on 9 May 2022).
- U.S. Food & Drug Administration. Adjusting for Covariates in Randomized Clinical Trials for Drugs and Biological Products; Draft Guidance for Industry, May 2021. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/adjusting-covariates-randomized-clinical-trials-drugs-and-biological-products (accessed on 9 May 2022).
- Fuller, W.A. Measurement Error Models; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models. A Modern Perspective, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Valeri, L.; Lin, X.; VanderWeele, T.J. Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model. Stat. Med. 2014, 33, 4875–4890. [Google Scholar] [CrossRef] [PubMed]
- Chien, I.; Enrique, A.; Palacios, J.; Regan, T.; Keegan, D.; Carter, D.; Tschiatschek, S.; Nori, A.; Thieme, A.; Richards, D.; et al. A Machine Learning Approach to Understanding Patterns of Engagement with Internet-Delivered Mental Health Interventions. JAMA Netw. Open 2020, 3, e2010791. [Google Scholar] [CrossRef] [PubMed]
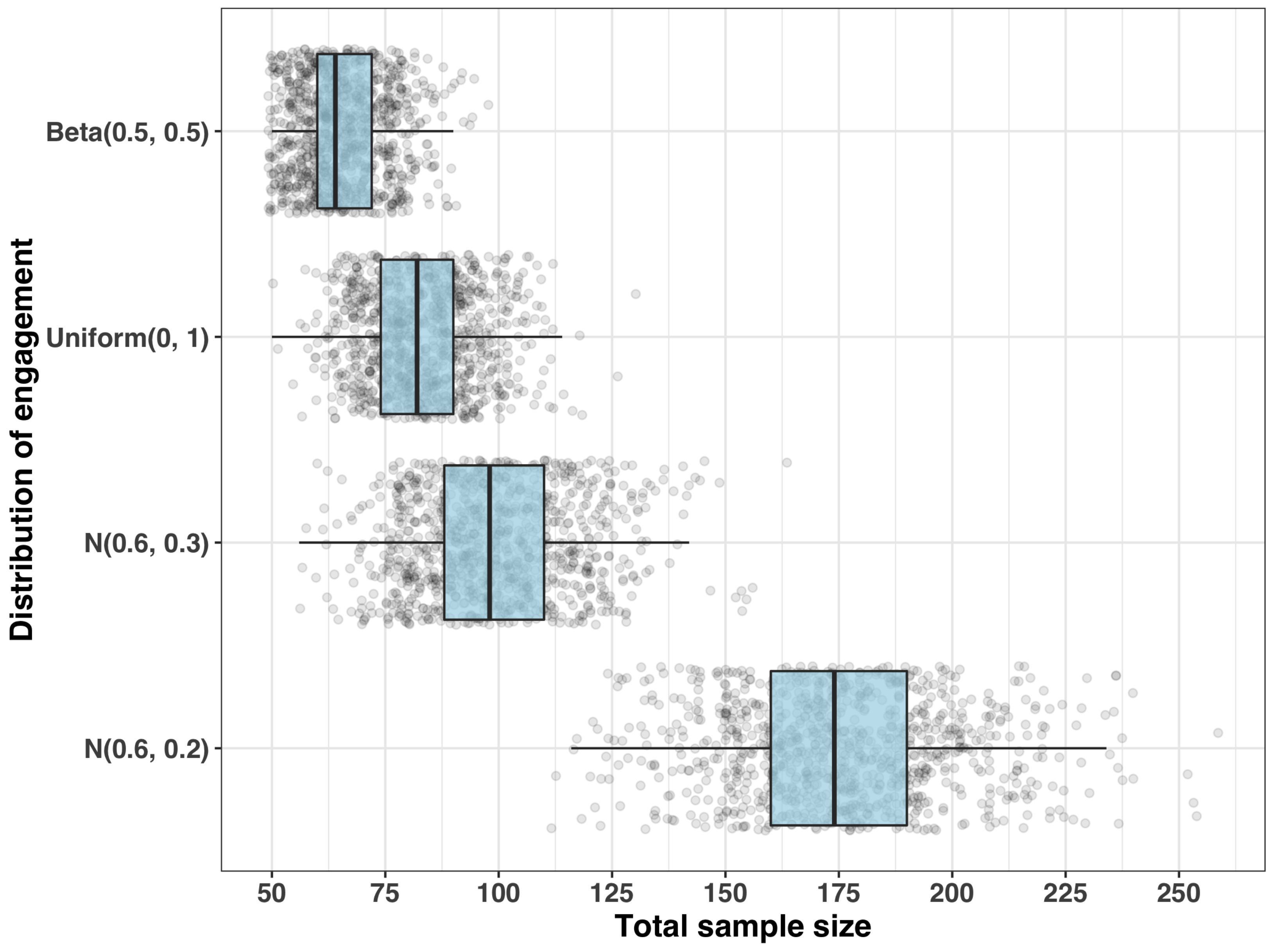
| Total Sample Size (n) | ||||
|---|---|---|---|---|
| Distribution of Engagement ( ) | Q50 | Q80 | Q90 | Max |
| 64 | 74 | 78 | 98 | |
| 82 | 92 | 98 | 130 | |
| 98 | 112 | 120 | 164 | |
| 174 | 194 | 206 | 258 | |
| Total Sample Size (n) | |||
|---|---|---|---|
| Q50 | Q80 | Q90 | |
| 0 | 98 | 110 | 114 |
| 0.3 | 40 | 46 | 50 |
| 0.5 | 24 | 26 | 30 |
| 22 | 24 | 24 | |
| 0.8 | 24 | 28 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sverdlov, O.; Ryeznik, Y. Accounting for Patient Engagement in Randomized Controlled Trials Evaluating Digital Cognitive Behavioral Therapies. Appl. Sci. 2022, 12, 4952. https://doi.org/10.3390/app12104952
Sverdlov O, Ryeznik Y. Accounting for Patient Engagement in Randomized Controlled Trials Evaluating Digital Cognitive Behavioral Therapies. Applied Sciences. 2022; 12(10):4952. https://doi.org/10.3390/app12104952
Chicago/Turabian StyleSverdlov, Oleksandr, and Yevgen Ryeznik. 2022. "Accounting for Patient Engagement in Randomized Controlled Trials Evaluating Digital Cognitive Behavioral Therapies" Applied Sciences 12, no. 10: 4952. https://doi.org/10.3390/app12104952
APA StyleSverdlov, O., & Ryeznik, Y. (2022). Accounting for Patient Engagement in Randomized Controlled Trials Evaluating Digital Cognitive Behavioral Therapies. Applied Sciences, 12(10), 4952. https://doi.org/10.3390/app12104952






