2. Literature Review
Customer churn prediction modeling has often been the focus of researchers, as evidenced by numerous studies published on this topic. Particularly well-explored are the contractual business settings in the B2C domain, such as those commonly encountered in the telecommunications [
19,
20,
21], banking [
22,
23], and insurance [
24,
25] sectors, where customers at risk of terminating or not renewing their contracts are identified and targeted with retention campaigns in efforts to persuade them otherwise. Non-contractual settings have also often been studied, where efforts have been put towards predicting which retail customers are least likely to make a purchase in the future [
26,
27], which users are at most risk to stop playing mobile games [
6], or which passengers are not planning to use a particular airline for their future flights [
28]. The B2B domain, on the other hand, has received less attention so far. Within the contractual settings in this domain, approaches have been proposed to identify business clients who are likely to close all contracts with a financial service provider [
29], business customers who are least likely to renew a subscription to a software service [
30,
31,
32], or the probability of corporate users switching to a different B2B telecommunications service provider given a set of incentives [
33].
Non-contractual B2B settings have started receiving more interest fairly recently, where efforts are being made to help companies identify customers at risk of leaving. However, even though some general guidelines in terms of the most promising approaches to the problem can be inferred from relevant studies, it may be difficult for practitioners to decide which approach (or combination of approaches) to use, as there is significant variability in methods used to create models (distinct algorithms and hyperparameter values used), leveraged data sources (spanning transactional, CRM, quality-of-service, and E-commerce systems), characteristics of raw datasets (in terms of the time span they cover, number of customers, and churn rates), and approaches to deriving features.
This is best illustrated within
Table 1, where we provide an overview of relevant studies with respect to:
Raw data characteristics (domain they come from, time period they span, number of customers included, and churn rates);
Source systems the data were extracted from (transactional, quality-of-service (QoS), Customer Relationship Management (CRM), and web data);
Churn definitions used (single or multiple);
Types of features extracted (L—length, R—recency, F—frequency, M—monetary, P—profit);
Type of feature extraction window considered (fixed or variable);
Approach to creating the training dataset (single-slicing or multi-slicing).
Table 1.
Relevant studies overview.
Table 1.
Relevant studies overview.
| Study | Chen et al. [34] | Schaeffer et al. [35] | Gordini et al. [9] | Gattermann-Itschert et al. [18] | Jahromi et al. [12] | Janssens et al. [36] | This Study |
|---|
| Domain | Logistics | Logistics | Wholesale (fast moving consumer goods) | Wholesale (fast moving consumer goods) | Retailer (fast moving consumer goods) | Retailer (beverages) | Wholesale (agricultural goods) |
| Dataset span | 29 months | 40 months | 12 months | 30 months | 12 months | 31 months | 38 months |
| # of Customers | 69,170 | 1968 | 80,000 | 5000 | 11,021 | 41,739 | 3470 |
| Churn definitions | 1 month | 3, 7 months | 12 months | 3 months | 6 months | 12 months | 1, 2, 3 months |
| Churn rates | 2% | 4–19% | 10% | 7–15% | 28% | 4% | 5–38% |
| Data sources | Transactions, QoS | Transactions | Transactions, QoS, web data | Transactions, QoS, CRM | Transactions | Transactions, QoS, CRM | Transactions |
| Features extracted | LRFMP | F | LRFM, QoS, platform usage | LRFM, QoS | RFM | LRFM | LRFM |
| Feature window | Fixed | Variable | Fixed | Fixed | Fixed | Fixed | Variable |
| Training set creation | Single-slicing | Single-slicing | Single-slicing | Multi-slicing | Single-slicing | Single-slicing | Multi-slicing |
In the remainder of this section, we describe each of the studies in more detail and put them in the context of gaps we aim to address within present study.
Chen et al. [
34] examined the importance of length, recency, frequency, monetary, and profit (LRFMP) variables for predicting churn in the case of one of the largest logistics companies in Taiwan. The company defines lost business customers (i.e., churners) as those who did not engage in any transactions in the past month. The dataset (after applying business-domain knowledge and relevant filtering) comprised 69,170 business customers, among which 1321 were churners. The authors applied common binary classification techniques for the domain—Decision Tree (DT), feed-forward Multi-Layer Perceptron neural network (MLP), Support Vector Machines (SVM) and Logistic Regression (LR)—to assess their effectiveness in predicting churn. Their experiment showed that the DT model is able to achieve superior results compared to other models on all reported measures (accuracy, precision, recall, and F1) and they report that the top three most influential predictors were recency of purchase, length of the relationship (i.e., tenure), and monetary indicator (i.e., amount spent).
Schaeffer et al. [
35] considered the case of a Mexican company that sells parcel-delivery as a prepaid service to business clients. Clients are able to purchase the desired number of delivery units from the company at any point in time and then consume them at their discretion, thus making this a non-contractual B2B scenario. The authors experimented with different definitions of churn (i.e., inactivity of customers in consecutive future time periods) and used inventory level-based (i.e., amount of services available) time series of varying lengths to derive features that are fed to selected machine learning algorithms in order to predict whether a client will be active or not. In particular, the authors extracted trend and level, magnitude, auto-correlations, and Fourier coefficients (as derived by fast Fourier transform) and used them as features. The dataset comprised transactions made by 1968 clients who ordered and spent services in a period of just over three years (between January 2014 and April 2017), among which, depending on the churn definition used, there were between 56 and 346 churners. The authors reported that Random Forest (RF) outperforms SVM, AdaBoost, and k-Nearest Neighbors (kNN) classifiers for the majority of time series lengths and churn definitions used when evaluated on specificity, but that SVM also performs acceptably over the majority of combinations when balanced accuracy is considered.
Gordini et al. [
9] proposed a novel parameter-selection approach for an established classification technique (SVM), which they used to create a predictive churn model that was subsequently tested on real-world data obtained from a major Italian on-line fast moving consumer goods company. The dataset used was derived from the activities of clients on a B2B e-commerce website (as well as the customer-level information provided by the company) and comprised 80,000 business customers, with their transactional records spanning the period from September 2013 to September 2014. According to company business rules, customers who do not make a purchase in the period of one year are considered churners and labeled accordingly in the dataset. While the training set contained equal percentage of churners and non-churners, the test set was imbalanced and contained 10% churners and 90% non-churners (both sets comprised 40,000 customers). The authors proposed the area under the receiver operating characteristic curve (AUC) as a metric on which to optimize model parameters (during the cross-validation in the training phase) and reported that such an approach outperforms the commonly used accuracy measure when evaluated on the number of correctly classified churners. In terms of performance when compared to LR and MLP, this approach also yields higher AUC and top-decile lift (TDL) when evaluated on the test set (holdout sample). Finally, the authors reported that recency of the latest purchase, frequency of purchases, and the length of relationship (i.e., tenure) are the top variables in terms of importance for successfully identifying churners.
Particularly relevant for the work presented in this paper is a recent study conducted by Gattermann-Itschert and Thonemann [
18], who demonstrated that the multi-slicing approach to creating the training dataset and testing on out-of-period data leads to superior churn prediction models when compared to the traditionally used single-slicing approach and testing on out-of-sample data. The authors obtained transactional data (invoicing, delivery, and CRM) from one of Europe’s largest convenience wholesalers selling goods (such as beverages, tobacco, food, and other essential supplies) to smaller retailers. The dataset comprised around 5000 active customers and spanned a period of 2.5 years (from January 2017 to June 2019). Then, instead of deriving features and churn labels only for the customers active in the fixed (i.e., most recent) observation period, they repeatedly shifted the origin of observation by one month backwards in time, thus yielding multiple snapshots of customer behavior (and corresponding labels) that they used for training predictive models. This approach is quite similar to the one presented by Mirkovic et al. in [
37]. The churn definition used was three consecutive months of inactivity (i.e., no purchases made during that period by a customer) and the reported churn rate fluctuated around 10%, but exhibited seasonality (ranging from around 7% to 15%). The authors hypothesized that using multi-slicing will yield more robust and accurate models, as the behavior of customers changes over time, so this approach reduces the chances of overfitting (which models trained on a single slice of data might be more susceptible to). Experimental results confirm this and the authors reported that both the increased sample size and training on observations from different time slices enhances predictive performance of classifiers. In particular, LR, SVM, and RF were compared and recursive feature elimination (RFE) and hyperparameter tuning (grid search) for each classification method was applied, RF has exhibited the best performance, showing a significantly higher AUC score compared to the other two classifiers, and significantly higher TDL than LR.
Jahromi et al. in [
12] proposed a method for maximizing the total profit of a retention campaign and determining the optimum number of customers to contact within it. They calculated the potential profit to be made at a customer level, provided that they respond favorably to an offer within the retention campaign and maintain average spending levels in the prediction period, which they then use as a sorting criterion for creating lists of customers to offer incentives to. An integral part of that calculation is the probability of a customer to become a churner, which is obtained via predictive churn models devised using DT and LR classifiers (in case of DT, they consider simple, cost-sensitive, and boosted variants). Two other important components of the calculation are the probability that a customer accepts the offer (which is kept constant across entire customer base at 30%) and the magnitude of incentive (the authors operate within a scenario where a 5% discount is offered). They then proceeded to test the proposed approach on a real-world dataset of 11,021 B2B customers of a major Australian online fast moving consumer goods retailer who made transactions within the span of one calendar year. Churn is defined as inactivity (no purchases made) in 6 consecutive months, with a reported churn rate of 28%. The authors reported that the boosting approach outperforms LR and simple and cost-sensitive DT, and that using this method for sorting and selecting potential churners can lead to significant business effects. They also identified recency and frequency as the most important predictors of churn.
Most recently, Janssens et al. [
36] proposed a novel measure that can be used to increase the profitability of retention campaigns called EMPB (Expected Maximum Profit measure for B2B customer churn). Unlike in [
12], where all customers are treated as equals, the authors of this study took into account the variability in customer base (i.e., high-value vs. low-value customers), which they proceeded to show can be leveraged to create retention campaigns that maximize expected profits. They compared the performance of customer churn prediction models devised with respect to the proposed measure and concluded that it can yield considerable and measurable business gains compared to traditionally-used metrics such as AUC. They used a dataset obtained from a large North American beverage retailer comprising purchases of 41,739 B2B customers spanning 12 months, out of which roughly 4% are churners, to create predictive models using algorithms such as XGBoost, ProfLogit, ProfTree, RF, and LASSO regression that leverage this measure to recommend customers to be included in retention campaigns to maximize profits. The most important features that the authors identified were monetary value and recency, as well as purchase quantity and the average difference in days with respect to the due date for handling reported issues (QoS).
As shown in this section, relevant studies consider a range of different case data that exhibit distinct characteristics in terms of the domain that they come from, the number of customers and time frame that they span, the churn definitions used, and churn rates reported. Source systems vary from transactional, CRM, and QoS, to web platform usage, and they are leveraged to construct pertinent informative features using a mostly-fixed window width and a single-slicing approach to dataset creation. The exception to this are [
35], where variable window widths are used, and [
18], where multi-slicing is assessed. What differentiates this study from all studies previously mentioned is the fact that it is, to the best of our knowledge, the first study to explore the effects of using different churn definitions and variable window widths for feature extraction and a multi-slicing approach to dataset creation on predictive model performance in one place, thus providing valuable insights on the most promising approaches to practitioners.
3. Materials and Methods
In work presented within this paper, we rely solely on invoice-level data, which can reasonably be expected to exist in virtually any company regardless of its industry or geographical region of operations. The motivation for this is twofold: one, it is our desire to make this approach as widely applicable as possible by using the smallest common denominator in terms of data, without taking into account any information which might be domain or business-specific (which is in line with [
9]) and two, relevant research has shown repeatedly that Length, Recency, Frequency, and Monetary (LRFM) features, which are easily derived from invoice-level data alone, often represent the most important features in predictive churn models [
38,
39,
40]. In the remainder of this section, we describe the raw data we obtained for the empirical study, the approach we take to derive the training and test sets from it, the algorithms we leverage to create predictive churn models, and the metrics we use to evaluate them.
3.1. Data
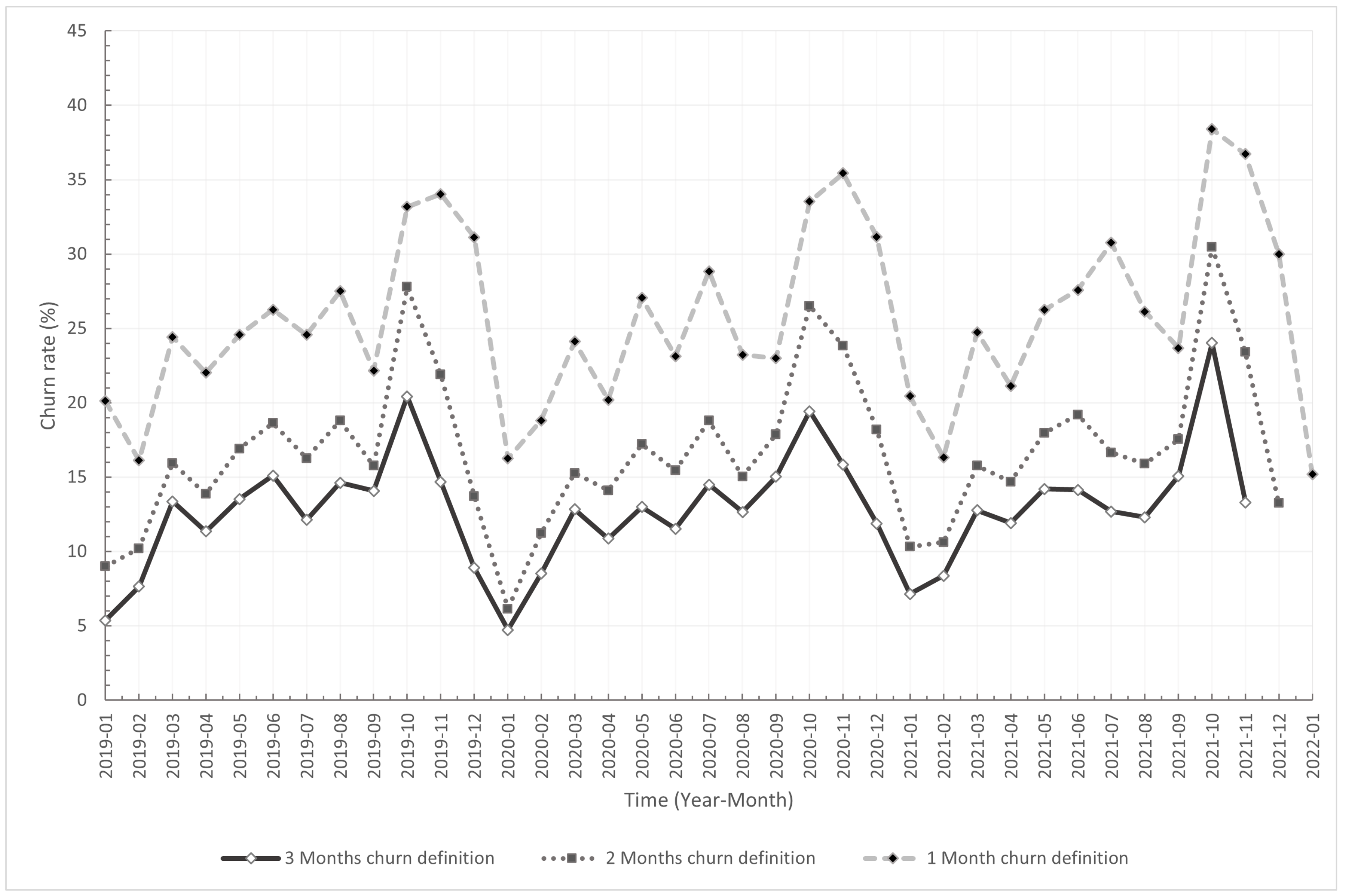
Our data comes from a major Eastern European seller and distributor of agricultural goods and equipment, operating predominantly in the Balkans region. We obtained invoice-level data for B2B transactions made between January 2019 and February 2022 (38 months in total). The dataset comprises 280,502 distinct invoices sent to 3470 different customers, containing 1,962,152 invoice lines in total. For each line, invoice ID, invoice date, customer ID, product ID, product price, and product quantity are recorded. Mean inter-purchase time over all customers is 15 days, with a standard deviation of 41 days. The company uses calendar months as grouping periods for reporting on key performance indicators and defines churn as three consecutive months of inactivity (i.e., if no purchases are made by a customer in three consecutive months, they are considered lost). However, the company is quite interested in assessing the potential benefits of using shorter churn definitions, as they might trigger new business initiatives (i.e., if customers who will not make a purchase in the following month or two can be reliably identified, they could be targeted with tailored promotions). Therefore, we also consider churn definitions of one and two consecutive months of inactivity.
In light of these business rules, the active customer base (i.e., customers making a purchase within a given month) varies between 800 and 1605 customers, with churn rates between 4.72% and 24.01% for churn definition of three months, 6.14% to 30.48% for churn definition of two months, and 16.12% and 38.38% for a one-month churn definition. Churn rates obtained by using different definitions are illustrated in
Figure 1.
3.2. Features, Training, and Test Sets
To construct features from the available data, we adopt a multi-slicing approach proposed by [
18] as a foundation, which we build upon by introducing what we refer to as Cumulative Features (
CF) and Delta Features (
DF). This approach is illustrated in
Figure 2. To create the training set, for every forecast origin
t (which occurs at the end of the observed month and is offset
K-times by one month for the length of the time period that the training data spans), we derive two sets of features:
CF, which comprise features constructed using all the data available in the time period between the date of the first available record (available data origin) and the date of forecast origin t;
DF, which comprise features constructed using monthly data for n number of non-overlapping monthly periods prior to the forecast origin t, such that .
Figure 2.
Deriving training and test sets by using the multi-slicing approach and delta features (illustrated for and DF length of ).
Figure 2.
Deriving training and test sets by using the multi-slicing approach and delta features (illustrated for and DF length of ).
These features are derived and merged at the customer level for customers who were active in the latest month relative to the forecast origin t (i.e., ). Then, all vectors comprising merged customer-level features at different forecast origins t (that is, for customers active in periods) are stacked in a feature matrix . Similarly, to create labels, for each active customer at a forecast origin t, we observe whether they had made purchases in any of the subsequent months reflecting different churn definitions (“Label window v”, spanning months for ) and if so, we designate them as non-churners (i.e., they are labeled “0”). Otherwise, we label them as churners (they are assigned label “1”). In that way, we obtain a label vector that we combine with the feature matrix to construct the final training set.
We rely on the out-of-period testing approach to assess predictive performance of models we devise, which has been argued to produce more realistic estimates than the more commonly used out-of-sample testing approach when there might be temporal changes in the factors driving churn and market conditions in general [
18,
41]. Within this approach, a portion of the data coming from a period more recent than the training data is used to evaluate model performance, which more closely resembles conditions encountered when making future predictions in real-world settings. This is illustrated in the lower part of
Figure 2, where the features and labels for the test set are derived for customers in
, such that the origin of forecast
.
As mentioned earlier, we use exclusively features that can be derived from invoice data alone. To illustrate, within
CF, we calculate the total and average amounts spent per purchase and per distinct products, number of purchases, and those of particular products, as well as the number of days since the latest purchase relative to the forecast origin
t, as some of the features. In terms of
DF, we derive these values as well as their differences between the latest month
and each preceding month
for
, where
is the length of the observation period for
DF in months. We use
values of
, which correspond to time periods usually used for comparisons in business settings (i.e., last month, last quarter, two previous quarters, three previous quarters, and last year). This way, we are able to explicitly quantify changes in purchasing patterns of customers between the latest observation period and previous periods, as well as to capture seasonality in their behavior. For the full set of features used in the experiment, we refer readers to
Table A1 in the
Appendix A.
3.3. Modeling
For creating predictive models, we employ three well-known techniques that are commonly used for churn prediction when the problem is cast as a binary classification one: Logistic Regression (LR) with L2 regularization, Support Vector Machines (SVM) with linear kernel, and Random Forests (RF). Given that we use different lengths of observation periods for deriving
DF (i.e.,
), which directly leads to different numbers of input features, for each
in our experiment and each classifier, we perform a nested 10-fold cross-validation where we use the inner loop to tune hyperparameters with respect to the chosen evaluation metric (AUC, which is described in the following subsection). To this end, we employ a grid search by using hyperparameter values within ranges reported in
Table 2. Prior to modeling, for LR and SVM we standardize features to have a zero-mean and unit-variance (which is not required for RF).
3.4. Evaluation Metrics
In binary classification problems, the performance of a model can be evaluated by using different metrics, the suitability of which will vary depending on the model’s ultimate purpose and the potential cost of misclassification. Even though accuracy, precision, recall, and F1 measures are often used with binary classifiers [
19,
26,
28], given the purpose for which we devise our models for (i.e., churn prediction), we opt for measures that are well established within the domain and which capture the overall model performance and allow for their assessment from a decision-making standpoint: AUC and TDL [
18,
42].
Probabilistic models, such as those devised within our work, enable the assignment of a particular class label to every instance based on a predefined threshold (e.g., if the probability output by the model is ≥50%, then assign label “1” or “churn”). This subsequently enables the construction of a confusion matrix: an overview of correctly and incorrectly classified instances where rows represent the number of ground-truth instances per class, while columns represent model predictions per class. Correctly classified instances are those where the model-assigned labels agree with the ground truth class and can be observed as either True Positives (
TP), when an actual churner is labeled as a churner by the model, or True Negatives (
TN) when an actual non-churner is labeled as a non-churner by the model. Incorrectly classified instances, on the other hand, occur when there is a disagreement between predictions and actual labels and can be either False Positives (
FP), when an actual non-churner is labeled as a churner by the model, or False Negatives (
FN), when an actual churner is labeled as a non-churner by the model. Depending on the threshold set, the number of
TP,
TN,
FP, and
FN will vary, so in order to assess the overall predictive performance of a model over all possible thresholds, a summary measure is required. This measure is known as
AUC and is calculated by approximating:
where the True Positive Rate (
TPR) and False Positive Rate (
FPR) are calculated for different probability thresholds as:
AUC ranges between 0 and 1, where a random classifier has a score of 0.5, while a perfect classifier has a score of 1.
While
AUC gives a good overall assessment of the classifier performance,
TDL is often used to estimate how useful the model would be if applied in a real-world setting, such as for retention activities. Given a list of churn probabilities obtained via a model and sorted in a descending order, one would expect a baseline classifier (i.e., random guessing) to capture a proportional percentage of churners within each decile of the list (e.g., the top 10% of the list would contain 10% of actual churners, the top 20% of the list would contain 20% of actual churners, and so on).
TDL expresses the improvement a model provides over this baseline for the top decile (i.e., top 10% of the list), since retention activities are usually directed towards customers most likely to churn. It is calculated for the top 10% of the customers predicted by the model as most likely to churn as:
where
is the overall churn rate. If
, it means that the model performs no better than what would be expected by random sampling, while values higher than 1 indicate improvement over the naive baseline.
4. Results
To obtain experimental results, we adopt the setup illustrated in
Figure 3. Starting with raw, invoice-level data, for each combination of churn definition (Label window
v) and length of
DF periods (
), we derive training and test sets by leveraging the multi-slicing approach described in
Section 3.2.
Within every iteration, datasets comprise delta and cumulative features, as well as appropriate churn labels. We then proceed to train and tune the selected algorithms by using the hyperparameter values presented in
Table 2, and evaluate the resulting models using out-of-period testing.
This setup resulted in a total of 45 models, the performance of which we assessed via AUC and TDL measures. The obtained results are shown in
Table 3, with the best performance for each measure (for each churn definition) outlined in bold and underlined.
In terms of AUC, the RF classifier yields the highest overall results among the three classifiers, over all combinations of churn definitions and DF length. The top AUC score of 0.9050 was obtained for a churn definition of two months when 12 months of historical data were used to construct DF, closely followed by AUC’s of 0.9020 for a churn definition of three months (also with period of 12 months) and 0.8970 for the one-month churn definition ( period was 9 months in this case).
RF also shows the best performance when TDL is in question, with a lift of 4.9090 obtained for churn definition of two months, 4.8091 for a churn definition of three months (in both cases with length of 12 for ) and 4.4604 for a one-month churn definition. In the last case, results were obtained with the model using of 3.
To test whether the observed differences in classifier performances are significant, we conducted a one-way ANOVA for both AUC and TDL measures, with Tukey’s HSD as a post-hoc test. The obtained results are summarized in
Figure 4. ANOVA for AUC showed that there are significant differences between classifiers at
p < 0.001 significance level (we use
= 0.05 threshold) and Tukey’s HSD revealed that differences exist between all three classifiers (
p < 0.001 for differences between SVM and LR/RF, and
p = 0.024 for differences between RF and LR). In terms of TDL, ANOVA also showed that there are differences between classifiers (
p < 0.001), but Tukey’s HSD revealed that significant differences at
= 0.05 exist only between SVM and the other classifiers. No significant differences were detected between LR and RF (
p = 0.235).
Then, to identify the features that are most important for making predictions in the top performing models (for each churn definition, that is label window
v), we adopted the permutation-based feature importance approach [
43], the results of which are reported in
Table 4. In this approach, values of a single feature are randomly shuffled and the change in model performance when using these values is measured repeatedly, the implication being that if the performance drops after permutation, the feature is important (i.e., the model depends on it).
Finally, to test whether the multi-slicing approach to dataset creation yields better performing models when compared to the more commonly employed single-slicing approach, by using the overall best-performing method identified previously (RF), we devised predictive models for all
and churn definition combinations, but leveraged only a single slice (i.e., the most recent one) of data. To make for a fair comparison, when devising models using a single-slicing approach, we adhered to the same experimental procedure described earlier. Results are presented in
Table 5 (for easier comparison, we also included relevant results from
Table 3). We then ran a two-sample
t-test for both AUC and TDL measures, which indicated that significant differences exist between the approaches in both cases (
p = 0.001 for AUC and
p < 0.001 for TDL at
= 0.05 level).
5. Discussion
The results presented in the previous section raise some interesting discussion points, both in terms of approaches to deriving predictive churn models and potential implications of applying them in real-world settings.
Regarding the overall performance, the random forest classifier ranked best in both measures we used for evaluation, which is not surprising given that studies comparable to ours in customer churn prediction domain have reported similar findings [
18,
38,
44,
45]. What is worth noting, however, is the apparent difference in the ability of selected classifiers to leverage distinct amounts of historical data. In particular, delta features generated using longer time periods (i.e., historical data spanning transactions recorded further from the forecasting origin
t) generally led to a higher AUC score when RF is in question, an observation further supported by the most important features identified for models created by using this method; all of them comprise features from the periods furthest away from the forecasting origin
t among the top 10, indicating that they are indeed relevant for making correct predictions. On the other hand, the same cannot be said for the other classifiers. LR, for example, when churn definition of three months is in question, appears to perform better if trained on less historical data, although the best model obtained using this method does not perform as well as the RF-based models. This might be a valuable insight for practitioners seeking to identify the most promising method for creating predictive churn models.
In terms of features and their contribution to model predictions it is interesting to observe that cumulative features do not appear as often among the most important 10 as do features from DF periods, but those that do rank highly. This is particularly true for “total number of invoices in CF”, which is the most significant feature when churn definitions of one and two months are used and ranks fourth for the model devised using a churn definition of three months. “Total number of invoice lines in CF” is another cumulative feature that is highly relevant, as it ranks third and seventh for models derived using two- and three-month churn definitions. This indicates that using the data originating further away in time from the forecasting thresholds for constructing features should not be neglected, as it could potentially contain valuable information for devising useful predictive models.
It is also worth noting that changes in customer purchasing patterns as captured by the DF we propose appear to be important for creating well-performing models. The evidence of this is the presence of features explicitly expressing the differences between values in the latest observation period (i.e., month ) and some of the previous periods in all three lists enumerating the top 10 most important features. Although they rank near the bottom of the lists, they are nevertheless present, which is a good indicator that there is value to be had by using them. The final thing worth mentioning regarding features is that, in our experiment, the recency group of features appears to bear less importance on model predictions than other groups, as there is only one feature from this group present among all the important features across all models (“Days since last invoice ()” is ranked as the eight most important feature for models using a one-month churn definition).
Regarding the performance of models created by using training datasets derived leveraging a multi-slicing approach, experimental results suggest that they perform better both in terms of AUC and TDL compared to models created using training data derived by single-slicing over all combinations of churn definitions and
widths. Given the similarity between the characteristics of datasets used in our study and the datasets of the study in which where multi-slicing was proposed ([
18]), we are excited to see this and believe our findings represent additional empirical evidence to the effectiveness of this approach.
6. Conclusions
In this study, we present an approach that relies on only a single source of common business data (i.e., invoice data) as a foundation for creating predictive models capable of reliably identifying churners in real-world settings. We find that using historical data spanning longer periods of time generally leads to better performing models and that periods of customer inactivity other than the one currently used to define churn might be used by the company. In that regard, this is one of the first studies to explore the effects of using different churn definitions, variable window widths for feature extraction, and the multi-slicing approach to dataset creation on predictive model performance in one place, thus providing valuable insights to practitioners on the most promising approaches to identifying churners in non-contractual B2B settings.
6.1. Managerial Implications
From a business perspective, our results indicate that top-performing models devised for any of the explored churn definitions have a significant potential to bring measurable gains to the company. To illustrate, reported TDL values show that by using this approach in cases of two and three-month churn definitions, a company would be able to identify almost five times more churners than by using random sampling within the top decile. This could directly lead to significant savings in retention activities, especially if they are in the form of giving a discount. As this is a rather customary approach to customers which the company expects will not make a purchase in the following period, assuming equal likelihood among both churners and non-churners to accept the incentive, the savings would directly depend on the number of actual churners targeted with the offer (otherwise, non-churners would be given a discount even though they would make a purchase anyway).
In addition to this, experimental results also indicate that the company in question could use not just one, but several churn definitions to reliably identify customers not likely to make a purchase in the following period. This directly opens up possibilities for tailoring custom retention strategies for groups of customers predicted to churn in distinct future time periods, thus maximizing the likelihood of keeping them active. Predictions of models devised using different churn definitions could also serve as a valuable input to client segmentation activities, especially if coupled with expected customer lifetime value calculations or other data sources potentially available at the company. For example, customers could be grouped according to their average spending and the most likely period in which they are expected not to make any purchases, and then offered customized incentives (e.g., different discount rates or discounts on particular product groups valid only for the number of months they are predicted to stay dormant in).
On that note, the simplicity of requirements in terms of data pertinent to the proposed approach is one of its greatest strengths. Even though it has been demonstrated that additional sources of data might be invaluable for creating even more accurate predictive models compared to using something as common as transactional data alone (i.e., without any additional customer or business-specific information), simple solutions often mean lower barriers for implementation in real-world settings and can thus potentially yield measurable business results faster. This especially holds for the B2B domain, which has been somewhat slower (compared to B2C) in adopting data gathering and analytics solutions, so this approach might be a good way to fairly quickly obtain some measurable results and hopefully convince management to consider exploring other approaches and devising more advanced strategies.
6.2. Limitations and Future Research Directions
To conclude this paper, we would like to highlight some of the limitations pertinent to our study, as well as to propose several future research directions.
In terms of data, we were limited by the fact that our data comes from a single company operating in the Balkans region dealing with agricultural goods and equipment. While the results we obtained seem to be in line with previous findings, it may be the case that they would not entirely hold for companies operating in different domains or geographical regions. Hence, even though this research is a step forward in terms of evidence that the multi-slicing approach generalizes well, additional studies covering more domains and business environments would certainly be even more beneficial to strengthening this conclusion.
We explored how different amounts of historical data for constructing
DF affect the predictive performance of models, but did not account for the possible effects of having fewer overall observable months of data (i.e., shorter
CF period). While the contemporary attitude in the era of big data appears to be “the more the better”, some studies suggest that beyond a point, using more historical data does not lead to better performing models [
42] and, depending on the design and resource requirements of the feature construction and model training processes, might in fact only mean more complexity while yielding only marginal gains in terms of model performance. Investigation into whether this holds for the dataset we have on hand is an avenue for future research.
Seasonality and changing purchase patterns are phenomena many companies experience in their operations. In this study, we used only the most recent data to derive churn labels (for all considered definitions), which is in line with the established practice in the domain. However, even though the multi-slicing approach implicitly addresses the issue of models devised at different prediction points in time (by creating ‘snapshots’ of customers at different possible prediction points), it would be interesting to check whether and to what extent this holds by devising models for high- and low-churn rate periods and assessing their performance.
The final limitation to this research pertains to the algorithms chosen for devising predictive churn models. We have opted for three established classifiers in this domain, as they have been demonstrated repeatedly to produce models applicable in real-world settings and they allowed us to easily compare our results to previous studies. However as deep-learning approaches gain more traction, it would be interesting to see whether and to what extent they could be leveraged when applied in this domain as a part of future research efforts. It would also be useful to gain more detailed insights into the reasons behind customer churn by employing some of the recent methods for explainable machine learning.