An Intelligent Nonlinear Control Method for the Multistage Electromechanical Servo System
Abstract
:1. Introduction
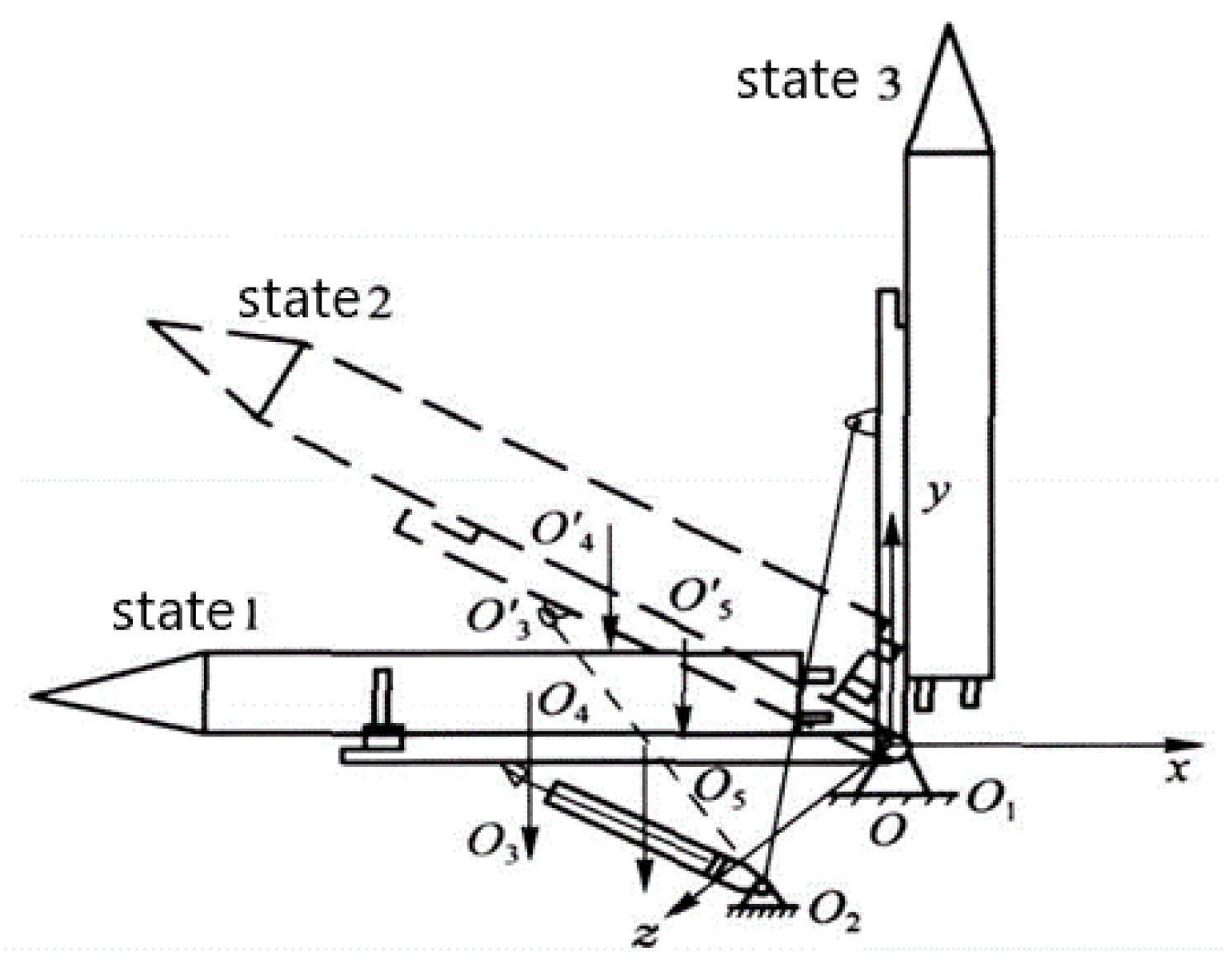
2. Model of Electromechanical Servo System
2.1. Mathematical Model of PMSM
2.2. Dynamic Model of Planetary Roller Screw
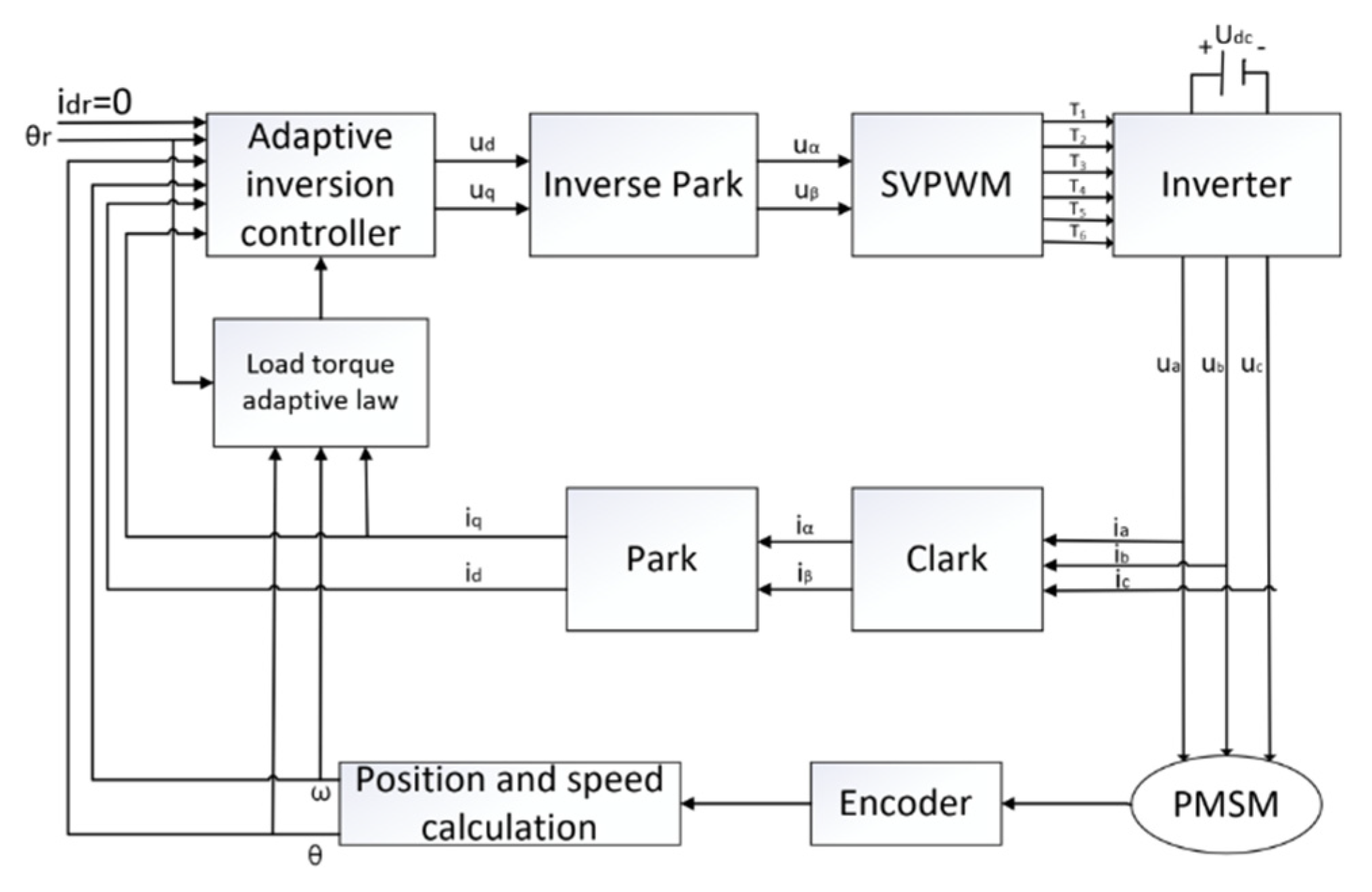
3. Adaptive Inversion Control
3.1. Design of Adaptive Inversion Controller
3.2. Design of Luenberger Observer
3.3. Stability Analysis
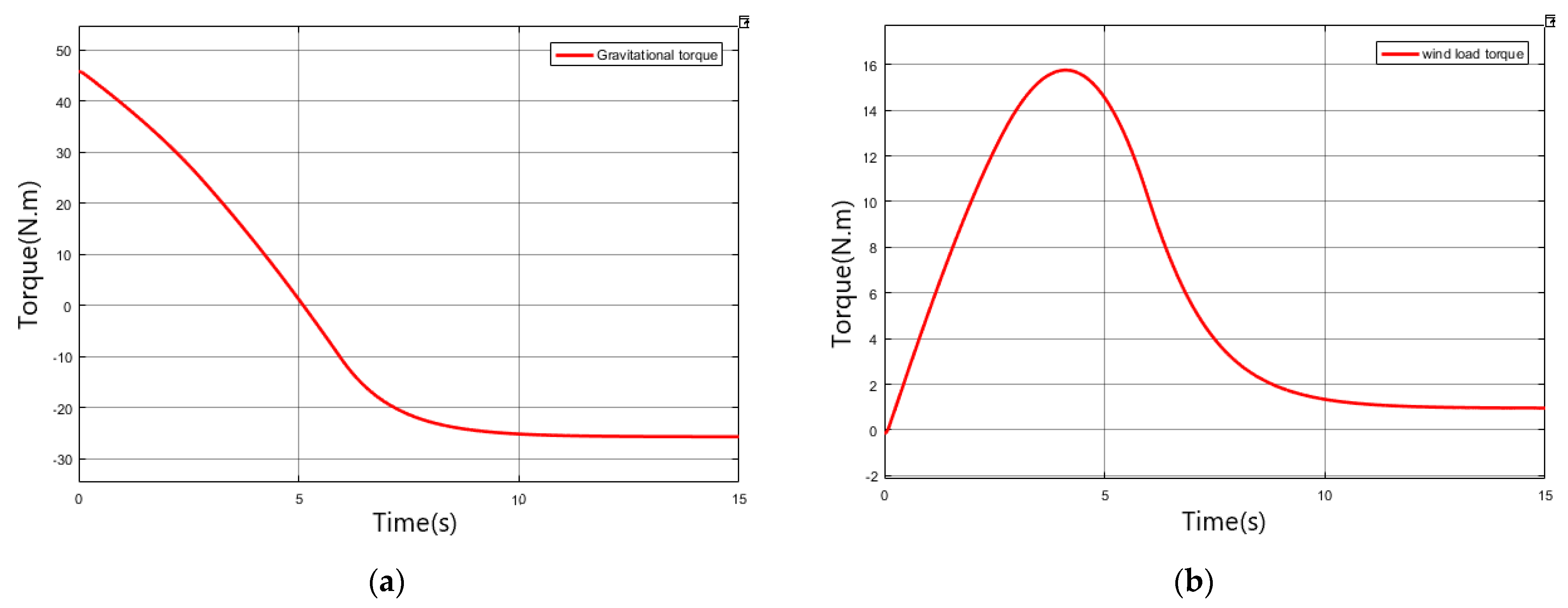
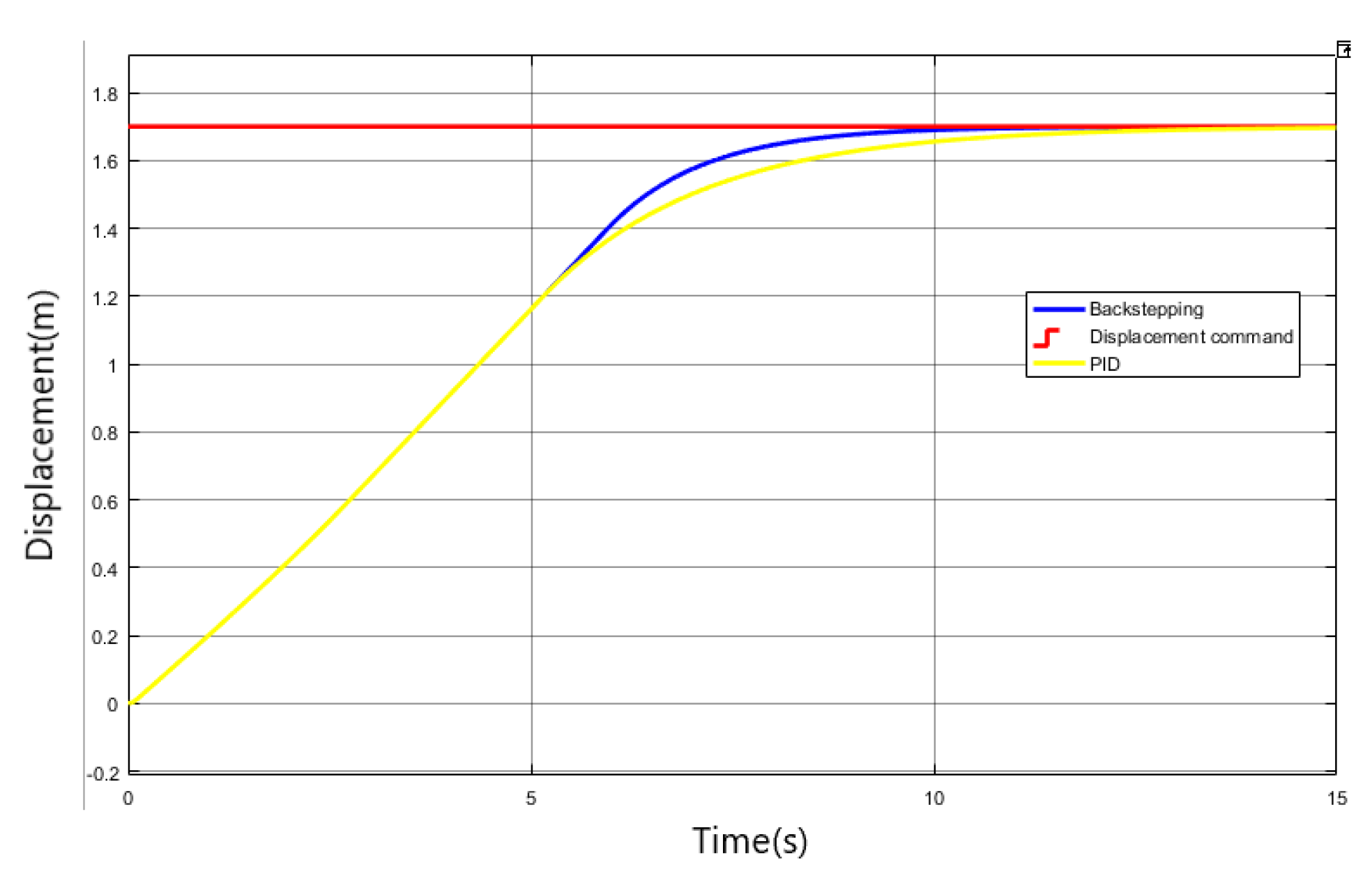
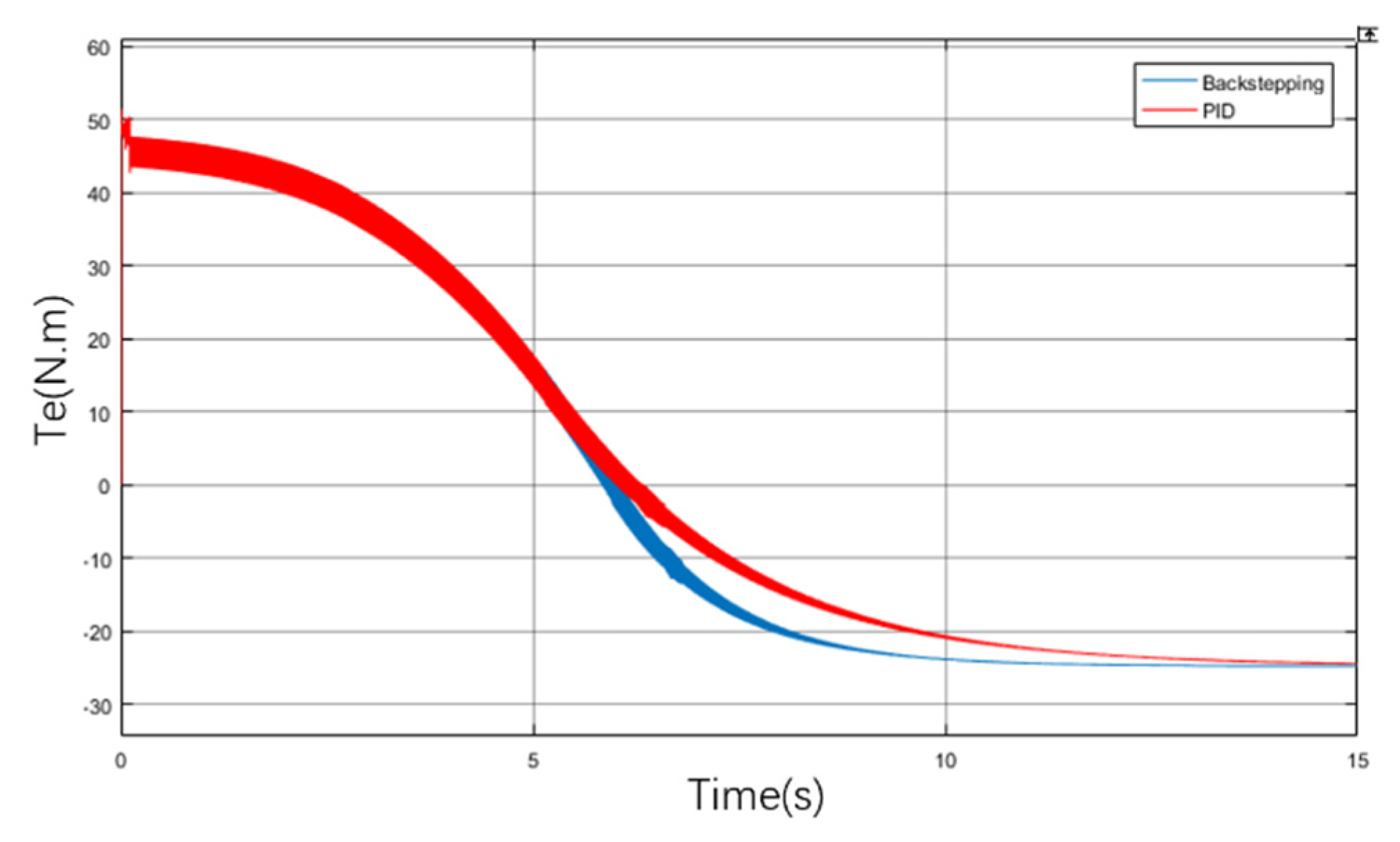
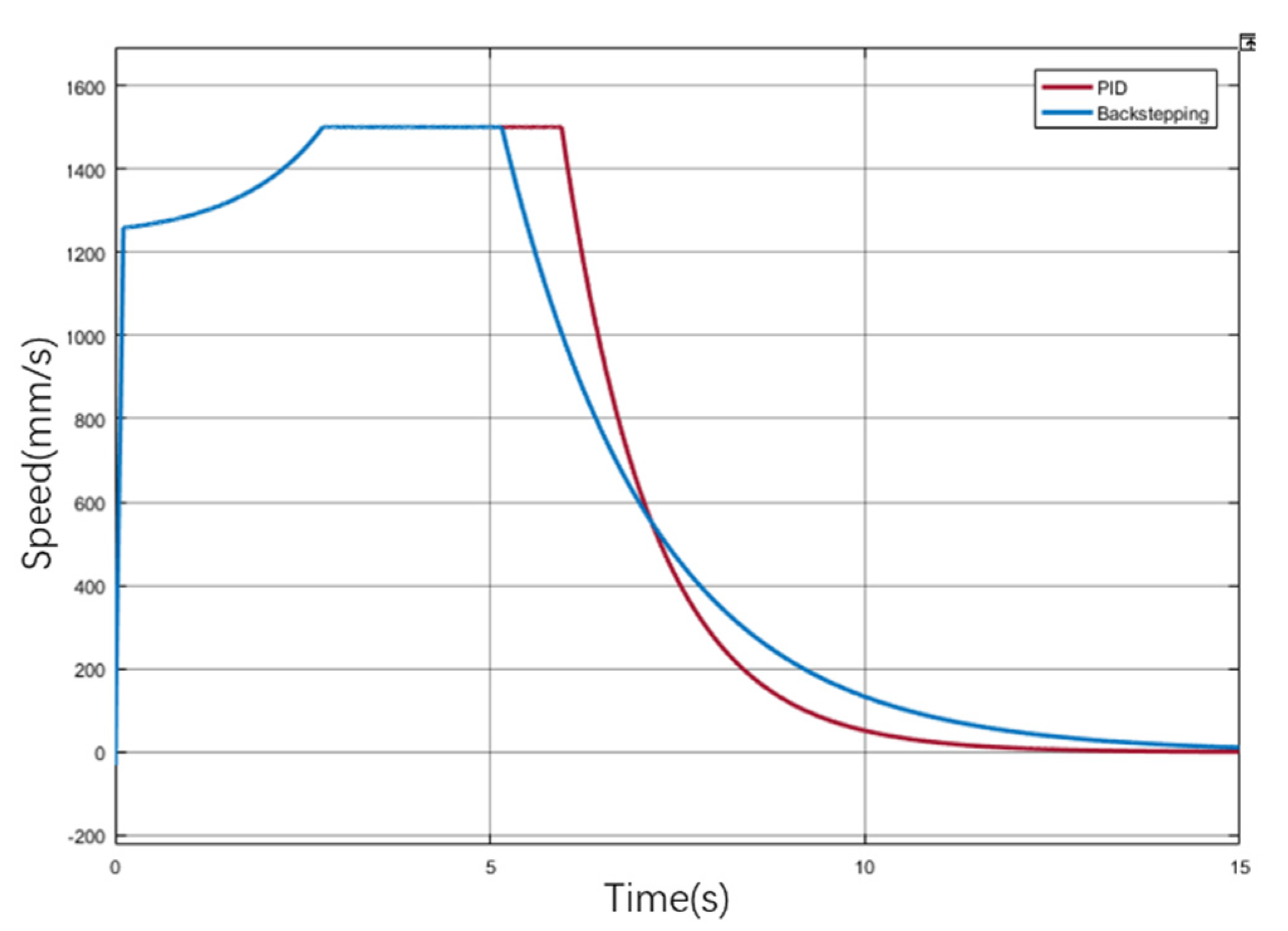
3.4. Joint Simulation Test
4. Experimental Research
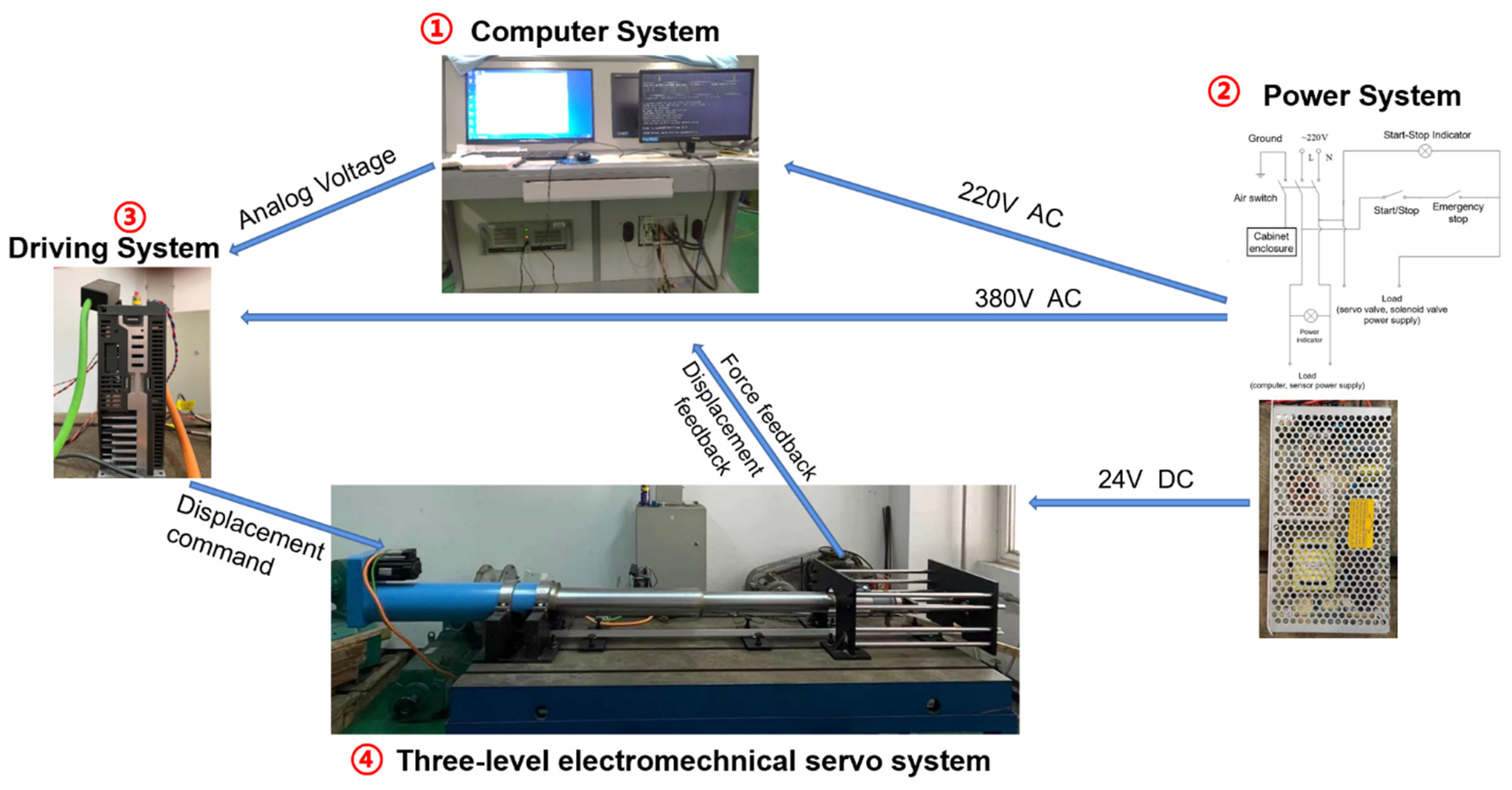
4.1. Experiment Platform
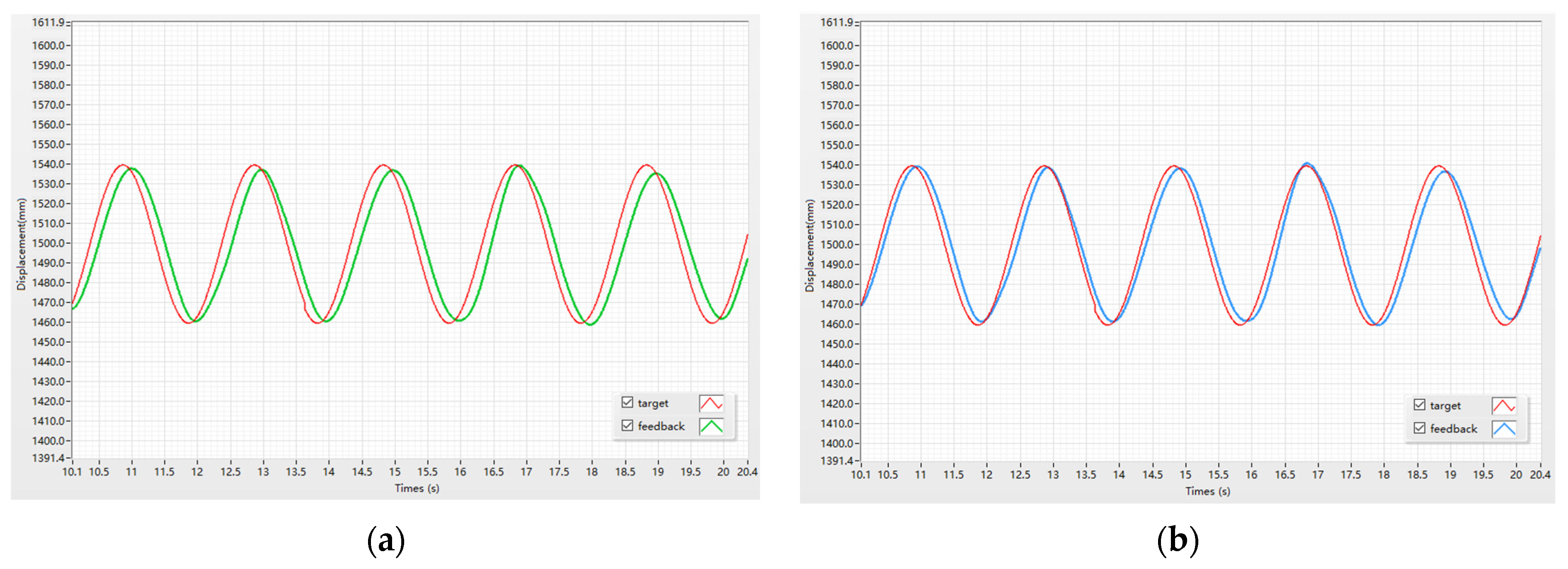
4.2. Experimental Results
5. Conclusions
- (1)
- In this paper, an adaptive inversion control method is proposed for the nonlinear problem of the multilevel electromechanical servo system. Through joint simulation with Simulink and ADAMS software, the displacement, torque, and speed results of a multistage electromechanical servo system under an adaptive inversion controller and a traditional PID controller are compared, to verify the feasibility and reliability of the designed controller. The designed control algorithm was debugged on the experimental platform, and the system step signal tracking and sinusoidal signal tracking tests were carried out. The test results verify that the designed adaptive inversion multistage EMA driving algorithm can respond quickly, has better tracking performance, and has better robustness and stability than the traditional PID controller.
- (2)
- Next, the future work is to replace the analog sensor with a digital sensor and change the loading mode to improve the experimental accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, S.; Meng, X.; Li, G. The Superior Election of Antiaircraft Missile Firing Mode Based on Advanced ADC. Guid. Fuze 2006. [Google Scholar]
- Li, X.; Liu, G.; Song, C. Rigid-Body Dynamic Analysis of Multi-Stage Planetary Roller Screw Mechanism. J. Northwest. Polytech. Univ. 2020, 38, 1001–1009. [Google Scholar] [CrossRef]
- Li, Y.; Yan, X. The Perspective and Status of PMSM Electrical Servo System. Micromotors 2021, 34, 30–33. [Google Scholar]
- Chen, X. Research on Control Strategy of Electromechanical Actuation Servo System for More Electric Aircraft; Northwestern Polytechnical University: Xi’an, China, 2016. [Google Scholar]
- Yuan, L.; Hu, B.; Wei, K. Control Principle and MATLAB Simulation of Modern Permanent Magnet Synchronous Motor; Beihang University Press: Beijing, China, 2016. [Google Scholar]
- Sun, G.; Su, Y.; Hong, M. Application of fuzzy control algorithm with variable scale factor to multimotor synchronization control system. In Proceedings of the 2013 8th IEEE Conference on Industrial Electronics and Applications (ICIEA), Melbourne, Australia, 18–21 June 2013; pp. 307–310. [Google Scholar]
- Li, J.; Kan, S. The study on multi-motor control system based on fuzzy pid control and bp neural network. Adv. Inf. Sci. Serv. Sci. 2012, 4, 100–107. [Google Scholar]
- Fu, Q. Fuzzy self-tuning PID-based multi-motor synchronization control study. Autom. Instrum. 2014, 10, 1–5. [Google Scholar]
- Safa, M.; Ahmadi, M.; Mehrmashadi, J. Selection of the most influential parameters on vectorial crystal growth of highly oriented vertically aligned carbon nanotubes by adaptive neuro-fuzzy technique. Int. J. Hydromechatron. 2020, 3, 238–251. [Google Scholar] [CrossRef]
- Liu, X.; Chen, C.; Liang, X. Study on double motor synchronous system of neural network control. Int. J. Model. Identif. Control 2009, 7, 376–381. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, G. Application of neural network PID in master-slave control system. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; pp. 320–322. [Google Scholar]
- Qi, D. Research on Precise Synchronous Control System of Multi-Motors; Shenyang University of Technology: Shenyang, China, 2018. [Google Scholar]
- Yepes, A.G.; Vidal, A.; López, O. Evaluation of techniques for cross-coupling decoupling between orthogonal axes in double synchronous reference frame current control. IEEE Trans. Ind. Electron. 2014, 61, 3527–3531. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, J.; Li, H. Robust Tracking Control for Direct Drive XY Table Based on GPC and DOB. Trans. China Electrotech. Soc. 2015, 30, 150–154. [Google Scholar]
- Han, J. Auto Disturbances Rejection Control Technique. Front. Sci. 2007, 1, 24–31. [Google Scholar]
- Kang, C.; Cong, P.; Shao, Y. ADRC-Based Speed Control for Permanent Magnet Synchronous Machine Drives Using Sliding-Mode Extended State Observer. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Rizvi, S.A.A.; Memon, A.Y. An extended observer-based robust nonlinear speed sensorless controller for a PMSM. Int. J. Control 2019, 92, 2123–2135. [Google Scholar] [CrossRef]
- Yan, Y. Disturbance Rejection Control for Nonlinear Systems with Multiple Disturbances and its Applications; Southeast University: Dhaka, Bangladesh, 2019. [Google Scholar] [CrossRef]
- Bodson, M. Adaptive Control: Stability, Convergence, and Robustness. J. Soc. Am. 1990, 88, 588. [Google Scholar]
- Jiang, D.; Jiang, W.; Pan, S. Adaptive Integral Back-stepping Sliding Mode Control for Uncertain Nonlinear Systems. Control Eng. China 2021, 28, 1780–1786. [Google Scholar]
- Astolfi, A.; Karagiannis, D.; Ortega, R. Nonlinear and Adaptive Control with Applications; Springer Publishing Company: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Song, L.; Chen, S.; Yao, Q. Adaptive Discrete Variable Structure Control and its Application to Power System. Proc. CSEE 2002, 22, 98–101. [Google Scholar]
- Wang, B. Model Reference Adaptive Control System with Strong Robustness. Control Decis. 2005, 20, 65–68. [Google Scholar]
- Wu, G.; Xiao, X. Speed Controller of Servo System Based on Self-tuning Control. Electr. Drive 2009, 39, 47–50. [Google Scholar]
- Zhang, E.; Shi, S.; Gao, W. Recent Researches and Developments on Fuzzy Control System. Control Theory Appl. 2001, 18, 7–11. [Google Scholar]
- Song, C. Fuzzy Neural Network Control of Permanent-Magnet Synchronous-Motor. Electr. Mach. Control Appl. 2008, 35, 24–26. [Google Scholar]
- Liu, Z.; Gui, Z.; Cai, Q. Present situation and development trend of neural network expert system. Comput. Sci. 1996, 23, 70–72. [Google Scholar]
- Lin, L.; Huang, S. Robust Control with Linearization Technique for Interior Permanent Magnet Synchronous Motor Servo System. Electr. Mach. Control 2009, 13, 541–547. [Google Scholar]
- Rahman, M.A.; Vilathgamuwa, D.M.; Uddin, M.N.; Tseng, K.-J. Nonlinear Control of Interior Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2003, 39, 408. [Google Scholar] [CrossRef]
- Sergeev, A.; Paterson, E.G.; Hajaiej, H. OpenFOAM computation of interacting wind turbine flows and control (I): Free rotating case. Int. J. Hydromechatron. 2020, 1, 1–26. [Google Scholar] [CrossRef]

| Parameters | Parameters Value |
|---|---|
| aerodynamic drag coefficient Cx | 0.6 |
| correction factor RH | 1.52 |
| gust dynamic coefficient β | 1.5 |
| roughness index α | 0.12 |
| local wind speed v (m/s) | 2.5 |
| air density ρ (kg/m3) | 1.35 |
| Step Displacement Command (mm) | Traditional PID Control | Adaptive Inversion Control | ||
|---|---|---|---|---|
| Average Adjustment Time | Average Overshoot | Average Adjustment Time | Average Overshoot | |
| (s) | (mm) | (s) | (mm) | |
| 100 | 3.3 | 1.1 | 2.6 | 0.3 |
| 200 | 4.2 | 2 | 3.1 | 0.4 |
| 400 | 6.8 | 1.2 | 5.1 | 0.4 |
| 800 | 11.5 | 1.8 | 9.0 | 0.3 |
| Sinusoidal Displacement Command (mm) | Frequency (Hz) | Traditional PID Control | Adaptive Inversion | ||
|---|---|---|---|---|---|
| Lag Time (s) | Amplitude Decay | Lag Time (s) | Amplitude Decay | ||
| 1100~1900 | 0.05 | 2.2 | 9.4% | 1.2 | 4.9% |
| 1300~1700 | 0.1 | 1.2 | 6.8% | 0.5 | 3.5% |
| 1400~1600 | 0.2 | 0.5 | 3.7% | 0.3 | 2.8% |
| 1460~1540 | 0.5 | 0.2 | 1.7% | 0.1 | 0.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Y.; Zhou, Y.; Zhang, J.; Ma, S.; Wu, S. An Intelligent Nonlinear Control Method for the Multistage Electromechanical Servo System. Appl. Sci. 2022, 12, 5053. https://doi.org/10.3390/app12105053
Lian Y, Zhou Y, Zhang J, Ma S, Wu S. An Intelligent Nonlinear Control Method for the Multistage Electromechanical Servo System. Applied Sciences. 2022; 12(10):5053. https://doi.org/10.3390/app12105053
Chicago/Turabian StyleLian, Yunxiao, Yong Zhou, Jianxin Zhang, Shangjun Ma, and Shuai Wu. 2022. "An Intelligent Nonlinear Control Method for the Multistage Electromechanical Servo System" Applied Sciences 12, no. 10: 5053. https://doi.org/10.3390/app12105053
APA StyleLian, Y., Zhou, Y., Zhang, J., Ma, S., & Wu, S. (2022). An Intelligent Nonlinear Control Method for the Multistage Electromechanical Servo System. Applied Sciences, 12(10), 5053. https://doi.org/10.3390/app12105053






