Granular Flow–Obstacle Interaction and Granular Dam Break Using the S-H Model with the TVD-MacCormack Scheme
Abstract
:1. Introduction
2. Research Methodology
2.1. Governing Equations
2.2. TVD-MacCormack Numerical Scheme
2.3. With/Without Grain Algorithm
3. Numerical Example
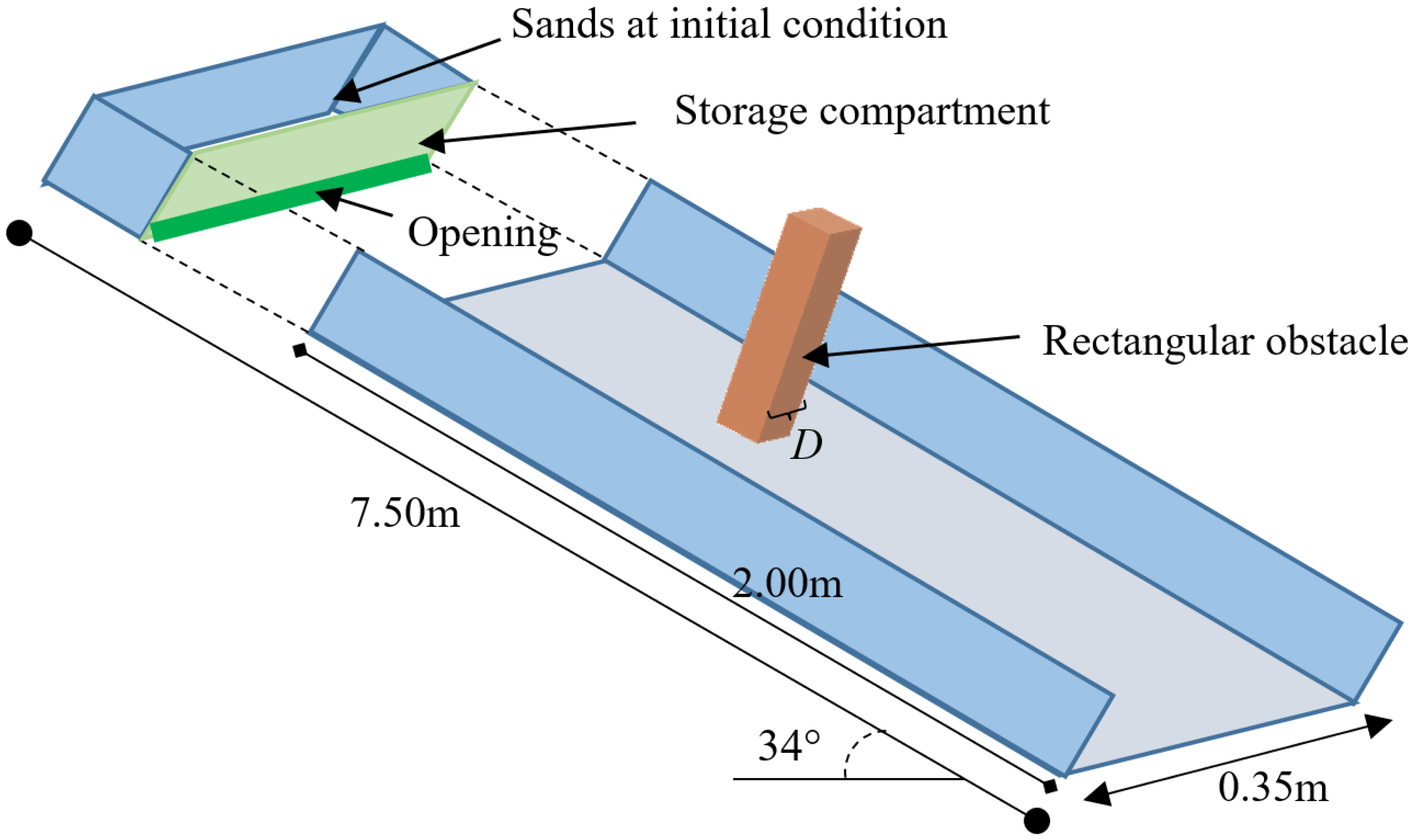
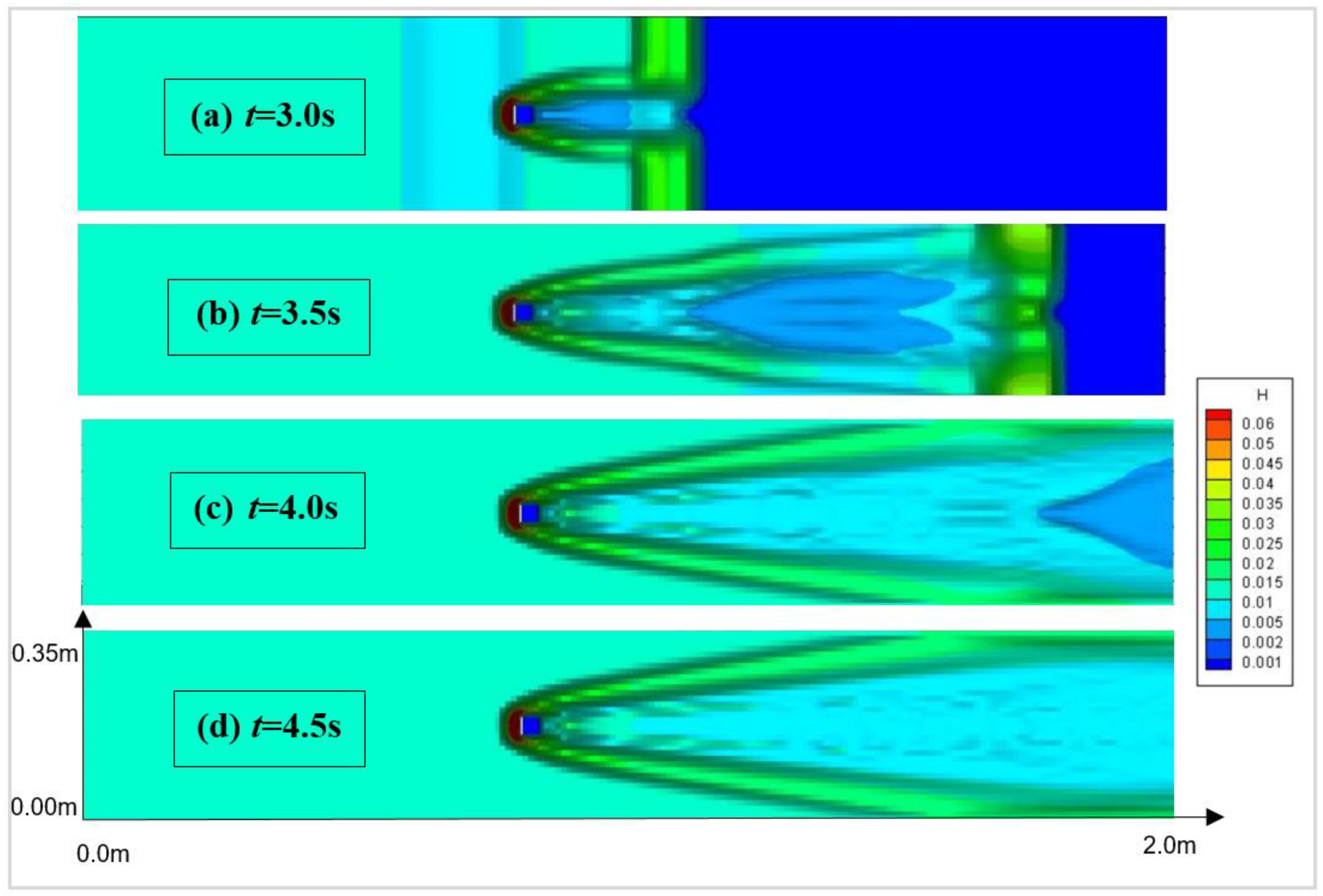
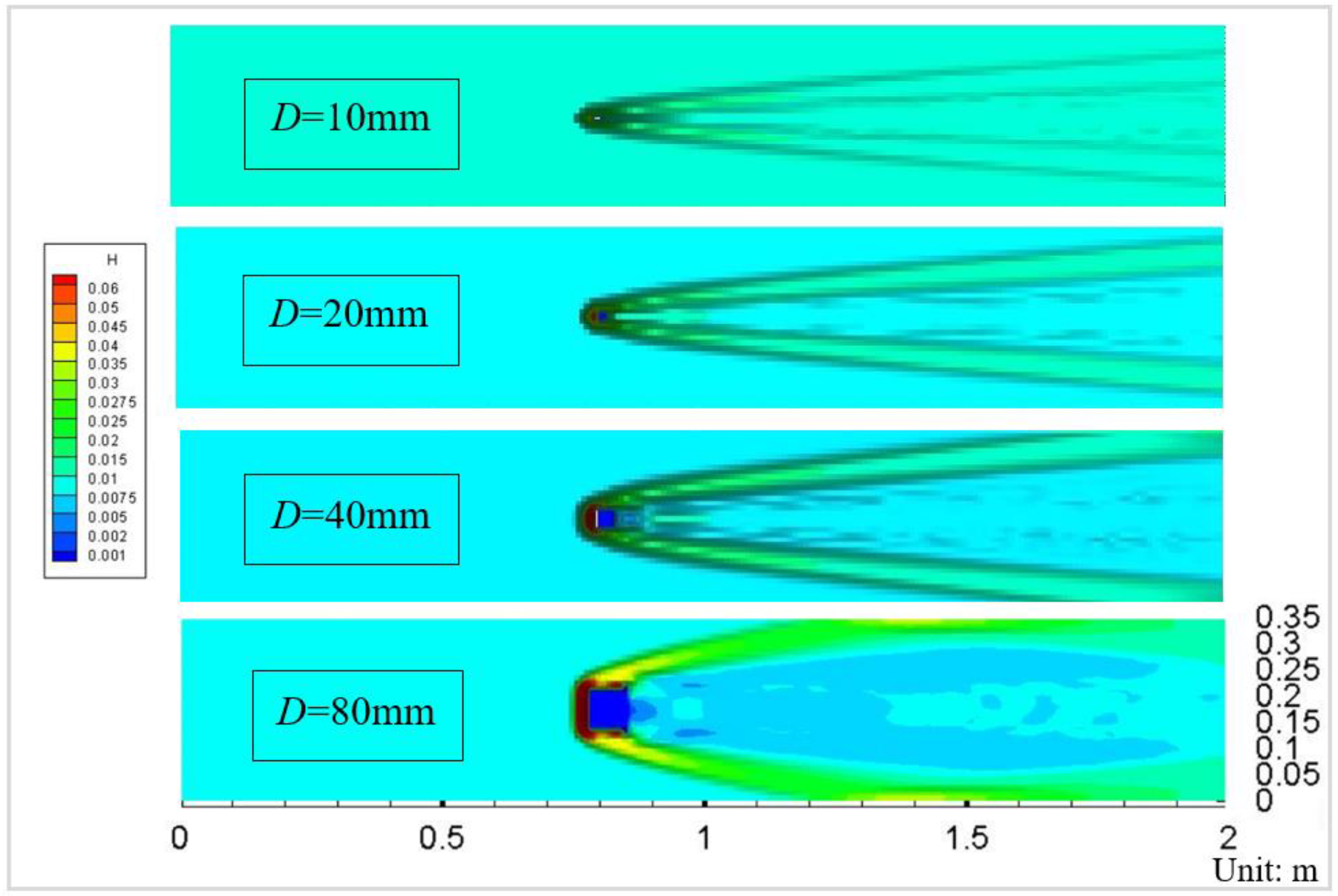
3.1. Granular Flume Flow Strike Mast-Like Obstacle
3.2. Granular Dam Break Simulation
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maccormack, R.W. An efficient explicit–implicit–characteristic method for solving the compressible Navier–Stokes equations. SIAM–AMS Proc. 1978, 11, 130–155. [Google Scholar]
- Savage, S.B.; Hutter, K. The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 1989, 199, 177–215. [Google Scholar] [CrossRef]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; McGraw-Hill Book Company: New York, NY, USA, 1984. [Google Scholar]
- Ferrand, M.; Harris, J.C. Finite volume arbitrary Lagrangian-Eulerian schemes using dual meshes for ocean wave applications. Comput. Fluids 2021, 219, 104860. [Google Scholar] [CrossRef]
- Huang, C.S.; Arbogast, T.; Hung, C.H. A semi-Lagrangian finite difference WENO scheme for scalar nonlinear conservation laws. J. Comput. Phys. 2016, 322, 559–585. [Google Scholar] [CrossRef] [Green Version]
- Forterre, Y.; Pouliquen, O. Long–surface–wave instability in dense granular flows. J. Fluid Mech. 2003, 486, 21–50. [Google Scholar] [CrossRef] [Green Version]
- Tai, Y.C.; Gray, J.M.N.T.; Hutter, K.; Noelle, S. Flow of dense avalanches past obstructions. Ann. Glaciol. 2001, 32, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Cui, X. Computational and experimental studies of rapid free–surface granular flows around obstacles. Comput. Fluids 2014, 89, 179–190. [Google Scholar] [CrossRef]
- Abdelrazek, A.M.; Kimura, I.; Shimizu, Y. Numerical simulation of granular flow past simple obstacles using the SPH method. J. Jpn. Soc. Civ. Eng. Ser. B1 2015, 71, 199–204. [Google Scholar] [CrossRef] [Green Version]
- Saghi, H.; Lakzian, E. Effects of using obstacles on the dam-break flow based on entropy generation analysis. Eur. Phys. J. Plus 2019, 134, 237. [Google Scholar] [CrossRef]
- Nessyahu, H.; Tadmor, E. Non–oscillatory central differencing for hyperbolic conservation laws. J. Comput. Phys. 1990, 87, 408–463. [Google Scholar] [CrossRef] [Green Version]
- Balbás, J.; Tadmor, E.; Wu, C.C. Non–oscillatory central schemes for one–and two–dimensional MHD equations. J. Comput. Phys. 2004, 201, 261–285. [Google Scholar] [CrossRef]
- Kurganov, A.; Tadmor, E. New high–resolution semi–discrete central schemes for Hamilton–Jacobi equations. J. Comput. Phys. 2000, 160, 720–742. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y. Central schemes on overlapping cells. J. Comput. Phys. 2005, 209, 82–104. [Google Scholar] [CrossRef]
- Gray, J.M.N.T.; Tai, Y.C.; Noelle, S. Shock waves, dead zones and particle–free regions in rapid granular free–surface flows. J. Fluid Mech. 2003, 491, 161–181. [Google Scholar] [CrossRef] [Green Version]
- Tai, Y.C.; Noelle, S.; Gray, J.M.N.T.; Hutter, K. Shock–capturing and front–tracking methods for granular avalanches. J. Comput. Phys. 2002, 175, 269–301. [Google Scholar] [CrossRef] [Green Version]
- Pitman, E.B.; Nichita, C.C.; Patra, A.; Bauer, A.; Sheridan, M.; Bursik, M. Computing granular avalanches and landslides. Phys. Fluids 2003, 15, 3638–3646. [Google Scholar] [CrossRef] [Green Version]
- Denlinger, R.P.; Iverson, R.M. Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res.-Solid Earth 2001, 106, 553–566. [Google Scholar] [CrossRef]
- Jeong, K.L.; Lee, Y.G. A numerical simulation method for the flow around floating bodies in regular waves using a three-dimensional rectilinear grid system. Int. J. Nav. Archit. Ocean. Eng. 2016, 8, 277–300. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, D.M.; Fernandes, C.V.S.; Kaviski, E.; Bleninger, T. Calibration of river hydrodynamic models: Analysis from the dynamic component in roughness coefficients. J. Hydrol. 2021, 598, 126136. [Google Scholar] [CrossRef]
- Heer, T.; Wells, M.G.; Mandrak, N.E. Asian carp spawning success: Predictions from a 3-D hydrodynamic model for a Laurentian Great Lake tributary. J. Great Lakes Res. 2021, 47, 37–47. [Google Scholar] [CrossRef]
- Zhang, X.X.; Li, D.; Wang, X.; Li, X.; Cheng, J.Y.; Zheng, B.Z. Exploration of polycyclic aromatic hydrocarbon distribution in the sediments of marine environment by hydrodynamic simulation model. Mar. Pollut. Bull. 2021, 171, 112697. [Google Scholar] [CrossRef]
- Tai, Y.C.; Kuo, C.Y.; Hui, W.H. An alternative depth–integrated formulation for granular avalanches over temporally varying topography with small curvature. Geophys. Astrophys. Fluid Dyn. 2012, 106, 596–629. [Google Scholar] [CrossRef]
- Murillo, C.J.J.; García-Navarro, P. 2D simulation of granular flow over irregular steep slopes using global and local coordinates. J. Comput. Phys. 2013, 255, 166–204. [Google Scholar]
- Mingham, C.G.; Causon, D.M.; Ingram, D.M. A TVD MacCormack scheme for transcritical flow. ICE Proc. Water Marit. Eng. 2001, 148, 167–175. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations. Adv. Water Resour. 2006, 29, 1833–1845. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. Simulation of rapidly varying flow using an efficient TVD–MacCormack scheme. Int. J. Numer. Methods Fluids 2007, 53, 811–826. [Google Scholar] [CrossRef]
- Khodadosti, F.; Khalsaraei, M.M. A new total variation diminishing implicit nonstandard finite difference scheme for conservation laws. Comput. Methods Differ. Equ. 2014, 2, 91–98. [Google Scholar]
- Zendrato, N.L.H.; Chrysanti, A.; Yakti, B.P.; Adityawan, M.B.; Suryadi, Y. Application of finite difference schemes to 1D St. venant for simulating weir overflow. MATEC Web Conf. 2018, 147, 03011. [Google Scholar] [CrossRef] [Green Version]
- Hauksson, S.; Pagliardi, M.; Barbolini, M.; Johannesson, T. Laboratory measurements of impact forces of supercritical granular flow against mast–like obstacles. Cold Reg. Sci. Technol. 2007, 49, 54–63. [Google Scholar] [CrossRef]
- Shirsath, S.S.; Padding, J.T.; Deen, N.G.; Clercx, H.J.H.; Kuipers, J.A.M. Experimental study of monodisperse granular flow through an inclined rotating chute. Powder Technol. 2013, 246, 235–246. [Google Scholar] [CrossRef]
- Ionescu, I.R.; Mangeney, A.; Bouchut, F.; Roche, O. Viscoplastic modeling of granular column collapse with pressure-dependent rheology. J. Non-Newton. Fluid Mech. 2015, 219, 1–18. [Google Scholar] [CrossRef]
- Daerr, A. Dynamical equilibrium of avalanches on a rough plane. Phys. Fluid 2001, 13, 2115–2124. [Google Scholar] [CrossRef] [Green Version]
- Prasad, S.N.; Pal, D.; Romkens, M.J.M. Wave formation on a shallow layer of flowing grains. J. Fluid Mech. 2000, 413, 89–110. [Google Scholar] [CrossRef]
- Louge, M.Y.; Keast, S.C. On dense granular flows down flat frictional inclines. Phys. Fluids 2001, 13, 1213–1233. [Google Scholar] [CrossRef]
- Forterre, Y. Kapiza waves as a test for three–dimensional granular flow rheology. J. Fluid Mech. 2006, 563, 123. [Google Scholar] [CrossRef] [Green Version]
- Johannesson, T.; Gauer, P.; Issler, D.; Lied, K.; Faug, T.; Naaim, M. The Design of Avalanche Protection Dams. Recent Practical and Theoretical Developments; European Commission, Directorate General for Research: Bruxelles, Belgium, 2009. [Google Scholar]
- Saghi, H.; Ketabdari, M.J.; Zamirian, M. A novel algorithm based on parameterization method for calculation of curvature of the free surface flows. Modelling 2013, 37, 570–585. [Google Scholar] [CrossRef] [Green Version]
- Saghi, H.; Hashemian, A. Multi-dimensional NURBS model for predicting maximum free surface oscillation in swaying rectangular storage tanks. Comput. Math. Appl. 2018, 76, 2496–2513. [Google Scholar] [CrossRef]



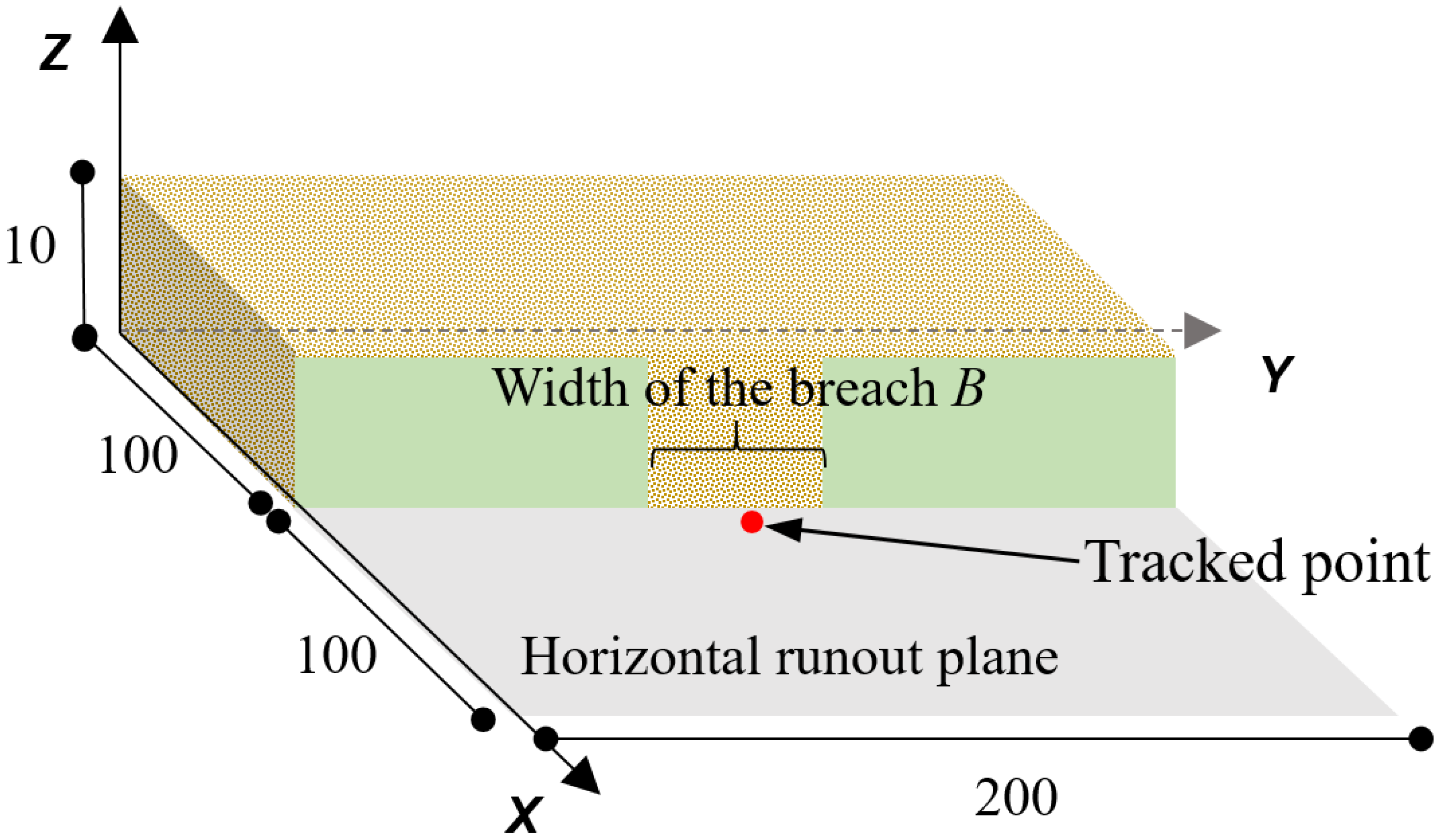
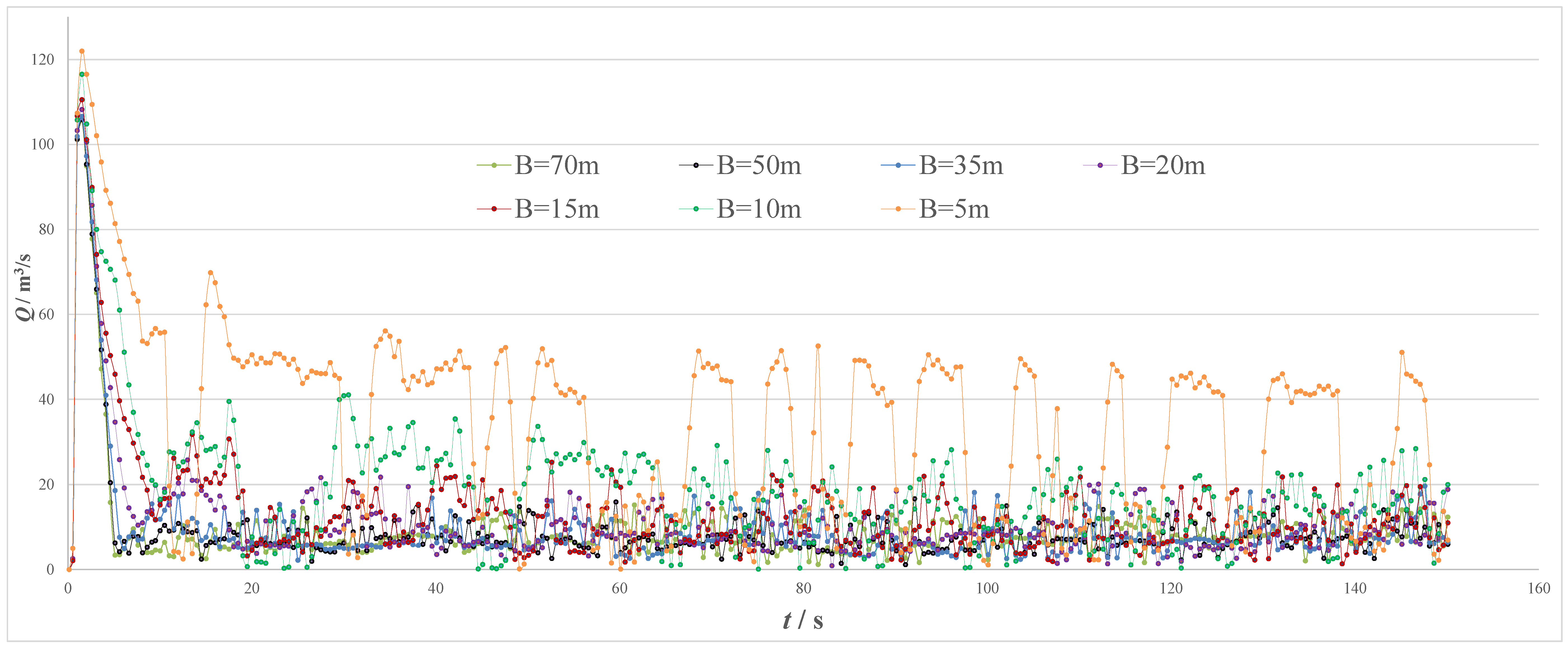
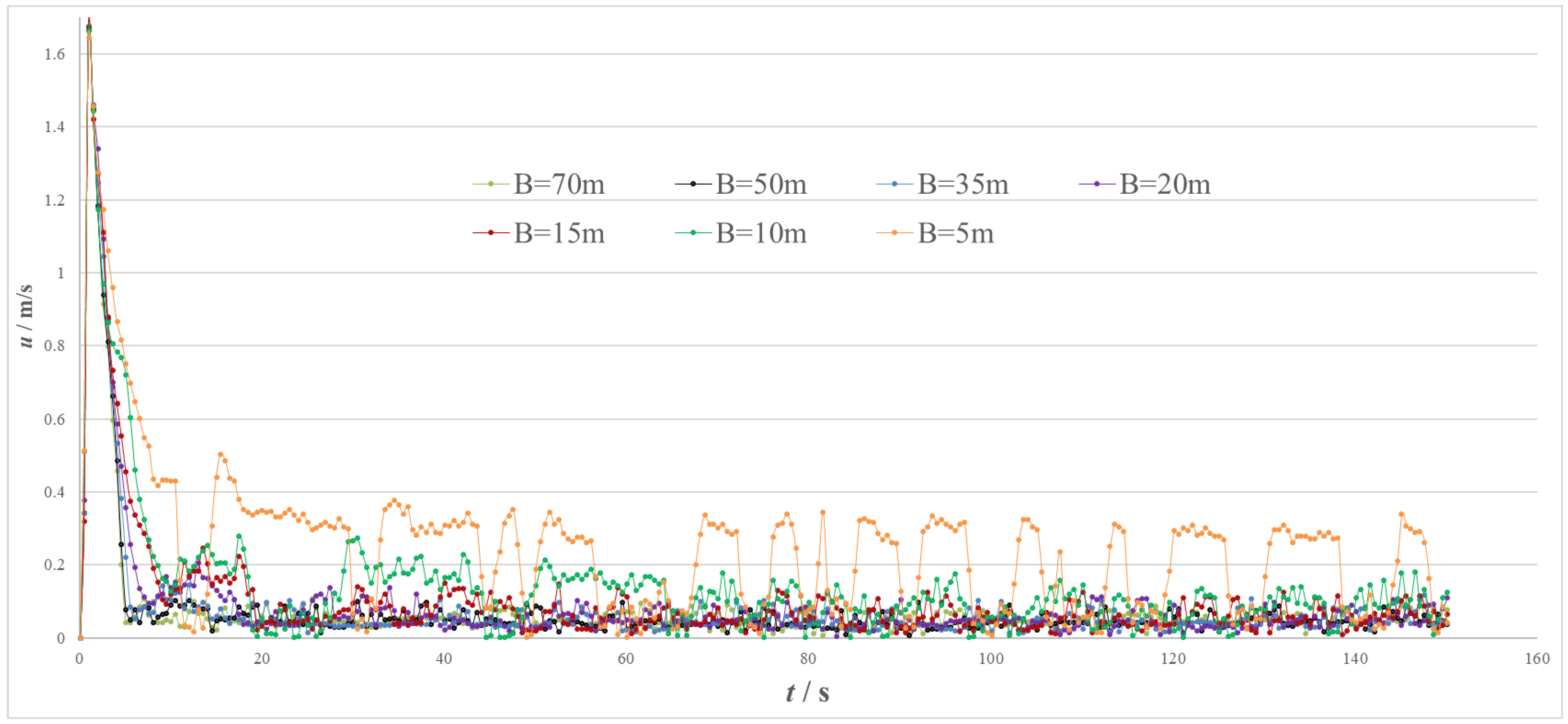
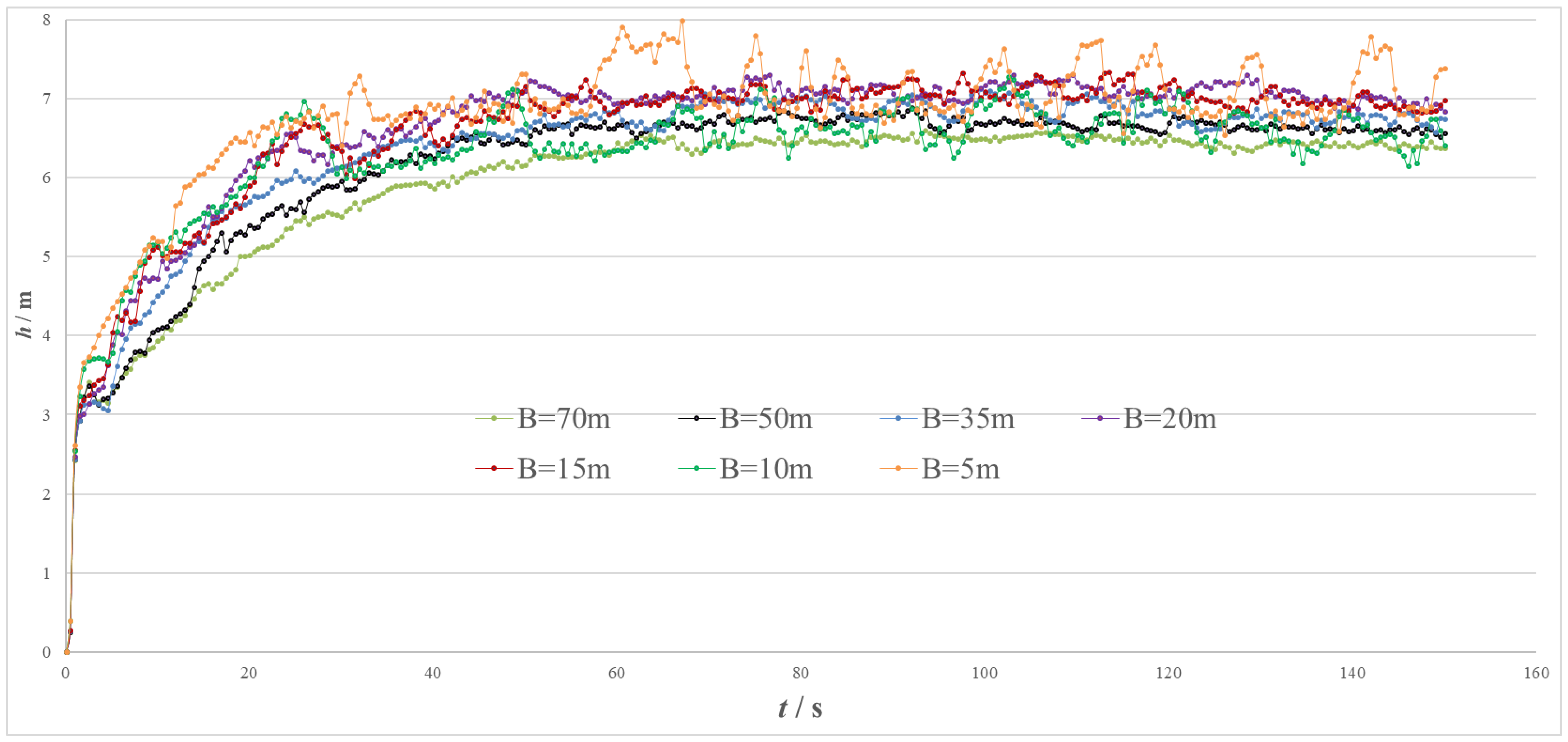

| Num. | B/m | hmax/m | τ/s |
|---|---|---|---|
| 1 | 5 | 6.692979 | 6.90883 |
| 2 | 10 | 6.135773 | 6.557069 |
| 3 | 15 | 9.688248 | 6.989259 |
| 4 | 20 | 9.814965 | 7.037584 |
| 5 | 35 | 10.08215 | 6.778386 |
| 6 | 50 | 11.97468 | 6.661324 |
| 7 | 70 | 13.35109 | 6.441027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, M.; Li, S.; Cao, Z.; Peng, A.; Huang, G.; Cao, L.; Fei, J. Granular Flow–Obstacle Interaction and Granular Dam Break Using the S-H Model with the TVD-MacCormack Scheme. Appl. Sci. 2022, 12, 5066. https://doi.org/10.3390/app12105066
Zhou H, Wang M, Li S, Cao Z, Peng A, Huang G, Cao L, Fei J. Granular Flow–Obstacle Interaction and Granular Dam Break Using the S-H Model with the TVD-MacCormack Scheme. Applied Sciences. 2022; 12(10):5066. https://doi.org/10.3390/app12105066
Chicago/Turabian StyleZhou, Hao, Mingsheng Wang, Shucai Li, Zhenxing Cao, Anjia Peng, Guang Huang, Liqiang Cao, and Jianbo Fei. 2022. "Granular Flow–Obstacle Interaction and Granular Dam Break Using the S-H Model with the TVD-MacCormack Scheme" Applied Sciences 12, no. 10: 5066. https://doi.org/10.3390/app12105066
APA StyleZhou, H., Wang, M., Li, S., Cao, Z., Peng, A., Huang, G., Cao, L., & Fei, J. (2022). Granular Flow–Obstacle Interaction and Granular Dam Break Using the S-H Model with the TVD-MacCormack Scheme. Applied Sciences, 12(10), 5066. https://doi.org/10.3390/app12105066






