The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder
Abstract
1. Introduction
2. Problem Analysis
3. Computational Technique
4. Results and Discussion
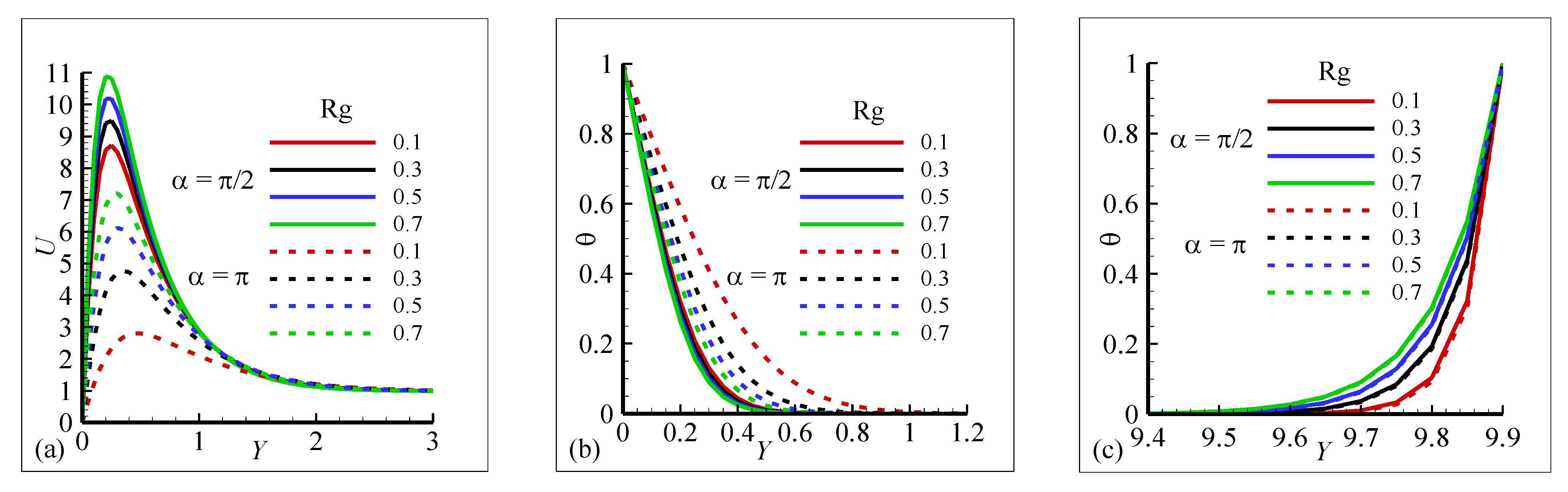
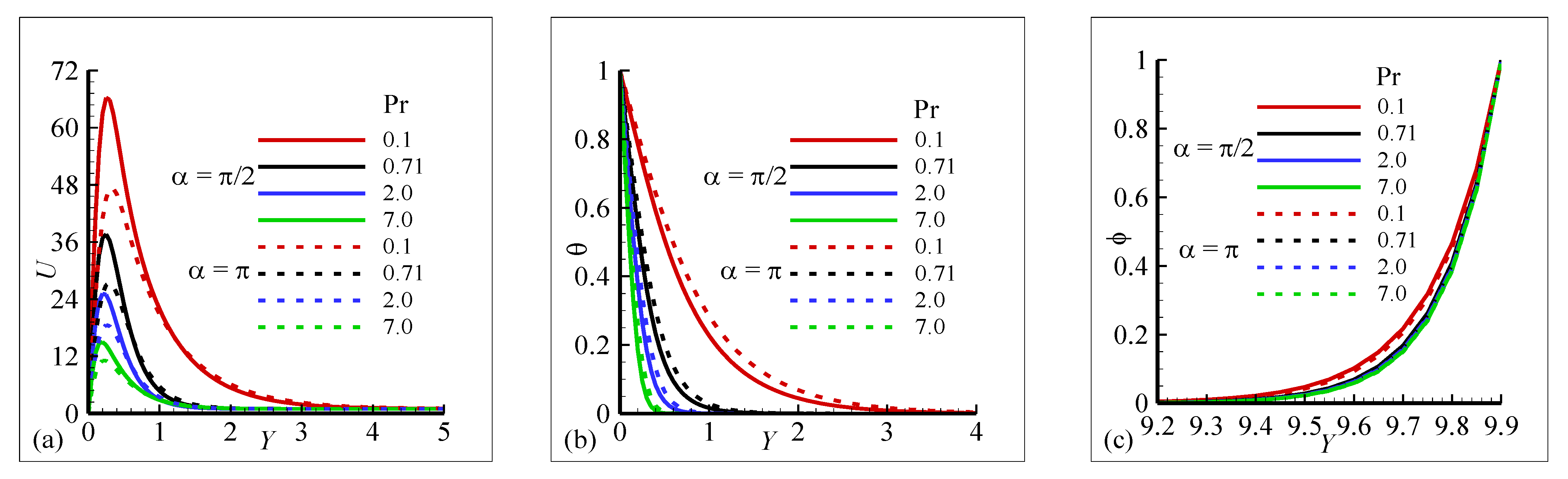
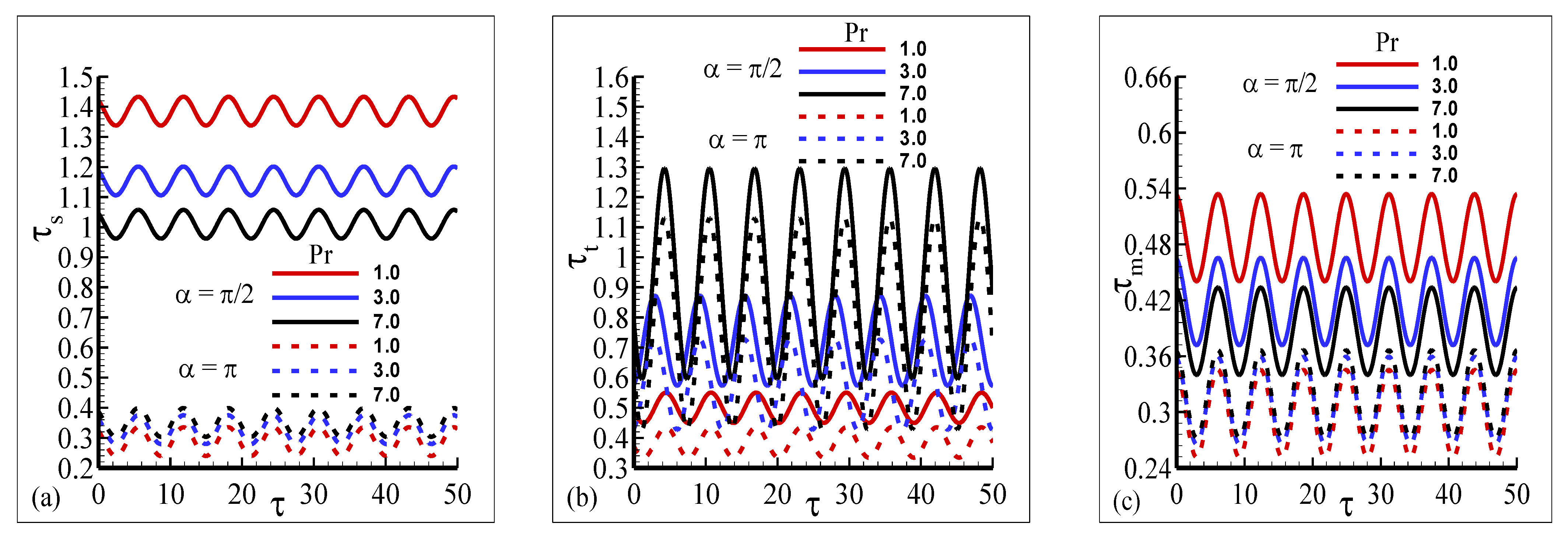
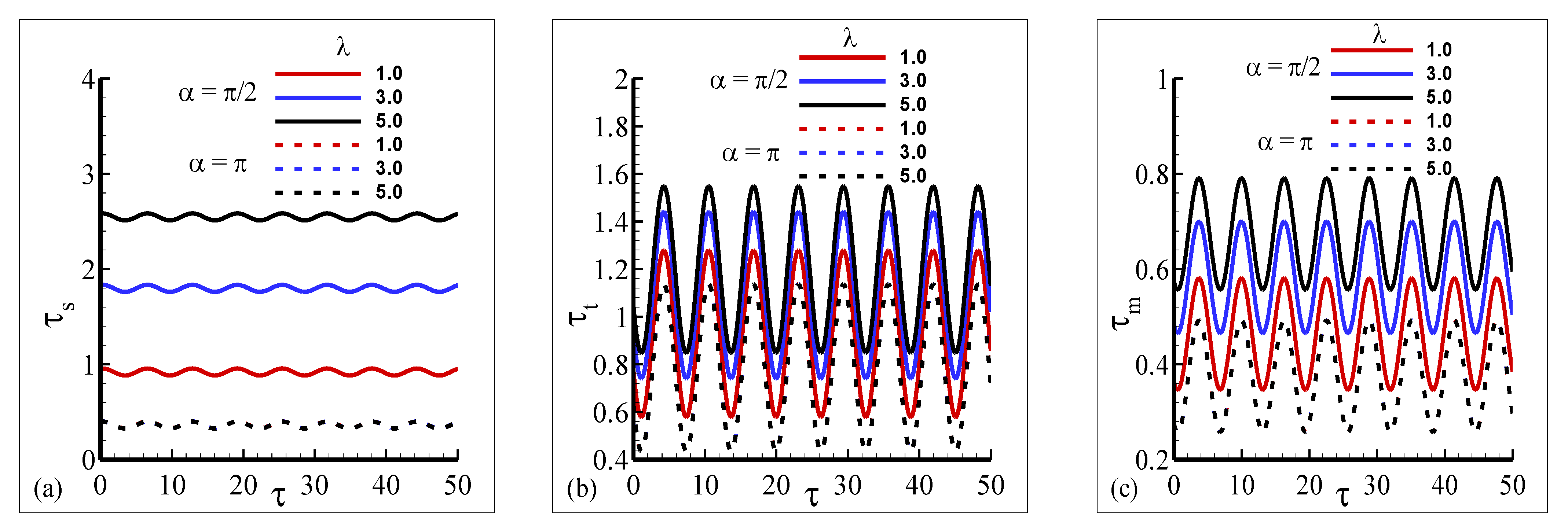
4.1. and Profiles to Check Accuracy of Numerical Data
4.2. Transient Shapes of , and Profiles to Check Accuracy of Numerical Data
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Velocity along and -coordinates (m s−1) | |
| Magnetic coordinates of velocities in direction (Tesla) | |
| Dynamicviscosity (kg m−1 s−1) | |
| Kinematicviscosity (m2 s−1) | |
| Fluid density (kg m−3) | |
| Gravity acceleration (m s−2) | |
| Coefficient of thermalexpansion (K−1) | |
| Magneticpermeability (H m−1) | |
| Thermaldiffusivity (m2 s−1) | |
| T | Fluidtemperature (K) |
| Specific heat (J kg−1 K−1) | |
| Temperature at maximum density | |
| Dimensionless magnetic field | |
| Transient heat transfer | |
| Dimensionless velocity | |
| Reduced gravity parameter | |
| Thermal conductivity | |
| MHD | Magnetohydrodynamic |
| Ambienttemperature (K) | |
| Reynolds number | |
| Grashof number | |
| Shearing stress (P a) | |
| Magnetic force parameter | |
| Mixedconvective number | |
| Dimensionalized temperature | |
| MagneticPrandtl parameter | |
| Pr | Prandtl parameter |
| Electrical conductivity (s m−1) | |
| Temperature difference | |
| Transient skin friction | |
| Transient current density | |
| Magnetic field intensity | |
| Maximum density | |
| Free stream velocity | |
| FDM | Finite difference method |
References
- Potter, J.M.; Riley, N. Free convection from a heated sphere at large Grashof number. J. Fluid Mech. 1980, 100, 769–783. [Google Scholar] [CrossRef]
- Ostrach, S. Convection phenomena at reduced gravity of importance in space processing of materials. Bull. Mater. Sci. 1982, 4, 109–123. [Google Scholar] [CrossRef][Green Version]
- Riley, N. The heat transfer from a sphere in free convective flow. Comput. Fluids 1986, 14, 225–237. [Google Scholar] [CrossRef]
- Herwing, H.; Klemp, K.; Stinnesbeck, J. Laminar entry flow in a pipe or channel: Effects of variable viscosity due to heat transfer across the wall. Numer. Heat Transf. 1990, 18, 51–70. [Google Scholar] [CrossRef]
- Kay, A.; Kuiken, H.K.; Merkin, J.H. Boundary-layer analysis of the thermal bar. J. Fluid Mech. 1995, 303, 253–278. [Google Scholar] [CrossRef]
- Cheng, C.Y. Natural convection boundary layer flow of fluid with temperature-dependent viscosity from a horizontal elliptical cylinder with constant surface heat flux. Appl. Math. Comput. 2010, 217, 83–91. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Effects of shear dependent viscosity and variable thermal conductivity on the flow and heat transfer in a slurry. Energies 2015, 8, 11546–11574. [Google Scholar] [CrossRef]
- Lotto, M.A.; Johnson, K.M.; Nie, C.W.; Klaus, D.M. The impact of reduced gravity on free convective heat transfer from a finite, flat, vertical plate. Microgravity Sci. Technol. 2017, 29, 371–379. [Google Scholar] [CrossRef]
- Ashraf, M.; Fatima, A.; Gorla, R.S.R. Periodic momentum and thermal boundary layer mixed convection flow around the surface of sphere in the presence of viscous dissipation. Can. J. Phys. 2017, 95, 976–986. [Google Scholar] [CrossRef]
- Ashraf, M.; Iqbal, I.; Ahmad, M.; Sultana, N. Numerical Prediction of natural convection flow in the presence of weak magnetic Prandtl number and strong magnetic field with algebraic decay in mainstream velocity. Adv. Appl. Math. Mech. 2017, 9, 349–361. [Google Scholar] [CrossRef]
- Ashraf, M.; Fatima, A. Numerical simulation of the effect of transient shear stress and rate of heat transfer around different position of sphere in the presence of viscous dissipation. J. Heat Transf. 2018, 140, 061701. [Google Scholar] [CrossRef]
- Muhammad, A.; Selvakumar, D.; Wu, J. Numerical investigation of laminar flow and heat transfer in a liquid metal cooled mini-channel heat sink. Int. J. Heat Mass Transf. 2020, 150, 119265. [Google Scholar] [CrossRef]
- Atif, S.M.; Hussain, S.; Sagheer, M. Effect of thermal radiation on MHD micropolar Carreau nanouid with viscous dissipation, Joule heating and internal heating. Sci. Iran. 2019, 26, 3875–3888. [Google Scholar]
- Liu, D.; Ling, X.; Peng, H.; Li, J.; Duan, L. Experimental and numerical analysis on heat transfer performance of slug flow in rectangular microchannel. Int. J. Heat Mass Transf. 2020, 147, 118963. [Google Scholar] [CrossRef]
- Makinde, O.D.; Reddy, M.G. MHD peristaltic slip flow of Casson fluid and heat transfer in channel filled with a porous medium. Sci. Iran. 2019, 26, 2342–2355. [Google Scholar] [CrossRef]
- Dixit, D.D.; Pattamatta, A. Effect of uniform external magnetic-field on natural convection heat transfer in a cubical cavity filled with magnetic nano-dispersion. Int. J. Heat Mass Transf. 2020, 146, 118828. [Google Scholar] [CrossRef]
- Vyas, A.; Mishra, B.; Srivastava, A. Experiments on flow and heat transfer characteristics of a rectangular channel with a built-in adiabatic square cylinder. Int. J. Heat Mass Transf. 2020, 147, 118908. [Google Scholar] [CrossRef]
- Raju BH, S.; Nath, D.; Pati, S.; Baranyi, L. Analysis of mixed convective heat transfer from a sphere with an aligned magnetic field. Int. J. Heat Mass Transf. 2020, 162, 120342. [Google Scholar] [CrossRef]
- Sekhar, T.V.S.; Sivakumar, R.; Kumar, T.R. Flow around a circular cylinder in an external magnetic field at high Reynolds numbers. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 740–759. [Google Scholar] [CrossRef]
- Yoon, H.S.; Chun, H.H.; Ha, M.Y.; Lee, H.G. A numerical study on the fluid flow and heat transfer around a circular cylinder in an aligned magnetic field. Int. J. Heat Mass Transf. 2004, 47, 4075–4087. [Google Scholar] [CrossRef]
- Alhamid, J.; Al-Obaidi, A.R.; Towsyfyan, H. A numerical study to investigate the effect of turbulators on thermal flow and heat performance of a 3D pipe. Heat Transf. 2021, 51, 2458–2475. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Alhamid, J. Investigation of flow pattern, thermohydraulic performance and heat transfer improvement in 3D corrugated circular pipe under varying structure configuration parameters with development different correlations. Int. Commun. Heat Mass Transf. 2021, 126, 105394. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Alhamid, J. Investigation of thermo-hydraulics flow and augmentation of heat transfer in the circular pipe by combined using corrugated tube with dimples and fitted with varying tape insert configurations investigation of thermo-hydraulics flow and augmentation of heat transfer in the circular pipe by combined using corrugated tube with dimples and fitted with varying tape insert configurations. Int. J. Heat Technol. 2021, 39, 365–374. [Google Scholar]
- Alhamid, J.; Al-Obaidi, R.A. Flow pattern investigation and thermohydraulic performance enhancement in three-dimensional circular pipe under varying corrugation configurations. J. Phys. Conf. Ser. 2021, 1845, 012061. [Google Scholar] [CrossRef]
- Gyergyek, S.; Kocjan, A.; Grilc, M.; Likozar, B.; Hočevar, B.; Makovec, D. A hierarchical Ru-bearing alumina/magnetic iron-oxide composite for the magnetically heated hydrogenation of furfural. Green Chem. 2020, 22, 5978–5983. [Google Scholar] [CrossRef]
- Gyergyek, S.; Kocjan, A.; Bjelić, A.; Grilc, M.; Likozar, B.; Makovec, D. Magnetically separable Ru-based nano-catalyst for the hydrogenation/hydro-deoxygenation of lignin-derived platform chemicals. Mater. Res. Lett. 2018, 6, 426–431. [Google Scholar] [CrossRef]
- Bjelić, A.; Grilc, M.; Gyergyek, S.; Kocjan, A.; Makovec, D.; Likozar, B. Catalytic hydrogenation, hydrodeoxygenation, and hydrocracking processes of a lignin monomer model compound eugenol over magnetic Ru/C–Fe2O3 and mechanistic reaction microkinetics. Catalysts 2018, 8, 425. [Google Scholar] [CrossRef]
- Ilyas, A.; Ashraf, M.; Rashad, A.M. Periodical Analysis of Convective Heat Transfer Along Electrical Conducting Cone Embedded in Porous Medium. Arab. J. Sci. Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Mahmood, M.; Asghar, S.; Hossain, M.A. Hydromagnetic flow of viscous incompressible fluid past a wedge with permeable surface. ZAMM-J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. Appl. Math. Mech. 2009, 89, 174–188. [Google Scholar] [CrossRef]
- Chawla, S.S. Magnetohydrodynamic oscillatory flow past a semi-infinite flat plate. Int. J. Non-Linear Mech. 1971, 6, 117–134. [Google Scholar] [CrossRef]



| Mehmood et al. [29] | Ilyas et al. [28] | Present Analysis | |
|---|---|---|---|
| 1 | 0.3148 | 0.3122 | 0.3040 |
| 10 | 0.3151 | 0.3137 | 0.3106 |
| 100 | 0.3156 | 0.3149 | 0.3118 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Ashraf, M.; Sarris, I.E.; Karakasidis, T.E. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Appl. Sci. 2022, 12, 5081. https://doi.org/10.3390/app12105081
Ullah Z, Ashraf M, Sarris IE, Karakasidis TE. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Applied Sciences. 2022; 12(10):5081. https://doi.org/10.3390/app12105081
Chicago/Turabian StyleUllah, Zia, Muhammad Ashraf, Ioannis E. Sarris, and Theodoros E. Karakasidis. 2022. "The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder" Applied Sciences 12, no. 10: 5081. https://doi.org/10.3390/app12105081
APA StyleUllah, Z., Ashraf, M., Sarris, I. E., & Karakasidis, T. E. (2022). The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Applied Sciences, 12(10), 5081. https://doi.org/10.3390/app12105081









