BearingCog: A Bearing Fault Diagnosis Method under Variable Operational Conditions
Abstract
:1. Introduction
- Signal processing is vital to feature extraction. Although numerous research has been developed in fault diagnosis, there is still a lack of analysis of the feature extraction effect with classifier accuracy. Inferior quality feature data will reduce the accuracy and efficiency of the classifier [7].
- A large number of features burden computational cost and execution speed. Moreover, the redundant features can decrease the diagnosis accuracy by misleading the classifier model in the training stage. Hence, the redundant features need to be recognized and eliminated.
- Benefiting from adaptive and robust properties, VMD is more capable of vibration signal decomposition and obtains more fault characteristics. The improvement in feature quantity increases the diversity of data selection and improves the quality of selected data.
- The SVM model combined with PCA feature selection is utilized, which improves generalization and detection accuracy for the classifier. Additionally, computational complexity is decreased in terms of feature selection. Furthermore, the SVM model benefits from a few adjustable parameters as well as better generalization capability.
- The effectiveness of the proposed algorithm is verified on numerous real-life bearing fault signals, either for the detected sensitivity or specificity.
2. Related Work
3. Methodology
3.1. BearingCog Overview
3.2. Signal Preprocessing
| Algorithm 1: Complete optimization of VMD |
| repeat for k = 1: K do end for Until |
3.3. Feature Extraction and Selection
3.4. Multiclass SVM Model for Recognition
4. Experimental Results and Discussion
4.1. Experimental Platform
4.2. Data Processing and Datasets
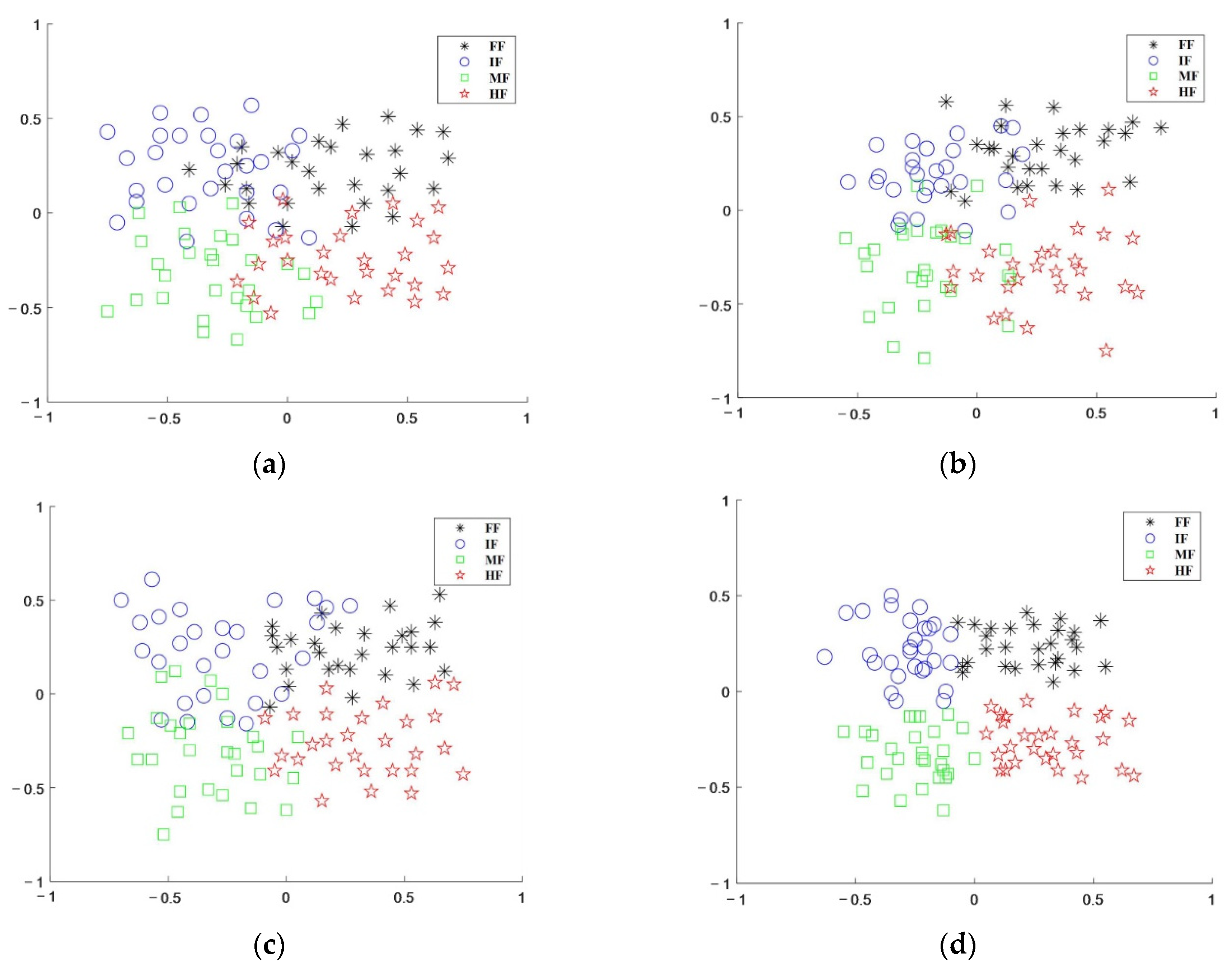
4.3. Feature Extraction Analysis
4.4. Classifier Model Optimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.P.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002–107023. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Din, Q. A robust intelligent fault diagnosis method for rolling element bearings based on deep distance metric learning. Neurocomputing 2018, 310, 77–95. [Google Scholar] [CrossRef]
- Liu, R.N.; Yang, B.Y.; Zio, E.; Chen, X.F. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mechanical Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.N.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, L. Naturally Damaged Wind Turbine Blade Bearing Fault Detection Using Novel Iterative Nonlinear Filter and Morphological Analysis. IEEE Trans. Ind. Electron. 2020, 67, 8713–8722. [Google Scholar] [CrossRef]
- Kong, L.; Wang, T.; Wang, P.; Zhou, Y. Research on Bearing Fault Diagnosis Method under Variable Operating Conditions Based on MWDCNN. J. Phys. Conf. Ser. 2022, 2173, 12088–12096. [Google Scholar] [CrossRef]
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Deep Residual Networks with Dynamically Weighted Wavelet Coefficients for Fault Diagnosis of Planetary Gearboxes. IEEE Trans. Ind. Electron. 2018, 65, 4290–4300. [Google Scholar] [CrossRef]
- Biswal, B.; Biswal, M.; Hasan, S.; Dash, P.K. Nonstationary power signal time series data classification using LVQ classifier. Appl. Soft Comput. 2014, 18, 158–166. [Google Scholar] [CrossRef]
- Ye, X.; Hu, Y.; Shen, J.; Chen, C.; Zhai, G. An Adaptive Optimized TVF-EMD Based on a Sparsity-Impact Measure Index for Bearing Incipient Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Gao, T.; Sheng, W.; Zhou, M.; Fang, B.; Luo, F.; Li, J. Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert-Huang Transform and Deep Learning. Sensors 2020, 20, 5633. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Process. 2020, 135, 106443–106463. [Google Scholar] [CrossRef]
- Fu, L.; Zhu, T.; Zhu, K.; Yang, Y. Condition Monitoring for the Roller Bearings of Wind Turbines under Variable Working Conditions Based on the Fisher Score and Permutation Entropy. Energies 2019, 12, 3085. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Zhu, T.; Pan, G.; Chen, S.; Zhong, Q.; Wei, Y. Power Quality Disturbance Recognition Using VMD-Based Feature Extraction and Heuristic Feature Selection. Appl. Sci. 2019, 9, 4901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lv, Y.; Ge, M. Complementary Ensemble Adaptive Local Iterative Filtering and Its Application to Rolling Bearing Fault Diagnosis. IEEE Access 2021, 9, 47275–47293. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A Novel Fault Diagnosis Method Based on Integrating Empirical Wavelet Transform and Fuzzy Entropy for Motor Bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Q.; Zhang, Y. Rolling Bearing Fault Diagnosis Based on CEEMDAN and Refined Composite Multiscale Fuzzy Entropy. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Amar, M.; Gondal, I.; Wilson, C. Vibration Spectrum Imaging: A Novel Bearing Fault Classification Approach. IEEE Trans. Ind. Electron. 2015, 62, 494–502. [Google Scholar] [CrossRef]
- Saidi, L.; Ben Ali, J.; Fnaiech, F. Application of higher order spectral features and support vector machines for bearing faults classification. ISA Trans. 2015, 54, 193–206. [Google Scholar] [CrossRef]
- Lei, Y.G.; Yang, B.; Jiang, X.W.; Jia, F.; Li, N.P.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587–106625. [Google Scholar] [CrossRef]
- Shao, H.D.; Xia, M.; Han, G.J.; Zhang, Y.; Wan, J.F. Intelligent Fault Diagnosis of Rotor-Bearing System Under Varying Working Conditions with Modified Transfer Convolutional Neural Network and Thermal Images. IEEE Trans. Ind. Inform. 2021, 17, 3488–3496. [Google Scholar] [CrossRef]
- Husari, F.; Seshadrinath, J. Incipient Interturn Fault Detection and Severity Evaluation in Electric Drive System Using Hybrid HCNN-SVM Based Model. IEEE Trans. Ind. Inform. 2022, 18, 1823–1832. [Google Scholar] [CrossRef]
- Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on Bearing Fault Diagnosis of Wind Turbine Gearbox Based on 1DCNN-PSO-SVM. IEEE Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
- Wang, T.; Lu, G.; Yan, P. A Novel Statistical Time-Frequency Analysis for Rotating Machine Condition Monitoring. IEEE Trans. Ind. Electron. 2020, 67, 531–541. [Google Scholar] [CrossRef]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.Y.; Qin, W.L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Sun, W.J.; Shao, S.Y.; Zhao, R.; Yan, R.Q.; Zhang, X.W.; Chen, X.F. A sparse auto-encoder-based deep neural network approach for induction motor faults classification. Measurement 2016, 89, 171–178. [Google Scholar] [CrossRef]
- Choudhary, A.; Goyal, D.; Letha, S.S. Infrared Thermography-Based Fault Diagnosis of Induction Motor Bearings Using Machine Learning. IEEE Sens. J. 2021, 21, 1727–1734. [Google Scholar] [CrossRef]
- Yan, X.A.; Jia, M.P. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Abdoos, A.A.; Mianaei, P.K.; Ghadikolaei, M.R. Combined VMD-SVM based feature selection method for classification of power quality events. Appl. Soft Comput. 2016, 38, 637–646. [Google Scholar] [CrossRef]







| Feature | Expression | Features | Expression |
|---|---|---|---|
| Mean (M) | Impulse factor (IF) | ||
| Root mean square (RMS) | Margin factor (MF) | ||
| Peak (PK) | Center frequency (FC) | ||
| Shape factor (SF) | Root mean square frequency (RMSF) | ||
| Kurtosis (KU) | Root variance frequency (RVF) |
| Technical Indicator | Measuring Range | Frequency Response Characteristic | Sensitivity | Constant Current Source Excitation |
|---|---|---|---|---|
| Values | −50~+50 g | 0.2 Hz~20 kHz | 93.7 mV/g | 2~10 mA |
| No. | Defected Bearing | Label | Cut Sectional Dimension |
|---|---|---|---|
| 1 | Little fault | LF | 0.5 mm × 0.5 mm |
| 2 | Medium fault | MF | 1.0 mm × 0.5 mm |
| 3 | High fault | HF | 1.5 mm × 0.5 mm |
| 4 | Fault-free | FF | - |
| Name of SVM Classifier | Characteristics of Training Samples | Number of Features |
|---|---|---|
| Dimensionless time domain characteristics | Mean, Peak, Kurtosis, Shape factor, Impulse factor Root mean square | 6 |
| EMD decomposition energy | Margin factor, Fuzzy entropy Sample entropy Center frequency Root variance frequency Root mean square frequency | 6 |
| VMD decomposition energy | Margin factor, Fuzzy entropy Sample entropy Center frequency Root variance frequency Root mean square frequency | 6 |
| Multi-information fusion | Mean, Peak, Kurtosis, Shape factor, Impulse factor Root mean square Margin factor, Fuzzy entropy Sample entropy Center frequency Root variance frequency Root mean square frequency | 12 |
| Data Set | Different Data Feature | Recognition Accuracy Rate |
|---|---|---|
| Experimental data | Dimensionless time domain characteristics | 63.6% |
| EMD decomposition energy | 71.0% | |
| VMD decomposition energy | 76.6% | |
| Multi-information fusion | 94.1% | |
| CWRU data | Dimensionless time domain characteristics | 75.3% |
| EMD decomposition energy | 84.5% | |
| VMD decomposition energy | 90.7% | |
| Multi-information fusion | 96.4% |
| Defected Bearing | Label | Fault Diameter (mm) | Motor Load (HP) | Motor Speed (r/min) | Outer Race Data Set Position |
|---|---|---|---|---|---|
| Little fault | LF | 0.1778 | 0 | 1797 | OR007@6_0 (130.mat) |
| 1 | 1772 | OR007@6_1 (131.mat) | |||
| Medium fault | MF | 0.3556 | 0 | 1797 | OR014@6_0 (197.mat) |
| 1 | 1772 | OR014@6_1 (198.mat) | |||
| High fault | HF | 0.5334 | 0 | 1797 | OR014@6_1 (198.mat) |
| 1 | 1772 | OR021@6_1 (235.mat) | |||
| Fault-free | FF | - | 0 | 1797 | Normal_0 (97.mat) |
| 1 | 1772 | Normal_1 (98.mat) |
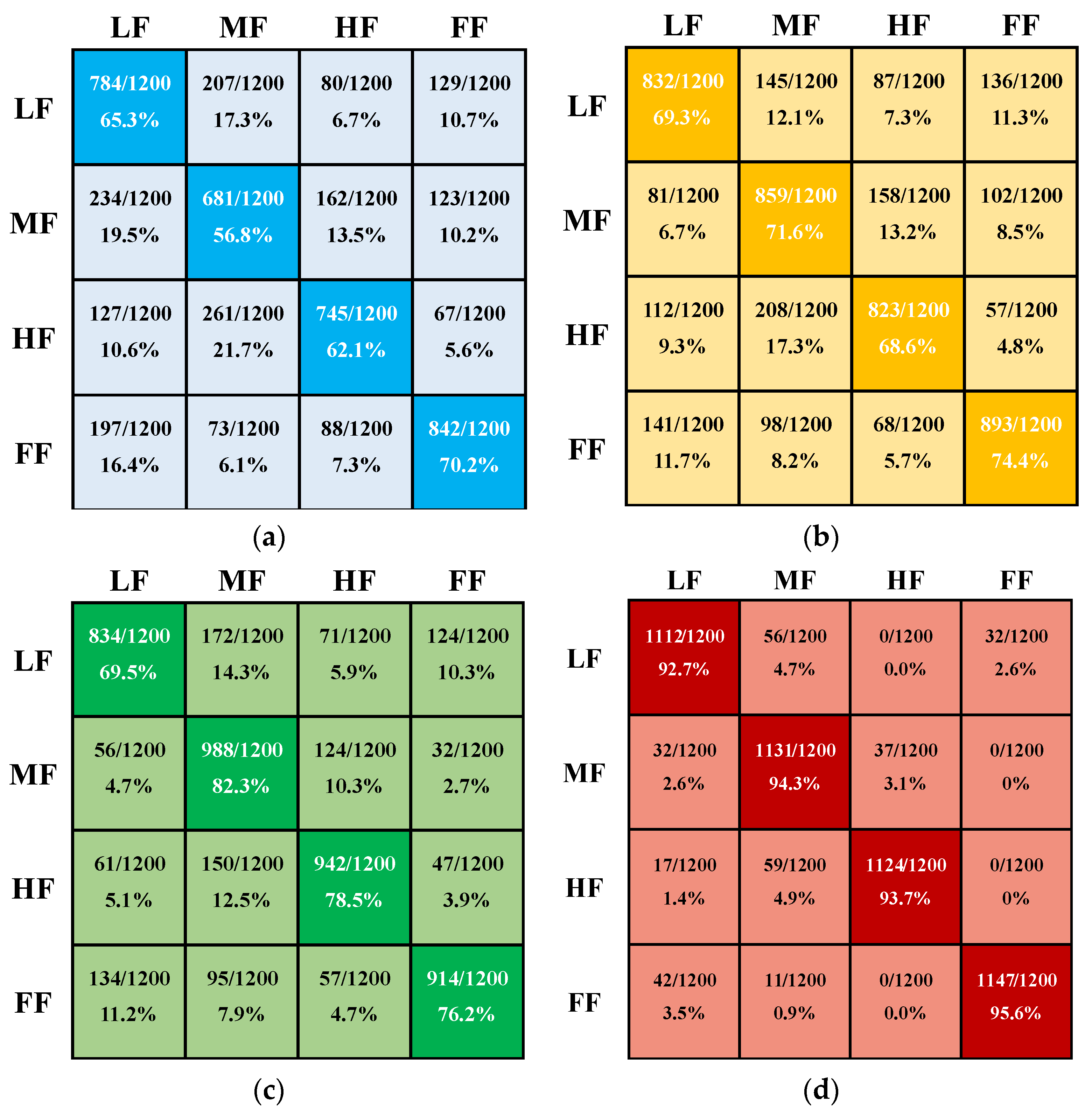
| Bearing State | Fault Free | Little Fault | Medium Fault | High Fault |
|---|---|---|---|---|
| Accuracy | Accuracy | Accuracy | Accuracy | |
| Linear kernel | 95.6% | 92.7% | 94.3% | 93.7% |
| Polynomial kernel | 95.7% | 93.3% | 94.6% | 94.1% |
| Radial basis function kernel | 96.8% | 94.5% | 96.7% | 97.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Ma, Z.; Wu, D.; Liu, J.; Xu, F.; Zhong, Q.; Zhu, T. BearingCog: A Bearing Fault Diagnosis Method under Variable Operational Conditions. Appl. Sci. 2022, 12, 5240. https://doi.org/10.3390/app12105240
Fu L, Ma Z, Wu D, Liu J, Xu F, Zhong Q, Zhu T. BearingCog: A Bearing Fault Diagnosis Method under Variable Operational Conditions. Applied Sciences. 2022; 12(10):5240. https://doi.org/10.3390/app12105240
Chicago/Turabian StyleFu, Lei, Zepeng Ma, Debin Wu, Jia Liu, Fang Xu, Qi Zhong, and Tiantian Zhu. 2022. "BearingCog: A Bearing Fault Diagnosis Method under Variable Operational Conditions" Applied Sciences 12, no. 10: 5240. https://doi.org/10.3390/app12105240
APA StyleFu, L., Ma, Z., Wu, D., Liu, J., Xu, F., Zhong, Q., & Zhu, T. (2022). BearingCog: A Bearing Fault Diagnosis Method under Variable Operational Conditions. Applied Sciences, 12(10), 5240. https://doi.org/10.3390/app12105240






