Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors
Abstract
:1. Introduction
2. Related Works
| Ref. | Year | DvC | Paradigm | Applications |
|---|---|---|---|---|
| [27] | 1971 | continuous | catenary | cable towed by aircraft |
| [22] | 1973 | both | Analytical methods (survey) | Ocean Science |
| [28] | 1981 | continuous | catenary | cable structures |
| [29] | 1995 | continuous | catenary | cable towed by aircraft |
| [30] | 1999 | both | catenary vs. rod elements | – |
| [31] | 2000 | continous | catenary | underwater towing |
| [32] | 2001 | continuous | catenary | ocean sciences, mooring |
| [33] | 2001 | continuous | catenary | underwater towing |
| [24] | 2006 | continuous | catenary | designs of nets of cables |
| [34] | 2007 | continuoys | rigid link | tethered UAV |
| [35] | 2008 | continuous | parabola | cable structures |
| [36] | 2008 | continuous | catenary | ocean sciences, mooring |
| [37] | 2009 | continuous | rigid link | cooperating UAV payload transport |
| [38] | 2010 | continuous | rigid link | cooperating UAV payload transport |
| [39] | 2012 | continuous | catenary | cable-driven parallel robot |
| [40] | 2012 | continuous | rigid link | cooperating UAV payload transport |
| [41] | 2013 | continuous | rigid link | tethered UAV |
| [42] | 2013 | continuous | catenary | cable-driven parallel robot |
| [43] | 2015 | continous | rigid link | tethered survillance UAV |
| [44] | 2015 | discrete | series of rigid links | cooperating UAV payload transport |
| [18,45] | 2015, 2017 | continuous | catenary | DLO transportation by UAVs |
| [46] | 2016 | continuous | catenary | tethered UAV |
| [47] | 2017 | continuous | catenary | tethered UAVs |
| [48] | 2017 | continuous | catenary | cable transportation by 2 UAVs |
| [25] | 2018 | continuous | catenary | suspension bridges |
| [26] | 2018 | continuous | catenary | suspension bridges |
| [49] | 2018 | continuous | catenary and parabola | cable vibrations |
| [15] | 2020 | discrete | chain of rigid links | hose transportation by 2 UAVs |
| [13] | 2021 | continuous | catenary | cable transportation by 2 UAVs |
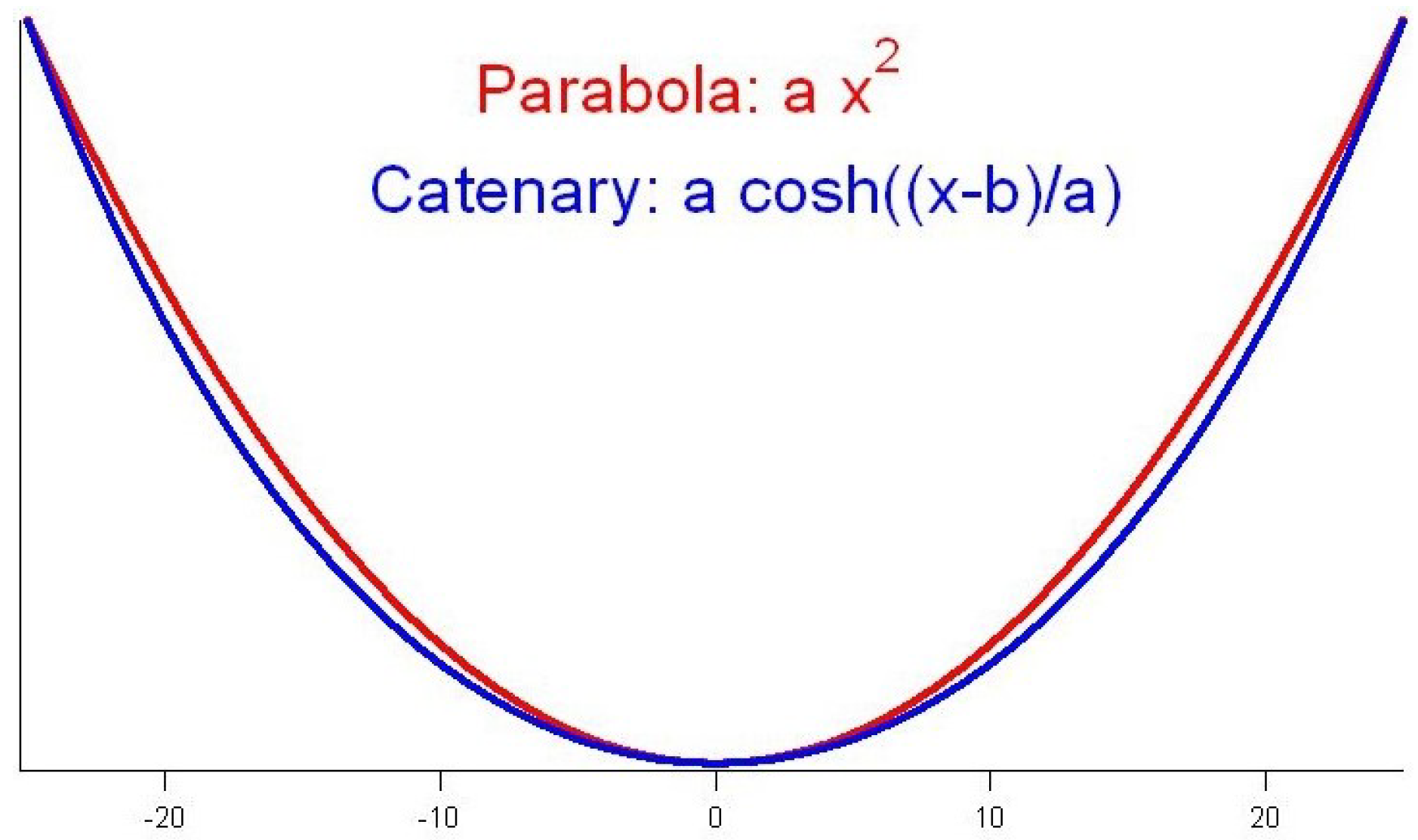
3. Parabola–Catenary Hybrid DLO Geometrical Model
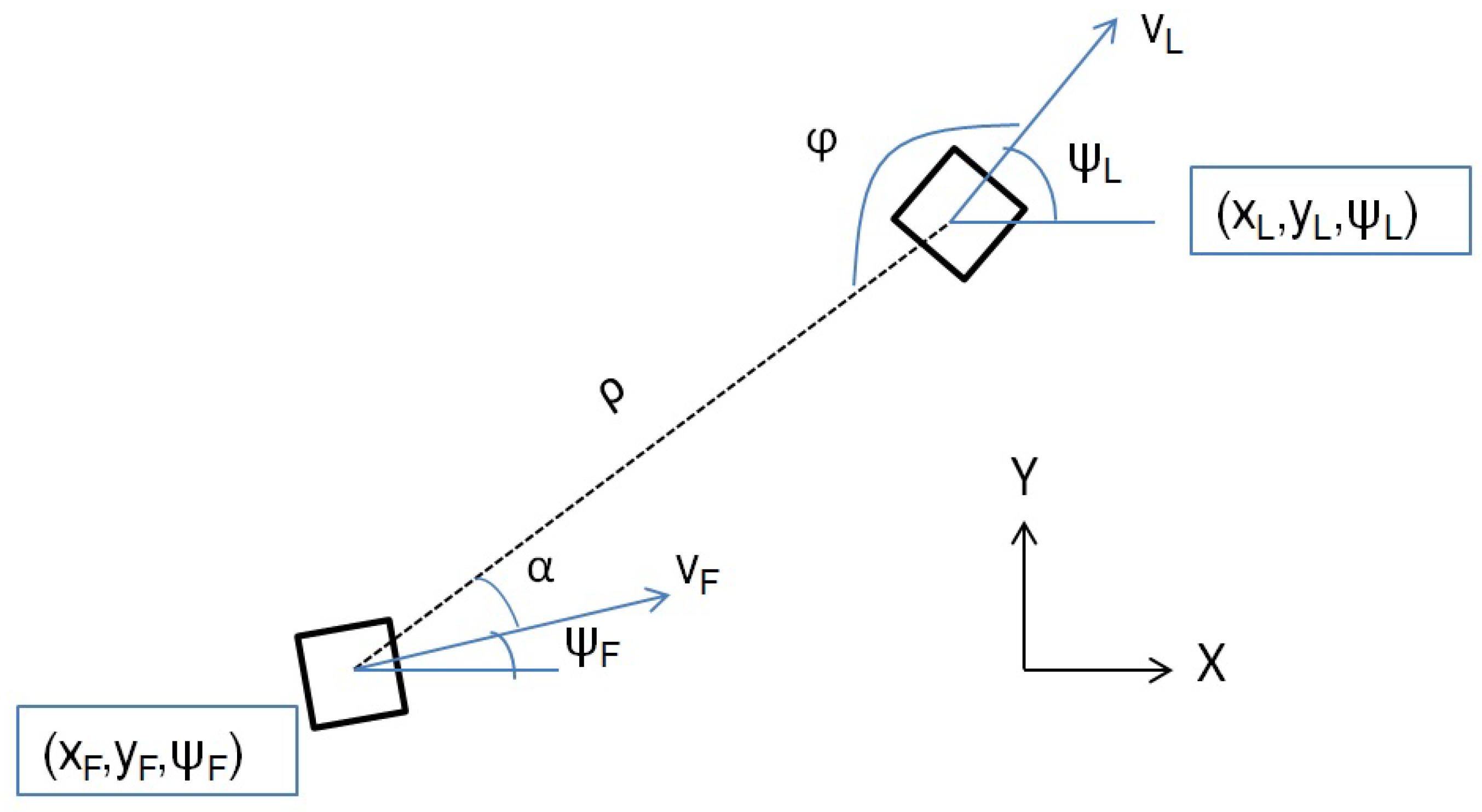
4. Quadrotor Team Formation Strategy
5. System Control
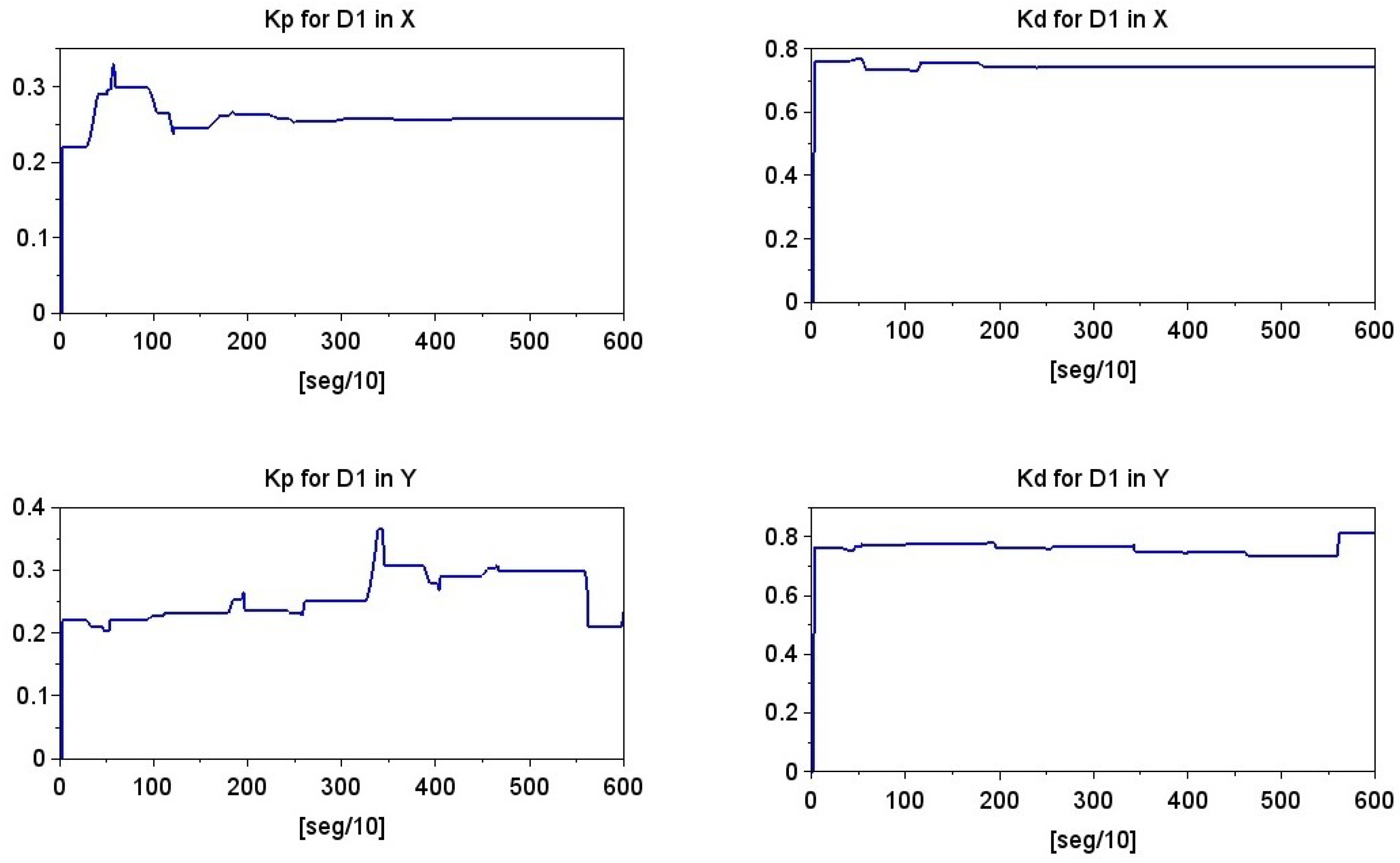
Online Adaptation of PD Controllers
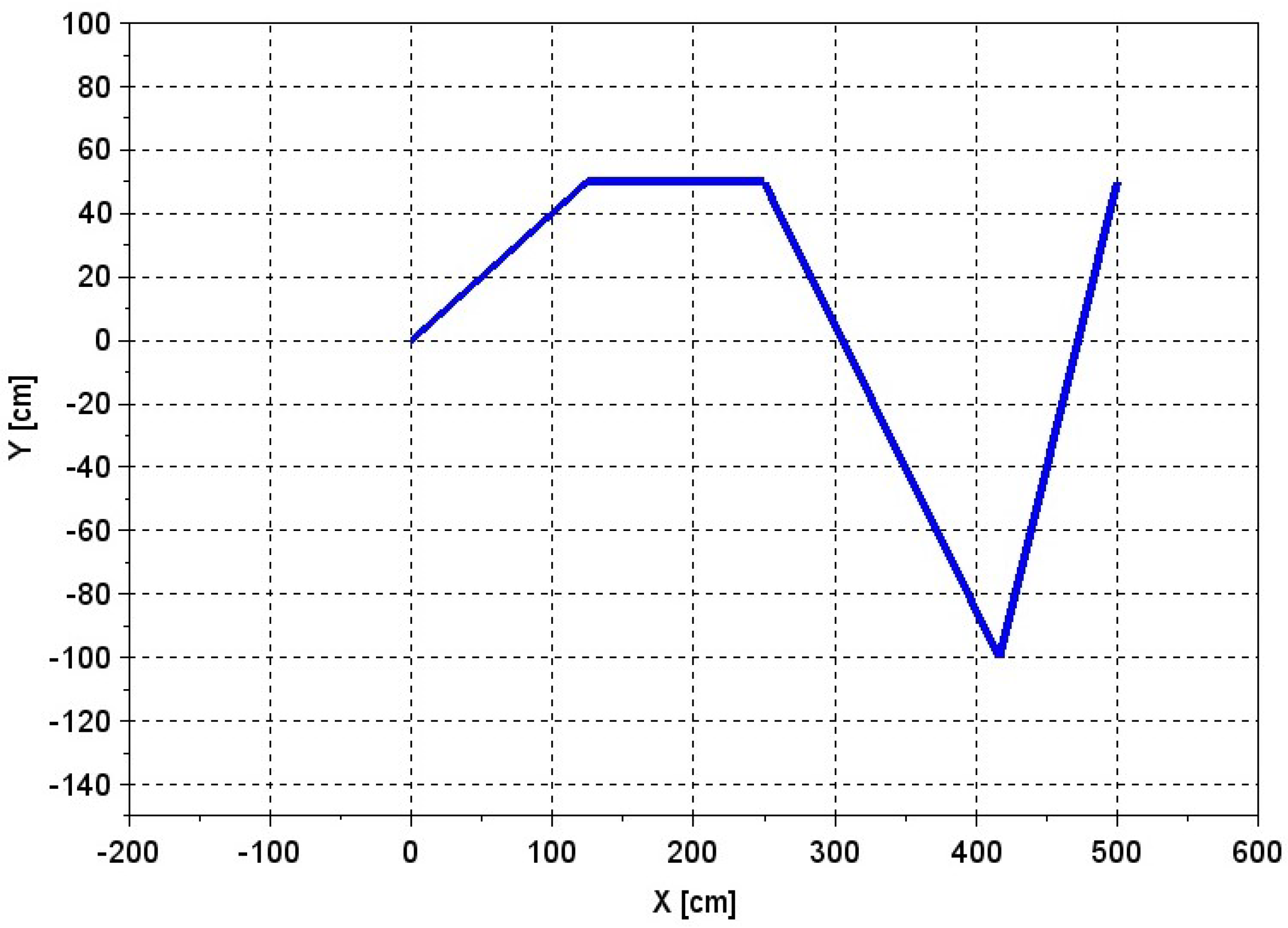
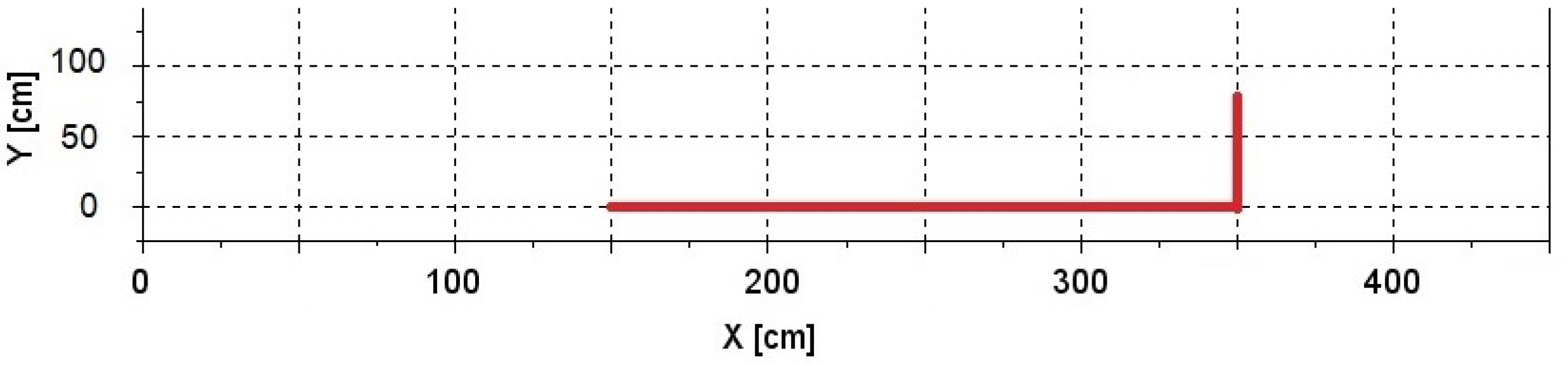
6. Experiments
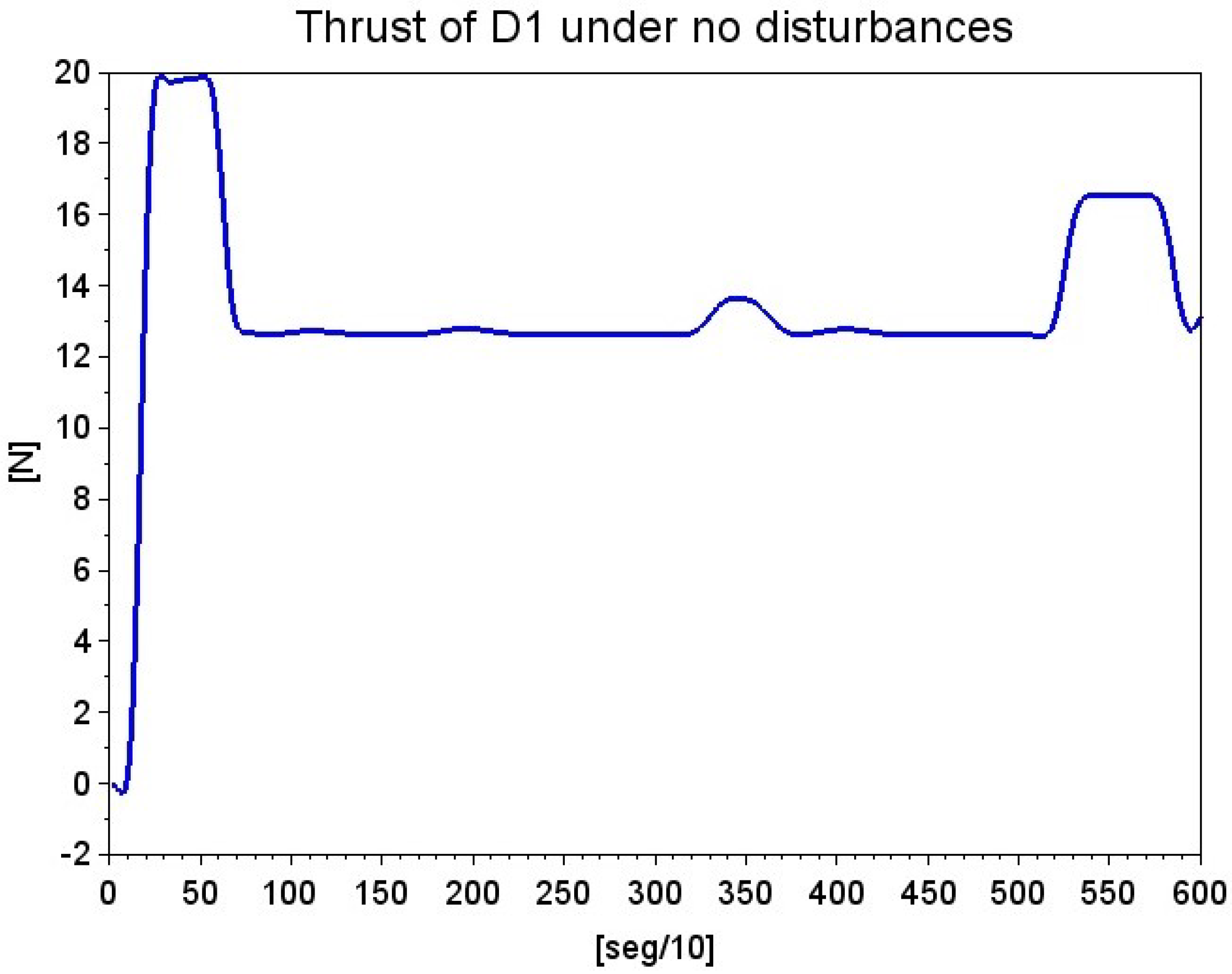
7. Results
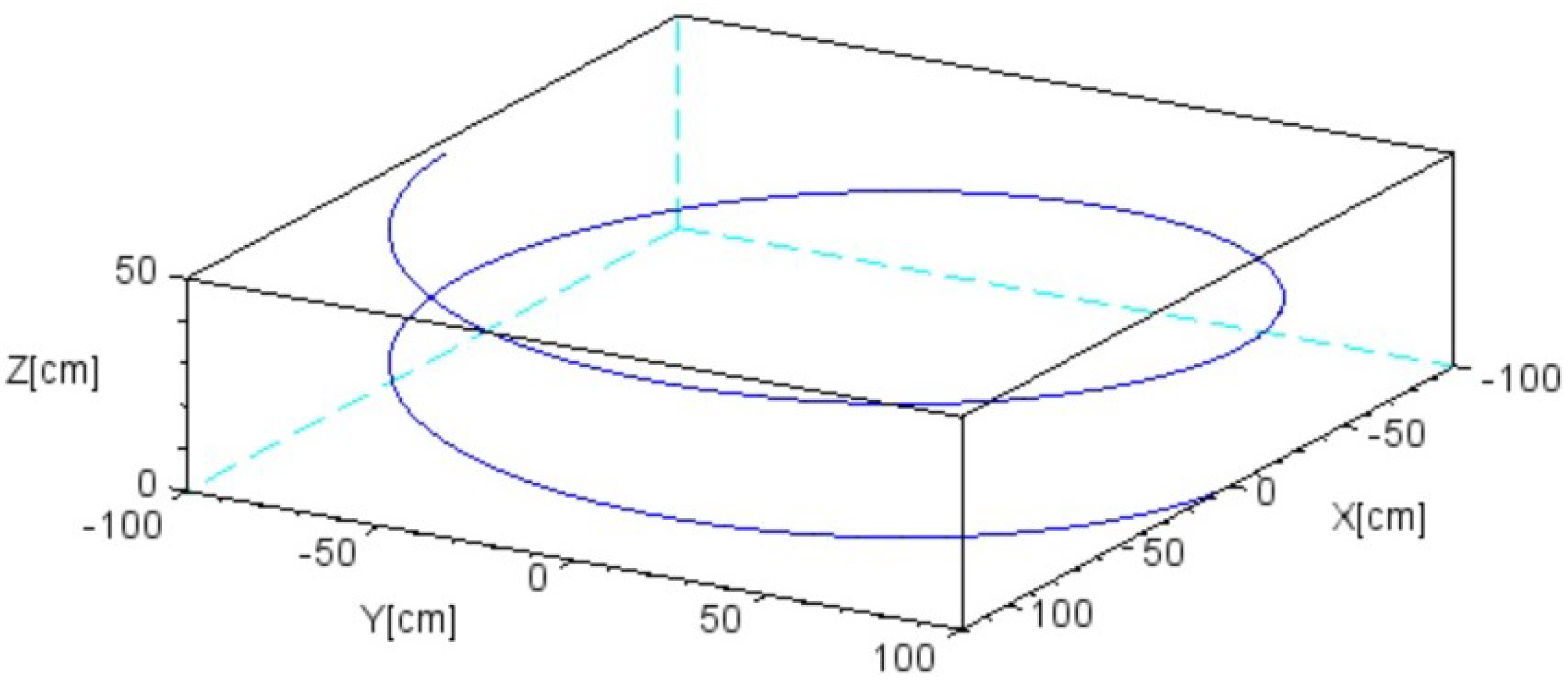
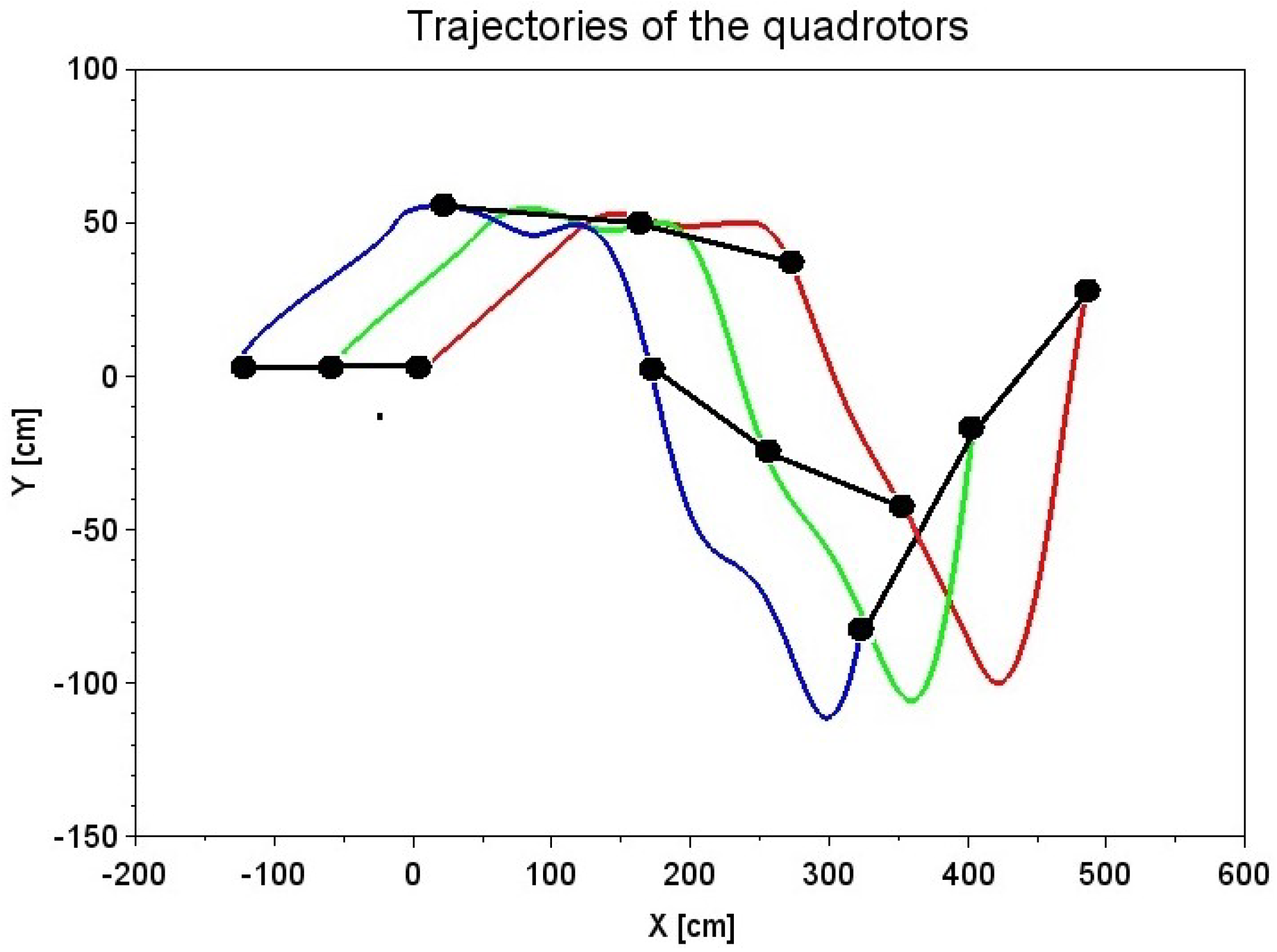
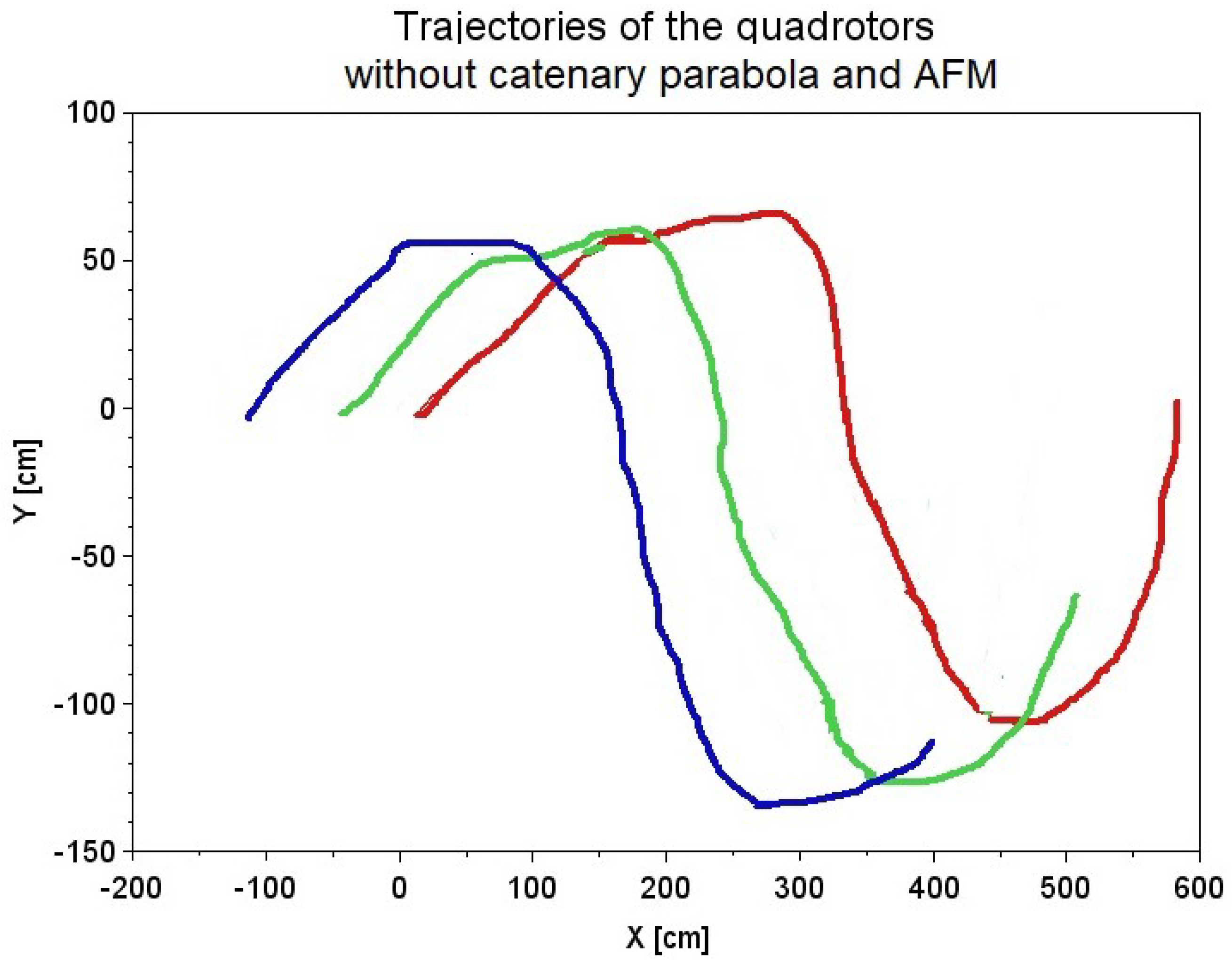
7.1. Experiment 1
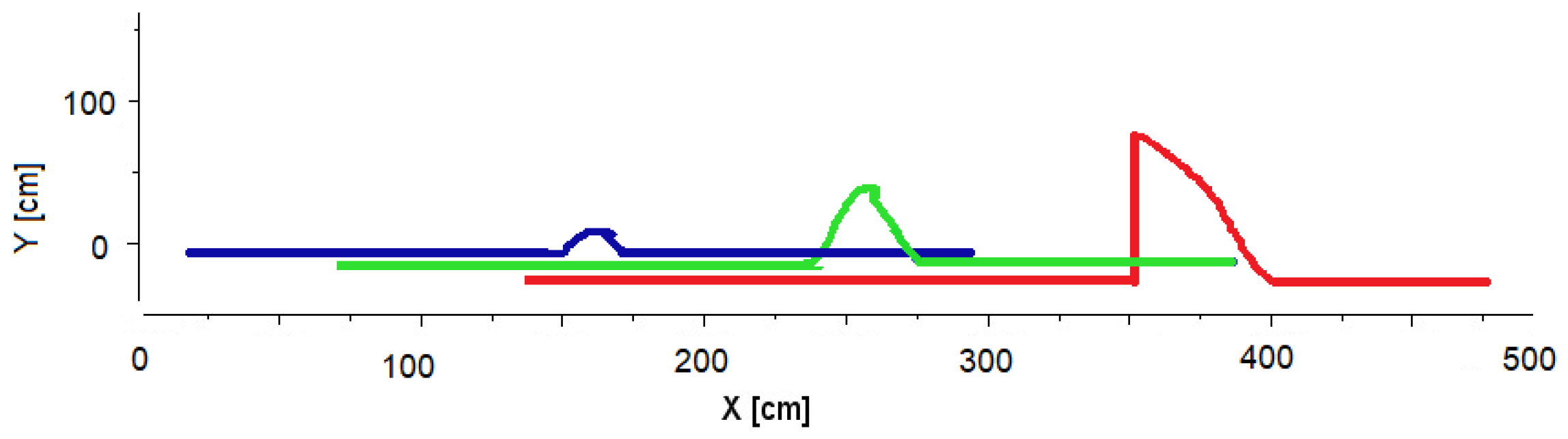
7.2. Experiment 2
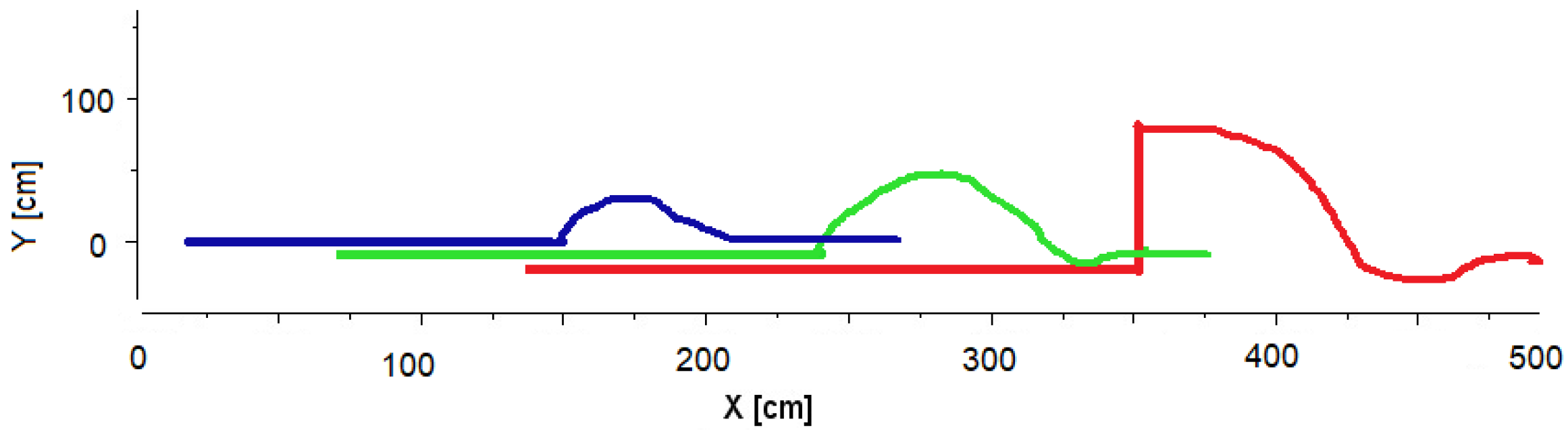
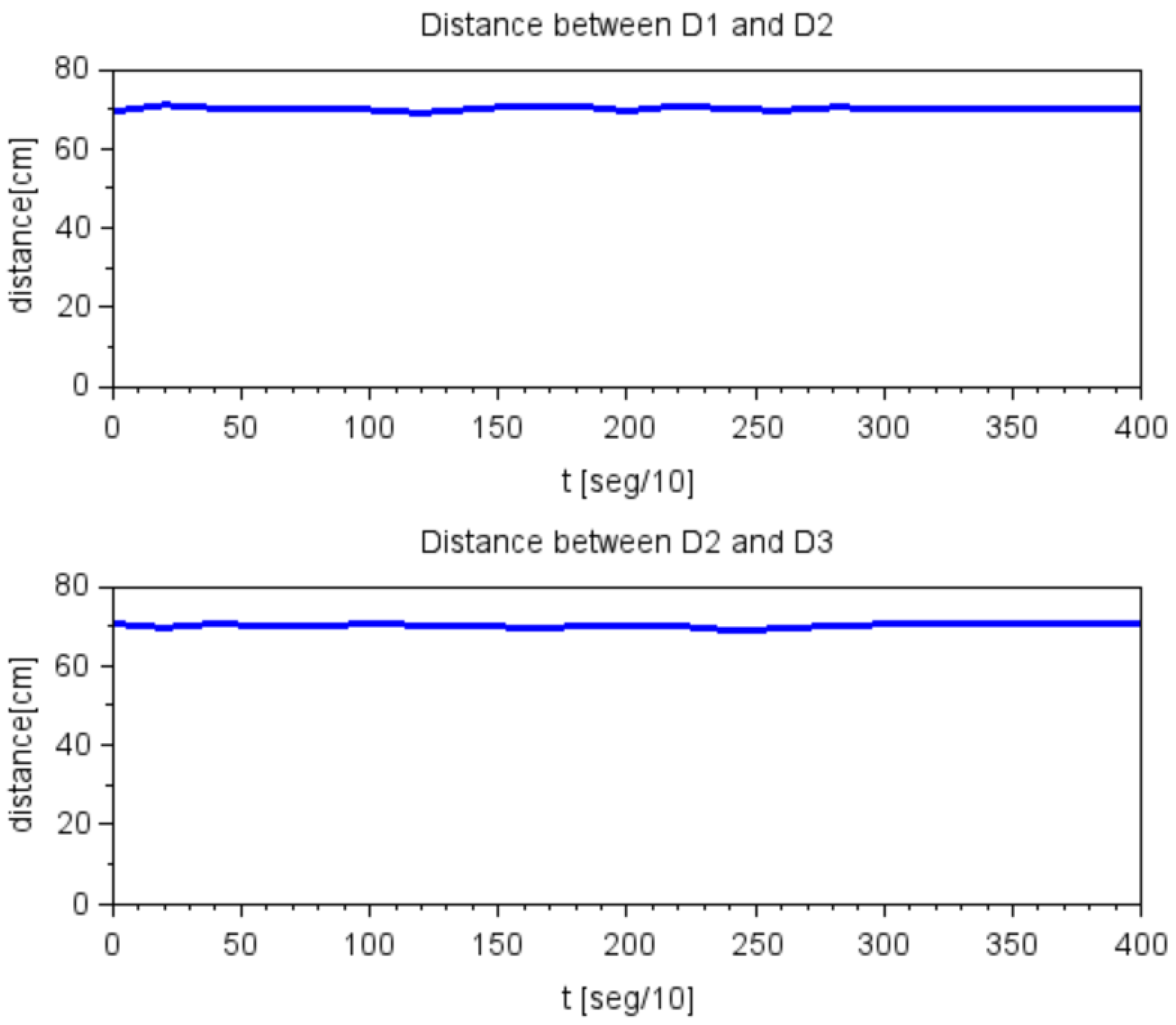
7.3. Experiment 3
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moshref-Javadi, M.; Hemmati, A.; Winkenbach, M. A truck and drones model for last-mile delivery: A mathematical model and heuristic approach. Appl. Math. Model. 2020, 80, 290–318. [Google Scholar] [CrossRef]
- Bonyan Khamseh, H.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Mohammadi, K.; Jafarinasab, M.; Sirouspour, S.; Dyer, E. Decentralized motion control in a cabled-based multi-drone load transport system. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4198–4203. [Google Scholar] [CrossRef]
- Mohammadi, K.; Sirouspour, S.; Grivani, A. Control of Multiple Quad-Copters With a Cable-Suspended Payload Subject to Disturbances. IEEE/ASME Trans. Mechatron. 2020, 25, 1709–1718. [Google Scholar] [CrossRef]
- Al-Kaff, A.; Armingol, J.M.; de La Escalera, A. A vision-based navigation system for Unmanned Aerial Vehicles (UAVs). Integr. Comput. Aided Eng. 2019, 26, 297–310. [Google Scholar] [CrossRef]
- Shirani, B.; Najafi, M.; Izadi, I. Cooperative load transportation using multiple UAVs. Aerosp. Sci. Technol. 2019, 84, 158–169. [Google Scholar] [CrossRef]
- Thapa, S.; Bai, H.; Acosta, J. Cooperative aerial load transport with force control. IFAC-PapersOnLine 2018, 51, 38–43. [Google Scholar] [CrossRef]
- Michael, N.; Shen, S.; Mohta, K.; Kumar, V.; Nagatani, K.; Okada, Y.; Kiribayashi, S.; Otake, K.; Yoshida, K.; Ohno, K.; et al. Collaborative mapping of an earthquake damaged building via ground and aerial robots. In Springer Tracts in Advanced Robotics; Springer: Cham, Switzerland, 2014; pp. 33–47. [Google Scholar]
- Ando, H.; Ambe, Y.; Ishii, A.; Konyo, M.; Tadakuma, K.; Maruyama, S.; Tadokoro, S. Aerial hose type robot by water jet for fire fighting. IEEE Robot. Autom. Lett. 2018, 3, 1128–1135. [Google Scholar] [CrossRef]
- Aminifar, F.; Rahmatian, F. Unmanned Aerial Vehicles in Modern Power Systems: Technologies, Use Cases, Outlooks, and Challenges. IEEE Electrif. Mag. 2020, 8, 107–116. [Google Scholar] [CrossRef]
- Suzuki, M.; Yokota, S.; Matsumoto, A.; Chugo, D.; Hashimoto, H. Liquid feeding system using cooperative towing by multiple drones—2nd Report: Position estimation of each drones based on catenary theory and tensile force of tube. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 19–22 February 2018; pp. 217–222. [Google Scholar] [CrossRef]
- Suzuki, M.; Yokota, S.; Imadu, A.; Matsumoto, A.; Chugo, D.; Hashimoto, H. Liquid feeding system using cooperative towing by multiple drones—1st report: Derivation of the flyable range while towing a tube. In Proceedings of the 2017 26th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Lisbon, Portugal, 28–31 August 2017; pp. 1228–1233. [Google Scholar] [CrossRef]
- D’Antonio, D.S.; Cardona, G.A.; Saldaña, D. The Catenary Robot: Design and Control of a Cable Propelled by Two Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3857–3863. [Google Scholar] [CrossRef]
- Sreenath, K.; Kumar, V. Dynamics, control and planning for cooperative manipulation of payloads suspended by cables from multiple quadrotor robots. In Proceedings of the Robotics: Science and Systems (RSS), Berlin, Germany, 24–28 June 2013. [Google Scholar]
- Kotaru, P.; Sreenath, K. Multiple quadrotors carrying a flexible hose: Dynamics, differential flatness and control. IFAC-PapersOnLine 2020, 53, 8832–8839. [Google Scholar] [CrossRef]
- Aström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Estevez, J.; Lopez-Guede, J.M.; Graña, M. Particle Swarm Optimization Quadrotor Control for Cooperative Aerial Transportation of Deformable Linear Objects. Cybern. Syst. 2016, 47, 4–16. [Google Scholar] [CrossRef]
- Estevez, J.; Graña, M.; Lopez-Guede, J.M. Online fuzzy modulated adaptive PD control for cooperative aerial transportation of deformable linear objects. Integr. Comput. Aided Eng. 2017, 24, 41–55. [Google Scholar] [CrossRef]
- Wei, K.; Zhang, L.X.; Ren, A.D. The analysis method of highline cable of alongside replenishment system based on suspended cable theory. In Advanced Materials Research; Trans Tech Publications: Zurich, Switzerland, 2012; Volume 490, pp. 633–637. [Google Scholar]
- Su, Y.; Qiu, Y.; Liu, P. Optimal cable tension distribution of the high-speed redundant driven camera robots considering cable sag and inertia effects. Adv. Mech. Eng. 2014, 6, 729020. [Google Scholar] [CrossRef] [Green Version]
- Hsu, Y.; Pan, C. The static WKB solution to catenary problems with large sag and bending stiffness. Math. Probl. Eng. 2014, 11, 231726. [Google Scholar] [CrossRef] [Green Version]
- Choo, Y.I.; Casarella, M.J. A Survey of Analytical Methods for Dynamic Simulation of Cable-Body Systems. J. Hydronaut. 1973, 7, 137–144. [Google Scholar] [CrossRef]
- Van Nieuwstadt, M.J.; Murray, R.M. Real-time trajectory generation for differentially flat systems. Int. J. Robust Nonlinear Control 1998, 8, 995–1020. [Google Scholar] [CrossRef]
- Andreu, A.; Gil, L.; Roca, P. A new deformable catenary element for the analysis of cable net structures. Comput. Struct. 2006, 84, 1882–1890. [Google Scholar] [CrossRef]
- Li, C.; He, J.; Zhang, Z.; Liu, Y.; Ke, H.; Dong, C.; Li, H. An improved analytical algorithm on main cable system of suspension bridge. Appl. Sci. 2018, 8, 1358. [Google Scholar] [CrossRef] [Green Version]
- Pan, Q.; Yan, D.; Yi, Z. Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges. Appl. Sci. 2018, 8, 2033. [Google Scholar] [CrossRef] [Green Version]
- Skop, R.A.; Choo, Y.I. The configuration of a cable towed in a circular path. J. Aircr. 1971, 8, 856–862. [Google Scholar] [CrossRef]
- Irvine, H.M. Cable Structures; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Clifton, J.M.; Schmidt, L.V.; Stuart, T.D. Dynamic modeling of a trailing wire towed by an orbiting aircraft. J. Guid. Control Dyn. 1995, 18, 875–881. [Google Scholar] [CrossRef]
- Dreyer, T.; Vuuren, J.H.V. A comparison between continuous and discrete modelling of cables with bending stiffness. Appl. Math. Model. 1999, 23, 527–541. [Google Scholar] [CrossRef]
- Yamaguchi, S.; Koterayama, W.; Yokobiki, T. Development of a motion control method for a towed vehicle with a long cable. In Proceedings of the 2000 International Symposium on Underwater Technology (Cat. No. 00EX418), Tokyo, Japan, 26 May 2000; pp. 491–496. [Google Scholar]
- Gobat, J.I.; Grosenbaugh, M.A. Dynamics in the touchdown region of catenary moorings. Int. J. Offshore Polar Eng. 2001, 11, 4. [Google Scholar]
- Turkyilmaz, Y.; Egeland, O. Active depth control of towed cables in 2D. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 1, pp. 952–957. [Google Scholar]
- McKerrow, P.J.; Ratner, D. The design of a tethered aerial robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation 2007, Rome, Italy, 10–14 April 2007; pp. 355–360. [Google Scholar]
- Ren, W.X.; Huang, M.G.; Hu, W.H. A parabolic cable element for static analysis of cable structures. Eng. Comput. 2008, 25, 366–384. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K. A finite differences formulation for the linear and nonlinear dynamics of 2D catenary risers. Ocean. Eng. 2008, 35, 616–636. [Google Scholar] [CrossRef]
- Maza, I.; Kondak, K.; Bernard, M.; Ollero, A. Multi-UAV Cooperation and Control for Load Transportation and Deployment. J. Intell. Robot. Syst. 2009, 57, 417–449. [Google Scholar] [CrossRef]
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2010, 30, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Gouttefarde, M.; Collard, J.F.; Riehl, N.; Baradat, C. Simplified static analysis of large-dimension parallel cable-driven robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 2299–2305. [Google Scholar]
- Jiang, Q.; Kumar, V. Determination and Stability Analysis of Equilibrium Configurations of Objects Suspended From Multiple Aerial Robots. J. Mech. Robot. 2012, 4, 021005. [Google Scholar] [CrossRef]
- Lupashin, S.; D’Andrea, R. Stabilization of a flying vehicle on a taut tether using inertial sensing. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2432–2438. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Gouttefarde, M.; Company, O.; Pierrot, F. On the simplifications of cable model in static analysis of large-dimension cable-driven parallel robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 928–934. [Google Scholar]
- Lee, T. Geometric controls for a tethered quadrotor UAV. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 2749–2754. [Google Scholar] [CrossRef] [Green Version]
- Goodarzi, F.A.; Lee, T. Dynamics and control of quadrotor UAVs transporting a rigid body connected via flexible cables. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4677–4682. [Google Scholar]
- Estevez, J.; Lopez-Guede, J.M.; Graña, M. Quasi-stationary state transportation of a hose with quadrotors. Robot. Auton. Syst. 2015, 63 Pt 2, 187–194. [Google Scholar] [CrossRef]
- Doroudgar, S. Static and Dynamic Modeling and Simulation of the Umbilical Cable in A Tethered Unmanned Aerial System. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2016. [Google Scholar]
- Laranjeira, M.; Dune, C.; Hugel, V. Catenary-based visual servoing for tethered robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 732–738. [Google Scholar]
- Abiko, S.; Kuno, A.; Narasaki, S.; Oosedo, A.; Kokubun, S.; Uchiyama, M. Obstacle avoidance flight and shape estimation using catenary curve for manipulation of a cable hanged by aerial robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, 5–8 December 2017; pp. 2099–2104. [Google Scholar]
- Mansour, A.; Mekki, O.B.; Montassar, S.; Rega, G. Catenary-induced geometric nonlinearity effects on cable linear vibrations. J. Sound Vib. 2018, 413, 332–353. [Google Scholar] [CrossRef]
- Ahmadi-Kashani, K. Development of Cable Elements and Their Applications in the Analysis of Cable Structures. Ph.D. Thesis, University of Manchester Institute of Science and Technology (UMIST), Oxford, MA, USA, 1983. [Google Scholar]
- Tibert, G. Numerical Analyses of Cable Roof Structures. Ph.D. Thesis, KTH, Stockholm, Sweden, 1999. [Google Scholar]
- White, N.N. Evolution of the Design and Modeling of the Eagle System. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2011. [Google Scholar]
- Chaterjee, N.; Nita, B.G. The hanging cable problem for practical applications. Atl. Electron. J. Math. 2010, 4, 70–77. [Google Scholar]
- Perkins, N.; Mote, C., Jr. Three-dimensional vibration of travelling elastic cables. J. Sound Vib. 1987, 114, 325–340. [Google Scholar] [CrossRef]
- Yao, R.; Tang, X.; Wang, J.; Huang, P. Dimensional optimization design of the four-cable-driven parallel manipulator in fast. IEEE/ASME Trans. Mechatron. 2009, 15, 932–941. [Google Scholar] [CrossRef]
- Larsen, L.; Pham, V.L.; Kim, J.; Kupke, M. Collision-free path planning of industrial cooperating robots for aircraft fuselage production. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2042–2047. [Google Scholar]
- Hatibovic, A.; Kádár, P. The application of autonomous drones in the environment of overhead lines. In Proceedings of the 2018 IEEE 18th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 21–22 November 2018; pp. 289–294. [Google Scholar]
- Oh, J.; Lee, C. 3D power line extraction from multiple aerial images. Sensors 2017, 17, 2244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, X. An overview of the development for cable-driven parallel manipulator. Adv. Mech. Eng. 2014, 6, 823028. [Google Scholar] [CrossRef] [Green Version]
- Qiu, H.; Duan, H. Pigeon interaction mode switch-based UAV distributed flocking control under obstacle environments. ISA Trans. 2017, 71, 93–102. [Google Scholar] [CrossRef]
- Cruz, P.J.; Fierro, R. Cable-suspended load lifting by a quadrotor UAV: Hybrid model, trajectory generation, and control. Auton. Robot. 2017, 41, 1629–1643. [Google Scholar] [CrossRef]
- Kang, Y.; Hedrick, J.K. Linear tracking for a fixed-wing UAV using nonlinear model predictive control. IEEE Trans. Control Syst. Technol. 2009, 17, 1202–1210. [Google Scholar] [CrossRef]
- Pruner, E.; Necsulescu, D.; Sasiadek, J.; Kim, B. Control of decentralized geometric formations of mobile robots. In Proceedings of the 2012 17th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2012; pp. 627–632. [Google Scholar]
- Brandão, A.S.; Sarcinelli-Filho, M. On the guidance of multiple uav using a centralized formation control scheme and delaunay triangulation. J. Intell. Robot. Syst. 2016, 84, 397–413. [Google Scholar] [CrossRef]
- Lee, T.; Sreenath, K.; Kumar, V. Geometric control of cooperating multiple quadrotor UAVs with a suspended payload. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 5510–5515. [Google Scholar]
- Mercado, D.A.; Castro, R.; Lozano, R. Quadrotors flight formation control using a leader-follower approach. In Proceedings of the 2013 European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013. [Google Scholar]
- Wen, N.; Zhao, L.; Su, X.; Ma, P. UAV online path planning algorithm in a low altitude dangerous environment. IEEE/CAA J. Autom. Sin. 2015, 2, 173–185. [Google Scholar] [CrossRef]
- Yeh, F.K. Attitude controller design of mini-unmanned aerial vehicles using fuzzy sliding-mode control degraded by white noise interference. Control. Theory Appl. IET 2012, 6, 1205–1212. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Liu, Z.; Mohammadzadeh, A.; Turabieh, H.; Mafarja, M.; Band, S.S.; Mosavi, A. A new online learned interval type-3 fuzzy control system for solar energy management systems. IEEE Access 2021, 9, 10498–10508. [Google Scholar] [CrossRef]
- Mosavi, A.; Qasem, S.N.; Shokri, M.; Band, S.S.; Mohammadzadeh, A. Fractional-order fuzzy control approach for photovoltaic/battery systems under unknown dynamics, variable irradiation and temperature. Electronics 2020, 9, 1455. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| mass, m | 0.5 kg |
| arm length, l | 25 cm |
| inertia moments, | |
| inertia moment, | |
| propeller thrust coefficient, b | |
| drag, d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estevez, J.; Lopez-Guede, J.M.; Garate, G.; Graña, M. Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors. Appl. Sci. 2022, 12, 5253. https://doi.org/10.3390/app12105253
Estevez J, Lopez-Guede JM, Garate G, Graña M. Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors. Applied Sciences. 2022; 12(10):5253. https://doi.org/10.3390/app12105253
Chicago/Turabian StyleEstevez, Julian, Jose Manuel Lopez-Guede, Gorka Garate, and Manuel Graña. 2022. "Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors" Applied Sciences 12, no. 10: 5253. https://doi.org/10.3390/app12105253
APA StyleEstevez, J., Lopez-Guede, J. M., Garate, G., & Graña, M. (2022). Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors. Applied Sciences, 12(10), 5253. https://doi.org/10.3390/app12105253







