Prediction of EPB Shield Tunneling Advance Rate in Mixed Ground Condition Using Optimized BPNN Model
Abstract
:1. Introduction
2. Methodology and Strategy
2.1. Multivariate Linear Regression
2.2. K-Nearest Neighbor
2.3. Support Vector Regression
2.4. Classification and Regression Tree
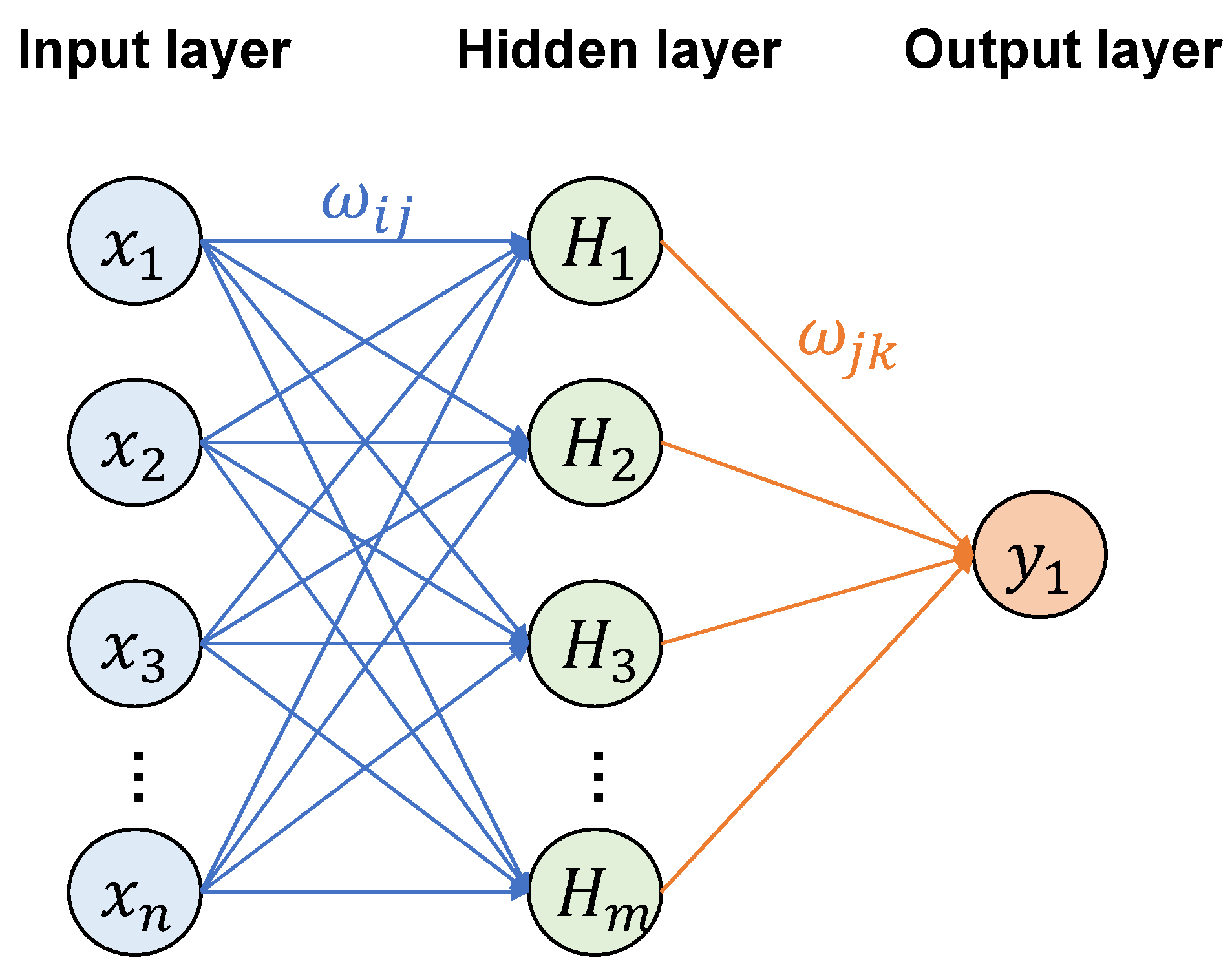
2.5. Back-Propagation Neural Network
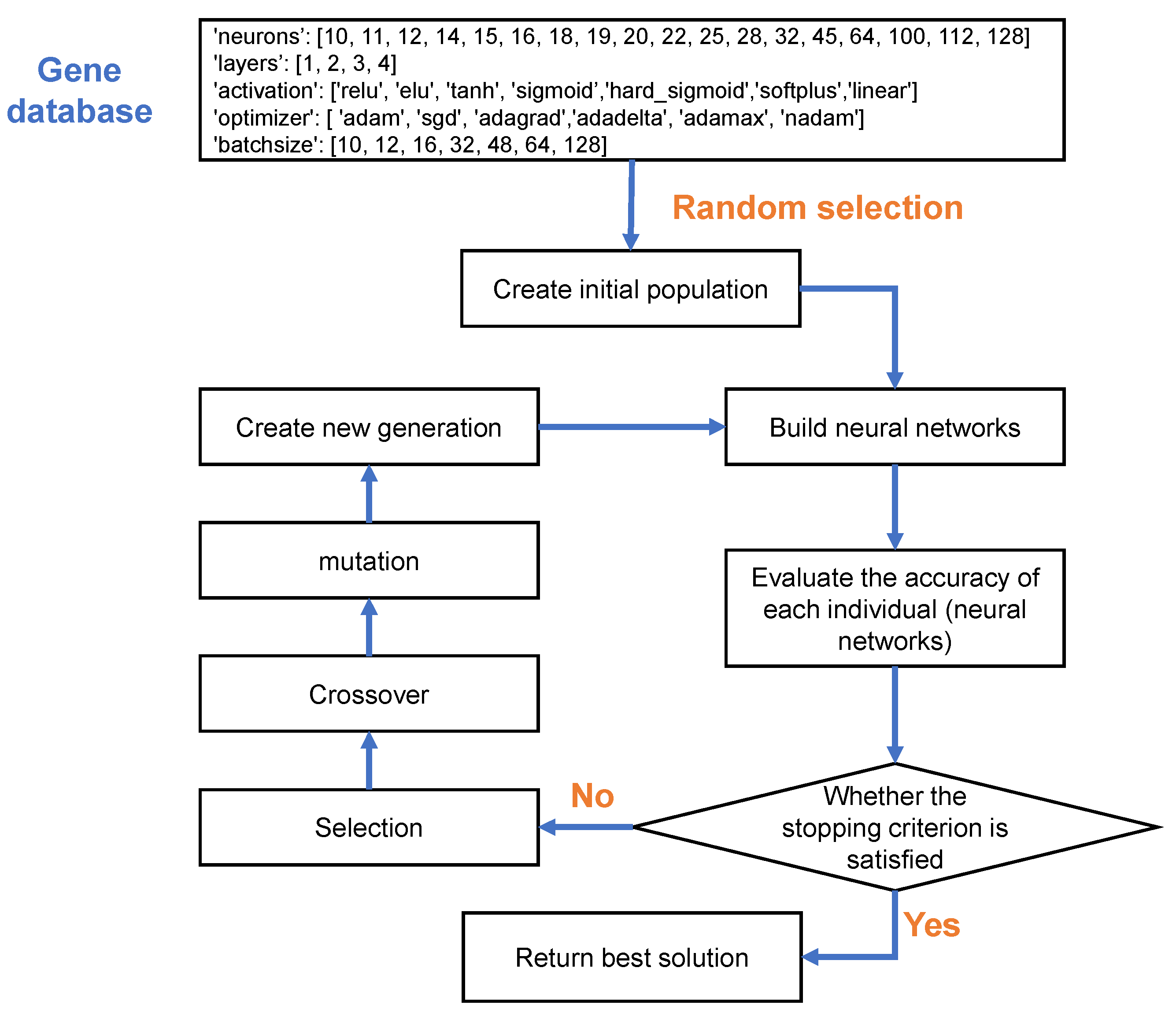
2.6. Genetic Algorithm
- Initialization: During the initialization process, the model will randomly select genes from the gene pool to form the chromosome. The random selection will increase the diversity of the population.
- Evaluation: The fitness (cost) function is then used to evaluate each chromosome to determine the fitness value.
- Selection: In this process, the model will select the superior individuals from the group and eliminate the inferior individuals. The purpose is to directly inherit the optimized individuals to the next generation or generate new individuals through pairing and crossover and then inherit them to the next generation, so as to continuously find the optimal one.
- Crossover: Just like genetic recombination in nature, it replaces and recombines part of the genes of two parent individuals to generate a new individual. Through crossover, the search ability of genetic algorithm can be improved by leaps and bounds;
- Mutation: This step will make changes in gene values at certain loci of individual strings of the population, by introducing another level of randomness. This will effectively avoid the model falling into the dilemma of local optimum.
- End: When the fitness of the optimal individual reaches a given threshold, or the fitness of the optimal individual and the fitness of the group no longer rise, or the number of iterations reaches a preset number of generations, the algorithm terminates.
2.7. Strategies for Mixed Ground
3. Case Study
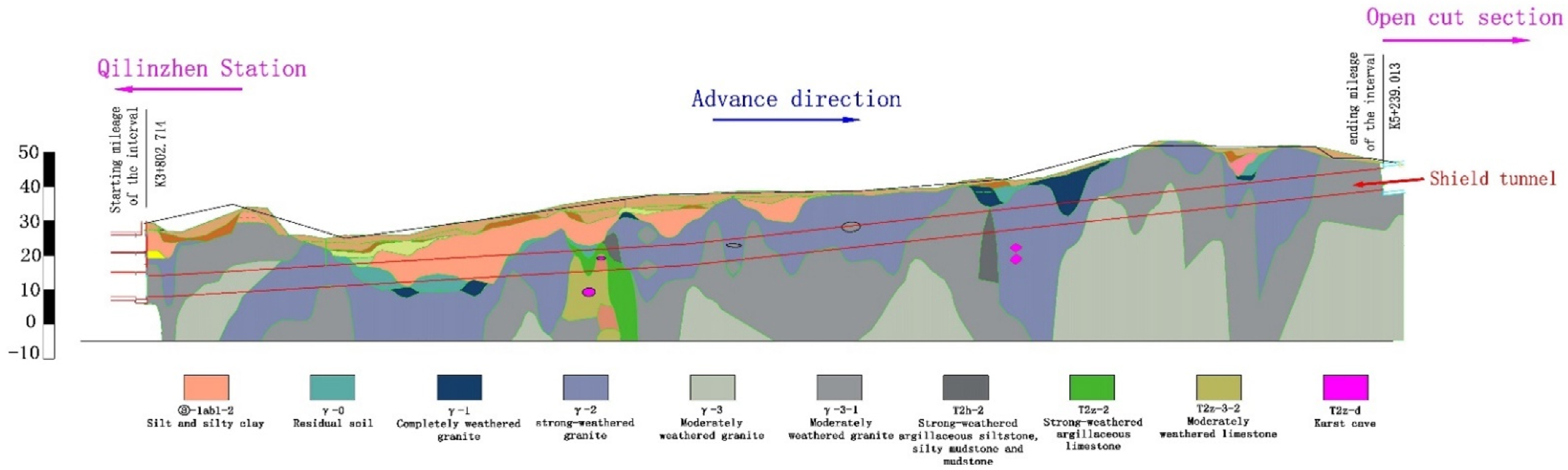
3.1. Project Description
3.2. Data Processing
3.3. Model Establishment
3.4. Assessment Index
4. Results and Discussion
4.1. Best BPNN Framework for Each Strategy
4.2. Model Assessment
4.3. Optimum Solution for Mixed Ground
4.4. AR Prediction Results
5. Conclusions
- It was feasible to combine genetic algorithm with back-propagation neural network. By optimizing the combination of hyperparameters, it can quickly find the best network structure and help the neural network achieve the best prediction effect.
- Compared with the other four models, the BPNN model provided the best performances. With the help of genetic algorithm, the optimal combination of model hyperparameters can be found in a short time.
- Shield tunneling parameter data of 1188 rings, combined with the geological parameter data obtained from the geological exploration, were used to train and test the models. Four error indicators were employed and the results showed that the model obtained by MLR had the worst fitting effect, while BPNN had a strong learning ability. The performance of the BPNN model was significantly better than the other four models, so the BPNN model was determined as the optimal advance rate prediction model in this study.
- Five strategies were proposed to solve the mixed ground engineering puzzle. The only difference between them was the treatment of the geological parameters of the mixed ground. After comparison, the best prediction was achieved by Strategy B, which took the geological parameters of the upper and lower layer as input, and introduced the parameter of the composite ratio at the same time. This provided a reference for the selection of input parameters for our subsequent model establishment of shield tunneling parameter prediction in mixed ground.
- A sample of 238 rings of data was randomly selected to test the performance of the model. The results showed that the BPNN obtained in scheme B can effectively predict the AR, and the R2 reached 0.920, which can be used for prediction and control of construction tunneling parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Su, C.; Qin, Q.; Cai, Z.; Hou, Z.; Kang, Y. Modeling and prediction for the thrust on EPB TBMs under different geological conditions by considering mechanical decoupling. Sci. China Technol. Sci. 2016, 59, 1428–1434. [Google Scholar] [CrossRef]
- Gong, Q.; Yin, L.; Ma, H.; Zhao, J. TBM Tunnelling under adverse geological conditions: An overview. Tunn. Undergr. Space Technol. 2016, 57, 4–17. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, J.S.; Chai, J.C.; Zhou, A. Analysis of disc cutter failure in shield tunnelling using 3D circular cutting theory. Eng. Fail. Anal. 2018, 90, 23–35. [Google Scholar] [CrossRef]
- Rehman, H.; Naji, A.M.; Nam, K.; Ahmad, S.; Muhammad, K.; Yoo, H.-K. Impact of Construction Method and Ground Composition on Headrace Tunnel Stability in the Neelum–Jhelum Hydroelectric Project: A Case Study Review from Pakistan. Appl. Sci. 2021, 11, 1655. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, X.; Shahrour, I. Deep learning model for shield tunneling advance rate prediction in mixed ground condition considering past operations. IEEE Access 2020, 8, 215310–215326. [Google Scholar] [CrossRef]
- Lin, S.S.; Zhang, N.; Zhou, A.; Shen, S.L. Time-series prediction of shield movement performance during tunneling based on hybrid model. Tunn. Undergr. Space Technol. 2022, 119, 104245. [Google Scholar] [CrossRef]
- Rostami, J. Development of a Force Estimation Model for Rock Fragmentation with Disc Cutters through Theoretical Modeling and Physical Measurement of Crushed Zone Pressure. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 1997. [Google Scholar]
- Shi, H.; Yang, H.; Gong, G.; Wang, L. Determination of the cutterhead torque for EPB shield tunneling machine. Autom. Constr. 2011, 20, 1087–1095. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Ryu, H.; Rehman, H.; Jafri, T.H.; Yoo, H.; Ha, S. Estimation Method for TBM Cutterhead Drive Design Based on Full-Scale Tunneling Tests for Application in Utility Tunnels. Appl. Sci. 2020, 10, 5187. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, Q.; Tian, Z.; Zhou, S.; Jiang, H. Torque fluctuation analysis and penetration prediction of EPB TBM in rock–soil interface mixed ground. Tunn. Undergr. Space Technol. 2019, 91, 103002. [Google Scholar] [CrossRef]
- Alsahly, A.; Stascheit, J.; Meschke, G. Advanced finite element modeling of excavation and advancement processes in mechanized tunneling. Adv. Eng. Softw. 2016, 100, 198–214. [Google Scholar] [CrossRef]
- Lee, H.; Choi, H.; Choi, S.W.; Chang, S.H.; Kang, T.H.; Lee, C. Numerical simulation of EPB shield tunnelling with TBM operational condition control using coupled DEM–FDM. Appl. Sci. 2021, 11, 2551. [Google Scholar] [CrossRef]
- Sheil, B.B.; Suryasentana, S.K.; Mooney, M.A.; Zhu, H. Machine learning to inform tunnelling operations: Recent advances and future trends. Proc. Inst. Civ. Eng. Smart Infrastruct. Constr. 2020, 173, 74–95. [Google Scholar] [CrossRef]
- Yagiz, S.; Gokceoglu, C.; Sezer, E.; Iplikci, S. Application of two non-linear prediction tools to the estimation of tunnel boring machine performance. Eng. Appl. Artif. Intell. 2009, 22, 808–814. [Google Scholar] [CrossRef]
- Mobarra, Y.; Hajian, A.; Rahgozar, M. Application of artificial neural networks to the prediction of TBM penetration rate in TBM-driven golab water transfer tunnel. In Proceedings of the International Conference on Civil Engineering Architecture & Urban Sustainable Development, Tabriz, Iran, 27–28 November 2013; Volume 27. [Google Scholar]
- Salimi, A.; Moormann, C.; Singh, T.; Jain, P. TBM Performance Prediction in rock tunneling using various artificial intelligence algorithms. In Proceedings of the 11th Iranian and 2nd Regional Tunnelling Conference “Tunnels and the Future”, Tehran, Iran, 2–5 November 2015. [Google Scholar]
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Kang, X.; Zhong, Z.; Liu, Y.; Wu, H. Prediction of maximum surface settlement caused by earth pressure balance (EPB) shield tunneling with ANN Methods. Soils Found. 2019, 59, 284–295. [Google Scholar] [CrossRef]
- Gao, X.; Shi, M.; Song, X.; Zhang, C.; Zhang, H. Recurrent neural networks for real-time prediction of TBM operating parameters. Autom. Constr. 2019, 98, 225–235. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, C.; Yao, Z.; Jiang, H.; Zhang, T.; Guan, Y. Prediction of TBM Tunneling Parameters through an LSTM neural network. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 702–707. [Google Scholar]
- Tóth, Á.; Gong, Q.; Zhao, J. Case studies of TBM tunneling performance in rock–soil interface mixed Ground. Tunn. Undergr. Space Technol. 2013, 38, 140–150. [Google Scholar] [CrossRef]
- Zhou, X.; Zhai, S. Estimation of the cutterhead torque for earth pressure balance TBM under mixed-face conditions. Tunn. Undergr. Space Technol. 2018, 74, 217–229. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhou, J.; Bejarbaneh, B.Y.; Armaghani, D.J.; Tahir, M.M. Forecasting of TBM advance rate in hard rock condition based on artificial neural network and genetic programming techniques. Bull. Eng. Geol. Environ. 2020, 79, 2069–2084. [Google Scholar] [CrossRef]
- Sampson, J.R. Adaptation in natural and artificial systems (John H. Holland). SIAM Rev. 1976, 18, 529–530. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar] [CrossRef]
- Whitley, D. A Genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Supervised machine learning techniques to the prediction of tunnel boring machine penetration rate. Appl. Sci. 2019, 9, 3715. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, S.; Mooney, M.A. Predicting EPBM advance rate performance using support vector regression modeling. Tunn. Undergr. Space Technol. 2020, 104, 103520. [Google Scholar] [CrossRef]

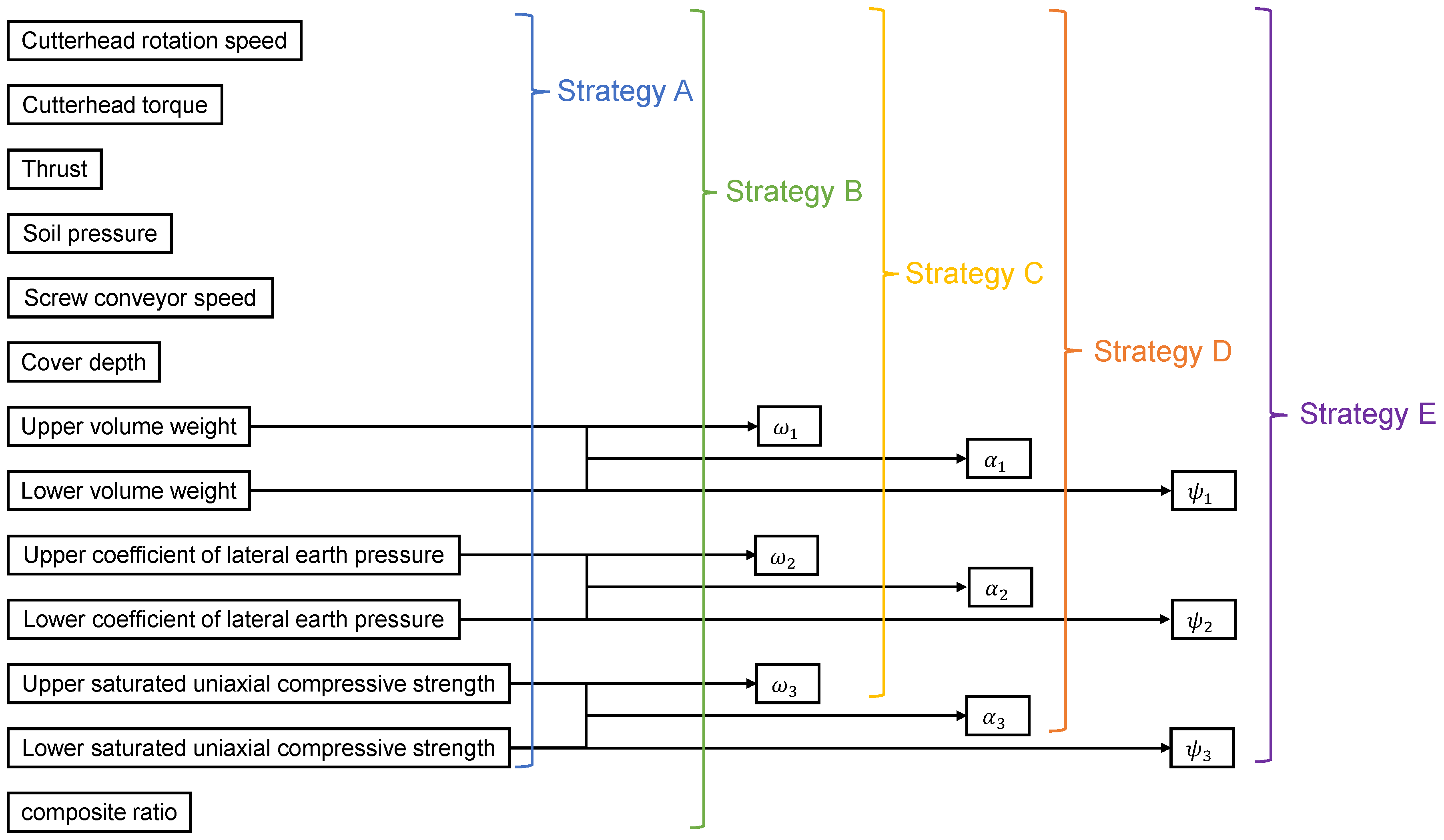

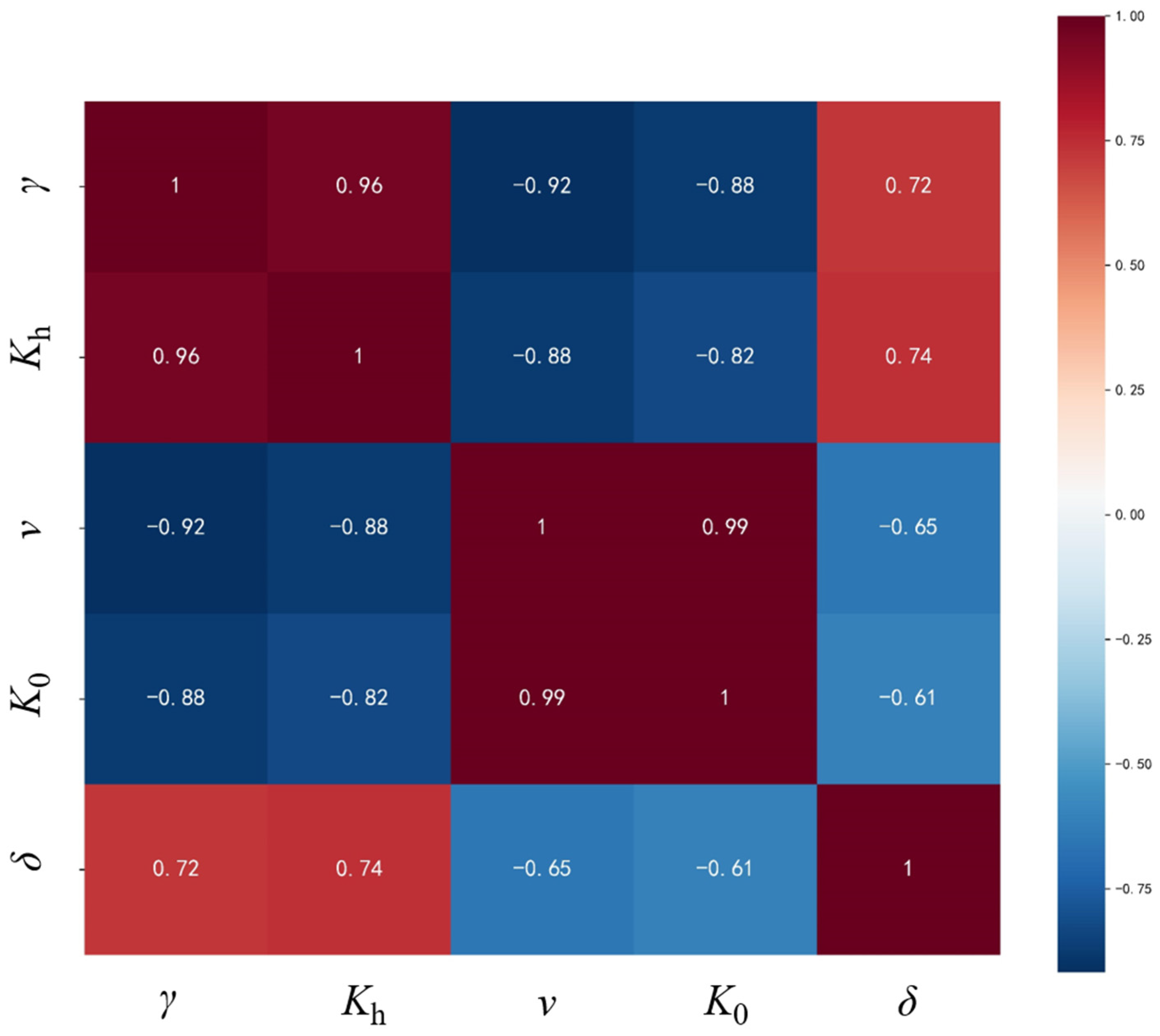
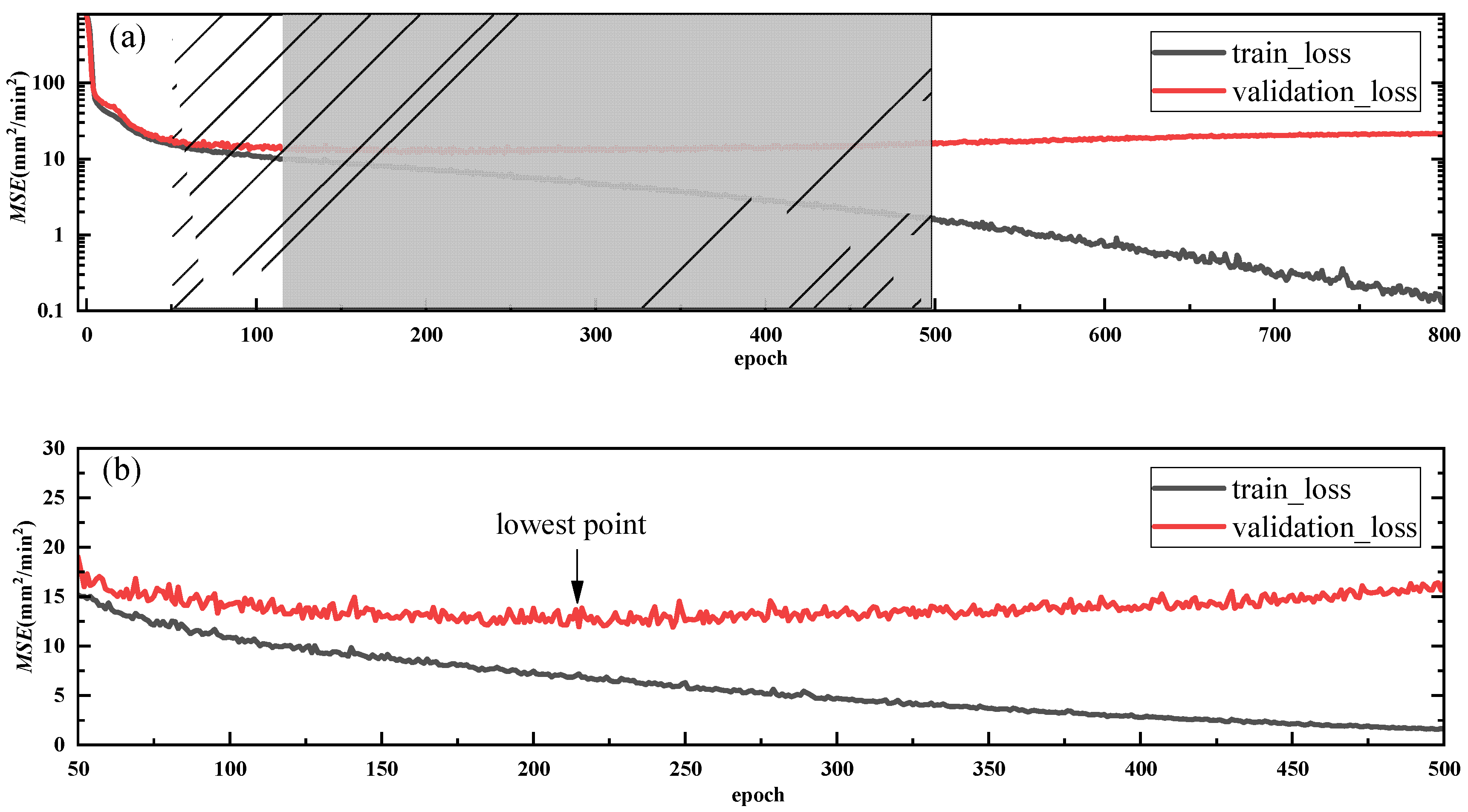

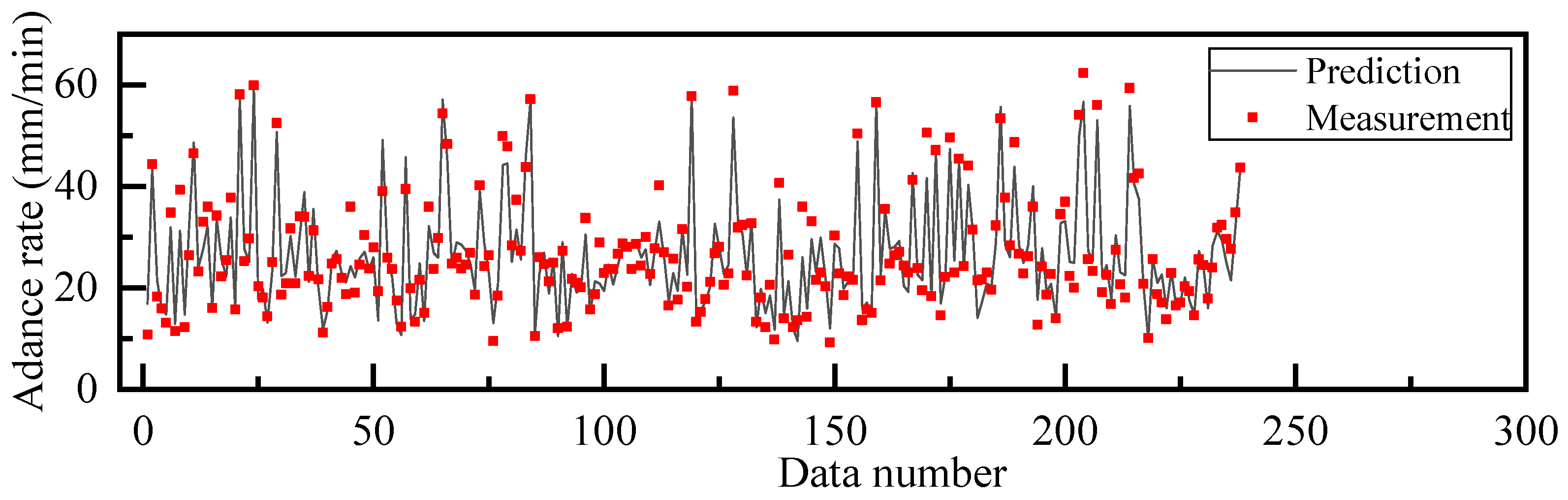
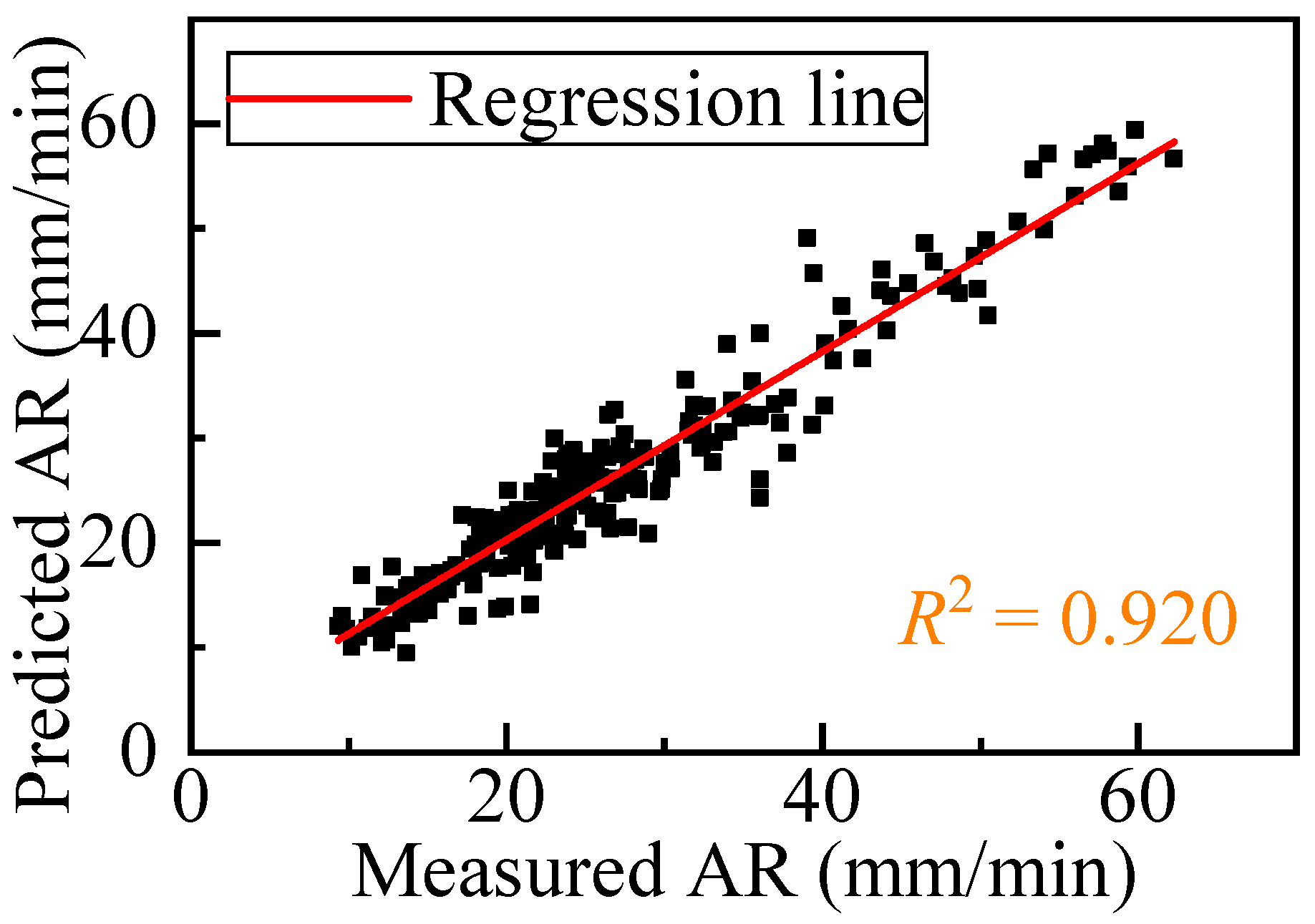

| Parameter | Unit | Strategy A | Strategy B | Strategy C | Strategy D | Strategy E |
|---|---|---|---|---|---|---|
| Cutterhead rotation speed (CS) | r/min | x1 | x1 | x1 | x1 | x1 |
| Cutterhead torque (CT) | KN·m | x2 | x2 | x2 | x2 | x2 |
| Thrust (T) | KN | x3 | x3 | x3 | x3 | x3 |
| Soil pressure (SP) | MPa | x4 | x4 | x4 | x4 | x4 |
| Screw conveyor speed (SS) | r/min | x5 | x5 | x5 | x5 | x5 |
| Cover depth (CD) | m | x6 | x6 | x6 | x6 | x6 |
| Upper volume weight (γu) | KN/m3 | x7 | x7 | |||
| Upper coefficient of lateral earth pressure (K0u) | / | x8 | x8 | |||
| Upper saturated uniaxial compressive strength (δu) | MPa | x9 | x9 | |||
| Lower volume weight (γd) | KN/m3 | x10 | x10 | |||
| Lower coefficient of lateral earth pressure (K0d) | / | x11 | x11 | |||
| Lower saturated uniaxial compressive strength (δd) | MPa | x12 | x12 | |||
| composite ratio (p) | / | x13 | ||||
| Comprehensive volume weight (ω1) | KN/m3 | x7 | ||||
| Comprehensive coefficient of lateral earth pressure (ω2) | / | x8 | ||||
| Comprehensive saturated uniaxial compressive strength (ω3) | MPa | x9 | ||||
| Comprehensive volume weight (α1) | KN/m3 | x7 | ||||
| Comprehensive coefficient of lateral earth pressure (α2) | / | x8 | ||||
| Comprehensive saturated uniaxial compressive strength (α3) | MPa | x9 | ||||
| Maximum volume weight (ψ1) | KN/m3 | x7 | ||||
| Maximum coefficient of lateral earth pressure (ψ2) | / | x8 | ||||
| Maximum saturated uniaxial compressive strength (ψ3) | MPa | x9 | ||||
| Advance rate (AR) | mm/min | y | y | y | y | y |
| Number | Name | γ | Kh | δ | ν | K0 | E | C | φ |
|---|---|---|---|---|---|---|---|---|---|
| KN/m3 | MPa/m | MPa | -- | -- | MPa | MPa | ° | ||
| ③-1ab1-2 | Silt and silty clay | 19.9 | 34 | -- | 0.32 | 0.46 | -- | 40.5 | 18.4 |
| γ-0 | Residual soil | 19.6 | 24 | -- | 0.31 | 0.45 | -- | 27 | 16 |
| γ-1 | Completely weathered granite | 20.6 | 40 | 16 | 0.3 | 0.42 | -- | 28 | 18 |
| γ-2 | strong-weathered granite | 22.5 | 100 | 39.06 | 0.29 | 0.41 | -- | 35 | 21 |
| γ-3 | Moderately weathered granite | 25.8 | 350 | 40.43 | 0.2 | 0.25 | 6000 | -- | -- |
| γ-3-1 | Moderately weathered granite | 25.1 | 280 | 38.49 | 0.21 | 0.26 | 3500 | -- | -- |
| T2h-2 | Strong-weathered argillaceous siltstone, silty mudstone, and mudstone | 21.5 | 90 | 0.49 | 0.29 | 0.41 | -- | 34 | 20 |
| T2z-2 | Strong-weathered argillaceous limestone | 21.5 | 90 | 2.73 | 0.29 | 0.41 | -- | 34 | 20 |
| T2z-3-2 | Moderately weathered limestone | 23.4 | 200 | 3.1 | 0.25 | 0.33 | 1500 | -- | -- |
| Dataset | Parameter | Unit | Mean | Std. | Min. | Max. |
|---|---|---|---|---|---|---|
| Training Set (950) | Cutterhead rotation speed (CS) | r/min | 1.28 | 0.07 | 1.00 | 1.54 |
| Cutterhead torque (CT) | KN·m | 3260.83 | 915.94 | 893.04 | 5401.23 | |
| Thrust (T) | KN | 11,751.07 | 2362.87 | 5522.75 | 19,048.84 | |
| Soil pressure (SP) | bar | 0.55 | 0.36 | 0.09 | 1.88 | |
| Screw conveyor speed (SS) | r/min | 4.07 | 1.84 | 0.21 | 10.12 | |
| Advance rate (AR) | mm/min | 27.07 | 10.47 | 9.07 | 66.79 | |
| Test Set (238) | Cutterhead rotation speed (CS) | r/min | 1.28 | 0.07 | 1.09 | 1.57 |
| Cutterhead torque (CT) | KN·m | 3309.93 | 1020.57 | 1007.39 | 5390.16 | |
| Thrust (T) | KN | 11,778.58 | 2294.79 | 6652.89 | 19,238.06 | |
| Soil pressure (SP) | bar | 0.57 | 0.39 | 0.10 | 1.90 | |
| Screw conveyor speed (SS) | r/min | 3.89 | 1.83 | 0.42 | 9.01 | |
| Advance rate (AR) | mm/min | 26.87 | 11.54 | 9.30 | 62.29 |
| Strategy/Parameters | Network Structure | Activation | Optimizer | Batch Size |
|---|---|---|---|---|
| Strategy A | [100, 112] | tanh | adam | 32 |
| Strategy B | [112, 128] | tanh | adam | 12 |
| Strategy C | [112, 112] | relu | nadam | 10 |
| Strategy D | [112, 112] | relu | adam | 10 |
| Strategy E | [112, 128] | tanh | nadam | 32 |
| Strategy | Model | Training Set (mm/min) | Test Set (mm/min) | ||
|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | ||
| A | MLR | 3.923 | 5.178 | 4.234 | 5.617 |
| KNN | 2.756 | 3.644 | 3.664 | 4.735 | |
| SVR | 3.026 | 4.183 | 3.740 | 4.753 | |
| CART | 2.754 | 3.639 | 3.590 | 4.663 | |
| BPNN | 1.948 | 2.595 | 2.742 | 3.552 | |
| B | MLR | 3.923 | 5.177 | 4.232 | 5.613 |
| KNN | 2.702 | 3.571 | 3.548 | 4.609 | |
| SVR | 2.984 | 4.206 | 3.722 | 4.822 | |
| CART | 2.736 | 3.621 | 3.737 | 4.995 | |
| BPNN | 1.768 | 2.480 | 2.411 | 3.249 | |
| C | MLR | 3.980 | 5.346 | 4.216 | 5.665 |
| KNN | 2.756 | 3.680 | 3.587 | 4.565 | |
| SVR | 3.067 | 4.234 | 3.721 | 4.699 | |
| CART | 2.433 | 3.343 | 3.754 | 4.885 | |
| BPNN | 2.251 | 3.016 | 2.960 | 3.724 | |
| D | MLR | 3.980 | 5.346 | 4.212 | 5.669 |
| KNN | 2.744 | 3.672 | 3.596 | 4.583 | |
| SVR | 3.059 | 4.214 | 3.714 | 4.689 | |
| CART | 1.970 | 2.833 | 3.892 | 5.098 | |
| BPNN | 2.097 | 2.814 | 2.853 | 3.618 | |
| E | MLR | 4.064 | 5.388 | 4.254 | 5.732 |
| KNN | 2.734 | 3.630 | 3.744 | 4.791 | |
| SVR | 3.074 | 4.224 | 3.746 | 4.724 | |
| CART | 2.818 | 3.682 | 3.793 | 4.884 | |
| BPNN | 1.996 | 2.659 | 2.889 | 3.700 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Gong, Q.; Wu, Y.; Zhao, Y.; Li, H. Prediction of EPB Shield Tunneling Advance Rate in Mixed Ground Condition Using Optimized BPNN Model. Appl. Sci. 2022, 12, 5485. https://doi.org/10.3390/app12115485
Fu X, Gong Q, Wu Y, Zhao Y, Li H. Prediction of EPB Shield Tunneling Advance Rate in Mixed Ground Condition Using Optimized BPNN Model. Applied Sciences. 2022; 12(11):5485. https://doi.org/10.3390/app12115485
Chicago/Turabian StyleFu, Xuesong, Quanmei Gong, Yaojie Wu, Yu Zhao, and Hui Li. 2022. "Prediction of EPB Shield Tunneling Advance Rate in Mixed Ground Condition Using Optimized BPNN Model" Applied Sciences 12, no. 11: 5485. https://doi.org/10.3390/app12115485
APA StyleFu, X., Gong, Q., Wu, Y., Zhao, Y., & Li, H. (2022). Prediction of EPB Shield Tunneling Advance Rate in Mixed Ground Condition Using Optimized BPNN Model. Applied Sciences, 12(11), 5485. https://doi.org/10.3390/app12115485






