A Practical Harmonic Admittance Matrix Derivation Approach for Fluctuating Power Photovoltaic Systems
Abstract
:1. Introduction
2. Methodology
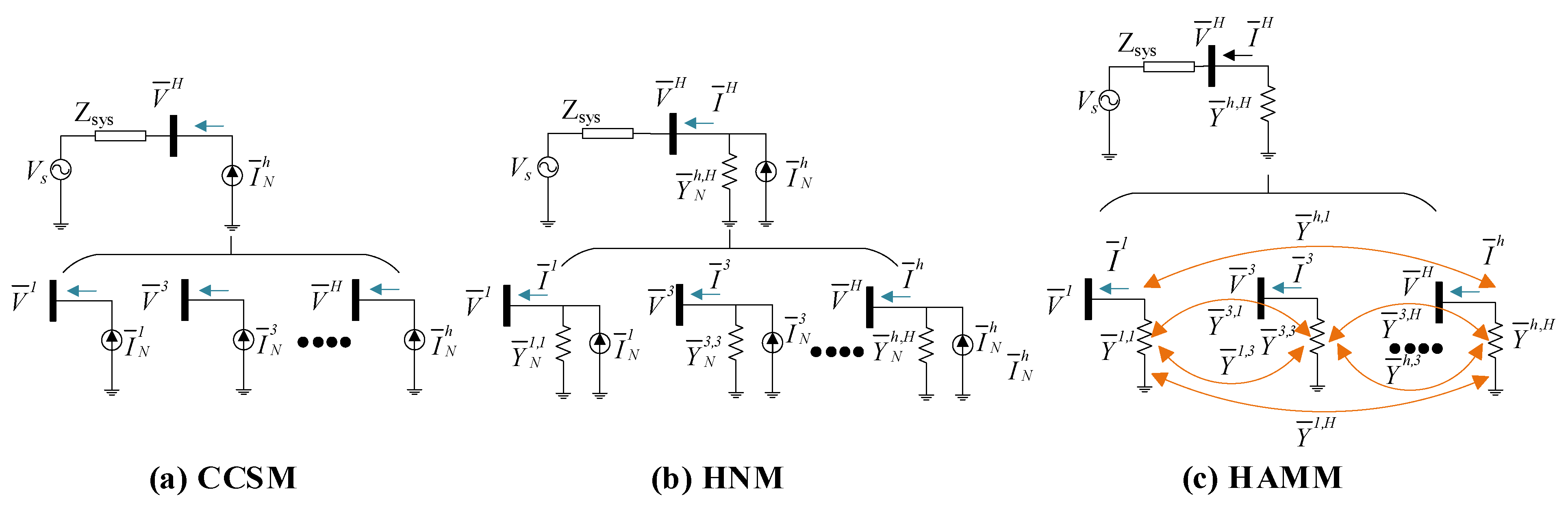
2.1. Conventional HAM Derivation Approach
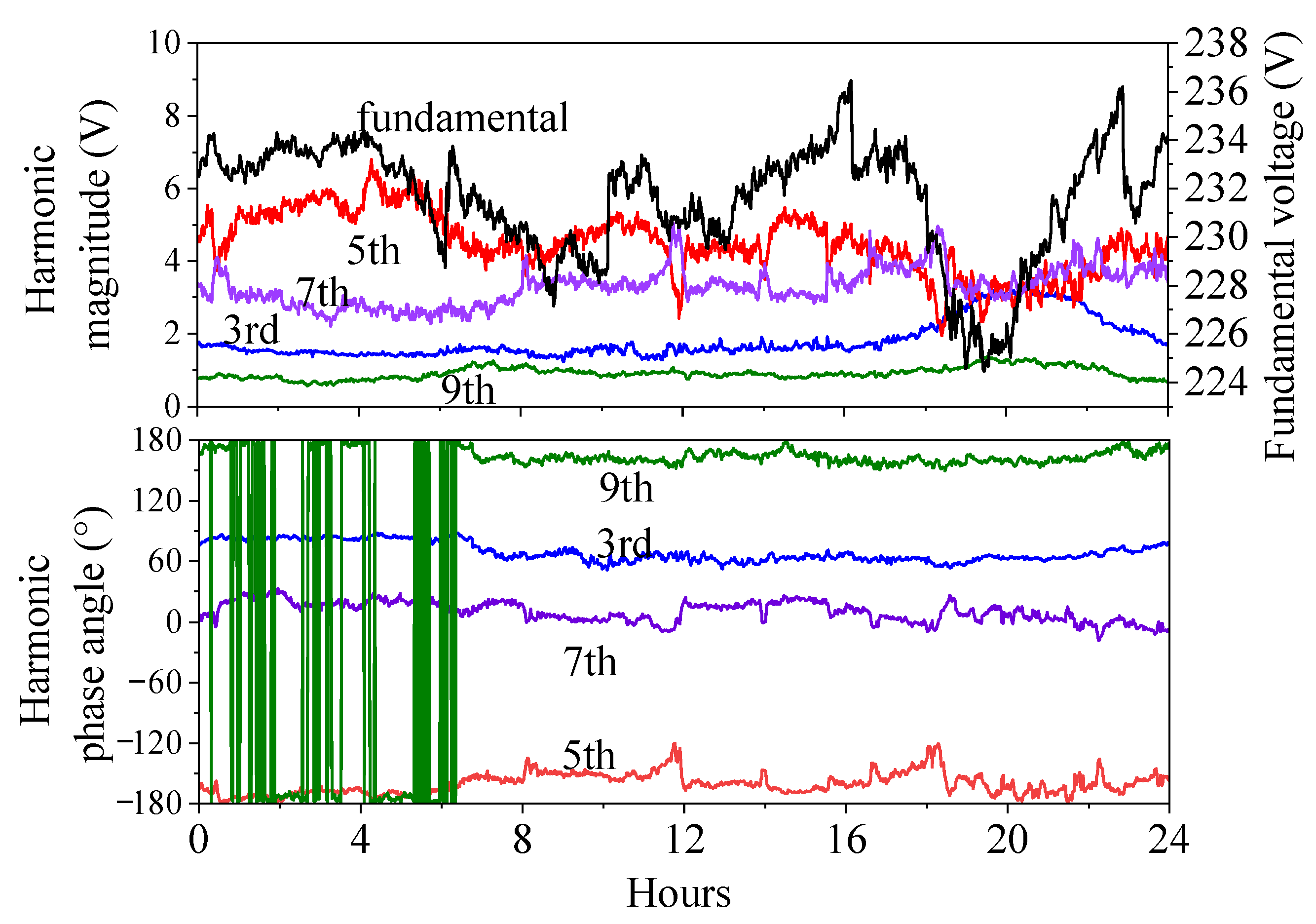
2.2. Harmonic Generation and Grid Interaction Mechanism of Rooftop PV Systems
2.3. The Power Dependency Evalution of HAM by Laboratory Tests
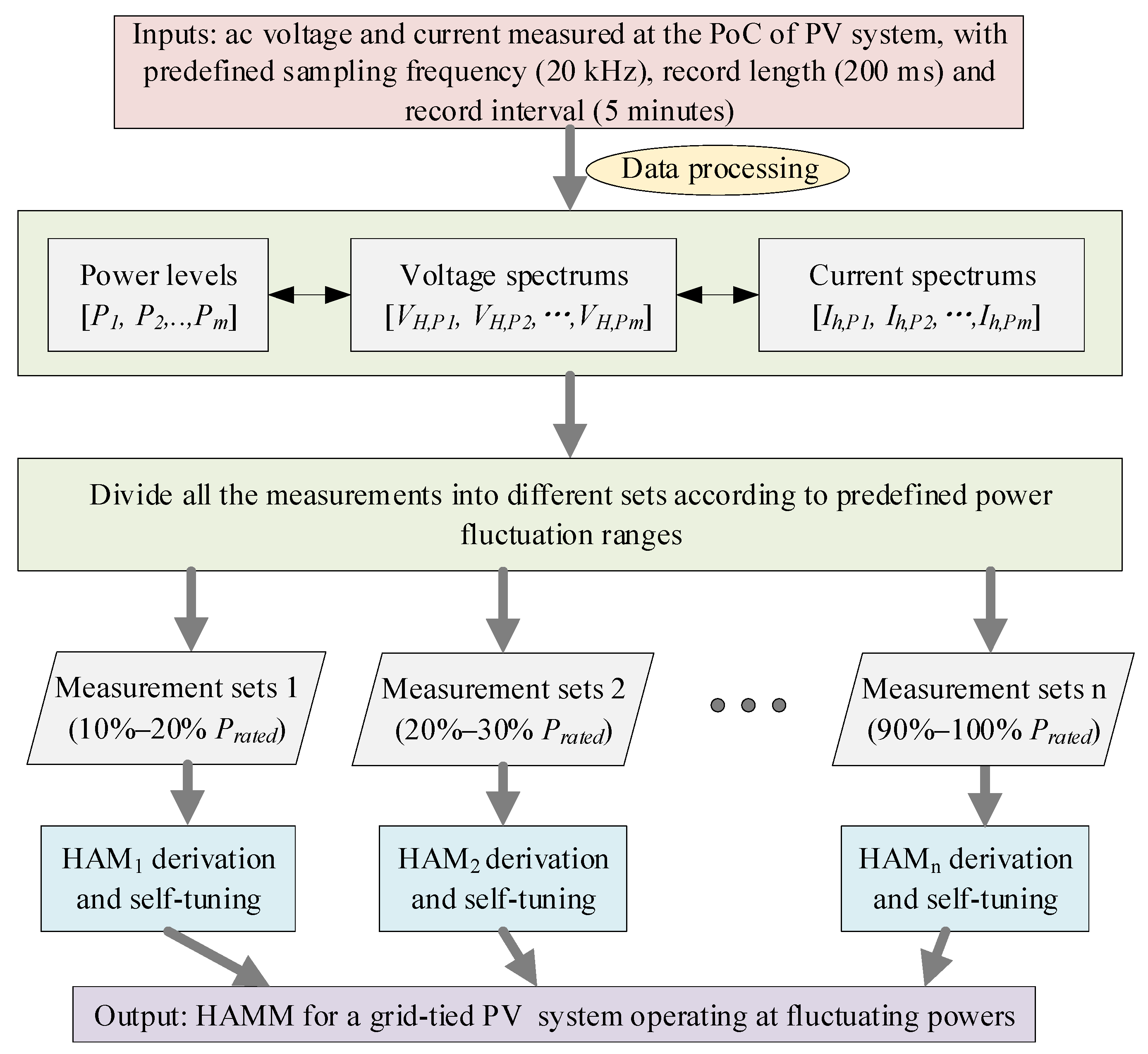
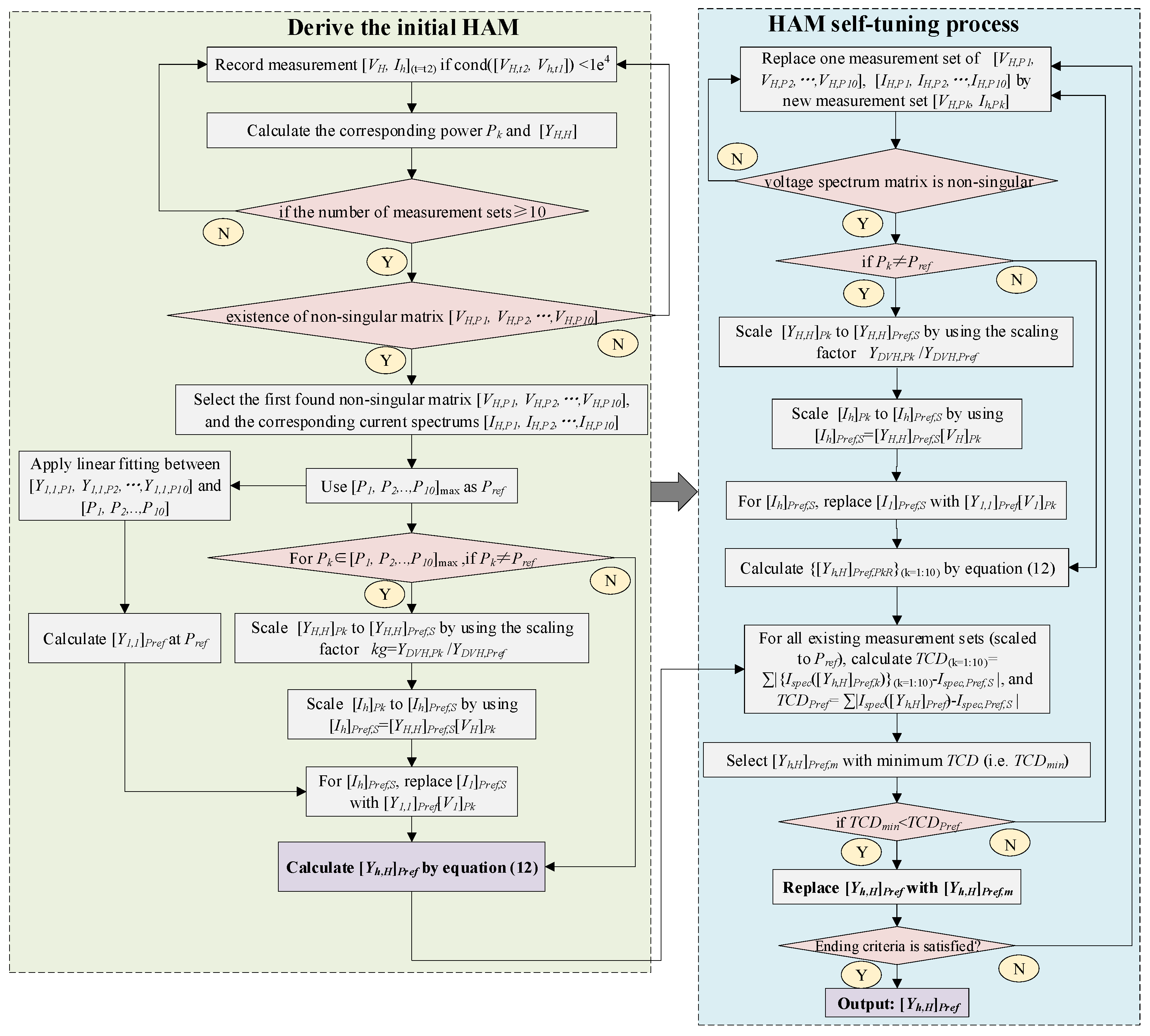
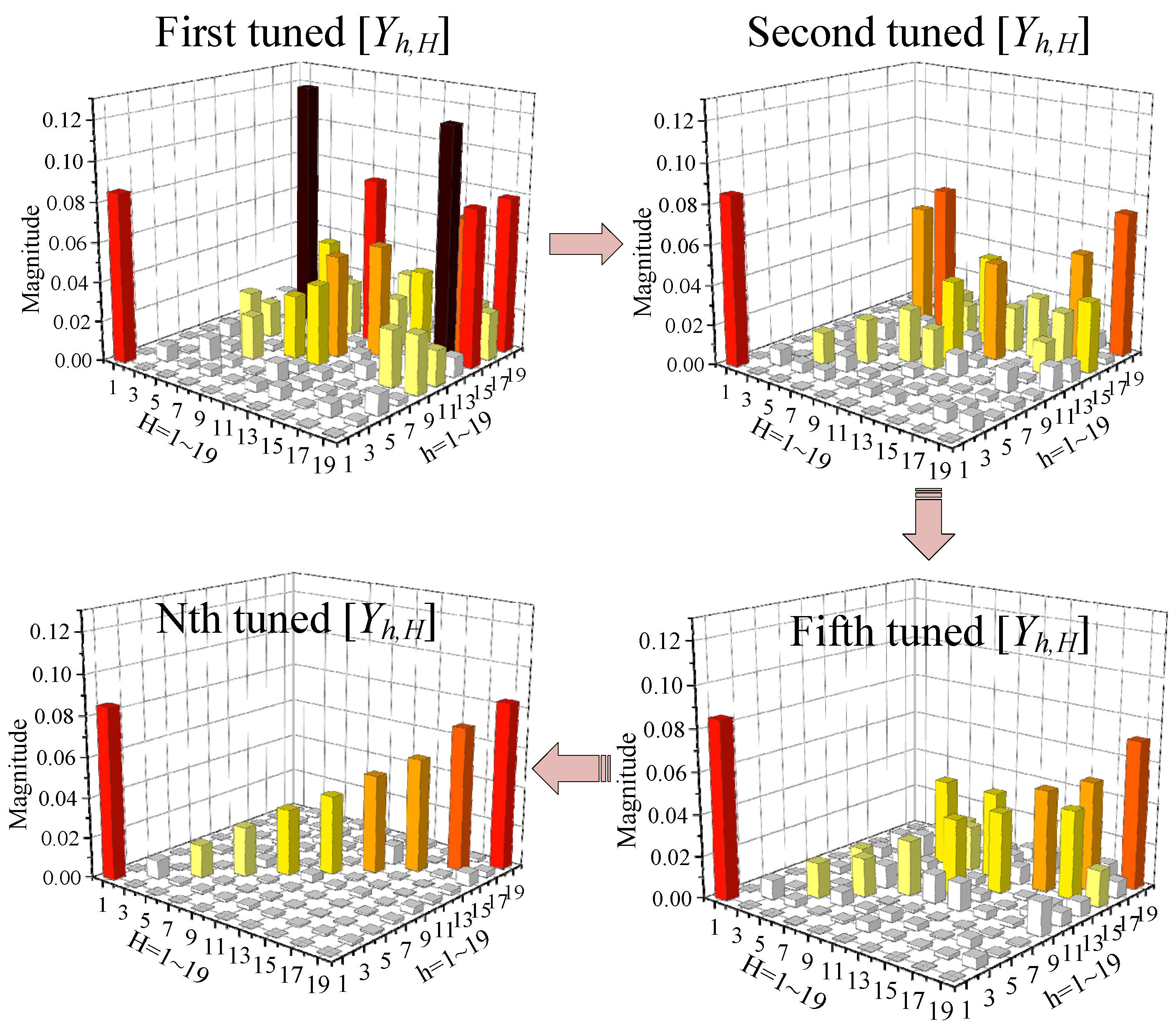
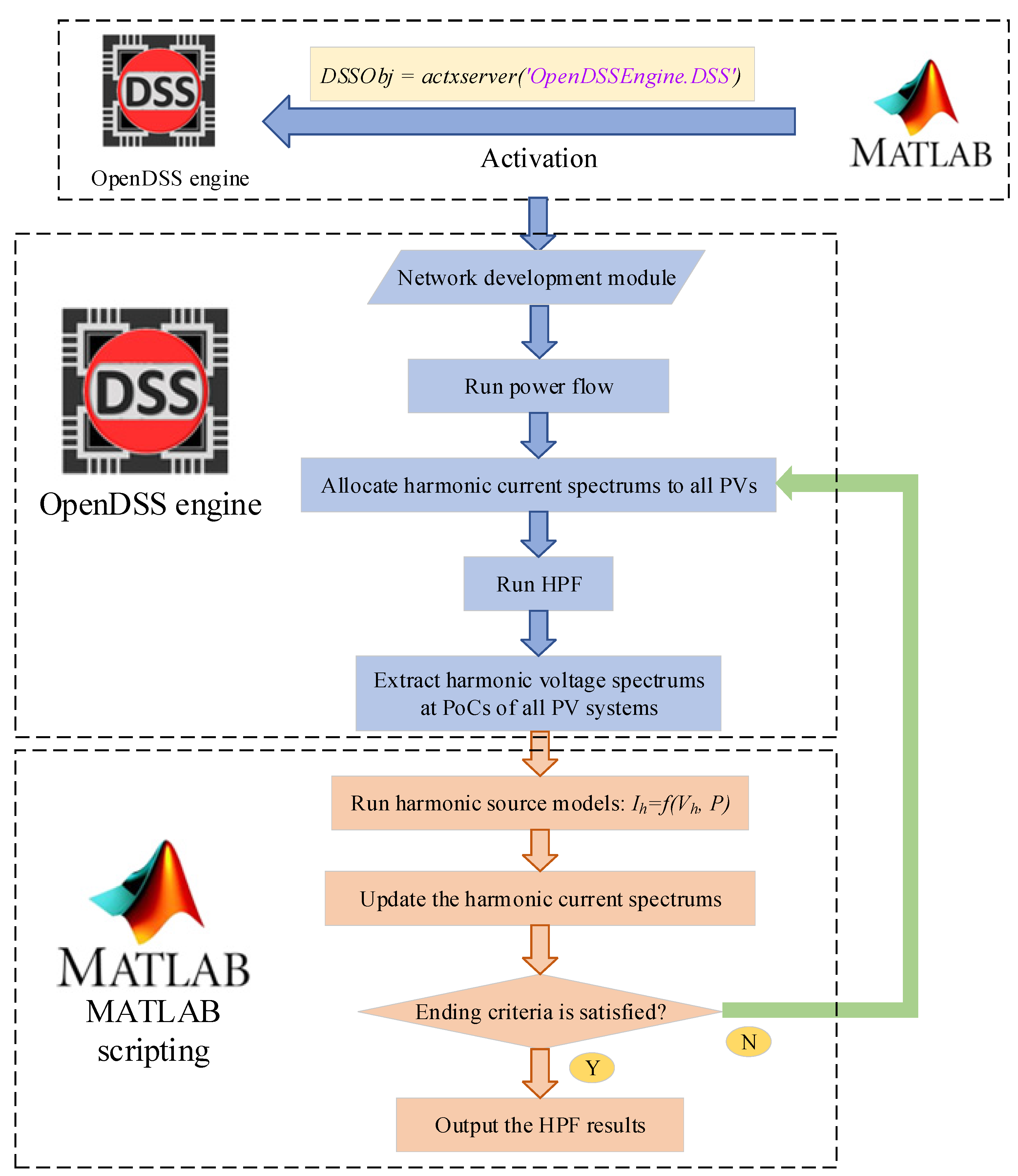
2.4. The Practical HAM Derivation Approach for Fluctuating Power PV Systems
3. Results and Discussions
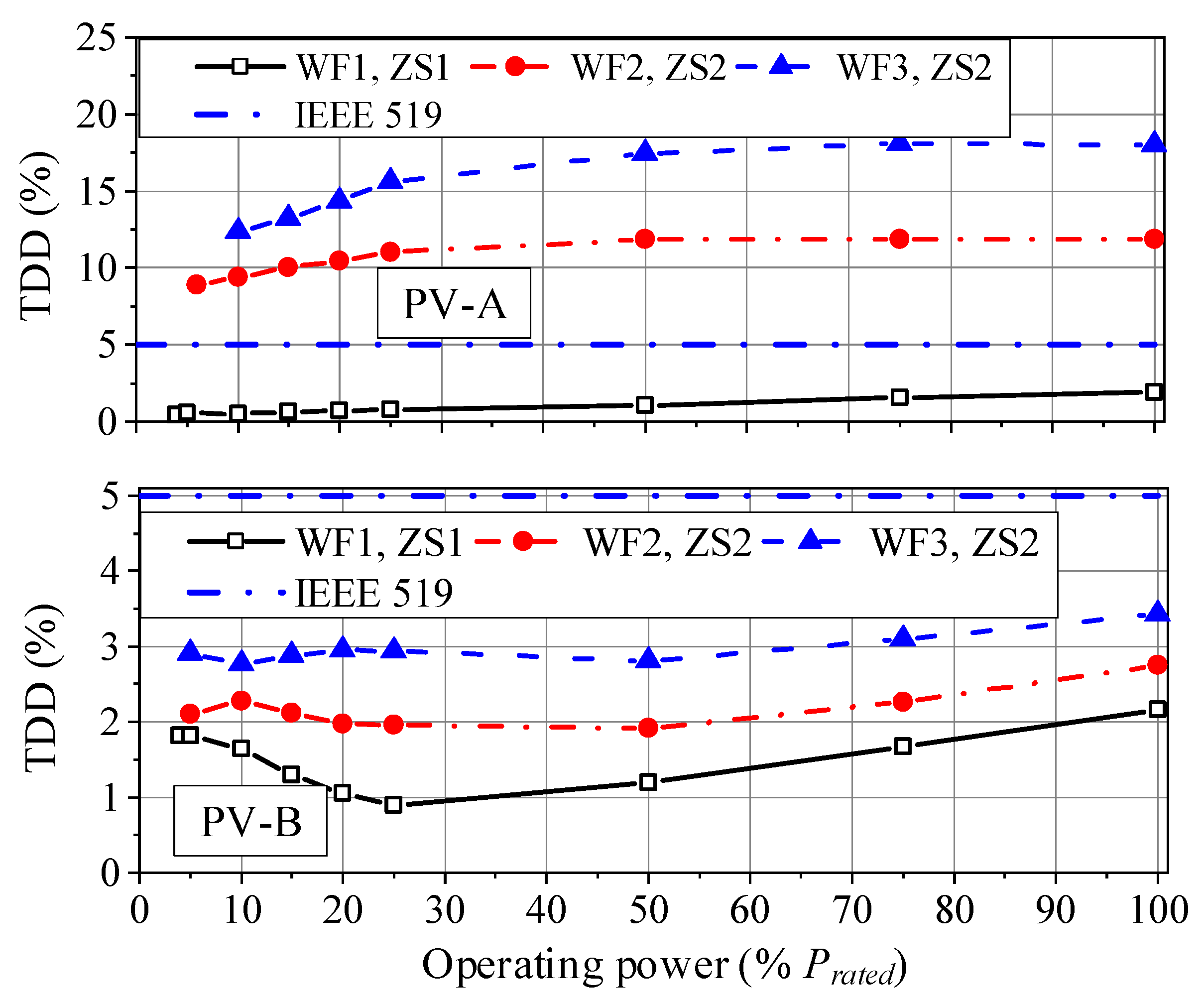
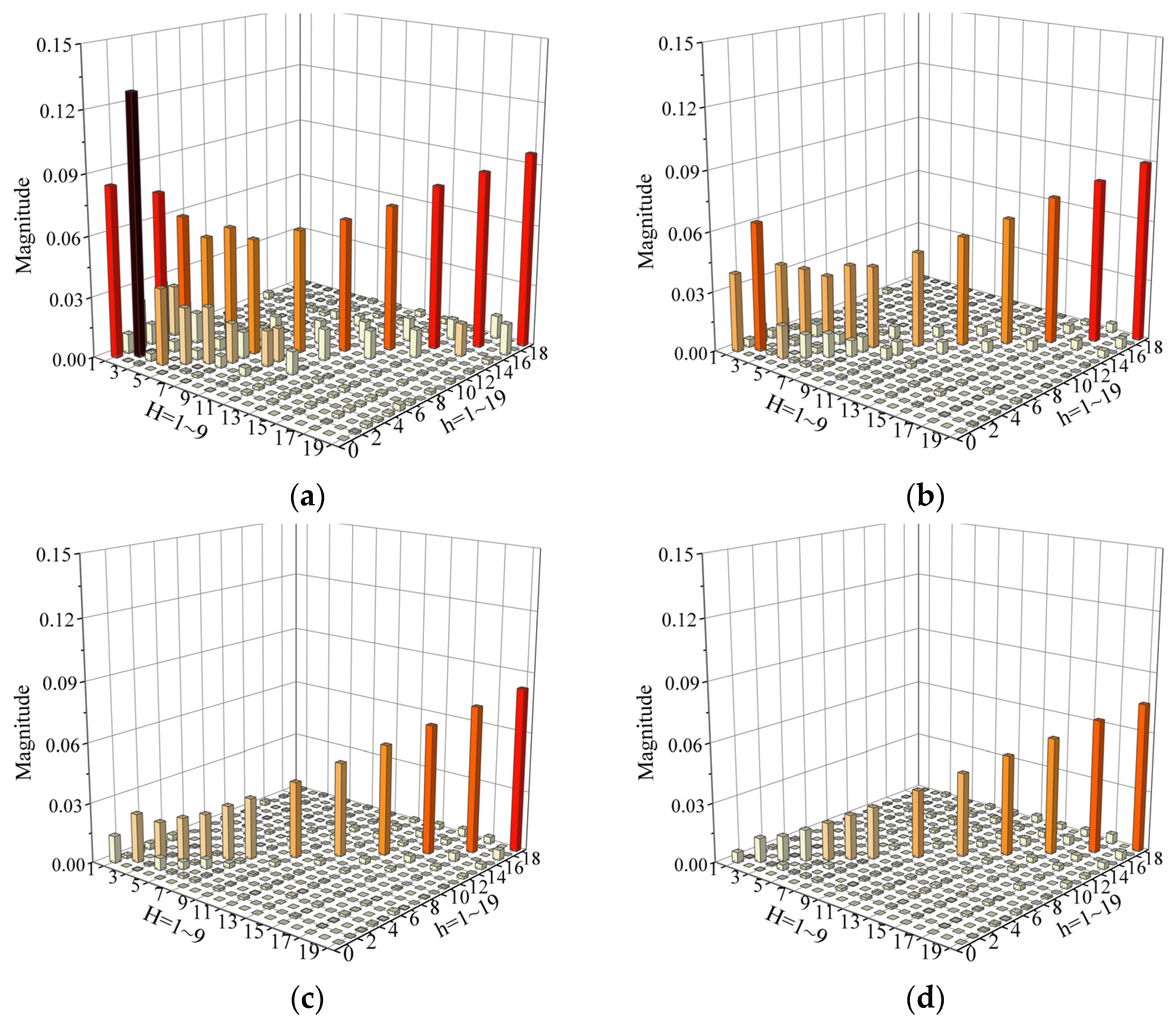
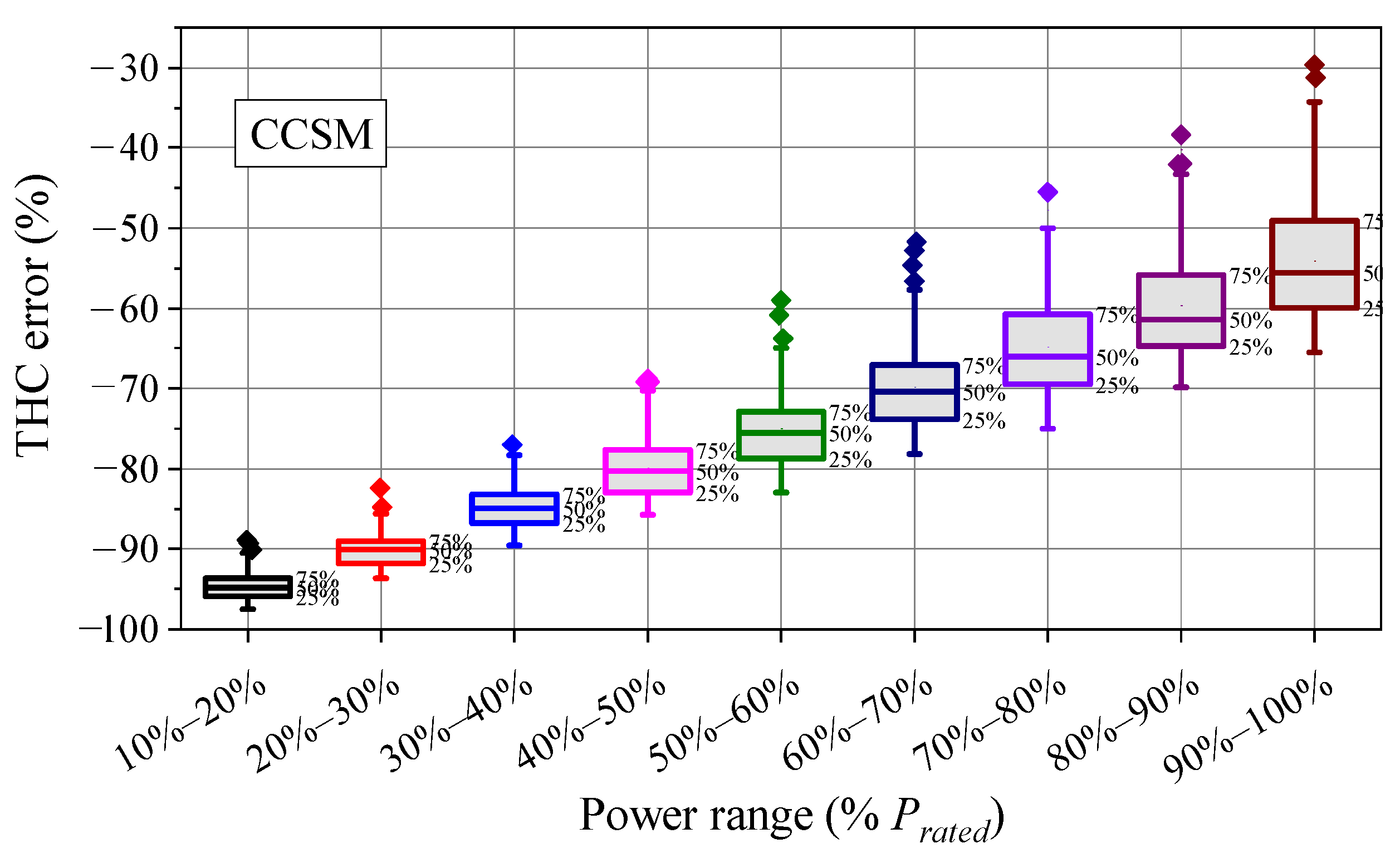
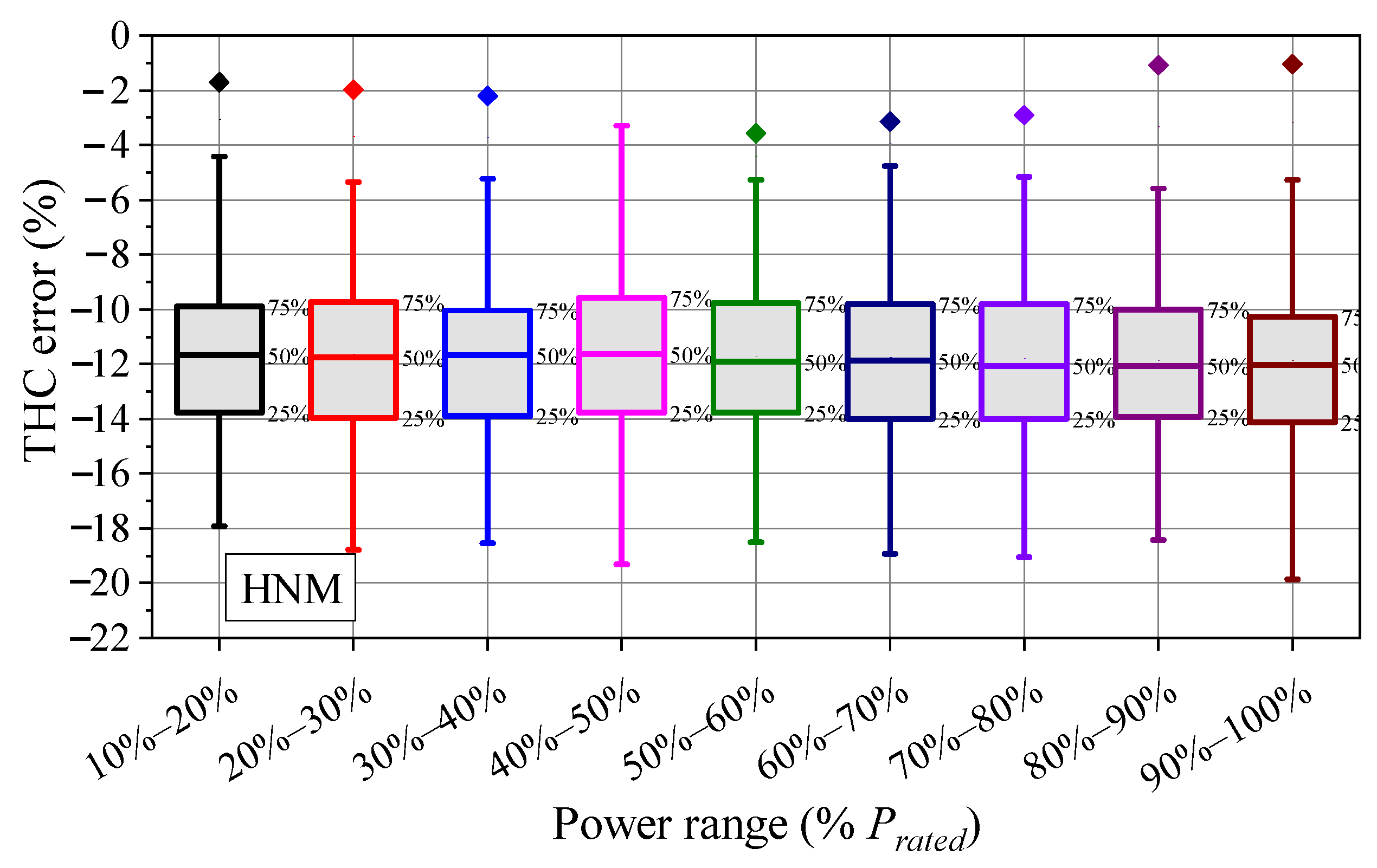
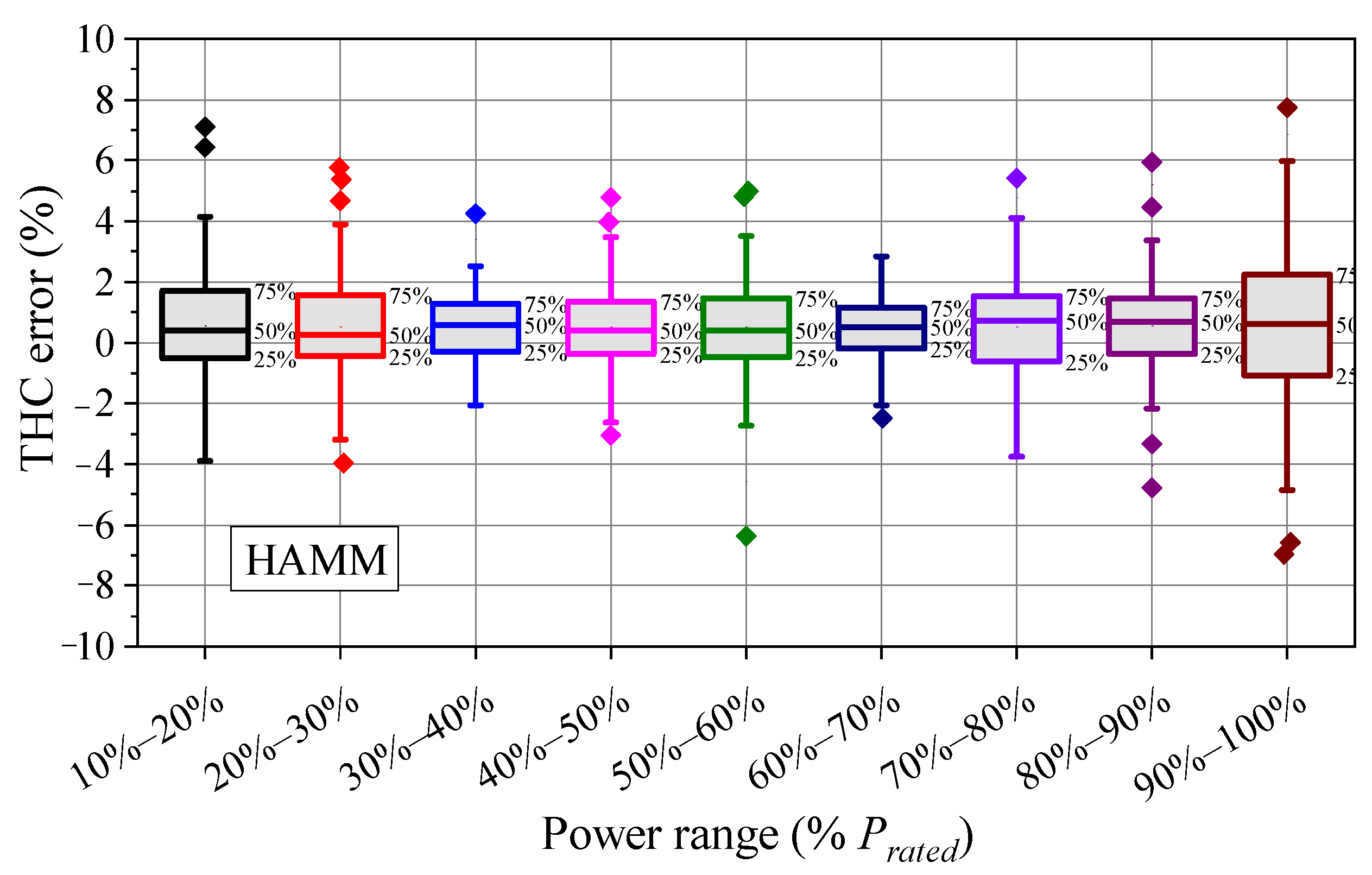
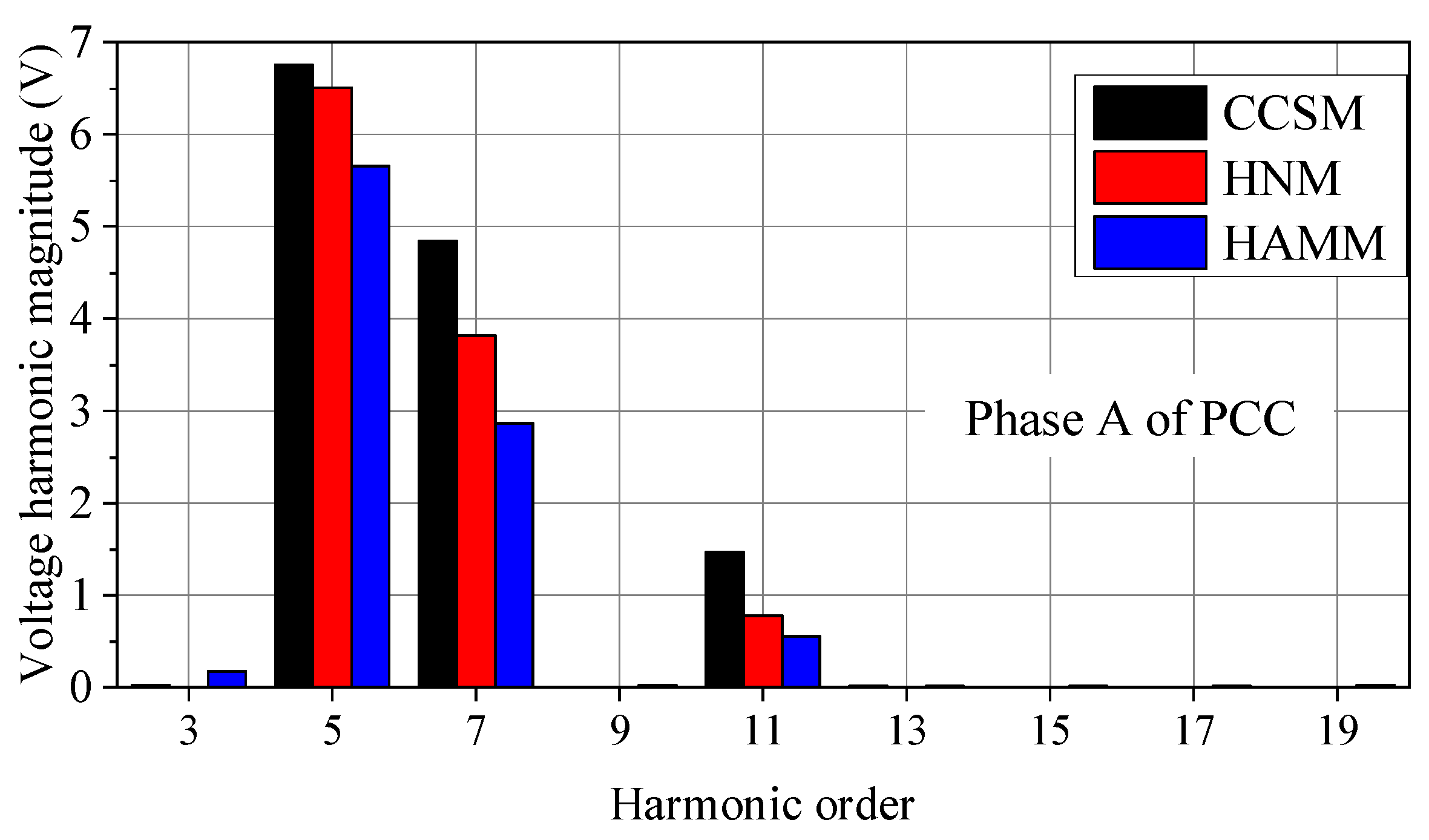
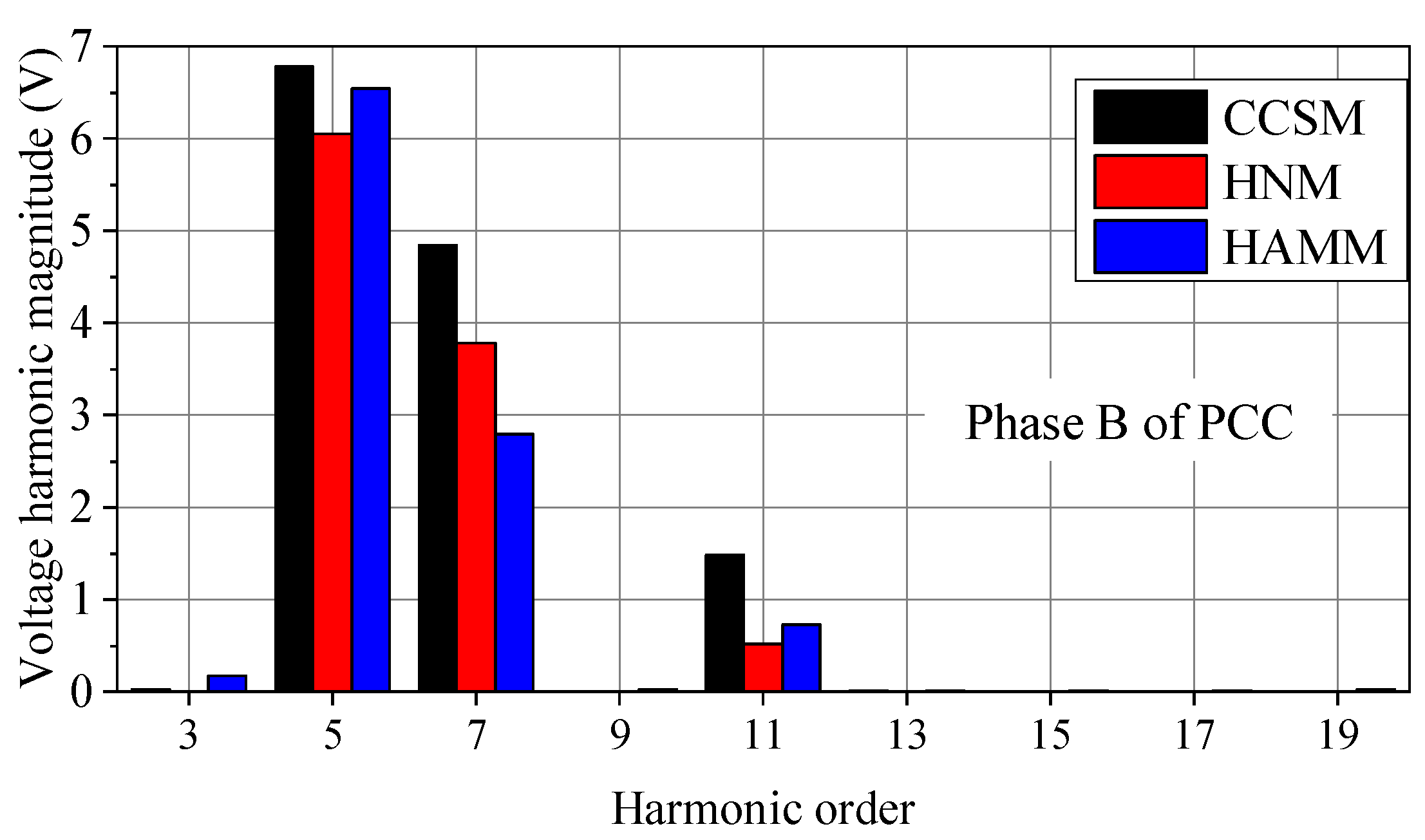
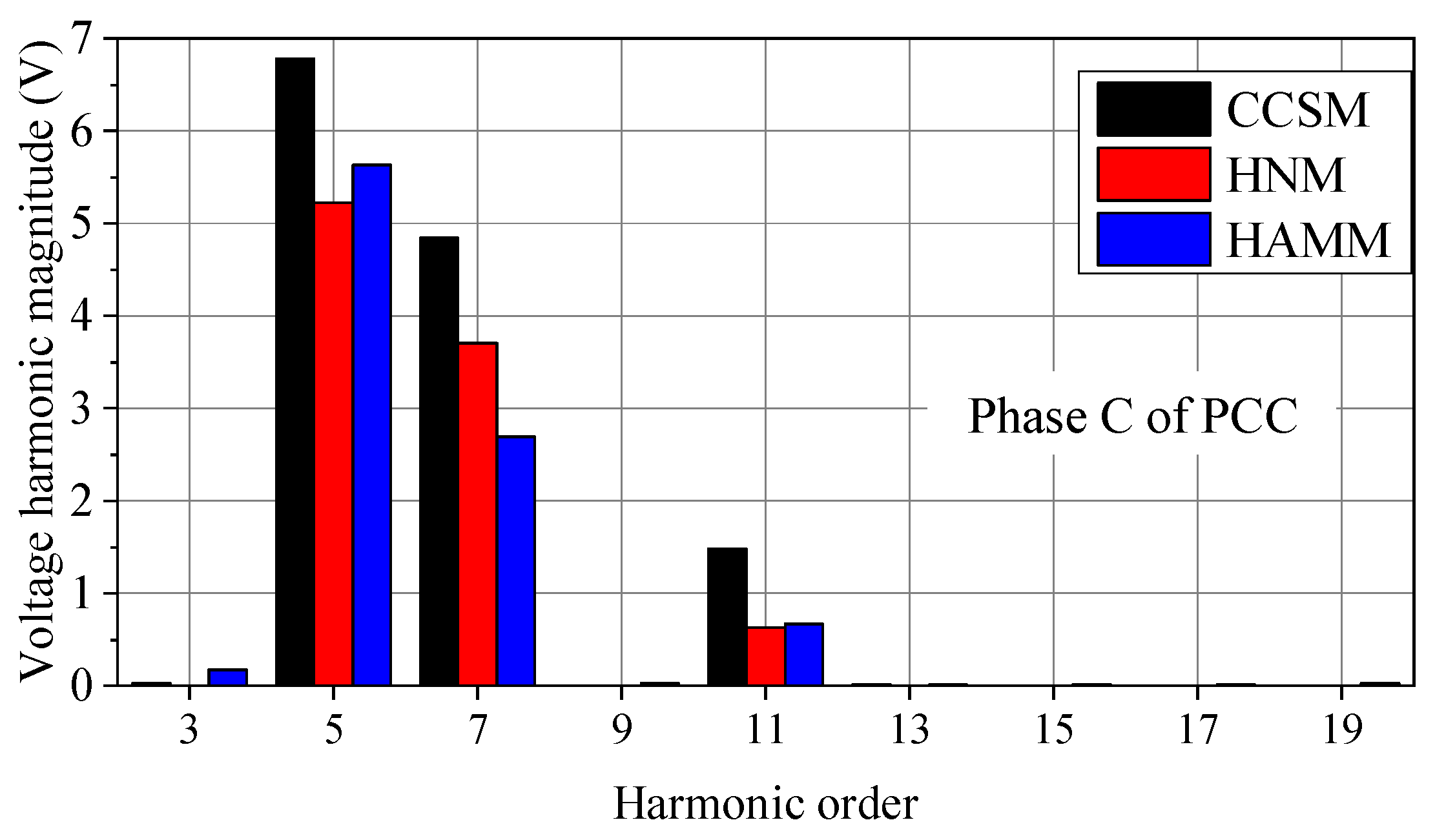
3.1. Accuracy Comparison among CCSM, HNM and HAMM
3.2. Comparison of Harmonic Power Flow Results among CCSM, HNM and HAMM
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forson, P.; Samuel, G.; Mark, A.B.; Eric, E.D. Impact assessment of grid tied rooftop PV systems on LV distribution network. Sci. Afr. 2022, 16, e01172. [Google Scholar]
- Oktoviano, G.; Dhivya, S.K.; Carlos, D.R.; Dipti, S. Review of power system impacts at high PV penetration Part I: Factors limiting PV penetration. Sol. Energy 2020, 210, 181–201. [Google Scholar]
- Erik, D.J.; Peter, V. The Impact of Large-Scale PV on Distribution Grid Operation and Protection; and Appropriate Testing. In Proceedings of the CIRED 2012 Workshop: Integration of Renewables into the Distribution Grid, Lisbon, Portugal, 29–30 May 2012; pp. 1–4. [Google Scholar]
- Li, W.; Yang, G.; Zhou, Z.; Lu, Q.; Du, D.; Liu, Y. Impact of the distributed photovoltaic on the current protection of 10kV distribution network. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 8–11 December 2013; pp. 1–4. [Google Scholar]
- IEEE Standard 1547-2003; IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems. IEEE Standard: New York, NY, USA, 2003.
- IEC 61727-2004; Photovoltaic (PV) Systems—Characteristics of the Utility Interface. IEC Standard: Geneva, Switzerland, 2004.
- IEEE Standard 519; IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems. IEEE Standard: New York, NY, USA, 2014.
- EN 50160:2010+A1:2015; Voltage Characteristics of the Electricity Supplied by Public Distribution Systems. British Standards Institution: London, UK, 2015.
- Tyagi, A.; Manisha. Harmonics Mitigation for Grid Connected PV Module with Integration of Multilevel Inverter Topology. In Proceedings of the 2020 International Conference on Advances in Computing, Communication & Materials (ICACCM), Dehradun, India, 21–22 August 2020; pp. 110–114. [Google Scholar]
- Renu, V.; Surasmi, N.L. Optimal control of selective harmonic elimination in a grid-connected single-phase PV inverter. In Proceedings of the 2014 International Conference on Advances in Green Energy (ICAGE), Thiruvananthapuram, India, 17–18 December 2014; pp. 265–271. [Google Scholar]
- Langella, R.; Testa, A.; Meyer, J.; Möller, F.; Stiegler, R.; Djokic, S.Z. Experimental-Based Evaluation of PV Inverter Harmonic and Interharmonic Distortion Due to Different Operating Conditions. Trans. Instrum. Meas. 2016, 65, 2221–2233. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Collin, A.J.; Djokic, S.Z.; Yanchenko, S.; Möller, F.; Meyer, J.; Langella, R.; Testa, A. Analysis and Modelling of Power-Dependent Harmonic Characteristics of Modern PE Devices in LV Networks. IEEE Trans. Power Deliv. I 2017, 32, 1014–1023. [Google Scholar] [CrossRef] [Green Version]
- Todeschini, G.; Balasubramaniam, S.; Igic, P. Time-domain Modeling of a Distribution System to Predict Harmonic Interaction Between PV Converters. IEEE Trans. Sustain. Energy 2019, 10, 1450–1458. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Lu, D.D.C.; Chu, G.M.L.; Xiao, W. Closed-Form Solution of Time-Varying Model and Its Applications for Output Current Harmonics in Two-Stage PV Inverter. IEEE Trans. Sustain. Energy 2015, 6, 142–150. [Google Scholar] [CrossRef]
- Perera, B.K.; Pulikanti, S.R.; Ciufo, P.; Perera, S. Simulation model of a grid connected single-phase photovoltaic system in PSCAD/EMTDC. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6. [Google Scholar]
- Ibrahim, C.B.; Engin, K.; Mutlu, B. Impact of harmonic limits on PV penetration levels in unbalanced distribution networks considering load and irradiance uncertainty. Int. J. Electr. Power Energy Syst. 2020, 118, 105780. [Google Scholar]
- Pablo, R.P.; Eduardo, C.; Araceli, H.; Mohamed, I. A Bottom-up model for simulating residential harmonic injections. Energy Build. 2022, 265, 112103. [Google Scholar]
- Tatiano, B.; Vineetha, R.; Anders, L.; Sarah, K.R.; Math, H.J.B.; Jan, M. Deviations between the commonly-used model and measurements of harmonic distortion in low-voltage installations. Electr. Power Syst. Res. 2020, 180, 106166. [Google Scholar]
- Karadeniz, A.; Ozturk, O.; Koksoy, A.; Atsever, M.B.; Balci, M.E.; Hocaoglu, M.H. Accuracy assessment of frequency-domain models for harmonic analysis of residential type photovoltaic-distributed generation units. Sol. Energy 2022, 233, 182–195. [Google Scholar] [CrossRef]
- Xu, X.; Collin, A.J.; Djokic, S.Z.; Yanchenko, S.; Möller, F.; Meyer, J.; Langella, R.; Testa, A. Aggregate Harmonic Fingerprint Models of PV Inverters, Part 1: Operation at Different Powers. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Safargholi, F. Harmonic Fingerprint Measurement for Characterization of LED Street Lighting. In PESS 2021-Power and Energy Student Summit; VDE VERLAG: Frankfurt, Germany, 2021; pp. 1–5. [Google Scholar]
- Cobben, J.F.G.; Kling, W.L.; Myrzik, J.M.A. The Making and Purpose of Harmonic Fingerprints. In Proceedings of the 19th International Conference on Electricity Distribution (CIRED 2007), Vienna, Austria, 21–24 May 2007; pp. 1–4. [Google Scholar]
- Zhao, E.; Han, Y.; Lin, X.; Liu, E.; Yang, P.; Zalhaf, A.S. Harmonic characteristics and control strategies of grid-connected photovoltaic inverters under weak grid conditions. Int. J. Electr. Power Energy Syst. 2022, 142, 108280. [Google Scholar] [CrossRef]
- IEEE PES Distribution Systems Analysis Subcommittee Radial Test Feeders. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 10 May 2022).




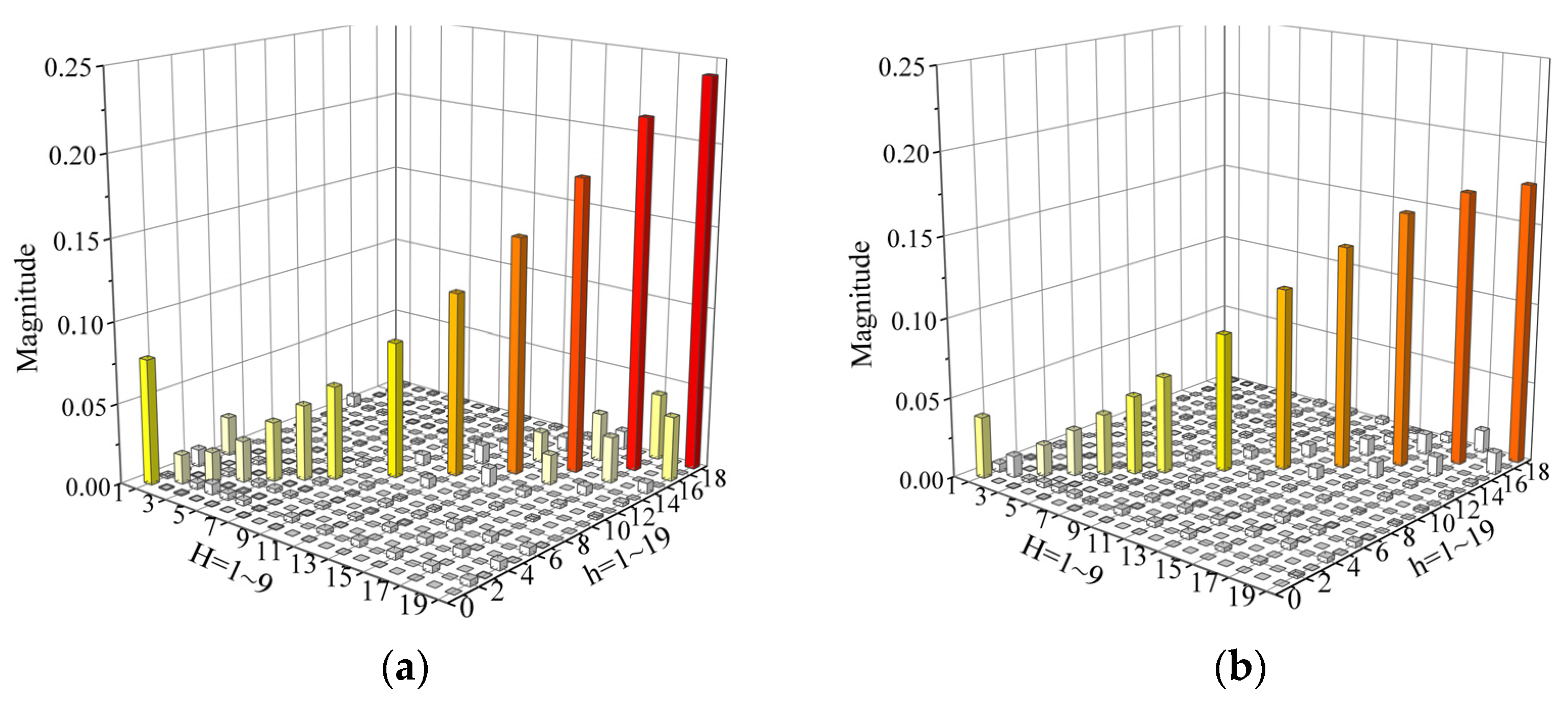
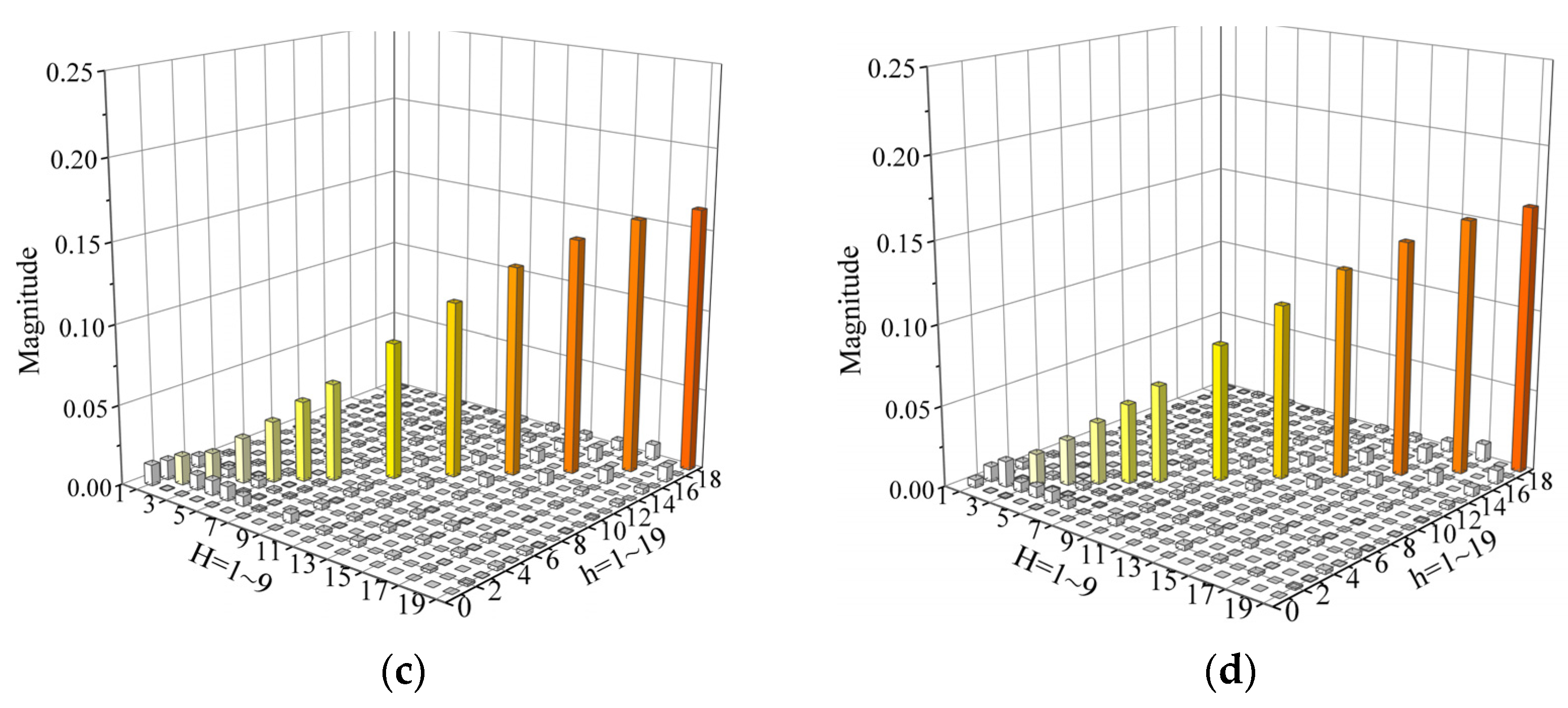

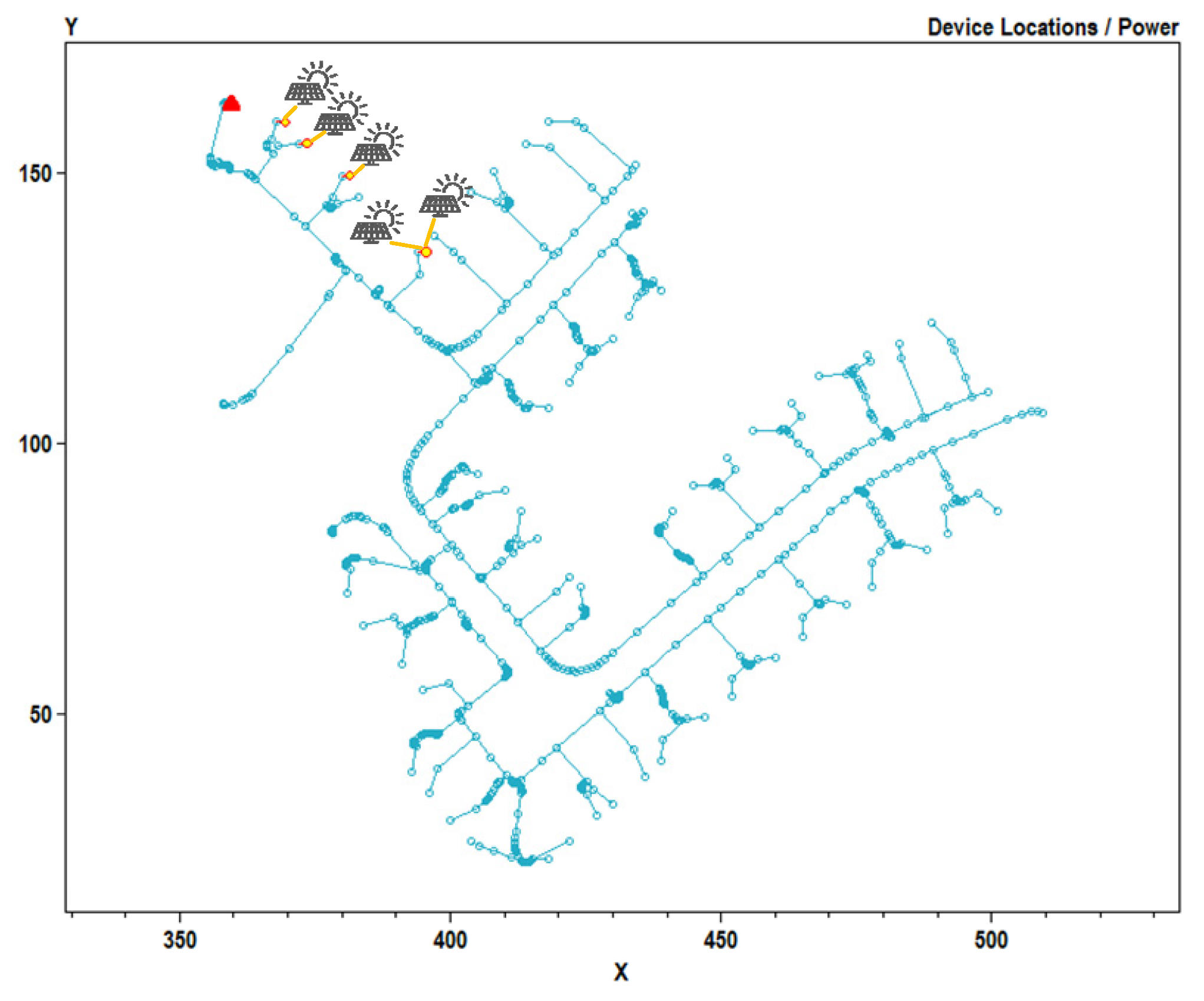
| Inverter | PV-A | PV-B |
|---|---|---|
| Technology | Transformerless | With low-frequency transformer |
| Rated power (kVA) | 4.6 | 4.6 |
| Phase connection | Single-phase | Single-phase |
| Rated/reference current (A) | 20 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Dong, A.; Li, Q.; Gao, H. A Practical Harmonic Admittance Matrix Derivation Approach for Fluctuating Power Photovoltaic Systems. Appl. Sci. 2022, 12, 5615. https://doi.org/10.3390/app12115615
Xu X, Dong A, Li Q, Gao H. A Practical Harmonic Admittance Matrix Derivation Approach for Fluctuating Power Photovoltaic Systems. Applied Sciences. 2022; 12(11):5615. https://doi.org/10.3390/app12115615
Chicago/Turabian StyleXu, Xiao, Anqi Dong, Qianting Li, and Hui Gao. 2022. "A Practical Harmonic Admittance Matrix Derivation Approach for Fluctuating Power Photovoltaic Systems" Applied Sciences 12, no. 11: 5615. https://doi.org/10.3390/app12115615






