Assessment of Appropriate Geometry for Thermally Efficient CO2 Adsorption Beds
Abstract
:1. Introduction
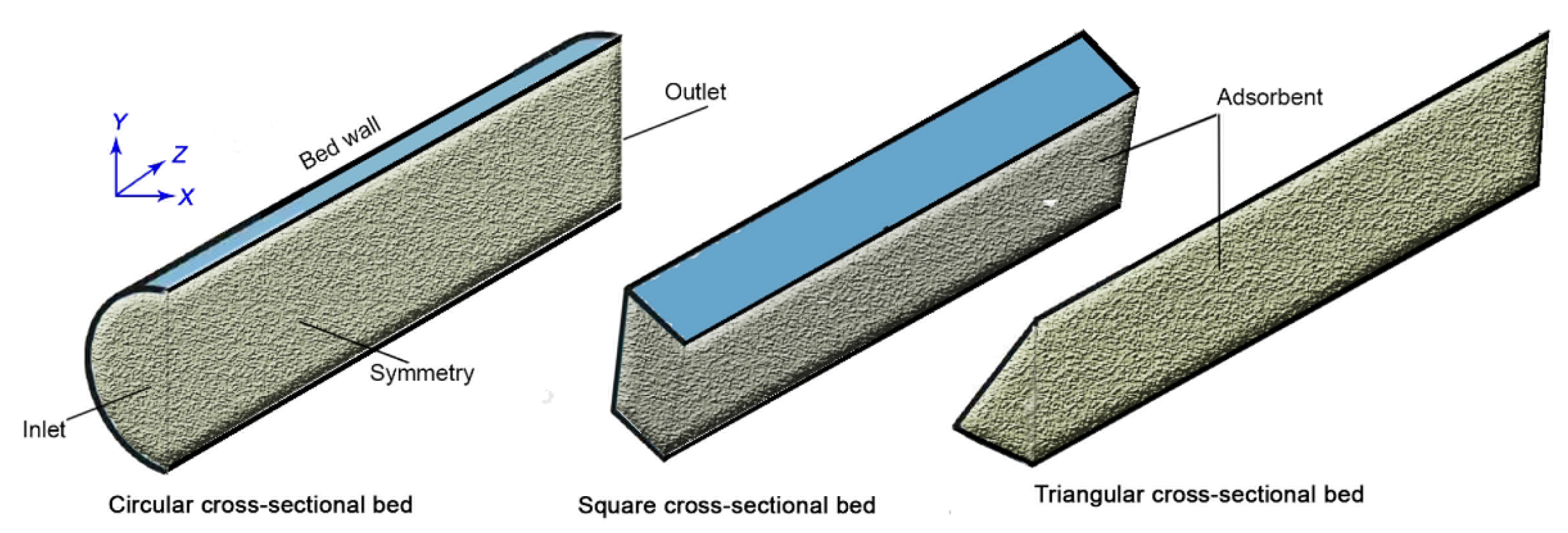
2. Adsorption Beds and Model Description
2.1. Governing Equations
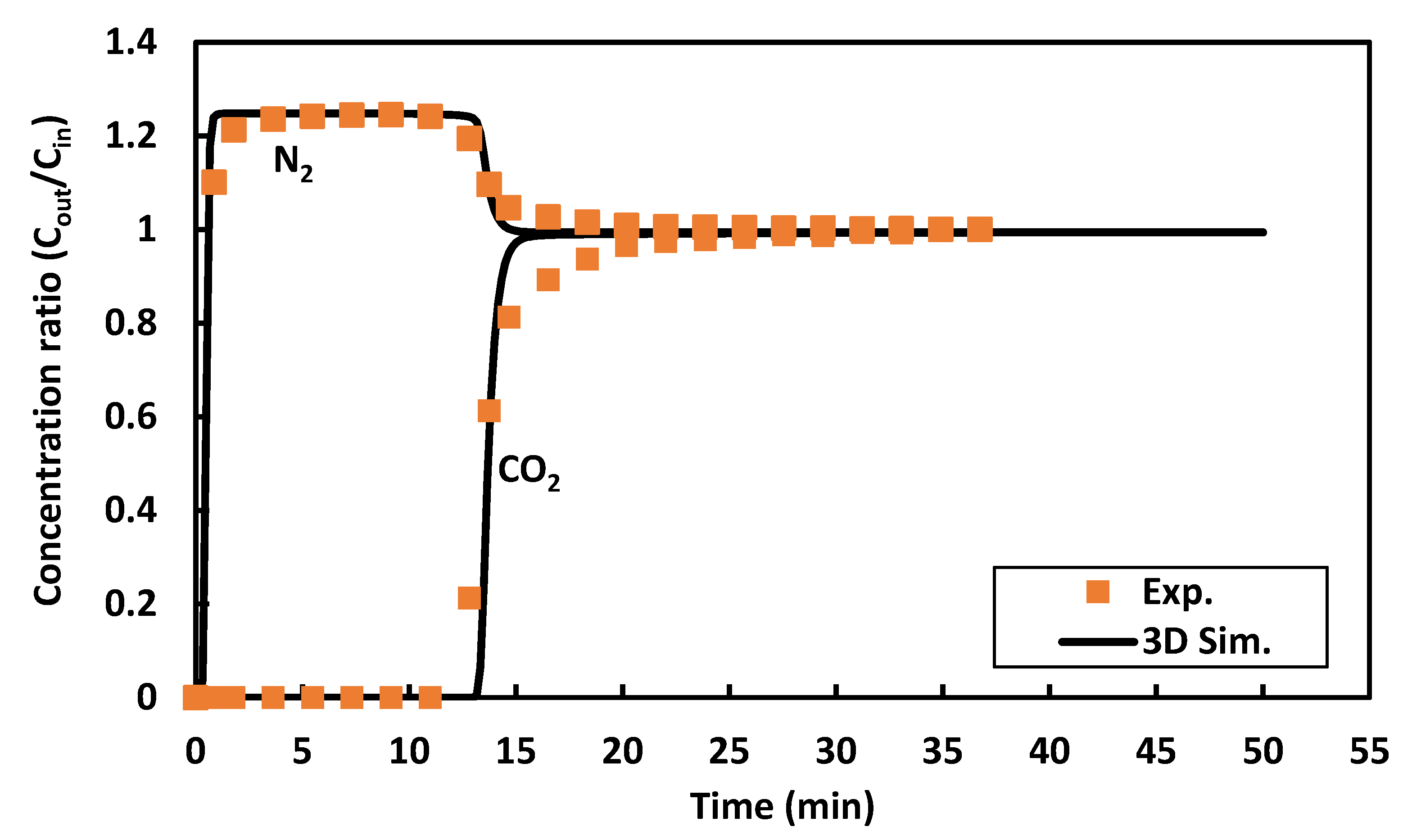
2.2. Mesh Independence and Model Validation
3. Results and Discussion
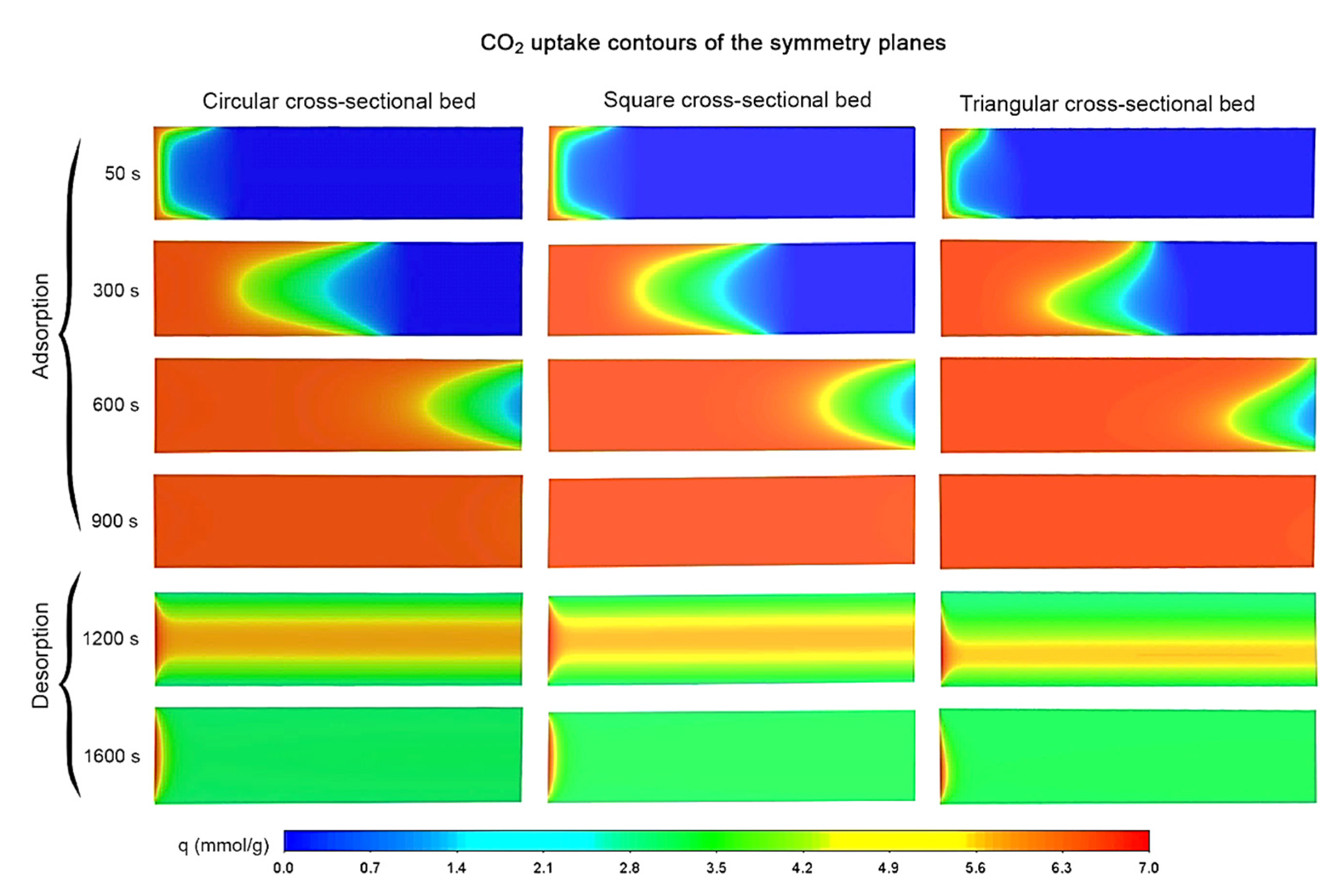
3.1. The General Behavior of Adsorption/Desorption Processes
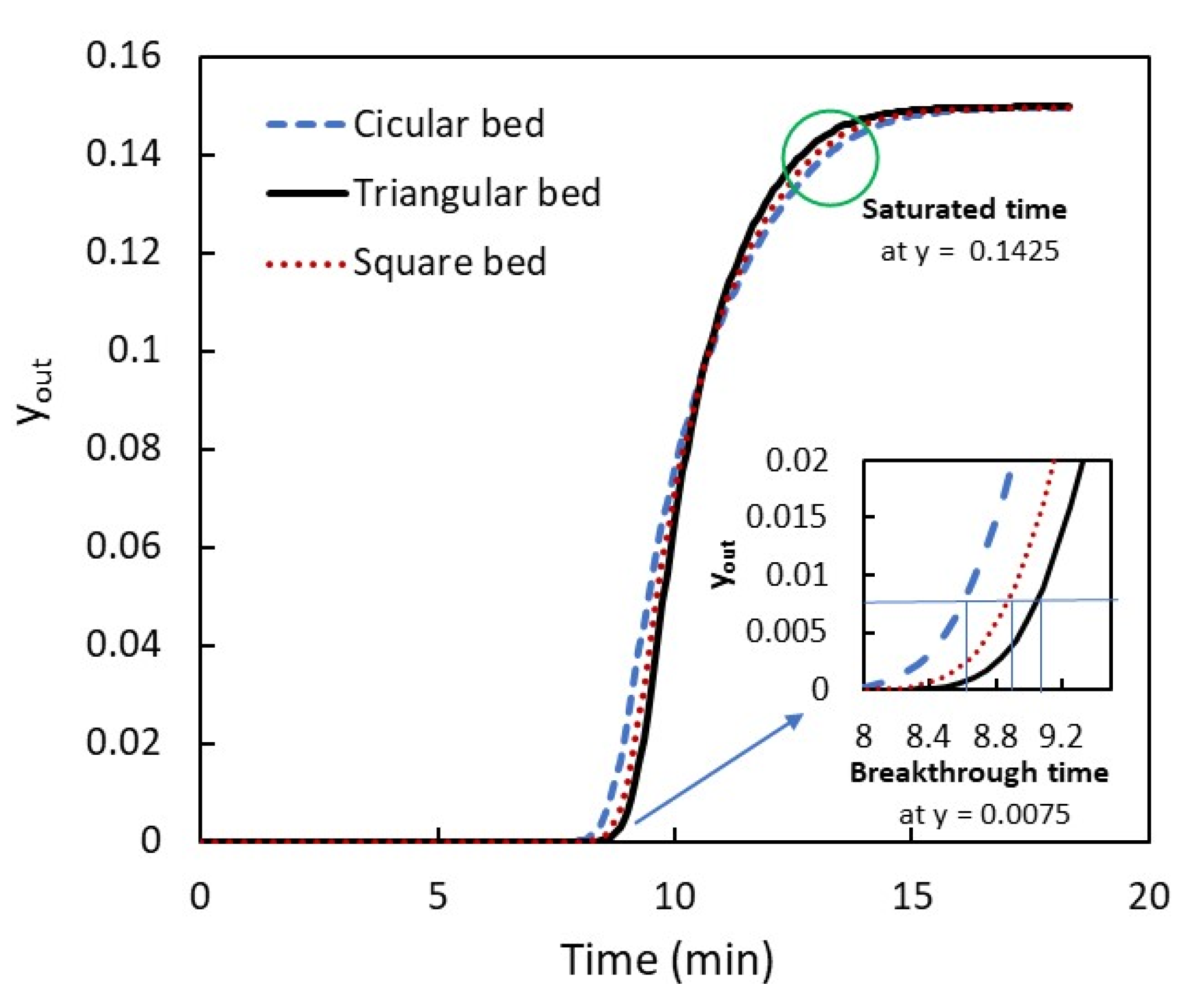
3.2. Adsorption Concentration
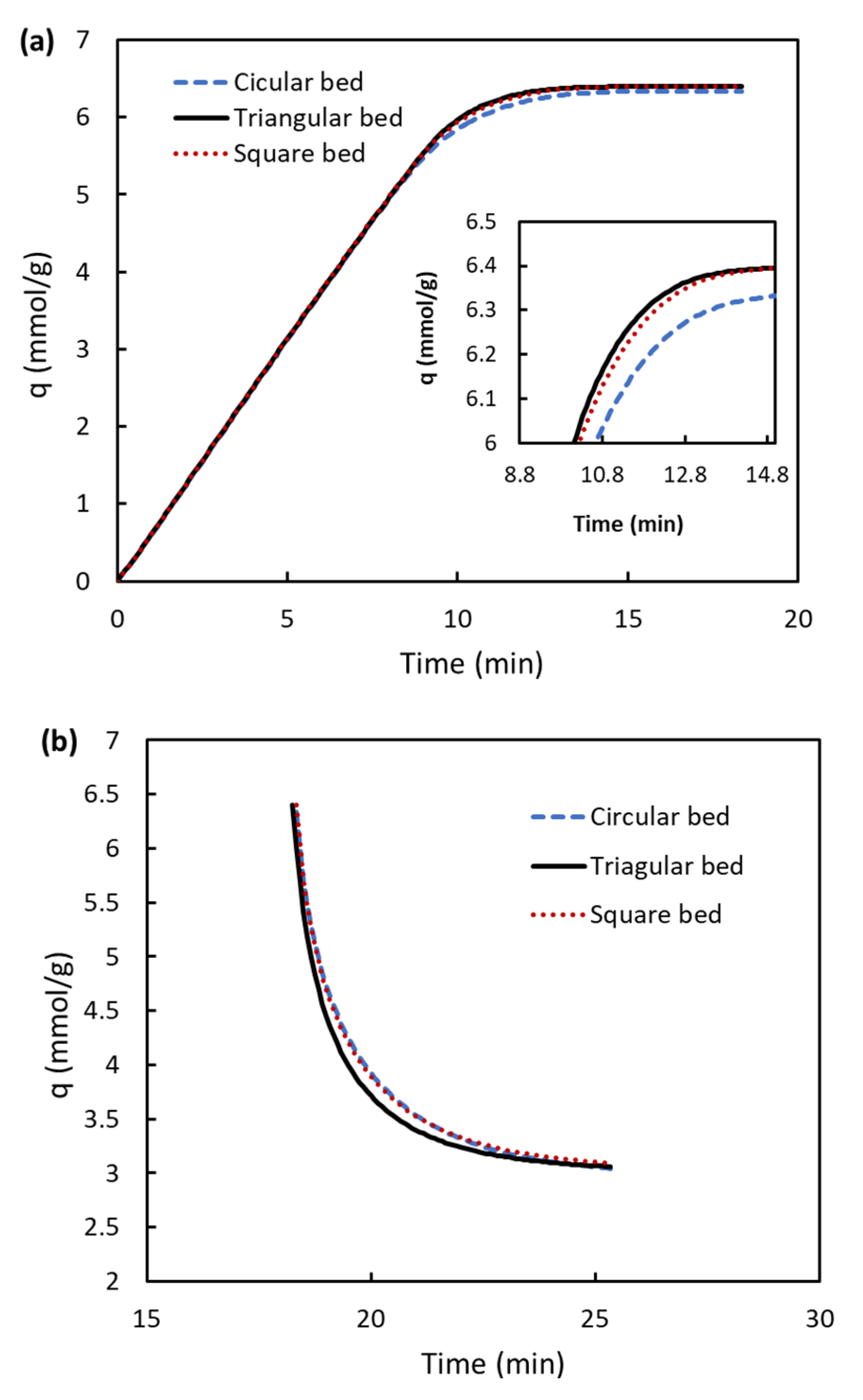
3.3. Adsorption Uptake
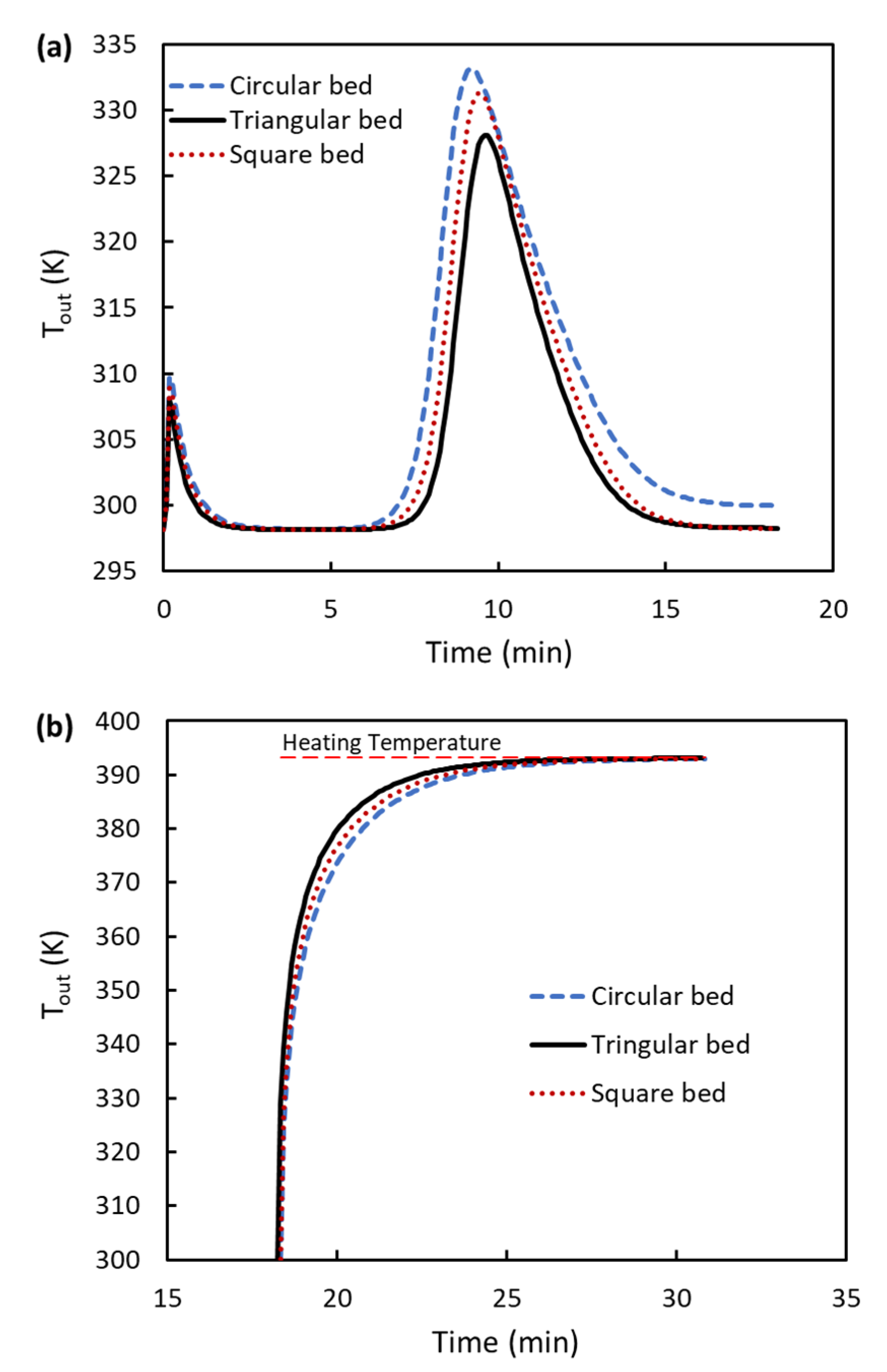
3.4. Temperature Profiles during Adsorption and Regeneration Processes
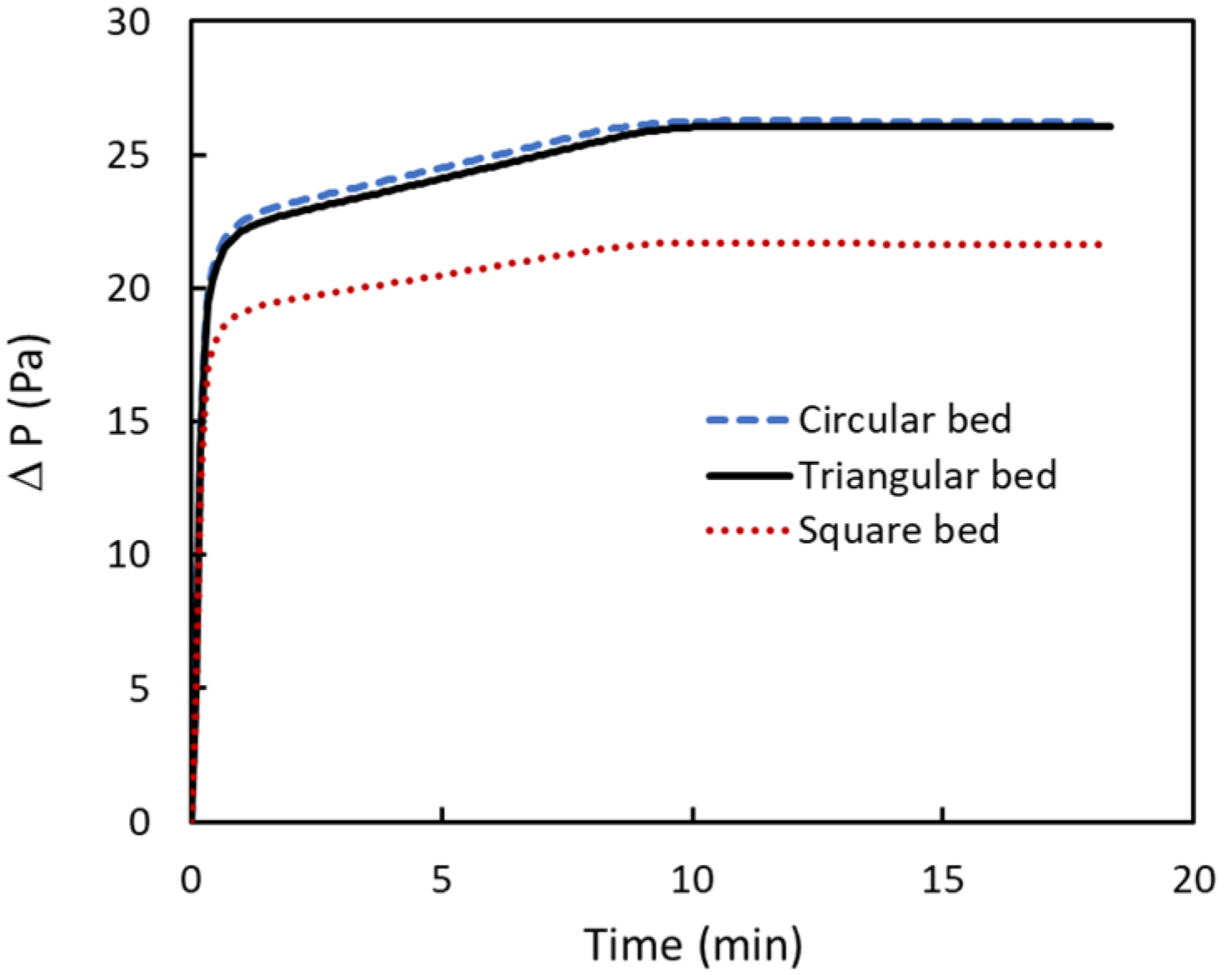
3.5. Pressure Drop
4. Conclusions
- Temperature values along the bed are lower for triangular cross-sectional beds than others, improving the adsorption and desorption processes. About 6 K is the reduction in temperature when a triangular cross-sectional bed is used compared to a circular one.
- Due to an enhancement in temperature cooling and heating of the triangular bed, the CO2 adsorption uptake has higher values for this bed than others.
- The pressure drop is lower for the square bed, about 17% less than the circular one. The triangular bed has slightly lower values compared to the circular beds.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ben-Mansour, R.; Habib, M.A.; Bamidele, O.E.; Basha, M.; Qasem, N.A.A.; Peedikakkal, A.; Laoui, T.; Ali, M. Carbon capture by physical adsorption: Materials, experimental investigations and numerical modeling and simulations—A review. Appl. Energy 2016, 161, 225–255. [Google Scholar] [CrossRef]
- Shah, G.; Ahmad, E.; Pant, K.K.; Vijay, V.K. Comprehending the contemporary state of art in biogas enrichment and CO2 capture technologies via swing adsorption. Int. J. Hydrog. Energy 2021, 46, 6588–6612. [Google Scholar] [CrossRef]
- D’Alessandro, D.M.; McDonald, T. Toward carbon dioxide capture using nanoporous materials. Pure Appl. Chem. 2010, 83, 57–66. [Google Scholar] [CrossRef]
- Ahsan, S.; Ayub, A.; Meeroff, D.; Lashaki, M.J. A comprehensive comparison of zeolite-5A molecular sieves and amine-grafted SBA-15 silica for cyclic adsorption-desorption of carbon dioxide in enclosed environments. Chem. Eng. J. 2022, 437, 135139. [Google Scholar] [CrossRef]
- Yao, X.; Cordova, K.E.; Zhang, Y.-B. Flexible Metal–Organic Frameworks as CO2 Adsorbents en Route to Energy-Efficient Carbon Capture. Small Struct. 2022, 3, 2100209. [Google Scholar] [CrossRef]
- Bermeo, M.; Vega, L.F.; Abu-Zahra, M.R.M.; Khaleel, M. Critical assessment of the performance of next-generation carbon-based adsorbents for CO2 capture focused on their structural properties. Sci. Total Environ. 2022, 810, 151720. [Google Scholar] [CrossRef] [PubMed]
- Akeeb, O.; Wang, L.; Xie, W.; Davis, R.; Alkasrawi, M.; Toan, S. Post-combustion CO2 capture via a variety of temperature ranges and material adsorption process: A review. J. Environ. Manag. 2022, 313, 115026. [Google Scholar] [CrossRef]
- Bai, R.; Song, X.; Yan, W.; Yu, J. Low-Energy Adsorptive Separation by Zeolites. Natl. Sci. Rev. 2022, nwac064. [Google Scholar] [CrossRef]
- Jung, W.; Lee, J. Economic evaluation for four different solid sorbent processes with heat integration for energy-efficient CO2 capture based on PEI-silica sorbent. Energy 2022, 238, 121864. [Google Scholar] [CrossRef]
- Samanta, A.; Zhao, A.; Shimizu, G.K.H.; Sarkar, P.; Gupta, R. Post-combustion CO2 capture using solid sorbents: A review. Ind. Eng. Chem. Res. 2012, 51, 1438–1463. [Google Scholar] [CrossRef]
- Siriwardane, R.V.; Shen, M.-S.; Fisher, E.P.; Poston, J.A. Adsorption of CO 2 on Molecular Sieves and Activated Carbon. Energy Fuels 2001, 15, 279–284. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Ben-Mansour, R. Energy and productivity efficient vacuum pressure swing adsorption process to separate CO2 from CO2/N2 mixture using Mg-MOF-74: A CFD simulation. Appl. Energy 2018, 209, 190–202. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Qadir, N.U.; Ben-Mansour, R.; Said, S.A.M. Synthesis, characterization, and CO2 breakthrough adsorption of a novel MWCNT/MIL-101(Cr) composite. J. CO2 Util. 2017, 22, 238–249. [Google Scholar] [CrossRef]
- Li, L.; Jung, H.S.; Lee, J.W.; Kang, Y.T. Review on applications of metal–organic frameworks for CO2 capture and the performance enhancement mechanisms. Renew. Sustain. Energy Rev. 2022, 162, 112441. [Google Scholar] [CrossRef]
- Pentyala, V.; Davydovskaya, P.; Ade, M.; Pohle, R.; Urban, G. Carbon dioxide gas detection by open metal site metal organic frameworks and surface functionalized metal organic frameworks. Sens. Actuators B Chem. 2016, 225, 363–368. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Ben-Mansour, R. Adsorption breakthrough and cycling stability of carbon dioxide separation from CO2/N2/H2O mixture under ambient conditions using 13X and Mg-MOF-74. Appl. Energy 2018, 230, 1093–1107. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Qasem, N.A.A.; Antar, M.A. Carbon dioxide adsorption separation from dry and humid CO2/N2 mixture. Comput. Chem. Eng. 2018, 117, 221–235. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Abuelyamen, A.; Ben-Mansour, R. Enhancing CO2 Adsorption Capacity and Cycling Stability of Mg-MOF-74, Arab. J. Sci. Eng. 2021, 46, 6219–6228. [Google Scholar] [CrossRef]
- Adhikari, A.K.; Lin, K.-S. Improving CO2 adsorption capacities and CO2/N2 separation efficiencies of MOF-74(Ni, Co) by doping palladium-containing activated carbon. Chem. Eng. J. 2016, 284, 1348–1360. [Google Scholar] [CrossRef]
- Lee, D.J.; Li, Q.; Kim, H.; Lee, K. Preparation of Ni-MOF-74 membrane for CO2 separation by layer-by-layer seeding technique. Microporous Mesoporous Mater. 2012, 163, 169–177. [Google Scholar] [CrossRef]
- Cho, H.Y.; Yang, D.A.; Kim, J.; Jeong, S.Y.; Ahn, W.S. CO2 adsorption and catalytic application of Co-MOF-74 synthesized by microwave heating. Catal. Today 2012, 185, 35–40. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Qasem, N.A.A.; Habib, M.A. Adsorption characterization and CO2 breakthrough of MWCNT/Mg-MOF-74 and MWCNT/MIL-100(Fe) composites. Int. J. Energy Environ. Eng. 2018, 9, 169–185. [Google Scholar] [CrossRef] [Green Version]
- Abdelnaby, M.M.; Qasem, N.A.A.; Al-Maythalony, B.A.; Cordova, K.E.; Al Hamouz, O.C.S. A Microporous Organic Copolymer for Selective CO2 Capture under Humid Conditions, ACS Sustain. Chem. Eng. 2019, 7, 13941–13948. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Abuelyamen, A.; Qasem, N.A.A. Thermal design and management towards high capacity CO2 adsorption systems. Energy Convers. Manag. 2020, 212, 112796. [Google Scholar] [CrossRef]
- Al Mesfer, M.K.; Danish, M.; Khan, M.I.; Ali, I.H.; Hasan, M.; Jery, A.E. Continuous Fixed Bed CO2 Adsorption: Breakthrough, Column Efficiency, Mass Transfer Zone. Processes 2020, 8, 1233. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Li, Z. Fast Adsorption Kinetics of CO2 on Solid Amine Sorbent Measured Using Microfluidized Bed Thermogravimetric Analysis. Ind. Eng. Chem. Res. 2020, 59, 6855–6866. [Google Scholar] [CrossRef]
- Jung, W.; Park, S.; Lee, K.S.; Jeon, J.-D.; Lee, H.K.; Kim, J.-H.; Lee, J.S. Rapid thermal swing adsorption process in multi-beds scale with sensible heat recovery for continuous energy-efficient CO2 capture. Chem. Eng. J. 2020, 392, 123656. [Google Scholar] [CrossRef]
- Boscherini, M.; Miccio, F.; Papa, E.; Medri, V.; Landi, E.; Doghieri, F.; Minelli, M. The relevance of thermal effects during CO2 adsorption and regeneration in a geopolymer-zeolite composite: Experimental and modelling insights. Chem. Eng. J. 2021, 408, 127315. [Google Scholar] [CrossRef]
- Abd, A.A.; Othman, M.R. Biogas upgrading to fuel grade methane using pressure swing adsorption: Parametric sensitivity analysis on an industrial scale. Fuel. 2022, 308, 121986. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Basha, M.; Qasem, N.A.A. Multicomponent and multi-dimensional modeling and simulation of adsorption-based carbon dioxide separation. Comput. Chem. Eng. 2017, 99, 255–270. [Google Scholar] [CrossRef]
- Xiao, J.; Peng, R.; Cossement, D.; Bénard, P.; Chahine, R. CFD model for charge and discharge cycle of adsorptive hydrogen storage on activated carbon. Int. J. Hydrog. Energy 2013, 38, 1450–1459. [Google Scholar] [CrossRef]
- Dantas, T.L.P.; Murilo, F.; Luna, T.; Silva, I.J.; de Azevedo, D.C.S.; Grande, C.A.; Rodrigues, A.E.; Moreira, R.F.P.M. Carbon dioxide—Nitrogen separation through adsorption on activated carbon in a fixed bed. Chem. Eng. J. 2011, 169, 11–19. [Google Scholar] [CrossRef]
- Dantas, T.L.P.; Murilo, F.; Luna, T.; Silva, I.J.; Eurico, A.; Torres, B.; de Azevedo, D.C.S.; Rodrigues, A.E.; Moreira, R.F.P.M. Carbon dioxide—Nitrogen separation through pressure swing adsorption. Chem. Eng. J. 2011, 172, 698–704. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Qasem, N.A.A. An efficient temperature swing adsorption (TSA) process for separating CO2 from CO2/N2 mixture using Mg-MOF-74. Energy Convers. Manag. 2018, 156, 10–24. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Bed length, m | 0.20 |
| Bed cross-sectional area, cm2 | 3.1416 |
| Bed density (kg/m3) | 297 [16] |
| Adsorbent thermal conductivity (W/m·K) | 0.3 [35] |
| Adsorbent heat capacity (J/kg·K) | 900 [35] |
| Particle density, ρp (kg/m3) | 911 [35] |
| Bed porosity, ε | 0.674 [16] |
| qm1,CO2 (Equation (4)) (mol/kg) | 6.80 [16] |
| qm2,CO2 (Equation (4)) (mol/kg) | 9.9 [16] |
| qm1,N2 (Equation (4)) (mol/kg) | 14.0 [16] |
| qm2,N2 (Equation (4)) (mol/kg) | 0 [16] |
| Ko1,CO2 (Equation (4)) (1/Pa) | 2.44 × 10−11 [16] |
| Ko2,CO2 (Equation (4)) (1/Pa) | 1.39 × 10−10 [16] |
| Ko1,N2 (Equation (4)) (1/Pa) | 4.96 × 10−10 [16] |
| Ko2,N2 (Equation (4)) (1/Pa) | 0 [16] |
| ΔH1,CO2 (Equation (4)) (J/mol) | −42,000 [16] |
| ΔH2,CO2 (Equation (4)) (J/mol) | −24,000 [16] |
| ΔH1,N2 (Equation (4)) (J/mol) | −18,000 [16] |
| ΔH2,N2 (Equation (4)) (J/mol) | 0 [16] |
| KL,CO2 (Equation (3)) (1/s) | 0.1213 [16] |
| KL,N2 (Equation (3)) (1/s) | 0.3055 [16] |
| CO2 adsorption heat (Equation (8)), ΔHCO2 (J/mol) | −(42,492.6 – 6568.83 q + 3973.75 q2 − 959.838 q3 + 69.1208 q4) J mol−1 (0 < q < 7.5 mmol g−1) [16] |
| N2 adsorption heat (Equation (8)), ΔHN2 (J/mol) | −18,000 [16] |
| Inlet velocity during adsorption, m/s | 0.1 |
| Pressure outlet during adsorption, kPa | 101.3 |
| Inlet temperature during adsorption, K | 298 |
| Inlet velocity during desorption, m/s | 0 |
| Wall temperature during adsorption, K | Equation (11) |
| Wall temperature during desorption, K | 393 |
| Cells Number | 7140 | 32,000 | 72,500 | 102,000 |
|---|---|---|---|---|
| Tavg (K) | 312.86 | 312.17 | 309.48 | 309.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasem, N.A.A.; Ben-Mansour, R. Assessment of Appropriate Geometry for Thermally Efficient CO2 Adsorption Beds. Appl. Sci. 2022, 12, 5726. https://doi.org/10.3390/app12115726
Qasem NAA, Ben-Mansour R. Assessment of Appropriate Geometry for Thermally Efficient CO2 Adsorption Beds. Applied Sciences. 2022; 12(11):5726. https://doi.org/10.3390/app12115726
Chicago/Turabian StyleQasem, Naef A. A., and Rached Ben-Mansour. 2022. "Assessment of Appropriate Geometry for Thermally Efficient CO2 Adsorption Beds" Applied Sciences 12, no. 11: 5726. https://doi.org/10.3390/app12115726
APA StyleQasem, N. A. A., & Ben-Mansour, R. (2022). Assessment of Appropriate Geometry for Thermally Efficient CO2 Adsorption Beds. Applied Sciences, 12(11), 5726. https://doi.org/10.3390/app12115726







