Investigation of the Heat Transfer and Pressure Drop in Tubes with Transverse Ribs of Zigzag Configurations

Abstract

Heat transfer through tube walls can be promoted using a ribbed tube configuration. Most of the ribs used in previous reports have equal height along the tube length. In this numerical study, we investigate the heat transfer and pressure drop in a transverse ribbed tube where ribs of unequal heights are mounted such that the tops of the ribs form a zigzag shape. Four configurations were studied. Each configuration had a set of two neighboring ribs of different heights. The set was repeated along the tube length to form a zigzag shape. The rib height ratios, e₂/e₁, of the four sets were 0.25, 0.5, 0.75, and 1.0. The ratios of the height of the taller rib, pitch, and width to the tube diameter were kept constant at values of e₁/d = 0.1, p/d = 1.0, and w/d = 0.05, respectively. The Reynolds number ranged from 10,000 to 60,000, while the Prandtl number ranged from 0.71 to 7.0. The results from the k-ε and k-ω models were first validated and compared with the experimental results of smooth and ribbed tubes. The two models showed comparable results, with the k-ε showing slightly better performance and was thus selected to perform the current study. It was found that the average Nusselt number increases along with increases in the rib height ratio, Prandtl number, and Reynolds number. The friction factor changed exponentially with the rib height ratio, while the Reynolds number showed a minor effect. At the same pumping power, a maximum thermal performance enhancement of approximately 8% was achieved at rib height ratios of 0.25 and 0.5. The rib height ratio of 0.5 has an advantage over that of 0.25 as it has a higher average Nusselt number. Two correlations were introduced to estimate the Nusselt number and friction factor for the current ribbed tube of zigzag configurations.

1. Introduction

Poor heat transfer through tube surfaces is mainly due to the boundary layer that develops inside pipes in addition to the low velocity of the fluid, leading to a decrease in the heat transfer coefficient. The utilization of ribs is one example of the artificial roughness methods used to overcome this problem by breaking the boundary layer. Moreover, ribs are used to increase the heat transfer surface area. Using ribs requires no external power; hence, it is considered a passive heat transfer augmentation technique. Numerous industrial applications and devices use ribs to increase heat transfer. One of these applications involves cooling the turbine blades, where the hot gases from combustion can reach up to 1700 °C [1,2,3,4]. Internal cooling is needed to prevent the temperature from rising above the material design limit. Other applications are the heat transfer enhancement of solar collectors, where ribs are mounted to increase solar energy absorption [5,6,7], and heat exchangers [8], where ribbed tubes are used to increase the heat transfer between the unmixed fluids. Other examples of passive techniques used to enhance the heat transfer through tubes are twisted tape inserts [9,10,11,12,13], strip inserts [14], parallel-type ribs [8], helical wires [15], helical ribs [16,17,18], and even the twisting of the whole tube, as performed by Tan et al. [19].

Ribs enhance heat transfer by separating the boundary layer upstream of the rib and then recirculating the fluid slightly downstream. The reattachment of the boundary layer occurs between the ribs, causing an increase in the heat transfer coefficient. One of the leading parameters affecting heat transfer and pressure drop is the rib height-to-diameter ratio, e/d.

The heat transfer and pressure drop in transverse ribbed circular tubes have been investigated numerically and experimentally. San and Huang [20] investigated the problem experimentally, considering the effect of the entrance region. An isothermal surface condition was considered. The rib pitch-to-tube diameter ratio (p/d) and the rib height-to-tube diameter ratio (e/d) were in the ranges of 0.304–5.72 and 0.015–0.143, respectively. The Reynolds number (Re) range was 4608–12,936. It was found that the entrance has little effect on Nu. The effect of the e/d ratio on Nu is larger than that of the p/d ratio. For e/d < 0.057 and e/d > 0.057, the friction factor f is proportional to e/d and (e/d)^2.55, respectively.

An experimental study of different grooved tubes at fully developed turbulent flow was performed by Bilen et al. [21]. Circular, trapezoidal, and rectangular geometries were investigated. Each groove has a depth of 3 mm, while the inner tube diameter is 36 mm. Heat transfer enhancements of 63%, 58%, and 47% for the circular, trapezoidal, and rectangular grooves, respectively, were obtained. Kim et al. [22] studied the experimentally and numerically angled ribs mounted on the inner surface of a tube. Two pairs of vortices were induced, which enhanced the heat transfer compared with conventional transverse ribs. Another experimental and numerical study was conducted by Li et al. [23] to study the turbulent heat transfer and flow resistance in ribbed tubes. The e/d ranged from 0.01 to 0.05. The standard k-ε model was used. Both the numerical and experimental results showed good agreement. The most significant discrepancies were 10% for the Nusselt numbers and 15% for the friction factors. When e/d < 0.02, the Nusselt number ratio and the friction factor ratio were comparable. The friction factor increased rapidly as e/d increased above 0.03.

A numerical investigation using k-ε was performed by Mohammed et al. [24] to study the effects of different geometrical parameters on the thermal and flow fields through transversely corrugated circular ribs. The roughness height (e/d) was changed from 0.025 up to 0.1. The Nusselt number and friction factor increased as e/d increased, but the rate of increase in the friction factor was much higher than that in the Nusselt number. Another numerical investigation using the SST k-ω model was performed by Kim et al. [25]. The values of e/d increased from 0.025 to 0.15. It was found that rib height was the dominant factor in heat transfer and friction loss. The highest thermal performance was found when e/d ranged from 0.1 to 0.125, apart from the rib width and the rib pitch values. Circular cross-sectional rings inserted near the tube wall were investigated numerically by Ozceyhan et al. [26]. Five pitches in the range of 0.5 d to 3.0 d were studied, whereas the Reynolds number was in the range of 4475–43,725. The best overall 18% enhancement was achieved at Re = 15,600. Another numerical investigation was conducted by Akermann et al. [27] using the LES method. The pipe insert was a helical rib shape. Two Re values and three Pr values were applied. There was a 190% heat transfer enhancement compared with a smooth pipe. It is also notable that while the enhancement in heat transfer was between 170% and 190%, the pressure loss was doubled compared with the results of the smooth tubes. A numerical and experimental study of heat transfer and pressure drop was performed by Khdher et al. [28] on a circumferential ribbed pipe using a nanofluid. The e/d ranged from 0.034 to 0.1. A realizable k-ε model was applied along with an enhanced wall treatment. Both the heat transfer and the friction coefficients increased as e/d increased.

Córcoles-Tendero et al. [29] conducted a 3D numerical investigation of the turbulent flow inside spirally corrugated tubes. The tube diameter and length were 18 mm and 6 m, respectively. The corrugation depth was 0.43 mm, and the helical pitch was 15.86 mm. The k-ε turbulence model was used. The error in predicting the Nusselt number was within 17%. Some authors performed their investigation on one e/d value, such as Wang et al. [30], who performed an experimental work using an e/d value of 0.055. In contrast, Jordan [31] used the LES numerical model to perform a study using e/d = 0.115. Helically finned and corrugated tubes with different geometric parameters were investigated by Aǧra et al. [32], where the k-ε model was applied. The Reynolds numbers ranged from 12,000 to 57,000. It was found that helically finned tubes worked better regarding thermal performance than corrugated ones. Another experimental and numerical study was conducted by Xu [33] on ribbed tubes of p/d = 0.225, e/d = 0.05, and a helix angle of 15° using Therminol-55 heat transfer fluid. The heat transfer increased 2.24-fold, while the friction factors increased by 2.4- and 2.8-fold compared with the smooth tube results.

As previous work indicates, the heat transfer is enhanced as the rib height increases. The drawback of increasing the rib height is the increase in the friction factor and, hence, an increase in the working fluid’s pumping power. Most of the previous research has focused on studying ribbed tubes comprising equal-height ribs along the tube length. In the present numerical work, the height of half of the transverse ribs was changed along the pipe length while the height of the other half remained unchanged. Thus, the ribs formed a zigzag shape configuration inside the tube. The effects of different rib height ratios as well as their effects on heat transfer and pressure drop were studied. The effects of the Prandtl number and the Reynolds numbers were also investigated. Correlations were deduced for estimating the Nusselt number and friction factor as functions of the studied parameters. The performances of the aforementioned configurations were investigated and compared, allowing for the selection of the configuration with the best performance.

2. Numerical Modeling

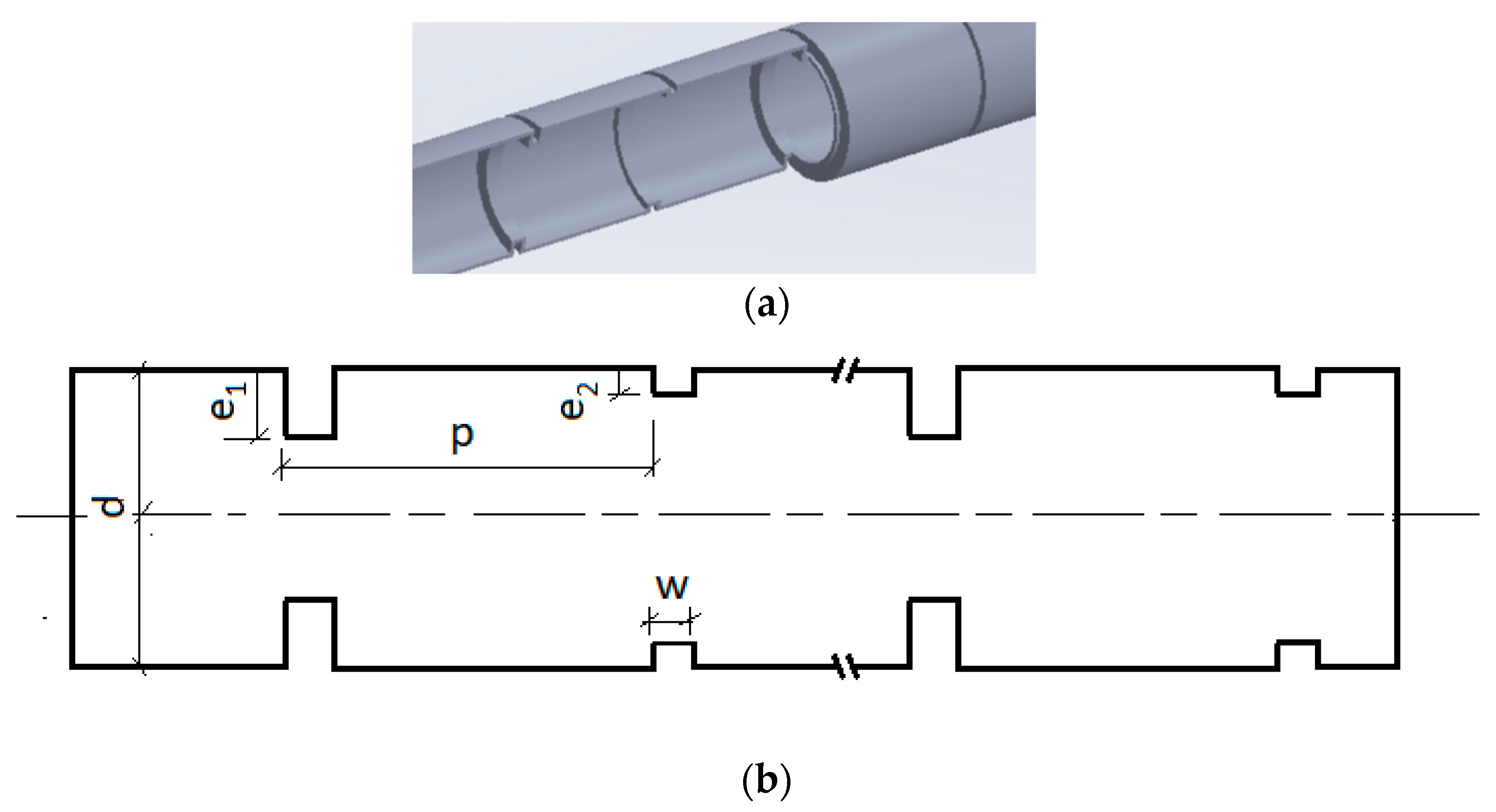
2.1. The Physical Model

The physical model is a tube with internal rectangular transverse ribs, as shown in Figure 1. The zigzag configuration consists of a set of two neighboring ribs with different heights, and the set is repeated along the tube length. The higher rib has a height of e₁, while that of the shorter rib is denoted e₂. Four ratios of e₂/e₁ (0.25, 0.5, 0.75, and 1.0) were tested. The e₁/d ratio was kept fixed at a value of 0.1. The pitch between the ribs, p, and the rib width, w, were held fixed throughout the current study. The values for the pitch-to-diameter (p/d) and width-to-diameter (w/d) ratios were 1.0 and 0.05, respectively.

2.2. Governing Equations

The first assumption of the current work is steady-state conditions for fluid flow and heat transfer, while the second assumption is that the fluid has constant properties. Hence, the fluid is considered to be incompressible. Three equations govern the current problem’s fluid flow and heat transfer: the continuity equation, the momentum equation, and the energy equation. The equations are presented in Reynolds averaging form as follows [34].

2.2.1. The Continuity Equation

The continuity equation for incompressible fluid flow can be represented as [34]:

$$\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}} \left({\mathrm{u}}_{\mathrm{i}}\right)=0$$

(1)

in which u_i is the mean velocity value. The problem under consideration is an axisymmetric one. The velocity values are in the axial and radial directions; hence, i = 1,2.

2.2.2. The Momentum Equation

The momentum equation is in the form [34]:

$$\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}} \left({\mathsf{\rho }\mathrm{u}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{j}}\right)=-\frac{\partial \mathrm{P}}{\partial {\mathrm{x}}_{\mathrm{i}}}+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}} \left[\mu \left(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}-\frac{2}{3}{\delta }_{ij}\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\right)\right]+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}} \left(-\rho \overline{ {\acute{\mathrm{u}}}_{\mathrm{i}}{\acute{\mathrm{u}}}_{\mathrm{j}}}\right)$$

(2)

where $\acute{\mathrm{u}}$ is the fluctuating velocity component and $-\rho \overline{ {\acute{\mathrm{u}}}_{\mathrm{i}}{\acute{\mathrm{u}}}_{\mathrm{j}}}$ are the Reynolds stresses [34].

2.2.3. The Energy Equation

The energy equation can be introduced as [34]:

$$\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}} \left[{\mathrm{u}}_{\mathrm{i}}\left(\mathsf{\rho }\mathrm{E}+\mathrm{P}\right)\right]=\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}} \left[{\mathrm{k}}_{\mathrm{eff}}\frac{\partial \mathrm{T}}{\partial {\mathrm{x}}_{\mathrm{j}}}+{\mathrm{u}}_{\mathrm{i}}{\left({\mathsf{\tau }}_{\mathrm{ji}}\right)}_{\mathrm{eff}}\right]$$

(3)

where the energy is defined as E = h − P/ρ + u²/2; h is the sensible enthalpy. The two terms on the right-hand side are the heat transfer by conduction and the viscous dissipation. K_eff is the effective thermal conductivity, while ${\left({\mathsf{\tau }}_{\mathrm{ji}}\right)}_{\mathrm{eff}}$ is the stress tensor that can be calculated as [34]:

$${\left({\mathsf{\tau }}_{\mathrm{ji}}\right)}_{\mathrm{eff}}={\mathsf{\mu }}_{\mathrm{eff}}\left(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}-\frac{2}{3}{\mathsf{\delta }}_{\mathrm{ij}}\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\right)$$

(4)

More details regarding the different models used to determine the values of Reynolds stresses and other quantities can be found in [26,34].

2.3. Data Reduction

The heat transfer and pressure drop were investigated via the calculation of the average Nusselt numbers and the pressure drop. First, the Reynolds number is defined as [35]:

$$\mathrm{Re}=\frac{\mathsf{\rho }\mathrm{ud}}{\mathsf{\mu }}$$

(5)

where $\mathsf{\rho }$ and $\mathsf{\mu }$ are the fluid density and viscosity, respectively, while $\mathrm{u}$ is the mean inlet velocity.

The local heat transfer coefficient, h_x, is calculated by determining the applied heat flux at the wall, $\mathrm{q}″$, as in [35]:

$${\mathrm{h}}_x=\frac{ \mathrm{q}″}{{\mathrm{T}}_{\mathrm{s},\mathrm{x}}-{\mathrm{T}}_{\mathrm{b},\mathrm{x}}}$$

(6)

where T_s,x is the wall surface temperature at the distance x that is found from the numerical solution. T_b,x is the bulk surface temperature at location x, and is calculated from [35]:

$${\mathrm{T}}_{\mathrm{b},\mathrm{x}}={\mathrm{T}}_{\mathrm{b},\mathrm{i}}+\frac{ \mathrm{q}″ \mathsf{\pi }\mathrm{d}\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{i}}\right)}{ \dot{\mathrm{m}}\mathrm{c}}$$

(7)

where T_b,i is the bulk temperature at location x_i.

The average heat transfer coefficient over the distance from x₁ to x₂ can be calculated as [35]:

$${\mathrm{h}}_{\mathrm{av}}=\frac{1}{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}\underset{{\mathrm{x}}_1}{\overset{{\mathrm{x}}_2}{{\displaystyle \int }}}{\mathrm{h}}_x\mathrm{dx}$$

(8)

The average Nusselt number can be calculated from the average heat transfer coefficient as [35]:

$${\mathrm{Nu}}_{\mathrm{av}}=\frac{{\mathrm{h}}_{\mathrm{av}}\mathrm{d}}{\mathrm{k}}$$

(9)

where k is the thermal conductivity of the flowing fluid. The friction factor is calculated over the distance x₂ − x₁, as [36]:

$$\mathrm{f}=\frac{2\mathrm{d}\left({\mathrm{P}}_1-{\mathrm{P}}_2\right)}{{\mathsf{\rho }\mathrm{u}}^2\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}$$

(10)

In order to evaluate the performance of the zigzag configuration in comparison to the traditional ribbed tube configuration, where the rib heights are the same, the performance evaluation criterion index, PEC, was applied. The performance evaluation criterion is a method for weighing the thermal enhancement of different cases at the same pumping power. Webb and Eckert [37] and Webb [38] coined an expression for the PEC. The PEC has been adapted in previous work [8,24], and in Karwa et al. [39], which mentions many references for studies that applied the PEC. The PEC can be evaluated as:

$$\mathrm{PEC}=\frac{\left(\mathrm{Nu}/{\mathrm{Nu}}_{\mathrm{s}}\right)}{{\left(\mathrm{f}/{\mathrm{f}}_{\mathrm{s}}\right)}^{1/3}}$$

(11)

where ${\mathrm{Nu}}_{\mathrm{s}}$ is the Nusselt number of a fully developed smooth tube, and ${\mathrm{f}}_{\mathrm{s}}$ is the corresponding friction factor. The friction factor for fully developed smooth tubes is a function of the Reynolds number and can be evaluated based on the Petukhov correlation in the range $3000 \le \mathrm{Re}\le {10}^6$ [40] as:

$${\mathrm{f}}_{\mathrm{s}}={\left(0.79 \ln \mathrm{Re}-1.64\right)}^{-2}$$

(12)

The Nusselt number value of a smooth tube depends on the Reynolds number, the Prandtl number, Pr, and the friction factor, as suggested by the Gnielinski correlation, such as [40]:

$${\mathrm{Nu}}_{\mathrm{s}}=\frac{\left({\mathrm{f}}_{\mathrm{s}}/8\right)\left(\mathrm{Re}-1000\right) \mathrm{Pr}}{1.07+12.7{\left({\mathrm{f}}_{\mathrm{s}}/8\right)}^{1/2}\left({\mathrm{Pr}}^{2/3}-1\right)}$$

(13)

Another widely used correlation to find the Nusselt number for smooth tubes and turbulent fully developed flow is the Dittus–Boelter correlation. When the working fluid is heated, the correlation can be presented as [35,41]:

$${\mathrm{Nu}}_{\mathrm{s}}=0.023{ \mathrm{Re}}^{0.8}{ \mathrm{Pr}}^{0.4}$$

(14)

2.4. Computational Domain and Boundary Conditions

The physical model was changed to a computational domain, as shown in Figure 2. As there is no change in velocity or temperature with the angular direction, the computational domain can be represented as an axisymmetric rectangular one. The tube diameter was kept the same as the physical one, at d = 10 mm. The computational domain has three sections: the inlet, test, and outlet sections. The inlet section is a smooth tube that expands for 20 d to allow for fully developed flow before the test section. Another benefit of this long inlet section is that testing is conducted using the fully developed flow of a smooth tube, as discussed below. The test section is approximately 9 d and comprises nine ribs. The first rib is a tall rib, followed by a short rib. This pattern of long and then short ribs is repeated along the test section. A 10th rib is added at the end of the test section between the test and the exit sections to maintain the same flow pattern over the test section. The outlet section is 5 d long to prevent reverse flow during the computational simulations. The lengths of the inlet and outlet sections are the same as in Mohammed et al. [24]. The test section of the present study has five tall ribs and four short ribs. The height of the tall ribs is 0.1 d and was kept fixed over the current study. The height of the shorter ribs was changed to allow its effect to be studied.

The domain was discretized using a quad structural grid. The grid was clustered close to the tube wall and around the ribbed regions to capture the gradients of the variables more precisely, as in Figure 3. The boundary conditions were as follows. The lower boundary at r = 0 was axisymmetric. The upper boundary was at the tube wall, r = d/2, where the velocity components are zero. A constant heat flux was applied at the tube wall, normal to the axial direction. At the inlet section, x = 0, a uniform axial velocity component value was applied. The inlet temperature was equal to 300 K. A constant pressure value was applied at the outlet section.

2.5. Verification of the Numerical Model

It is crucial to verify the computation model in two ways. The first is to perform a grid independence study to ensure that the obtained results are not affected by the grid size or number. In the second verification process, the numerical results are compared with the experimental or numerical data obtained from the literature. Two grid distributions were tested, as well as two numerical models. The Ansys Fluent software package was used to generate the computational domain and results. The two most widely used models, which are the k-ε and k-ω models, were compared to determine and select the model that is more suitable for the current application.

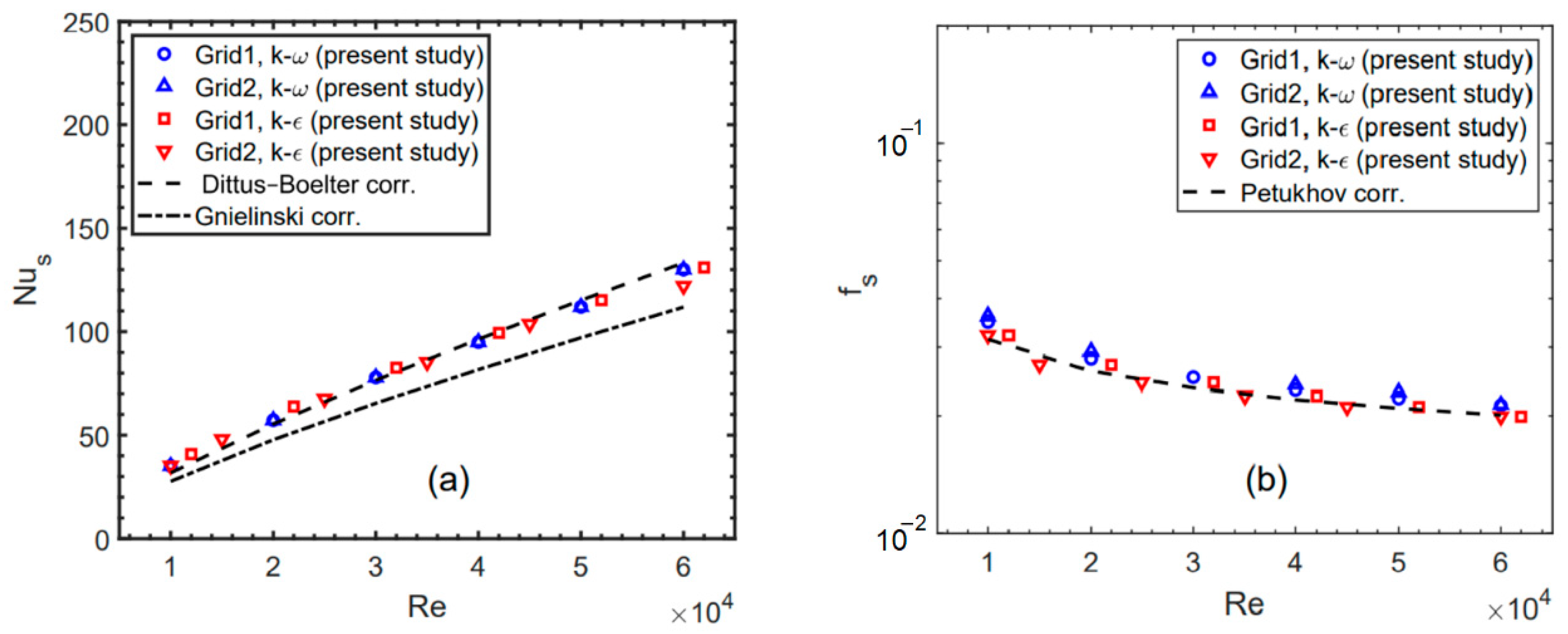
2.5.1. Smooth Pipe Verification

The numerical domain has two smooth sections, which are the inlet and exit sections. The grid distribution in the radial direction at the test section of the ribbed tube is the same as that of the smooth sections. Figure 4 depicts comparisons of the average Nusselt number of a smooth pipe, Nu_s, obtained from the current numerical simulation to that obtained from the Gnielinski and Dittus–Boelter correlations, Equations (13) and (14), respectively. Two grids were applied. Grid1 has 87,271 nodes, while Grid2 has 238,321 nodes. Heat flux was applied at the inlet section of the computational domain, as it represents a smooth pipe of a length more than 10 times its diameter to ensure fully developed flow. The Nusselt number was calculated 15 d from the inlet. The Prandtl number was 0.71, which may represent the flow of air as a working fluid. The k-ε and k-ω models were investigated. The numerical results show a very high degree of agreement with the Dittus–Boelter correlation. On the other hand, the numerical results overestimate the values obtained by the Gnielinski correlation. The two grids almost indicate identical results.

The friction factor for a smooth tube was compared against the Petukhov correlation, Equation (12), as shown in Figure 4b. Very good predictions of the friction factor were obtained, and the two grids have almost identical prediction values. The discrepancies between the predicted and correlation results decrease as Re increases. The predicted results of the two tested numerical models are close, though are marginally better for the the k-ε model than the k-ω prediction model.

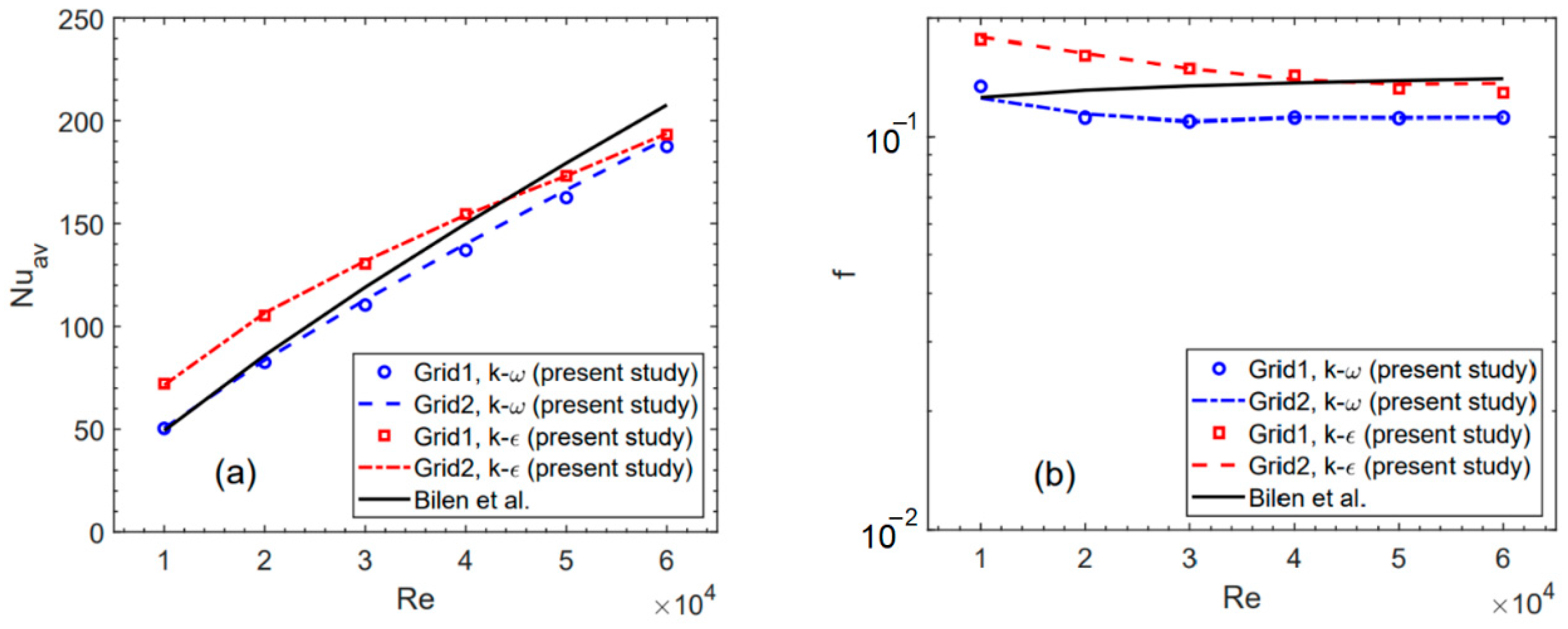
2.5.2. Ribbed Pipe Verification

In the case of a ribbed tube, the results were verified by comparison with the experimental results of Bilen et al. [21], in which a tube of rectangular grooves was studied. The height, pitch, and width of the groove are 3, 12, and 6 mm, respectively. The inner tube diameter is 36 mm, while the diameter at the groove section is 42 mm. It is important to note that the Re and other parameters are based on the inner diameter of 36 mm. The k-ε and k-ω models were tested as well as Grid 1 and Grid 2.

Both the average Nusselt number, Nu_av, and the friction factor, f, were compared at a Prandtl number of 0.71, as shown in Figure 5. For the same numerical model, the results of Grid1 and Grid2 of the current simulation are almost identical. The results for both the numerical models show good agreement with those of Bilen et al. [21]. The k-ω numerical model shows better agreement at low Re values, while the k-ε model results in better estimations at higher Re values. Either of the two numerical models can be used. Based on the overall verification, k-ε was selected for use as the simulation model of the current study.

3. Results and Discussion

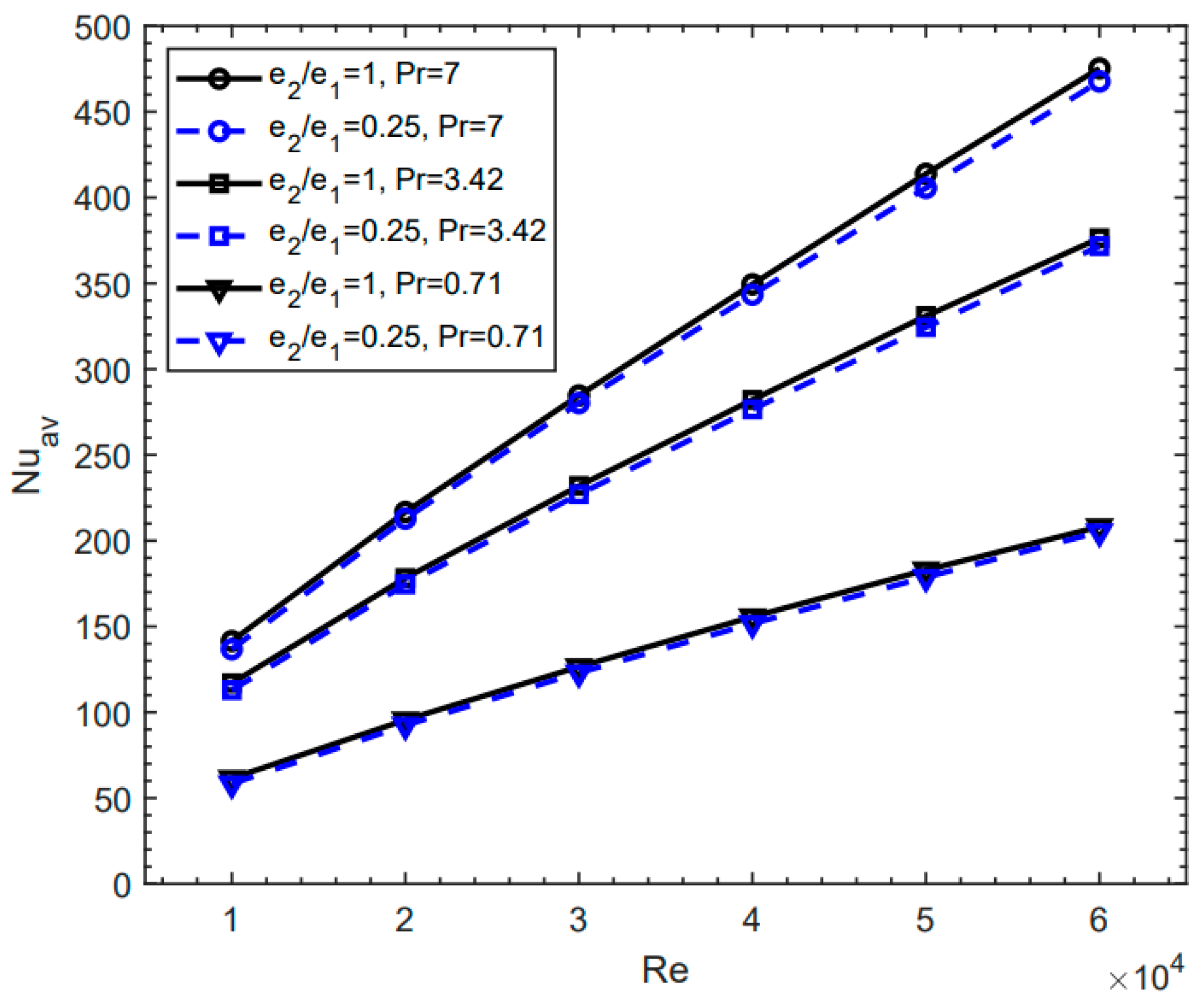
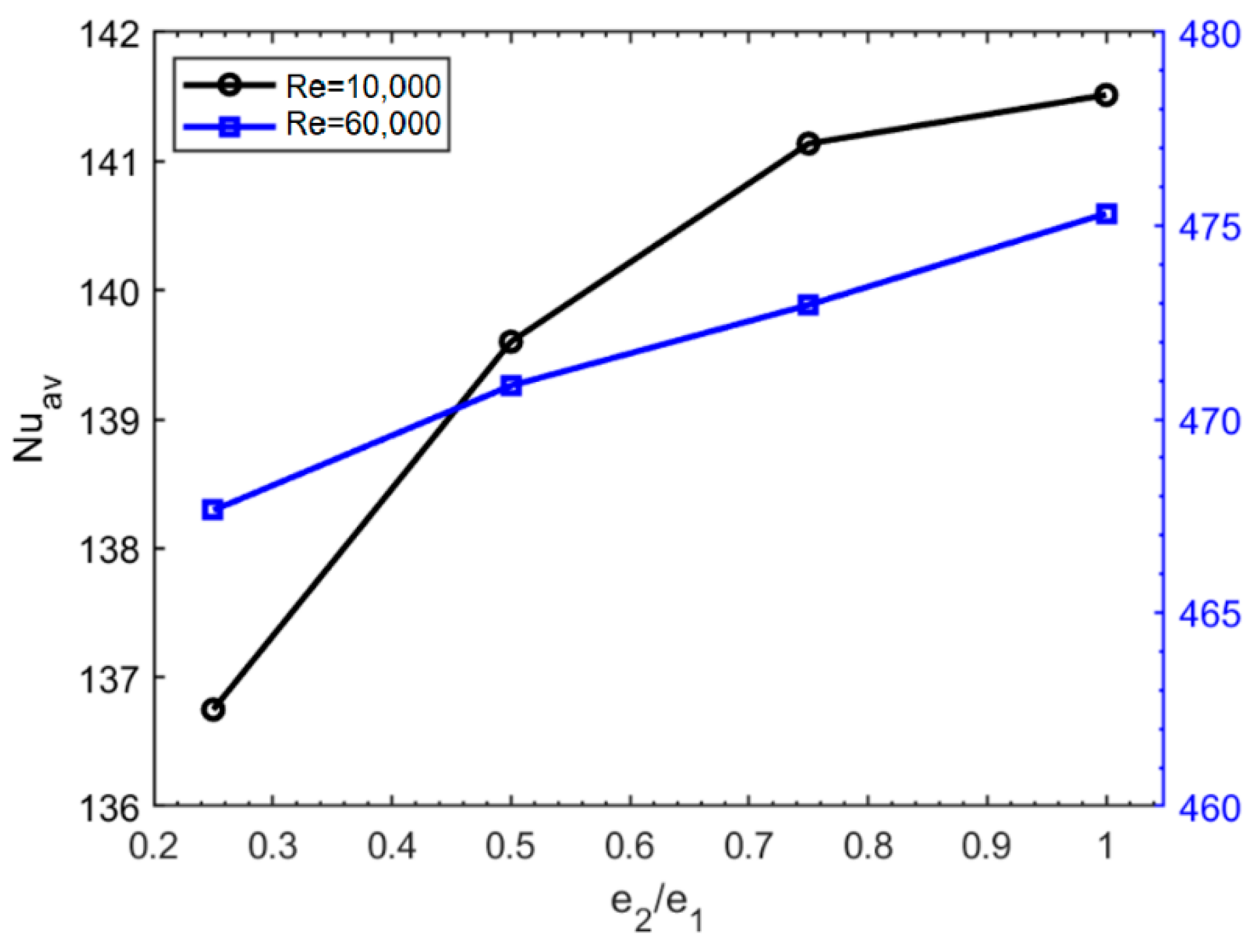
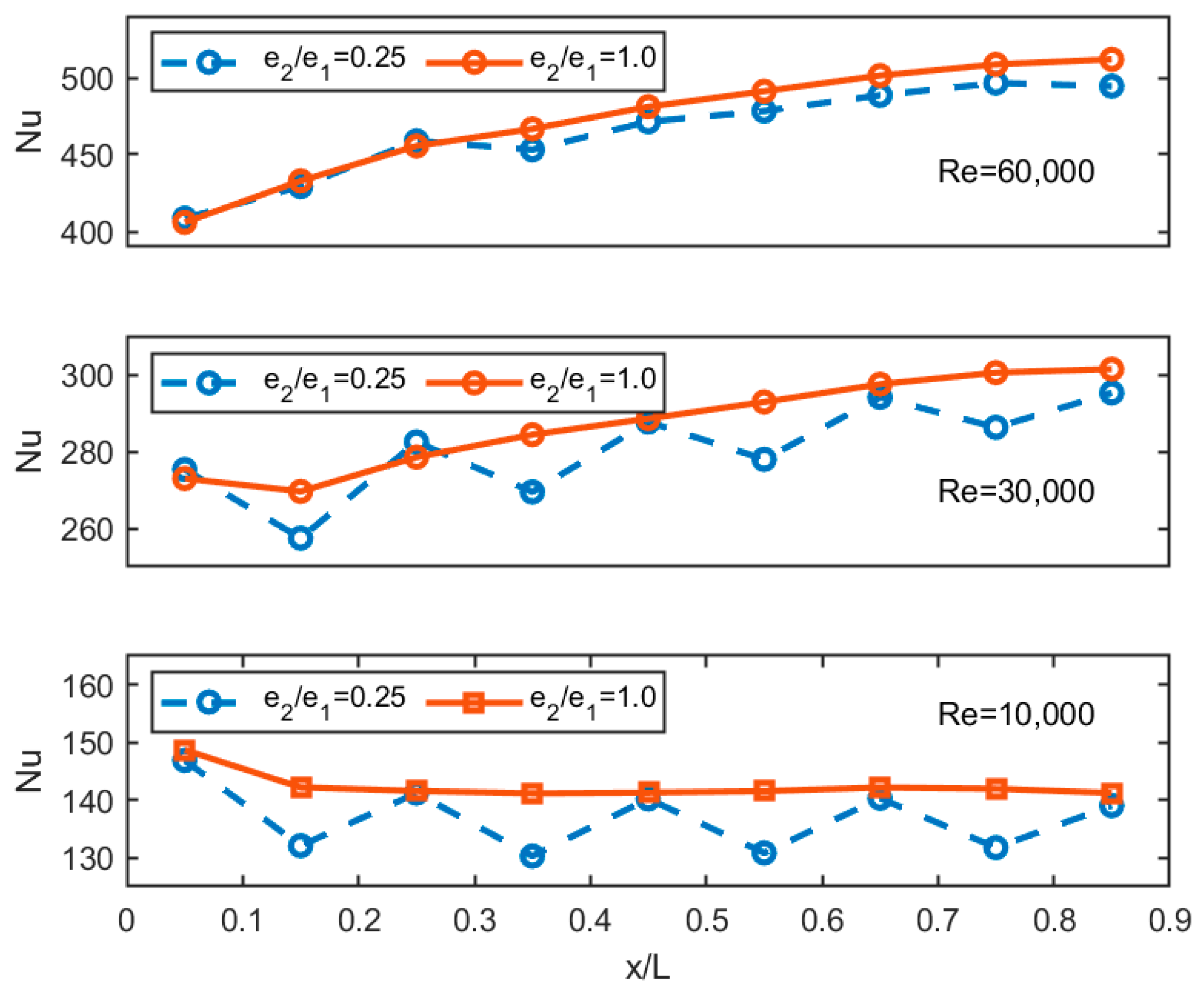
3.1. Effect of the Zigzag Ratio and Pr Number on the Nu Number

The effect of changing the ratio e₂/e₁ on the average Nusselt number, Nu_av, while keeping the rib width and pitch fixed, is presented in Figure 6. Two cases are shown. The first case is a ribbed tube of equal rib height ratio, e₂/e₁ = 1, while the second case is a ribbed tube with a zigzag rib arrangement, e₂/e₁ = 0.25. The first rib height to tube diameter is e₁/d = 0.1, the width of the ribs to the tube diameter is w/d = 0.05, and the pitch between ribs to the diameter is p/d = 1. Three Prandtl number (Pr) values (0.71, 3.42, and 7.0) were investigated. The presence of the ribs increases the Nu values compared with that of the smooth tubes, due to the disturbance of the viscous sublayer as a direct effect of the ribs’ presence. The average Nusselt number increases almost linearly as the Reynolds number increases. The slope of such lines increases with the Pr number. Likewise, the higher the Pr number, the higher the average Nu number. The higher Pr number indicates that heat transfer is higher via fluid momentum than via conduction diffusion. The decrease in the e₂/e₁ value decreases the average Nusselt number at all values of the Re number and Pr numbers. At a Pr of 7.0, Re = 10,000 and 60,000, and the reductions in Nu_av were only 3.4 and 1.6%, respectively, although the decrease in the rib height e₂ was by 75% compared with e₁.

The detailed effect of changing e₂/e₁ on the average Nusselt number is better presented in Figure 7. Four values of e₂/e₁ (0.25, 0.5, 0.75, and 1) are plotted while keeping the values of e1/d = 0.1, w/d = 0.05, and p/d = 1. Two Reynolds number values of 10,000 and 60,000 were selected to represent the minimum and maximum values, respectively, of the present study, while the Pr number was kept constant at 7.0. The average Nusselt number increases as e₂/e₁ increases. At a lower Reynolds number, the change in the average Nusselt number was nonlinear. The rate of change in the average Nusselt number decreases as e₂/e₁ increases. At a high Reynolds number, the change in the average Nusselt number is almost linear, with e₂/e₁.

Figure 8 demonstrates the average Nusselt number between the ribs, Nu, plotted at the midspan between the ribs at three values of the Reynolds number (10,000, 30,000, and 60,000). Two values of e₂/e₁ (0.25 and 1) are presented, while the Pr number is 7.0. At a Re of 10,000, the Nusselt number between the ribs decreases slightly as the Reynolds number increases. Equal-height ribbed tubes, e₂/e₁ = 1, show almost identical Nu values between the ribs. When a zigzag arrangement of e₂/e₁ = 0.25 is used, a zigzag pattern of the Nu is clear, and its lower values are downstream of the shorter ribs. This zigzag behavior of the Nu decreases as the Reynolds number increases and almost vanishes at Re = 60,000. At this Re value, the Nu values are not affected by reducing the value of e₂ upstream of the test section.

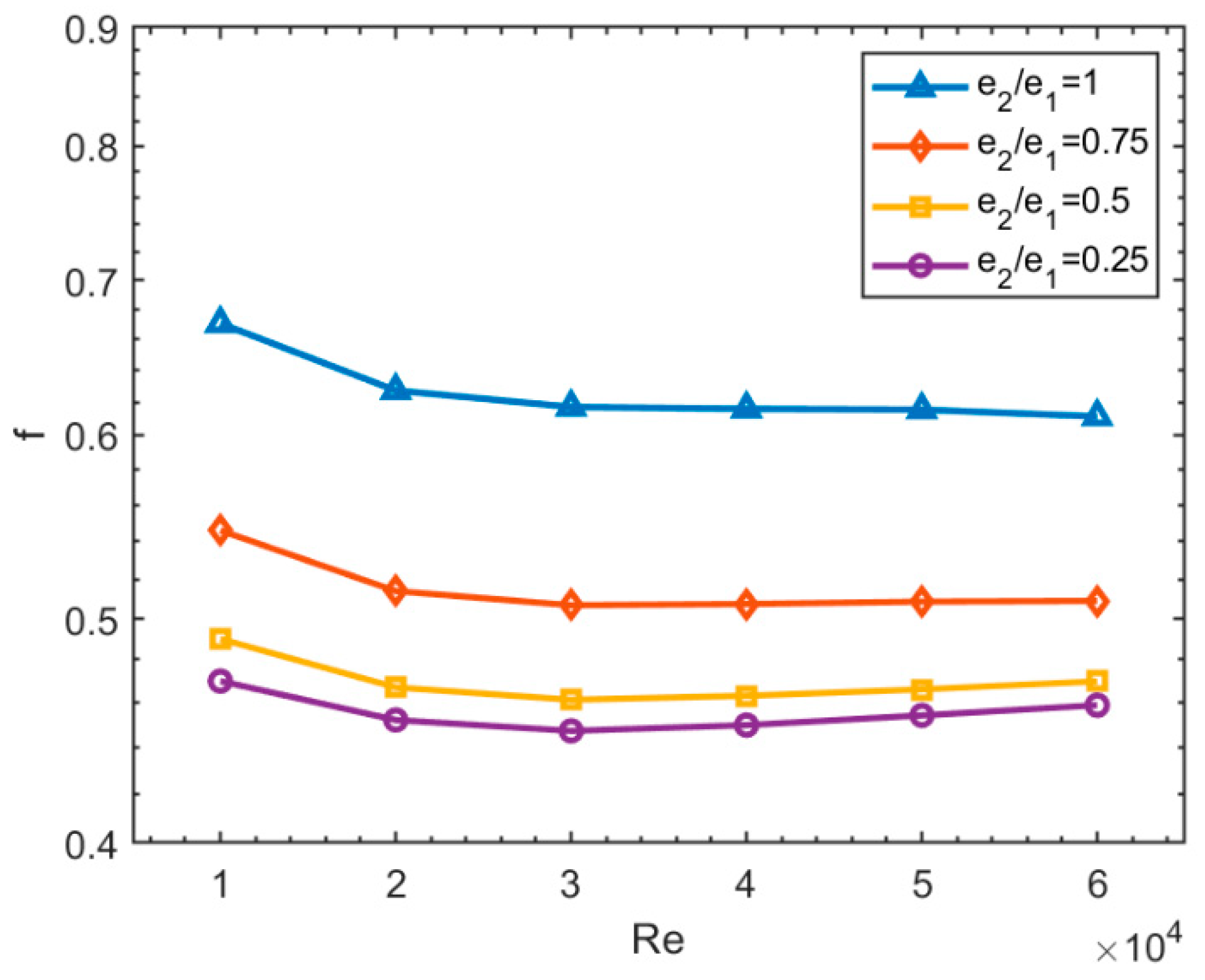
3.2. Effect of the Zigzag Ratio on the Friction Factor

The effect of zigzagging the rib heights on the friction factor is shown in Figure 9. The friction factor values decrease considerably as the e₂/e₁ ratio decreases. At e₂/e₁ values of 0.25 and 0.5, the friction values decrease by 27 and 25%, respectively, compared with the equal rib height case, e₂/e₁ = 1, respectively. The highest friction factors occur at Re = 10,000, and then they decrease up to Re = 30,000 for each value of e₂/e₁. After Re = 30,000, the behavior of the friction factor changes according to the values of e₂/e₁. The friction factor increases after Re = 30,000 for e₂/e₁ = 0.25 and 0.5, remains constant at e₂/e₁ = 0.75, and continues decreasing at e₂/e₁ = 1. However, approximation of the behavior of the friction factor shows that it does not change with Re for Re > 20,000.

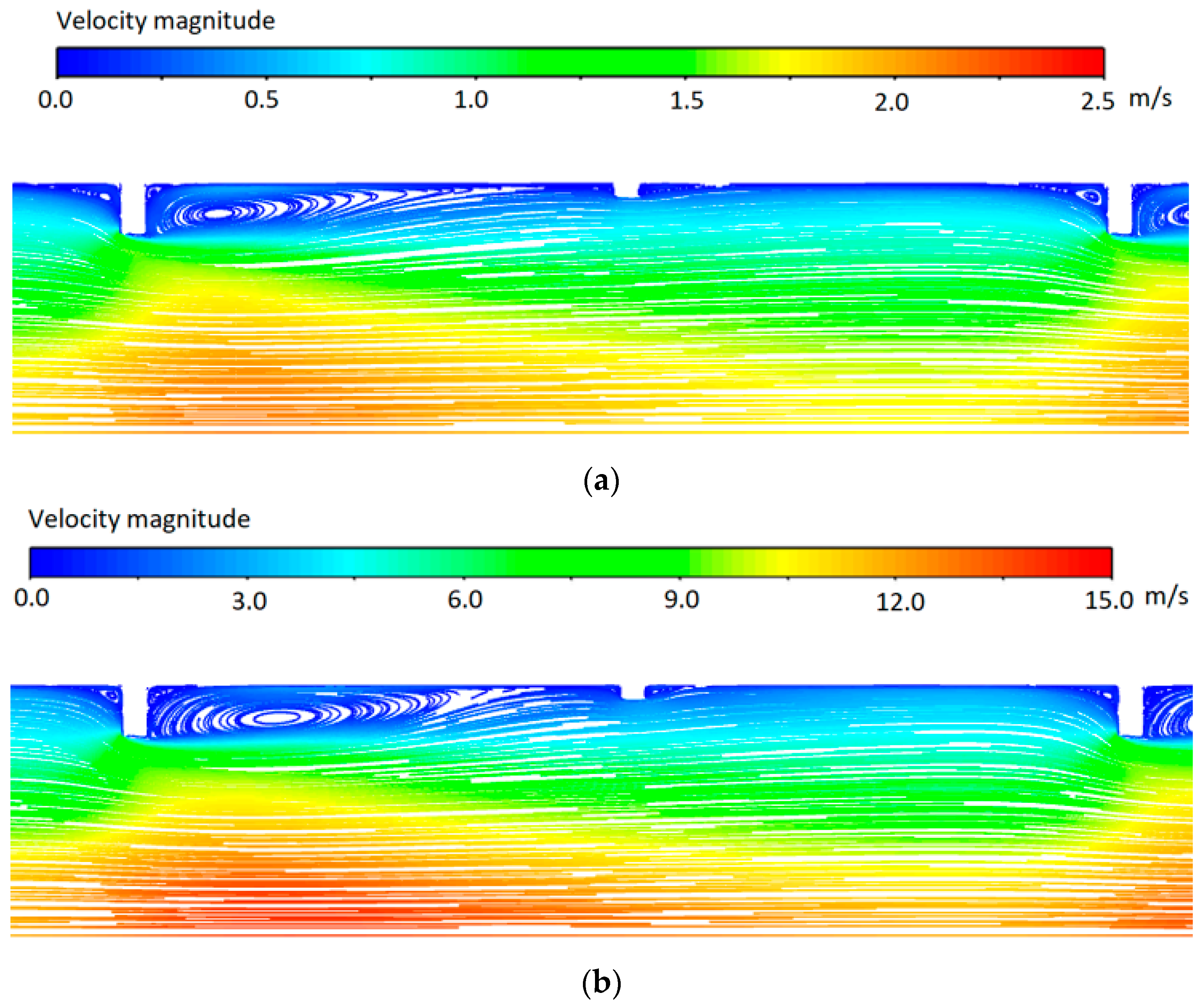
3.3. Streamlines and Velocity Flow Fields

To understand the flow patterns, it is helpful to demonstrate how the flow fields change with the Reynolds number. Figure 10a,b illustrate the flow field streamlines and the velocity fields in the region between the fifth and the seventh ribs at Reynolds numbers of 10,000 and 60,000, respectively. The maximum velocity value of each color legend is 2.5 times that of the inlet velocity. The high-velocity values occur just downstream of the opposite higher ribs, with a maximum value at the tube axis.

A large circulation zone exists downstream of the taller ribs and occupies most of the length up to the shorter rib. A small circulation zone can be observed downstream of the shorter rib. Other smaller circulation zones exist upstream and downstream of each rib. The circulation enhances fluid mixing by bringing the cold fluid from the middle region to the hot fluid region near the tube wall.

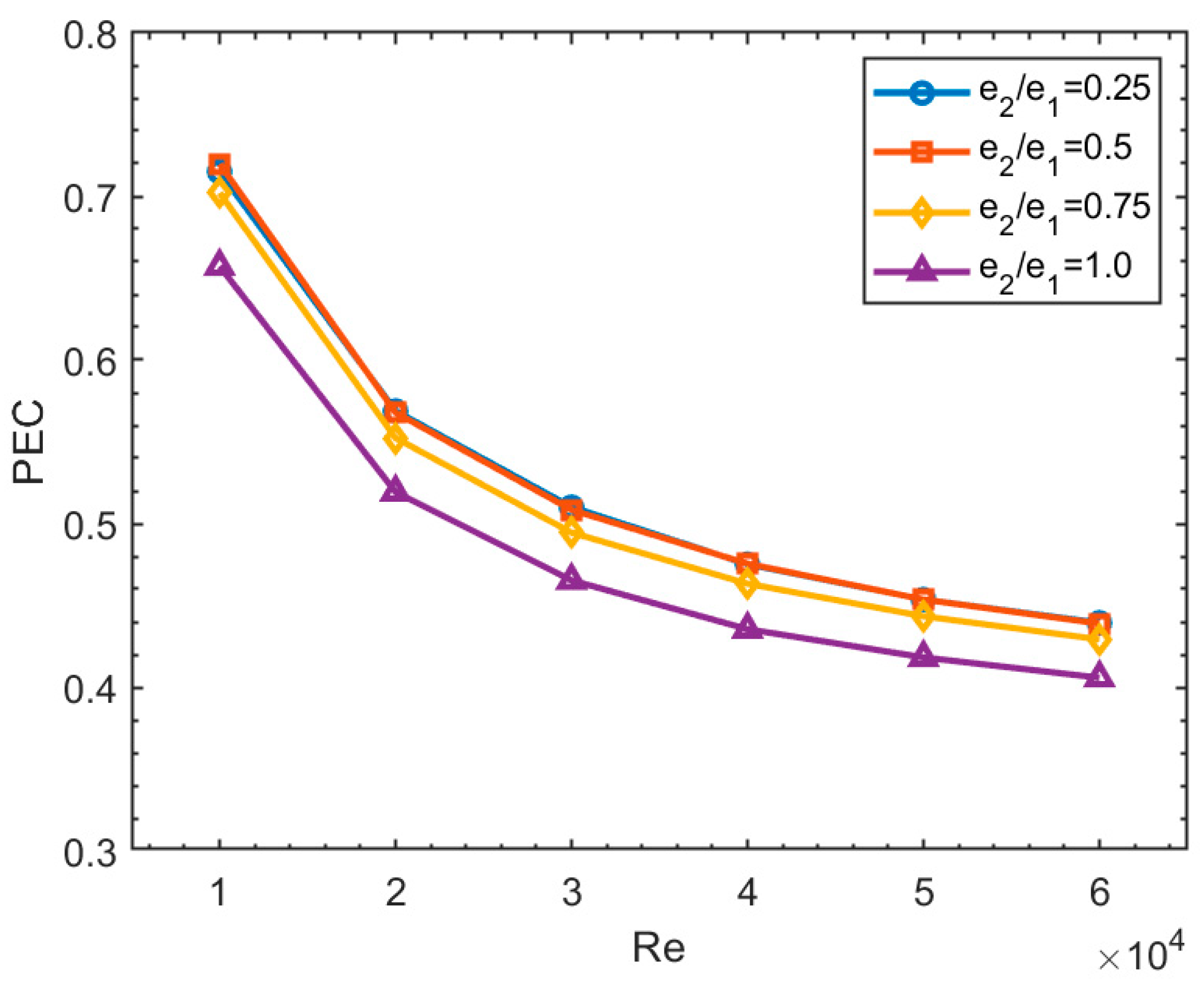
3.4. The Performance Evaluation Criterion, PEC

The performance evaluation criterion, PEC, of four zigzag ratios and Pr = 7.0 is shown in Figure 11. For the same e₂/e₁ ratio value, the PEC values nonlinearly decrease with an increase in the Reynolds number. The lower the e₂/e₁ ratio value, the better the performance. The best performance is achieved at e₂/e₁ values of 0.25 and 0.5. Both ratios show almost identical PEC values. The value of e₂/e₁ = 0.5 has an advantage over the 0.25 value, since it has a higher Nusselt number, as mentioned above. Therefore, the best performance is achieved at an e₂/e₁ value of 0.5. This indicates that, compared with the traditional equal-height rib corrugated arrangement, the performance associated with a ribbed tube with a zigzag arrangement is enhanced by 8.2%.

3.5. Average Nusselt Number and Friction Factor Correlations

Based on the results obtained from the numerical investigations of the 49 ribbed tube cases, the following correlations for the average Nusselt number and friction factor were obtained. The correlations are limited to ribbed tubes, where e₁/d = 0.1, p/d = 1, and w/d = 0.05. The average Nusselt number can be correlated as:

$${\mathrm{Nu}}_{\mathrm{av}}=0.1365 {\left({\mathrm{e}}_2/{\mathrm{e}}_1\right)}^{0.01544}{ \mathrm{Re}}^{0.6766}{ \mathrm{Pr}}^{0.3604}$$

(15)

which has an R² value of 0.997. The maximum deviation of Nu_av is 7.5% at Re = 10,000, Pr = 3.42, and e₂/e₁ = 1, while the average deviation of all values is 2.2%. The exponent of the Prandtl number is 0.3604, which is in the range between 0.3 and 0.4, as found in many previous studies [9,12].

Likewise, the friction factor correlation can be presented as:

$$\mathrm{f}=0.5422 \exp \left[0.4192\left({\mathrm{e}}_2/{\mathrm{e}}_1\right)\right]{ \mathrm{Re}}^{-0.03093}$$

(16)

The friction factor changes exponentially with the zigzag ratio e₂/e₁. The R² value is 0.88. The maximum deviation is 7.5% at Re value of 10,000, and e₂/e₁ = 1, while the average deviation is 4.1%.

4. Conclusions

In the current work, parameters associated with heat transfer and pressure drop were investigated in corrugated tubes with a zigzag rib configuration, where two ribs of different heights were repeated along the tube length. The following can be concluded:

• For Reynolds number increases in the range of 20,000 up to 60,000, the average Nusselt number increases almost linearly with the Re, but the friction factor shows an almost constant value;
• By increasing the value of e₂/e₁, the average Nu and f values increase. At low Re values, the growth of Nu is nonlinear, which is different to the behavior of the average Nu at high Re values. The average Nu increases nonlinearly with the Pr number;
• The friction factor varies exponentially with e₂/e₁;
• The average Nu between the ribs shows a fluctuating behavior at low and high average Re values when the rib height ratios are less than 1.0;
• The circulation zone behind the higher rib dominates the downstream region up to the short rib, which has a smaller downstream circulation zone;
• The performance evaluation criteria index (PEC) values decrease with increases in the Re values and the rib height ratio. PEC values of approximately 8.2% were achieved at rib height ratios of 0.25 and 0.5. A rib height ratio of 0.5 is to be preferred when considering higher values of Nusselt numbers.

In the future, the present work should be extended to determine the effects with varying e₁/d, p/d, and w/d.