Parameter Identification of Structures with Different Connections Using Static Responses
Abstract
:1. Introduction
2. Formulation for Parameter Identification
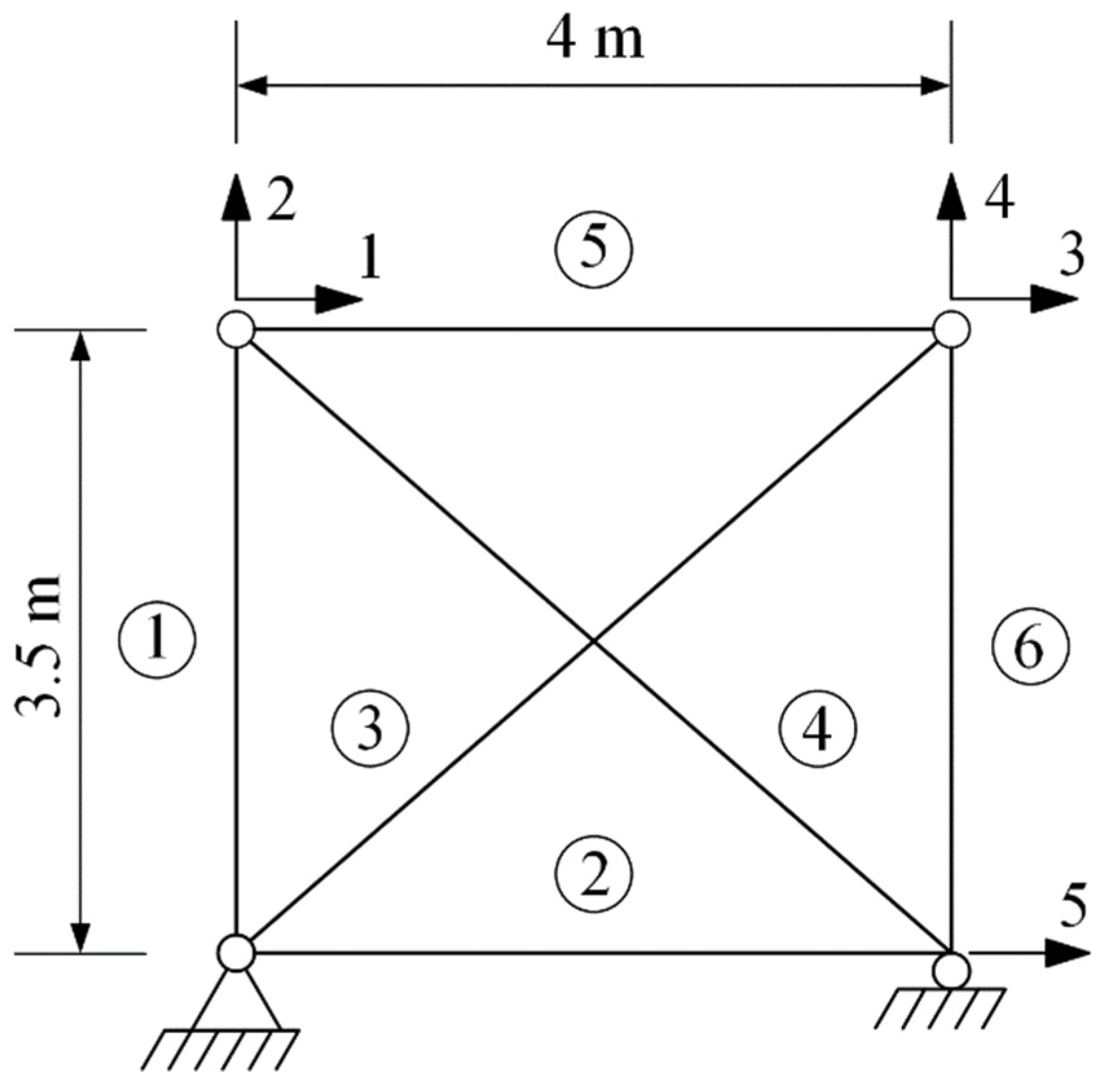
3. Parameter Identification for Truss
3.1. Member Stiffness Matrix of Truss
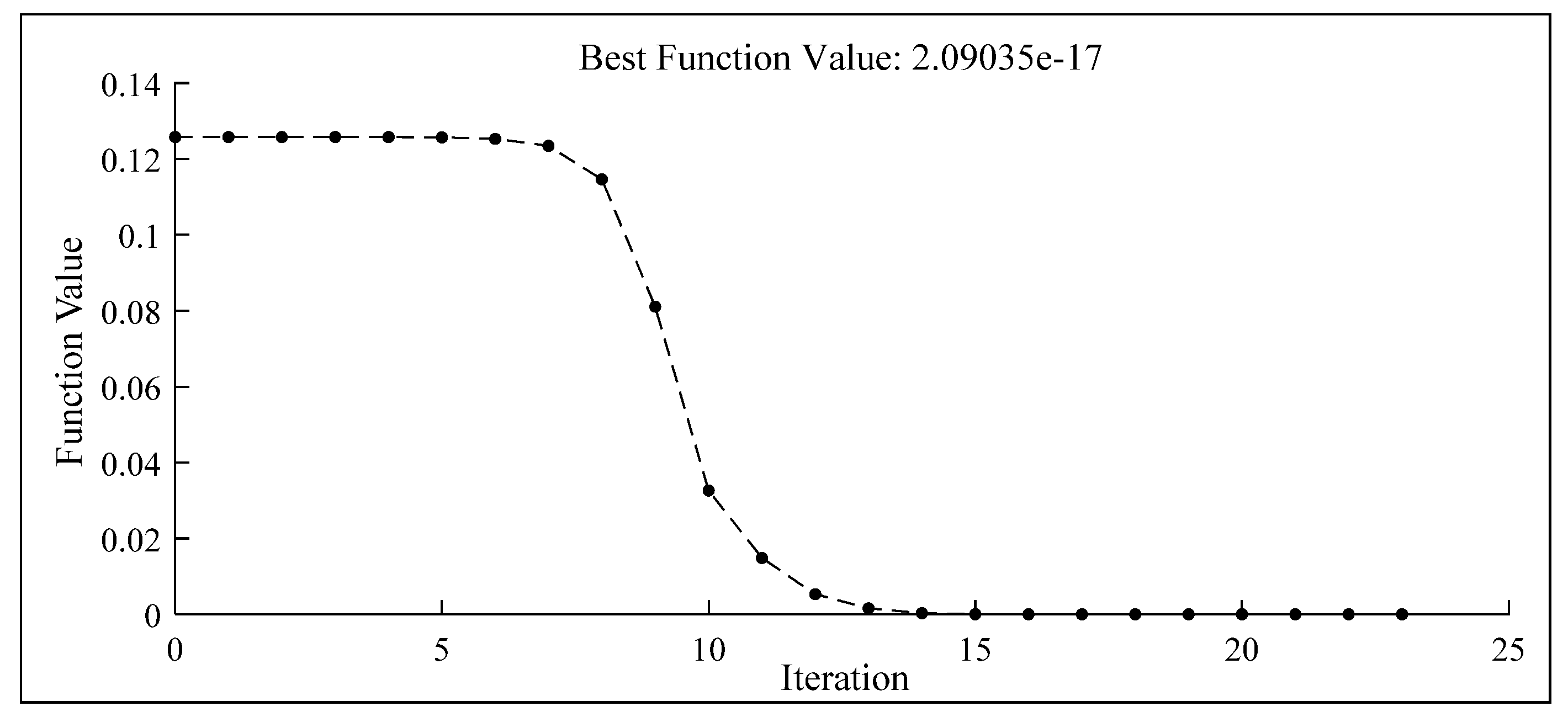
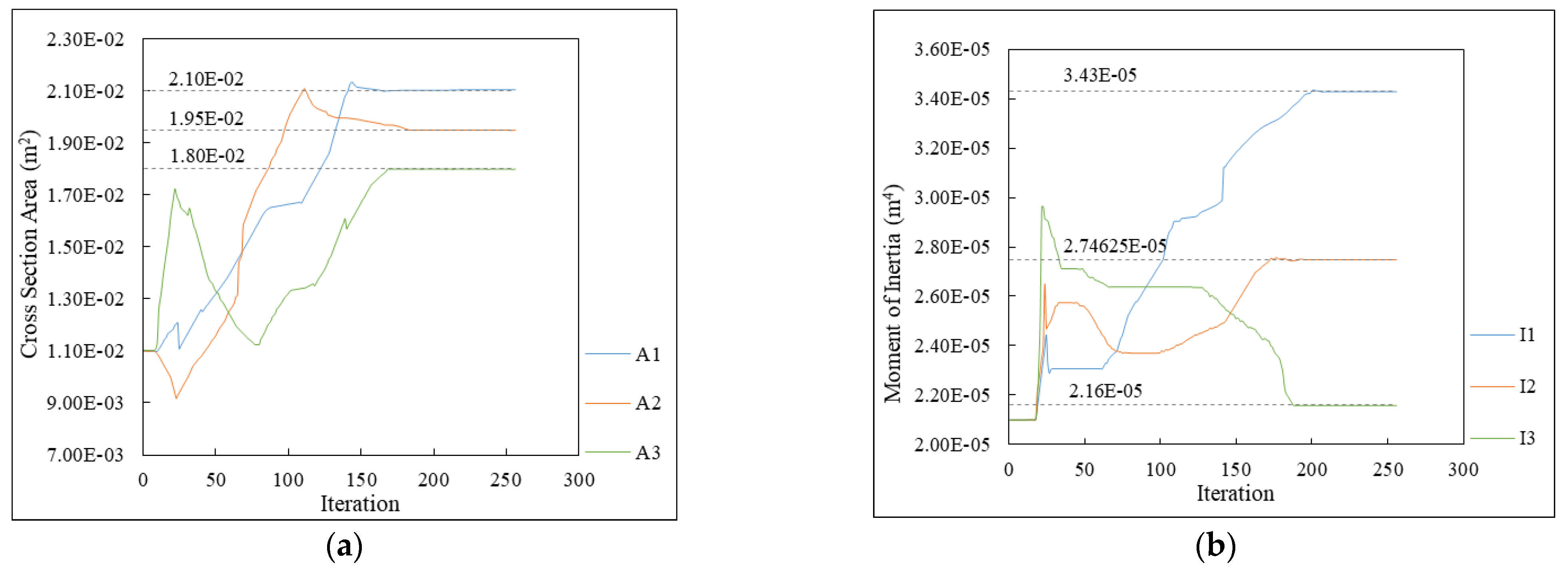
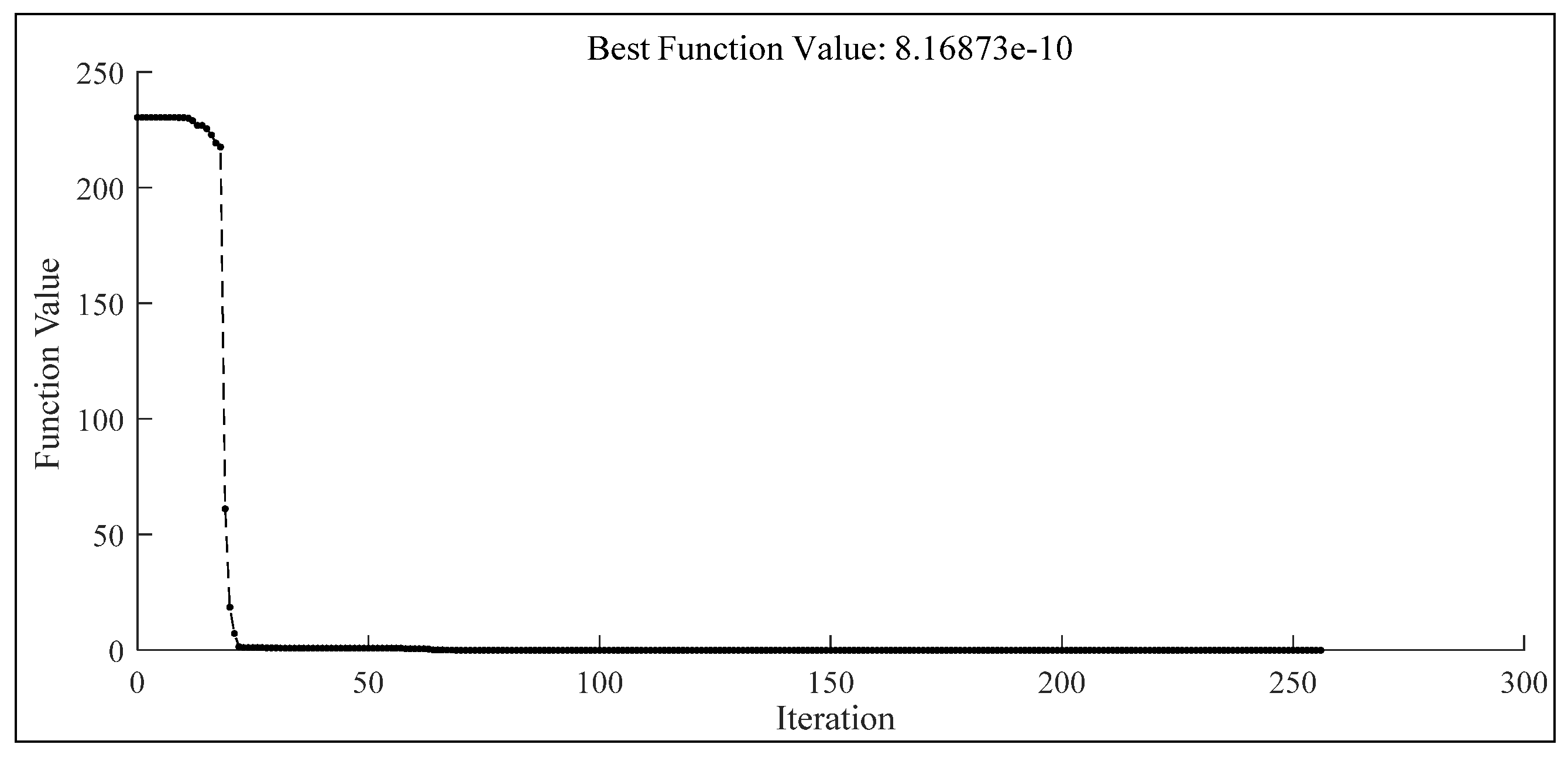
3.2. Parameter Identification for Truss Sample
4. Parameter Identification for a Rigid Frame
4.1. Member Stiffness Matrix of a Rigid Frame
4.2. Parameter Identification for a Rigid Frame Sample
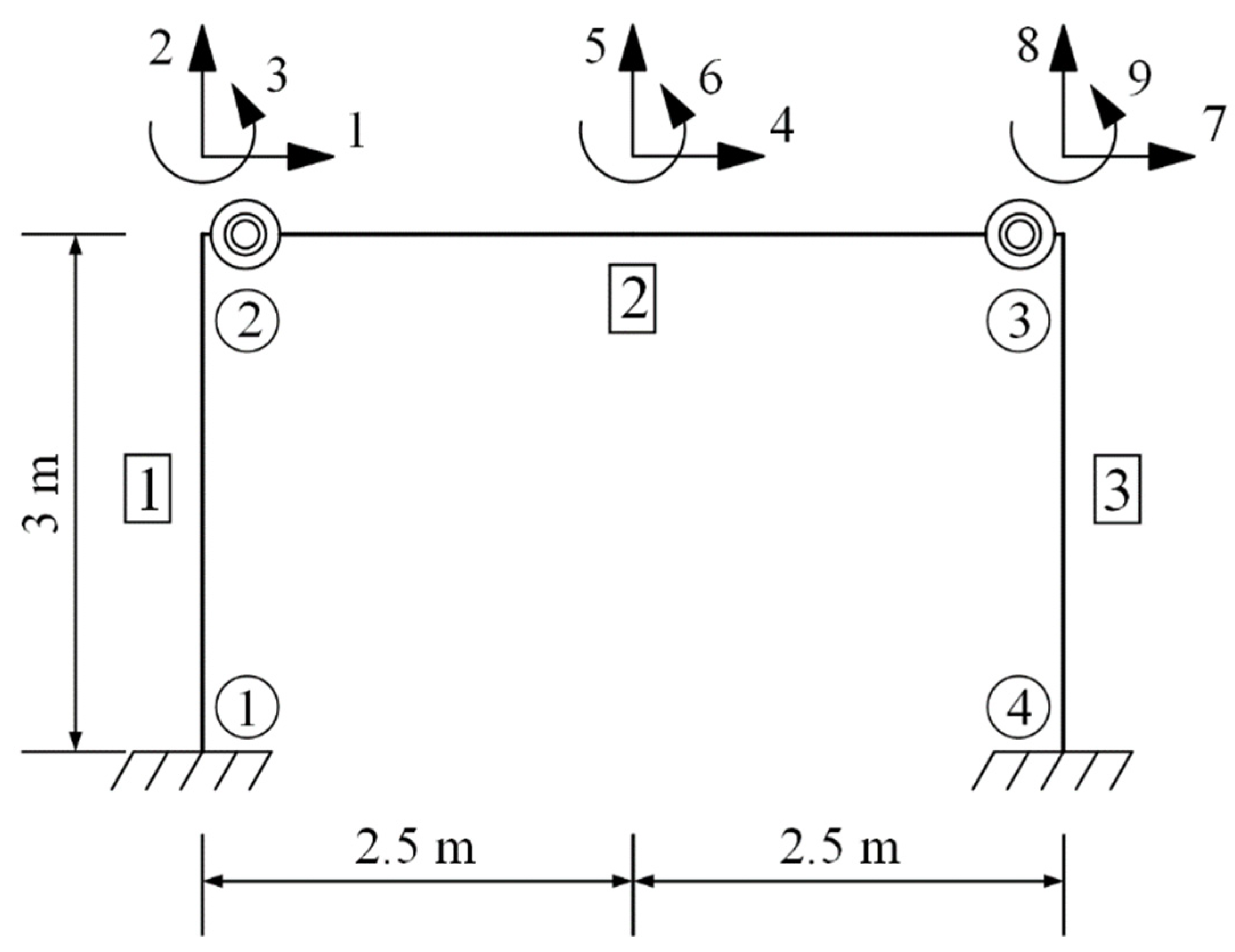
5. Parameter Identification for a Frame with Semi-Rigid Connections
5.1. Member Stiffness Matrix of Semi-Rigid Frame
5.2. Nodal Displacement Error Analysis Caused by Nodal Rotational Stiffness Changes
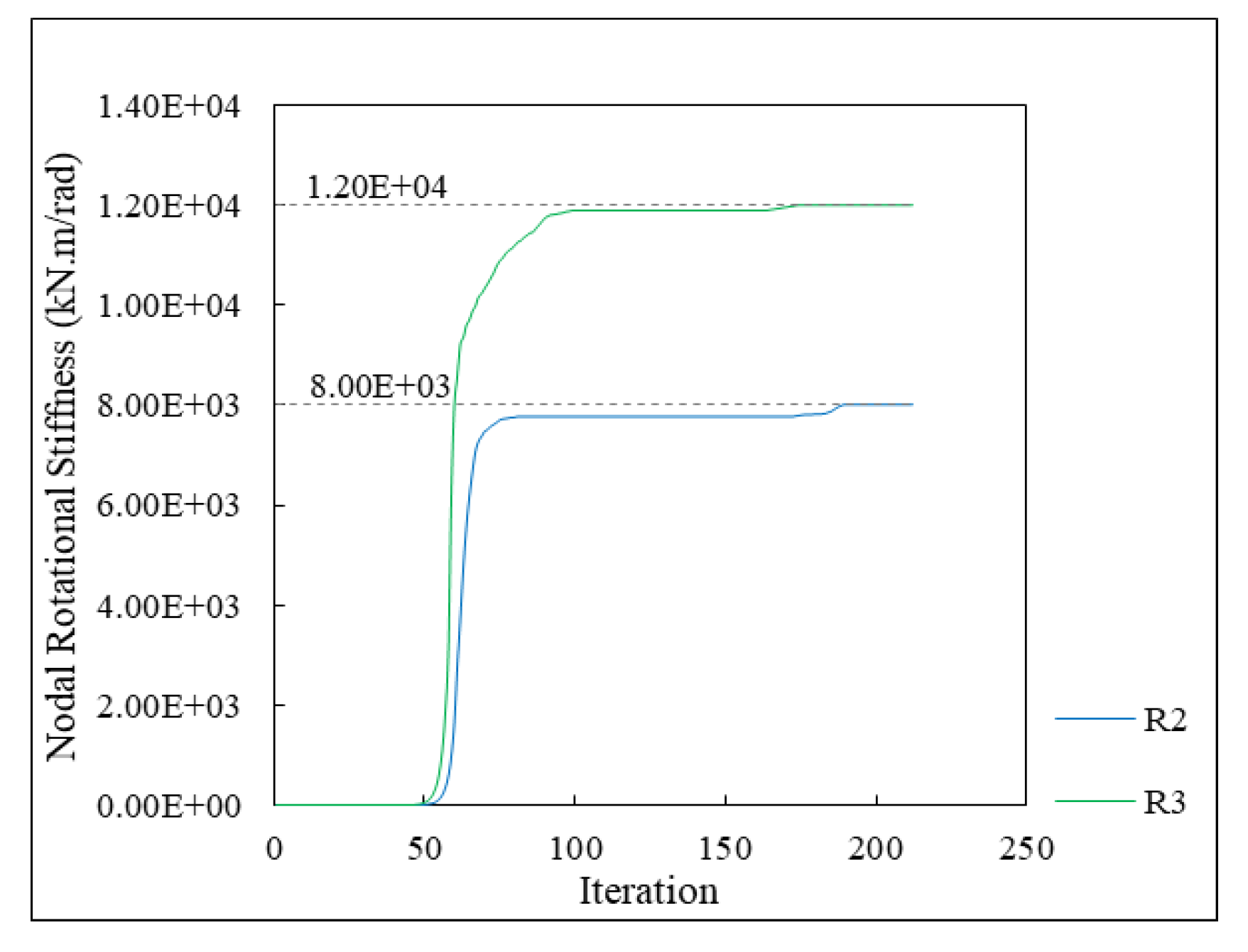
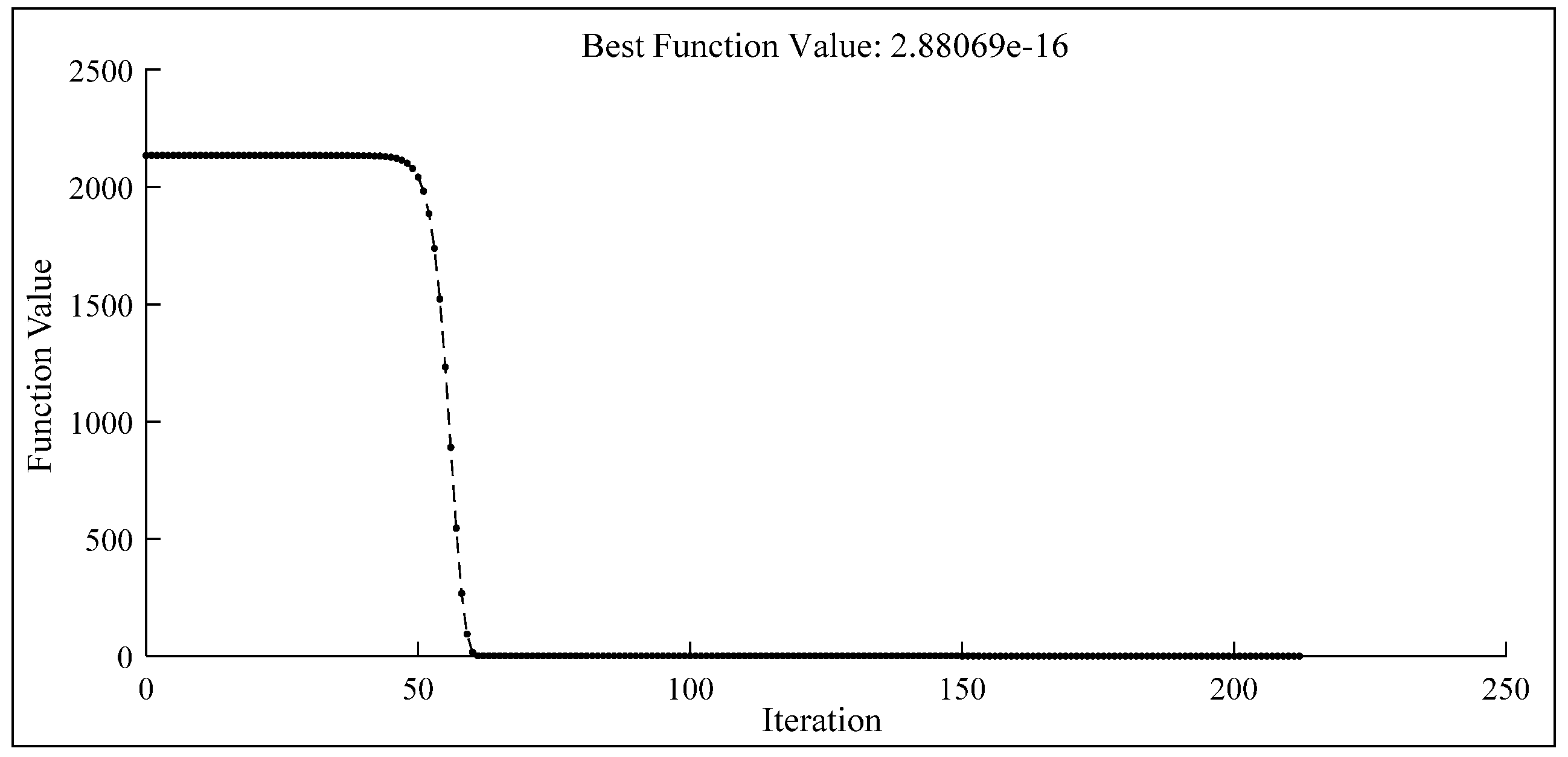
5.3. Parameter Identification for a Frame Sample with Joint Damage
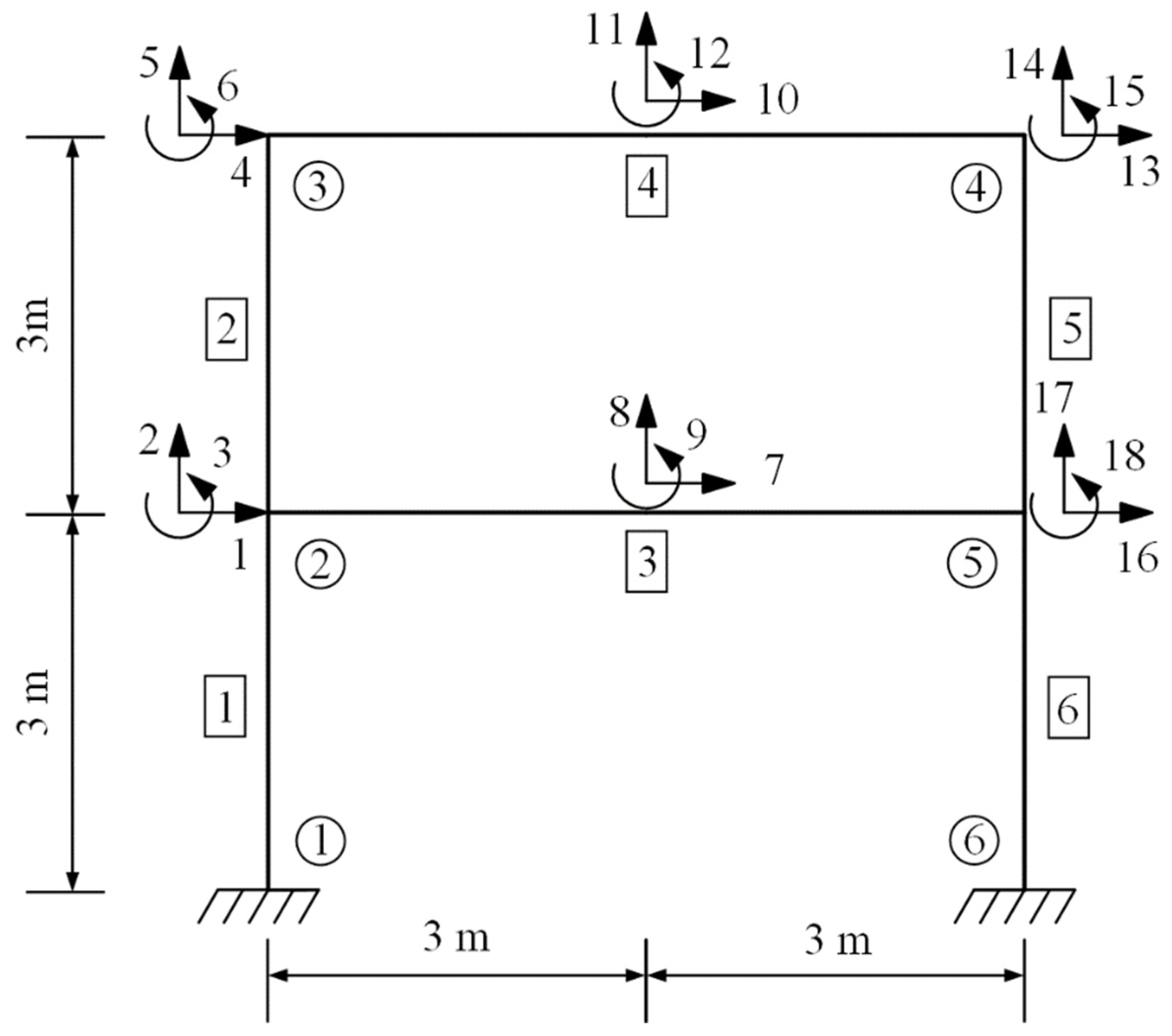
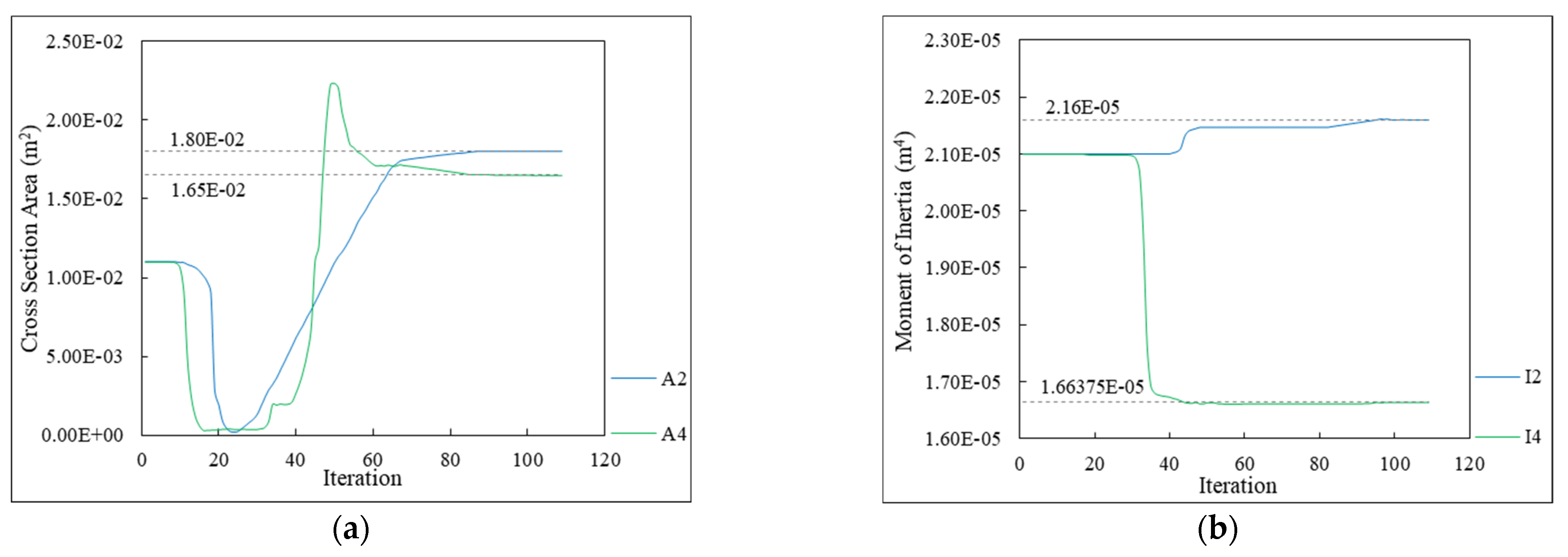
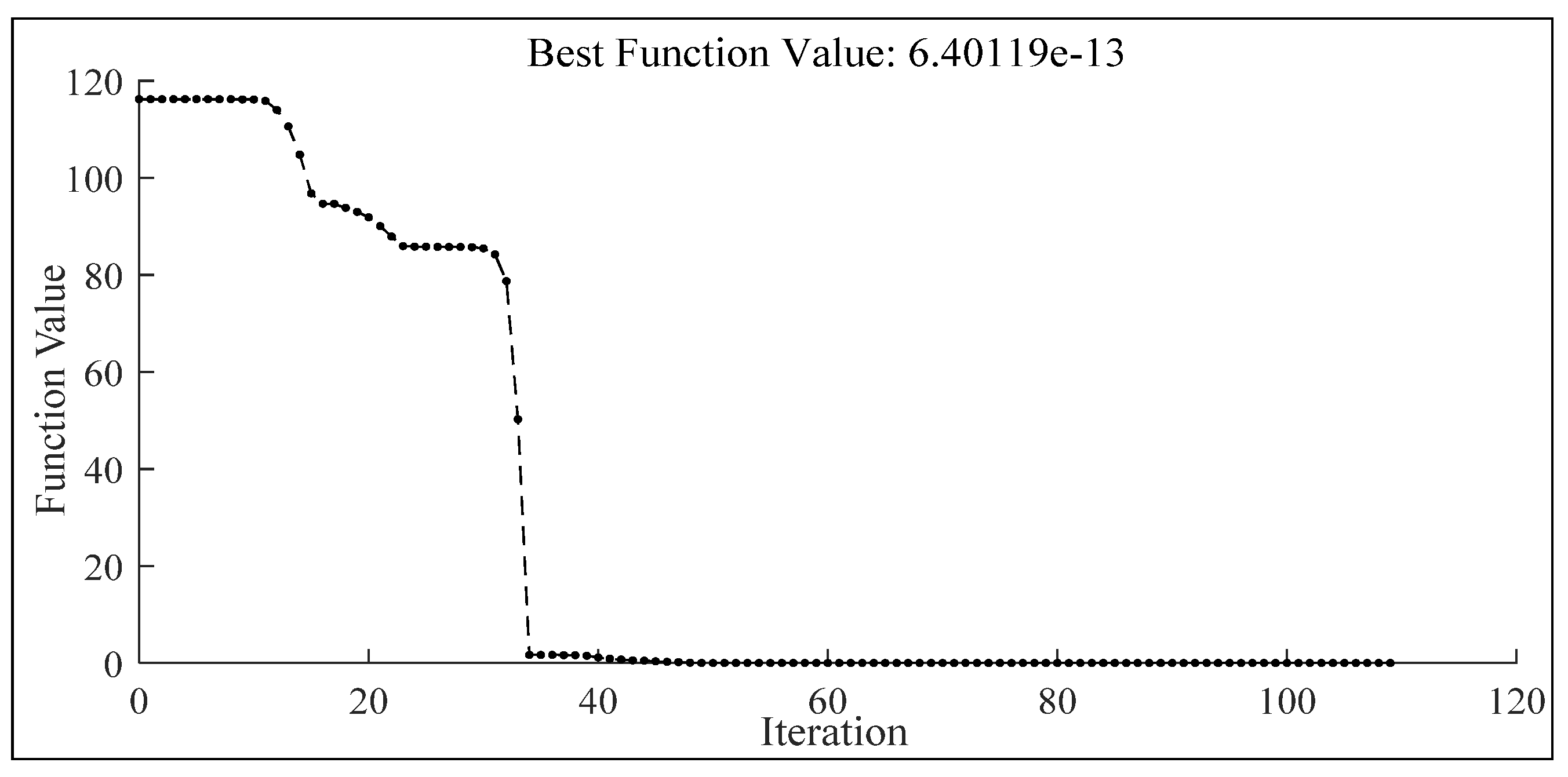
5.4. Parameter Identification for a Frame with Cross-Sectional Damage and Joint Damage
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zapico-Valle, J.L.; García-Diéguez, M.; Alonso-Camblor, R. Nonlinear modal identification of a steel frame. Eng. Struct. 2013, 56, 246–259. [Google Scholar] [CrossRef]
- Beskhyroun, S.; Wegner, L.D.; Sparling, B.F. New methodology for the application of vibration-based damage detection techniques. Struct. Control Health Monit. 2012, 19, 632–649. [Google Scholar] [CrossRef]
- Nick, H.; Aziminejad, A.; Hosseini, M.H.; Laknejadi, K. Damage identification in steel girder bridges using modal strain energy-based damage index method and artificial neural network. Eng. Fail. Anal. 2020, 119, 105010. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Saha, S.; Sohail, T. Identification of Parameter of Truss Structure by Limited Static Strain Measurement. Recent Advances in Structural Engineering; Springer: Singapore, 2019; pp. 375–388. [Google Scholar] [CrossRef]
- Schommer, S.; Nguyen, V.H.; Maas, S.; Zürbes, A. Model updating for structural health monitoring using static and dynamic measurements. Procedia Eng. 2017, 199, 2146–2153. [Google Scholar] [CrossRef]
- Budipriyanto, A. Blind source separation based dynamic parameter identification of a multi-story moment-resisting frame building under seismic ground motions. Procedia Eng. 2013, 54, 299–307. [Google Scholar] [CrossRef]
- Bu, H.; Wang, D.; Zhou, P.; Zhu, H. An improved wavelet–Galerkin method for dynamic response reconstruction and parameter identification of shear-type frames. J. Sound Vib. 2018, 419, 140–157. [Google Scholar] [CrossRef]
- Sanayei, M.; Onipede, O. Damage assessment of structures using static test data. AIAA J. 1990, 29, 1174–1179. [Google Scholar] [CrossRef]
- Terlaje, A.S.; Truman, K.Z. Parameter Identification and Damage Detection Using Structural Optimization and Static Response Data. Adv. Struct. Eng. 2007, 10, 607–621. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13, 1–11. [Google Scholar] [CrossRef]
- Xiao, F.; Fan, J.; Chen, G.S.; Hulsey, J.L. Bridge health monitoring and damage identification of truss bridge using strain measurements. Adv. Mech. Eng. 2019, 11, 1–7. [Google Scholar] [CrossRef]
- Reyes-Salazar, A.; Haldar, A. Nonlinear Seismic Response of Steel Structures with Semi-Rigid and Compo-site Connections. J. Constr. Steel Res. 1999, 51, 37–59. [Google Scholar] [CrossRef]
- Llanes-Tizoc, M.D.; Reyes-Salazar, A.; Ruiz, S.E.; Valenzuela-Beltrán, F.; Bojorquez, E.; Chávez, R. Reliability analysis of steel buildings considering the flexibility of the connections of the GFs. Structures 2020, 27, 2170–2181. [Google Scholar] [CrossRef]
- Rigi, A.; JavidSharifi, B.; Hadianfard, M.A.; Yang, T. Study of the seismic behavior of rigid and semi-rigid steel moment-resisting frames. J. Constr. Steel Res. 2021, 186, 106910. [Google Scholar] [CrossRef]
- Chen, W.F.; Goto, Y.; Richard-Liew, J.Y. Stability Design of Semi-Rigid Frames; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Reyes-Salazar, A.; Sauceda-Pimentel, J.M.; Ruiz, S.E.; Bojórquez, E.; Bojorquez, J. Seismic response and energy dissipation of 3D complex steel buildings considering the influence of interior semi-rigid connections: Low- medium- and high-rise. Bull. Earthq. Eng. 2018, 16, 5557–5590. [Google Scholar] [CrossRef]
- de Araújo, F.C.; Ribeiro, I.S.; Machado, R.M. Nonlinear analysis of semi-rigid steel frames having nonprismatic shear-deformable members. Eng. Struct. 2022, 257, 114047. [Google Scholar] [CrossRef]
- Yi, J.H.; Yuri, C.B.; Feng, M.Q. Model updating and joint damage assessment for steel frame structures using structural identification techniques. Steel Struct. 2003, 3, 83–94. [Google Scholar]
- Altunişik, A.C.; Bayraktar, A.; Sevim, B.; Kartal, M.E.; Adanur, S.; Sevim, B. Finite element model updating of an arch type steel laboratory bridge model using semi-rigid connection. Steel Compos. Struct. 2010, 10, 541–561. [Google Scholar] [CrossRef]
- Machavaram, R.; Shankar, K. Joint damage identification using Improved Radial Basis Function (IRBF) networks in frequency and time domain. Appl. Soft Comput. 2013, 13, 3366–3379. [Google Scholar] [CrossRef]
- Nanda, B.; Maity, D.; Maiti, D.K. Modal parameter based inverse approach for structural joint damage assessment using unified particle swarm optimization. Appl. Math. Comput. 2014, 242, 407–422. [Google Scholar] [CrossRef]
- Pal, J.; Banerjee, S. Identification of semi-rigid joints in steel frame structures using vibration-based technique. Recent Adv. Struct. Eng. 2017, 1, 363–374. [Google Scholar]
- Seyedpoor, S.M.; Nopour, M.H. A two-step method for damage identification in moment frame connections using support vector machine and differential evolution algorithm. Appl. Soft Comput. 2020, 88, 106008. [Google Scholar] [CrossRef]
- Hou, R.; Beck, J.L.; Zhou, X.; Xia, Y. Structural damage detection of space frame structures with semi-rigid connections. Eng. Struct. 2021, 235, 112029. [Google Scholar] [CrossRef]
- Hibbeler, R.C.; Tan, K.H. Structural Analysis; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Forsgren, A.; Gill, P.E.; Wright, M.H. Interior methods for nonlinear optimization. Soc. Ind. Appl. Math. 2002, 44, 525–597. [Google Scholar] [CrossRef]
- Logan, D.L. A First Course in the Finite Element Method; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Xu, L.; Grierson, D.E. Computer-Automated Design of Semirigid Steel Frameworks. J. Struct. Eng. 1993, 119, 1740–1760. [Google Scholar] [CrossRef]
- Yun, C.B.; Yi, J.H.; Bahng, E.Y. Joint damage assessment of framed structures using a neural networks technique. Eng. Struct. 2001, 23, 425–435. [Google Scholar] [CrossRef]
- McGuire, W.; Gallagher, R.H.; Ziemian, R.D. Matrix Structural Analysis, 2nd ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Simoes, L. Optimization of frames with semi-rigid connections. Comput. Struct. 1996, 60, 531–539. [Google Scholar] [CrossRef]
- Lyu, M.; Zhu, X.; Yang, Q. Connection stiffness identification of historic timber buildings using temperature-based sensitivity analysis. Eng. Struct. 2017, 131, 180–191. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, F.; Zhu, W.; Meng, X.; Chen, G.S. Parameter Identification of Structures with Different Connections Using Static Responses. Appl. Sci. 2022, 12, 5896. https://doi.org/10.3390/app12125896
Xiao F, Zhu W, Meng X, Chen GS. Parameter Identification of Structures with Different Connections Using Static Responses. Applied Sciences. 2022; 12(12):5896. https://doi.org/10.3390/app12125896
Chicago/Turabian StyleXiao, Feng, Weiwei Zhu, Xiangwei Meng, and Gang S. Chen. 2022. "Parameter Identification of Structures with Different Connections Using Static Responses" Applied Sciences 12, no. 12: 5896. https://doi.org/10.3390/app12125896





