Seismic Response Study of L-Shaped Frame Structure with Magnetorheological Dampers
Abstract
:1. Introduction
2. The Tests of the MRD
2.1. Structure of the MRD
2.2. Test Loading of the MRD
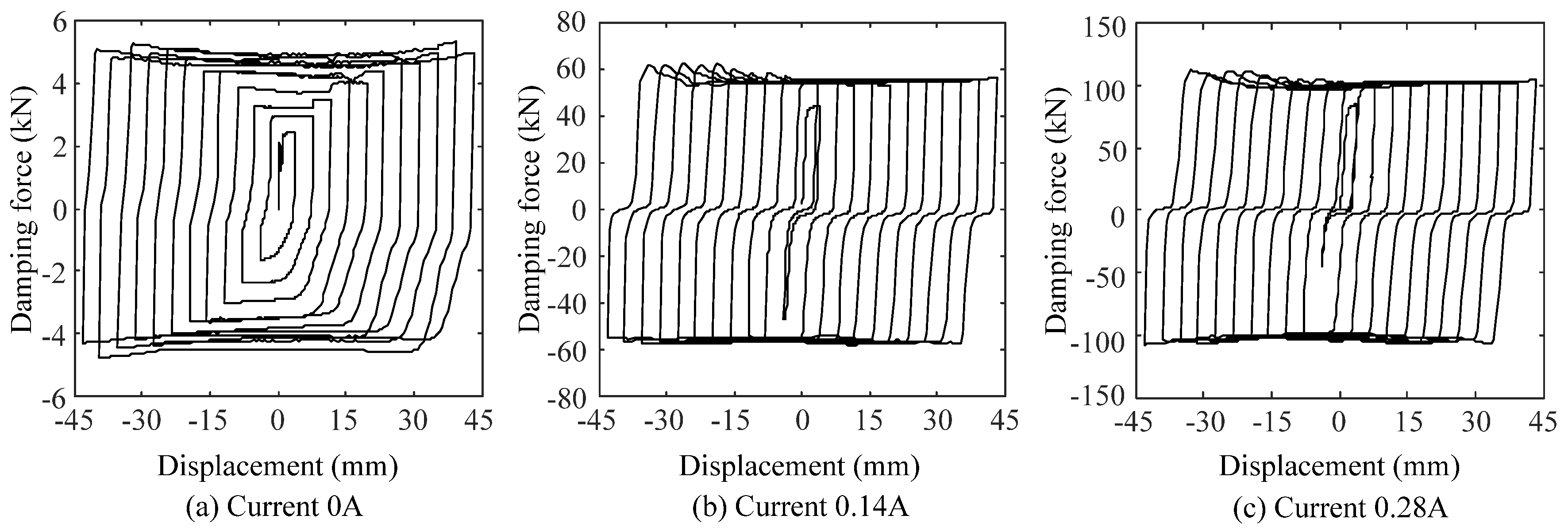
2.3. Test Results Analysis
3. Modeling Theory of the L-Shaped Frame Structure
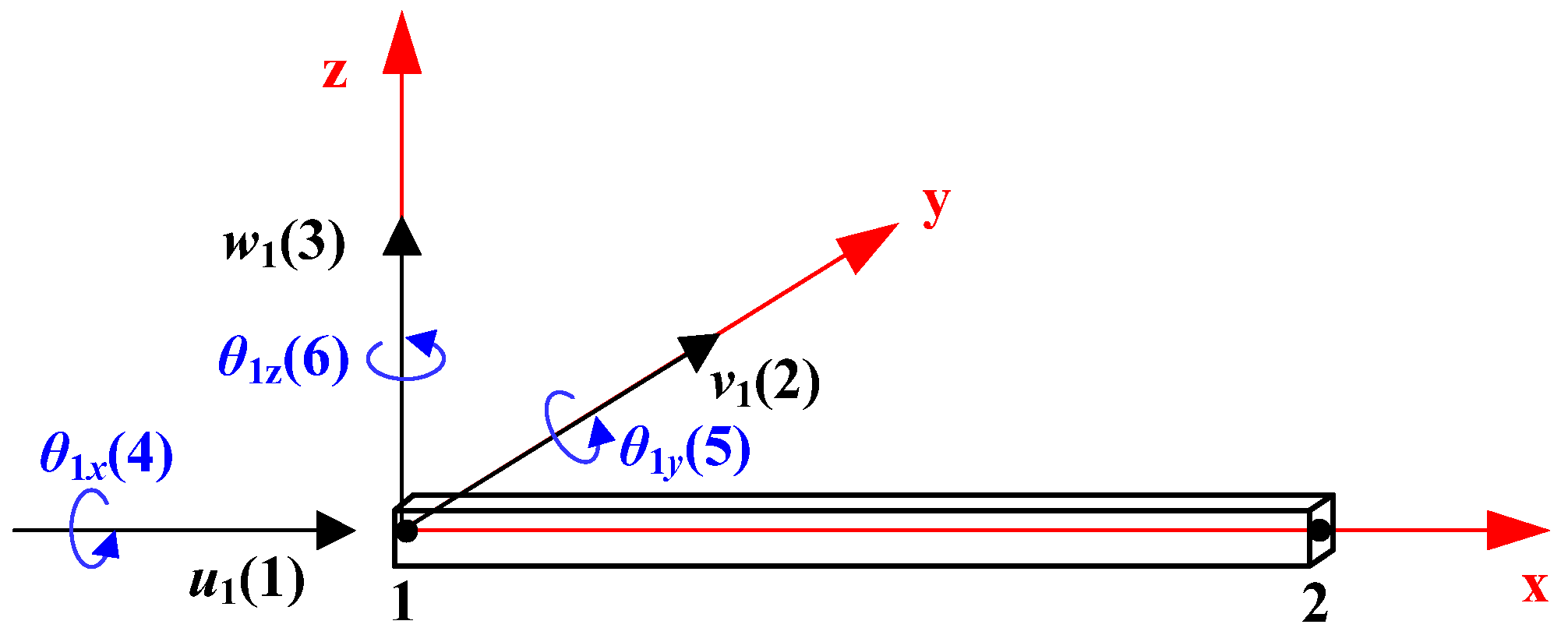
3.1. Theory of Spatial Beam Element
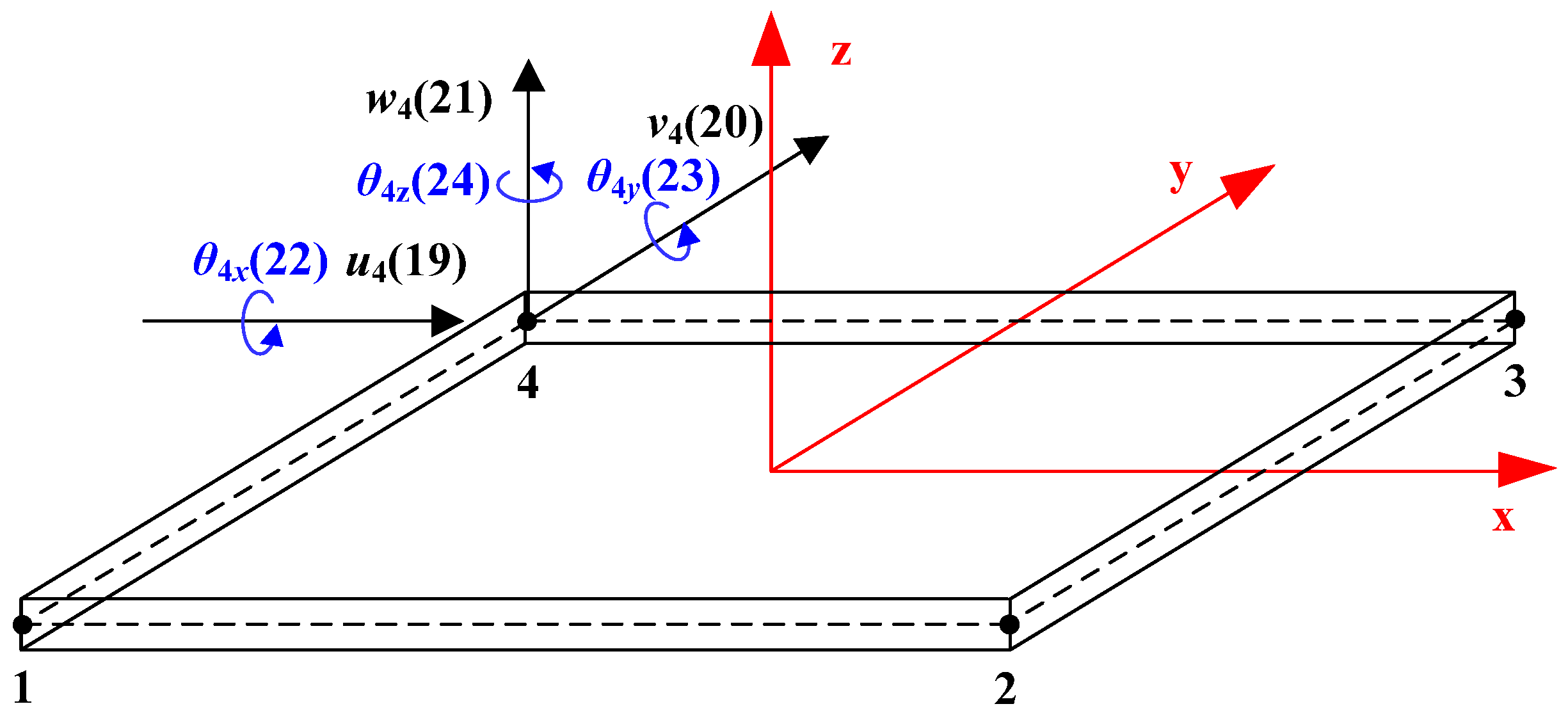
3.2. Theory of the Shell Element
3.3. Coordinate Transformation
3.4. Equation of Motion
3.5. Semi-Active Control Algorithm
3.6. Determination of the MRD Location Matrix
4. Model Description and Verification
4.1. Model Description
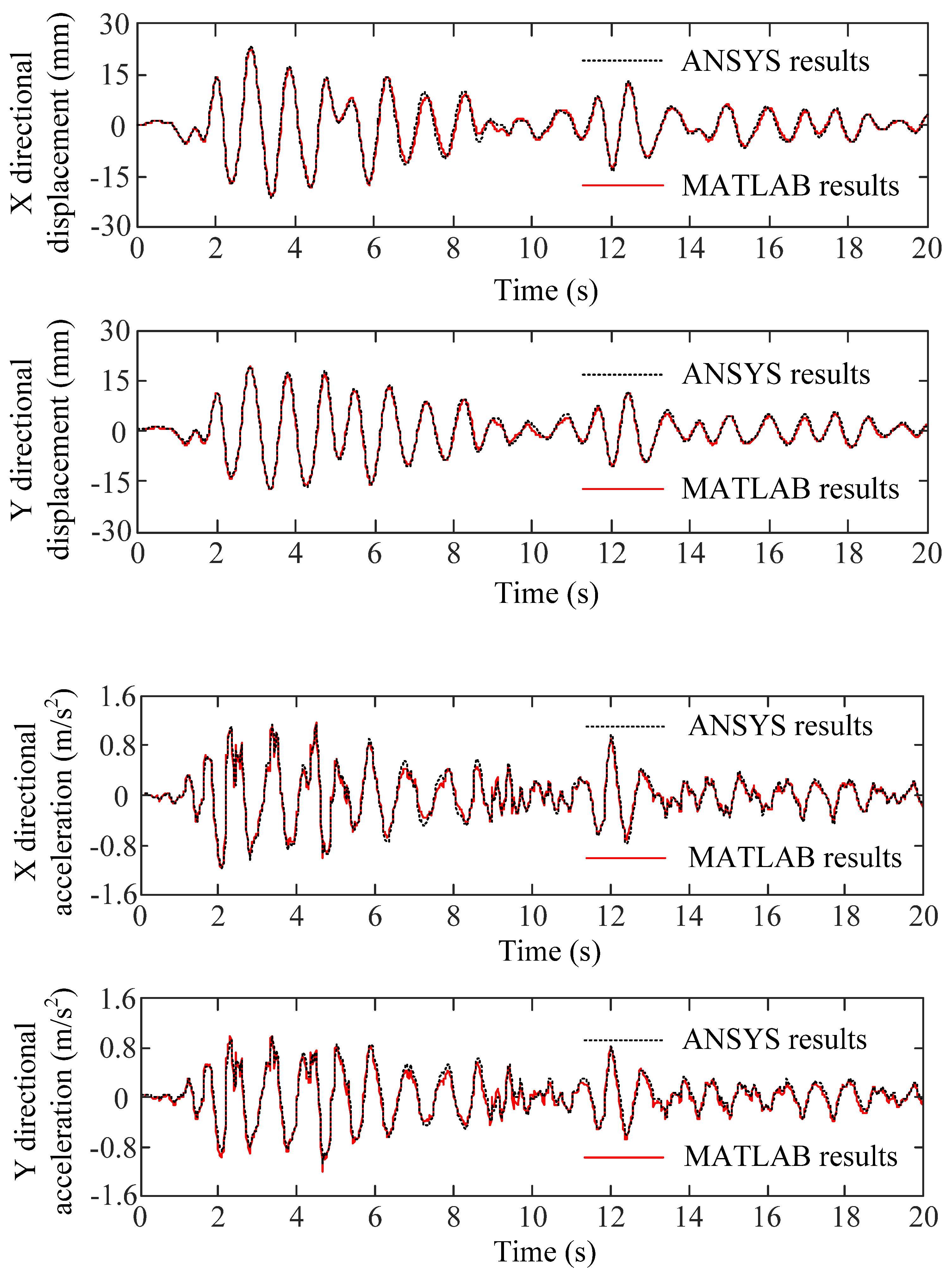
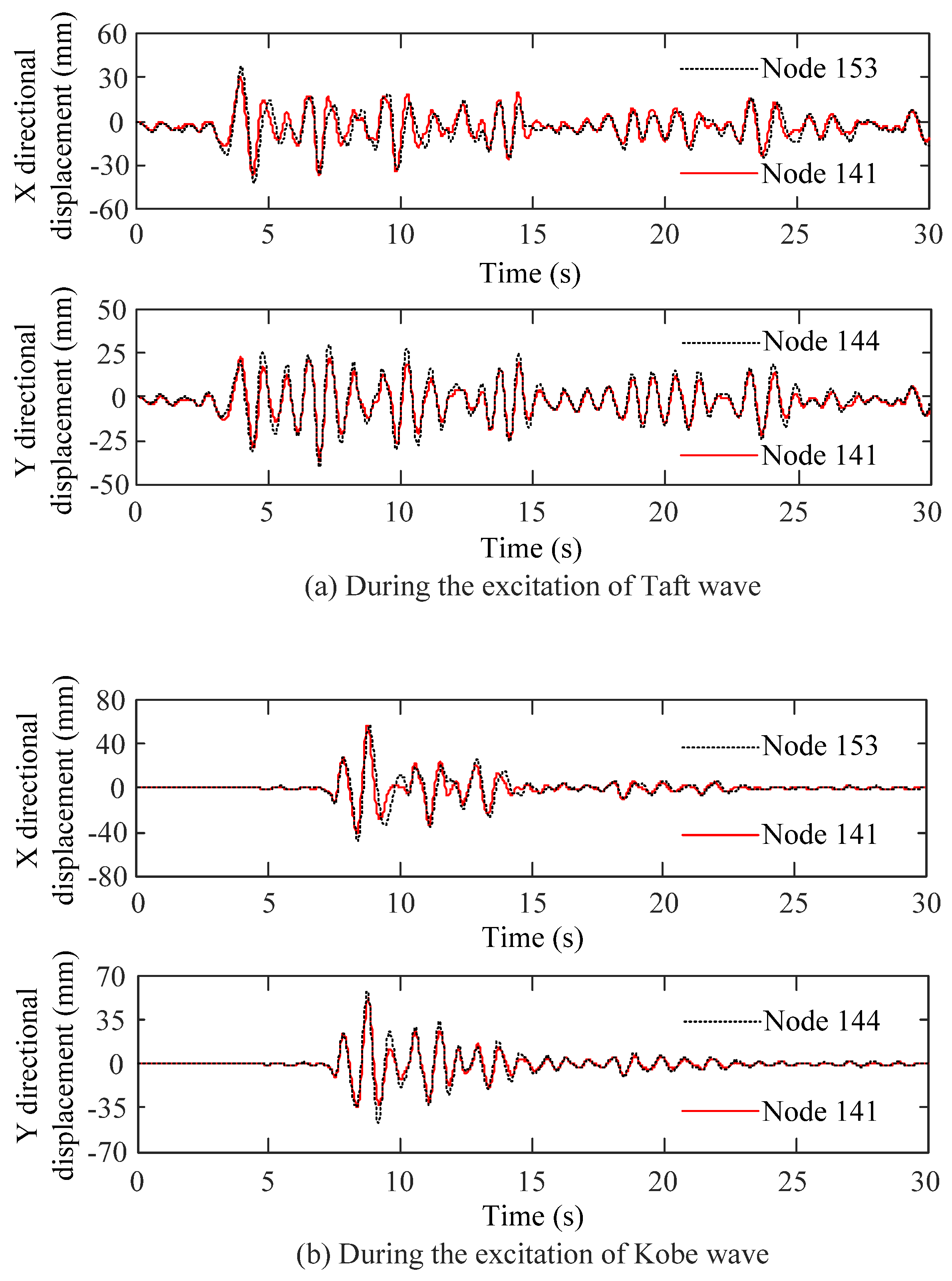
4.2. Model Verification
5. Analysis and Interpretation of Results
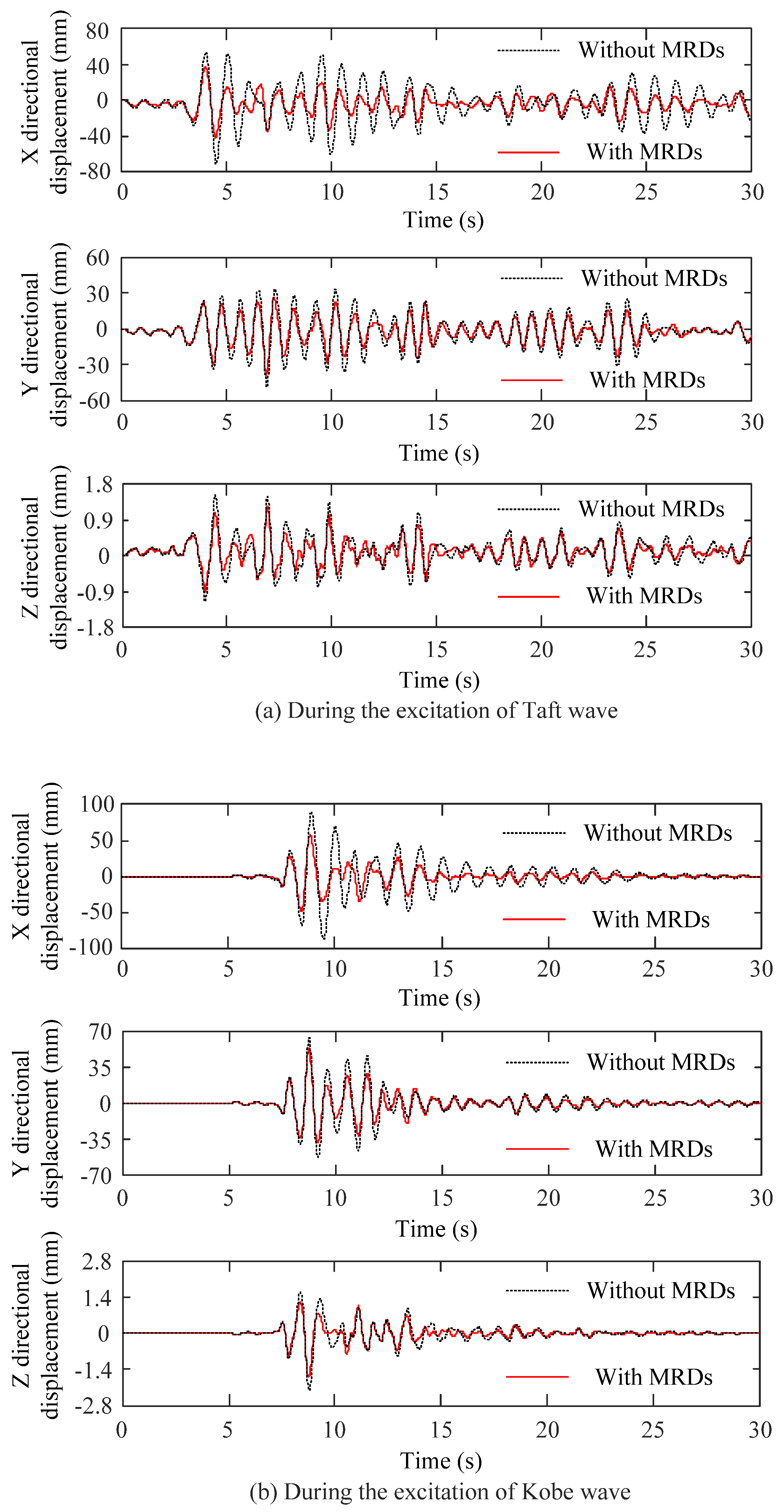
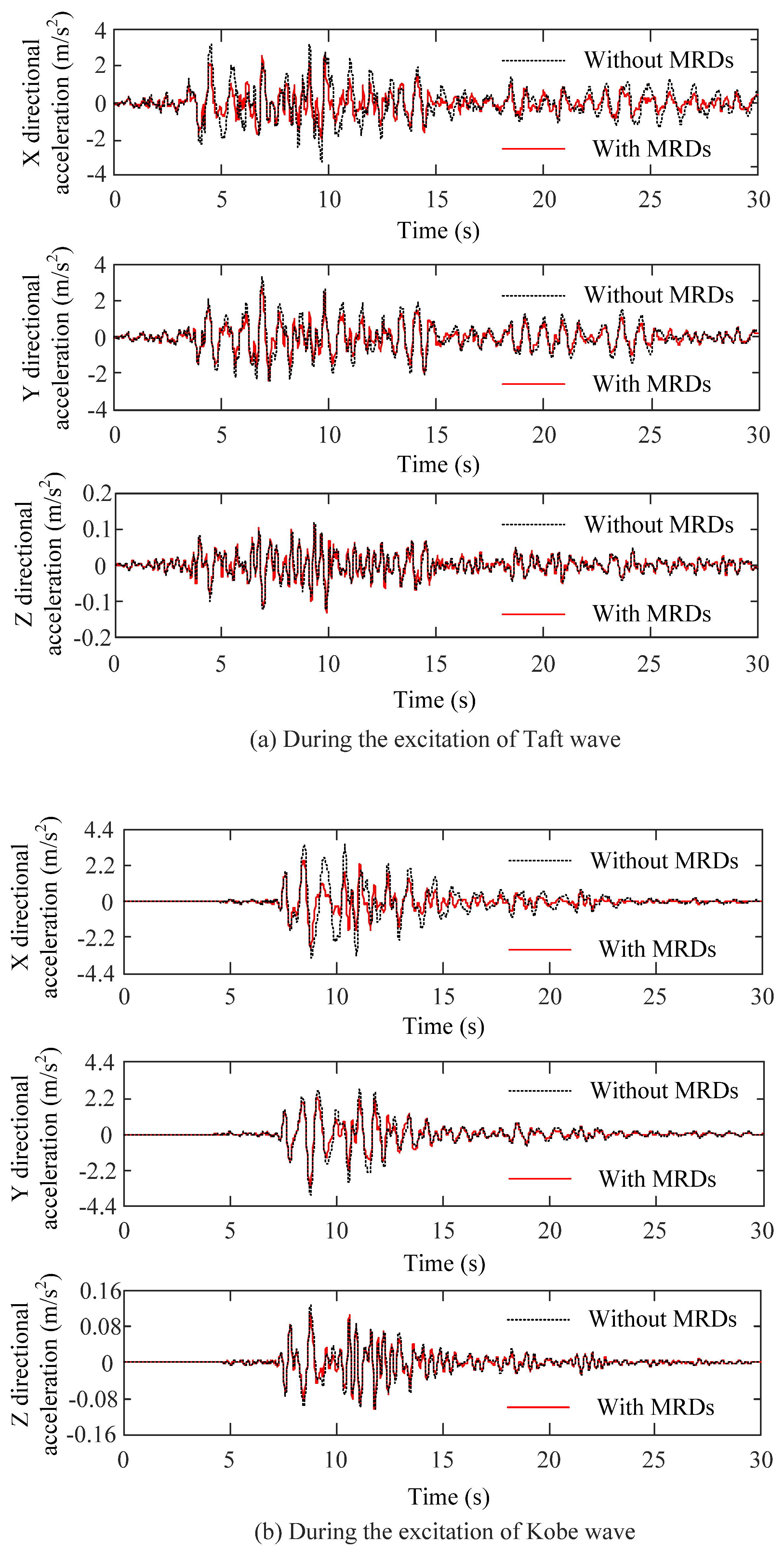
5.1. Results Analysis on Multi-Dimensional Vibration Reduction of the Structure
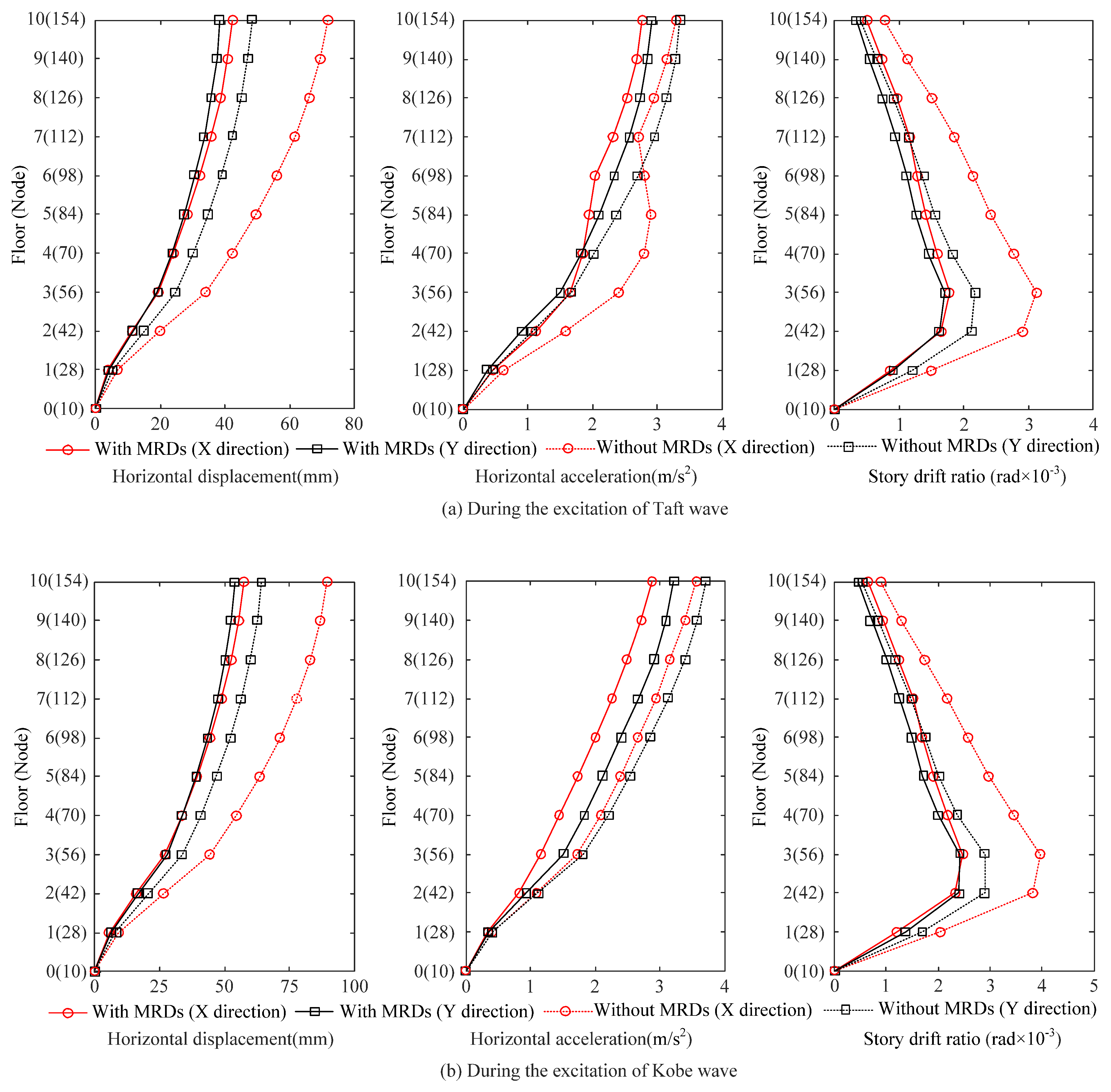
5.2. Results Analysis on the Maximum Displacement, Acceleration, and Story Drift Ratio of the Structure
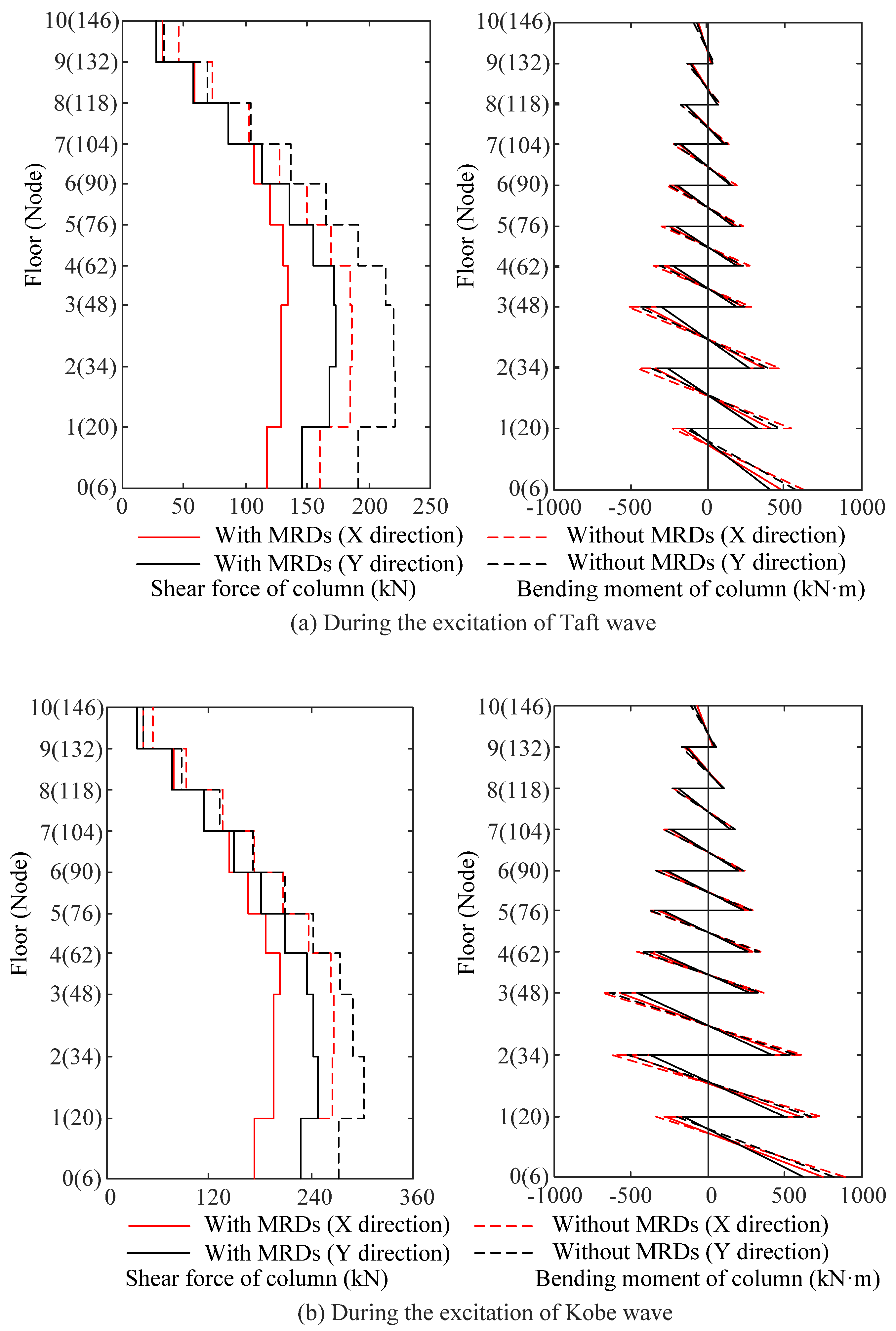
5.3. Results Analysis on Shear Force and Bending Moment of the Structural Columns
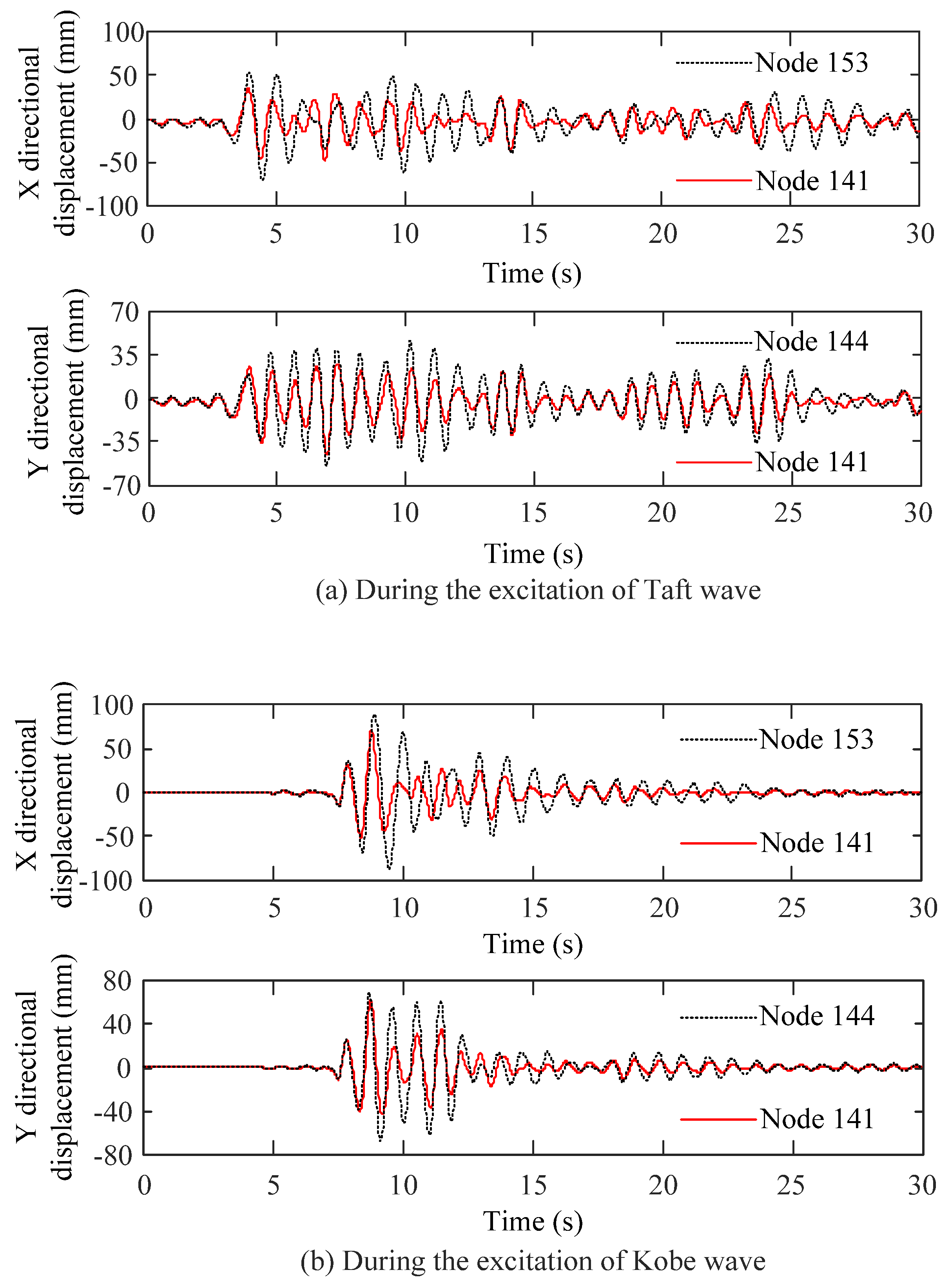
5.4. Results Analysis on Torsional Vibration Control of the Structure
6. Conclusions
- The damping force provided by the MRD gradually increases with the current, and the adjustable scope of damping force is from 3.1 to 120 kN when the current level increases from 0 to 0.28 A.
- The programs of the calculation model and time history analysis of the L-shaped frame structure without and with MRDs are proposed, which offers a new way for seismic response analysis of frame structures with MRDs.
- In contrast with the L-shaped frame structure without MRDs, the three-directional displacement and acceleration, story drift ratio, shear force, and bending moment of each floor of the L-shaped frame structure with MRDs have been significantly decreased.
- Throughout the duration of seismic waves, the L-shaped frame structure has the obvious response of torsional vibration, and the response of torsional vibration can be controlled by reasonably arranging MRDs in the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kolekar, S.; Venkateshv, K.; Oh, J.S.; Choi, S.B. Vibration controllability of sandwich structures with smart materials of electrorheological fluids and magnetorheological materials: A review. J. Vib. Eng. Technol. 2019, 7, 359–377. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Julai, S.; Ferdaus, M.M.; Ahamed, R. A review of advances in magnetorheological dampers: Their design optimization and applications. J. Zhejiang Univ.-Sci. A (Appl. Phys. Eng.) 2017, 18, 991–1010. [Google Scholar] [CrossRef]
- Bahman, F.A.; Hedayat, V.; Farzad, R.; Siamak, T. Control of the nonlinear building using an optimum inverse TSK model of MR damper based on modified grey wolf optimizer. Eng. Struct. 2020, 214, 110657. [Google Scholar]
- Ding, Y.; Zhang, L.; Zhu, H.T.; Li, Z.X. A new magnetorheological damper for seismic control. Smart Mater Struct. 2013, 22, 115003-1–115003-12. [Google Scholar] [CrossRef]
- Wang, W.; Hua, X.; Wang, X.; Wu, J.; Sun, H.; Song, G. Mechanical behavior of magnetorheological dampers after long-term operation in a cable vibration control system. Struct. Control Health Monit. 2019, 26, e22801-19. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.D.; Shen, Y.P. Intelligent Bi-State Control for the Structure with Magnetorheological Dampers. J. Intell. Mater. Syst. Struct. 2003, 14, 35–42. [Google Scholar] [CrossRef]
- Xu, Z.D.; Ge, T.; Liu, J. Experimental and theoretical study of high energy dissipation viscoelastic dampers based on acrylate rubber matrix. J. Eng. Mech. 2020, 146, 04020057. [Google Scholar] [CrossRef]
- Xu, Z.D.; Xu, F.H.; Chen, X. Vibration suppression on a platform by using vibration isolation and mitigation devices. Nonlinear Dynam. 2016, 83, 1341–1353. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhang, X.; Zhao, Y.; Zhao, J.; Xu, Z. Experimental and numerical studies on a composite MR damper considering magnetic saturation effect. Eng. Struct. 2017, 132, 576–585. [Google Scholar] [CrossRef]
- Lv, H.Z.; Zhang, S.S.; Sun, Q.; Chen, R.; Zhang, W.J. The dynamic models, control strategies and applications for magnetorheological damping systems A Systematic Review. J. Vib. Eng. Technol. 2020, 9, 131–147. [Google Scholar] [CrossRef]
- Parlak, Z.; Engin, T. Time-dependent CFD and quasi-static analysis of magnetorheological fluid dampers with experimental validation. Int. J. Mech. Sci. 2012, 64, 22–31. [Google Scholar] [CrossRef]
- Carlson, J.D.; Spencer, B.F. Magnetorheological fluid dampers for semi-active seismic control. Motion Vibr. Control 1996, 2, 35–40. [Google Scholar]
- Fujitani, H.; Sodeyama, H.; Tomura, T.; Hiwatashi, T.; Hata, K.; Sunakoda, K.; Morishita, S.; Soda, S. Development of 400 kN magnetorheological damper for a real base-isolated building. Proc. SPIE-Int. Soc. Opt. Eng. 2003, 5052, 265–276. [Google Scholar]
- Xu, Z.D.; Sha, L.F.; Zhang, X.C.; Ye, H.H. Design, performance test and analysis on magnetorheological damper for earthquake mitigation. Struct. Control Health Monit. 2013, 20, 956–970. [Google Scholar] [CrossRef]
- Tu, J.W.; Liu, J.; Qu, W.L.; Zhou, Q.; Cheng, H.B.; Cheng, X.D. Design and Fabrication of 500-kN Large-scale MR Damper. J. Intell. Mater. Syst. Struct. 2011, 22, 475–487. [Google Scholar] [CrossRef]
- Khanal, B.; Chaulagain, H. Seismic elastic performance of L-shaped building frames through plan irregularities. Structures 2020, 27, 22–36. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E.; Ahmed, M.M.M.; Ahmed, M.M.; Abdel-shafy, A.G.A. Evaluation of plan configuration irregularity effects on seismic response demands of L-shaped MRF buildings. Bull. Earthq. Eng. 2018, 16, 3845–3869. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E.; Ahmed, M.M.M.; Ahmed, M.M.; Ahmed, M.M.; Abdel-shafy, A.G.A. Seismic performance of L-shaped multi-storey buildings with moment-resisting frames. Proc. Inst. Civil Eng. Struct. Build. 2018, 171, 395–408. [Google Scholar] [CrossRef]
- Amarloo, N.; Emami, A.R. A 3-dimensional perspective for inter-storey drift, ductility and damage distributions in plan-irregular RC buildings considering seismic orientation effect. Bull. Earthq. Eng. 2019, 17, 3447–3474. [Google Scholar] [CrossRef]
- Zafarani, M.M.; Halabian, A.M. Supervisory adaptive nonlinear control for seismic alleviation of inelastic asymmetric buildings equipped with MR dampers. Eng. Struct. 2018, 176, 849–858. [Google Scholar] [CrossRef]
- Li, Z.X.; Lv, Y.; Xu, L.H.; Ding, Y.; Zhao, Q. Experimental studies on nonlinear seismic control of a steel-concrete hybrid structure using MR dampers. Eng. Struct. 2013, 49, 248–263. [Google Scholar] [CrossRef]
- Bhatti, A.Q. Performance of viscoelastic dampers (VED) under various temperatures and application of magnetorheological dampers (MRD) for seismic control of structures. Mech. Time-Depend. Mater. 2012, 17, 275–284. [Google Scholar] [CrossRef]
- Sakurai, T.; Morishita, S. Seismic response reduction of a three-story building by an MR grease damper. Front. Mech. Eng. 2017, 12, 224–233. [Google Scholar] [CrossRef]
- Ali, S.F.; Ramaswamy, A. Hybrid structural control using magnetorheological dampers for base isolated structures. Smart Mater. Struct. 2009, 18, 055011. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F.; Sain, M.K.; Carlson, J.D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater. Struct. 1996, 5, 565–575. [Google Scholar] [CrossRef]
- Xu, Z.D.; Zhao, Y.L.; Guo, Y.Q.; Yang, X.L.; Sarwar, W. Shaking table tests of magnetorheological damped frame to mitigate the response under real-time online control. Smart Mater. Struct. 2019, 28, 115021. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F.; Sain, M.K.; Carlson, J.D. An experimental study of MR dampers for seismic protection. Smart Mater. Struct. 1998, 7, 693–703. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, O.; Dyke, S.J.; Giacosa, L.M.; Truman, K.Z. Experimental verification of torsional response control of asymmetric buildings using MR dampers. Earthq. Eng. Struct. Dyn. 2003, 32, 2085–2105. [Google Scholar] [CrossRef]
- Zhang, X.C.; Xu, Z.D. Testing and modeling of a CLEMR damper and its application in structural vibration reduction. Nonlinear Dyn. 2012, 70, 1575–1588. [Google Scholar] [CrossRef]
- Bhaiya, V.; Shrimali, M.K.; Bharti, S.D.; Datta, T.K. Modified semi-active control with MR dampers for partially observed systems. Eng. Struct. 2019, 191, 129–147. [Google Scholar] [CrossRef]
- Xu, F.H.; Xu, Z.D.; Zhang, X.C. Study on the space frame structures incorporated with magnetorheological dampers. Smart Struct. Syst. 2017, 19, 279–288. [Google Scholar] [CrossRef]
- Zhao, J.; Li, K.; Zhang, X.C.; Sun, Y.P.; Xu, Z.D. Multidimensional vibration reduction control of the frame structure with magnetorheological damper. Struct. Control Health Monit. 2020, 27, e2572. [Google Scholar] [CrossRef]
- Qian, R.J.; Yuan, X.F.; Lin, Z.B. The Analysis Theory and Finite Element Method for Solid and Structure; Southeast University Press: Nanjing, China, 2013; pp. 425–427+436–437. (In Chinese) [Google Scholar]
- Motra, G.B.; Mallik, W.; Chandiramani, N.K. Semi-active vibration control of connected buildings using magnetorheological dampers. J. Intell. Mater. Syst. Struct. 2011, 22, 1811–1827. [Google Scholar] [CrossRef]
- Ubaidillah, H.K.; Kadir, F.A.A. Modelling, characterisation and force tracking control of a magnetorheological damper under harmonic excitation. Int. J. Model. Identif. Control 2011, 13, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Russo, R.; Terzo, M. Modelling, parameter identification, and control of a shear mode magnetorheological device. Proc. Inst. Mech. Eng. I 2011, 225, 549–562. [Google Scholar] [CrossRef]
- Weber, F. Robust force tracking control scheme for MR dampers. Struct. Control Health Monit. 2015, 22, 1373–1395. [Google Scholar] [CrossRef]
- Ribeiro, T.; Bernardo, L.; Carrazedo, R.; Domenico, D. Seismic Design of Bolted Connections in Steel Structures—A Critical Assessment of Practice and Research. Buildings 2022, 12, 32. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Hong, W.-K. A novel erection technique of the l-shaped precast frames utilizing laminated metal plates. J. Asian Archit. Build. Eng. 2021, 20, 674–688. [Google Scholar] [CrossRef]
- Chhatani, Y.; Pawade, P.Y.; Dabhekar, K.R.; Khedikar, I.P. Seismic performance of l-shaped building through plan irregularities. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1197, 012050. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Li, F.; Mou, B.; Wang, T. Experimental and numerical study on the seismic performance of an L-Shaped double-steel plate composite shear wall. J. Build. Eng. 2022, 49, 104015. [Google Scholar] [CrossRef]
- Ping, C.Z.; Weiwei, S.; Yang, Y. Seismic behavior of reinforced concrete t-shaped columns under compression-bending-shear and torsion. Earthq. Struct. 2021, 20, 431–444. [Google Scholar]
- Zhang, X.; Xia, Q.; Ye, B.; Yan, W.; Deng, Z.; Xiang, P. Seismic performances of src special-shaped columns and rc beam joints under double-direction low-cyclic reversed loading. Front. Mater. 2021, 8, 438. [Google Scholar] [CrossRef]
- Zhang, M.J.; Xu, F.Y. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104836. [Google Scholar] [CrossRef]
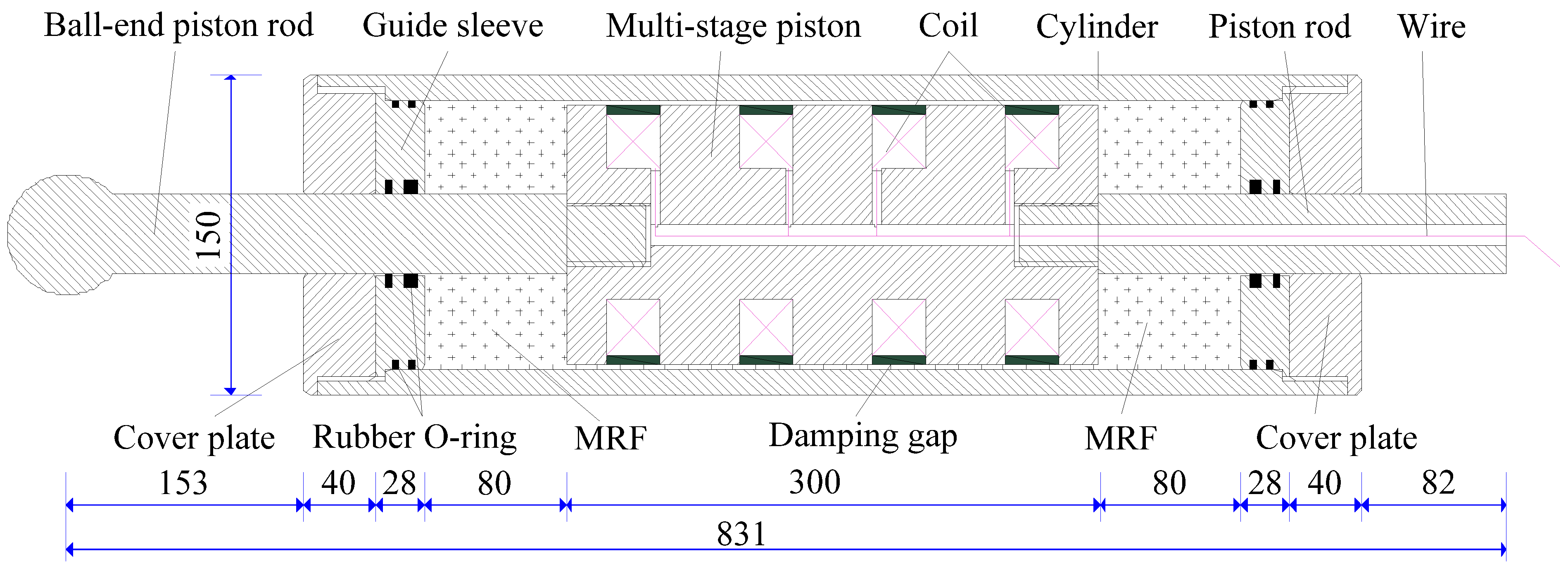

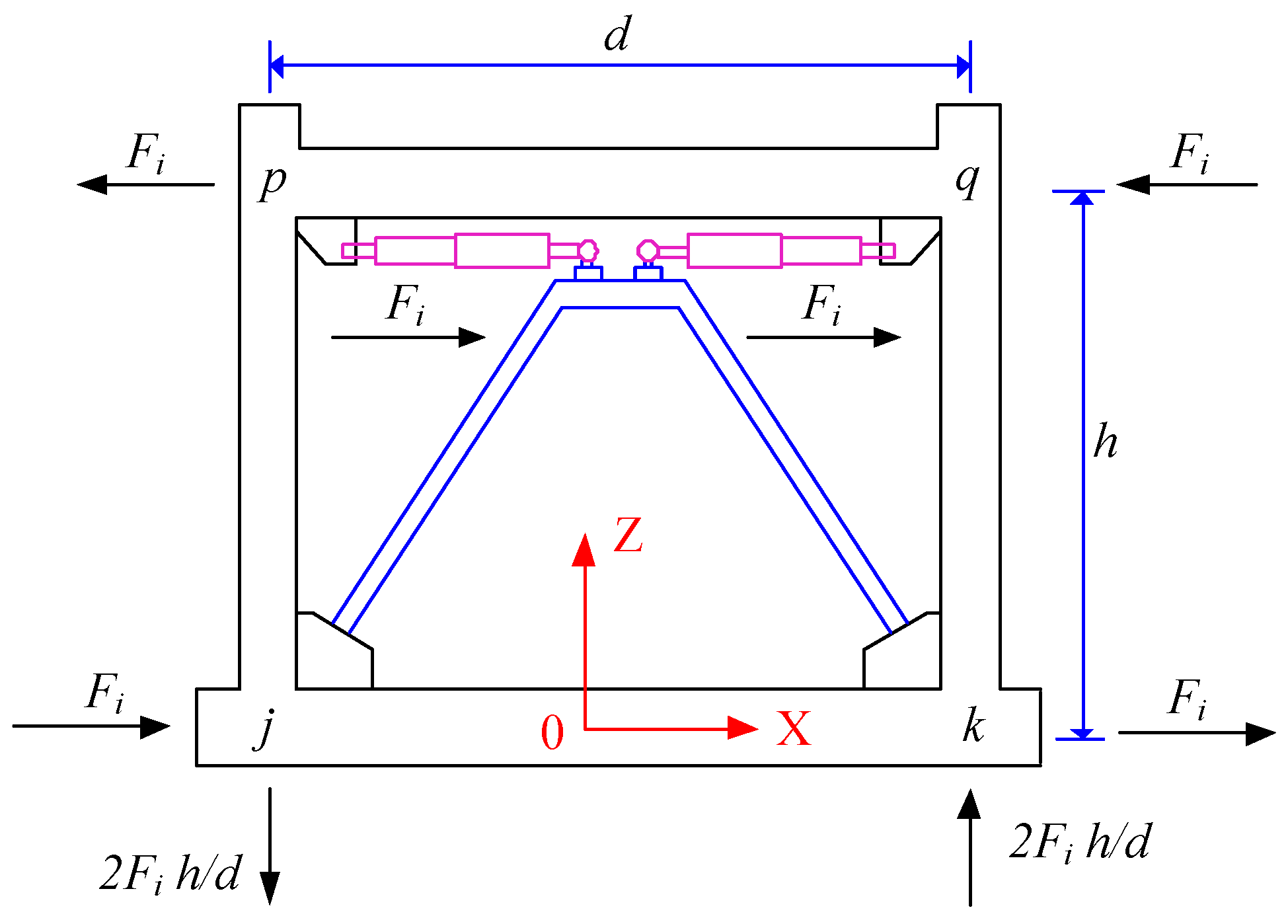
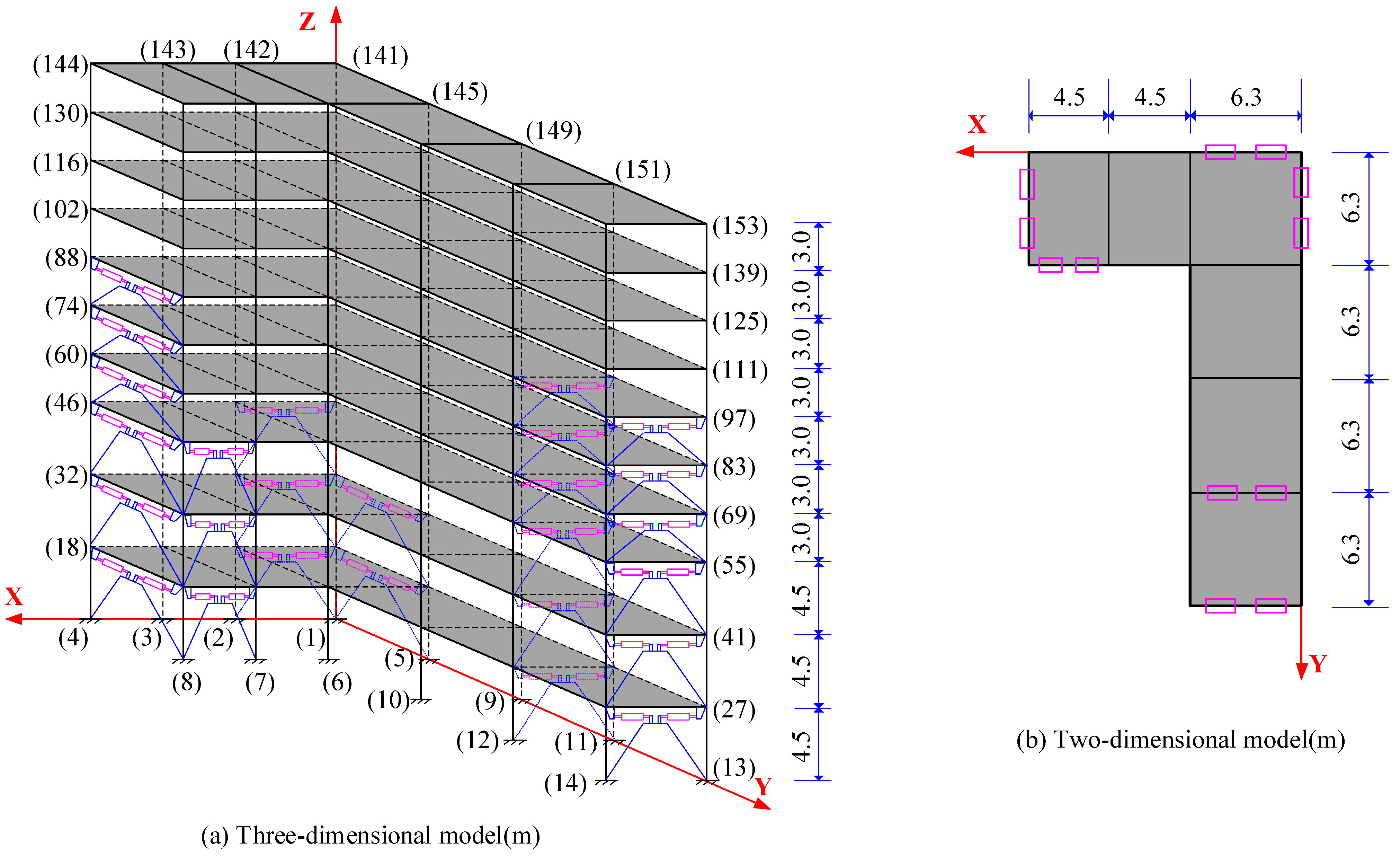
| Parameter | Size | Parameter | Size |
|---|---|---|---|
| Outer diameter of cylinder (mm) | 150 | Stroke (mm) | ±80 |
| Inner diameter of cylinder (mm) | 120 | Coil groove depth (mm) | 25 |
| Diameter of piston (mm) | 118 | Damping gap (mm) | 1 |
| Magnetic Field Intensity (T) | 0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Shear stress (Pa) | 304.8 | 1340 | 4062.9 | 7928 | 10,921 | 15,016.7 | 18,346 | 21,312 | 23,550 | 25,498 | 26,732 |
| Floor (Node) | 10 (154) | 10 (148) | 10 (141) | 9 (140) | 9 (134) | 9 (127) | 8 (126) | 8 (120) | 8 (113) | |
|---|---|---|---|---|---|---|---|---|---|---|
| X direction | ANSYS (mm) | 44.10 | 24.11 | 22.73 | 42.48 | 23.42 | 22.06 | 40.50 | 22.48 | 21.10 |
| Self-compiled (mm) | 42.34 | 23.34 | 22.20 | 40.94 | 22.71 | 21.57 | 38.89 | 21.75 | 20.64 | |
| Relative error (%) | 3.97 | 3.20 | 2.33 | 3.63 | 3.05 | 2.22 | 3.96 | 3.26 | 2.18 | |
| Y direction | ANSYS (mm) | 22.78 | 32.91 | 19.38 | 22.17 | 31.93 | 18.91 | 21.20 | 30.54 | 18.18 |
| Self-compiled (mm) | 21.97 | 31.65 | 18.93 | 21.41 | 30.76 | 18.47 | 20.50 | 29.45 | 17.74 | |
| Relative error (%) | 3.54 | 3.84 | 2.32 | 3.44 | 3.65 | 2.34 | 3.31 | 3.56 | 2.45 | |
| Floor (Node) | 10 (154) | 10 (148) | 10 (141) | 9 (140) | 9 (134) | 9 (127) | 8 (126) | 8 (120) | 8 (113) | |
|---|---|---|---|---|---|---|---|---|---|---|
| X direction | ANSYS (m/s2) | 2.32 | 1.47 | 1.17 | 2.19 | 1.39 | 1.14 | 2.05 | 1.29 | 1.09 |
| Self-compiled (m/s2) | 2.22 | 1.43 | 1.18 | 2.11 | 1.37 | 1.135 | 1.98 | 1.27 | 1.088 | |
| Relative error (%) | 4.47 | 2.45 | −0.95 | 3.52 | 1.52 | 0.43 | 3.41 | 1.89 | 0.12 | |
| Y direction | ANSYS (m/s2) | 1.53 | 2.01 | 1.19 | 1.49 | 1.96 | 1.17 | 1.43 | 1.87 | 1.13 |
| Self-compiled (m/s2) | 1.50 | 1.93 | 1.20 | 1.46 | 1.87 | 1.165 | 1.39 | 1.79 | 1.11 | |
| Relative error (%) | 2.16 | 3.96 | −0.52 | 2.24 | 4.51 | 0.38 | 2.70 | 4.52 | 1.36 | |
| Floor (Node/Node) | X Direction | Floor (Node/Node) | Y Direction | ||
|---|---|---|---|---|---|
| Without MRDs | With MRDs | Without MRDs | With MRDs | ||
| 1 (27/15) | 1.395 | 1.046 | 1 (18/15) | 1.253 | 1.103 |
| 2 (41/29) | 1.445 | 1.087 | 2 (32/29) | 1.261 | 1.112 |
| 3 (55/43) | 1.480 | 1.109 | 3 (46/43) | 1.249 | 1.101 |
| 4 (69/57) | 1.503 | 1.116 | 4 (60/57) | 1.243 | 1.103 |
| 5 (83/71) | 1.506 | 1.122 | 5 (74/71) | 1.235 | 1.102 |
| 6 (97/85) | 1.499 | 1.127 | 6 (88/85) | 1.226 | 1.097 |
| 7 (111/99) | 1.494 | 1.135 | 7 (105/99) | 1.218 | 1.092 |
| 8 (125/113) | 1.491 | 1.141 | 8 (116/113) | 1.212 | 1.086 |
| 9 (139/127) | 1.489 | 1.140 | 9 (130/127) | 1.208 | 1.081 |
| 10 (153/141) | 1.489 | 1.140 | 10 (144/141) | 1.208 | 1.081 |
| Floor (Node/Node) | X Direction | Floor (Node/Node) | Y Direction | ||
|---|---|---|---|---|---|
| Without MRDs | With MRDs | Without MRDs | With MRDs | ||
| 1 (27/15) | 1.232 | 0.937 | 1 (18/15) | 1.119 | 1.104 |
| 2 (41/29) | 1.237 | 0.974 | 2 (32/29) | 1.133 | 1.121 |
| 3 (55/43) | 1.237 | 0.986 | 3 (46/43) | 1.131 | 1.119 |
| 4 (69/57) | 1.242 | 0.989 | 4 (60/57) | 1.130 | 1.124 |
| 5 (83/71) | 1.247 | 0.988 | 5 (74/71) | 1.128 | 1.125 |
| 6 (97/85) | 1.248 | 0.987 | 6 (88/85) | 1.125 | 1.124 |
| 7 (111/99) | 1.247 | 0.990 | 7 (105/99) | 1.123 | 1.120 |
| 8 (125/113) | 1.246 | 0.993 | 8 (116/113) | 1.122 | 1.116 |
| 9 (139/127) | 1.244 | 0.995 | 9 (130/127) | 1.121 | 1.113 |
| 10 (153/141) | 1.245 | 0.998 | 10 (144/141) | 1.123 | 1.113 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.; Yang, Y.; Fan, Y.; Zhang, X. Seismic Response Study of L-Shaped Frame Structure with Magnetorheological Dampers. Appl. Sci. 2022, 12, 5976. https://doi.org/10.3390/app12125976
You J, Yang Y, Fan Y, Zhang X. Seismic Response Study of L-Shaped Frame Structure with Magnetorheological Dampers. Applied Sciences. 2022; 12(12):5976. https://doi.org/10.3390/app12125976
Chicago/Turabian StyleYou, Jiangtao, Yang Yang, Yongfeng Fan, and Xiangcheng Zhang. 2022. "Seismic Response Study of L-Shaped Frame Structure with Magnetorheological Dampers" Applied Sciences 12, no. 12: 5976. https://doi.org/10.3390/app12125976
APA StyleYou, J., Yang, Y., Fan, Y., & Zhang, X. (2022). Seismic Response Study of L-Shaped Frame Structure with Magnetorheological Dampers. Applied Sciences, 12(12), 5976. https://doi.org/10.3390/app12125976





