Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector
Abstract
:1. Introduction
2. Numerical Model
2.1. Mass Conservation
2.2. Energy Conservation
2.3. Charge Transport
3. Numerical Methodology
3.1. Numerical Solution
3.2. Model Validation
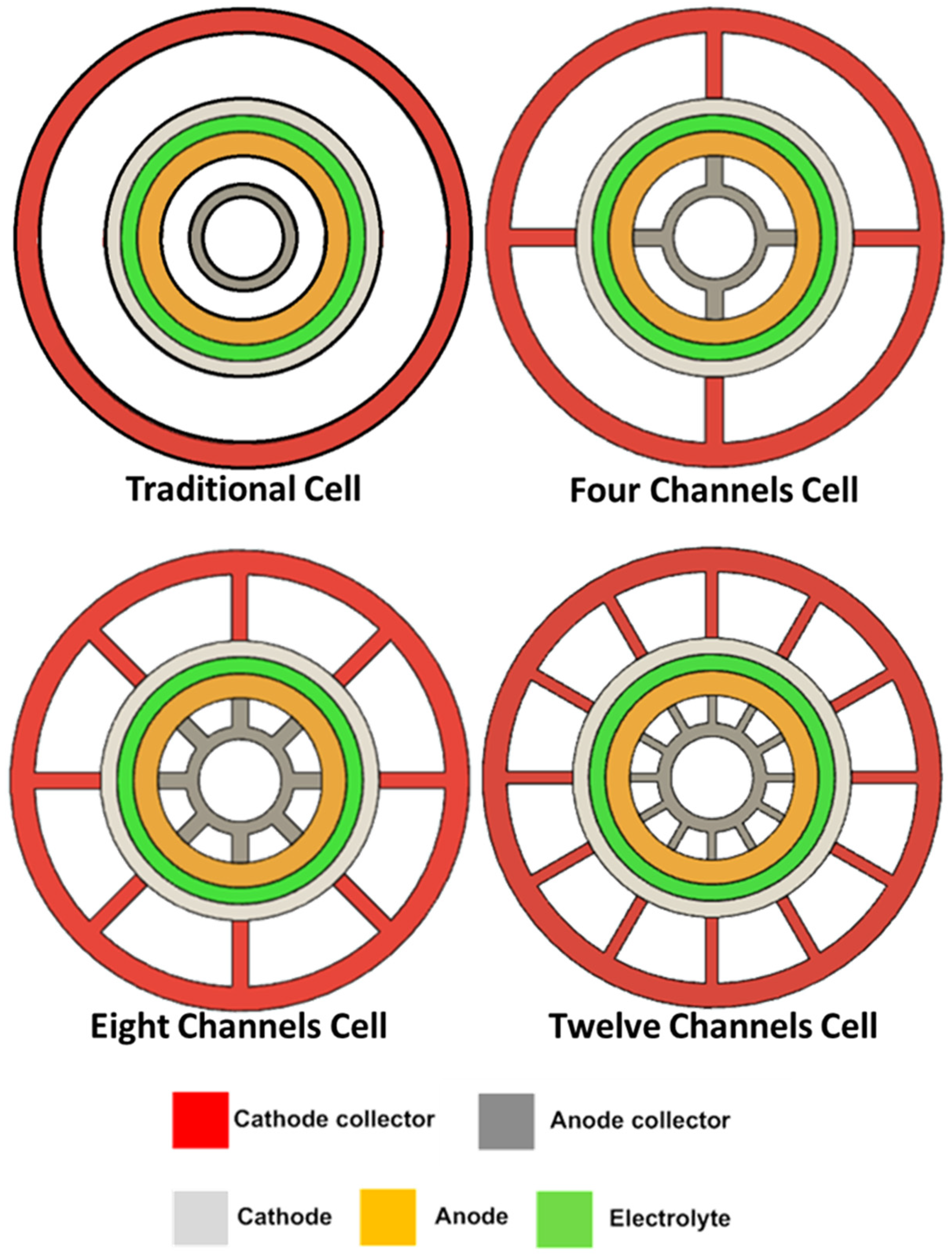
4. New Current Collector Design
5. Results and Discussion
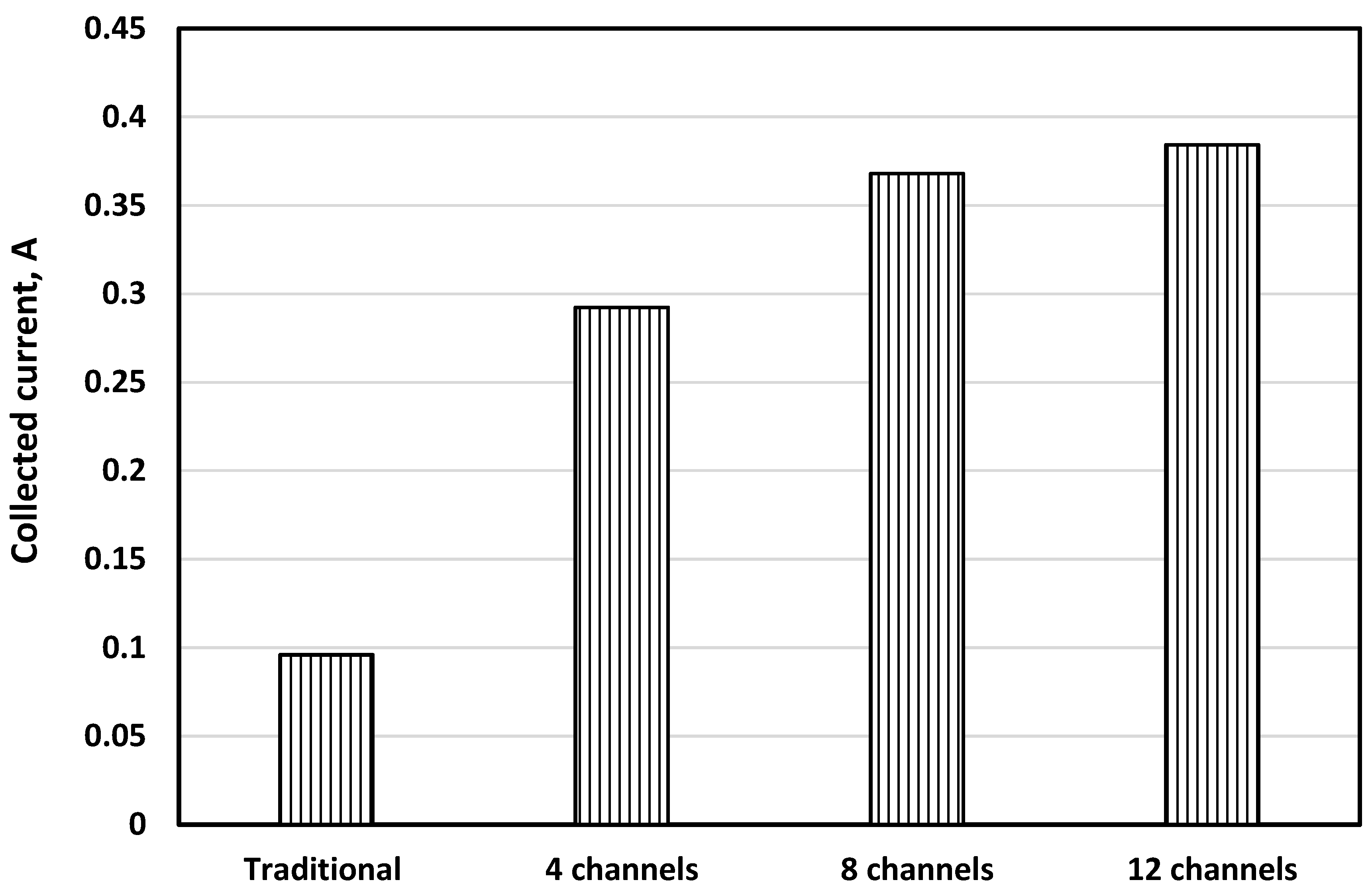
5.1. Cell Performance
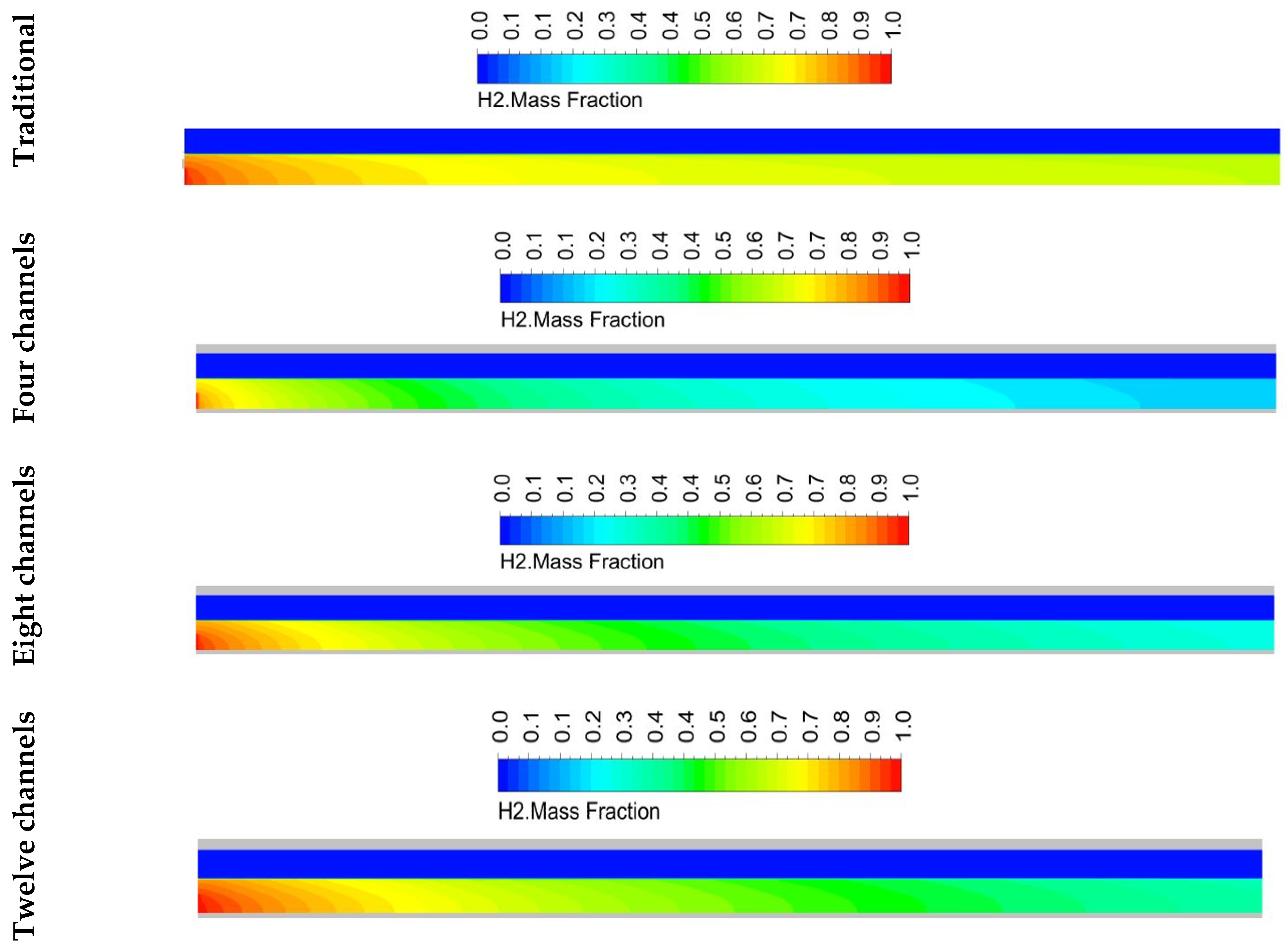
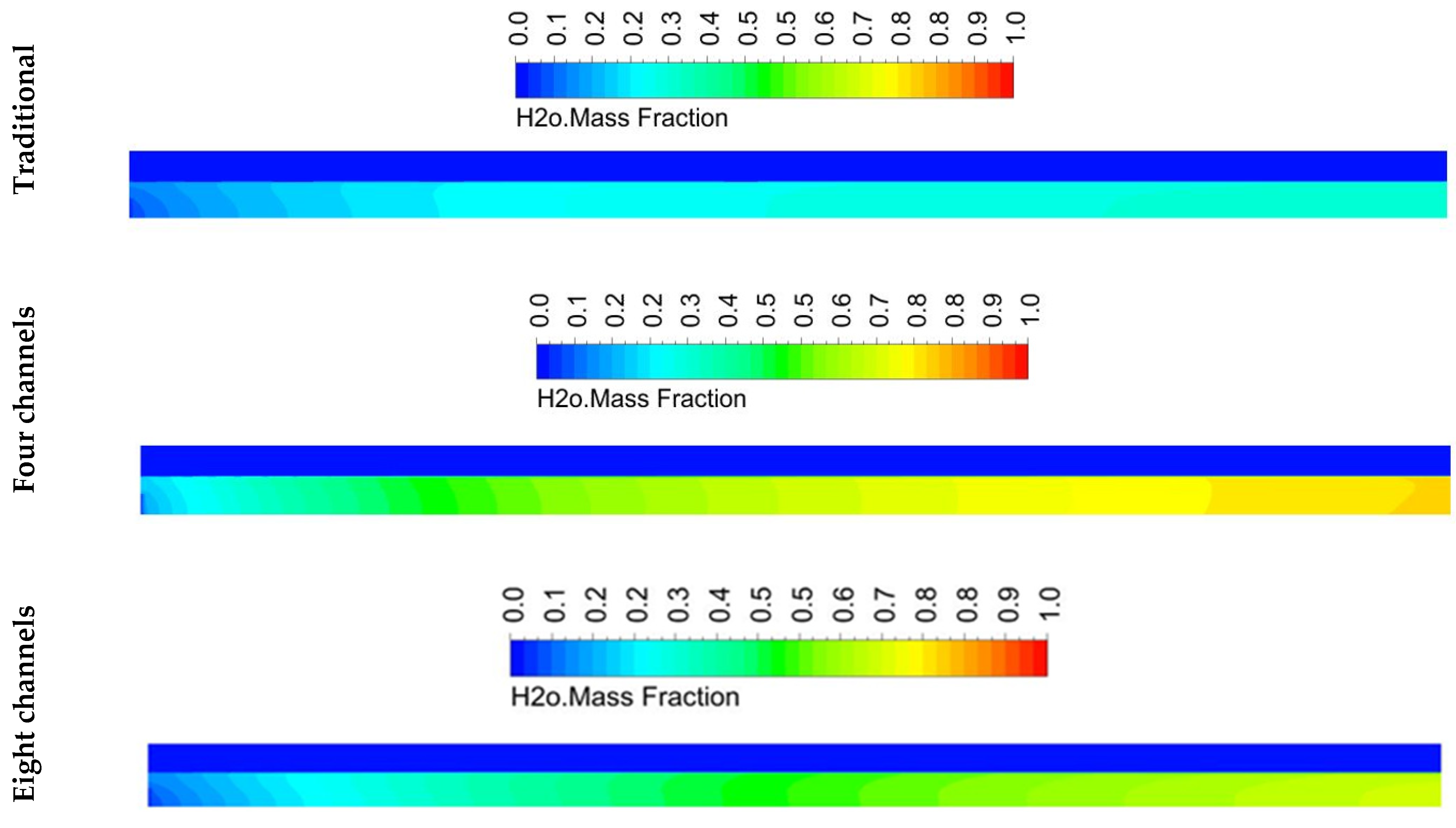
5.2. Species Distribution
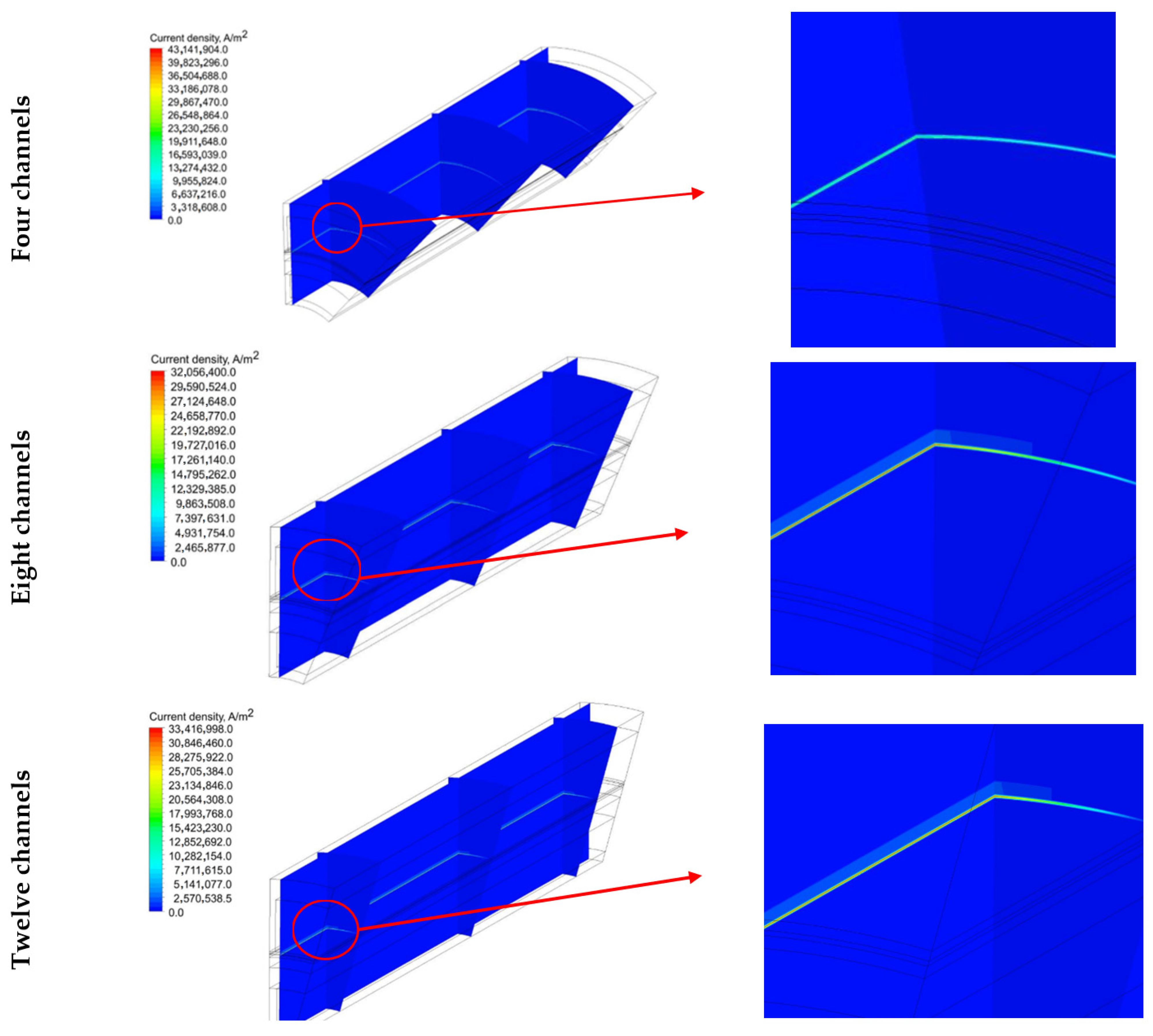
5.3. Current Density Distribution
6. Conclusions
- The numerical model could predict the cell performance with the newly developed current collector designs.
- The developed trapezoidal design achieves high performance compared with the traditional design.
- Increasing the number of channels enhances cell performance by increasing the contact surface, leading to efficient current collection.
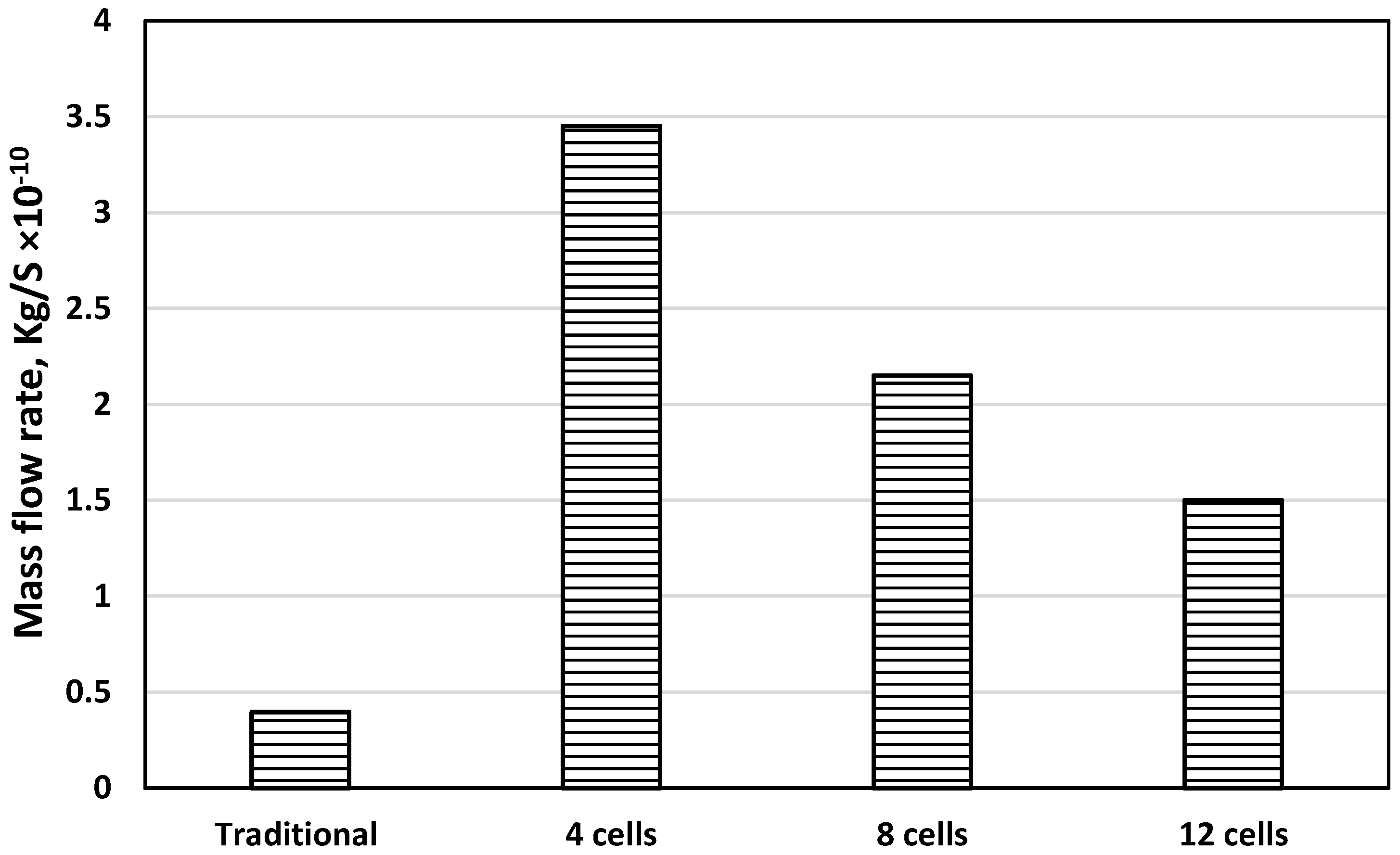
- Increasing the number of channels from 8 to 12 did not achieve a significant high-performance difference, and any further improvement should be directed to the SOFC microstructure.
- The design with twelve channels gave a high concentration of hydrogen at the outlet compared to the designs with four and eight channels. However, it achieved a greater performance than the designs with four and eight channels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| volumetric reaction surface area (m−1) | |
| pore diameter in the porous electrode (m) | |
| binary mass diffusion coefficient of a mixture of species i and j (m2 s−1) | |
| Faraday’s constant: 96,487 C mol−1 | |
| enthalpy | |
| current density (A m−2) | |
| species radius | |
| electrode radius | |
| average molecular weight (kg mol−1) | |
| number fraction | |
| exchange current (A m−2) | |
| permeability of porous electrode (m2) | |
| pressure (Pa) | |
| universal gas constant (J mol−1 K−1) | |
| mass source term (kg m−3 s−1) | |
| heat generation due to electrochemical reaction (W m−3) | |
| heat generation due to joule heating (W m−3) | |
| reaction source term for species i (kg m−3 s−1) | |
| temperature (K) | |
| velocity (m s−1) | |
| Po | reference pressure (pa) |
| To | reference temperature (K) |
| exponent of pore blockage | |
| mole fraction of species i | |
| direction perpendicular to electrolyte layer (m) | |
| Greek Symbols | |
| electron transfer coefficient (usually 0.5) | |
| viscosity (N s m−2) | |
| density (kg m−3) | |
| weight fraction of species i | |
| overpotential (V) | |
| exchange potential (V) | |
| reaction order for oxidation or reduction | |
| electrical conductivity (S m−1) | |
References
- Dhathathreyan, K.S.; Rajalakshmi, N.; Basu, S. Recent Trends in Fuel Cell Science and Technology; Basu, S., Ed.; Springer: New York, NY, USA; Springer: New Delhi, India, 2007; ISBN 978-0-387-35537-5. [Google Scholar]
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained; J. Wiley: Chichester, UK, 2003; Volume 2, ISBN 978-0-470-84857-9. [Google Scholar]
- Saied, M.; Ahmed, K.; Ahmed, M.; Nemat-Alla, M.; El-Sebaie, M. Investigations of Solid Oxide Fuel Cells with Functionally Graded Electrodes for High Performance and Safe Thermal Stress. Int. J. Hydrogen Energy 2017, 42, 15887–15902. [Google Scholar] [CrossRef]
- Sun, C.; Hui, R.; Roller, J. Cathode Materials for Solid Oxide Fuel Cells: A Review. J. Solid State Electrochem. 2010, 14, 1125–1144. [Google Scholar] [CrossRef]
- Zhu, J.H.; Ghezel-Ayagh, H. Cathode-Side Electrical Contact and Contact Materials for Solid Oxide Fuel Cell Stacking: A Review. Int. J. Hydrog. Energy 2017, 42, 24278–24300. [Google Scholar] [CrossRef]
- Ivers-Tiffée, E.; Weber, A.; Herbstritt, D. Materials and Technologies for SOFC-Components. J. Eur. Ceram. Soc. 2001, 21, 1805–1811. [Google Scholar] [CrossRef]
- Dokiya, M. SOFC System and Technology. Solid State Ion. 2002, 152–153, 383–392. [Google Scholar] [CrossRef]
- Collins, C.; Lucas, J.; Buchanan, T.L.; Kopczyk, M.; Kayani, A.; Gannon, P.E.; Deibert, M.C.; Smith, R.J.; Choi, D.-S.; Gorokhovsky, V.I. Chromium Volatility of Coated and Uncoated Steel Interconnects for SOFCs. Surf. Coat. Technol. 2006, 201, 4467–4470. [Google Scholar] [CrossRef]
- Davies, D.P.; Adcock, P.L.; Turpin, M.; Rowen, S.J. Stainless Steel as a Bipolar Plate Material for Solid Polymer Fuel Cells. J. Power Sources 2000, 86, 237–242. [Google Scholar] [CrossRef]
- Demeneva, N.V.; Bredikhin, S.I. Oxide Film Formation and Diffusion Processes in Near-Surface Layers of Current Collectors in Solid Oxide Fuel Cells. Russ J. Electrochem. 2014, 50, 725–729. [Google Scholar] [CrossRef]
- Gao, J.-T.; Li, J.-H.; Feng, Q.-Y.; Li, C.-J.; Li, C.-X. High Performance of Ceramic Current Collector Fabricated at 550 °C through In-Situ Joining of Reduced Mn1.5Co1.5O4 for Metal-Supported Solid Oxide Fuel Cells. Int. J. Hydrogen Energy 2020, 45, 29123–29130. [Google Scholar] [CrossRef]
- Qu, Z.; Aravind, P.V.; Boksteen, S.Z.; Dekker, N.J.J.; Janssen, A.H.H.; Woudstra, N.; Verkooijen, A.H.M. Three-Dimensional Computational Fluid Dynamics Modeling of Anode-Supported Planar SOFC. Int. J. Hydrogen Energy 2011, 36, 10209–10220. [Google Scholar] [CrossRef]
- Guillodo, M.; Vernoux, P.; Fouletier, J. Electrochemical Properties of Ni–YSZ Cermet in Solid Oxide Fuel Cells: Effect of Current Collecting. Solid State Ion. 2000, 127, 99–107. [Google Scholar] [CrossRef]
- Wei, S.-S.; Wang, T.-H.; Wu, J.-S. Numerical Modeling of Interconnect Flow Channel Design and Thermal Stress Analysis of a Planar Anode-Supported Solid Oxide Fuel Cell Stack. Energy 2014, 69, 553–561. [Google Scholar] [CrossRef]
- Saied, M.; Ahmed, K.; Nemat-Alla, M.; Ahmed, M.; El-Sebaie, M. Performance Study of Solid Oxide Fuel Cell with Various Flow Field Designs: Numerical Study. Int. J. Hydrog. Energy 2018, 43, 20931–20946. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Hu, B.; Yan, C.; Lu, L. Investigation of Proper External Air Flow Path for Tubular Fuel Cell Stacks with an Anode Support Feature. Energy Convers. Manag. 2018, 171, 807–814. [Google Scholar] [CrossRef]
- Sammes, N.M.; Du, Y.; Bove, R. Design and Fabrication of a 100W Anode Supported Micro-Tubular SOFC Stack. J. Power Sources 2005, 145, 428–434. [Google Scholar] [CrossRef]
- Zhu, H.; Kee, R.J. The Influence of Current Collection on the Performance of Tubular Anode-Supported SOFC Cells. J. Power Sources 2007, 169, 315–326. [Google Scholar] [CrossRef]
- Cui, D.; Liu, L.; Dong, Y.; Cheng, M. Comparison of Different Current Collecting Modes of Anode Supported Micro-Tubular SOFC through Mathematical Modeling. J. Power Sources 2007, 174, 246–254. [Google Scholar] [CrossRef]
- Calise, F.; Restucccia, G.; Sammes, N. Experimental Analysis of Micro-Tubular Solid Oxide Fuel Cell Fed by Hydrogen. J. Power Sources 2010, 195, 1163–1170. [Google Scholar] [CrossRef]
- Li, T.; Wu, Z.; Li, K. A Dual-Structured Anode/Ni-Mesh Current Collector Hollow Fibre for Micro-Tubular Solid Oxide Fuel Cells (SOFCs). J. Power Sources 2014, 251, 145–151. [Google Scholar] [CrossRef]
- Hatchwell, C.E.; Sammes, N.M.; Kendall, K. Cathode Current-Collectors for a Novel Tubular SOFC Design. J. Power Sources 1998, 70, 85–90. [Google Scholar] [CrossRef]
- Lee, S.; Lim, T.; Song, R.; Shin, D.; Dong, S. Development of a 700W Anode-Supported Micro-Tubular SOFC Stack for APU Applications. Int. J. Hydrogen Energy 2008, 33, 2330–2336. [Google Scholar] [CrossRef]
- Hodjati-Pugh, O.; Dhir, A.; Steinberger-Wilckens, R. Internal Current Collection and Thermofluidynamic Enhancement in a Microtubular SOFC. Int. J. Heat Mass Transf. 2021, 173, 121255. [Google Scholar] [CrossRef]
- Shi, J.; Fan, J.; Wang, Y.; Shi, Y.; Cai, N. A New Design Using Metal Wire Brushes as the Current Collector and Catalyst Carrier for Internal Reforming of Micro-Tubular SOFCs. J. Electrochem. Soc. 2021, 168, 104508. [Google Scholar] [CrossRef]
- Montero, X.; Tietz, F.; Stöver, D.; Cassir, M.; Villarreal, I. Evaluation of Commercial Alloys as Cathode Current Collector for Metal-Supported Tubular Solid Oxide Fuel Cells. Corros. Sci. 2009, 51, 110–118. [Google Scholar] [CrossRef]
- Doraswami, U.; Droushiotis, N.; Kelsall, G.H. Modelling Effects of Current Distributions on Performance of Micro-Tubular Hollow Fibre Solid Oxide Fuel Cells. Electrochim. Acta 2010, 55, 3766–3778. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, Y.; Wei, Z.; Zhang, Y.; Wang, Y. Effect of Tube Radius on Creep for an Anode Supported Tubular Solid Oxide Fuel Cell: Experimental and Finite Element Simulation. Int. J. Hydrogen Energy 2017, 42, 23198–23206. [Google Scholar] [CrossRef]
- Funahashi, Y.; Shimamori, T.; Suzuki, T.; Fujishiro, Y.; Awano, M. Simulation Study for the Optimization of Microtubular Solid Oxide Fuel Cell Bundles. J. Fuel Cell Sci. Technol. 2010, 7, 021015. [Google Scholar] [CrossRef]
- Cordiner, S.; Mariani, A.; Mulone, V. CFD-Based Design of Microtubular Solid Oxide Fuel Cells. J. Heat Transf. 2010, 132, 062801. [Google Scholar] [CrossRef]
- Zhang, Z.; Yue, D.; Yang, G.; Chen, J.; Zheng, Y.; Miao, H.; Wang, W.; Yuan, J.; Huang, N. Three-Dimensional CFD Modeling of Transport Phenomena in Multi-Channel Anode-Supported Planar SOFCs. Int. J. Heat Mass Transf. 2015, 84, 942–954. [Google Scholar] [CrossRef]
- Mollayi Barzi, Y.; Raoufi, A.; Manafi Rasi, N.; Davari, S. Three Dimensional Simulation of a Counter-Flow Planar Solid Oxide Fuel Cell. ECS Trans. 2019, 35, 1021–1033. [Google Scholar] [CrossRef]
- Wilberforce, T.; Ijaodola, O.; Emmanuel, O.; Thompson, J.; Olabi, A.G.; Abdelkareem, M.A.; Sayed, E.T.; Elsaid, K.; Maghrabie, H.M. Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes 2021, 11, 146. [Google Scholar] [CrossRef] [PubMed]
- Hart, N.T.; Brandon, N.P.; Day, M.J.; Lapeña-Rey, N. Functionally Graded Composite Cathodes for Solid Oxide Fuel Cells. J. Power Sources 2002, 106, 42–50. [Google Scholar] [CrossRef]
- Anandakumar, G.; Li, N.; Verma, A.; Singh, P.; Kim, J.-H. Thermal Stress and Probability of Failure Analyses of Functionally Graded Solid Oxide Fuel Cells. J. Power Sources 2010, 195, 6659–6670. [Google Scholar] [CrossRef]
- Eaton, B.M. FLUENT Fuel Cell Modules Manual. Available online: https://documents.pub/document/fluent-fuel-cell-modules-manual-cfd-is-a-trademark-used-by-ansys-inc-the.html (accessed on 2 April 2022).
- Cable, T.L.; Sofie, S.W. A Symmetrical, Planar SOFC Design for NASA’s High Specific Power Density Requirements. J. Power Sources 2007, 174, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Li, W.; Zhang, S.; Bi, L.; Peng, R.; Chen, C.; Liu, W. Fabrication and Characterization of an Anode-Supported Hollow Fiber SOFC. J. Power Sources 2009, 187, 90–92. [Google Scholar] [CrossRef]
- Chaisantikulwat, A.; Diaz-Goano, C.; Meadows, E.S. Dynamic Modelling and Control of Planar Anode-Supported Solid Oxide Fuel Cell. Comput. Chem. Eng. 2008, 32, 2365–2381. [Google Scholar] [CrossRef]
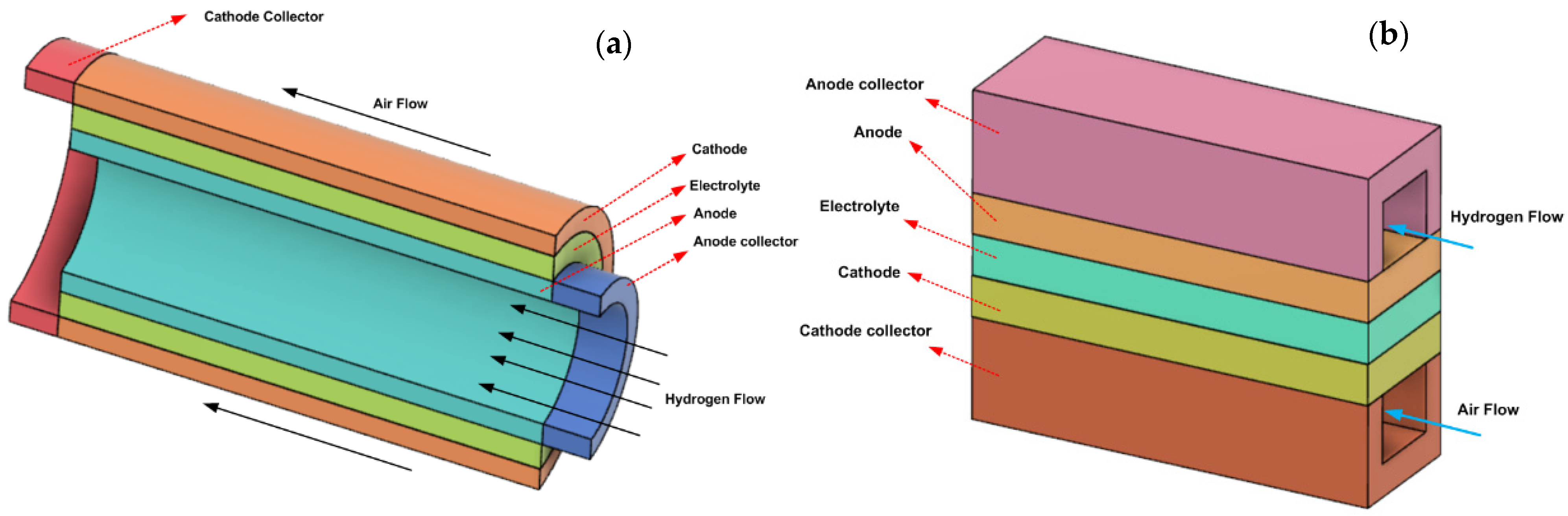
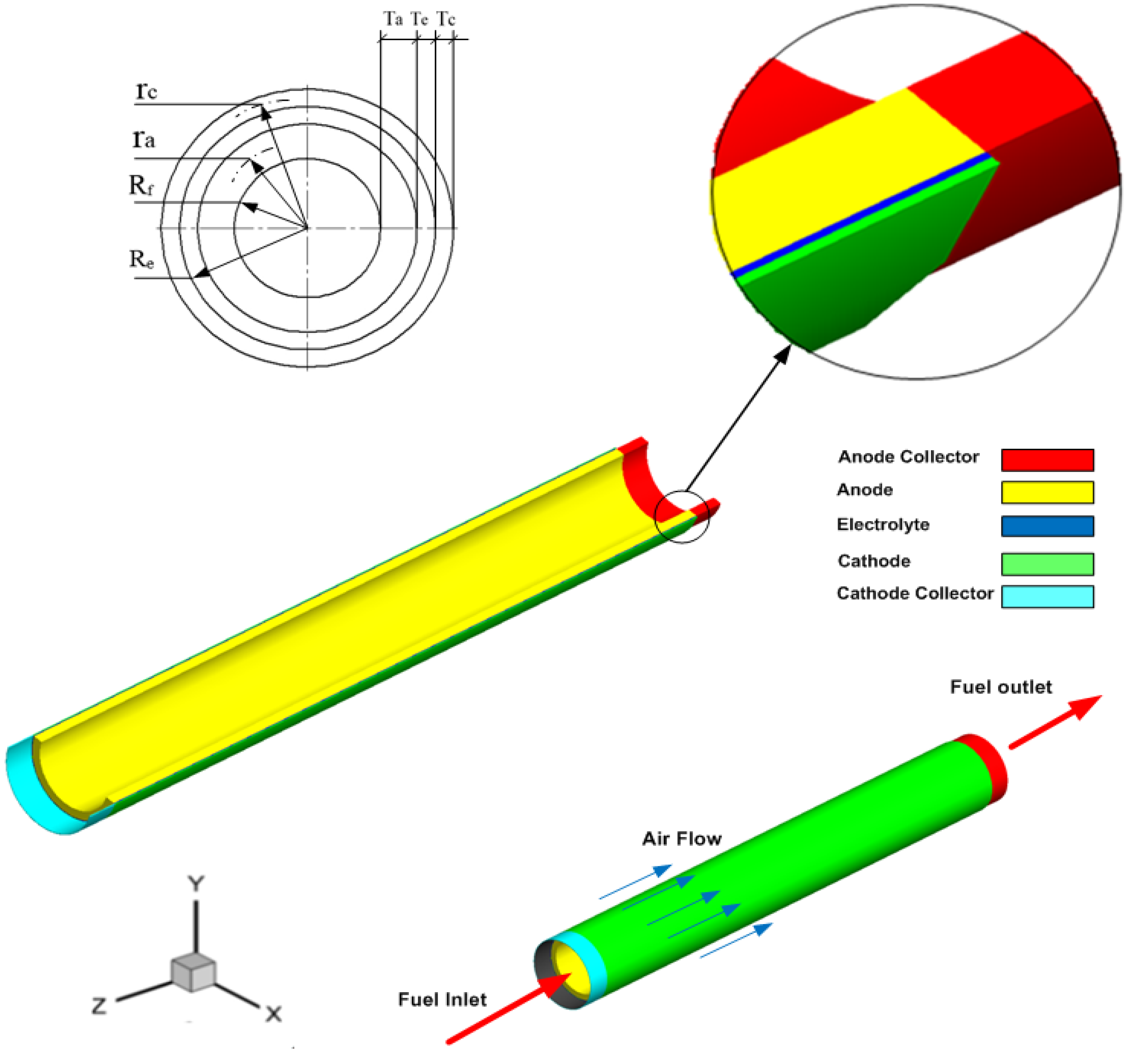
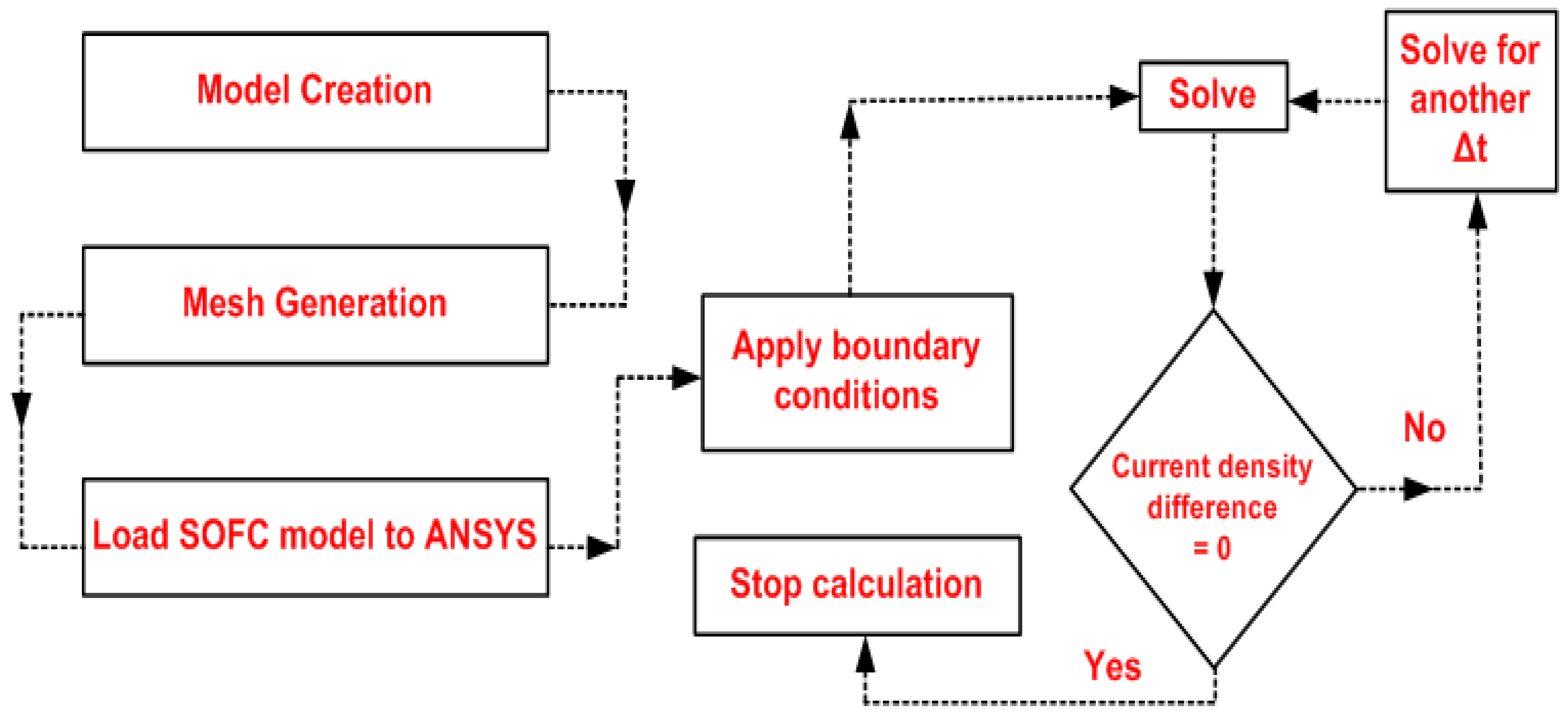
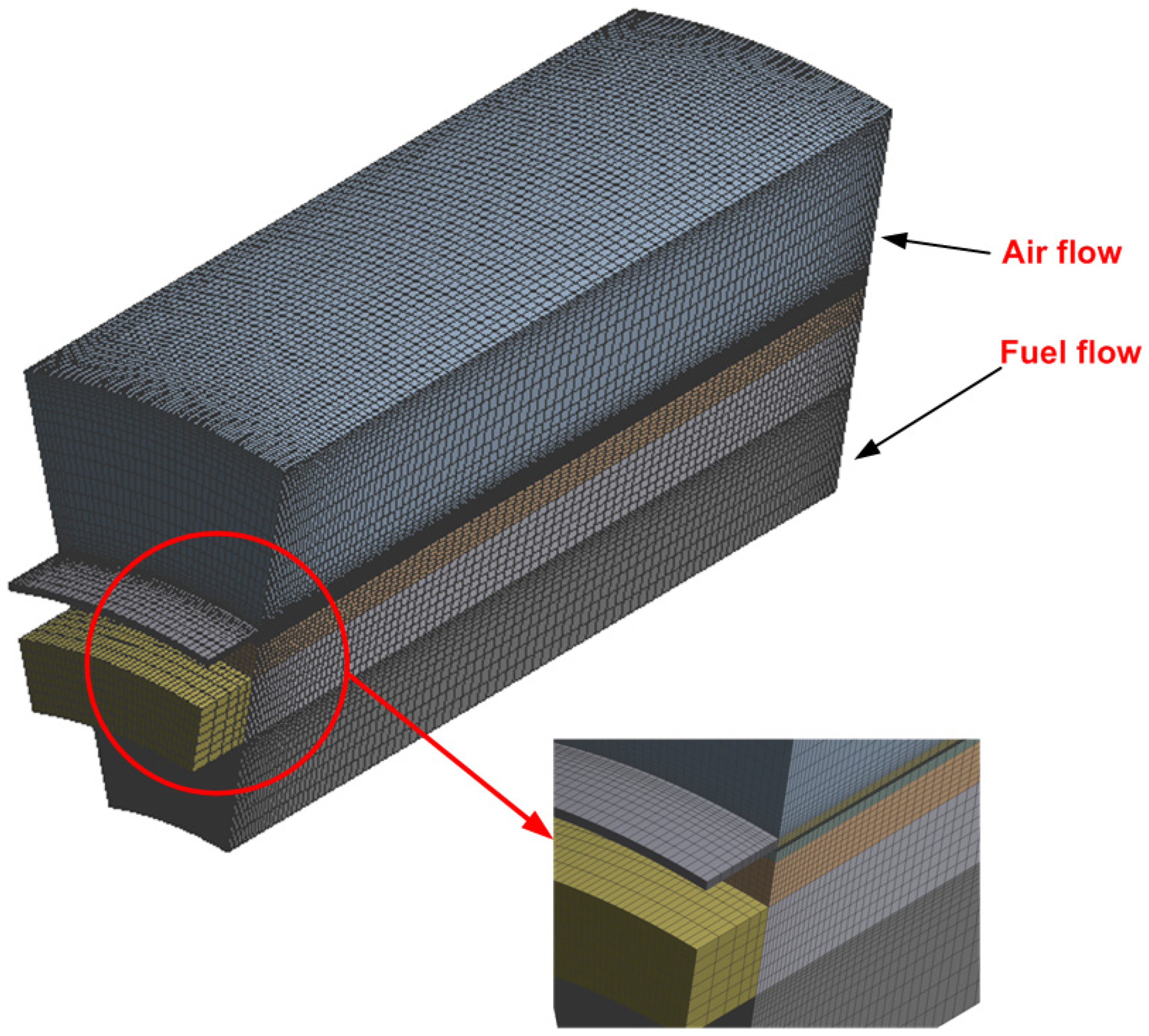



| Item | Dimension, mm |
|---|---|
| Cell length | 11.8 |
| Anode thickness | 0.15 |
| Cathode thickness | 0.015 |
| Electrolyte thickness | 0.012 |
| Anode flow Diameter | 1.35 |
| Cathode flow Diameter | 3.4 |
| Parameter | Anode | Cathode | Electrolyte |
|---|---|---|---|
| Material | Ni-YSZ | LSM | YSZ |
| Density (kg/m3) | 4200 | 6350 | 6010 |
| Specific heat (j/kg-K) | 377 | 377 | 2000 |
| Items | Anode Inlet | Cathode Inlet | Collector | Cell Surroundings | |
|---|---|---|---|---|---|
| Mass flow inlet (kg/s) | 1.334 × 10−8 | Exposed to air | None | None | |
| Temperature, K | 1073 | 1073 | Adiabatic | Adiabatic | |
| Species | H2 | 97% | None | None | None |
| O2 | None | 21% | |||
| H2O | 3% | None | |||
| Mesh | A | B |
|---|---|---|
| Element size | 0.2 mm sizing | 0.125 mm sizing |
| Mesh size | 1,057,997 | 1,617,846 |
| No. of cores used | 7 | 7 |
| Iteration time (sec) | 15 | 20 |
| Amp. at 0.6 volt | 0.636838 | 0.635234 |
| Error (%) | 5.78 | 5.5466 |
| No. of iterations | 17,650 | 17,650 |
| Solving time (hr) | 73.54 | 98.06 |
| Item | Yang et al. [38] | Chaisantikulwat et al. [39] |
|---|---|---|
| Fuel cell configuration | Tubular | Planar |
| 3D representation | 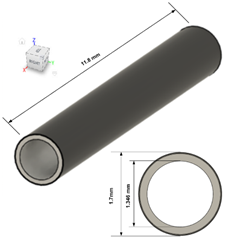 |  |
| Fuel composition | H2 (∼3% H2O) | H2 (∼3% H2O) |
| Fuel flow rate | 40 mL min−1 | 10 cm3/min |
| Reduction medium | Exposed to air | O2 (21%) + N2 (79%) |
| Reduction of medium flow rate | 15 cm3/min | |
| Operating temperature | 873.15 K | 1023 K |
| Pressure | 1.01325 bar | 1.01325 bar |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.I.; Ahmed, M.H. Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector. Appl. Sci. 2022, 12, 6003. https://doi.org/10.3390/app12126003
Ahmed KI, Ahmed MH. Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector. Applied Sciences. 2022; 12(12):6003. https://doi.org/10.3390/app12126003
Chicago/Turabian StyleAhmed, Khaled I., and Mohamed H. Ahmed. 2022. "Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector" Applied Sciences 12, no. 12: 6003. https://doi.org/10.3390/app12126003
APA StyleAhmed, K. I., & Ahmed, M. H. (2022). Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector. Applied Sciences, 12(12), 6003. https://doi.org/10.3390/app12126003






