A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions
Abstract
:1. Introduction
2. Generalized Dynamic Model
2.1. Establishment of Global Dynamics Model
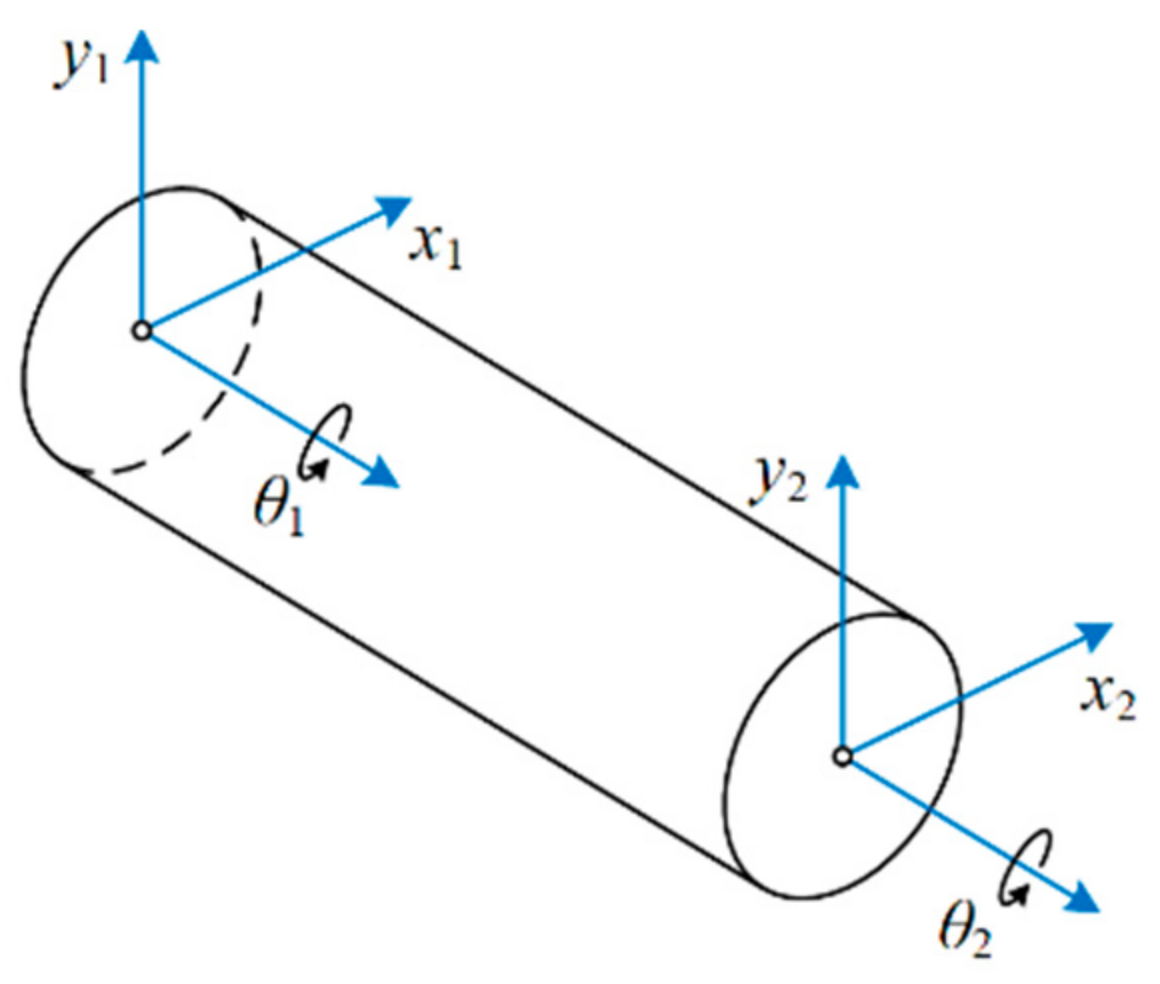
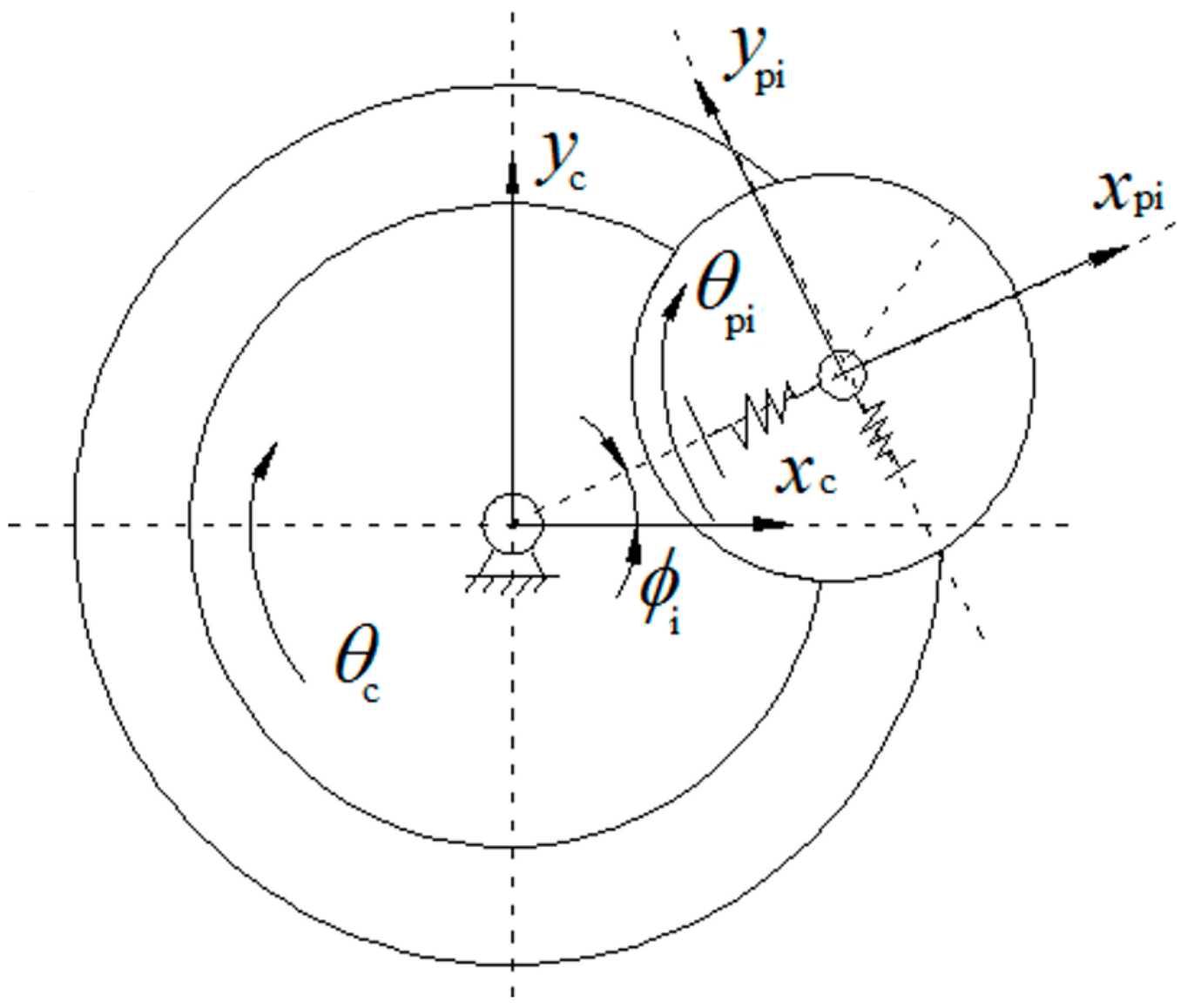
2.1.1. Shaft Element
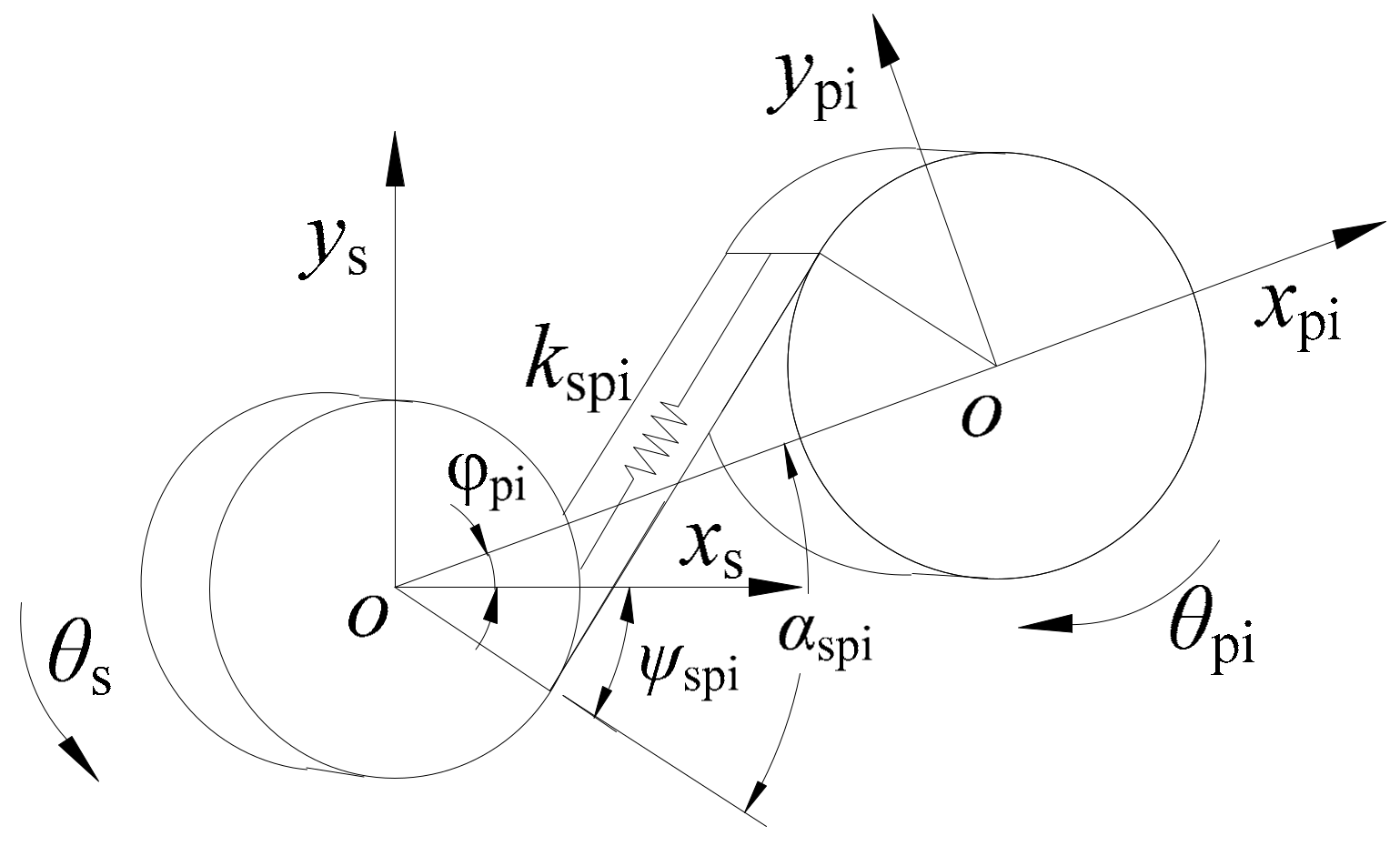
2.1.2. External Meshing Element
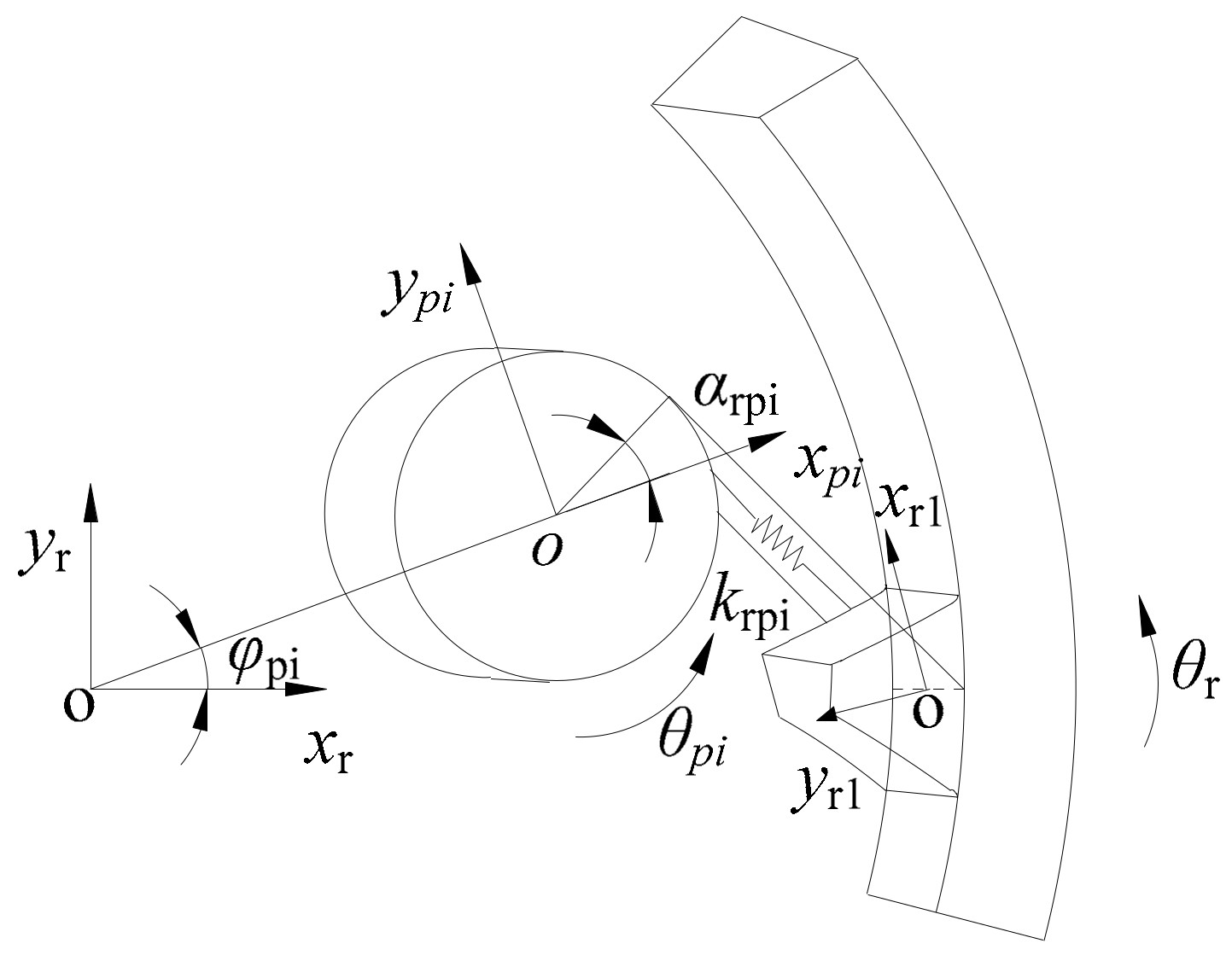
2.1.3. Internal Meshing Element
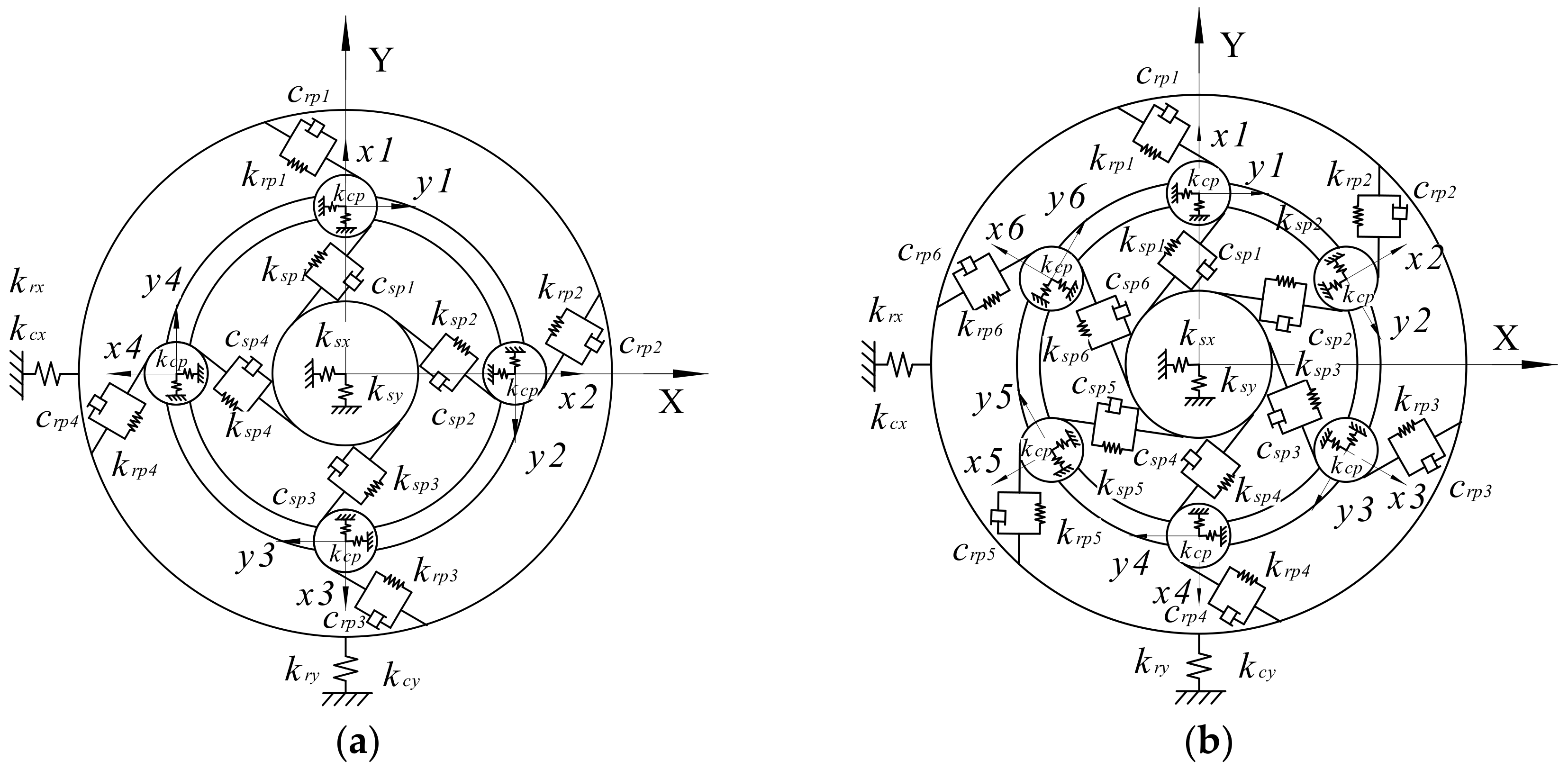
2.1.4. Planetary Carrier Element
2.2. A Generalized Dynamic Model for Planetary Gear Set Transmissions
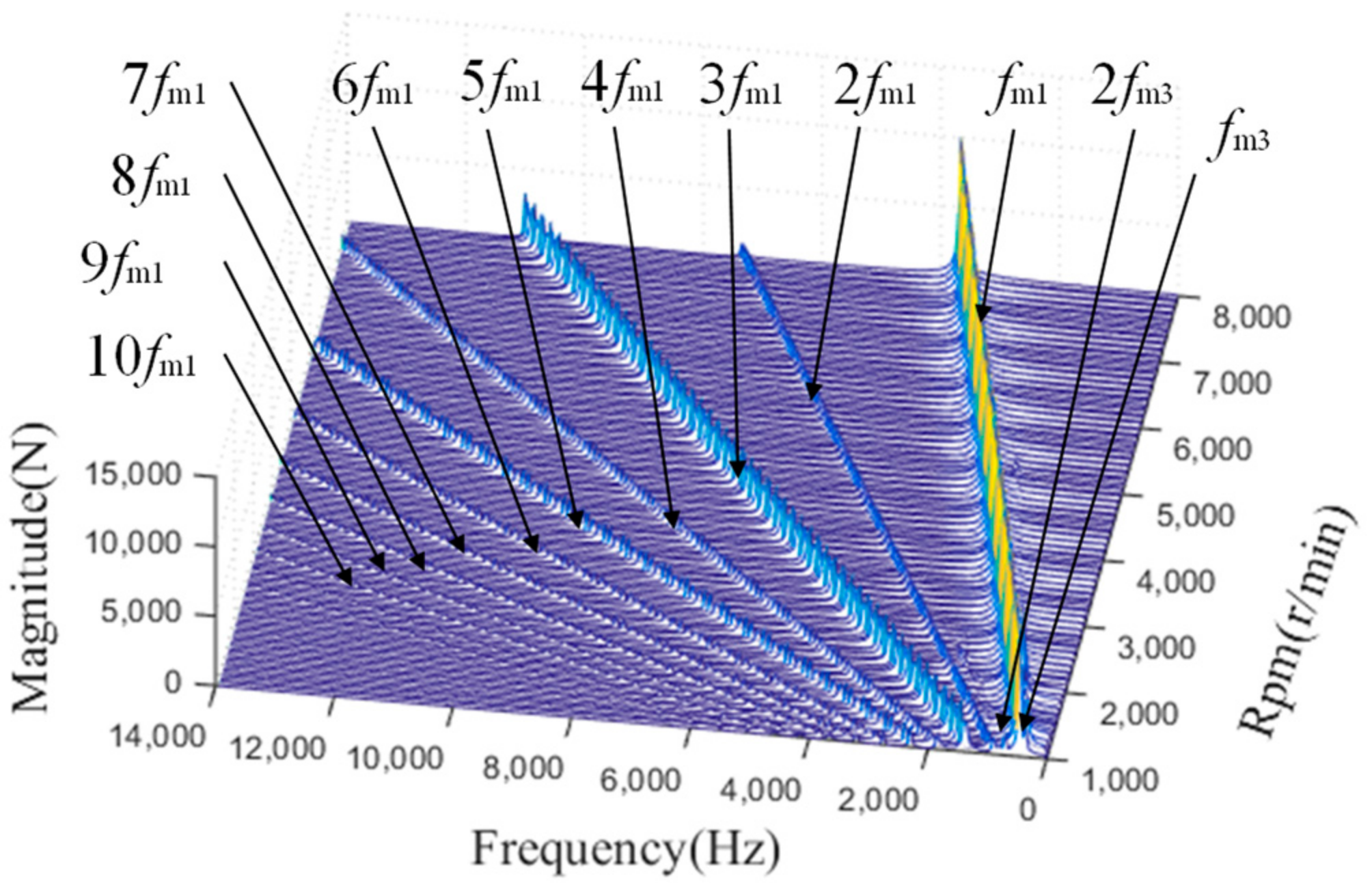
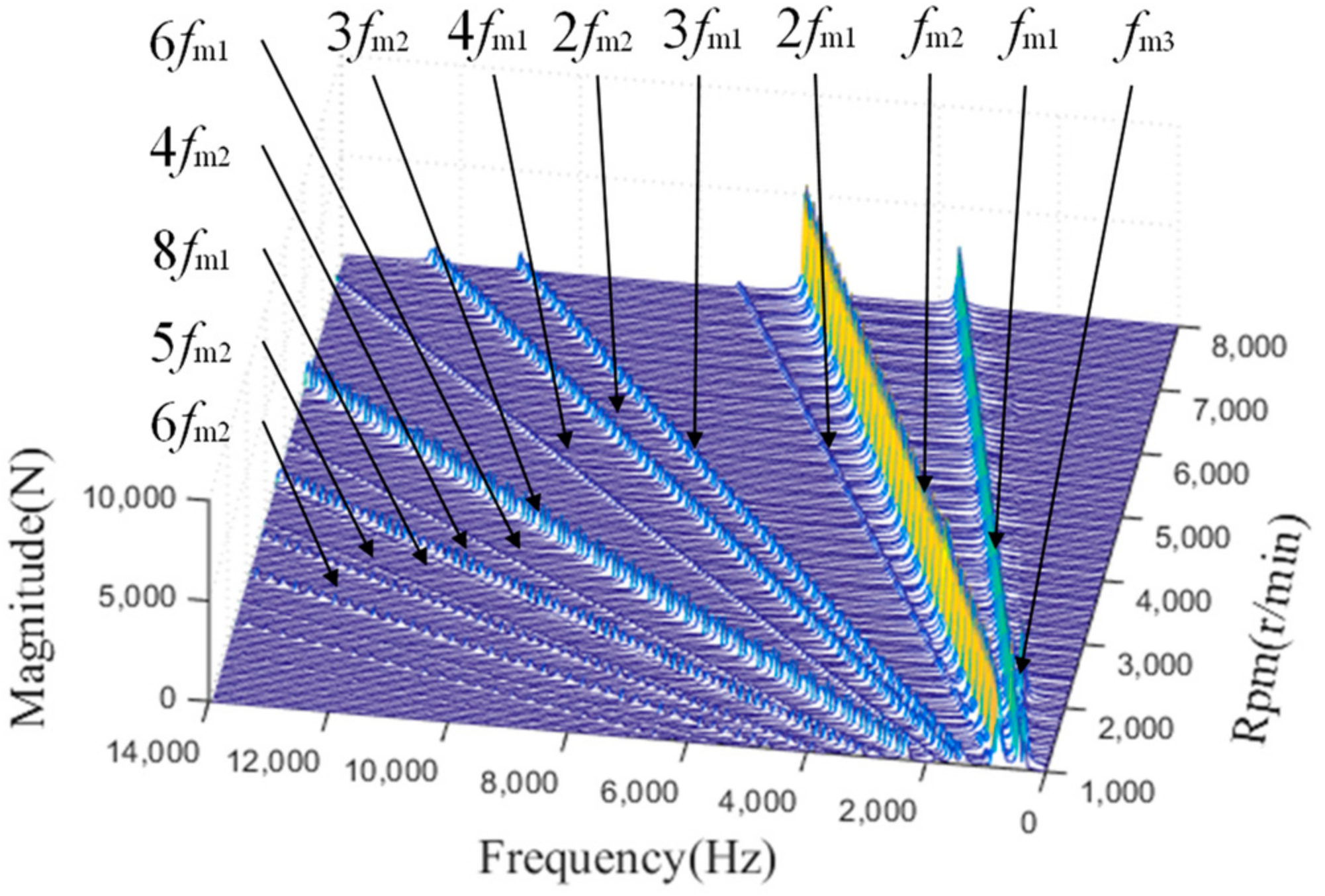
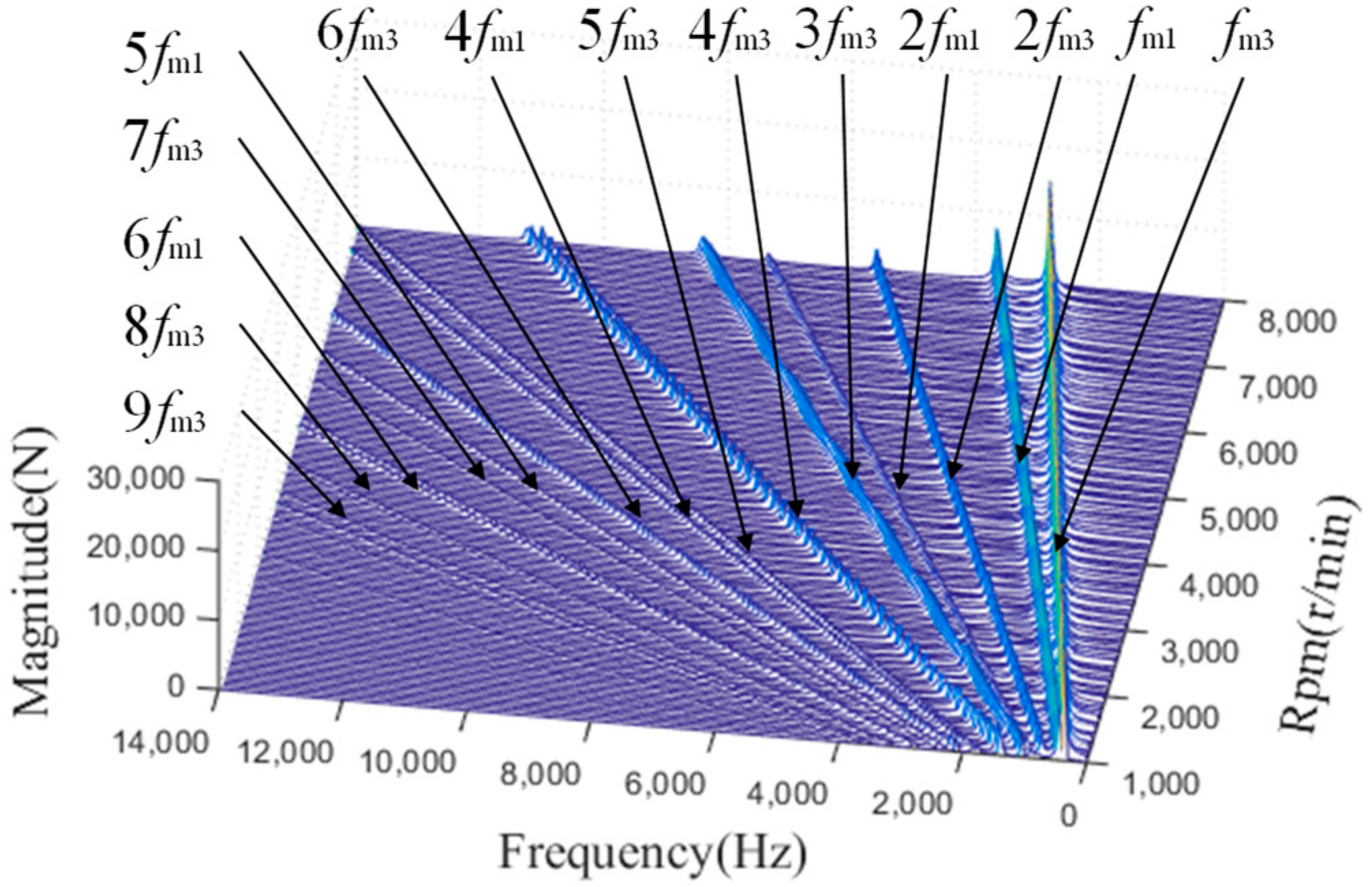
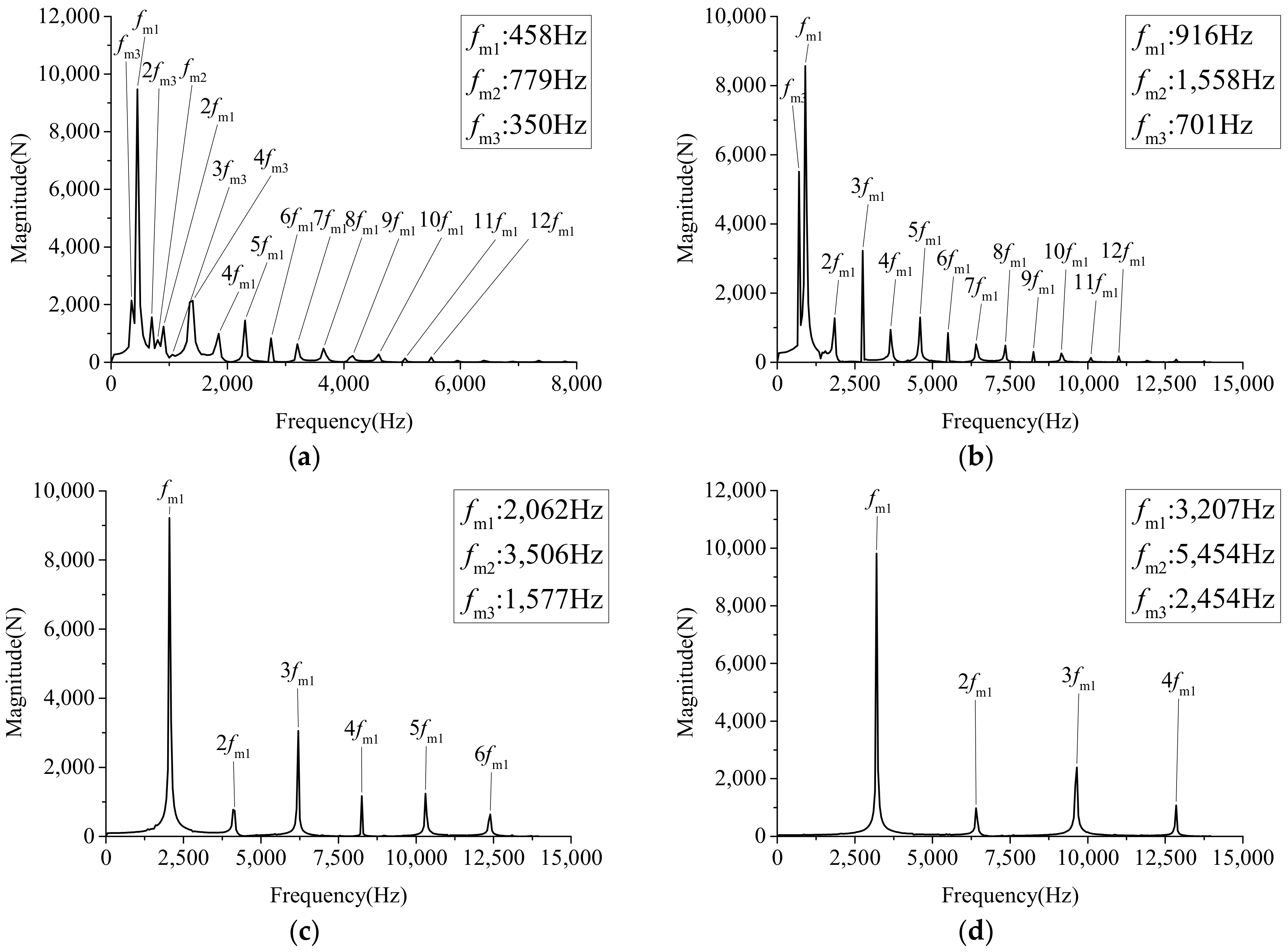
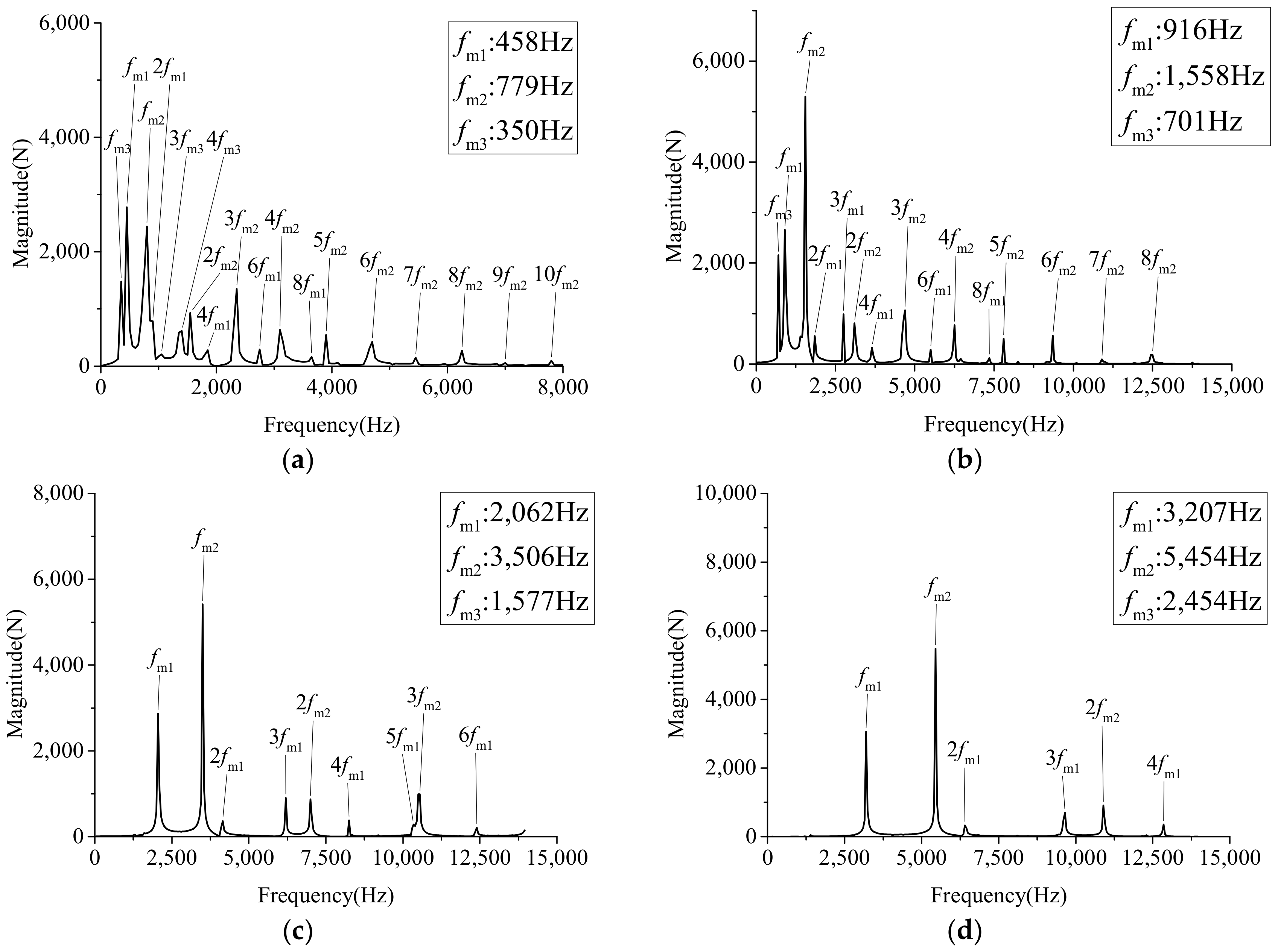
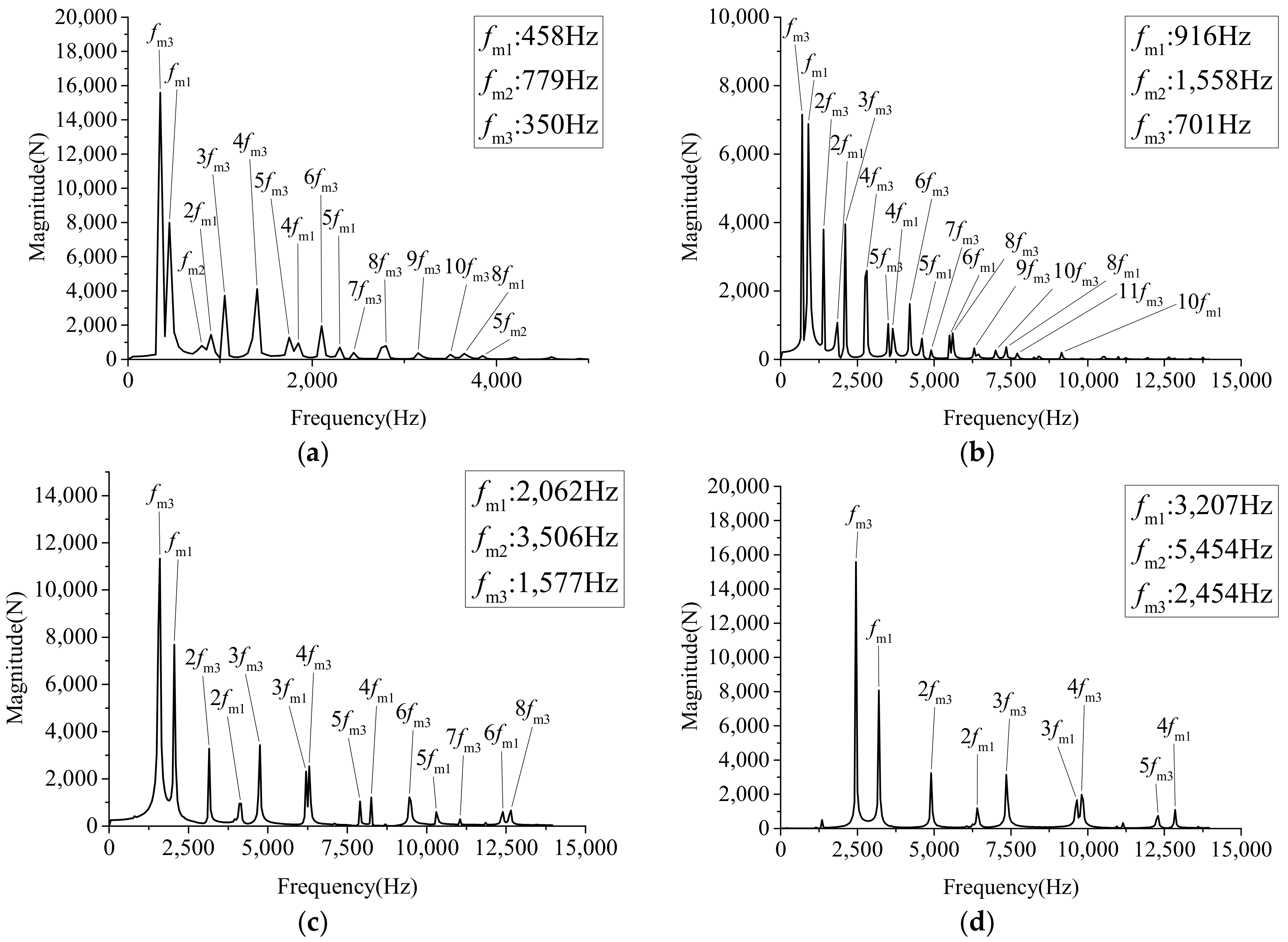
3. Meshing Force Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kahraman, A. Natural modes of planetary gear trains. J. Sound Vib. 1994, 173, 125–130. [Google Scholar] [CrossRef]
- Lin, J.; Parker, R.G. Analytical characterization of the unique properties of planetary gear free vibration. J. Vib. Acoust. 1999, 121, 316–321. [Google Scholar] [CrossRef]
- Bang, Y. Multi-speed transmission mechanism using a compound planetary gear set and brakes. Int. J. Automot. Technol. 2019, 20, 739–748. [Google Scholar] [CrossRef]
- Ambarisha, V.K.; Parker, R.G. Nonlinear dynamics of planetary gears using analytical and finite element models. J. Sound Vib. 2007, 302, 577–595. [Google Scholar] [CrossRef]
- Zhao, L.; Xiong, X. Research on dynamic characteristics based on flexible body model of planetary gear system. Coal Mine Mach. 2012, 33, 117–119. [Google Scholar]
- Lai, J.; Liu, Y.; Xu, X.; Li, H.; Xu, J.; Wang, S.; Guo, W. Dynamic modeling and analysis of Ravigneaux planetary gear set with unloaded floating ring gear. Mech. Mach. Theory 2022, 170, 104696. [Google Scholar] [CrossRef]
- Benford, H.L.; Leising, M.B. The lever analogy: A new tool in transmission analysis. SAE Trans. 1981, 90, 429–437. [Google Scholar]
- Kim, H.; Kum, D. Comprehensive design methodology of input-and output-split hybrid electric vehicles: In search of optimal configuration. IEEE/ASME Trans. Mechatron. 2016, 21, 2912–2923. [Google Scholar] [CrossRef]
- Kahraman, A.; Ligata, H.; Kienzle, K.; Zini, D.M. A kinematics and power flow analysis methodology for automatic transmission planetary gear trains. J. Mech. Des. 2004, 126, 1071–1081. [Google Scholar] [CrossRef]
- Lang, S.Y.T. Graph-theoretic modelling of epicyclic gear systems. Mech. Mach. Theory 2005, 40, 511–529. [Google Scholar] [CrossRef]
- Tian, L.; Li, Q. Matrix system for the analysis of planetary transmissions. J. Mech. Des. 1997, 119, 333–337. [Google Scholar] [CrossRef]
- Chang, L.; He, Z.; Liu, G. Dynamic modeling of parallel shaft gear transmissions using finite element method. J. Vib. Shock 2016, 35, 47–53. [Google Scholar]
- Qian, B.; Wu, S.; Zhou, G. Research on dynamic characteristics of planetary gear sets. J. Syst. Simul. 2009, 20, 6608–6612. [Google Scholar]
- Wei, J.; Zhang, A.; Qin, D.; Lim, T.C.; Shu, R.; Lin, X.; Meng, F. A coupling dynamics analysis method for a multistage planetary gear system. Mech. Mach. Theory 2017, 110, 27–49. [Google Scholar] [CrossRef]
- Lv, H.; Li, Z.; Zhu, W.; Tang, X.; Gao, J.; Zhu, R. Construction of 12 DOFs spur gear coupling dynamic model. Vibroengineering PROCEDIA 2019, 28, 241–245. [Google Scholar]
- Xiao, Z.; Qin, D.; Wang, J.; Wu, W.; Chen, L. Study on torsional dynamics of 3-stage planetary gears of main reducer used in driving cutterhead of shield tunnelling machine. China Mech. Eng. 2010, 21, 2176. [Google Scholar]
- Liu, H.; Cai, Z.; Xiang, C. Frequency coupling and dynamic characteristics of nonlinear meshing force for two-stage planetary Gears. J. Vib. Shock 2015, 34, 13–23. [Google Scholar]
- Wei, J.; Zhang, A.; Qin, D.; Shu, R.Z. Coupling vibration analysis for planetary gear system considering flexible structure. J. Mech. Eng. 2017, 53, 1–12. [Google Scholar]
- Zhang, Q.; Li, H. Torsional vibration analysis and optimization of vehicle multi-stage planetary transmission system. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 339–343. [Google Scholar]
- Dou, Z.; Li, Y.; Zeng, Z.; Du, M.; Yang, Y. Frequency coupling and coupling resonance of a composite planetary transmission system under complex excitations. J. Vib. Shock 2019, 38, 16–23. [Google Scholar]
- Hao, X.; Yuan, X.; Bai, J.; Li, F.; Qin, J. Analysis of factor affecting frequency coupling of double planetary gear system. J. Mech. Transm. 2020, 44, 110–117, 165. [Google Scholar] [CrossRef]
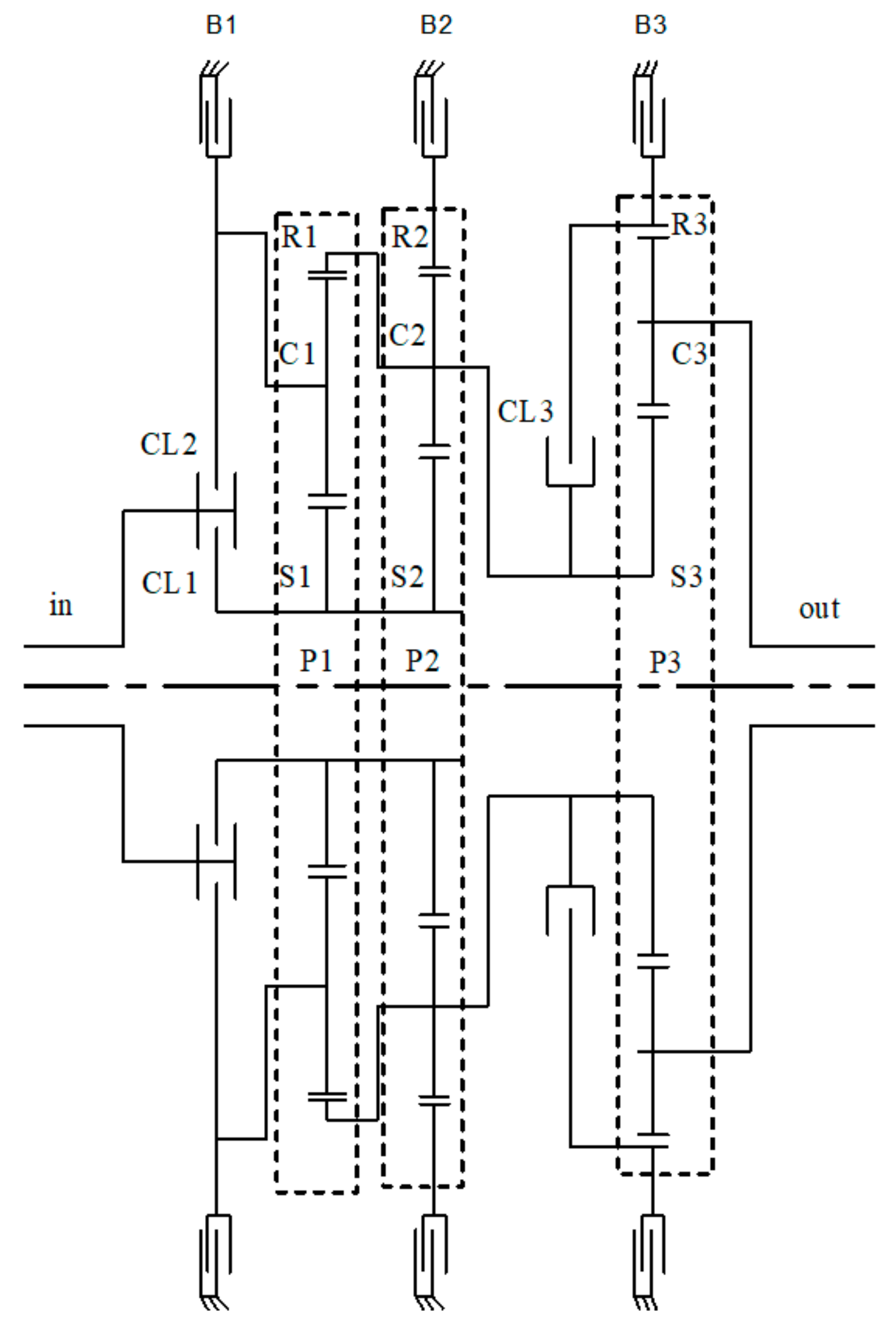
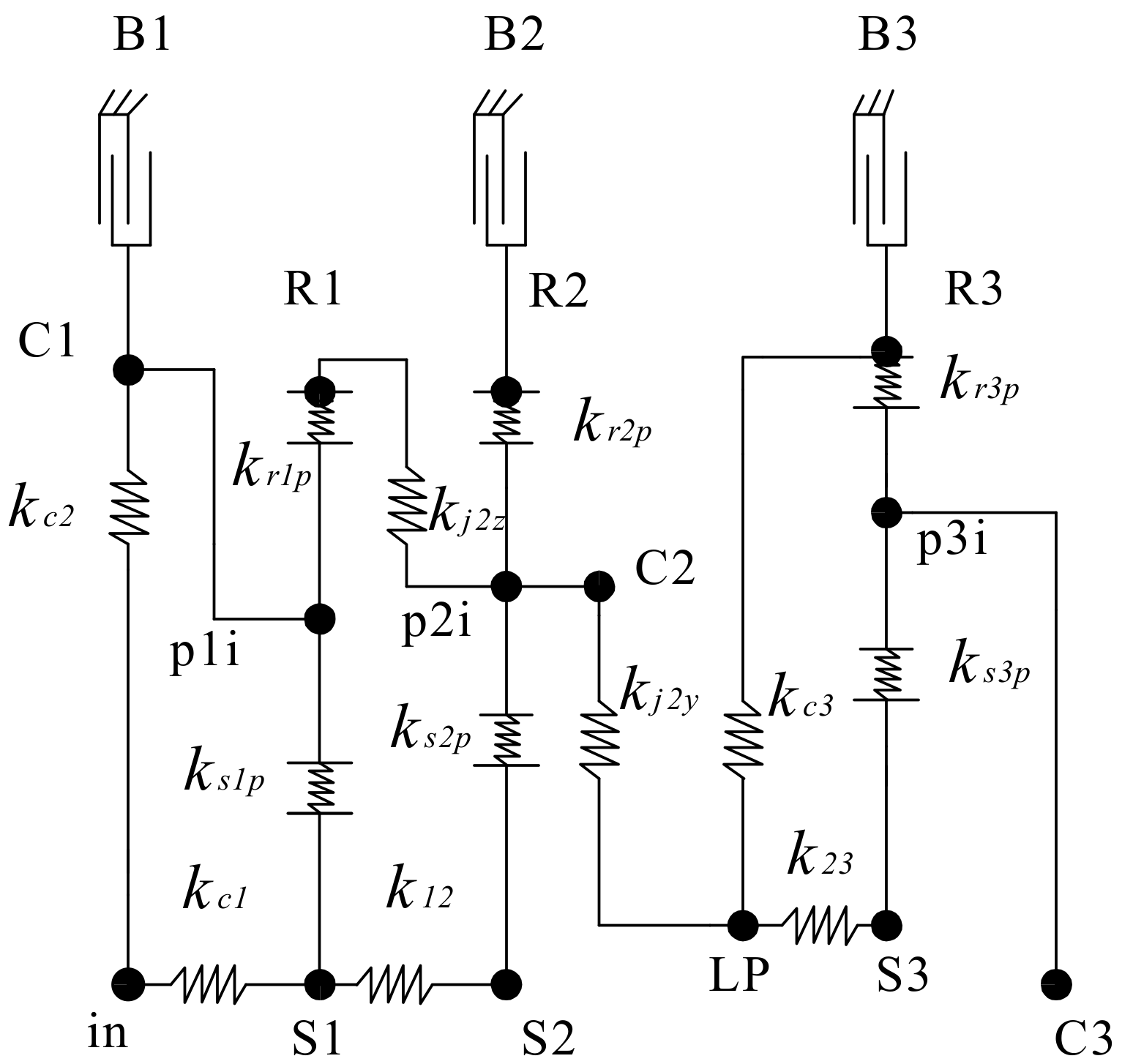

| Stiffness Symbol | The Meaning of Stiffness Symbol |
|---|---|
| kc1 | Connection stiffness between input shaft and S1 when clutch CL1 engages |
| kc2 | Connection stiffness between input shaft and C1 when clutch CL2 engages |
| k12 | Connection stiffness between sun gear S1 and sun gear S1 |
| kj2z | Connection stiffness between ring gear R1 and planetary carrier C2 |
| kj2y | Connection stiffness between planetary carrier C2 and connecting gear |
| k23 | Connection stiffness between connecting gear and sun gear S3 |
| kc3 | Connection stiffness between connecting disc and ring gear R3 |
| Gear | CL1 | CL2 | CL3 | B1 | B2 | B3 |
|---|---|---|---|---|---|---|
| First gear | ○ | × | × | × | ○ | ○ |
| Second gear | × | ○ | × | × | ○ | ○ |
| Third gear | ○ | ○ | × | × | × | ○ |
| Fourth gear | × | ○ | ○ | × | ○ | × |
| Fifth gear | ○ | ○ | ○ | × | × | × |
| First reverse gear | ○ | × | × | ○ | × | ○ |
| Second reverse gear | ○ | × | ○ | ○ | × | × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ji, C.; Lu, F.; Wang, C.; Sun, X. A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions. Appl. Sci. 2022, 12, 6279. https://doi.org/10.3390/app12126279
Wang H, Ji C, Lu F, Wang C, Sun X. A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions. Applied Sciences. 2022; 12(12):6279. https://doi.org/10.3390/app12126279
Chicago/Turabian StyleWang, Haiwei, Cheng Ji, Fengxia Lu, Cheng Wang, and Xueyan Sun. 2022. "A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions" Applied Sciences 12, no. 12: 6279. https://doi.org/10.3390/app12126279
APA StyleWang, H., Ji, C., Lu, F., Wang, C., & Sun, X. (2022). A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions. Applied Sciences, 12(12), 6279. https://doi.org/10.3390/app12126279





