Real-Time Short-Term Voltage Stability Assessment Using Combined Temporal Convolutional Neural Network and Long Short-Term Memory Neural Network
Abstract
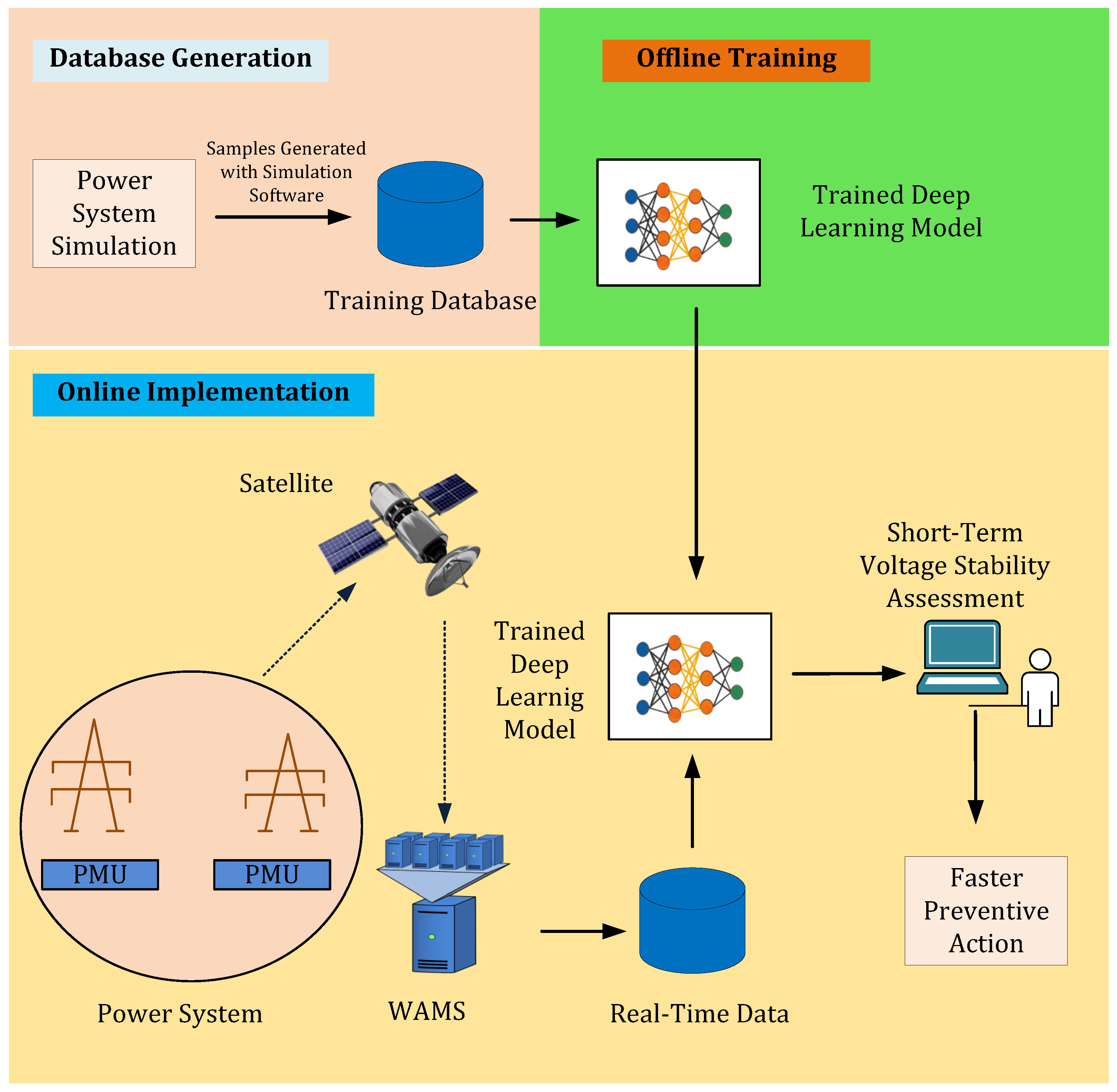
:1. Introduction
- Proposal of an approach for real-time STVS assessment, including both voltage instability and FIDVR pheomenon based on a deep learning algorithm combining a temporal convolutional neural network and a long short-term memory neural network (TempCNN-LSTM). The proposed TempCNN-LSTM model can extract spatiotemporal STVS features from the data samples available through PMUs.
- The performance of the proposed approach in assessing STVS is compared with other deep learning models and conventional machine learning models under different conditions such as PMUs measurement error, missing PMUs data, and different observation time windows.
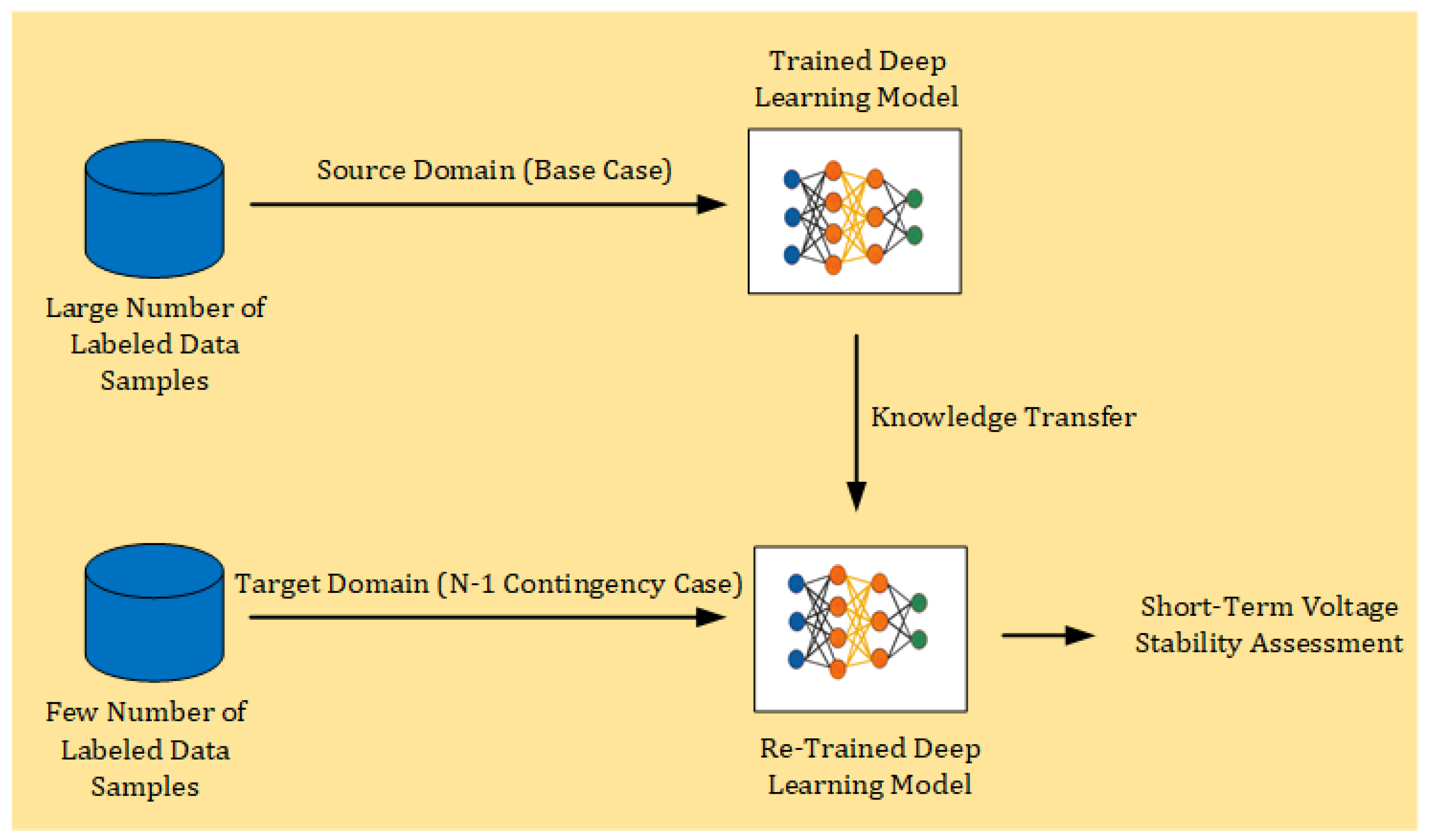
- The proposed approach also uses a transfer learning technique for the assessment of STVS that can adapt to the new environment (N-1 contingency case) with a few labeled data samples.
2. Methodology
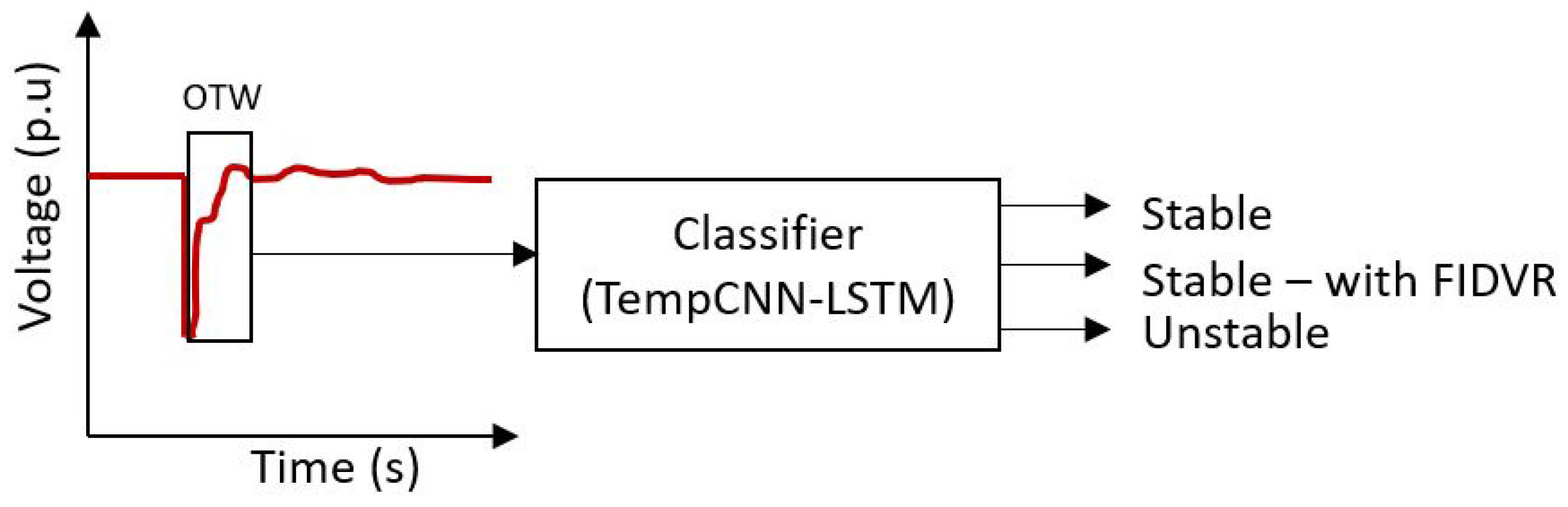
2.1. Short-Term Voltage Stability Assessment
2.2. Short-Term Voltage Stability Assessment along with Fault-Induced Delayed Voltage Recovery
3. Framework of Proposed Temporal Convolutional Neural Network-Long Short-Term Memeory Neural Network
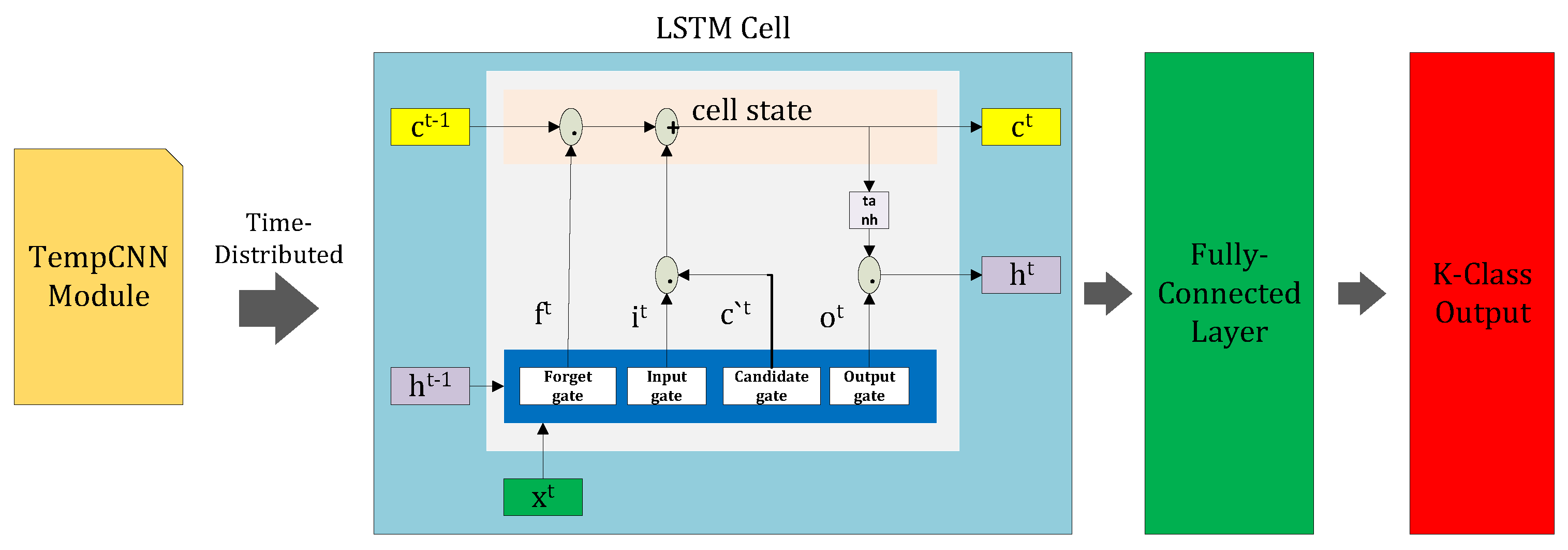
3.1. Temporal Convolutional Neural Network
3.2. Long Short-Term Memory Neural Network
3.3. Transfer Learning
3.4. Performance Evaluation
4. Simulation Result and Discussion
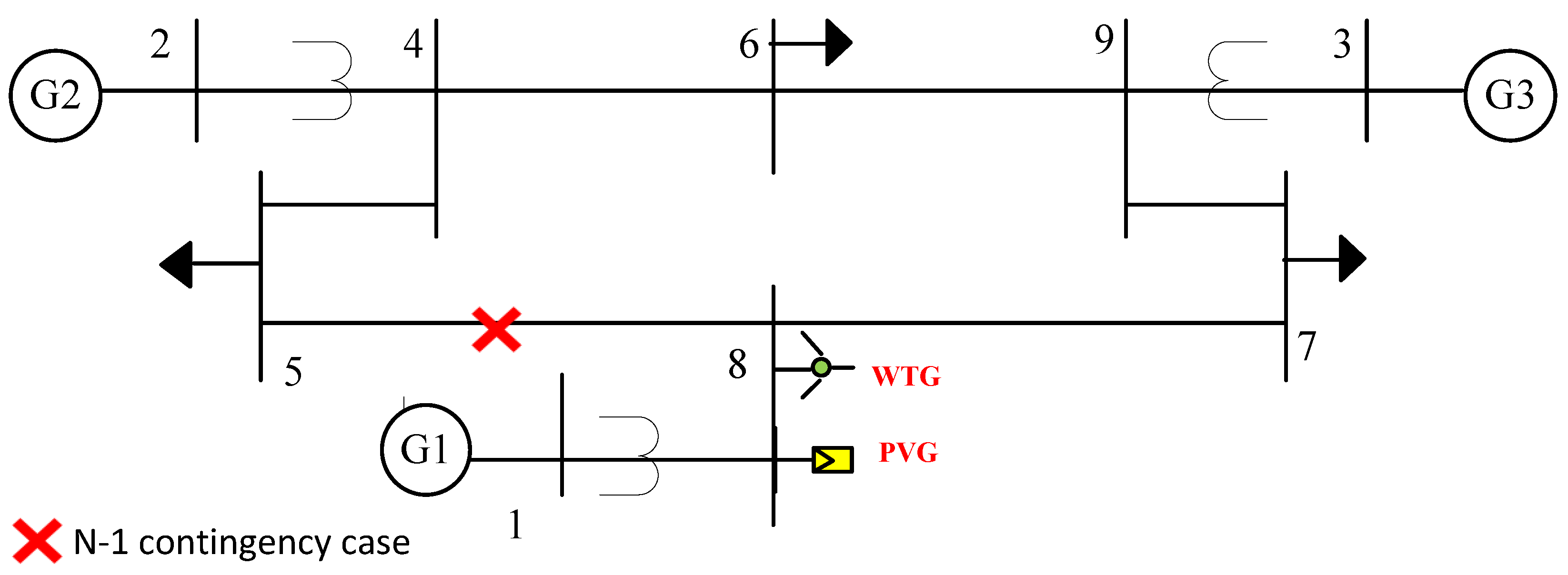
4.1. Test System
4.2. Data Generation
4.3. Analysis of Case Studies
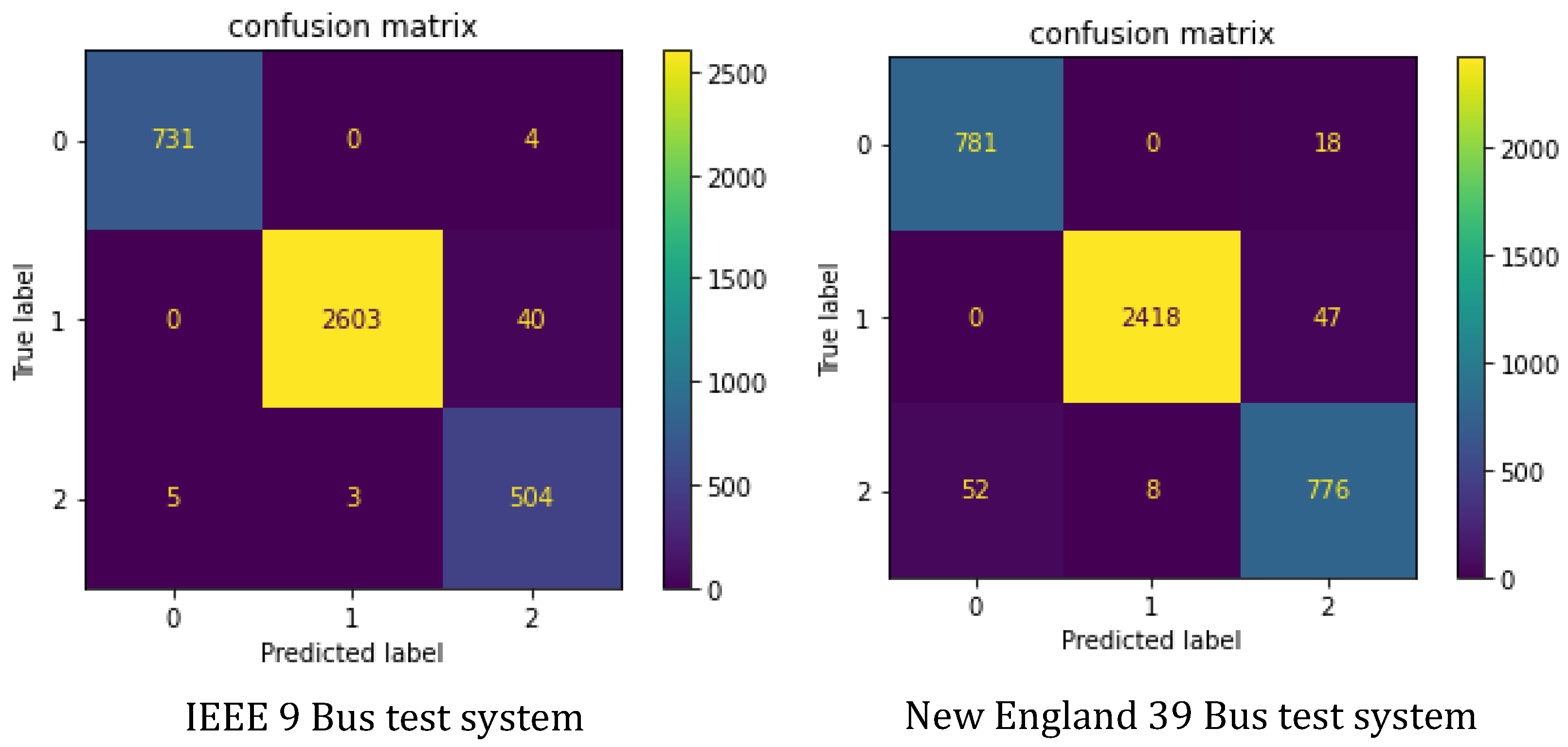
4.3.1. Case I: Base Case
4.3.2. Case II: PMUs Measurement Error Case
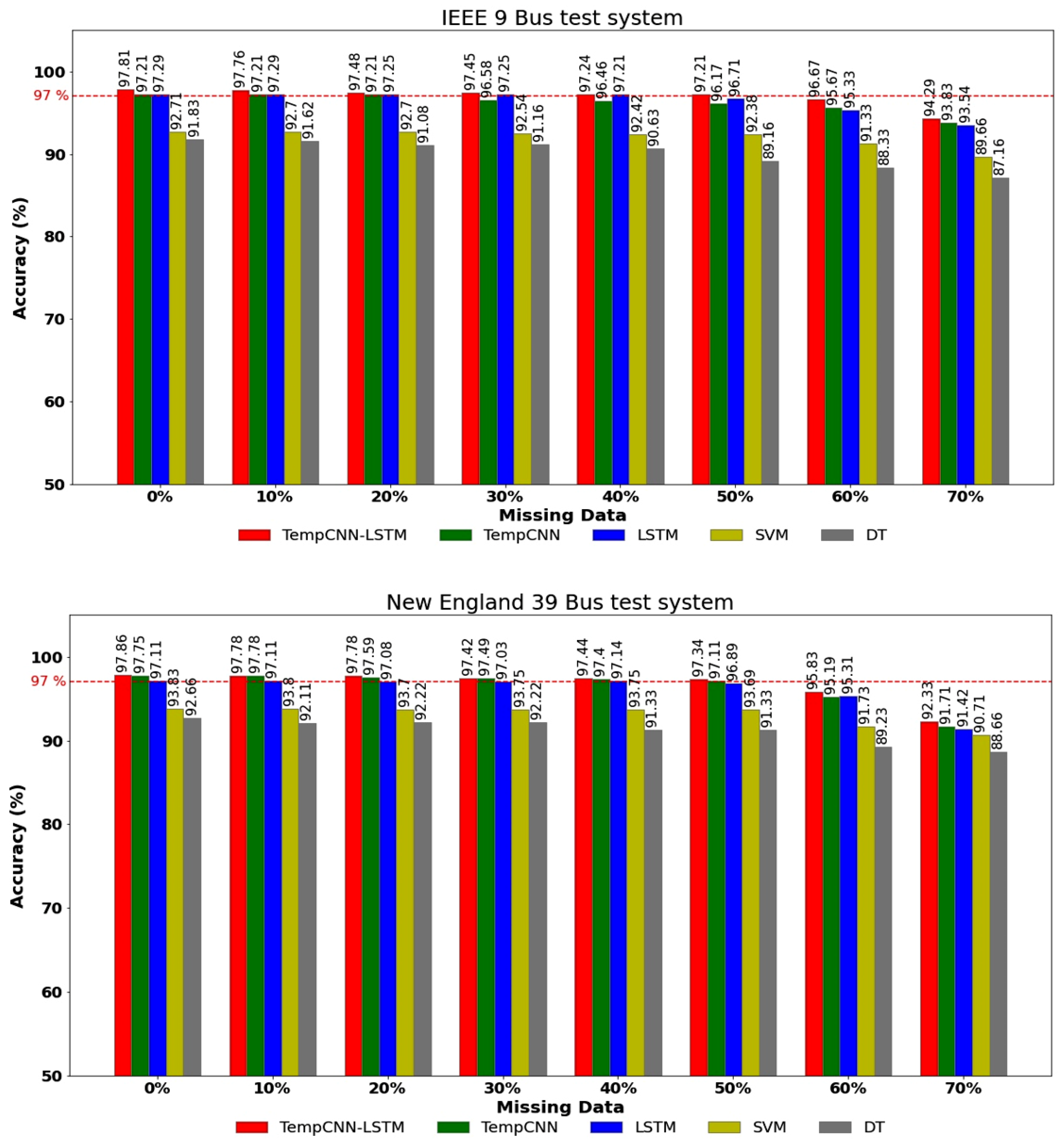
4.3.3. Case III: Missing PMUs Data Case
4.3.4. Case IV: Impact of Assessment Time
4.3.5. Case V: Transfer Learning for N-1 Contingency Case
5. Conclusions
- The performance of the proposed model evaluated in terms of classification accuracy shows 98.66% accuracy for the IEEE 9 Bus test system and more than 96.95% accuracy for the New England 39 Bus Test System with efficient computational time for the online assessment of STVS.
- The proposed model shows the superior performance compared to other deep learning models (TempCNN and LSTM) and conventional machine learning models (SVM and DT). The performance of the proposed model in terms of classification accuracy, precison, recall and F1-score is significantly high compared to other classification models.
- The proposed model is more tolerant to the PMUs measurement error/losses and thus is suitable for online assessment of STVS.
- The accuracy of the proposed model under the variation of different assessment time shows the superior performance compared to the existing state-of-art deep learning-based time series classification models (TempCNN and LSTM) and machine learning models (SVM and DT). Furthermore, for all these models, the accuracy increases with the increase in the OTW length.
- Using the deep learning-based transfer learning approach, the proposed model can predict the STVS state of the system under topology change condition (N-1 contingency) with more than 97% accuracy for both the test systems with few labeled samples. It eliminates the need to train different learning models. Furthermore, it reduces the computational time required for re-training the model for online application.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Van Cutsem, T.; Vournas, C. Voltage Stability of Electric Power Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 441. [Google Scholar]
- Potamianakis, E.; Vournas, C. Short-term voltage instability: Effects on synchronous and induction machines. IEEE Trans. Power Syst. 2006, 21, 791–798. [Google Scholar] [CrossRef]
- Adetokun, B.B.; Muriithi, C.M.; Ojo, J.O. Voltage stability assessment and enhancement of power grid with increasing wind energy penetration. Int. J. Electr. Power Energy Syst. 2020, 120, 105988. [Google Scholar] [CrossRef]
- Xu, X.; Yan, Z.; Shahidehpour, M.; Wang, H.; Chen, S. Power system voltage stability evaluation considering renewable energy with correlated variabilities. IEEE Trans. Power Syst. 2017, 33, 3236–3245. [Google Scholar] [CrossRef]
- Liu, K.y.; Sheng, W.; Hu, L.; Liu, Y.; Meng, X.; Jia, D. Simplified probabilistic voltage stability evaluation considering variable renewable distributed generation in distribution systems. IET Gener. Transm. Distrib. 2015, 9, 1464–1473. [Google Scholar] [CrossRef]
- Prusty, B.R.; Jena, D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 1286–1302. [Google Scholar] [CrossRef]
- Operator, A.E.M. Black System South Australia 28 September 2016. 2017. Available online: https://www.aemo.com.au (accessed on 16 October 2021).
- Kundur, P.S.; Balu, N.J.; Lauby, M.G. Power System Dynamics and Stability; CRC Press: Boca Raton, FL, USA, 2017; Volume 3. [Google Scholar]
- Zhang, Y.; Xu, Y.; Dong, Z.Y.; Zhang, R. A hierarchical self-adaptive data-analytics method for real-time power system short-term voltage stability assessment. IEEE Trans. Ind. Inform. 2018, 15, 74–84. [Google Scholar] [CrossRef]
- Safavizadeh, A.; Kordi, M.; Eghtedarnia, F.; Torkzadeh, R.; Marzooghi, H. Framework for real-time short-term stability assessment of power systems using PMU measurements. IET Gener. Transm. Distrib. 2019, 13, 3433–3442. [Google Scholar] [CrossRef]
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inform. 2011, 7, 529–539. [Google Scholar] [CrossRef] [Green Version]
- Dasgupta, S.; Paramasivam, M.; Vaidya, U.; Ajjarapu, V. Real-time monitoring of short-term voltage stability using PMU data. IEEE Trans. Power Syst. 2013, 28, 3702–3711. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, C.; Dong, Z.Y.; Hong, C. Imbalance learning machine-based power system short-term voltage stability assessment. IEEE Trans. Ind. Inform. 2017, 13, 2533–2543. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Hagmar, H.; Tong, L.; Eriksson, R.; Tuan, L.A. Voltage instability prediction using a deep recurrent neural network. IEEE Trans. Power Syst. 2020, 36, 17–27. [Google Scholar] [CrossRef]
- Yang, W.; Zhu, Y.; Liu, Y. Fast Assessment of Short-Term Voltage Stability of AC/DC Power Grid Based on CNN. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 4 December 2019; pp. 1–4. [Google Scholar]
- Zhang, M.; Li, J.; Li, Y.; Xu, R. Deep Learning for Short-Term Voltage Stability Assessment of Power Systems. IEEE Access 2021, 9, 29711–29718. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Z.; Bian, Z.; Xu, Z. A short-term voltage stability online prediction method based on graph convolutional networks and long short-term memory networks. Int. J. Electr. Power Energy Syst. 2021, 127, 106647. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Chen, C. A deep-learning intelligent system incorporating data augmentation for short-term voltage stability assessment of power systems. Appl. Energy 2022, 308, 118347. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, C.; Zhu, L.; Song, J. Data-driven short-term voltage stability assessment based on spatial-temporal graph convolutional network. Int. J. Electr. Power Energy Syst. 2021, 130, 106753. [Google Scholar] [CrossRef]
- Su, H.Y.; Liu, T.Y. Enhanced-Online-Random-Forest Model for Static Voltage Stability Assessment Using Wide Area Measurements. IEEE Trans. Power Syst. 2018, 33, 6696–6704. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Annakkage, U.D.; Rajapakse, A.D. Online Monitoring of Voltage Stability Margin Using an Artificial Neural Network. IEEE Trans. Power Syst. 2010, 25, 1566–1574. [Google Scholar] [CrossRef]
- Zheng, C.; Malbasa, V.; Kezunovic, M. Regression tree for stability margin prediction using synchrophasor measurements. IEEE Trans. Power Syst. 2012, 28, 1978–1987. [Google Scholar] [CrossRef]
- Beiraghi, M.; Ranjbar, A. Online voltage security assessment based on wide-area measurements. IEEE Trans. Power Deliv. 2013, 28, 989–997. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Motiian, S.; Piccirilli, M.; Adjeroh, D.A.; Doretto, G. Unified Deep Supervised Domain Adaptation and Generalization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5716–5726. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Zhang, Y.J.A.; Wen, H. Voltage Stability Monitoring Based on Disagreement-Based Deep Learning in a Time-Varying Environment. IEEE Trans. Power Syst. 2021, 36, 28–38. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Y. Transfer Learning-Based Power System Online Dynamic Security Assessment: Using One Model to Assess Many Unlearned Faults. IEEE Trans. Power Syst. 2020, 35, 821–824. [Google Scholar] [CrossRef]
- Adhikari, A.; Naetiladdanon, S.; Sangswang, A. Real-Time Short-Term Voltage Stability Assessment using Temporal Convolutional Neural Network. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies-Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021; pp. 1–5. [Google Scholar]
- Bravo, R.J.; Yinger, R.; Arons, P. Fault induced delayed voltage recovery (FIDVR) indicators. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Medellin, Colombia, 10–13 September 2014; pp. 1–5. [Google Scholar]
- Li, Q.; Xu, Y.; Ren, C. A Hierarchical Data-Driven Method for Event-Based Load Shedding Against Fault-Induced Delayed Voltage Recovery in Power Systems. IEEE Trans. Ind. Inform. 2020, 17, 699–709. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, C.; Sun, Y. Time series shapelet classification based online short-term voltage stability assessment. IEEE Trans. Power Syst. 2015, 31, 1430–1439. [Google Scholar] [CrossRef]
- Boričić, A.; Torres, J.L.R.; Popov, M. Fundamental study on the influence of dynamic load and distributed energy resources on power system short-term voltage stability. Int. J. Electr. Power Energy Syst. 2021, 131, 107141. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Shekar, M.C.; Aarthi, N. Contingency Analysis of IEEE 9 Bus System. In Proceedings of the 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bengaluru, India, 18–19 May 2018; pp. 2225–2229. [Google Scholar]
- Pai, M. Energy Function Analysis for Power System Stability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Secretariat, R. Global Status Report; REN21 Secretariat: Paris, France, 2018. [Google Scholar]
- Gurung, S.; Naetiladdanon, S.; Sangswang, A. Probabilistic small-signal stability analysis of power system with solar farm integration. Turk. J. Electr. Eng. Comput. Sci. 2019, 27, 1276–1289. [Google Scholar] [CrossRef]
- Gurung, S.; Naetiladdanon, S.; Sangswang, A. Coordination of power-system stabilizers and battery energy-storage system controllers to improve probabilistic small-signal stability considering integration of renewable-energy resources. Appl. Sci. 2019, 9, 1109. [Google Scholar] [CrossRef] [Green Version]
- PowerFactory, D. User Manual; DigSILENT Gmbh: Gomaringen, Germany, 2014. [Google Scholar]
- Ahmad, T.; Senroy, N. Statistical characterization of PMU error for robust WAMS based analytics. IEEE Trans. Power Syst. 2019, 35, 920–928. [Google Scholar] [CrossRef]
- Martin, K.E.; Benmouyal, G.; Adamiak, M.; Begovic, M.; Burnett, R.; Carr, K.; Cobb, A.; Kusters, J.; Horowitz, S.; Jensen, G.; et al. IEEE standard for synchrophasors for power systems. IEEE Trans. Power Deliv. 1998, 13, 73–77. [Google Scholar] [CrossRef]
- Zhu, L.; Hill, D.; Lu, C. Intelligent Short-Term Voltage Stability Assessment via Spatial Attention Rectified RNN Learning. IEEE Trans. Ind. Inform. 2020, 17, 7005–7016. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, R.; Zhao, J.; Dong, Z.Y.; Wang, D.; Yang, H.; Wong, K.P. Assessing short-term voltage stability of electric power systems by a hierarchical intelligent system. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1686–1696. [Google Scholar] [CrossRef]
- Shi, Z.; Yao, W.; Zeng, L.; Wen, J.; Fang, J.; Ai, X.; Wen, J. Convolutional neural network-based power system transient stability assessment and instability mode prediction. Appl. Energy 2020, 263, 114586. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Zhang, R.; Dong, Z.Y. A missing-data tolerant method for data-driven short-term voltage stability assessment of power systems. IEEE Trans. Smart Grid 2018, 10, 5663–5674. [Google Scholar] [CrossRef]







| No. of Samples | Bus ID | Input Data (p.u.) | Output (STVS Class) | |||
|---|---|---|---|---|---|---|
| Vt1 | Vt2 | … | Vt | |||
| 1 | 0.45 | 0.47 | … | 0.65 | ||
| 1 | … | … | … | … | … | 0 (Unstable) |
| 0.67 | 0.71 | … | 0.87 | |||
| 1 | 0.78 | 0.81 | … | 0.97 | ||
| 2 | … | … | … | … | … | 1 (Stable) |
| 0.82 | 0.87 | … | 0.98 | |||
| … | … | … | … | … | … | … |
| 1 | 0.72 | 0.75 | … | 0.96 | ||
| N | … | … | … | … | … | 2 (Stable-with FIDVR) |
| 0.62 | 0.68 | … | 0.97 | |||
| Reference Class | Predicted Class | |
|---|---|---|
| Positive | Negative | |
| Positive | True Positive (TP) | False Negative (FN) |
| Negative | False Positive (FP) | True Negative (TN) |
| Load level | of initial loading |
| Fault lines | All the transmission lines |
| Load model | Complex load model in DIgSILENT |
| Load dynamics | 0–80% of induction motor load |
| Fault locations | 0–80% of all fault lines |
| Fault type | Three-phase bolted fault |
| Fault duration | 0.1 s |
| Simulation time | 5 s |
| Length of OTW | 0.25 s of post fault voltage trajectories |
| Sampling per time step | 0.01 s |
| Parameters | Values |
|---|---|
| Optimizer | Adam |
| Exponential decay rate () | 0.9 |
| Exponential decay rate () | 0.999 |
| Constant () | 10 |
| Learning rate | 0.001 |
| Batch size | 32 |
| Number of epochs | 200 |
| Test System | Model | Performance Evaluation | |||||
|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | Training Time | Testing Time | ||
| Proposed | 98.66% | 98.74% | 98.66% | 98.68% | 8 min 23 s | 406 ms | |
| TempCNN | 97.87% | 97.86% | 97.87% | 97.85% | 5 min 59 s | 359 ms | |
| IEEE 9 Bus | LSTM | 97.86% | 97.85% | 97.86% | 97.81% | 19 min 59 s | 915 ms |
| SVM | 92.87% | 95.95% | 92.87% | 93.73% | 1 min 9 s | 1.2 s | |
| DT | 91.84% | 95.42% | 91.84% | 92.87% | 56 s | 4.99 ms | |
| Proposed | 96.95% | 97.01% | 96.95% | 96.97% | 24 min 42 s | 658 ms | |
| TempCNN | 96.44% | 96.55% | 96.44% | 96.47% | 9 min 11 s | 325 ms | |
| New England 39 Bus | LSTM | 96.37% | 96.60% | 96.36% | 96.42% | 22 min 54 s | 714 ms |
| SVM | 92.69% | 96.82% | 92.69% | 92.65% | 3 min 44 s | 1.27 s | |
| DT | 91.36% | 92.28% | 91.36% | 91.48% | 3 min 3 s | 6 ms | |
| Test System | Model | Performance Evaluation | |||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | ||
| Proposed | 97.93% | 97.97% | 97.93% | 97.94% | |
| TempCNN | 97.29% | 97.48% | 97.29% | 97.35% | |
| IEEE 9 Bus | LSTM | 97.19% | 97.49% | 98.18% | 97.26% |
| SVM | 92.75% | 95.93% | 92.75% | 93.64% | |
| DT | 88.71% | 93.89% | 88.71% | 90.38% | |
| Proposed | 96.66% | 96.65% | 96.66% | 96.65% | |
| TempCNN | 95.78% | 95.84% | 95.78% | 95.76% | |
| New England 39 Bus | LSTM | 95.02% | 95.14% | 95.03% | 95.06% |
| SVM | 92.48% | 92.64% | 92.48% | 92.44% | |
| DT | 87.24% | 88.53% | 87.24% | 87.48% | |
| Model | Parameter | IEEE 9 Bus | New England 39 Bus | ||
|---|---|---|---|---|---|
| With TL | Without TL | With TL | Without TL | ||
| Proposed | Accuracy | 98.08% | 66.35% | 97.06% | 58.82% |
| Precision | 98.17% | 76.92% | 97.16% | 69.13% | |
| Recall | 98.08% | 61.54% | 97.06% | 58.82% | |
| F1-Score | 97.78% | 53.15% | 96.59% | 45.38% | |
| Re-Training Time | 9.3 s | - | 27.2 s | - | |
| Testing Time | 45.7 ms | 59 ms | 55 ms | 57 ms | |
| TempCNN | Accuracy | 96.15% | 76.92% | 95.59% | 63.73% |
| Precision | 98.07% | 87.23% | 95.13% | 72.66% | |
| Recall | 96.15% | 76.92% | 95.59% | 63.72% | |
| F1-Score | 96.75% | 74.69% | 95.28% | 56.16% | |
| Re-Training Time | 8.39 s | - | 9.53 s | - | |
| Testing Time | 48.6 ms | 71.5 ms | 48 ms | 142 ms | |
| LSTM | Accuracy | 96.15% | 61.54% | 94.12% | 80.88% |
| Precision | 96.15% | 78.71% | 94.34% | 82.92% | |
| Recall | 96.15% | 61.54% | 94.12% | 80.88% | |
| F1-Score | 96.15% | 55.41% | 93.65% | 79.88% | |
| Re-Training Time | 18.1 s | - | 26.5 s | - | |
| Testing Time | 52 ms | 188 ms | 54 ms | 451 ms | |
| SVM | Accuracy | 94.23% | 59.61% | 92.64% | 82.35% |
| Precision | 88.84% | 79.01% | 87.19% | 86.20% | |
| Recall | 94.23% | 59.61% | 92.06% | 82.35% | |
| F1-Score | 91.44% | 54.61% | 89.83% | 81.58% | |
| Re-Training Time | 740 ms | - | 3.54 s | - | |
| Testing Time | 2 ms | 14 ms | 7 ms | 71 ms | |
| DT | Accuracy | 92.31% | 46.15% | 92.65% | 75.00% |
| Precision | 97.98% | 84.62% | 92.70% | 83.65% | |
| Recall | 92.31% | 46.15% | 92.65% | 75.00% | |
| F1-Score | 95.06% | 49.36% | 92.57% | 74.74% | |
| Re-Training Time | 1.41 s | - | 3.29 s | - | |
| Testing Time | 1 ms | 1 ms | 1 ms | 2 ms | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhikari, A.; Naetiladdanon, S.; Sangswang, A. Real-Time Short-Term Voltage Stability Assessment Using Combined Temporal Convolutional Neural Network and Long Short-Term Memory Neural Network. Appl. Sci. 2022, 12, 6333. https://doi.org/10.3390/app12136333
Adhikari A, Naetiladdanon S, Sangswang A. Real-Time Short-Term Voltage Stability Assessment Using Combined Temporal Convolutional Neural Network and Long Short-Term Memory Neural Network. Applied Sciences. 2022; 12(13):6333. https://doi.org/10.3390/app12136333
Chicago/Turabian StyleAdhikari, Ananta, Sumate Naetiladdanon, and Anawach Sangswang. 2022. "Real-Time Short-Term Voltage Stability Assessment Using Combined Temporal Convolutional Neural Network and Long Short-Term Memory Neural Network" Applied Sciences 12, no. 13: 6333. https://doi.org/10.3390/app12136333
APA StyleAdhikari, A., Naetiladdanon, S., & Sangswang, A. (2022). Real-Time Short-Term Voltage Stability Assessment Using Combined Temporal Convolutional Neural Network and Long Short-Term Memory Neural Network. Applied Sciences, 12(13), 6333. https://doi.org/10.3390/app12136333






