Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eggleton, B.J.; Poulton, C.G.; Rakich, P.T. Brillouin integrated photonics. Nat. Photonics 2019, 13, 664–677. [Google Scholar] [CrossRef]
- Wolff, C.; Steel, M.J.; Eggleton, B.J. Stimulated Brillouin scattering in integrated photonic waveguides: Forces, scattering mechanisms, and coupled-mode analysis. Phys. Rev. A 2015, 92, 013836. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Gauthier, D.J.; Boyd, R.W. Stored light in an optical fiber via stimulated Brillouin scattering. Science 2007, 318, 1748–1750. [Google Scholar] [CrossRef]
- Zhu, Z.; Dawes, A.M.C.; Gauthier, D.J. Broadband SBS slow light in an optical fiber. J. Lightw. Technol. 2007, 25, 201–206. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Sun, J. Design of Silicon Phoxonic Crystal Waveguides for Slow Light Enhanced Forward Stimulated Brillouin Scattering. J. Lightw. Technol. 2017, 35, 2917–2925. [Google Scholar] [CrossRef]
- Willner, A.E.; Zhang, B.; Zhang, L. Optical signal processing using tunable Delay elements based on slow light. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 691–705. [Google Scholar] [CrossRef]
- Deng, D.; Gao, W.; Cheng, T. Highly Efficient Fast Light Generation in a Tellurite Fiber Embedded in Brillouin Laser Ring Cavity. IEEE Photonics Technol. Lett. 2014, 26, 1758–1761. [Google Scholar] [CrossRef]
- Pant, R.; Byrnes, A.; Poulton, C.G. Photonic-chip-based tunable slow and fast light via stimulated Brillouin scattering. Opt. Lett. 2012, 37, 969–971. [Google Scholar] [CrossRef]
- Zhang, W.; Minasian, R.A. Widely Tunable Single-Passband Microwave Photonic Filter Based on Stimulated Brillouin Scattering. IEEE Photonics Technol. Lett. 2011, 23, 1775–1777. [Google Scholar] [CrossRef]
- Marpaung, D.; Morrison, B.; Pagani, M. Low-power, chip-based stimulated Brillouin scattering microwave photonic filter with ultrahigh selectivity. Optica 2015, 2, 76–83. [Google Scholar] [CrossRef]
- Minasian, R.A.; Chan, E.H.W.; Yi, X. Microwave photonic signal processing. Opt. Express 2013, 21, 22918–22936. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, A.; Morrison, B.; Aryanfar, I. Advanced Integrated Microwave Signal Processing With Giant On-Chip Brillouin Gain. J. Lightw. Technol. 2017, 35, 846–854. [Google Scholar] [CrossRef]
- Horiguchi, T.; Shimizu, K.; Kurashima, T. Development of a Distributed Sensing Technique Using Brillouin Scattering. J. Lightw. Technol. 1995, 13, 1296–1302. [Google Scholar] [CrossRef]
- Hotate, K.; Ong, S.S.L. Distributed dynamic strain measurement using a correlation-based Brillouin sensing system. IEEE Photonics Technol. Lett. 2003, 15, 272–274. [Google Scholar] [CrossRef]
- Kittlaus, E.A.; Otterstrom, N.T.; Rakich, P.T. On-chip inter-modal Brillouin scattering. Nat. Commun. 2017, 8, 15819. [Google Scholar] [CrossRef]
- Merklein, M.; Casas-Bedoya, A.; Marpaung, D. Stimulated Brillouin Scattering in Photonic Integrated Circuits: Novel Applications and Devices. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 336–346. [Google Scholar] [CrossRef]
- Ippen, E.P.; Stolen, R.H. Stimulated Brillouin scattering in optical fibers. Appl. Phys. Lett. 1972, 21, 539–541. [Google Scholar] [CrossRef]
- Kobyakov, A.; Sauer, M.; Chowdhury, D. Stimulated Brillouin Scattering in Optical Fibers. Adv. Opt. Photonics 2009, 2, 1–59. [Google Scholar] [CrossRef]
- Hill, K.O.; Kawasaki, B.S.; Johnson, D.C. cw Brillouin laser. Appl. Phys. Lett. 1976, 28, 608–609. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Kramer, G.; Winzer, P.J. Capacity Limits of Optical Fiber Networks. J. Lightw. Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Poulton, C.G.; Pant, R. Inducing and harnessing stimulated Brillouin scattering in photonic integrated circuits. Adv. Opt. Photonics 2013, 5, 536. [Google Scholar] [CrossRef]
- Song, K.Y.; Kim, Y.H. Characterization of stimulated Brillouin scattering in a few-mode fiber. Opt. Lett. 2013, 38, 4841–4844. [Google Scholar] [CrossRef]
- Li, A.; Hu, Q.; Shieh, W. Characterization of stimulated Brillouin scattering in a circular-core two-mode fiber using optical time-domain analysis. Opt. Express 2013, 21, 31894–31906. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wang, Y.; Hu, Q. Few-mode fiber based optical sensors. Opt. Express 2015, 23, 1139–1150. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ren, M.; Lu, Y. Multi-parameter sensor based on stimulated Brillouin scattering in inverse-parabolic graded-index fiber. Opt. Lett. 2016, 41, 1138. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Guo, Z.; Ke, C. Simultaneous temperature and strain sensing utilizing Brillouin frequency shifts contributed by multiple acoustic modes. In Proceedings of the IEEE 2016 IEEE Photonics Conference (IPC), Waikoloa, HI, USA, 2–6 October 2016; pp. 817–818. [Google Scholar]
- Fang, J.; Milione, G.; Stone, J. Multi-parameter distributed fiber sensing with higher-order optical and acoustic modes. Opt. Lett. 2019, 44, 1096. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Song, K.Y. Recent Progress in Distributed Brillouin Sensors Based on Few-Mode Optical Fibers. Sensors 2021, 21, 2168. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Y. Integrated lithium niobate photonics. Nanophotonics 2020, 9, 1287–1320. [Google Scholar] [CrossRef]
- Lin, J.; Bo, F.; Cheng, Y. Advances in on-chip photonic devices based on lithium niobate on insulator. Photonics Res. 2020, 8, 1910–1936. [Google Scholar] [CrossRef]
- Wang, J.-S.; Tseng, Y.-H. ITO electrode-embedded double-cladding single-crystal LiNbO3 optical fiber. Opt. Lett. 2013, 38, 452–454. [Google Scholar] [CrossRef]
- Russell, P.S.J.; Culverhouse, D. Experimental observation of forward stimulated Brillouin scattering in dual-mode single-core fibre. Electron. Lett. 1990, 26, 1195–1196. [Google Scholar] [CrossRef]
- Beugnot, J.C.; Sylvestre, T.; Maillotte, H.; Melin, G.; Laude, V. Guided acoustic wave Brillouin scattering in photonic crystal fibers. Opt. Lett. 2007, 32, 17–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, W.; Rakich, P.T.; Shin, H. Stimulated Brillouin scattering in nanoscale silicon step-index waveguides: A general framework of selection rules and calculating SBS gain. Opt. Express 2013, 21, 31402–31419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jen, C.K.; Safaai-Jazi, A.; Farnell, G.W. Leaky Modes in Weakly Guiding Fiber Acoustic Waveguides. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1986, 33, 634–643. [Google Scholar]

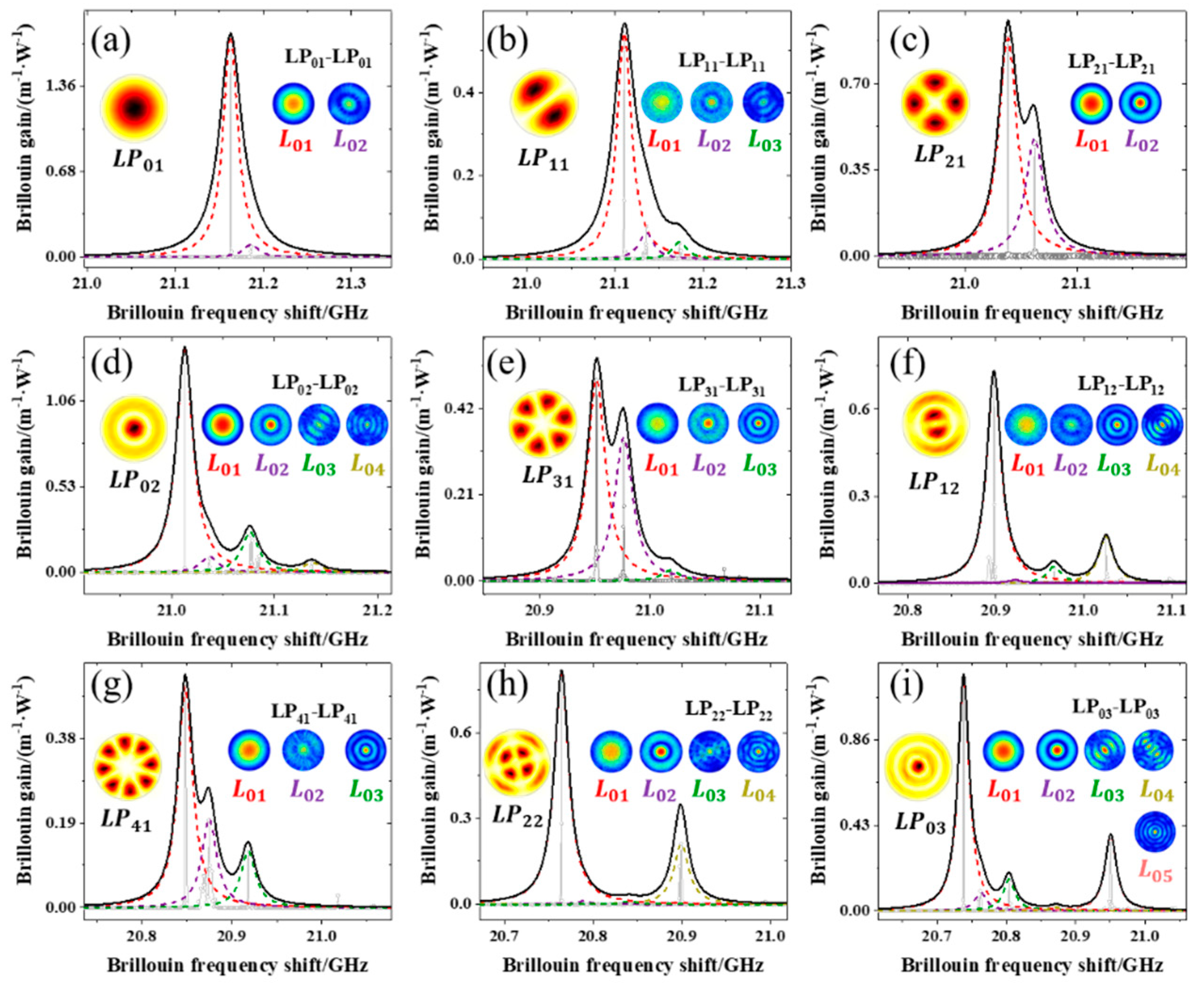

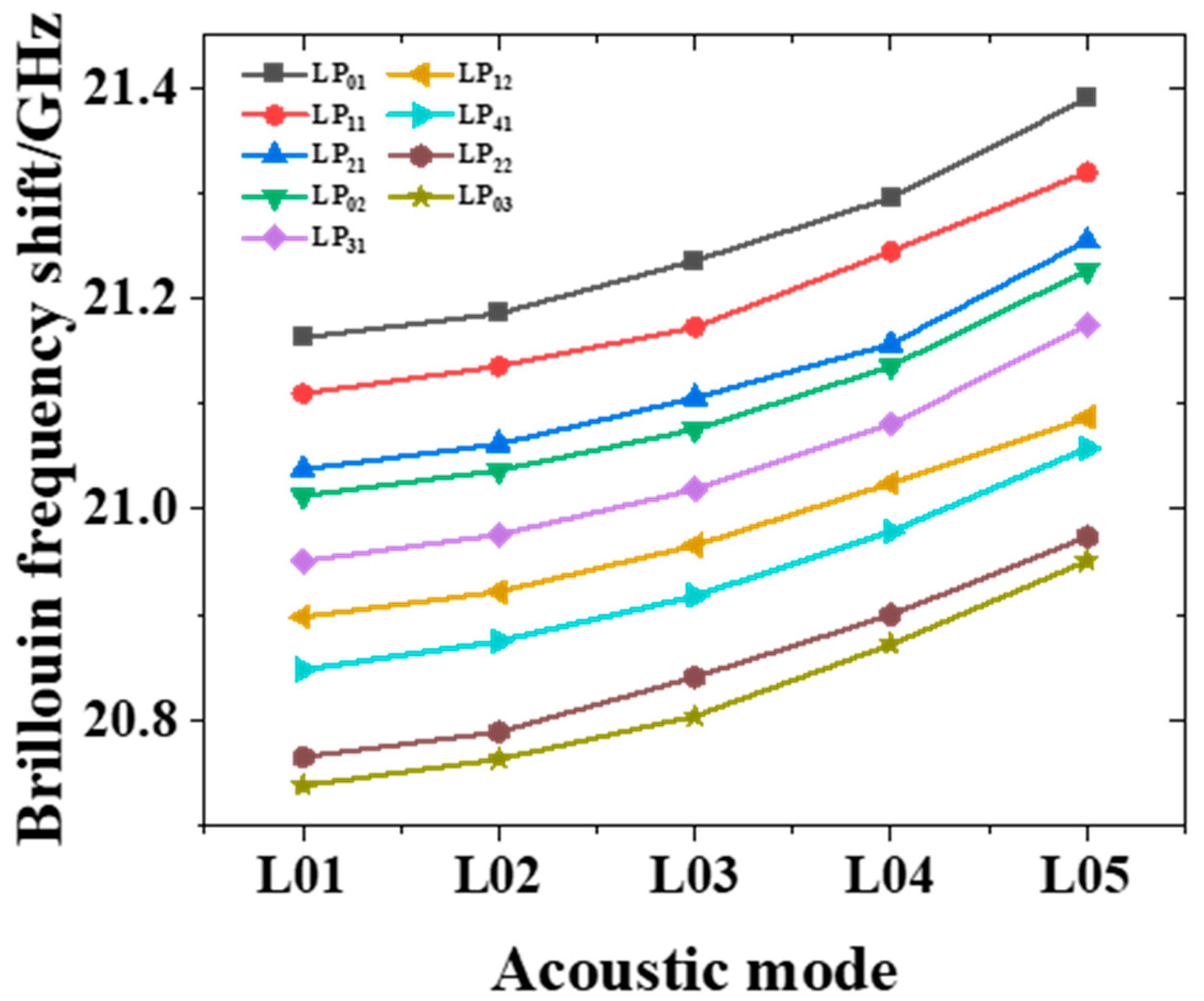
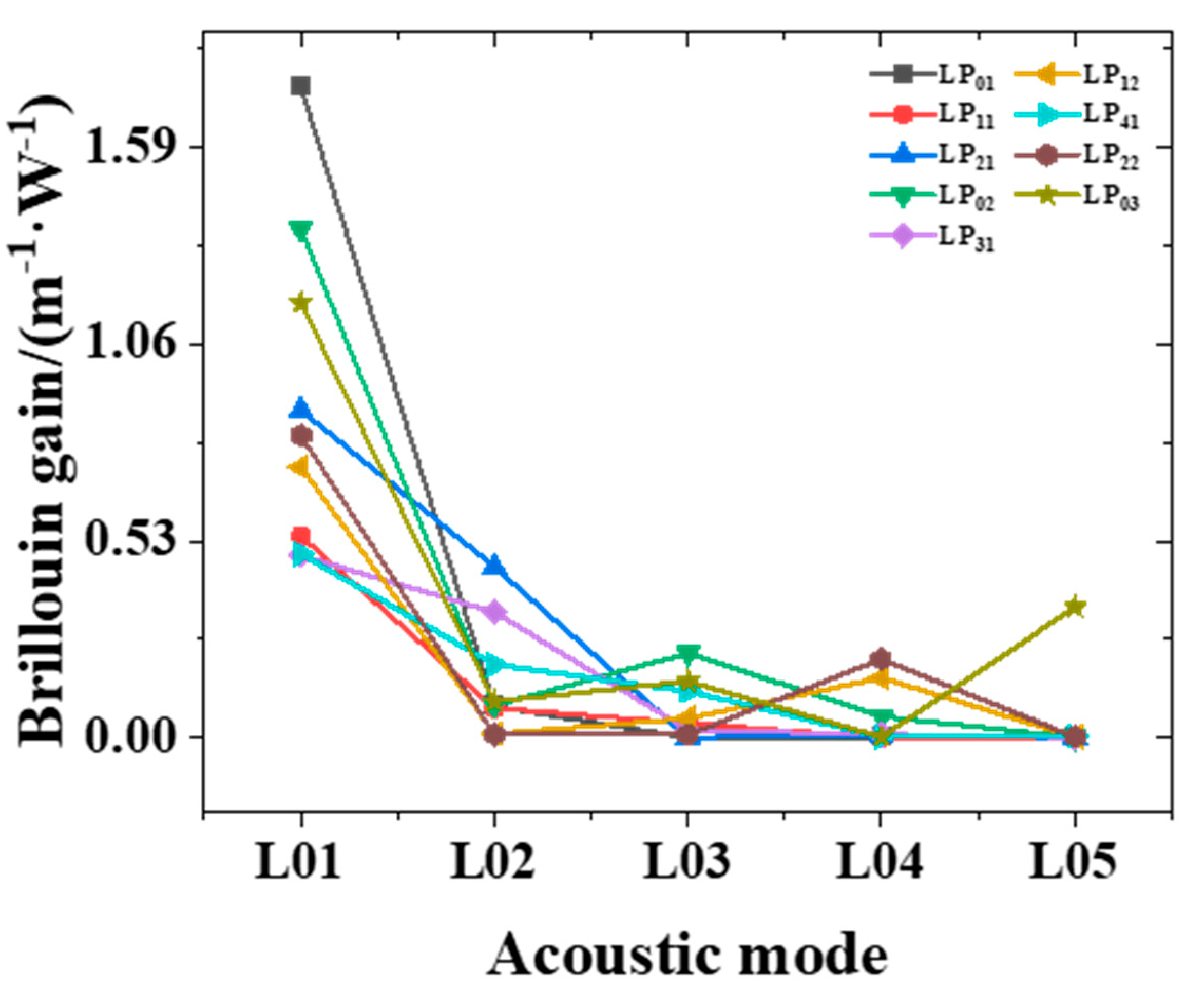
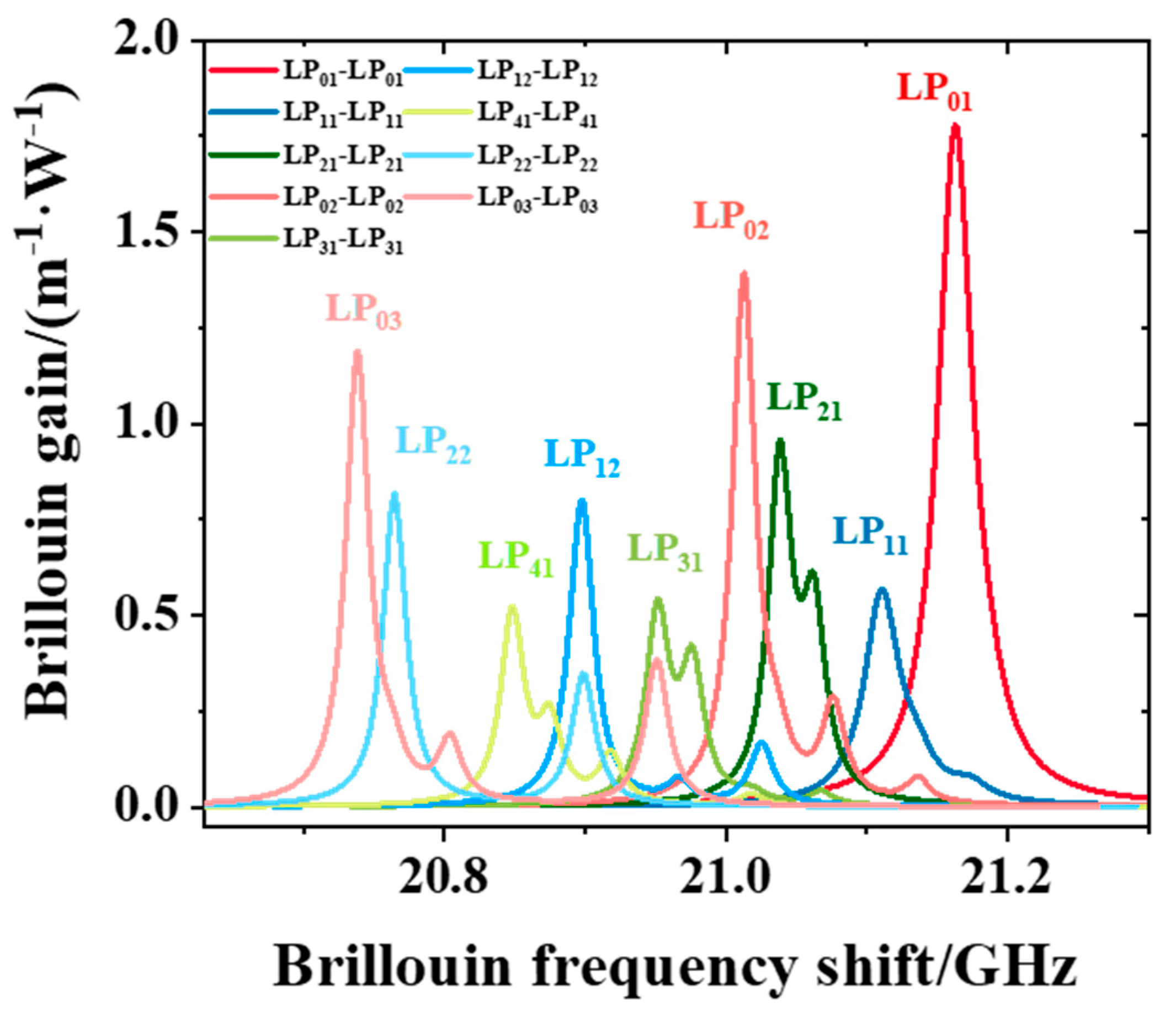
| Values | ||
|---|---|---|
| Parameters | Core | Cladding |
| Radius (μm) | ||
| Refractive index | ||
| ) | ||
| Longitudinal acoustic velocity (m/s) | ||
| Photo-elastic coefficients | , , | |
| Transmission loss at 1550 nm (dB/cm) a | 0.89 | |
| Mode | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Effective refractive index |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Liu, Y.; He, W.; You, Y.; Wang, L.; Xu, X.; Chou, X. Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber. Appl. Sci. 2022, 12, 6476. https://doi.org/10.3390/app12136476
Feng L, Liu Y, He W, You Y, Wang L, Xu X, Chou X. Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber. Applied Sciences. 2022; 12(13):6476. https://doi.org/10.3390/app12136476
Chicago/Turabian StyleFeng, Liuyan, Yi Liu, Wenjun He, Yajun You, Linyi Wang, Xin Xu, and Xiujian Chou. 2022. "Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber" Applied Sciences 12, no. 13: 6476. https://doi.org/10.3390/app12136476
APA StyleFeng, L., Liu, Y., He, W., You, Y., Wang, L., Xu, X., & Chou, X. (2022). Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber. Applied Sciences, 12(13), 6476. https://doi.org/10.3390/app12136476






