A Hybrid Early Warning Method for the Landslide Acceleration Process Based on Automated Monitoring Data
Abstract
:1. Introduction
2. Methods
2.1. The Proposed Hybrid Early Warning Method
2.1.1. Conventional Early Warning
2.1.2. Critical Sliding Early Warning
2.1.3. Strategies for Determining Early Warning Levels
- Conservative Strategy: choose the higher warning level of the two methods’ results. This strategy is conservative and can ensure the immediacy of early warning, but there may be many false warnings;
- Real Early Warning Strategy: choose the lower warning level of the two methods’ results. This strategy has relatively fewer false warnings but poorer immediacy;
- Single-Method Strategy: use either the conventional early warning method or the critical sliding early warning method to determine the early warning level. Compared with the proposed hybrid early warning method, it obtains less information, so the real early warning rate and immediacy are lower.
- Whether a genuine warning for the current landslide existed in the past. If a landslide warning has been issued previously, the conservative strategy should be taken to ensure the warning’s immediacy;
- The risk of landslide instability and the degree of disaster impact. Conservative strategy should be chosen if the risk of landslide instability is high and the impact of a disaster is severe;
- Computing resources for monitoring and early warning systems. If system computing resources are limited, the single-method strategy should be chosen to reduce the amount of calculation for most landslides with low instability risk;
- The quality of monitoring data of the current landslide. If the quality of monitoring data is poor, the real early warning strategy should be chosen to reduce false warnings.
2.2. Method for Determining Early Warning Parameter Values
2.2.1. Velocity Calculation in CDS
2.2.2. Determination of the Time Window
2.3. Threshold Setting
2.3.1. Thresholds in the Conventional Early Warning Method
2.3.2. Normalized Tangent Angle Threshold Criterion
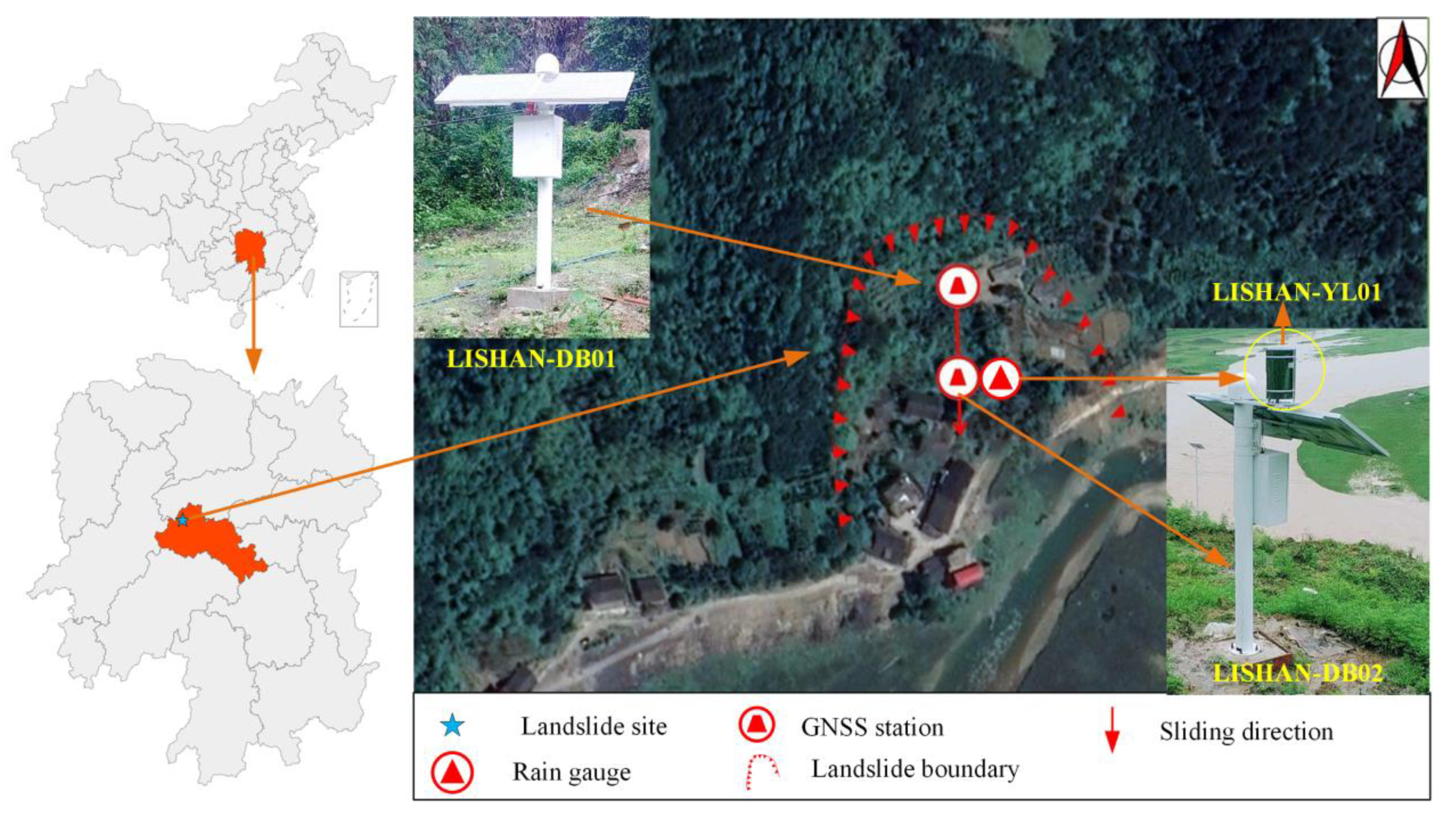
3. Case Study: Lishanyuan Landslide
3.1. Landslide Overview
3.2. Overview of Landslide Monitoring
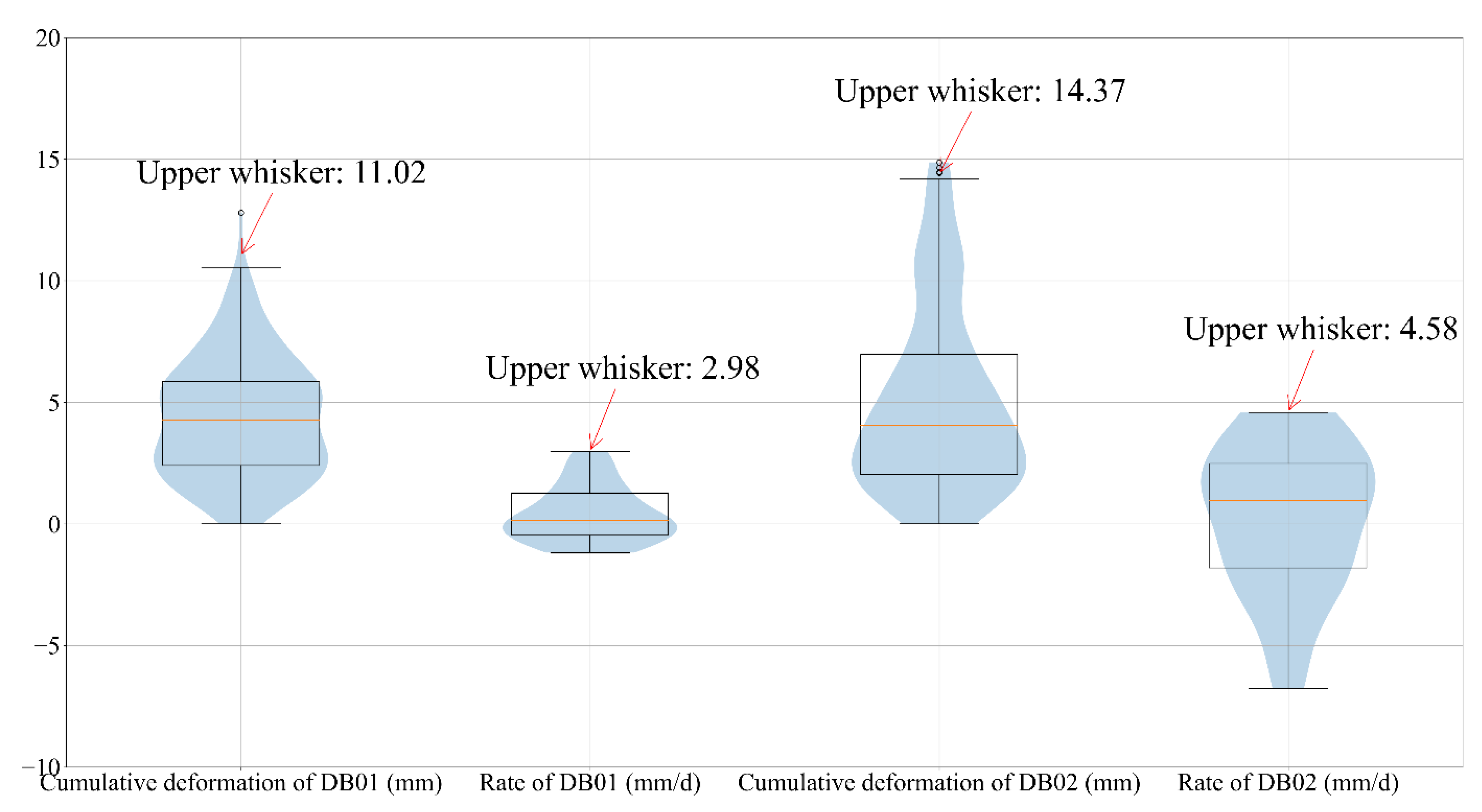
3.3. Thresholds Setting
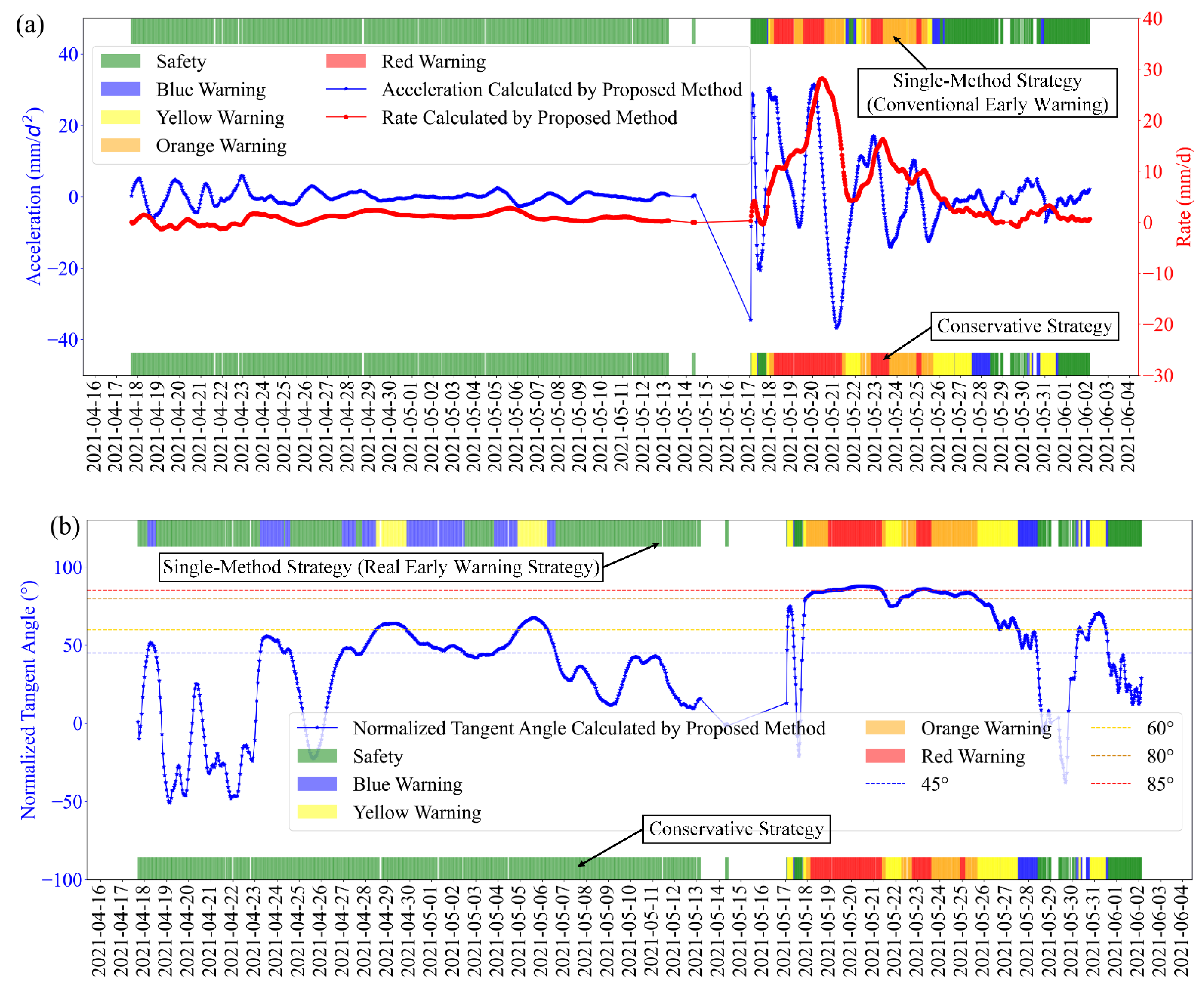
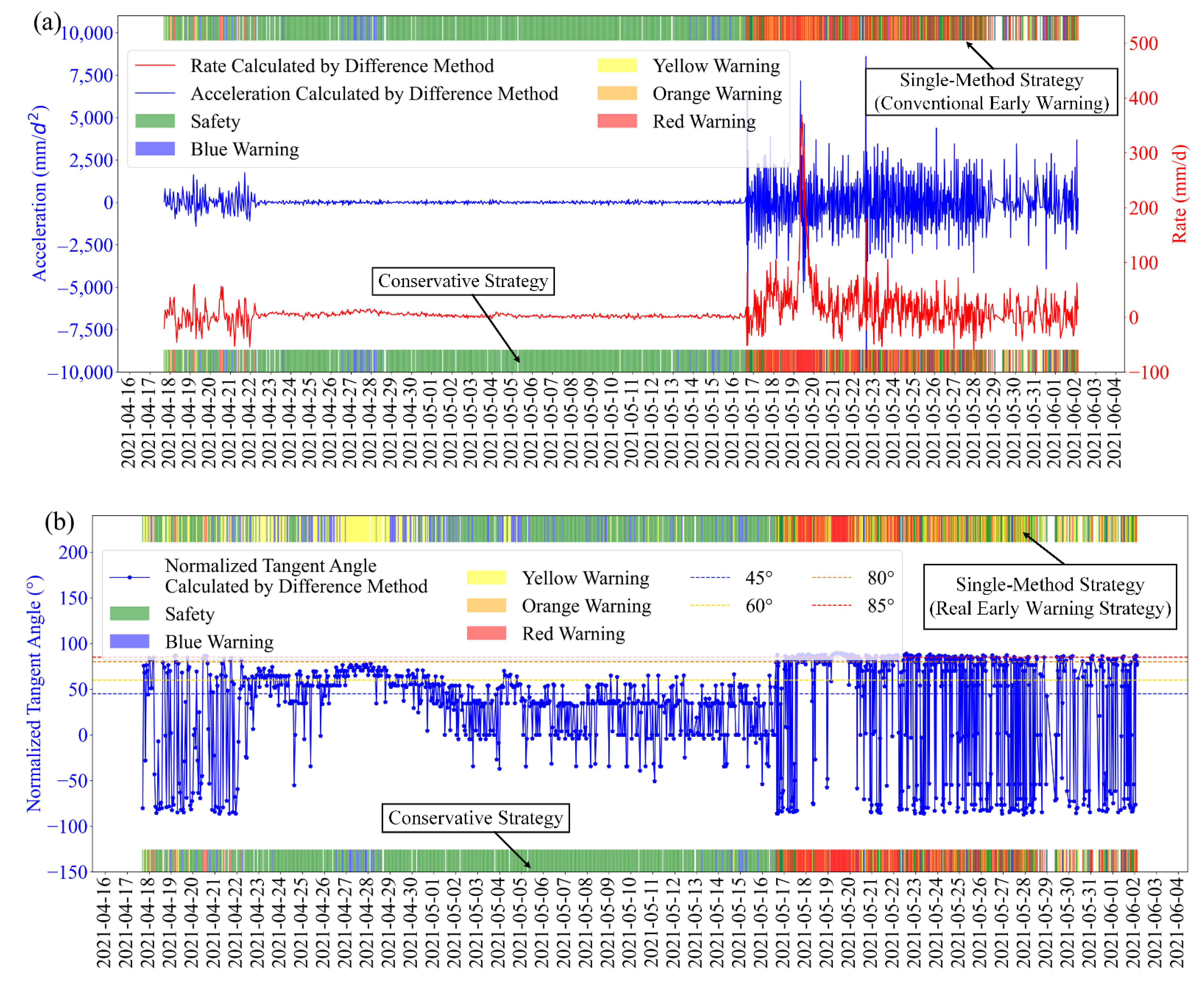
3.4. Early Warning Analysis
3.5. Comparative Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Bureau of Statistics of People’s Republic of China. China Statistical Yearbook 2020; China Statistics Press: Beijing, China, 2021; ISBN 1671-2552. [Google Scholar]
- Bai, D.; Tang, J.; Lu, G.; Zhu, Z.; Liu, T.; Fang, J. The Design and Application of Landslide Monitoring and Early Warning System Based on Microservice Architecture. Geomat. Nat. Hazards Risk 2020, 11, 928–948. [Google Scholar] [CrossRef]
- Benoit, L.; Briole, P.; Martin, O.; Thom, C.; Malet, J.P.; Ulrich, P. Monitoring Landslide Displacements with the Geocube Wireless Network of Low-Cost GPS. Eng. Geol. 2015, 195, 111–121. [Google Scholar] [CrossRef]
- Ju, N.; Huang, J.; He, C.; Van Asch, T.W.J.; Huang, R.; Fan, X.; Xu, Q.; Xiao, Y.; Wang, J. Landslide Early Warning, Case Studies from Southwest China. Eng. Geol. 2020, 279, 105917. [Google Scholar] [CrossRef]
- Xu, Q.; Peng, D.; Zhang, S.; Zhu, X.; He, C.; Qi, X.; Zhao, K.; Xiu, D.; Ju, N. Successful Implementations of a Real-Time and Intelligent Early Warning System for Loess Landslides on the Heifangtai Terrace, China. Eng. Geol. 2020, 278, 105817. [Google Scholar] [CrossRef]
- Wu, Y.; Niu, R.; Wang, Y.; Chen, T. A Fast Deploying Monitoring and Real-Time Early Warning System for the Baige Landslide in Tibet, China. Sensors 2020, 20, 6619. [Google Scholar] [CrossRef]
- Scoppettuolo, M.R.; Cascini, L.; Babilio, E. Typical Displacement Behaviours of Slope Movements. Landslides 2020, 17, 1105–1116. [Google Scholar] [CrossRef]
- Fukuzono, T. New Methods for Predicting the Failure Time of a Slope: Fukuzono, T Proc 4th International Conference and Field Workshop on Landslides, Japan, 23–31 Aug 1985 P145–150. Publ Tokyo: Japan Landslide Society, 1985. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, A34. [Google Scholar] [CrossRef]
- Saito, M. Forecasting the Time of Occurrence of a Slope Failure. Int. Soc. Soil Mech. Geotech. Eng. 1965, 6, 537–541. [Google Scholar]
- Wang, L.; Xie, M.; Chai, X. Research on Method of Displacement Speed Ratio for Spatial Evaluation of Landslide Deformation. Rock Soil Mech. (Chin.) 2014, 35, 519–528. [Google Scholar] [CrossRef]
- Zhou, X.-P.; Liu, L.-J.; Xu, C. A Modified Inverse-Velocity Method for Predicting the Failure Time of Landslides. Eng. Geol. 2020, 268, 105521. [Google Scholar] [CrossRef]
- Valletta, A.; Carri, A.; Segalini, A. Definition and Application of a Multi-Criteria Algorithm to Identify Landslide Acceleration Phases. Georisk 2021, 1–15. [Google Scholar] [CrossRef]
- Xu, Q.; Zeng, Y.; Qian, J.; Wang, C.; He, C. Study on a Improved Tangential Angle and the Corresponding Landslide Pre-Warning Criteria. Geol. Bull. China 2009, 28, 501–505. [Google Scholar]
- Xu, Q.; Yuan, Y.; Zeng, Y.; Hack, H. Some New Pre-Warning Criteria for Creep Slope Failure. Sci. China Technol. Sci. 2011, 54, 210–220. [Google Scholar] [CrossRef]
- Bao, L.; Zhang, G.; Hu, X.; Wu, S.; Liu, X. Stage Division of Landslide Deformation and Prediction of Critical Sliding Based on Inverse Logistic Function. Energies 2021, 14, 1091. [Google Scholar] [CrossRef]
- Carri, A.; Valletta, A.; Cavalca, E.; Savi, R.; Segalini, A. Advantages of IoT-Based Geotechnical Monitoring Systems Integrating Automatic Procedures for Data Acquisition and Elaboration. Sensors 2021, 21, 2249. [Google Scholar] [CrossRef]
- Gamperl, M.; Singer, J.; Thuro, K. Internet of Things Geosensor Network for Cost-Effective Landslide Early Warning Systems. Sensors 2021, 21, 2609. [Google Scholar] [CrossRef] [PubMed]
- Jin, D.; Li, J.; Gong, J.; Li, Y.; Zhao, Z.; Li, Y.; Li, D.; Yu, K.; Wang, S. Shipborne Mobile Photogrammetry for 3D Mapping and Landslide Detection of the Water-Level Fluctuation Zone in the Three Gorges Reservoir Area, China. Remote Sens. 2021, 13, 1007. [Google Scholar] [CrossRef]
- Khan, M.W.; Dunning, S.; Bainbridge, R.; Martin, J.; Diaz-Moreno, A.; Torun, H.; Jin, N.; Woodward, J.; Lim, M. Low-Cost Automatic Slope Monitoring Using Vector Tracking Analyses on Live-Streamed Time-Lapse Imagery. Remote Sens. 2021, 13, 893. [Google Scholar] [CrossRef]
- Liu, B.; He, K.; Han, M.; Hu, X.; Ma, G.; Wu, M. Application of UAV and GB-SAR in Mechanism Research and Monitoring of Zhonghaicun Landslide in Southwest China. Remote Sens. 2021, 13, 1653. [Google Scholar] [CrossRef]
- Cenni, N.; Fiaschi, S.; Fabris, M. Integrated Use of Archival Aerial Photogrammetry, GNSS, and InSAR Data for the Monitoring of the Patigno Landslide (Northern Apennines, Italy). Landslides 2021, 18, 2247–2263. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Wang, L.; Hu, H.; Lu, X.; Qian, C.; Liu, J.; Jin, S.; Chen, R. Short-Term Landslide Displacement Detection Based on GNSS Real-Time Kinematic Positioning. IEEE Trans. Instrum. Meas. 2021, 70, 1004714. [Google Scholar] [CrossRef]
- Tan, Q.; Wang, P.; Hu, J.; Zhou, P.; Bai, M.; Hu, J. The Application of Multi-Sensor Target Tracking and Fusion Technology to the Comprehensive Early Warning Information Extraction of Landslide Multi-Point Monitoring Data. Measurement 2020, 166, 108044. [Google Scholar] [CrossRef]





| Cumulative Deformation S | Acceleration | Warning Level | |
|---|---|---|---|
| / | / | Safe | |
| / | Safe | ||
| positive | Blue Warning | ||
| negative | Safe | ||
| positive | Yellow Warning | ||
| negative | Blue Warning | ||
| / | Safe | ||
| positive | Blue Warning | ||
| negative | Safe | ||
| positive | Yellow Warning | ||
| negative | Blue Warning | ||
| positive | Orange Warning | ||
| negative | Yellow Warning | ||
| positive | Red Warning | ||
| negative | Orange Warning |
| Station | Start Time | End Time | Calculation Methods (mm/d) | Average Value (mm/d) | ||
|---|---|---|---|---|---|---|
| GKDEM | AVM | RFM | ||||
| DB01 | 23 April 05:00 | 12 May 23:00 | 1.073 | 1.114 | 1.244 | 1.144 |
| DB02 | 6 May 03:00 | 13 May 00:00 | 1.726 | 1.732 | 1.754 | 1.737 |
| Time | 22 April | 13 May | ||
|---|---|---|---|---|
| Station | DB01 | DB02 | DB01 | DB02 |
| (mm) | 16.5 | 21 | 16.5 | 21 |
| (mm) | 33 | 42 | 33 | 42 |
| (mm/d) | 12 | 20 | 12 | 20 |
| (mm/d) | 24 | 40 | 24 | 40 |
| (mm/d) | 6 | 10 | 2.288 | 3.474 |
| (mm/d) | 12 | 20 | 4.576 | 6.948 |
| (mm/d) | 18 | 30 | 6.864 | 10.422 |
| (mm/d) | 24 | 40 | 9.152 | 13.896 |
| (mm/d) | / | / | 1.144 | 1.737 |
| Warning Strategy | Single-method strategy (Conventional warning) | Conservative strategy | ||
| Event Time | Cumulative Deformation (mm) | Velocity zhangxinyu (mm/d) | Acceleration (mm/d2) | Normalized Tangent Angle (°) | Warning Event |
|---|---|---|---|---|---|
| 25 April 21:00 | 21.11 | 4.34 | 0.85 | 68.18 | = 21 mm |
| 28 April 05:00 | 42.29 | 10.16 | 3.65 | 80.30 | = 42 mm Blue warning |
| 28 April 18:00 | 46.75 | 10.84 | −0.69 | 80.89 | Blue warning cancelled |
| 17 May 08:00 | 93.65 | 1.77 | 3.62 | 45.47 | Blue warning |
| 17 May 17:30 | 99.12 | 3.36 | 6.7 | 62.64 | Yellow warning |
| 18 May 00:30 | 114.63 | 10.15 | 24.63 | 80.29 | Orange warning |
| 18 May 03:30 | 123.01 | 14.08 | 32.85 | 82.97 | Red warning, Alternative red and orange warnings |
| 26 May 11:30 | 392.11 | 9.78 | −7.34 | 79.93 | Yellow warning |
| 28 May 12:30 | 400.91 | 2.92 | −4.49 | 59.24 | Blue warning |
| 29 May 09:00 | 401.6 | 1.61 | −2.1 | 42.90 | Safety |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Lu, G.; Zhu, Z.; Zhu, X.; Tao, C.; Fang, J. A Hybrid Early Warning Method for the Landslide Acceleration Process Based on Automated Monitoring Data. Appl. Sci. 2022, 12, 6478. https://doi.org/10.3390/app12136478
Bai D, Lu G, Zhu Z, Zhu X, Tao C, Fang J. A Hybrid Early Warning Method for the Landslide Acceleration Process Based on Automated Monitoring Data. Applied Sciences. 2022; 12(13):6478. https://doi.org/10.3390/app12136478
Chicago/Turabian StyleBai, Dongxin, Guangyin Lu, Ziqiang Zhu, Xudong Zhu, Chuanyi Tao, and Ji Fang. 2022. "A Hybrid Early Warning Method for the Landslide Acceleration Process Based on Automated Monitoring Data" Applied Sciences 12, no. 13: 6478. https://doi.org/10.3390/app12136478
APA StyleBai, D., Lu, G., Zhu, Z., Zhu, X., Tao, C., & Fang, J. (2022). A Hybrid Early Warning Method for the Landslide Acceleration Process Based on Automated Monitoring Data. Applied Sciences, 12(13), 6478. https://doi.org/10.3390/app12136478






