Tension Force Detection of Short Suspender by Using Laser Doppler Vibrometer
Abstract
:1. Introduction
2. Experimental Design
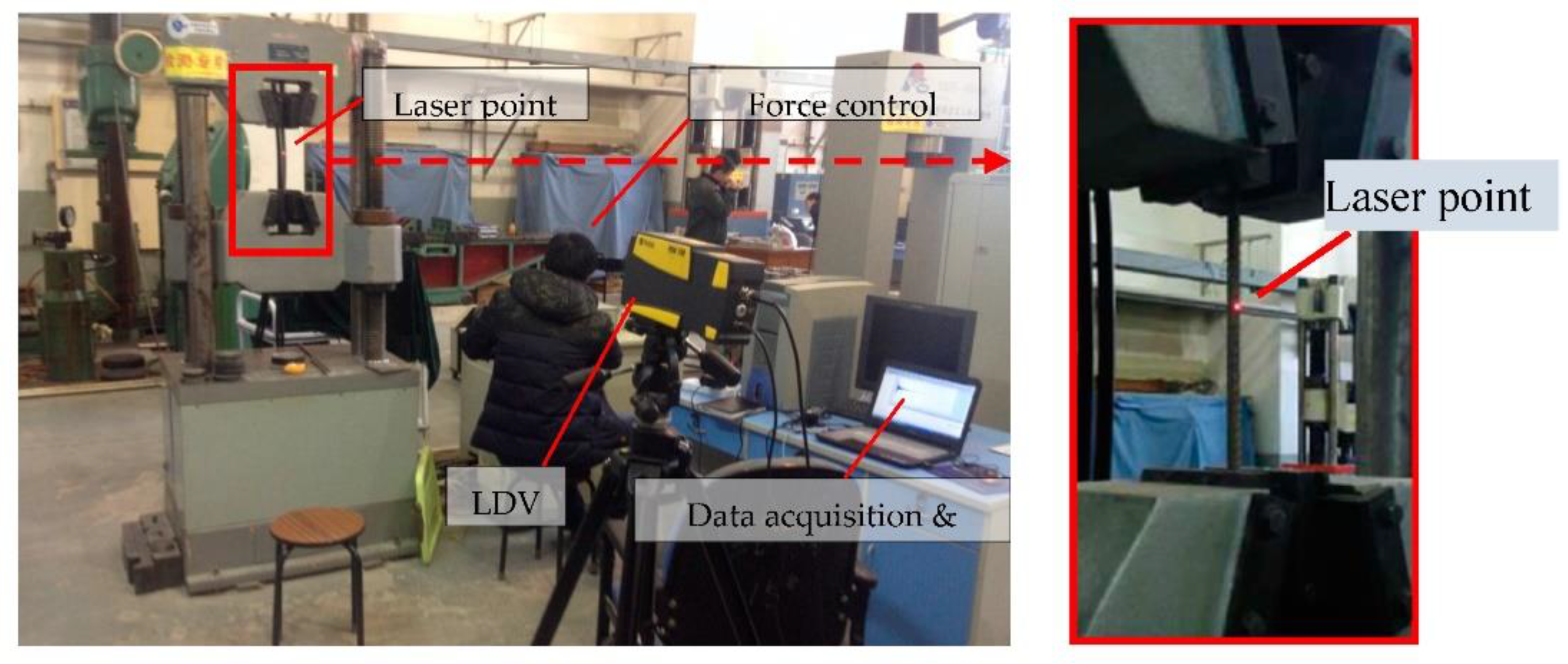
2.1. Laser Doppler Vibrometer (LDV)
2.2. Raw Materials
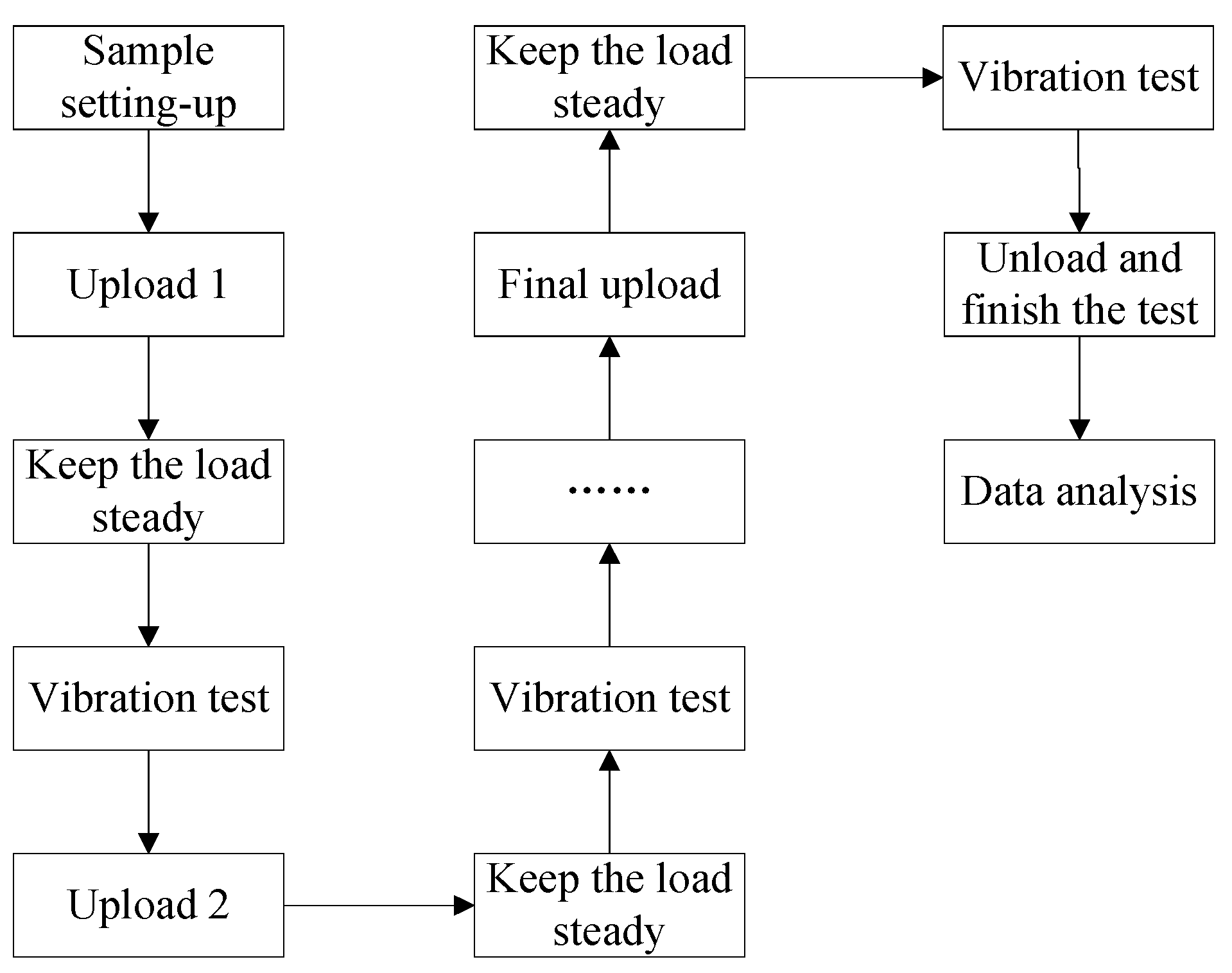
2.3. Testing Process
3. Results
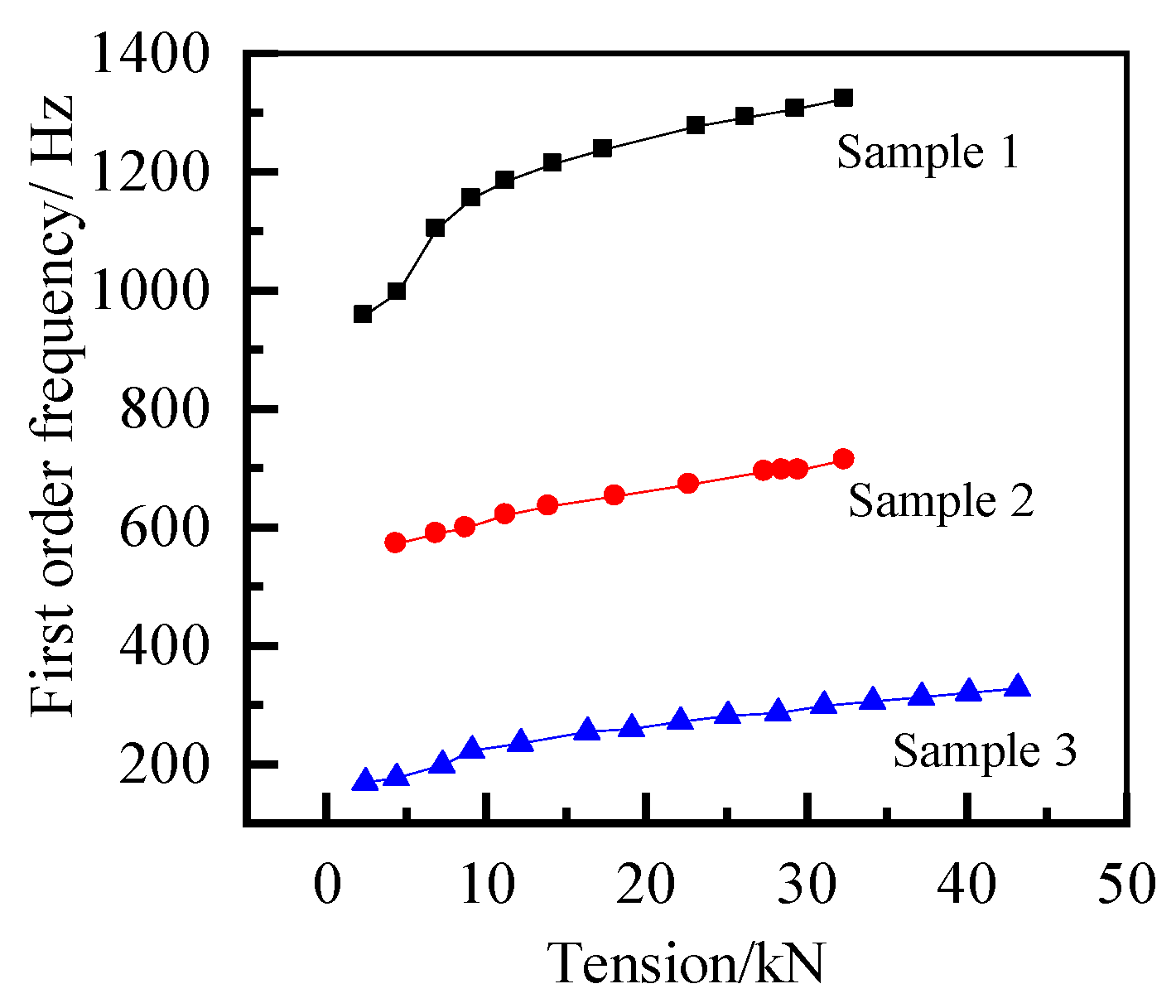
3.1. Vibration Frequency under Different Tension Force
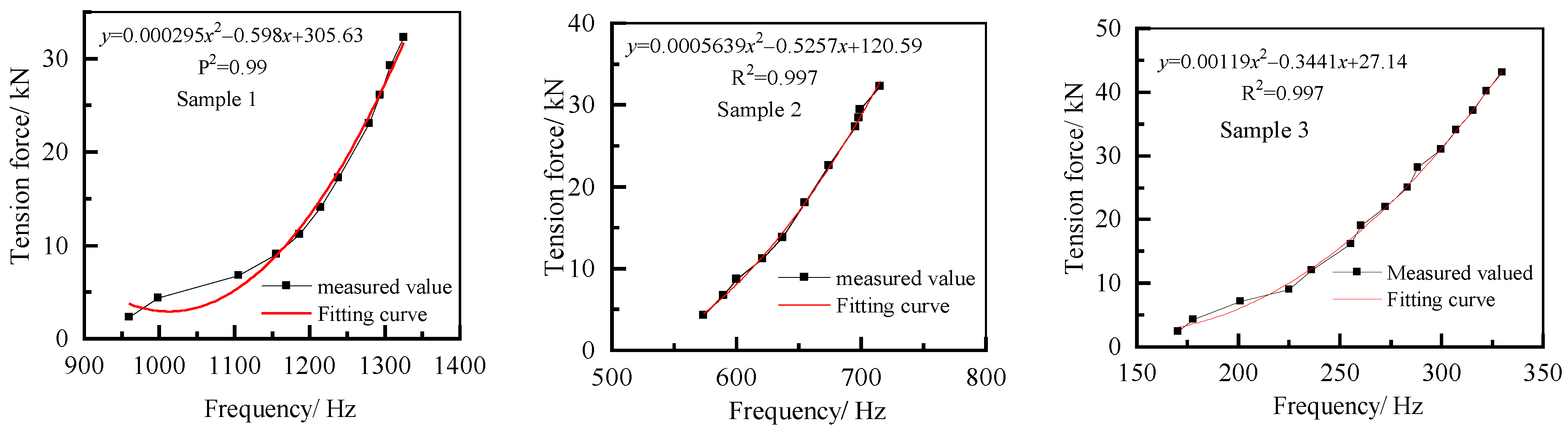
3.2. Quadratic Regression Relationships for Vibration Frequency and Tension Force for Short Suspenders
4. Discussion
5. Conclusions
- (1)
- There is a good correlation between tension force and vibration frequency for short suspenders. With the increase of tension force and aspect ratio, vibration frequency displays an increasing trend, indicating the possibility of using vibration frequency for real-time detection of the tension force state of short suspenders.
- (2)
- The relationships between vibration frequency and tension force of steel rod-type short suspenders is influenced mainly by boundary constraints and flexibility of suspenders, leading to the inadaptability of typical tension string theory. It has been found that for steel rod-type short suspenders, there is a quadratic regression relationship between vibration frequency and tension force, controlling the error between experimental and calculated tension force within 5%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zui, H.; Shinke, T.; Namita, Y. Practical formulas for estimation of cable tension by vibration method. J. Struct. Eng. 1980, 525, 651–656. [Google Scholar] [CrossRef]
- Syamsi, M.; Wang, C.; Nguyen, V. Tension force identification for cable of various end-restraints using equivalent effective vibration lengths of mode pairs. Mesurement 2022, 197, 111319. [Google Scholar] [CrossRef]
- Li, S.; Wei, S.; Bao, Y.; Li, H. Condition assessment of cables by pattern recognition of vehicle-induced cable tension ratio. Eng. Struct. 2018, 155, 1–15. [Google Scholar] [CrossRef]
- Rango, B.J.; Serralunga, F.J.; Piovan, M.T.; Ballaben, J.S.; Rosales, M.B. Identification of the tension force in cables with insulators. Meccanica 2019, 54, 33–46. [Google Scholar] [CrossRef]
- Hassan, M.; Khajepour, A. Optimization of actuator forces in cable-based parallel manipulators using convex analysis. IEEE Trans. Robot. 2008, 24, 736–740. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-H.; Chen, S.-Y.; Lai, G. A novel tension estimation approach for elastic cables by elimination of complex boundary condition effects employing mode shape functions. Eng. Struct. 2018, 166, 152–166. [Google Scholar] [CrossRef]
- Yu, C. Tension prediction for straight cables based on effective vibration length with a two-frequency approach. Eng. Struct. 2020, 222, 111121. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, X.; Cui, J. Failure Mechanism of unbonded preforceed Thru-Anchor Cables: In situ investigation in large underground caverns. Rock Mech. Rock Eng. 2015, 48, 873–878. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, X.; Hou, S.; Sun, H. Non-iterative geometric method for cable-tension optimization of cable-driven parallel robots with 2 redundant cables. Mechatronics 2019, 59, 49–60. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Huang, S.; Li, L. Measured frequency for the estimation of cable force by vibration method. J. Eng. Mech. 2014, 141, 06014020. [Google Scholar] [CrossRef]
- Avanzini, F.; Marogna, R.; Bank, B. Efficient synthesis of tension modulation in strings and membranes based on energy estimation. J. Acoust. Soc. Am. 2012, 131, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-H.; Lee, C.-H.; Shih, K.-J.; Wang, Y.-J. Frequency estimation of distorted power system signals using a robust algorithm. IEEE Trans. Power Deliv. 2007, 23, 41–51. [Google Scholar] [CrossRef]
- Wen, H.; Guo, S.; Teng, Z.; Li, F.; Yang, Y. Frequency estimation of distorted and noisy signals in power systems by FFT-based approach. IEEE Trans. Power Syst. 2014, 29, 765–774. [Google Scholar] [CrossRef]
- Ahmad, J.; Cheng, S.; Ghrib, F. An analytical approach to evaluate damping property of orthogonal cable networks. Eng. Struct. 2014, 75, 225–236. [Google Scholar] [CrossRef]
- Yan, W.; Xu, X.; Li, Y.; Chen, Y. Cable force measurement based on vibration frequency method and optimization function. J. Highw. Transp. Res. Dev. 2015, 32, 61–67. (In Chinese) [Google Scholar]
- Kim, B.; Park, T. Estimation of cable tension force using the frequency-based system identification method. J. Sound Vib. 2007, 304, 660–676. [Google Scholar] [CrossRef]
- Agbezuge, L.; Wieloch, F. Estimation of interfacial tension components for liquid–solid systems from contact angle measurements. J. Appl. Polym. Sci. 1982, 27, 271–275. [Google Scholar] [CrossRef]
- Xu, H.; Huang, P.; Han, W. Boundary conditions and calculating method of tension for short rigid suspenders. J. Chang. Univ. (Nat. Sci. Ed.) 2008, 28, 58–65. (In Chinese) [Google Scholar]
- Sun, Z.; Ning, S.; Shen, Y. Failure investigation and replacement implementation of short suspenders in a suspension bridge. J. Bridge Eng. 2017, 22, 05017007. [Google Scholar] [CrossRef]
- Deng, Y.; Deng, L. Suspender replacement method for long-span concrete-filled steel tubular arch bridges and cable force measurement based on frequency method. Adv. Civ. Eng. 2021, 2021, 7308816. [Google Scholar] [CrossRef]
- Stromquist-Levoir, G.; Mcmullen, K.F.; Zaghi, A.E.; Christenson, R. Determining time variation of cable tension forces in suspended bridges using time-frequency analysis. Adv. Civ. Eng. 2018, 2018, 1053232. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Deng, N.; Wang, X.; Dong, J.; Jiang, W. Comparative analysis of method for measuring cable force of short suspender in arch bridge. J. Guilin Univ. Technol. 2021, 11, 11–15. (In Chinses) [Google Scholar]
- Ni, Y.; Chen, Q. Research on accurate measurement of cable force of short hanging rod of arch bridge. West. China Commun. Sci. Technol. 2019, 9, 4. (In Chinses) [Google Scholar]
- Huang, Z.; Xie, M.; Chen, C.; Du, Y.; Zhao, J. Engineering application of a safety-state evaluation model for hidden frame-supported glass curtain walls based on remote vibration. J. Build. Eng. 2019, 26, 100915. [Google Scholar] [CrossRef]
- Huang, Z.; Xie, M.; Du, Y.; Song, H. Application of Laser Doppler Vibration in cable force detection. Highway 2018, 5, 109–111. (In Chinese) [Google Scholar]
- Abbas, S.H.; Jang, J.-K.; Kim, D.-H.; Lee, J.-R. Underwater vibration analysis method for rotating propeller blades using laser Doppler vibrometer. Opt. Lasers Eng. 2020, 132, 106133. [Google Scholar] [CrossRef]
- Rothberg, S.J.; Allen, M.S.; Castellini, P.; Di Maio, D.; Dirckx, J.J.; Ewins, D.J.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2016, 99, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Ma, G.; Sawada, K.; Yashima, A.; Saito, H. Experimental Study of the applicability of the remotely positioned laser doppler vibrometer to rock-block stability assessment. Rock Mech. Rock Eng. 2015, 48, 787–802. [Google Scholar] [CrossRef]
- Du, Y.; Xie, M.; Jiang, Y.; Jiang, Y.; Li, B.; Liu, Q. A new method for landslide safety assessments based on natural vibration frequency. Chin. J. Eng. 2015, 37, 1118–1123. (In Chinese) [Google Scholar]
- Armin, B.; Mehrabi, L. A unified finite difference formulation for free vibration of cables. Struct. Eng. 1998, 124, 1313–1322. [Google Scholar]


| NO. | l/mm | l/d | ρ/(kg·m−1) | EI/(N·mm2) | Yield Strength/MPa | Tensile Strength/MPa |
|---|---|---|---|---|---|---|
| 1# | 168 | 14 | 0.89 | 2.03 × 108 | 410 | 645 |
| 2# | 250 | 20.8 | 0.89 | 2.03 × 108 | 410 | 645 |
| 3# | 453 | 37.8 | 0.89 | 2.03 × 108 | 410 | 645 |
| Tension/kN | /Hz | Typical Model in Equation (1) | Modified Model in Equation (2) | ||
|---|---|---|---|---|---|
| 2.3 | 959.38 | 151.70 | 84.19 | 154.00 | 83.95 |
| 4.4 | 997.81 | 208.91 | 79.06 | 210.59 | 78.89 |
| 6.8 | 1105.63 | 259.90 | 76.49 | 261.25 | 76.37 |
| 9.1 | 1155.94 | 300.11 | 74.04 | 301.28 | 73.94 |
| 11.2 | 1186.56 | 333.30 | 71.91 | 334.36 | 71.82 |
| 14.1 | 1214.06 | 373.97 | 69.20 | 374.91 | 69.12 |
| 17.3 | 1238.44 | 413.64 | 66.60 | 414.49 | 66.53 |
| 23.1 | 1278.75 | 478.98 | 62.54 | 479.72 | 62.49 |
| 26.2 | 1293.44 | 509.29 | 60.62 | 509.98 | 60.57 |
| 29.3 | 1307.50 | 538.91 | 58.78 | 539.56 | 58.73 |
| 32.4 | 1325.0 | 566.46 | 57.25 | 567.08 | 57.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Zhang, G.; Xie, M.; Du, Y. Tension Force Detection of Short Suspender by Using Laser Doppler Vibrometer. Appl. Sci. 2022, 12, 6536. https://doi.org/10.3390/app12136536
Huang Z, Zhang G, Xie M, Du Y. Tension Force Detection of Short Suspender by Using Laser Doppler Vibrometer. Applied Sciences. 2022; 12(13):6536. https://doi.org/10.3390/app12136536
Chicago/Turabian StyleHuang, Zhide, Guihong Zhang, Mowen Xie, and Yan Du. 2022. "Tension Force Detection of Short Suspender by Using Laser Doppler Vibrometer" Applied Sciences 12, no. 13: 6536. https://doi.org/10.3390/app12136536
APA StyleHuang, Z., Zhang, G., Xie, M., & Du, Y. (2022). Tension Force Detection of Short Suspender by Using Laser Doppler Vibrometer. Applied Sciences, 12(13), 6536. https://doi.org/10.3390/app12136536





