Shape Optimization with a Flattening-Based Morphing Method
Abstract
:1. Introduction
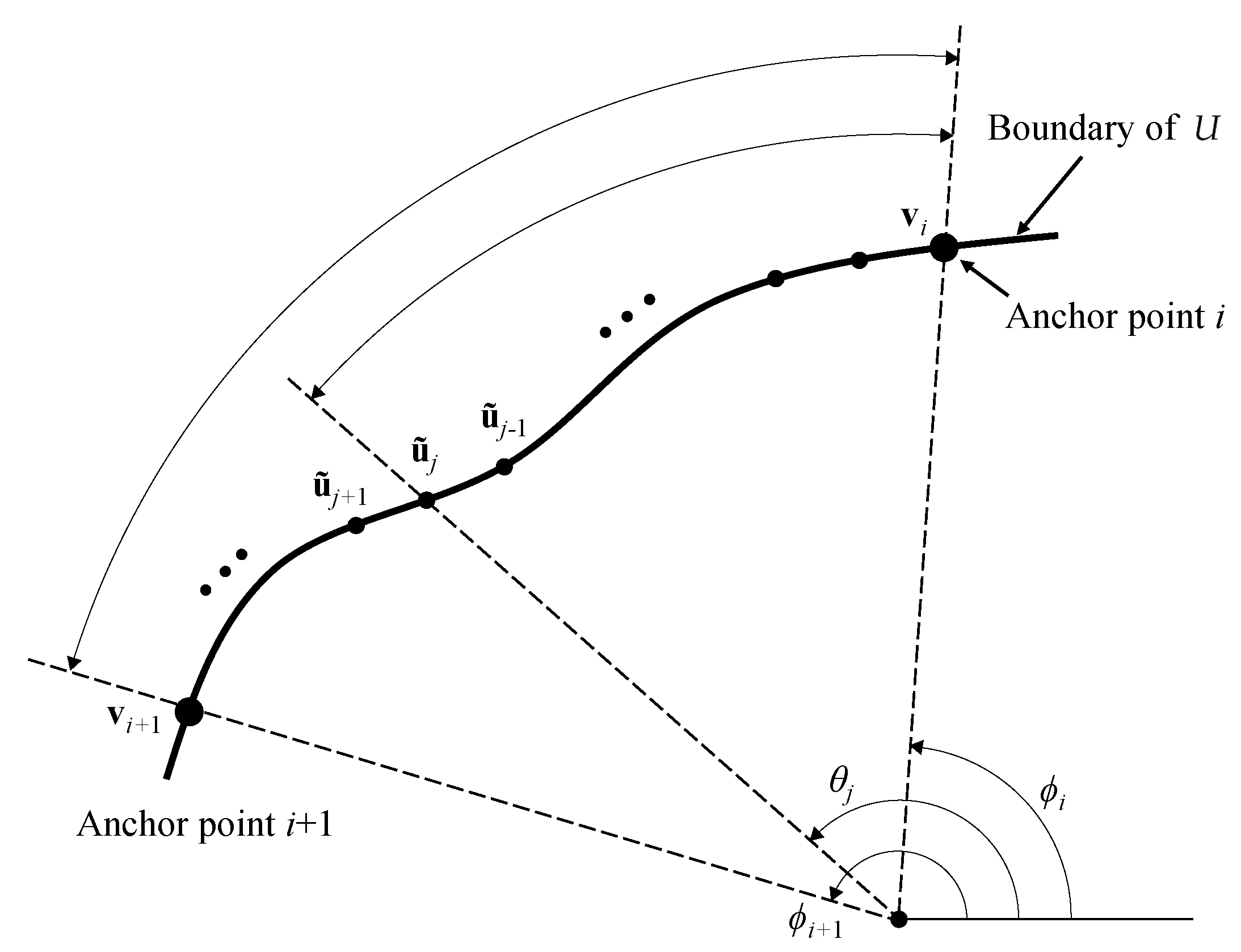
2. Flattening-Based Morphing Method
3. Application
3.1. Baseline Models
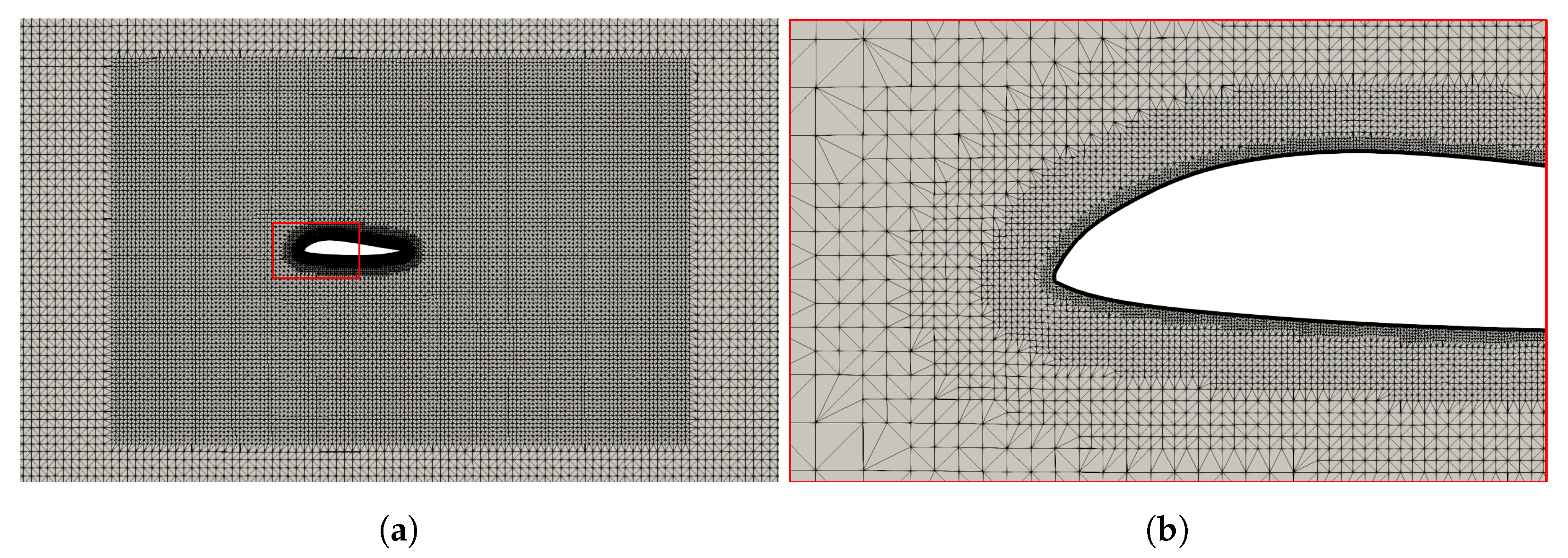
3.2. CFD Simulation
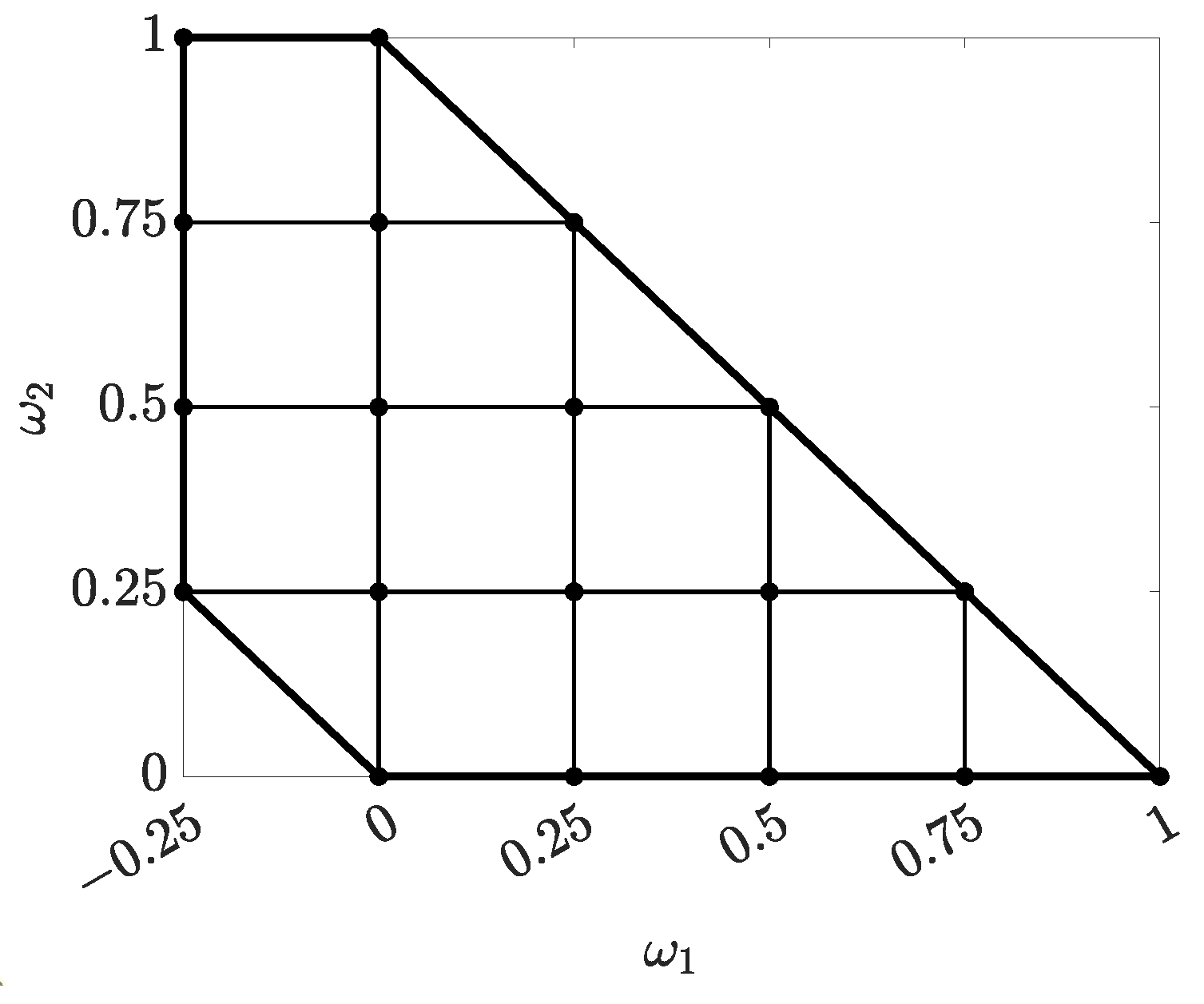
3.3. Design Parameters and Objective Function
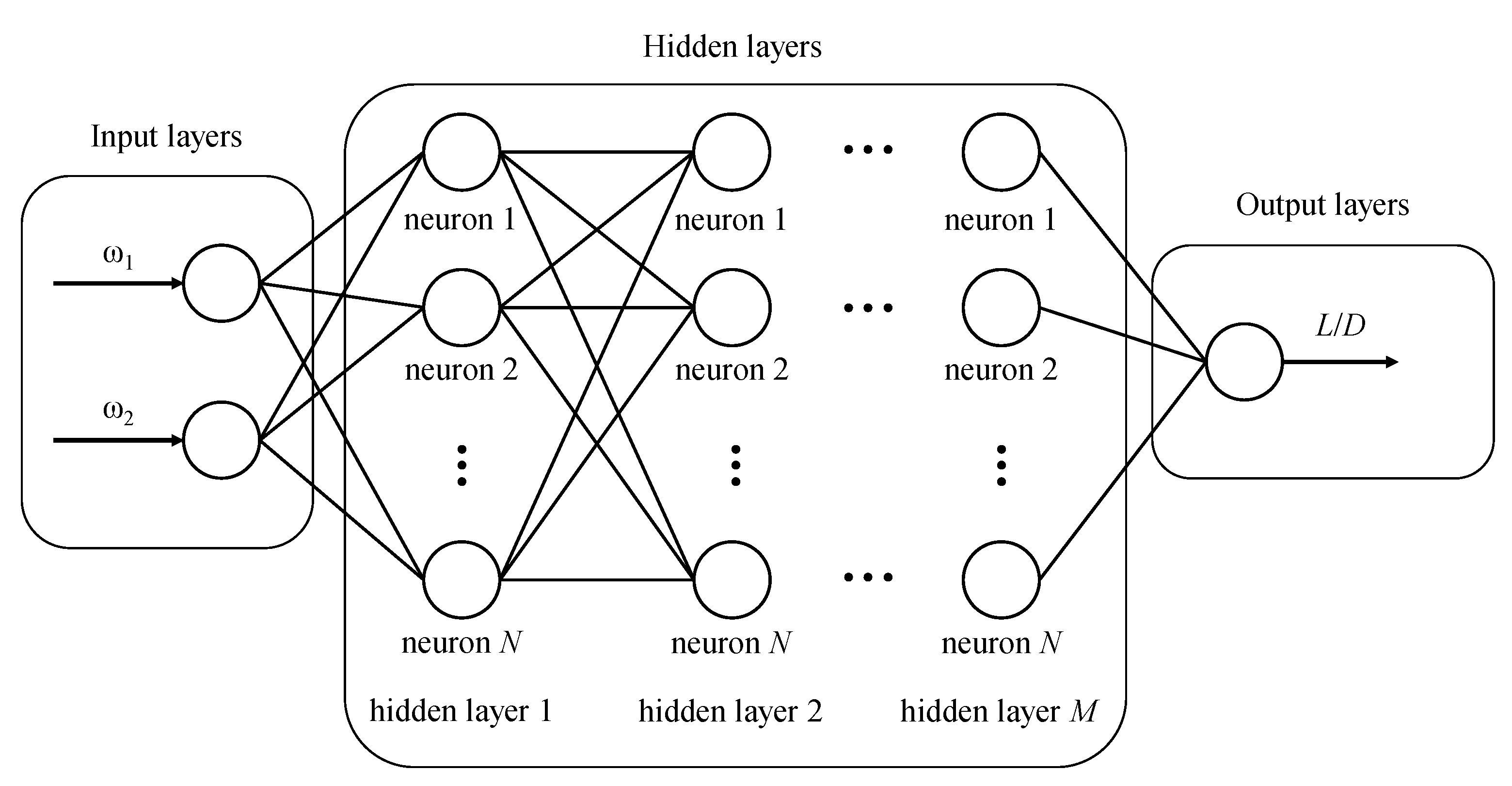
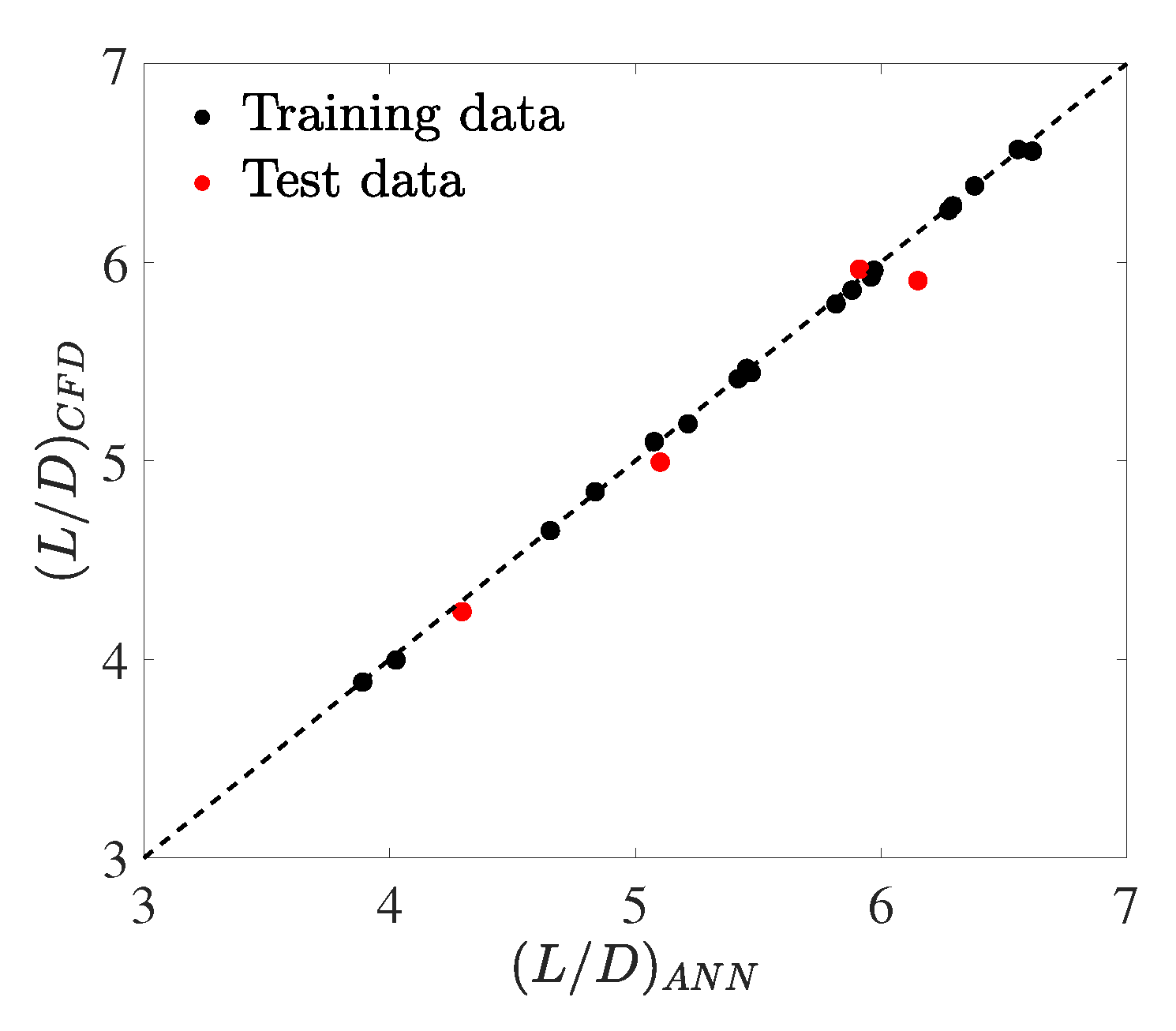
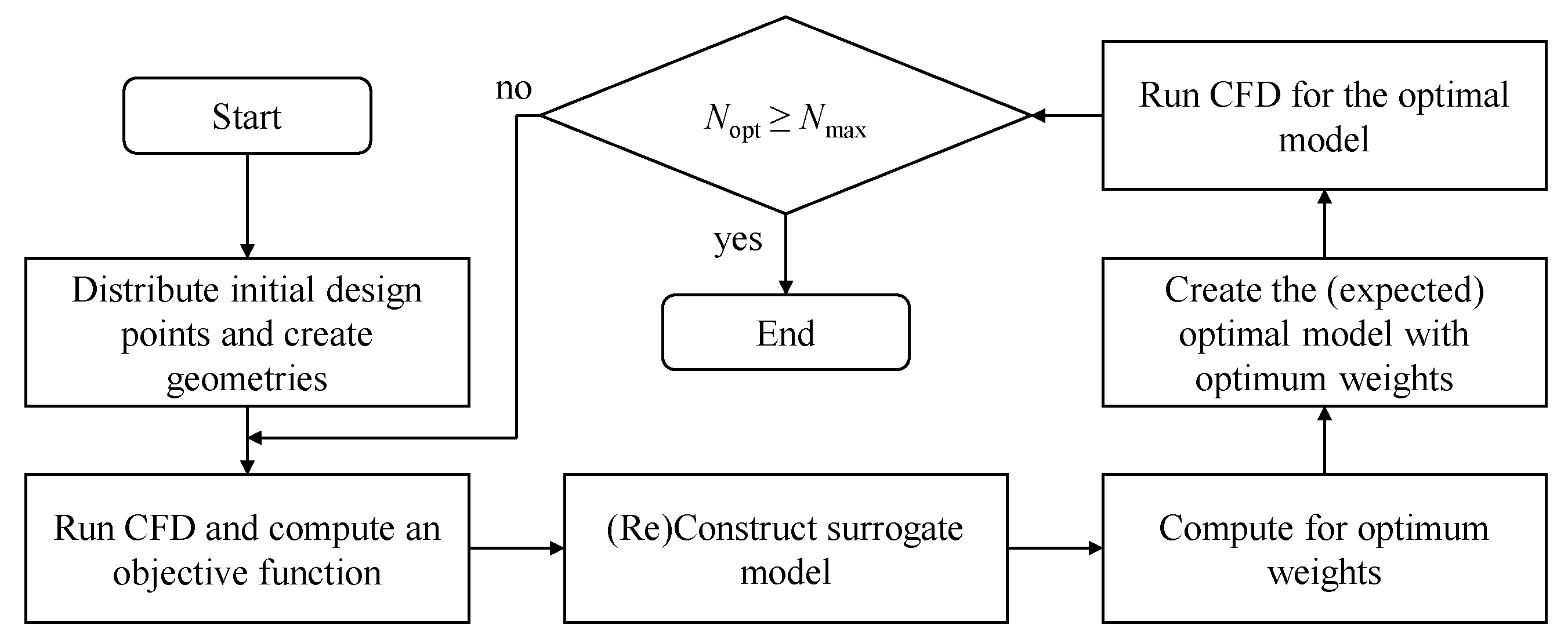
3.4. Optimization
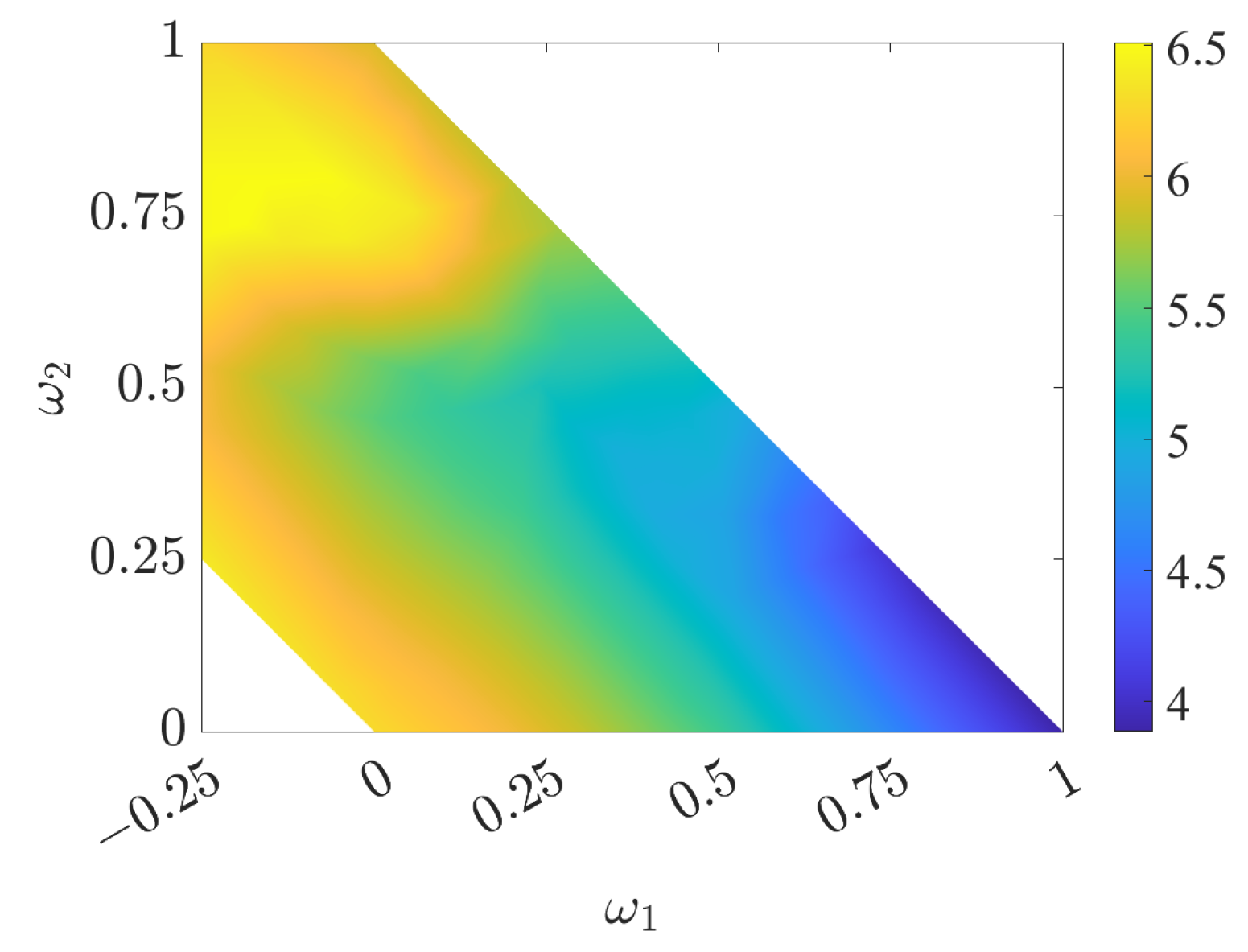
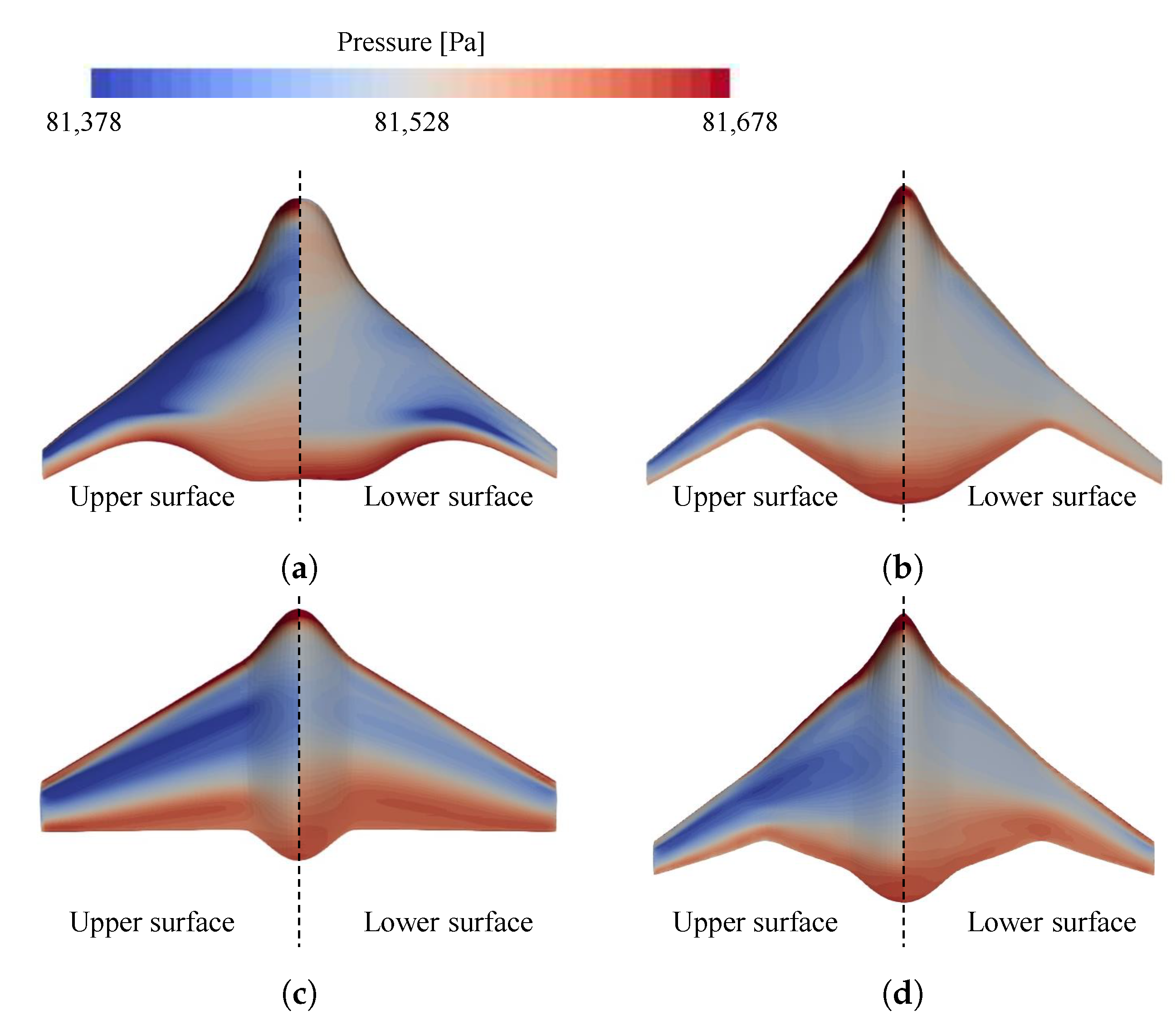
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, Z.; Yao, S.; Yang, G. Research on aerodynamic optimization of high-speed train’s slipstream. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1106–1127. [Google Scholar] [CrossRef]
- Sudin, M.N.; Abdullah, M.A.; Shamsuddin, S.A.; Ramli, F.R.; Tahir, M.M. Review of research on vehicles aerodynamic drag reduction methods. Int. J. Mech. Mechatron. Eng. 2014, 14, 37–47. [Google Scholar]
- Lyu, Z.; Martins, J.R. Aerodynamic shape optimization of an adaptive morphing trailing-edge wing. J. Aircr. 2015, 52, 1951–1970. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, A.; Castilla, R.; Eid, G. A numerical aerodynamic analysis on the effect of rear underbody diffusers on road cars. Appl. Sci. 2022, 12, 3763. [Google Scholar] [CrossRef]
- Sun, Z.; Yao, S.; Wei, L.; Yao, Y.; Yang, G. Numerical Investigation on the Influence of the Streamlined Structures of the High-Speed Train’s Nose on Aerodynamic Performances. Appl. Sci. 2021, 11, 784. [Google Scholar] [CrossRef]
- Ju, S.; Sun, Z.; Guo, D.; Yang, G.; Wang, Y.; Yan, C. Aerodynamic-Aeroacoustic Optimization of a Baseline Wing and Flap Configuration. Appl. Sci. 2022, 12, 1063. [Google Scholar] [CrossRef]
- Maizi, M.; Mohamed, M.; Dizene, R.; Mihoubi, M. Noise reduction of a horizontal wind turbine using different blade shapes. Renew. Energy 2018, 117, 242–256. [Google Scholar] [CrossRef]
- Sanaye, S.; Hassanzadeh, A. Multi-objective optimization of airfoil shape for efficiency improvement and noise reduction in small wind turbines. J. Renew. Sustain. Energy 2014, 6, 053105. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Song, B.; Wang, P. Parametric geometric model and shape optimization of an underwater glider with blended-wing-body. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 995–1006. [Google Scholar] [CrossRef] [Green Version]
- Jha, A.K.; Kudva, J.N. Morphing aircraft concepts, classifications, and challenges. In Proceedings of the Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies, San Diego, CA, USA, 14–18 March 2004; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5388, pp. 213–224. [Google Scholar]
- Wang, Y.; Shen, S.; Li, G.; Huang, D.; Zheng, Z. Investigation on aerodynamic performance of vertical axis wind turbine with different series airfoil shapes. Renew. Energy 2018, 126, 801–818. [Google Scholar] [CrossRef]
- Peifeng, L.; Zhang, B.; Yingchun, C.; Changsheng, Y.; Yu, L. Aerodynamic design methodology for blended wing body transport. Chin. J. Aeronaut. 2012, 25, 508–516. [Google Scholar]
- Panagiotou, P.; Yakinthos, K. Parametric aerodynamic study of Blended-Wing-Body platforms at low subsonic speeds for UAV applications. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3737. [Google Scholar]
- Brujic, D.; Ristic, M.; Mattone, M.; Maggiore, P.; De Poli, G.P. CAD based shape optimization for gas turbine component design. Struct. Multidiscip. Optim. 2010, 41, 647–659. [Google Scholar] [CrossRef]
- Sun, J.; Frazer, J.H.; Mingxi, T. Shape optimisation using evolutionary techniques in product design. Comput. Ind. Eng. 2007, 53, 200–205. [Google Scholar] [CrossRef]
- Luo, X.; Yang, B.; Sheng, L.; Chen, J.; Li, H.; Xie, L.; Chen, G.; Yu, M.; Guo, W.; Tian, W. CAD based design sensitivity analysis and shape optimization of scaffolds for bio-root regeneration in swine. Biomaterials 2015, 57, 59–72. [Google Scholar] [CrossRef]
- Gordon, W.J.; Riesenfeld, R.F. B-spline curves and surfaces. In Computer Aided Geometric Design; Elsevier: Amsterdam, The Netherlands, 1974; pp. 95–126. [Google Scholar]
- Boehm, W. Inserting new knots into B-spline curves. Comput.-Aided Des. 1980, 12, 199–201. [Google Scholar] [CrossRef]
- Farin, G.; Rein, G.; Sapidis, N.; Worsey, A.J. Fairing cubic B-spline curves. Comput. Aided Geom. Des. 1987, 4, 91–103. [Google Scholar] [CrossRef]
- Piegl, L. On NURBS: A survey. IEEE Comput. Graph. Appl. 1991, 11, 55–71. [Google Scholar] [CrossRef]
- Xie, W.C.; Zou, X.F.; Yang, J.D.; Yang, J.B. Iteration and optimization scheme for the reconstruction of 3D surfaces based on non-uniform rational B-splines. Comput.-Aided Des. 2012, 44, 1127–1140. [Google Scholar] [CrossRef]
- Liang, Y.; Cheng, X.; Li, Z.; Xiang, J. Multi-objective robust airfoil optimization based on non-uniform rational B-spline (NURBS) representation. Sci. China Technol. Sci. 2010, 53, 2708–2717. [Google Scholar] [CrossRef]
- Tang, P.S.; Chang, K.H. Integration of topology and shape optimization for design of structural components. Struct. Multidiscip. Optim. 2001, 22, 65–82. [Google Scholar] [CrossRef]
- Han, X.; Zingg, D.W. An adaptive geometry parametrization for aerodynamic shape optimization. Optim. Eng. 2014, 15, 69–91. [Google Scholar] [CrossRef]
- Qian, X. Full analytical sensitivities in NURBS based isogeometric shape optimization. Comput. Methods Appl. Mech. Eng. 2010, 199, 2059–2071. [Google Scholar] [CrossRef]
- Painchaud-Ouellet, S.; Tribes, C.; Trepanier, J.Y.; Pelletier, D. Airfoil shape optimization using NURBS representation under thickness constraint. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–9 January 2004; p. 1095. [Google Scholar]
- Yu, G.; Müller, J.D.; Jones, D.; Christakopoulos, F. CAD-based shape optimisation using adjoint sensitivities. Comput. Fluids 2011, 46, 512–516. [Google Scholar] [CrossRef]
- Samareh, J. Aerodynamic shape optimization based on free-form deformation. In Proceedings of the 10th AIAA/ISSMO multidisciplinary analysis and optimization conference, Albany, NY, USA, 30 August–1 September 2004; p. 4630. [Google Scholar]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Lyu, Z.; Martins, J.R. Aerodynamic design optimization studies of a blended-wing-body aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef] [Green Version]
- Allen, C.B.; Rendall, T. CFD-based optimization of hovering rotors using radial basis functions for shape parameterization and mesh deformation. Optim. Eng. 2013, 14, 97–118. [Google Scholar] [CrossRef]
- De Boer, A.; Van der Schoot, M.S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Jakobsson, S.; Amoignon, O. Mesh deformation using radial basis functions for gradient-based aerodynamic shape optimization. Comput. Fluids 2007, 36, 1119–1136. [Google Scholar] [CrossRef]
- Sieger, D.; Menzel, S.; Botsch, M. On shape deformation techniques for simulation-based design optimization. In New Challenges in Grid Generation and Adaptivity for Scientific Computing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 281–303. [Google Scholar]
- Oh, S.; Jiang, C.H.; Jiang, C.; Marcus, P.S. Finding the optimal shape of the leading-and-trailing car of a high-speed train using design-by-morphing. Comput. Mech. 2018, 62, 23–45. [Google Scholar] [CrossRef]
- Kim, H.; Oh, S. Shape optimization of a hyperloop pod’s head and tail using a multi-resolution morphing method. Int. J. Mech. Sci. 2022, 223, 107227. [Google Scholar] [CrossRef]
- Karimmaslak, H.; Najafi, B.; Band, S.S.; Ardabili, S.; Haghighat-Shoar, F.; Mosavi, A. Optimization of performance and emission of compression ignition engine fueled with propylene glycol and biodiesel–diesel blends using artificial intelligence method of ANN-GA-RSM. Eng. Appl. Comput. Fluid Mech. 2021, 15, 413–425. [Google Scholar] [CrossRef]
- Oh, S. Comparison of a response surface method and artificial neural network in predicting the aerodynamic performance of a wind turbine airfoil and its optimization. Appl. Sci. 2020, 10, 6277. [Google Scholar] [CrossRef]
- Seo, Y.M.; Pandey, S.; Lee, H.U.; Choi, C.; Park, Y.G.; Ha, M.Y. Prediction of heat transfer distribution induced by the variation in vertical location of circular cylinder on Rayleigh-Bénard convection using artificial neural network. Int. J. Mech. Sci. 2021, 209, 106701. [Google Scholar] [CrossRef]
- Yoo, S.; Oh, S. Flow analysis and optimization of a vertical axis wind turbine blade with a dimple. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1666–1681. [Google Scholar] [CrossRef]
- Varrecchia, T.; De Marchis, C.; Draicchio, F.; Schmid, M.; Conforto, S.; Ranavolo, A. Lifting activity assessment using kinematic features and neural networks. Appl. Sci. 2020, 10, 1989. [Google Scholar] [CrossRef] [Green Version]
- Pinkall, U.; Polthier, K. Computing discrete minimal surfaces and their conjugates. Exp. Math. 1993, 2, 15–36. [Google Scholar] [CrossRef]
- Desbrun, M.; Meyer, M.; Alliez, P. Intrinsic parameterizations of surface meshes. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2002; Volume 21, pp. 209–218. [Google Scholar]
- Oh, S. A new triangular mesh repairing method using a mesh distortion energy minimization-based mesh flattening method. Adv. Eng. Softw. 2019, 131, 48–59. [Google Scholar] [CrossRef]
- Sorkine, O. Laplacian mesh processing. Eurographics (State Art Rep.) 2005, 4. [Google Scholar] [CrossRef]
- Karim, R.; Ma, Y.; Jang, M.; Housden, R.J.; Williams, S.E.; Chen, Z.; Ataollahi, A.; Althoefer, K.; Rinaldi, C.A.; Razavi, R.; et al. Surface flattening of the human left atrium and proof-of-concept clinical applications. Comput. Med. Imaging Graph. 2014, 38, 251–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dehpanah, P.; Nejat, A. The aerodynamic design evaluation of a blended-wing-body configuration. Aerosp. Sci. Technol. 2015, 43, 96–110. [Google Scholar] [CrossRef]
- Siouris, S.; Qin, N. Study of the effects of wing sweep on the aerodynamic performance of a blended wing body aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 47–55. [Google Scholar] [CrossRef]
- Giguere, P.; Dumas, G.; Lemay, J. Gurney flap scaling for optimum lift-to-drag ratio. AIAA J. 1997, 35, 1888–1890. [Google Scholar] [CrossRef]
- Haryanto, I.; Utomo, T.S.; Sinaga, N.; Rosalia, C.A.; Putra, A.P. Optimization of maximum lift to drag ratio on airfoil design based on artificial neural network utilizing genetic algorithm. In Applied Mechanics and Materials; Trans Tech Publ: Zurich, Switzerland, 2014; Volume 493, pp. 123–128. [Google Scholar]
- Fatehi, M.; Nili-Ahmadabadi, M.; Nematollahi, O.; Minaiean, A.; Kim, K.C. Aerodynamic performance improvement of wind turbine blade by cavity shape optimization. Renew. Energy 2019, 132, 773–785. [Google Scholar] [CrossRef]
- Conn, A.; Gould, N.; Toint, P. A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Math. Comput. 1997, 66, 261–288. [Google Scholar] [CrossRef]
- Wang, S.; Jian, G.; Xiao, J.; Wen, J.; Zhang, Z. Optimization investigation on configuration parameters of spiral-wound heat exchanger using Genetic Aggregation response surface and Multi-Objective Genetic Algorithm. Appl. Therm. Eng. 2017, 119, 603–609. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]








| Meshes | Number of Cells () | Number of Layers | Averaged | First Layer Thickness ( m) | Drag Coefficients | Relative Error (%) |
|---|---|---|---|---|---|---|
| Coarse | 5.51 | 20 | 2.36 | 3.58 | 0.01492 | 2.40 |
| Intermediate | 8.75 | 20 | 2.09 | 3.17 | 0.01473 | 1.10 |
| Fine | 13.08 | 20 | 1.82 | 2.76 | 0.01457 | - |
| Parameters | Lower Bounds | Upper Bounds |
|---|---|---|
| 1 | ||
| 1 | ||
| Constraint | 0 1 | |
| Optimization Iteration | Error (%) | ||||
|---|---|---|---|---|---|
| 1 | 0.7907 | 6.7128 | 6.6567 | 0.8432 | |
| 2 | 0.8047 | 6.7110 | 6.6816 | 0.4386 | |
| 3 | 0.7853 | 6.6935 | 6.6812 | 0.1847 | |
| 4 | 0.7792 | 6.6784 | 6.6958 | 0.2600 | |
| 5 | 0.7751 | 6.6941 | 6.7030 | 0.1332 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Oh, S. Shape Optimization with a Flattening-Based Morphing Method. Appl. Sci. 2022, 12, 6565. https://doi.org/10.3390/app12136565
Kim H, Oh S. Shape Optimization with a Flattening-Based Morphing Method. Applied Sciences. 2022; 12(13):6565. https://doi.org/10.3390/app12136565
Chicago/Turabian StyleKim, Honghee, and Sahuck Oh. 2022. "Shape Optimization with a Flattening-Based Morphing Method" Applied Sciences 12, no. 13: 6565. https://doi.org/10.3390/app12136565
APA StyleKim, H., & Oh, S. (2022). Shape Optimization with a Flattening-Based Morphing Method. Applied Sciences, 12(13), 6565. https://doi.org/10.3390/app12136565





