Pressure- and Size-Dependent Aerodynamic Drag Effects on Mach 0.3–2.2 Microspheres for High-Precision Micro-Ballistic Characterization
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
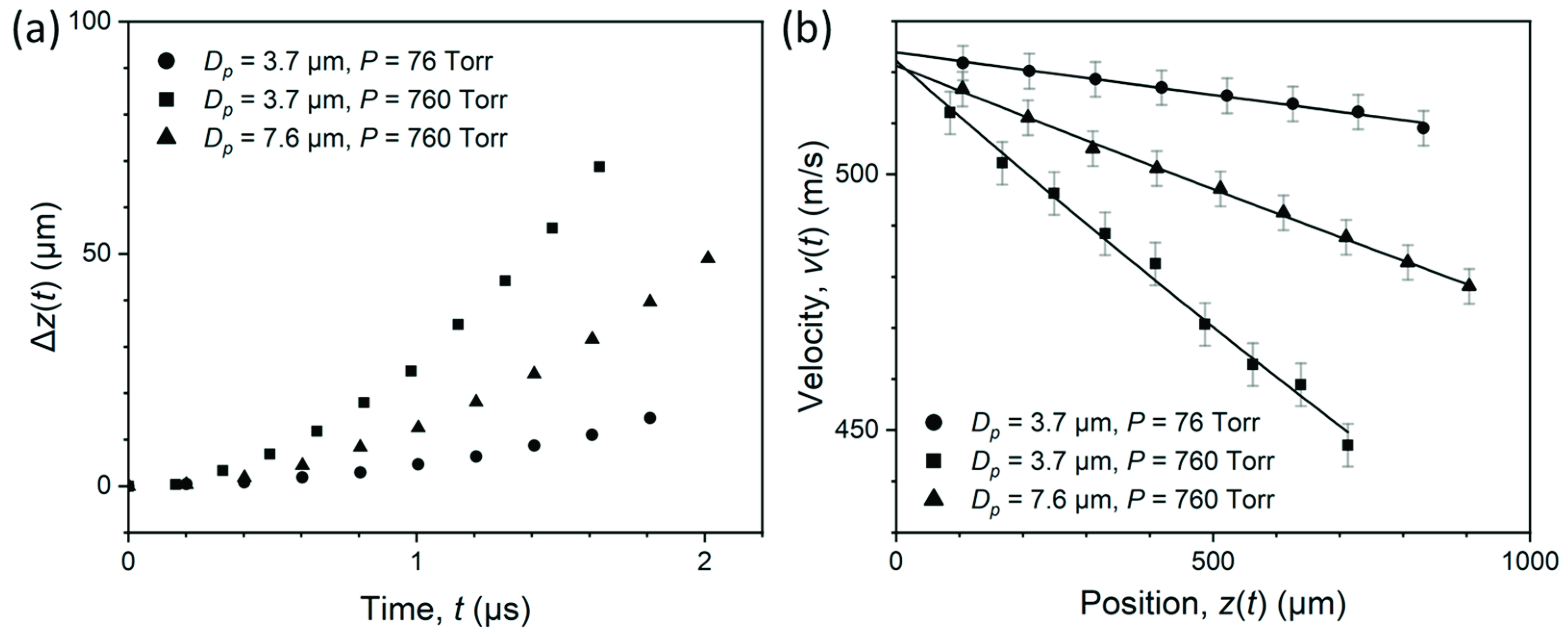
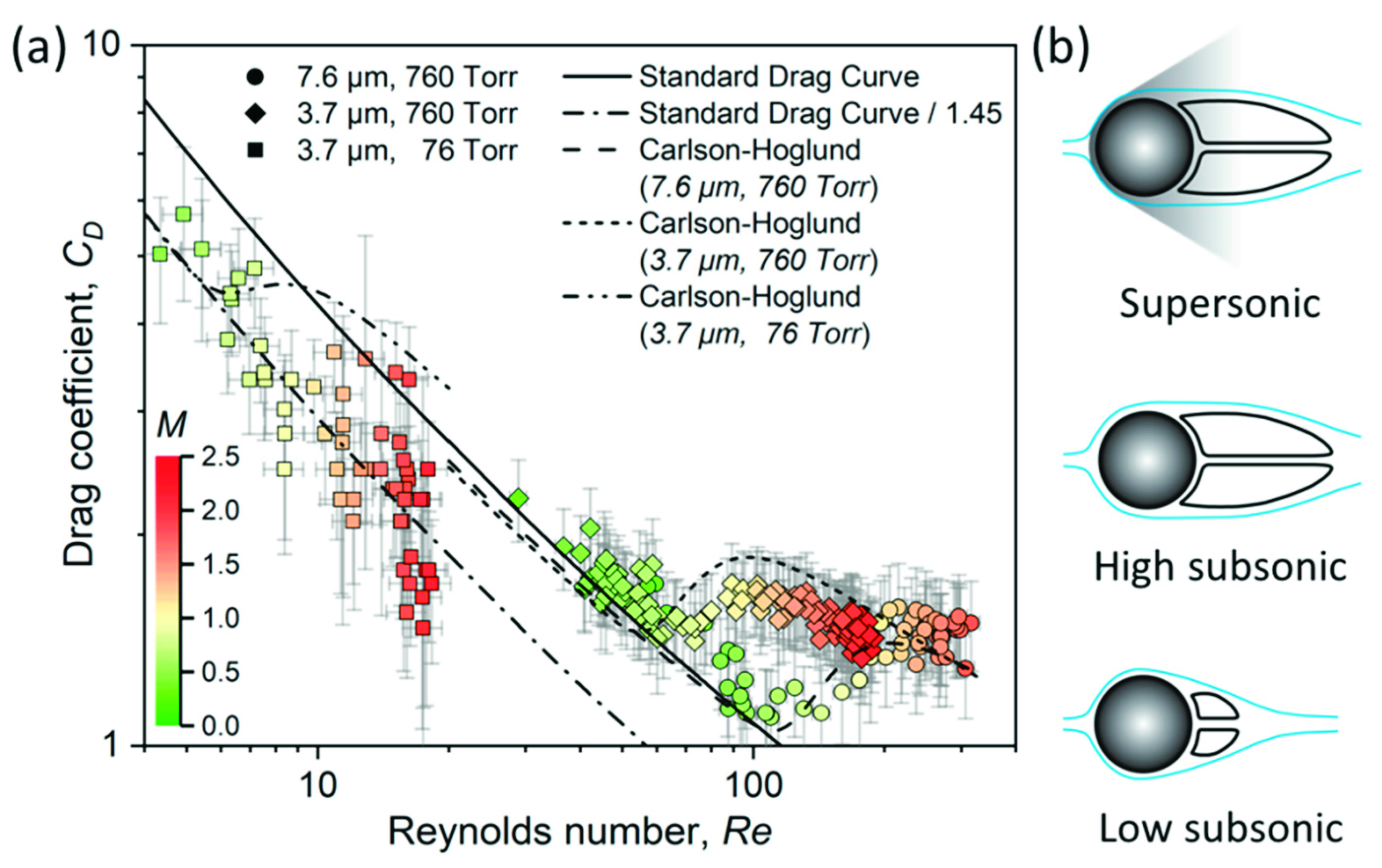
3. Results and Discussion

4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoerner, S.F. Fluid-Dynamic Drag. 1965. Available online: https://cir.nii.ac.jp/crid/1572543026233935872 (accessed on 23 May 2022).
- Lee, J.-H.; Veysset, D.; Singer, J.P.; Retsch, M.; Saini, G.; Pezeril, T.; Nelson, K.A.; Thomas, E.L. High Strain Rate Deformation of Layered Nanocomposites. Nat. Commun. 2012, 3, 1164. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-H.; Loya, P.E.; Lou, J.; Thomas, E.L. Dynamic Mechanical Behavior of Multilayer Graphene via Supersonic Projectile Penetration. Science 2014, 346, 1092–1096. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Lee, J.-H. Intrinsic Dynamics and Toughening Mechanism of Multilayer Graphene upon Microbullet Impact. ACS Appl. Nano Mater. 2020, 3, 9185–9191. [Google Scholar] [CrossRef]
- Sanford, J.C.; Klein, T.M.; Wolf, E.D.; Allen, N. Delivery of Substances into Cells and Tissues Using a Particle Bombardment Process. Part. Sci. Technol. 1987, 5, 27–37. [Google Scholar] [CrossRef]
- Iida, A.; Seki, M.; Kamada, M.; Yamada, Y.; Morikawa, H. Gene Delivery into Cultured Plant Cells by DNA-Coated Gold Particles Accelerated by a Pneumatic Particle Gun. Theor. Appl. Genet. 1990, 80, 813–816. [Google Scholar] [CrossRef] [PubMed]
- Mellott, A.J.; Forrest, M.L.; Detamore, M.S. Physical Non-Viral Gene Delivery Methods for Tissue Engineering. Ann. Biomed. Eng. 2013, 41, 446–468. [Google Scholar] [CrossRef] [Green Version]
- Klein, T.M.; Gradziel, T.; Fromm, M.E.; Sanford, J.C. Factors Influencing Gene Delivery into Zea Mays Cells by High-Velocity Microprojectiles. Nat. Biotechnol. 1988, 6, 559–563. [Google Scholar] [CrossRef]
- Menezes, V.; Takayama, K.; Ohki, T.; Gopalan, J. Laser-Ablation-Assisted Microparticle Acceleration for Drug Delivery. Appl. Phys. Lett. 2005, 87, 163504. [Google Scholar] [CrossRef]
- Kendall, M.; Mitchell, T.; Wrighton-Smith, P. Intradermal Ballistic Delivery of Micro-Particles into Excised Human Skin for Pharmaceutical Applications. J. Biomech. 2004, 37, 1733–1741. [Google Scholar] [CrossRef]
- Quinlan, N.J.; Kendall, M.A.F.; Bellhouse, B.J.; Ainsworth, R.W. Investigations of Gas and Particle Dynamics in First Generation Needle-Free Drug Delivery Devices. Shock Waves 2001, 10, 395–404. [Google Scholar] [CrossRef]
- Kane, E.D. Sphere Drag Data at Supersonic Speeds and Low Reynolds Numbers. J. Aeronaut. Sci. 1951, 18, 259–270. [Google Scholar] [CrossRef]
- Wegener, P.P.; Ashkenas, H. Wind Tunnel Measurements of Sphere Drag at Supersonic Speeds and Low Reynolds Numbers. J. Fluid Mech. 1961, 10, 550–560. [Google Scholar] [CrossRef]
- Aroesty, J. Sphere Drag in a Low Density Supersonic Flow; California University: Berkeley, CA, USA, 1962. [Google Scholar]
- Bailey, A.B.; Hiatt, J. Free-Flight Measurements of Sphere Drag at Subsonic, Transonic, Supersonic, and Hypersonic Speeds for Continuum, Transition, and Near-Free-Molecular Flow Conditions; Arnold Air Force Station: Tullahoma, TN, USA, 1971. [Google Scholar]
- Pritchard, P.J. Introduction to Fluid Dynamics; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bailey, A.B. Sphere Drag Measurements in an Aeroballistics Range at High Velocities and Low Reynolds Numbers; Arnold Air Force Station: Tullahoma, TN, USA, 1966. [Google Scholar]
- Lawrence, W.R. Free-Flight Range Measurements of Sphere Drag at Low Reynolds Numbers and Low Mach Numbers; Arnold Air Force Station: Tullahoma, TN, USA, 1967. [Google Scholar]
- Bailey, A.B.; Hiatt, J. Sphere Drag Coefficients for a Broad Range of Mach and Reynolds Numbers. AIAA J. 1972, 10, 1436–1440. [Google Scholar] [CrossRef]
- Veysset, D.; Sun, Y.; Kooi, S.E.; Lem, J.; Nelson, K.A. Laser-Driven High-Velocity Microparticle Launcher in Atmosphere and under Vacuum. Int. J. Impact Eng. 2020, 137, 103465. [Google Scholar] [CrossRef] [Green Version]
- Parmar, M.; Haselbacher, A.; Balachandar, S. Generalized Basset-Boussinesq-Oseen Equation for Unsteady Forces on a Sphere in a Compressible Flow. Phys. Rev. Lett. 2011, 106, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Johnson, T.A.; Patel, V.C. Flow Past a Sphere up to a Reynolds Number of 300. J. Fluid Mech. 1999, 378, 19–70. [Google Scholar] [CrossRef]
- Nagata, T.; Nonomura, T.; Takahashi, S.; Mizuno, Y.; Fukuda, K. Investigation on Subsonic to Supersonic Flow around a Sphere at Low Reynolds Number of between 50 and 300 by Direct Numerical Simulation. Phys. Fluids 2016, 28, 056101. [Google Scholar] [CrossRef] [Green Version]
- Zaehringer, E.; Schwabe, M.; Zhdanov, S.; Mohr, D.P.; Knapek, C.A.; Huber, P.; Semenov, I.L.; Thomas, H.M. Interaction of a Supersonic Particle with a Three-Dimensional Complex Plasma. Phys. Plasmas 2018, 25, 033703. [Google Scholar] [CrossRef]
- Nakamura, I. Steady Wake behind a Sphere. Phys. Fluids 1976, 19, 5–8. [Google Scholar] [CrossRef]
- Wu, Z.; Jin, H.; Guo, L. Investigation on the Drag Coefficient of Supercritical Water Flow Past Sphere-Particle at Low Reynolds Numbers. Therm. Sci. 2017, 21, 217–223. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Dehn, J. A Unified Theory of Penetration. Int. J. Impact Eng. 1987, 5, 239–248. [Google Scholar] [CrossRef]
- Kendall, M.A.F. The Delivery of Particulate Vaccines and Drugs to Human Skin with a Practical, Hand-Held Shock Tube-Based System. Shock Waves 2002, 12, 23–30. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Schiller, L.; Naumann, A. Über Die Grundlegenden Berechnungen Bei Der Schwerkraftaufbereitung. Z. Des Ver. Dtsch. Ing. 1933, 77, 318–320. [Google Scholar]
- Morsi, S.A.; Alexander, A.J. An Investigation of Particle Trajectories in Two-Phase Flow Systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Lapple, C.E. Particle Dynamics; E.I. Dupont de Nemours and Company: Wilmington, DE, USA, 1951. [Google Scholar]
- Langmuir, I.; Blodgett, K.B. Technical Report No. 5418: A Mathematical Investigation of Water Droplet Trajectories; Army Air Forces Headquarters, Air Technical Service Command: Washington, DC, USA, 1948. [Google Scholar]
- Allen, H.S. The Motion of a Sphere in a Viscous Fluid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 519–534. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, M.; Davis, L.; Altman, D. Velocity Lag of Particles in Linearly Accelerated Combustion Gases. Jet Propuls. 1955, 25, 26–30. [Google Scholar] [CrossRef]
- Kürten, H.; Raasch, J.; Rumpf, H. Beschleunigung Eines Kugelförmigen Feststoffteilchens Im Strömungsfeld Konstanter Geschwindigkeit. Chem. Ing. Tech. 1966, 38, 941–948. [Google Scholar] [CrossRef]
- Abraham, F.F. Functional Dependence of Drag Coefficient of a Sphere on Reynolds Number. Phys. Fluids 1970, 13, 2194–2195. [Google Scholar] [CrossRef]
- Ihme, F.; Schmidt-Traub, H.; Brauer, H. Theoretische Untersuchung Über Die Umströmung Und Den Stoffübergang an Kugeln. Chem. Ing. Tech. 1972, 44, 306–313. [Google Scholar] [CrossRef]
- Clift, R.; Gauvin, W. Proceedings of Chemeca 70. Chemeca 1970, 70, 14–27. [Google Scholar]
- Brauer, H.; Mewes, D. Strömungswiderstand Sowie Stationärer Und Instationärer Stoff-und Wärmeübergang an Kugeln. Chem. Ing. Tech. 1972, 44, 865–868. [Google Scholar] [CrossRef]
- Tanaka, Z.; Iinoya, K. New Approximate Equation of Drag Coefficient for Spherical Particles. J. Chem. Eng. Japan 1970, 3, 261–262. [Google Scholar] [CrossRef] [Green Version]
- Moshfegh, A.; Shams, M.; Ahmadi, G.; Ebrahimi, R. A New Expression for Spherical Aerosol Drag in Slip Flow Regime. J. Aerosol. Sci. 2010, 41, 384–400. [Google Scholar] [CrossRef]
- Barber, R.W.; Emerson, D.R. Numerical Simulation of Low Reynolds Number Slip Flow Past a Confined Microsphere; CLRC Daresbury Laboratory: Daresbury, UK, 2001. [Google Scholar]
- Barber, R.W.; Gu, X.J.; Emerson, D.R. Simulation of Low Knudsen Number Isothermal Flow Past a Confined Spherical Particle in a Micro-Pipe. In Proceedings of the Second International Conference on Microchannels and Minichannels, Rochester, NY, USA, 17–19 June 2004; pp. 1–8. [Google Scholar]
- Stefanov, S.K.; Barber, R.W.; Ota, M.; Emerson, D.R. Comparison between Navier-Stokes and DSMC Calculations for Low Reynolds Number Slip Flow Past a Confined Microsphere. In AIP Conference Proceedings; American Institute of Physics: Bari, Italy, 2005; Volume 762, pp. 701–706. [Google Scholar]
- Carlson, D.J.; Hoglund, R.F. Particle Drag and Heat Transfer in Rocket Nozzles. AIAA J. 1964, 2, 1980–1984. [Google Scholar] [CrossRef]
- Emmons, H.W. Fundamentals of Gas Dynamics: Volume 3, High Speed Aerodynamics and Jet Propulsion; Princeton University Press: Princeton, NJ, USA, 1958. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figliola, N.; Schmidt, D.; Lee, J.-H. Pressure- and Size-Dependent Aerodynamic Drag Effects on Mach 0.3–2.2 Microspheres for High-Precision Micro-Ballistic Characterization. Appl. Sci. 2022, 12, 6622. https://doi.org/10.3390/app12136622
Figliola N, Schmidt D, Lee J-H. Pressure- and Size-Dependent Aerodynamic Drag Effects on Mach 0.3–2.2 Microspheres for High-Precision Micro-Ballistic Characterization. Applied Sciences. 2022; 12(13):6622. https://doi.org/10.3390/app12136622
Chicago/Turabian StyleFigliola, Nino, David Schmidt, and Jae-Hwang Lee. 2022. "Pressure- and Size-Dependent Aerodynamic Drag Effects on Mach 0.3–2.2 Microspheres for High-Precision Micro-Ballistic Characterization" Applied Sciences 12, no. 13: 6622. https://doi.org/10.3390/app12136622
APA StyleFigliola, N., Schmidt, D., & Lee, J.-H. (2022). Pressure- and Size-Dependent Aerodynamic Drag Effects on Mach 0.3–2.2 Microspheres for High-Precision Micro-Ballistic Characterization. Applied Sciences, 12(13), 6622. https://doi.org/10.3390/app12136622






