A Switched Variational Estimation Algorithm for Continuous Discrete Measurement Information Loss in Underwater Navigation: Linear versus Nonlinear
Abstract
:1. Introduction
- (1)
- A new method searching for the optimal solution is designed, in which the initial loss parameter makes a valuable contribution toward state estimation;
- (2)
- The problem of measurement information loss in a continuous discrete underwater navigation model (i.e., the state model is continuous and the measurement model is discrete) is effectively solved by the proposed SVEF algorithm;
- (3)
- In the VE method, linear or nonlinear filtering is employed to effectively determine the state vector; moreover, the measurement error covariance matrix and predicted error covariance matrix are accurately calculated.
2. Problem Statement
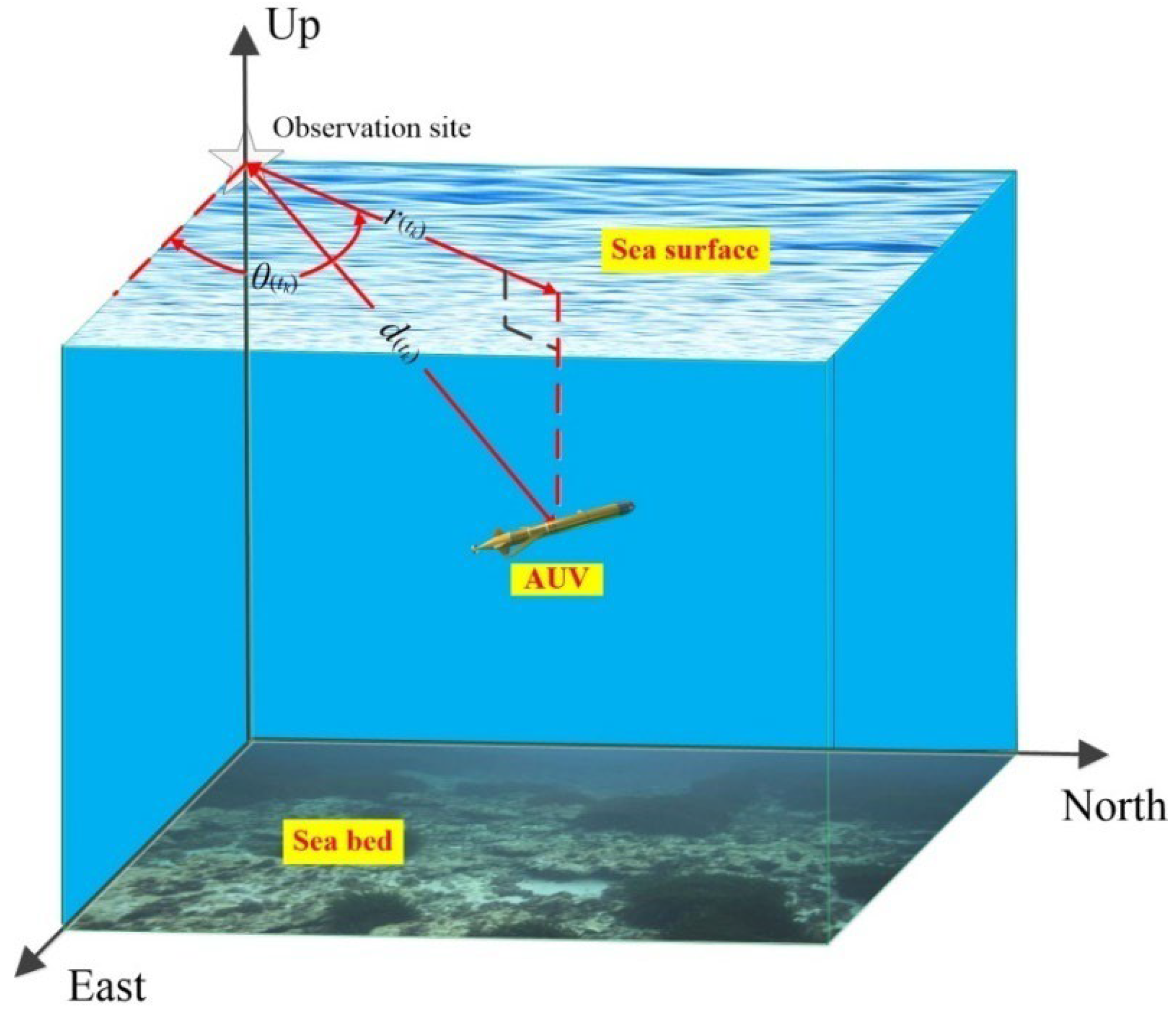
2.1. Underwater Navigation Model
2.2. Preliminaries of the Measurement Information Loss
3. Switched Variational Estimation Filtering in Underwater Navigation
3.1. Mixture Probabilistic Model
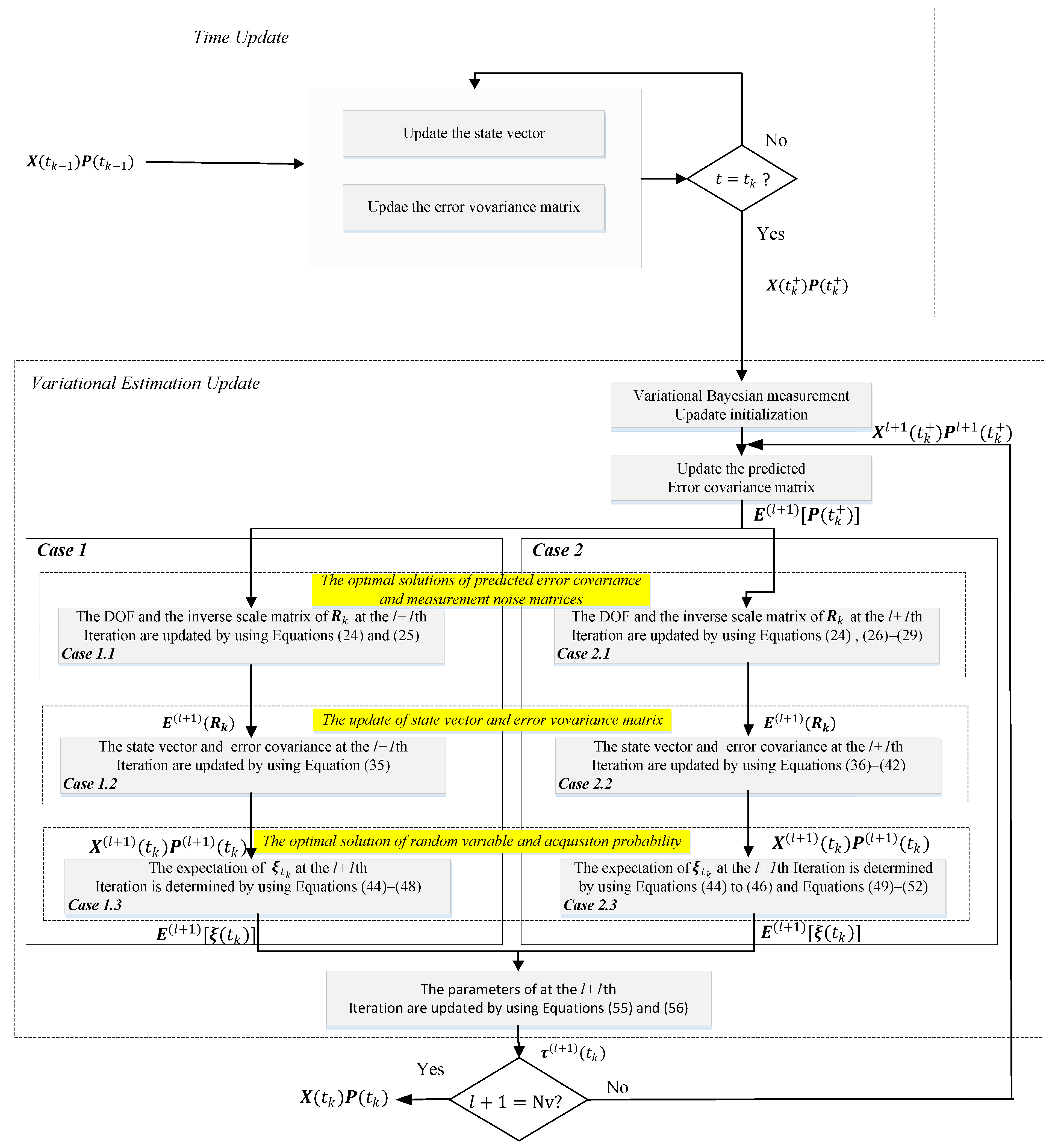
3.2. Proposed Optimal Variational Estimation in Navigation Information Acquisition
- (1)
- The optimal solutions of predicted error covariance and observation noise matrices.
- (2)
- The update of state vector and error covariance matrix.
- (3)
- The optimal solutions of the random variable and acquisition probability.
| Algorithm 1: The proposed switched variational estimation filtering algorithm. |
| Input:, , , . Time Update: for i = 0:0.01:1 Update and using Equations (15)–(17); end Variational Estimation Update: Variational estimation initialization: , . for l = 0: Nv − 1 (1) The optimal solutions of the predicted error covariance and measurement noise matrices. The DOF and inverse scale matrix of in iteration l + 1 are updated by using Equation (22). The update of the DOF and the inverse scale matrix of in iteration l + 1: Case 1.1 updated by using Equations (24) and (25). Case 2.1 updated by using Equations (24), (26)–(29). and are calculated by Equations (30)–(32). (2) The update of state vector and error covariance matrix in iteration l + 1. Case 1.2 updated by using Equation (35). Case 2.2 updated by using Equations (36)–(42). (3) The optimal solutions of the random variable and acquisition probability. The expectation of in iteration l + 1: Case 1.3 determined by using Equations (44)–(48). Case 2.3 determined by using Equations (44)–(46) and (49)–(52). The parameters of in iteration l + 1 are updated by using Equations (55)–(56) End Output: and . |
4. Experiments and Results
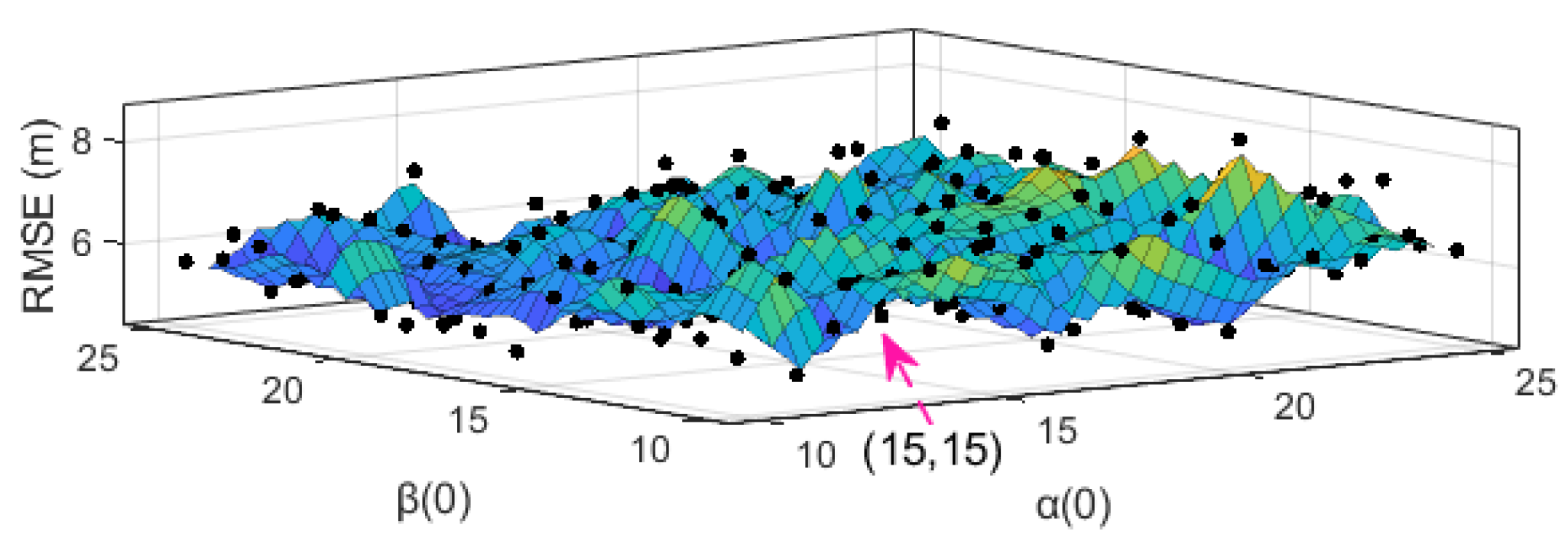
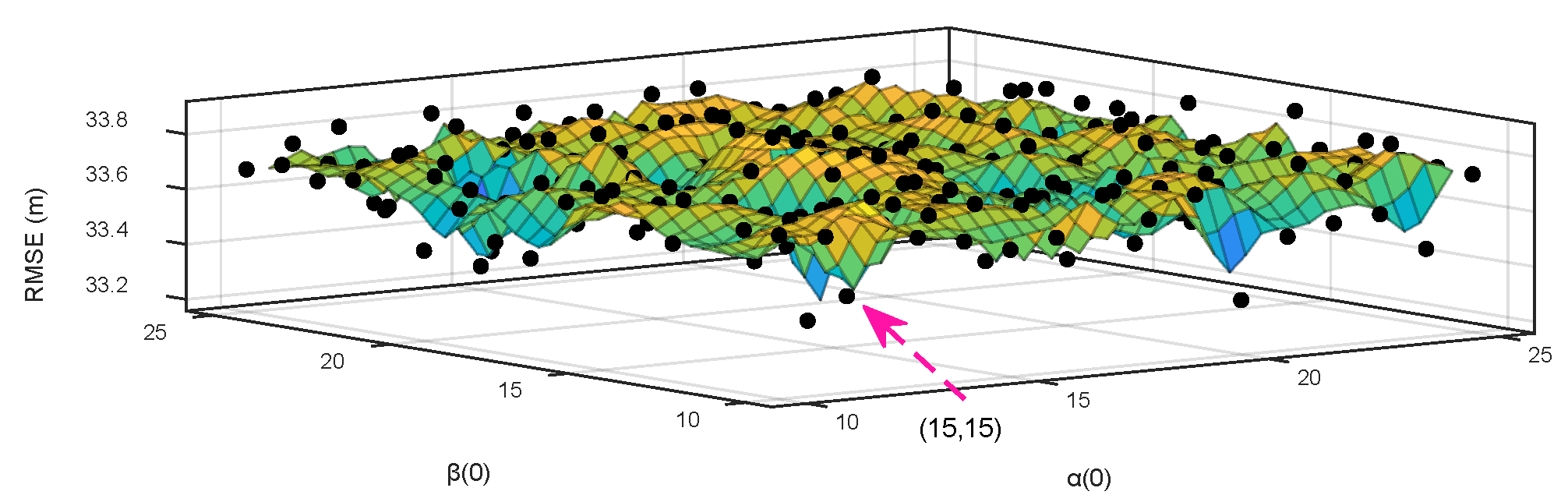
4.1. Selection of Initialization Values
4.2. Comparison of State Estimation Algorithms
- Case 1: The measurement model is linear
- Case 2: The measurement model is nonlinear
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Teeneti, C.R.; Truscott, T.T.; Beal, D.N.; Pantic, Z. Review of Wireless Charging Systems for Autonomous Underwater Vehicles. IEEE J. Oceanic. Eng. 2021, 46, 68–87. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, C.; He, B.; Guo, J.; Wang, D.; Lv, P.-F. Actuator fault diagnosis in autonomous underwater vehicle based on neural network. Sens. Actuator A Phys. 2021, 324, 112668. [Google Scholar] [CrossRef]
- Huang, H.; Tang, J.; Liu, C.; Zhang, B.; Wang, B. Variational Bayesian-Based Filter for Inaccurate Input in Underwater Navigation. IEEE Trans. Veh. Technol. 2021, 70, 8441–8452. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, M.; Cao, J.; Liu, Y.; Yu, R.; Cai, S. An Underwater Gravimetry Method Using Inertial Navigation System and Depth Gauge Based on Trajectory Constraint. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1510–1514. [Google Scholar] [CrossRef]
- Xiong, Z.; Cao, J.; Wu, M.; Cai, S.; Yu, R.; Wang, M. A Method for Underwater Dynamic Gravimetry Combining Inertial Navigation System, Doppler Velocity Log, and Depth Gauge. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1294–1298. [Google Scholar] [CrossRef]
- Donovan, G.T. Position Error Correction for an Autonomous Underwater Vehicle Inertial Navigation System (INS) Using a Particle Filter. IEEE J. Oceanic. Eng. 2012, 37, 431–445. [Google Scholar] [CrossRef]
- Lu, J.; Xie, L. Ocean Vehicle Inertial Navigation Method based on Dynamic Constraints. J. Navig. 2018, 71, 1553–1566. [Google Scholar] [CrossRef]
- Lv, P.-F.; He, B.; Guo, J. Position Correction Model Based on Gated Hybrid RNN for AUV Navigation. IEEE Trans. Veh. Technol. 2021, 70, 5648–5657. [Google Scholar] [CrossRef]
- Mahboub, V.; Mohammadi, D. A Constrained Total Extended Kalman Filter for Integrated Navigation. J. Navig. 2018, 71, 971–988. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Yang, D.; Xu, X. An IMM-UKF Aided SINS/USBL Calibration Solution for Underwater Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 3740–3747. [Google Scholar] [CrossRef]
- Wang, G.; Xu, X.; Zhang, T. M-M Estimation-Based Robust Cubature Kalman Filter for INS/GPS Integrated Navigation System. IEEE Trans. Instrum. Meas. 2021, 70, 9501511. [Google Scholar] [CrossRef]
- Karmozdi, A.; Hashemi, M.; Salarieh, H.; Alasty, A. INS-DVL Navigation Improvement Using Rotational Motion Dynamic Model of AUV. IEEE Sens. J. 2020, 20, 14329–14336. [Google Scholar] [CrossRef]
- Kepper, J.H.; Claus, B.C.; Kinsey, J.C. A Navigation Solution Using a MEMS IMU, Model-Based Dead-Reckoning, and One-Way-Travel-Time Acoustic Range Measurements for Autonomous Underwater Vehicles. IEEE J. Oceanic. Eng. 2019, 44, 664–682. [Google Scholar] [CrossRef]
- Song, S.; Liu, J.; Guo, J.; Wang, J.; Xie, Y.; Cui, J.-H. Neural-Network-Based AUV Navigation for Fast-Changing Environments. IEEE Internet Things J. 2020, 7, 9773–9783. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xu, B.; Wu, Z.; Chambers, J.A. A New Adaptive Extended Kalman Filter for Cooperative Localization. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 353–368. [Google Scholar] [CrossRef]
- Sabzevari, D.; Chatraei, A. INS/GPS Sensor Fusion based on Adaptive Fuzzy EKF with Sensitivity to Disturbances. IET Radar Sonar Navig. 2021, 15, 1535–1549. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Eberts, M.D.; El-Shafie, A. Performance Enhancement of MEMS-Based INS/GPS Integration for Low-Cost Navigation Applications. IEEE Trans. Veh. Technol. 2009, 58, 1077–1096. [Google Scholar] [CrossRef]
- Duník, J.; Biswas, S.K.; Dempster, A.G.; Pany, T.; Closas, P. State Estimation Methods in Navigation: Overview and Application. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 16–31. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, W.; Li, H.; Mo, Y.; Ni, W.; Huang, Q. A New Kind of Accurate Calibration Method for Robotic Kinematic Parameters Based on the Extended Kalman and Particle Filter Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 3337–3345. [Google Scholar] [CrossRef]
- Lyu, X.; Hu, B.; Li, K.; Chang, L. An Adaptive and Robust UKF Approach Based on Gaussian Process Regression-Aided Variational Bayesian. IEEE Sens. J. 2021, 21, 9500–9514. [Google Scholar] [CrossRef]
- Yang, Y.; Bin, L.; Xinjie, W.; Lijian, Y. Application of Adaptive Cubature Kalman Filter to In-Pipe Survey System for 3D Small-Diameter Pipeline Mapping. IEEE Sens. J. 2020, 20, 6331–6337. [Google Scholar] [CrossRef]
- Yang, H.; Rao, Y.; Li, L.; Liang, H.; Luo, T.; Luo, B. Dynamic Measurement of Well Inclination Based on UKF and Correlation Extraction. IEEE Sens. J. 2021, 21, 4887–4899. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, Y.; Guo, X.; Chen, X.; Cao, H.; Tang, J.; Li, J.; Liu, J. Seamless GPS/Inertial Navigation System Based on Self-Learning Square-Root Cubature Kalman Filter. IEEE Trans. Ind. Electron. 2021, 68, 499–508. [Google Scholar] [CrossRef]
- Zhang, L.; Li, S.; Zhang, E.; Chen, Q.; Guo, J. Improved square root adaptive cubature Kalman filter. IET Signal Process. 2019, 13, 641–649. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, J.; Zhang, J.; Yang, Y.; Song, R.; Chen, J.; Zhang, J. Attitude Estimation Fusing Quasi-Newton and Cubature Kalman Filtering for Inertial Navigation System Aided With Magnetic Sensors. IEEE Access 2018, 6, 28755–28767. [Google Scholar] [CrossRef]
- He, J.; Sun, C.; Zhang, B.; Wang, P. Variational Bayesian-Based Maximum Correntropy Cubature Kalman Filter with Both Adaptivity and Robustness. IEEE Sens. J. 2021, 21, 1982–1992. [Google Scholar] [CrossRef]
- Turlapaty, A.C. Variational Bayesian Estimation of Statistical Properties of Composite Gamma Log-Normal Distribution. IEEE Trans. Signal Process. 2020, 68, 6481–6492. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, B.; Zhao, C. Online Probabilistic Estimation of Sensor Faulty Signal in Industrial Processes and Its Applications. IEEE Trans. Ind. Electron. 2021, 68, 8853–8862. [Google Scholar] [CrossRef]
- Miao, Z.; Shi, H.; Zhang, Y.; Xu, F. Neural Network-Aided Variational Bayesian Adaptive Cubature Kalman Filtering for Nonlinear State Estimation. Meas. Sci. Technol. 2017, 28, 105003–105013. [Google Scholar] [CrossRef] [Green Version]
- Dong, P.; Jing, Z.; Leung, H.; Shen, K. Variational Bayesian Adaptive Cubature Information Filter Based on Wishart Distribution. IEEE Trans. Automat. Contr. 2017, 62, 6051–6057. [Google Scholar] [CrossRef]
- Xu, B.; Li, S.; Razzaqi, A.A.; Zhang, J. Cooperative Localization in Harsh Underwater Environment Based on the MC-ANFIS. IEEE Access 2019, 7, 55407–55421. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Yu, W.; Guan, X. Multiple Autonomous Underwater Vehicle Cooperative Localization in Anchor-Free Environments. IEEE J. Ocean. Eng. 2019, 44, 895–911. [Google Scholar] [CrossRef]
- Jørgensen, E.K.; Fossen, T.I.; Bryne, T.H.; Schjølberg, I. Underwater Position and Attitude Estimation Using Acoustic, Inertial, and Depth Measurements. IEEE J. Ocean. Eng. 2020, 45, 1450–1465. [Google Scholar] [CrossRef]
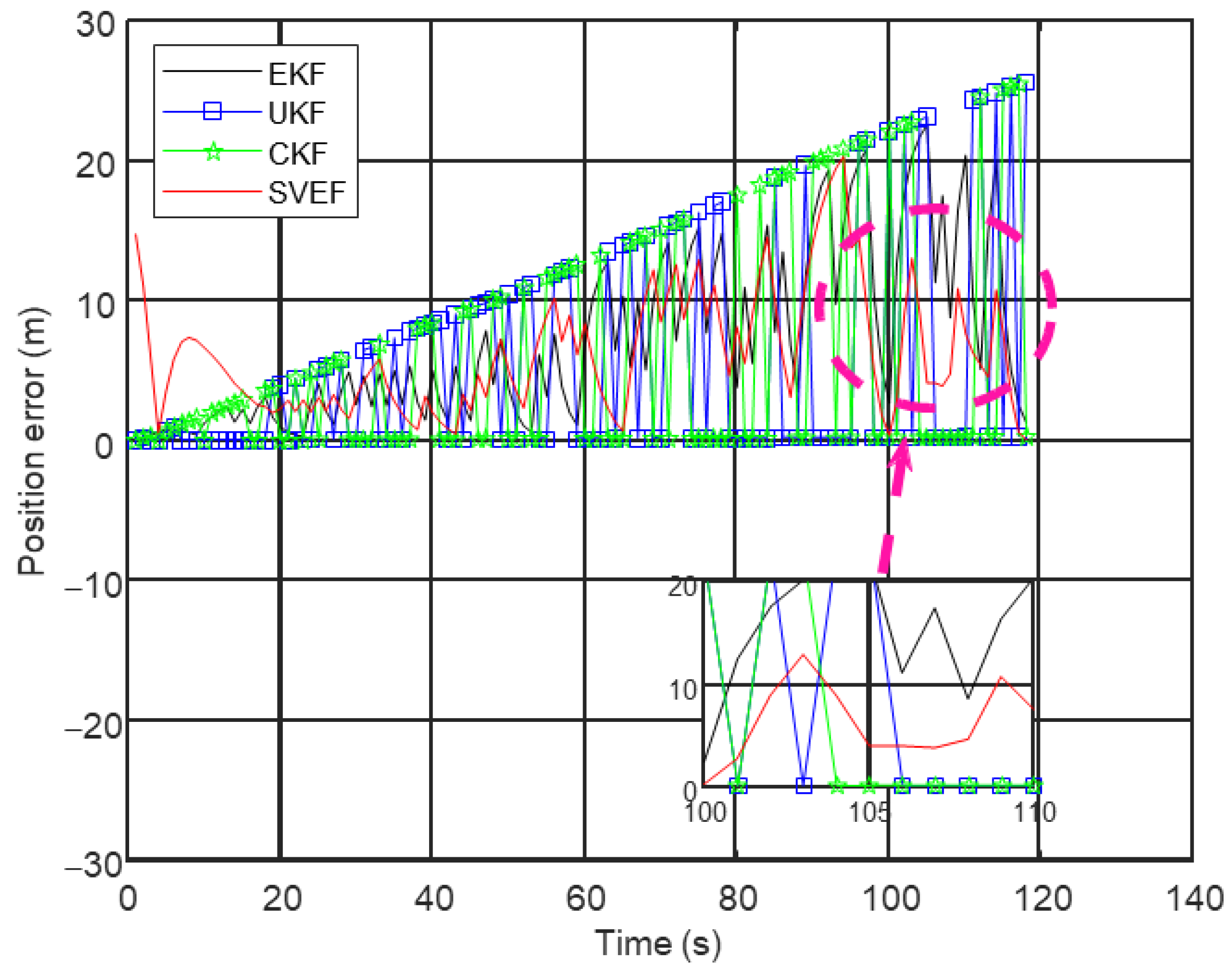
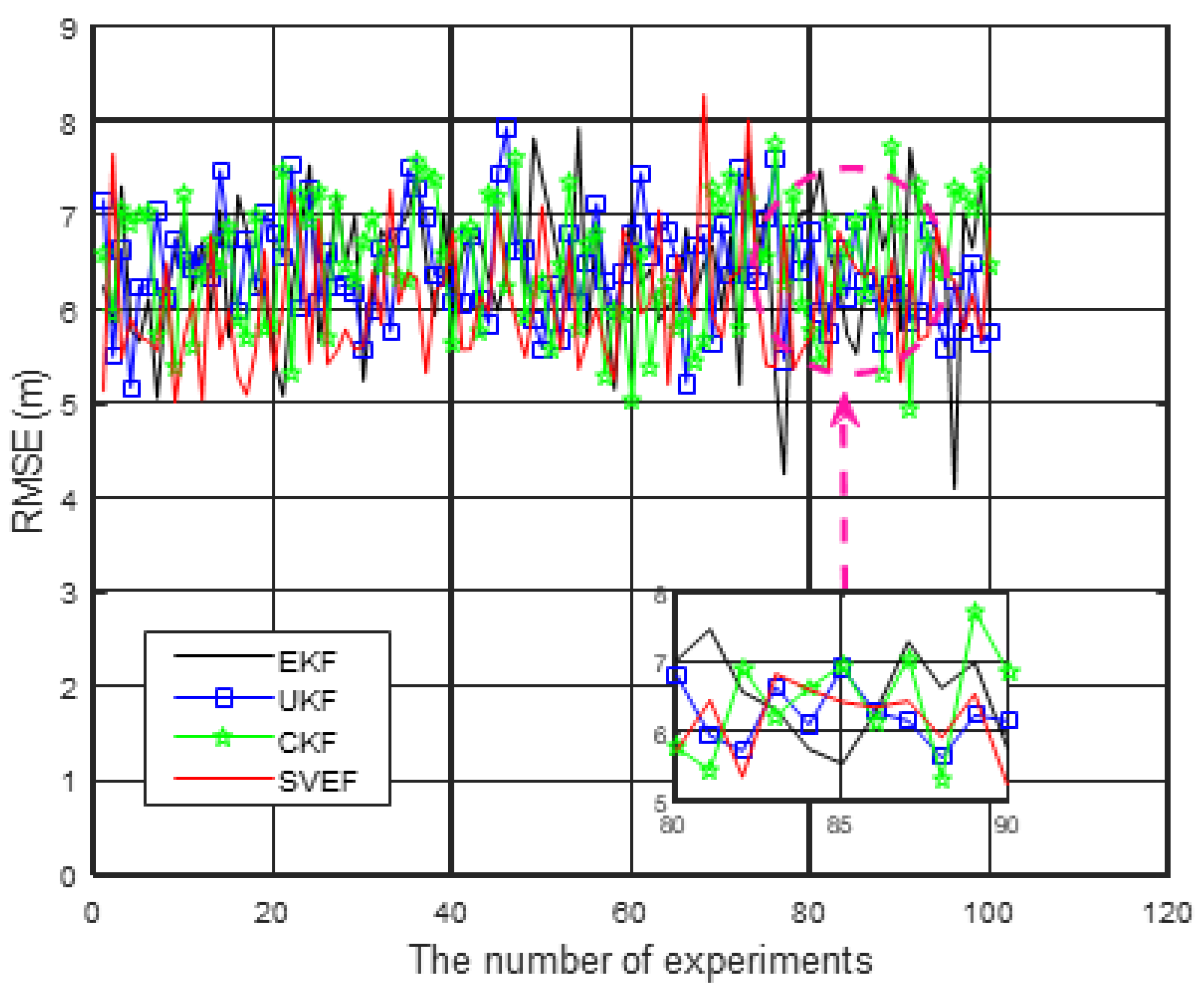
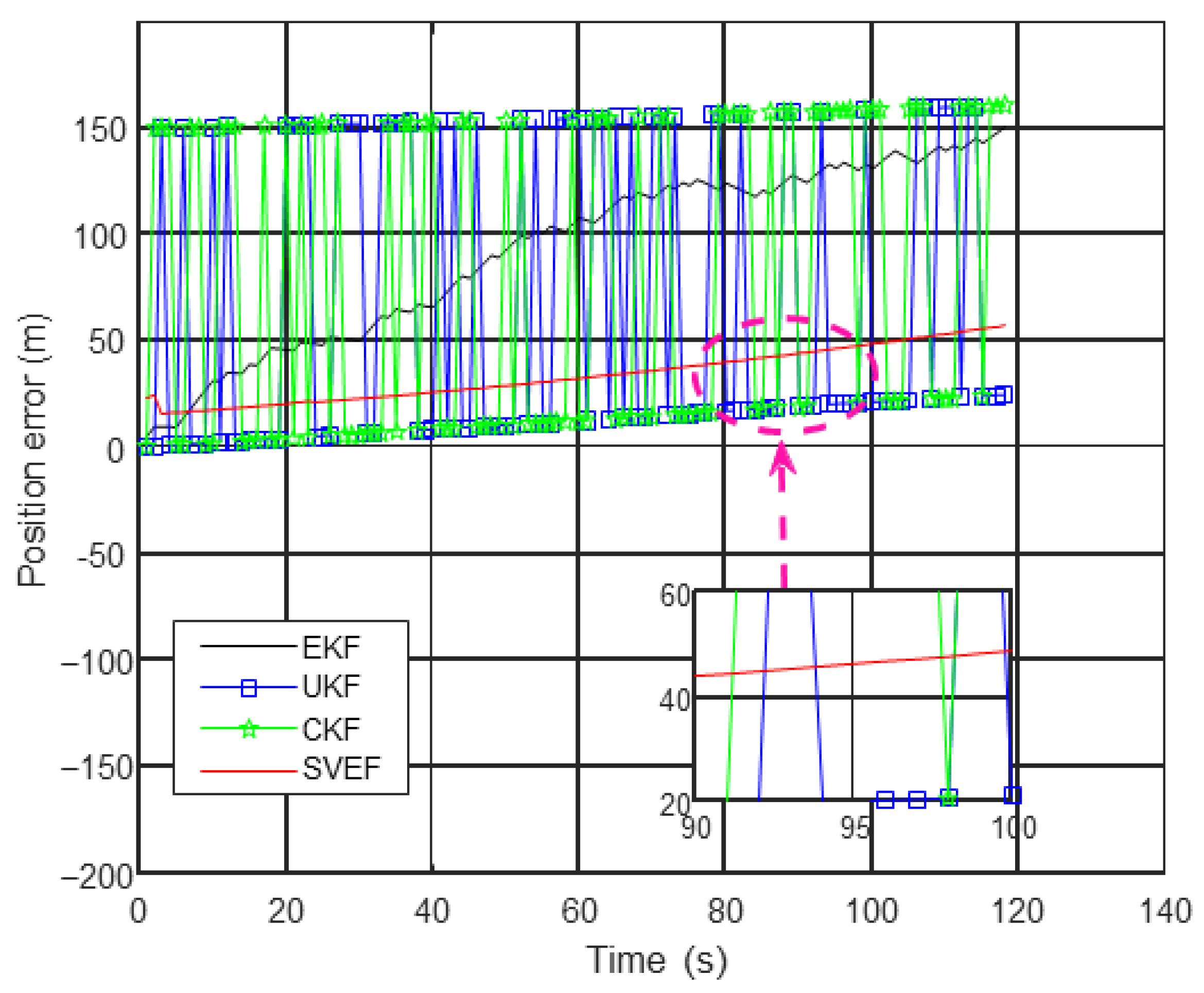
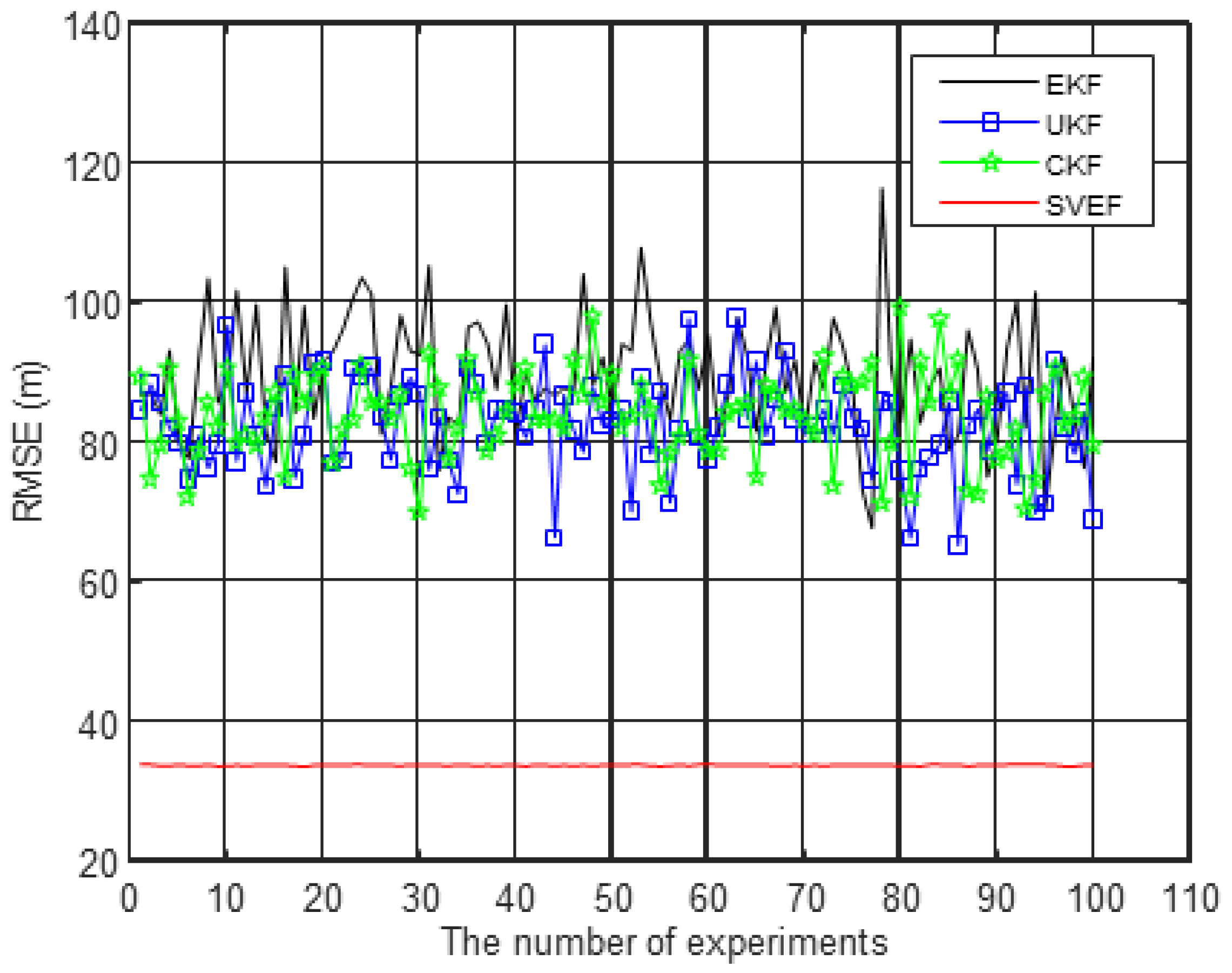
| Initialization Parameter | Value |
|---|---|
| Algorithms | EKF | UKF | CKF | SVEF |
|---|---|---|---|---|
| MC RMSE (m) | 6.6054 | 6.4225 | 6.5284 | 6.0907 |
| Algorithms | EKF | UKF | CKF | SVEF |
|---|---|---|---|---|
| MC RMSE (m) | 90.6664 | 84.0154 | 82.9580 | 33.6932 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Huang, H.; Ren, C. A Switched Variational Estimation Algorithm for Continuous Discrete Measurement Information Loss in Underwater Navigation: Linear versus Nonlinear. Appl. Sci. 2022, 12, 6663. https://doi.org/10.3390/app12136663
Song X, Huang H, Ren C. A Switched Variational Estimation Algorithm for Continuous Discrete Measurement Information Loss in Underwater Navigation: Linear versus Nonlinear. Applied Sciences. 2022; 12(13):6663. https://doi.org/10.3390/app12136663
Chicago/Turabian StyleSong, Xiang, Haoqian Huang, and Chunxiao Ren. 2022. "A Switched Variational Estimation Algorithm for Continuous Discrete Measurement Information Loss in Underwater Navigation: Linear versus Nonlinear" Applied Sciences 12, no. 13: 6663. https://doi.org/10.3390/app12136663
APA StyleSong, X., Huang, H., & Ren, C. (2022). A Switched Variational Estimation Algorithm for Continuous Discrete Measurement Information Loss in Underwater Navigation: Linear versus Nonlinear. Applied Sciences, 12(13), 6663. https://doi.org/10.3390/app12136663







