Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities
Abstract
:1. Introduction
- Transformation: We perform tensor decompositions as a preprocessing step to project the tensors within coherent segments into a more suitable space for reduction. We obtain core tensors (or coefficients) and bases. The tensor basis functions are similar to wavelets and/or local spatial frequencies, and are therefore good at expressing the correlations among the tensors.
- Autoencoder-based compression: AEs are trained on the transformed tensor coefficient space. Since tensor basis functions can take care of spatial correlation, AEs encode and decode tensor basis coefficients. We use AEs to obtain the encoded coefficients using standard loss measures and employ a quantization scheme to store the encoded coefficients.
- Error guarantees on PD: Error guarantees in the form of bounded reconstruction error are achieved by selectively applying error-bounded compressors on the residuals. (The residual is the difference between the reconstructed data of the AE and the PD). The residuals are processed with error-bounded lossy compressors to guarantee bounds on the overall PD error.
- QoI satisfaction: Preservation of QoI is addressed using constraint satisfaction on the reconstructed PD. After residual post-processing, we perform constrained optimization while minimizing the changes to the PD reconstruction. The parameters produced as a result of the QoI satisfaction step are quantized and stored with the encoded coefficients and residuals.
2. XGC Application
3. The Compression Framework
3.1. Reduction of the Primary Data
3.1.1. Data Transformation
3.1.2. The Autoencoder
3.1.3. Quantization of the Latent Space
3.1.4. Residual Post-Processing
3.2. Preservation of the Derived Quantities
3.2.1. Constraint Satisfaction
3.2.2. Quantization of the Lagrange Parameters
4. Experimental Results
4.1. Error Metrics
- NRMSE. Since the XGC dataset represents the velocity of electrons, the scale of the data is extremely large (∼10). Therefore, instead of using the Root Mean Squared Error (RMSE), we measure the error using the Normalized Root Mean Square Error (NRMSE), defined as follows:where x is the primary or original data (PD), is the reconstructed data, and N is the number of nodes. We will ensure that error bounds for PD are met. Some of these may be tight error bounds and some of them may be probabilistic and vary within the PD.
- Amount of Data Reduction. The key feature of the data reduction algorithms is the amount of reduction achieved. We measure the storage sizes of the compressed data and residuals, and Lagrange multipliers as well as the size of the models, Tucker bases, and the dictionaries of product quantizers. Once the machine architecture is fixed (after training), the decoder size becomes a fixed compression cost in terms of the size, and it should be included in the overall size when computing the compression levels. Tucker bases are fixed compression costs, since the decoded coefficients need to be projected back into the original data space. The product quantizer’s dictionaries for both compressed data and Lagrange multipliers are also fixed compression costs which need to be included in all calculations. Considering all the costs that are needed for the reconstruction, we compute the compression ratio (CR) defined as shown below:The in Equation (31) includes encoded coefficients of the AE, compressed residuals and quantized Lagrange multipliers. The encompasses the models of AE and MGARD, Tucker bases, and PQ dictionaries for the AE and Lagrange multipliers.
4.2. Baseline
4.3. Parameter Settings
4.4. Results
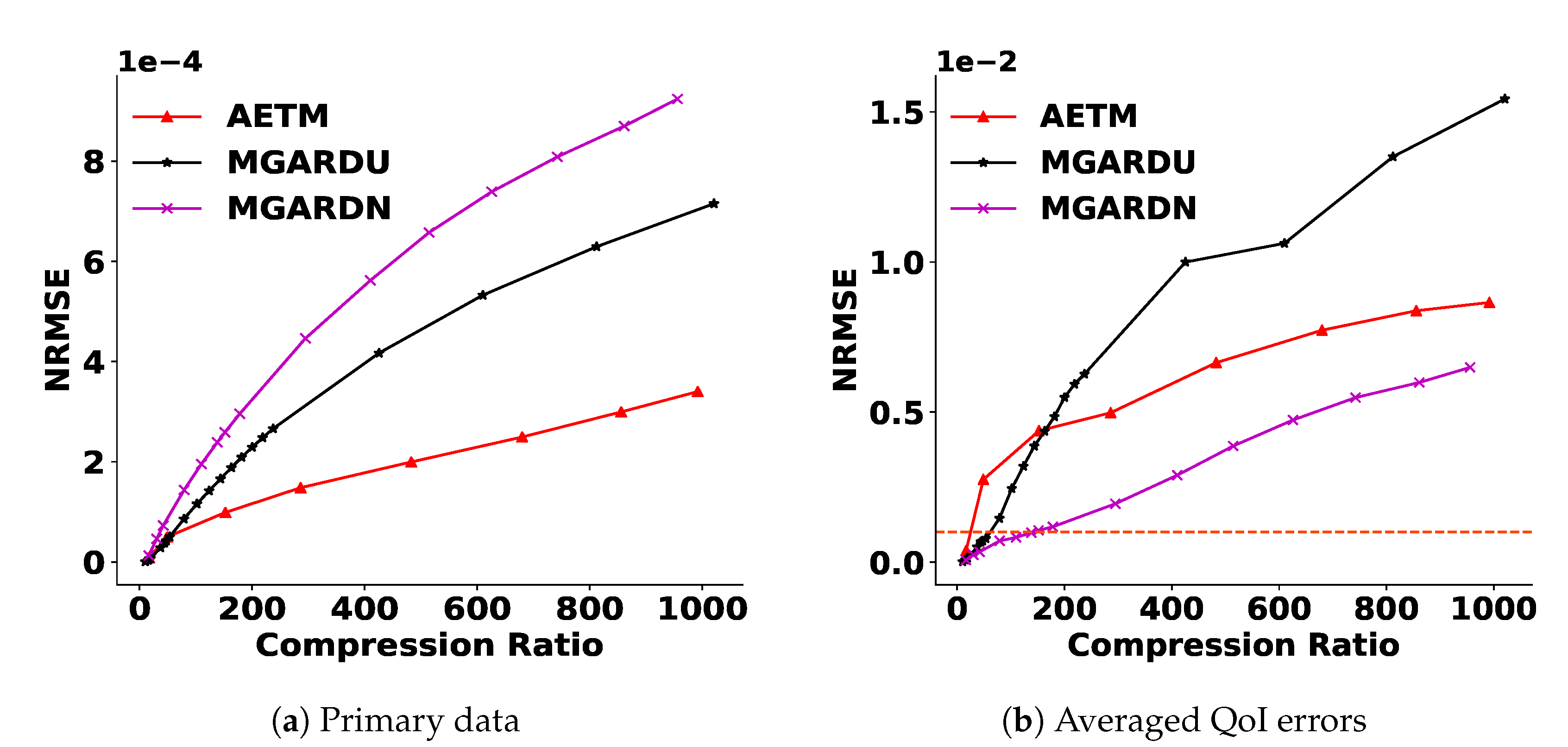
4.4.1. Reduction of the Primary Quantities
4.4.2. Satisfaction of Derived Quantities
4.4.3. Framework with Test Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Implementation Details
| Encoder | Decoder | |
|---|---|---|
| Layer | 1 FC | 1FC |
| Weight | ||
| Activation | Linear | Linear |
| Parameter | Setting |
|---|---|
| Epochs | 300 |
| Learning rate | 0.001 |
| Optimizer | Adam |
Appendix B. Algorithms

Appendix C. Computation Time
| AETMC | MGARD | ||
|---|---|---|---|
| AE Compression | Residual Post-Processing | Constraint Satisfaction | |
| 3 min | 3 min | 30 s | 5 min |
| Algorithm A1 AETMC. | |
Input:, , and : a 16,395 × 39 × 39 tensor per each cross-section. Each represents a 2D velocity histogram. There are eight cross-sections per each timestep and each cross-section has 16,395 nodes. : a 16,395 × 4 tensor representing four true QoI values of histograms computed using per each cross-section. : geometry metadata where in Equation (21). | |
|
|
References
- Foster, I. Computing Just What You Need: Online Data Analysis and Reduction at Extreme Scales. In Proceedings of the 2017 IEEE 24th International Conference on High Performance Computing (HiPC), Jaipur, India, 18–21 December 2017; p. 306. [Google Scholar] [CrossRef] [Green Version]
- Grois, D.; Marpe, D.; Mulayoff, A.; Itzhaky, B.; Hadar, O. Performance comparison of H.265/MPEG-HEVC, VP9 and H.264/MPEG-AVC encoders. In Proceedings of the 2013 Picture Coding Symposium (PCS), San Jose, CA, USA, 8–11 December 2013; pp. 394–397. [Google Scholar] [CrossRef]
- Lindstrom, P.; Isenburg, M. Fast and Efficient Compression of Floating-Point Data. IEEE Trans. Vis. Comput. Graph. 2006, 12, 1245–1250. [Google Scholar] [CrossRef] [PubMed]
- Collet, Y.; Kucherawy, M.S. Zstandard Compression and the ‘application/zstd’ Media Type. RFC 2021, 8878, 1–45. [Google Scholar] [CrossRef]
- Lindstrom, P. Error Distributions of Lossy Floating-Point Compressors; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2017. Technical Report LLNL-CONF-740547. Available online: https://www.osti.gov/servlets/purl/1526183 (accessed on 6 June 2022).
- Di, S.; Cappello, F. Fast Error-Bounded Lossy HPC Data Compression with SZ. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Chicago, IL, USA, 23–27 May 2016; pp. 730–739. [Google Scholar] [CrossRef]
- Tao, D.; Di, S.; Chen, Z.; Cappello, F. Significantly Improving Lossy Compression for Scientific Data Sets Based on Multidimensional Prediction and Error-Controlled Quantization. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Orlando, FL, USA, 29 May–2 June 2017; pp. 1129–1139. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Di, S.; Tao, D.; Li, S.; Li, S.; Guo, H.; Chen, Z.; Cappello, F. Error-Controlled Lossy Compression Optimized for High Compression Ratios of Scientific Datasets. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 438–447. [Google Scholar] [CrossRef]
- Lindstrom, P. Fixed-Rate Compressed Floating-Point Arrays. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2674–2683. [Google Scholar] [CrossRef] [PubMed]
- Ainsworth, M.; Tugluk, O.; Whitney, B.; Klasky, S. Multilevel techniques for compression and reduction of scientific data—The univariate case. Comput. Vis. Sci. 2018, 19, 65–76. [Google Scholar] [CrossRef]
- Ainsworth, M.; Tugluk, O.; Whitney, B.; Klasky, S. Multilevel techniques for compression and reduction of scientific data—The multivariate case. SIAM J. Sci. Comput. 2019, 41, A1278–A1303. [Google Scholar] [CrossRef]
- Ainsworth, M.; Tugluk, O.; Whitney, B.; Klasky, S. Multilevel techniques for compression and reduction of scientific data-quantitative control of accuracy in derived quantities. SIAM J. Sci. Comput. 2019, 41, A2146–A2171. [Google Scholar] [CrossRef]
- Ibarria, L.; Lindstrom, P.; Rossignac, J.; Szymczak, A. Out-of-core compression and decompression of large n-dimensional scalar fields. Comput. Graph. Forum 2003, 22, 343–348. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zuo, W.; Gu, S.; Zhao, D.; Zhang, D. Learning convolutional networks for content-weighted image compression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3214–3223. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Deep convolutional autoencoder-based lossy image compression. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 253–257. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Cai, C.; Gao, Y.; Su, S.; Wu, J. Variational autoencoder for low bit-rate image compression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2617–2620. Available online: https://openaccess.thecvf.com/content_cvpr_2018_workshops/papers/w50/Zhou_Variational_Autoencoder_for_CVPR_2018_paper.pdf (accessed on 6 June 2022).
- Liu, T.; Wang, J.; Liu, Q.; Alibhai, S.; Lu, T.; He, X. High-Ratio Lossy Compression: Exploring the Autoencoder to Compress Scientific Data. IEEE Trans. Big Data 2021. [Google Scholar] [CrossRef]
- Glaws, A.; King, R.; Sprague, M. Deep learning for in situ data compression of large turbulent flow simulations. Phys. Rev. Fluids 2020, 5, 114602. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef] [Green Version]
- Bar-Sinai, Y.; Hoyer, S.; Hickey, J.; Brenner, M.P. Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. USA 2019, 116, 15344–15349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bézenac, E.; Pajot, A.; Gallinari, P. Deep learning for physical processes: Incorporating prior scientific knowledge. J. Stat. Mech. Theory Exp. 2019, 2019, 124009. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D. Nonlinear Programming; Athena Scientific: Chestnut, NH, USA, 1999. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Dener, A.; Miller, M.A.; Churchill, R.M.; Munson, T.; Chang, C.S. Training neural networks under physical constraints using a stochastic augmented Lagrangian approach. arXiv 2020, arXiv:2009.07330. [Google Scholar] [CrossRef]
- Miller, M.A.; Churchill, R.M.; Dener, A.; Chang, C.S.; Munson, T.; Hager, R. Encoder–decoder neural network for solving the nonlinear Fokker–Planck–Landau collision operator in XGC. J. Plasma Phys. 2021, 87, 905870211. [Google Scholar] [CrossRef]
- Beucler, T.; Pritchard, M.; Rasp, S.; Ott, J.; Baldi, P.; Gentine, P. Enforcing analytic constraints in neural networks emulating physical systems. Phys. Rev. Lett. 2021, 126, 098302. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Ku, S.; Chang, C.; Diamond, P. Full-f gyrokinetic particle simulation of centrally heated global ITG turbulence from magnetic axis to edge pedestal top in a realistic tokamak geometry. Nucl. Fusion 2009, 49, 115021. [Google Scholar] [CrossRef]
- Chang, C.; Ku, S. Spontaneous rotation sources in a quiescent tokamak edge plasma. Phys. Plasmas 2008, 15, 062510. [Google Scholar] [CrossRef]
- Hager, R.; Chang, C.S.; Ferraro, N.M.; Nazikian, R. Gyrokinetic study of collisional resonant magnetic perturbation (RMP)-driven plasma density and heat transport in tokamak edge plasma using a magnetohydrodynamic screened RMP field. Nucl. Fusion 2019, 59. [Google Scholar] [CrossRef]
- Tucker, L. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Sheehan, B.N.; Saad, Y. Higher Order Orthogonal Iteration of Tensors (HOOI) and its Relation to PCA and GLRAM. In Proceedings of the 2007 SIAM International Conference on Data Mining (SDM), Minneapolis, MN, USA, 26–28 April 2007. [Google Scholar] [CrossRef] [Green Version]
- Jégou, H.; Douze, M.; Schmid, C. Product Quantization for Nearest Neighbor Search. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 117–128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gray, R. Vector quantization. IEEE ASSP Mag. 1984, 1, 4–29. [Google Scholar] [CrossRef]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Censor, Y.; Lent, A. An iterative row-action method for interval convex programming. J. Optim. Theory Appl. 1981, 34, 321–353. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Dennis, J.; Moré, J. Quasi-Newton Methods, Motivation and Theory. SIAM Rev. 1977, 19, 46–89. [Google Scholar] [CrossRef] [Green Version]
- Rebut, P.H. ITER: The first experimental fusion reactor. Fusion Eng. Des. 1995, 30, 85–118. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 8026–8037. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar] [CrossRef]






| Acronyms | Meaning |
|---|---|
| PD | Primary data (original data) |
| QoI | Quantities of interest |
| AE | Autoencoder |
| PQ | Product quantizer |
| AET | Combination of Tucker decomposition, AE, and PQ |
| AETM | AET followed by MGARD for residual post-processing |
| AETMC | AETM followed by constraint satisfaction for QoI preservation |
| MGARDU | MGARD uniform |
| MGARDN | MGARD non-uniform |
| Reduction | Components | Parameters | |||
|---|---|---|---|---|---|
| PD | AET Compression | Bottleneck layer | 5 | ⋯ | 300 |
| PQ bits | 4 | ⋯ | 12 | ||
| Residual post-processing | PD threshold | ⋯ | |||
| MGARD error bound | ⋯ | ||||
| QoI | Lagrange Multipliers | PQ bits | 6 | ⋯ | 10 |
| Framework | PD Error Increase |
|---|---|
| AETMC (6) | 10 |
| AETMC (8) | 9.4 |
| AETMC (10) | 9.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Gong, Q.; Choi, J.; Banerjee, T.; Klasky, S.; Ranka, S.; Rangarajan, A. Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities. Appl. Sci. 2022, 12, 6718. https://doi.org/10.3390/app12136718
Lee J, Gong Q, Choi J, Banerjee T, Klasky S, Ranka S, Rangarajan A. Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities. Applied Sciences. 2022; 12(13):6718. https://doi.org/10.3390/app12136718
Chicago/Turabian StyleLee, Jaemoon, Qian Gong, Jong Choi, Tania Banerjee, Scott Klasky, Sanjay Ranka, and Anand Rangarajan. 2022. "Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities" Applied Sciences 12, no. 13: 6718. https://doi.org/10.3390/app12136718
APA StyleLee, J., Gong, Q., Choi, J., Banerjee, T., Klasky, S., Ranka, S., & Rangarajan, A. (2022). Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities. Applied Sciences, 12(13), 6718. https://doi.org/10.3390/app12136718







