Getting over High-Dimensionality: How Multidimensional Projection Methods Can Assist Data Science
Abstract
:1. Introduction
2. Method of the Systematic Review
Literature Search Procedure
- Papers published in peer-reviewed journals as articles and available online in English are the priority sources. In addition to these papers, we extended our scope to conference proceedings, arXiv e-Prints, thesis, dissertations, and books;
- Papers explicitly employ multidimensional data and multidimensional projection techniques. Then, we excluded those articles that only list multidimensional projection in keywords, allude to multidimensional data as datasets, or apply multidimensional projection without further explanation or reference to the specific methodology employed to processing and presenting the information.
3. Ground Theory
3.1. Data Multidimensionality
3.2. Basic Terminology
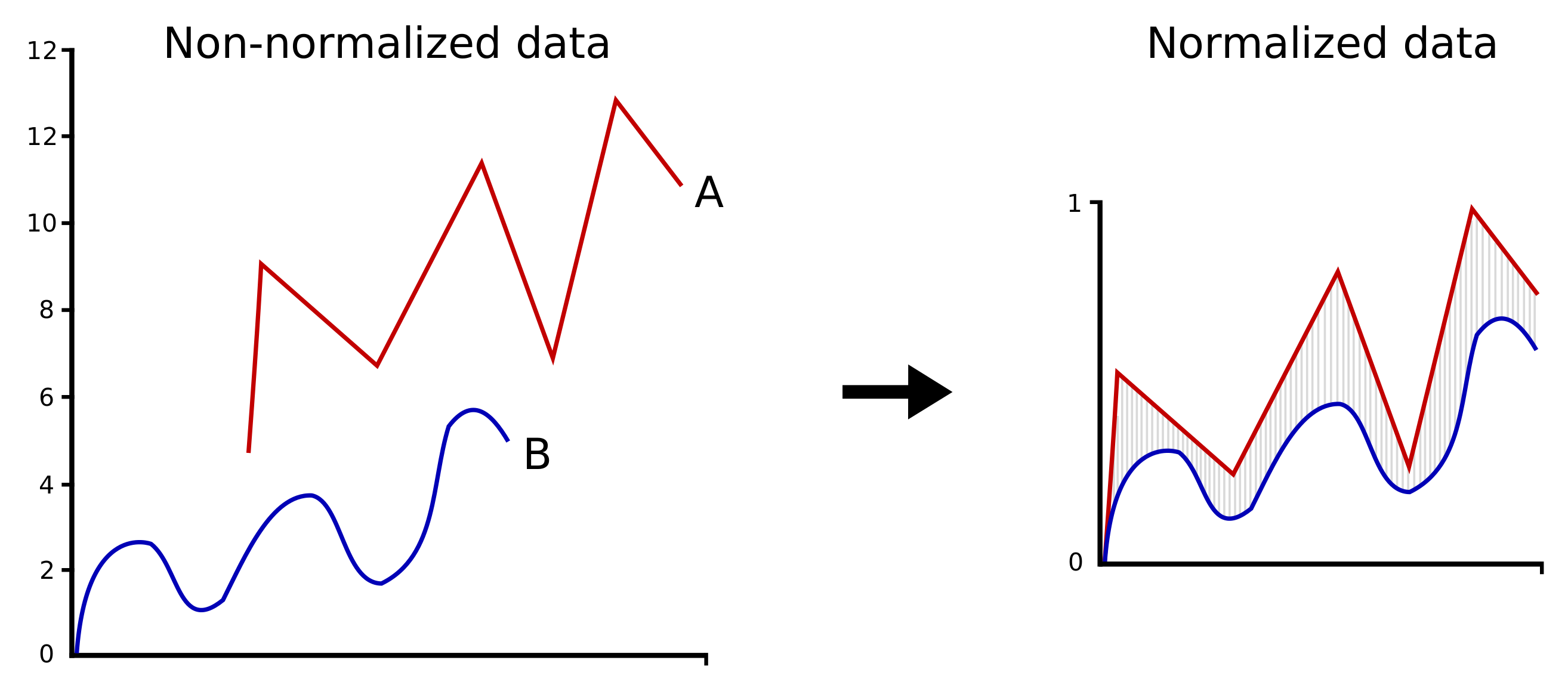
3.3. Multidimensional Projection
3.4. Taxonomies Used in the Multidimensional Projection Area
- (I)
- According to the transformation type
- (II)
- According to the projection nature
- (III)
- Other classifications
3.5. Evaluation of Projected Spaces
3.6. Influence of Graphical Perception and Visual Properties in Projection Analysis
- Proximity principle—visual elements close in the visual space are preattentive (intrinsic and uncontrolled) processed as a group that shares similar features, even if instances are grouped in a not explicit way;
- Similarity principle—elements represented by visual structures that share similar features (size, color, orientation, symmetry, parallelism) are perceptually grouped;
- “Common fate” principle—visual elements that undergo similar visual transformations tend to be mentally grouped. The dynamism of movement helps the viewer to perceive which objects are related to the same action;
- Closure principle—elements delimited in areas with clear contours tend to be visually grouped, even if they are not entirely continuous.
4. Multidimensional Projection Approaches and Domains
4.1. Principal Component Analysis
4.2. Multidimensional Scaling
4.3. Sammon’s Mapping and Related Projections
4.4. Isometric Feature Mapping
4.5. FastMap
4.6. Force-Based Placement
4.7. Stochastic Neighbor Embedding
4.8. Least Square Projection
4.9. Part-Linear Multidimensional Projection
4.10. Local Affine Multidimensional Projection
4.11. Hierarchical Approaches
4.12. Local Convex Hull
4.13. Uniform Manifold Approximation for Dimension Reduction
4.14. TopoMap
4.15. Graph Regularization Multidimensional Projection
4.16. SHAP Clustering
5. Discussions about the Multidimensional Projection Techniques
5.1. Real Data Applications
5.1.1. Text Mining Data
5.1.2. Bio-Informatics (Cancer Classification Data)
6. Challenges, Open Questions, and Future Research Directions
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Javed, W.; McDonnel, B.; Elmqvist, N. Graphical Perception of Multiple Time Series. IEEE Trans. Vis. Comput. Graph. 2010, 16, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Shneiderman, B. The Eyes Have It: A Task by Data Type Taxonomy for Information Visualizations. In Proceedings of the 1996 IEEE Symposium on Visual Languages, VL’96, Boulder, CO, USA, 3–6 September 1996; IEEE Computer Society: Washington, DC, USA, 1996; p. 336. [Google Scholar]
- Heer, J.; Kong, N.; Agrawala, M. Sizing the Horizon: The Effects of Chart Size and Layering on the Graphical Perception of Time Series Visualizations. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems CHI’09, Boston, MA, USA, 4–9 April 2009; ACM: New York, NY, USA, 2009; pp. 1303–1312. [Google Scholar]
- Chi, E.H. A Framework for Visualization Information; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Telea, A.C. Data Visualization: Principles and Practice, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Fadel, S.G.; Fatore, F.M.; Duarte, F.S.L.G.; Paulovich, F.V. LoCH: A neighborhood-based multidimensional projection technique for high-dimensional sparse spaces. Neurocomputing 2015, 150, 546–556. [Google Scholar] [CrossRef]
- Nonato, L.G.; Aupetit, M. Multidimensional projection for visual analytics: Linking techniques with distortions, tasks, and layout enrichment. IEEE Trans. Vis. Comput. Graph. 2018, 25, 2650–2673. [Google Scholar] [CrossRef] [PubMed]
- Cantareira, G.D.; Etemad, E.; Paulovich, F.V. Exploring Neural Network Hidden Layer Activity Using Vector Fields. Information 2020, 11, 426. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Nonato, L.G.; Minghim, R.; Levkowitz, H. Least Square Projection: A Fast High-Precision Multidimensional Projection Technique and Its Application to Document Mapping. IEEE Trans. Vis. Comput. Graph. 2008, 14, 564–575. [Google Scholar] [CrossRef] [PubMed]
- Paulovich, F.V.; Minghim, R. HiPP: A Novel Hierarchical Point Placement Strategy and Its Application to the Exploration of Document Collections. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1229–1236. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Moraes, M.L.; Maki, R.M.; Ferreira, M.; Oliveira, O.N.; de Oliveira, M.C.F. Information visualization techniques for sensing and biosensing. Anal. R. Soc. Chem. 2011, 136, 1344–1350. [Google Scholar] [CrossRef]
- Joia, P.; Coimbra, D.; Cuminato, J.A.; Paulovich, F.V.; Nonato, L.G. Local Affine Multidimensional Projection. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2563–2571. [Google Scholar] [CrossRef]
- Berkhin, P. A Survey of Clustering Data Mining Techniques; Springer: Berlin/Heidelberg, Germany, 2006; pp. 25–71. [Google Scholar]
- Lee, J.; Verleysen, M. Nonlinear Dimensionality Reduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Buja, A.; Swayne, D.F.; Littman, M.L.; Dean, N.; Hofmann, H.; Chen, L. Data Visualization With Multidimensional Scaling. J. Comput. Graph. Stat. 2008, 17, 444–472. [Google Scholar] [CrossRef]
- Maaten, L.V.D.; Postma, E.; Herik, J.V.D. Dimensionality Reduction: A Comparative Review. J. Mach. Learn Res. 2009, 10, 13. [Google Scholar]
- Osipyan, H.; Kruliš, M.; Marchand-Maillet, S. A Survey of CUDA-based Multidimensional Scaling on GPU Architecture. In Proceedings of the 2015 Imperial College Computing Student Workshop (ICCSW 2015), London, UK, 24–25 September 2015; Schulz, C., Liew, D., Eds.; Schloss Dagstuhl—Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2015; Volume 49, pp. 37–45. [Google Scholar]
- Sacha, D.; Zhang, L.; Sedlmair, M.; Lee, J.A.; Peltonen, J.; Weiskopf, D.; North, S.C.; Keim, D.A. Visual Interaction with Dimensionality Reduction: A Structured Literature Analysis. IEEE Trans. Vis. Comput. Graph. 2017, 23, 241–250. [Google Scholar] [CrossRef] [Green Version]
- Konyha, Z.; Lez, A.; Matković, K.; Jelović, M.; Hauser, H. Interactive Visual Analysis of Families of Curves Using Data Aggregation and Derivation. In Proceedings of the 12th International Conference on Knowledge Management and Knowledge Technologies, i-KNOW’12, Graz, Austria, 5–7 September 2012; ACM: New York, NY, USA, 2012; pp. 24:1–24:8. [Google Scholar]
- Fua, Y.H.; Ward, M.O.; Rundensteiner, E.A. Hierarchical Parallel Coordinates for Exploration of Large Datasets. In Proceedings of the Conference on Visualization’99: Celebrating Ten Years, VIS’99, Los Alamitos, CA, USA, 24–29 October 1999; IEEE Computer Society Press: Los Alamitos, CA, USA, 1999; pp. 43–50. [Google Scholar]
- Ware, C. Information Visualization: Perception for Design, 2nd ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2004. [Google Scholar]
- Pudil, P.; Novovicova, J. Novel Methods for Subset Selection with Respect to Problem Knowledge. IEEE Intell. Syst. 1998, 13, 66–74. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Kirby, M. Geometric Data Analysis: An Empirical Approach to Dimensionality Reduction and the Study of Patterns, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Tejada, E.; Minghim, R.; Nonato, L.G. On Improved Projection Techniques to Support Visual Exploration of Multidimensional Data Sets. Inf. Vis. 2003, 2, 218–231. [Google Scholar] [CrossRef]
- Cox, T.F.; Cox, M.A.A. Multidimensional Scaling, 2nd ed.; Chapman and Hall–CRC: New York, NY, USA, 2000. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Zezula, P.; Amato, G.; Dohnal, V.; Batko, M. Similarity Search: The Metric Space Approach, 1st ed.; Advances in Database Systems, Book 32; Springer Publishing Company, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Paulovich, F.V. Mapeamento de Dados Multi-Dimensionais-Integrando Mineração e Visualização. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2008. [Google Scholar]
- Ward, M.O.; Grinstein, G.; Keim, D. Interactive Data Visualizaton: Foundations, Techniques, and Applications, 2nd ed.; CRC Press: New York, NY, USA, 2015; p. 578. [Google Scholar]
- Keogh, E.; Kasetty, S. On the Need for Time Series Data Mining Benchmarks: A Survey and Empirical Demonstration. Data Min. Knowl. Discov. 2003, 7, 349–371. [Google Scholar] [CrossRef]
- Law, M.H.C.; Jain, A.K. Incremental Nonlinear Dimensionality Reduction by Manifold Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 377–391. [Google Scholar] [CrossRef]
- Kruskal, J.B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Heulot, N.; Fekete, J.D.; Aupetit, M. Visualizing dimensionality reduction artifacts: An evaluation. arXiv 2017, arXiv:1705.05283. [Google Scholar]
- Rousseeuw, P. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Coimbra, D.B. Multidimensional Projections for the Visual Exploration of Multimedia Data. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2016. [Google Scholar]
- Marcilio, W.E.; Eler, D.M.; Garcia, R.E. An approach to perform local analysis on multidimensional projection. In Proceedings of the 2017 30th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Niteroi, Brazil, 17–18 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 351–358. [Google Scholar]
- Bertini, E.; Tatu, A.; Keim, D. Quality Metrics in High-Dimensional Data Visualization: An Overview and Systematization. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2203–2212. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S.; McGill, R. Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods. J. Am. Stat. Assoc. 1984, 79, 531–554. [Google Scholar] [CrossRef]
- Wagemans, J.; Elder, J.H.; Kubovy, M.; Palmer, S.E.; Peterson, M.A.; Singh, M.; Heydt, R.V.D. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure-ground organization. Psychol. Bull. 2012, 138, 1172–1217. [Google Scholar] [CrossRef] [Green Version]
- Becker, R.A.; Cleveland, W.S. Brushing Scatterplots. Technometrics 1987, 29, 127–142. [Google Scholar] [CrossRef]
- Alexandrina, E.C.; Ortigossa, E.S.; Lui, E.S.; Gonçalves, J.A.S.; Corrêa, N.A.; Nonato, L.G.; Aguiar, M.L. Analysis and visualization of multidimensional time series: Particulate matter (PM10) from São Carlos-SP (Brazil). Atmos. Pollut. Res. 2019, 10, 1299–1311. [Google Scholar] [CrossRef]
- McLachlan, P.; Munzner, T.; Koutsofios, E.; North, S. LiveRAC: Interactive Visual Exploration of System Management Time-series Data. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, CHI’08, Florence, Italy, 5–10 April 2008; ACM: New York, NY, USA, 2008; pp. 1483–1492. [Google Scholar]
- Jugel, U.; Jerzak, Z.; Hackenbroich, G.; Markl, V. M4: A Visualization-oriented Time Series Data Aggregation. Proc. Very Large Database Endow. 2014, 7, 797–808. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2002. [Google Scholar]
- Li, L.; Su, X.; Zhang, Y.; Lin, Y.; Li, Z. Trend Modeling for Traffic Time Series Analysis: An Integrated Study. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3430–3439. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control, 2nd ed.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Torgerson, W.S. Multidimensional scaling: I. Theory and method. Psychometrika 1952, 17, 401–419. [Google Scholar] [CrossRef]
- Silva, V.D.; Tenenbaum, J.B. Sparse Multidimensional Scaling Using Landmark Points; Technical Report; Stanford University: Stanford, CA, USA, 2004. [Google Scholar]
- Brandes, U.; Pich, C. Eigensolver Methods for Progressive Multidimensional Scaling of Large Data. In Proceedings of the 14th International Conference on Graph Drawing, GD’06, Tübingen, Germany, 18–20 September 2007; Springer: Berlin, Heidelberg, 2007; pp. 42–53. [Google Scholar]
- Sammon, J.W. A Nonlinear Mapping for Data Structure Analysis. IEEE Trans. Comput. 1969, 18, 401–409. [Google Scholar] [CrossRef]
- Pekalska, E.; de Ridder, D.; Duin, R.P.; Kraaijveld, M.A. A new method of generalizing Sammon mapping with application to algorithm speed-up. In Proceedings of the 5th Annual Conference of the Advanced School for Computing and Imaging, ASCI’99, Heijen, The Netherlands, 15–17 June 1999; Delft: Heijen, The Netherlands, 1999; pp. 221–228. [Google Scholar]
- Tenenbaum, J.B.; Silva, V.d.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Doraiswamy, H.; Tierny, J.; Silva, P.J.; Nonato, L.G.; Silva, C. TopoMap: A 0-dimensional homology preserving projection of high-dimensional data. IEEE Trans. Vis. Comput. Graph. 2020, 27, 561–571. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, M.; Schwartz, E.L. The Isomap Algorithm and Topological Stability. Science 2002, 295, 7a. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, V.D.; Tenenbaum, J.B. Global Versus Local Methods in Nonlinear Dimensionality Reduction. In Proceedings of the 15th International Conference on Neural Information Processing Systems, NIPS’02, Vancouver, BC, Canada, 9–14 December 2002; MIT Press: Cambridge, MA, USA, 2002; pp. 721–728. [Google Scholar]
- Faloutsos, C.; Lin, K.I. FastMap: A Fast Algorithm for Indexing, Data-mining and Visualization of Traditional and Multimedia Datasets. ACM SIGMOD Rec. 1995, 24, 163–174. [Google Scholar] [CrossRef]
- Chalmers, M. A Linear Iteration Time Layout Algorithm for Visualising High-dimensional Data. In Proceedings of the 7th Conference on Visualization’96, VIS ’96, San Francisco, CA, USA, 27 October–1 November 1996; IEEE Computer Society Press: Los Alamitos, CA, USA, 1996; p. 127. [Google Scholar]
- Morrison, A.; Ross, G.; Chalmers, M. A Hybrid Layout Algorithm for Sub-Quadratic Multidimensional Scaling. In Proceedings of the IEEE Symposium on Information Visualization, INFOVIS’02, Boston, MA, USA, 27 October–1 November 2002; IEEE Computer Society: Washington, DC, USA, 2002; p. 152. [Google Scholar]
- Brodbeck, D.; Girardin, L. Combining topological clustering and multidimensional scaling for visualising large data sets. In Proceedings of the IEEE Information Visualization 1998, Research Triangle Park, NC, USA, 19–20 October 1998; pp. 1–4. [Google Scholar]
- Ingram, S.; Munzner, T.; Olano, M. Glimmer: Multilevel MDS on the GPU. IEEE Trans. Vis. Comput. Graph. 2009, 15, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.; Roweis, S. Stochastic Neighbor Embedding. In Proceedings of the 15th International Conference on Neural Information Processing Systems, NIPS’02. Vancouver, BC, Canada, 9–14 December 2002; MIT Press: Cambridge, MA, USA, 2002; pp. 857–864. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Maaten, L.V.D. Accelerating t-SNE Using Tree-based Algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lee, J.A.; Verleysen, M. Shift-invariant similarities circumvent distance concentration in stochastic neighbor embedding and variants. Procedia Comput. Sci. 2011, 4, 538–547. [Google Scholar] [CrossRef] [Green Version]
- Wattenberg, M.; Viégas, F.; Johnson, I. How to use t-SNE effectively. Distill 2016, 1, e2. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Eler, D.M.; Poco, J.; Botha, C.P.; Minghim, R.; Nonato, L.G. Piecewise Laplacian-based Projection for Interactive Data Exploration and Organization. In Proceedings of the 13th Eurographics/IEEE—VGTC Conference on Visualization, EuroVis’11, Bergen, Norway, 1–3 June 2011; The Eurographs Association and John Wiley & Sons, Ltd.: Chichester, UK, 2011; pp. 1091–1100. [Google Scholar]
- Paulovich, F.V.; Silva, C.T.; Nonato, L.G. Two-Phase Mapping for Projecting Massive Data Sets. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1281–1290. [Google Scholar] [CrossRef] [PubMed]
- Gower, J.C.; Dijksterhuis, G.B. Procrustes Problems; Oxford Statistical Science Series; Oxford University Press: Oxford, UK, 2004; Volume 30. [Google Scholar]
- Steinbach, M.; Karypis, G.; Kumar, V. A comparison of document clustering techniques. In Proceedings of the KDD Workshop on Text Mining, Boston, MA, USA, 20 August 2000; pp. 525–526. [Google Scholar]
- Dias, F.; Minghim, R. xHiPP: eXtended Hierarchical Point Placement Strategy. In Proceedings of the 2018 31st SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Foz do Iguaçu, Brazil, 29 October–1 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 361–368. [Google Scholar]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Dal Col, A.; Petronetto, F. Graph regularization multidimensional projection. Pattern Recognit. 2022, 129, 108690. [Google Scholar] [CrossRef]
- Goerss, P.G.; Jardine, J.F. Simplicial Homotopy Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Davis, C. The norm of the Schur product operation. Numer. Math. 1962, 4, 343–344. [Google Scholar] [CrossRef]
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (COIL-20); Columbia University: New York, NY, USA, 1996. [Google Scholar]
- LeCun, Y.; Cortes, C.; Burges, C.J. The MNIST Database of Handwritten Digits. 1998, Volume 10, p. 34. Available online: http://yann.lecun.com/exdb/mnist (accessed on 10 April 2022).
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 3111–3119. [Google Scholar]
- Wagner, A.; Solomon, E.; Bendich, P. Improving Metric Dimensionality Reduction with Distributed Topology. arXiv 2021, arXiv:2106.07613. [Google Scholar]
- Nelson, B.J.; Luo, Y. Topology-Preserving Dimensionality Reduction via Interleaving Optimization. arXiv 2022, arXiv:2201.13012. [Google Scholar]
- Bauer, U. Ripser: Efficient computation of Vietoris–Rips persistence barcodes. J. Appl. Comput. Topol. 2021, 5, 391–423. [Google Scholar] [CrossRef]
- Sohns, J.T.; Schmitt, M.; Jirasek, F.; Hasse, H.; Leitte, H. Attribute-based Explanation of Non-Linear Embeddings of High-Dimensional Data. IEEE Trans. Vis. Comput. Graph. 2021, 28, 540–550. [Google Scholar] [CrossRef]
- Ortega, A.; Frossard, P.; Kovačević, J.; Moura, J.M.F.; Vandergheynst, P. Graph Signal Processing: Overview, Challenges, and Applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef] [Green Version]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Shapley, L.S. A value for n-person games Contributions to the Theory of Games (AM-28); Princeton University Press: Princeton, NJ, USA, 1953; Volume 2, pp. 307–318. [Google Scholar]
- Molnar, C. Interpretable Machine Learning; Lulu Press, Inc.: Durham, NC, USA, 2019. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Long Beach, CA, USA, 2017; pp. 4768–4777. [Google Scholar]
- Hong, C.W.; Lee, C.; Lee, K.; Ko, M.S.; Hur, K. Explainable Artificial Intelligence for the Remaining Useful Life Prognosis of the Turbofan Engines. In Proceedings of the 2020 3rd IEEE International Conference on Knowledge Innovation and Invention (ICKII), Taiwan, China, 21–23 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 144–147. [Google Scholar]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.W.; Newman, S.F.; Kim, J.; et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2018, 2, 749–760. [Google Scholar] [CrossRef]
- Vilarino, R.; Vicente, R. An Experiment on Leveraging SHAP Values to Investigate Racial Bias. arXiv 2020, arXiv:2011.09865. [Google Scholar]
- Marcílio, W.E., Jr.; Eler, D.M. Explaining dimensionality reduction results using Shapley values. Expert Syst. Appl. 2021, 178, 115020. [Google Scholar]
- Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE Smartworld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (Smartworld/SCALCOM/UIC/ATC/CBDcom/IOP/SCI), San Francisco, CA, USA, 4–8 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Zhang, Q.; Zhu, S.C. Visual interpretability for deep learning: A survey. arXiv 2018, arXiv:1802.00614. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, A.; Yosinski, J.; Clune, J. Multifaceted feature visualization: Uncovering the different types of features learned by each neuron in deep neural networks. arXiv 2016, arXiv:1602.03616. [Google Scholar]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic representation and inverse design of metamaterials based on a deep generative model with semi-supervised learning strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Jiang, X.; Hu, X.; Li, G. Visualization of genetic disease-phenotype similarities by multiple maps t-SNE with Laplacian regularization. BMC Med Genom. 2014, 7, S1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial; Centrum Voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Kaggle. Women’s E-Commerce Clothing Reviews. 2018. Available online: https://www.kaggle.com/datasets/nicapotato/womens-ecommerce-clothing-reviews (accessed on 10 April 2022).
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaggle. Gene Expression Classification; Kaggle: San Francisco, CA, USA, 2019. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 3rd ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2011. [Google Scholar]
- Vernier, E.F.; Garcia, R.; Silva, I.d.; Comba, J.L.D.; Telea, A.C. Quantitative Evaluation of Time-Dependent Multidimensional Projection Techniques. Comput. Graph. Forum 2020, 39, 241–252. [Google Scholar] [CrossRef]
- Rauber, P.E.; Falcão, A.X.; Telea, A.C. Visualizing Time-Dependent Data Using Dynamic t-SNE. In Proceedings of the Eurographics/IEEE VGTC Conference on Visualization, Groningen, The Netherlands, 6–10 June 2016. [Google Scholar]
- Rauber, P.E.; Fadel, S.G.; Falcao, A.X.; Telea, A.C. Visualizing the hidden activity of artificial neural networks. IEEE Trans. Vis. Comput. Graph. 2016, 23, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.; Purushotham, S.; To, H.; Shahabi, C. m-tsne: A framework for visualizing high-dimensional multivariate time series. arXiv 2017, arXiv:1708.07942. [Google Scholar]
- Mao, Y.; Dillon, J.; Lebanon, G. Sequential document visualization. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1208–1215. [Google Scholar] [CrossRef]
- Fujiwara, T.; Chou, J.K.; Shilpika, S.; Xu, P.; Ren, L.; Ma, K.L. An incremental dimensionality reduction method for visualizing streaming multidimensional data. IEEE Trans. Vis. Comput. Graph. 2019, 26, 418–428. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.M.; Paulovich, F.V. RankViz: A visualization framework to assist interpretation of Learning to Rank algorithms. Comput. Graph. 2020, 93, 25–38. [Google Scholar] [CrossRef]
- Gleicher, M.; Correll, M.; Nothelfer, C.; Franconeri, S. Perception of average value in multiclass scatterplots. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2316–2325. [Google Scholar] [CrossRef] [Green Version]
- Rensink, R.A.; Baldridge, G. The perception of correlation in scatterplots. Comput. Graph. Forum 2010, 29, 1203–1210. [Google Scholar] [CrossRef]
- Sedlmair, M.; Tatu, A.; Munzner, T.; Tory, M. A taxonomy of visual cluster separation factors. Comput. Graph. Forum 2012, 31, 1335–1344. [Google Scholar] [CrossRef]
- Pandey, A.V.; Krause, J.; Felix, C.; Boy, J.; Bertini, E. Towards understanding human similarity perception in the analysis of large sets of scatter plots. In Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016; pp. 3659–3669. [Google Scholar]
- Chao, G.; Luo, Y.; Ding, W. Recent advances in supervised dimension reduction: A survey. Mach. Learn. Knowl. Extr. 2019, 1, 341–358. [Google Scholar] [CrossRef] [Green Version]
- Espadoto, M.; Martins, R.M.; Kerren, A.; Hirata, N.S.T.; Telea, A.C. Toward a Quantitative Survey of Dimension Reduction Techniques. IEEE Trans. Vis. Comput. Graph. 2021, 27, 2153–2173. [Google Scholar] [CrossRef] [PubMed]








| Technique | Transformation | Nature | Complexity |
|---|---|---|---|
| PCA | Linear | Global | |
| Classical MDS | Linear | Global | |
| Kruskal | Nonlinear | Global | |
| Sammon’s | Nonlinear | Global | |
| FastMap | Nonlinear | Global | |
| Chalmers | Nonlinear | Local | |
| Pekalska | Nonlinear | Global | |
| Isomap | Nonlinear | Global | |
| Chalmers Hybrid | Nonlinear | Local | |
| L-Isomap | Nonlinear | Global | |
| SNE | Nonlinear | Local | |
| Force Scheme | Nonlinear | Global | |
| LMDS | Nonlinear | Global | |
| LSP | Nonlinear | Global | |
| HiPP | Nonlinear | Global | |
| t-SNE | Nonlinear | Local | |
| Glimmer | Nonlinear | Global | |
| PLMP | Partially linear | Global | |
| PLP | Nonlinear | Local | |
| LAMP | Nonlinear | Local-Hybrid | |
| LoCH | Nonlinear | Local | |
| UMAP | Nonlinear | Local | |
| TopoMap | Nonlinear | Global | |
| GRMP | Nonlinear | Local |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortigossa, E.S.; Dias, F.F.; Nascimento, D.C.d. Getting over High-Dimensionality: How Multidimensional Projection Methods Can Assist Data Science. Appl. Sci. 2022, 12, 6799. https://doi.org/10.3390/app12136799
Ortigossa ES, Dias FF, Nascimento DCd. Getting over High-Dimensionality: How Multidimensional Projection Methods Can Assist Data Science. Applied Sciences. 2022; 12(13):6799. https://doi.org/10.3390/app12136799
Chicago/Turabian StyleOrtigossa, Evandro S., Fábio Felix Dias, and Diego Carvalho do Nascimento. 2022. "Getting over High-Dimensionality: How Multidimensional Projection Methods Can Assist Data Science" Applied Sciences 12, no. 13: 6799. https://doi.org/10.3390/app12136799







