Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China
Abstract
:Featured Application
Abstract
1. Introduction
2. Study Area and Data
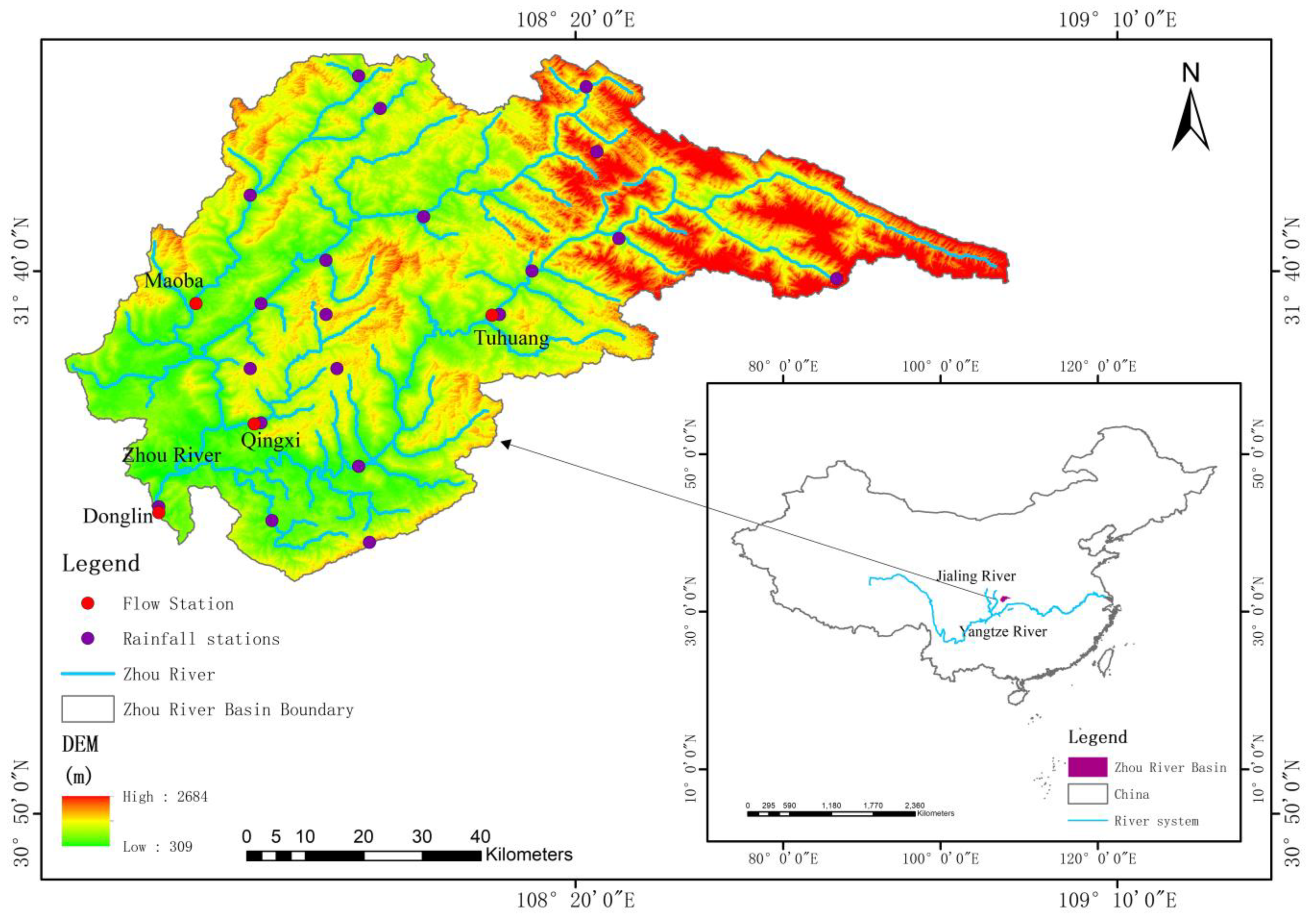
2.1. Study Area
2.2. Data
3. Methodology
3.1. Hydrological Model: The Block-Wise Use of TOPMODEL (BTOP Model)
- (1)
- Runoff generation process
- (2)
- Flow routing process
- (3)
- Model parameters
3.2. Autoregressive Integrated Moving Average Model (ARIMA Model)
- (1)
- Autoregressive (AR) model
- (2)
- Moving average (MA) model
- (3)
- Autoregressive integrated moving average (ARIMA) model
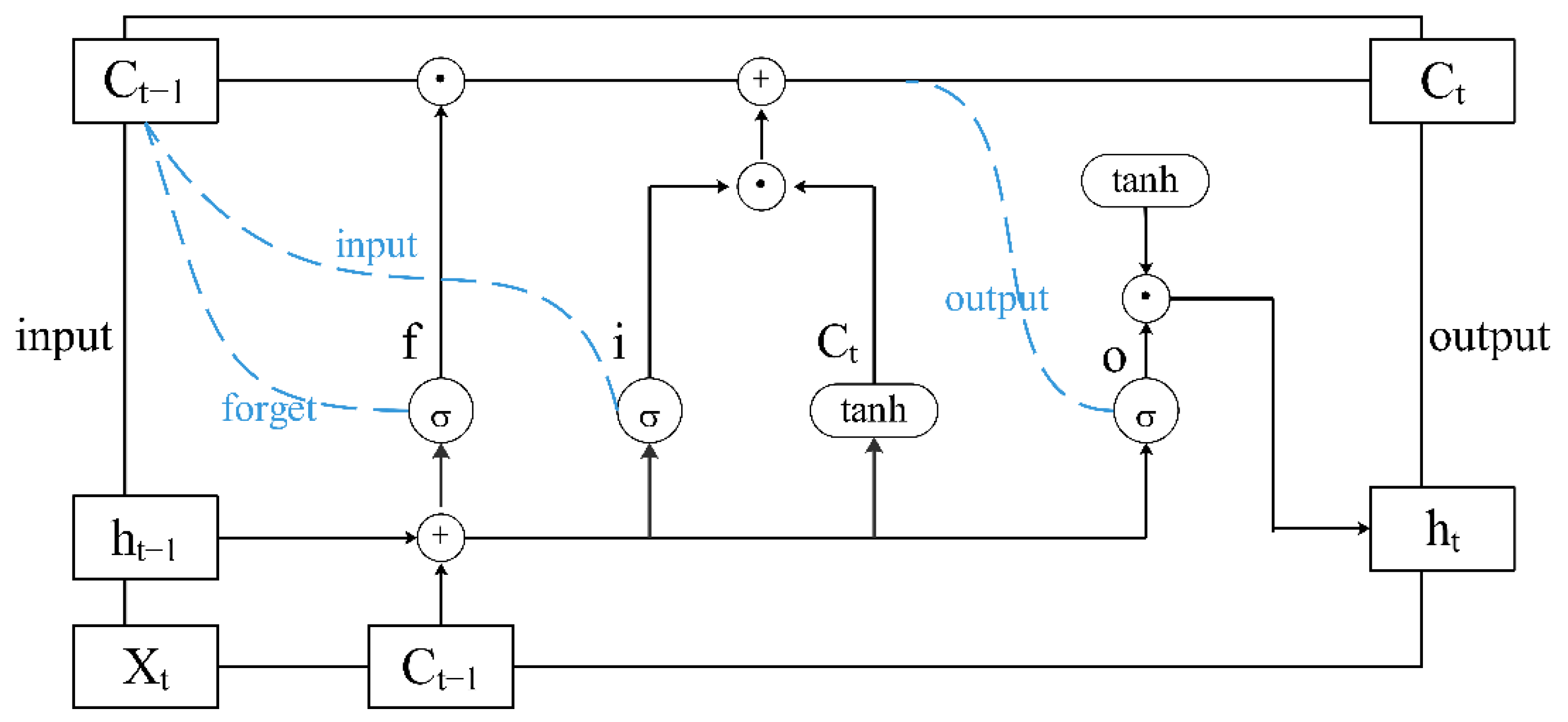
3.3. Long Short-Term Memory (LSTM)-Based Prediction
3.4. Improved Prophet Model
- (1)
- Trend function
- (2)
- Periodic function
- (3)
- Flow function
- (4)
- White noise function
3.5. Evaluation Indicators
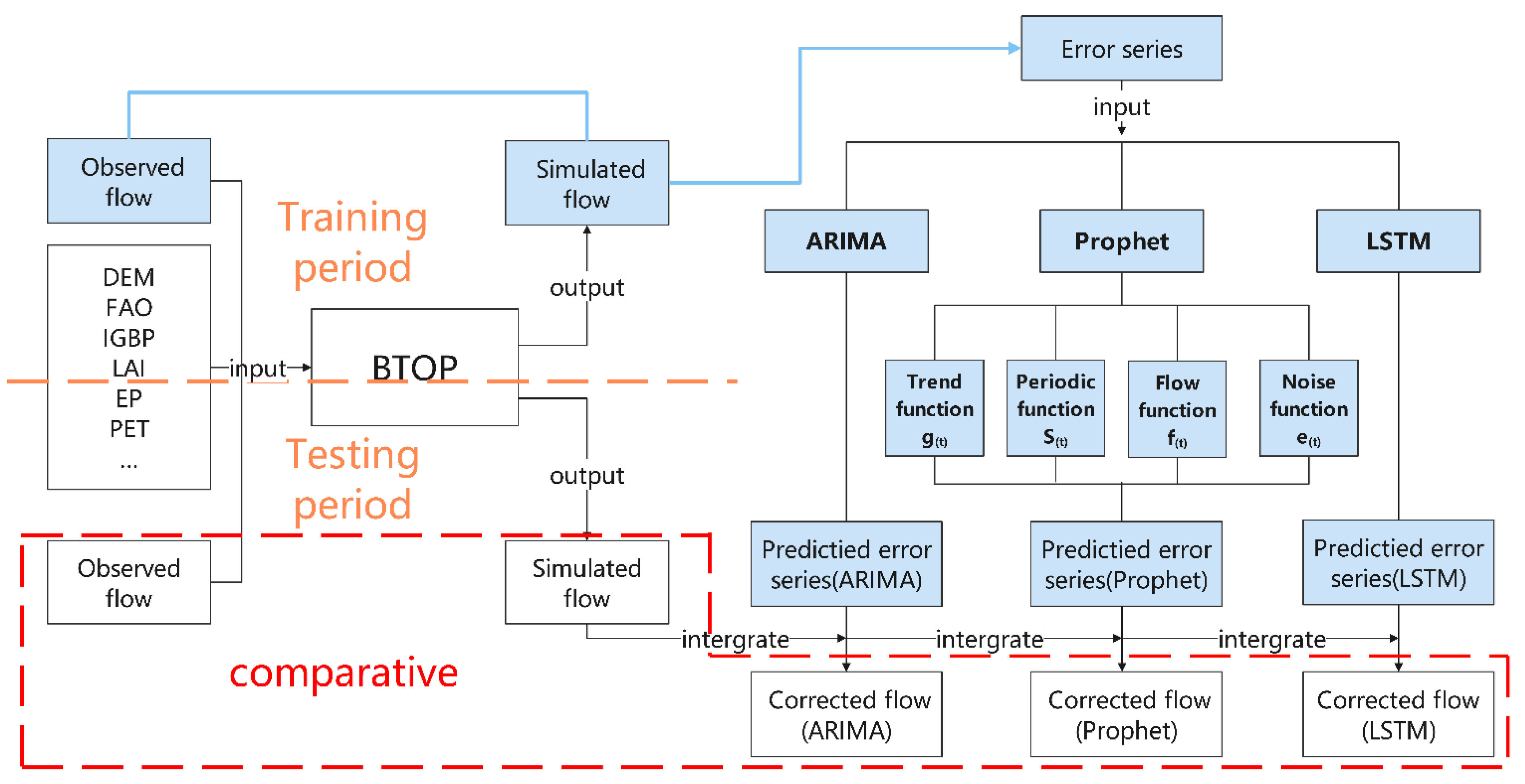
3.6. Methodology Structure
4. Results and Discussion
4.1. Performance of Each Time Series Model
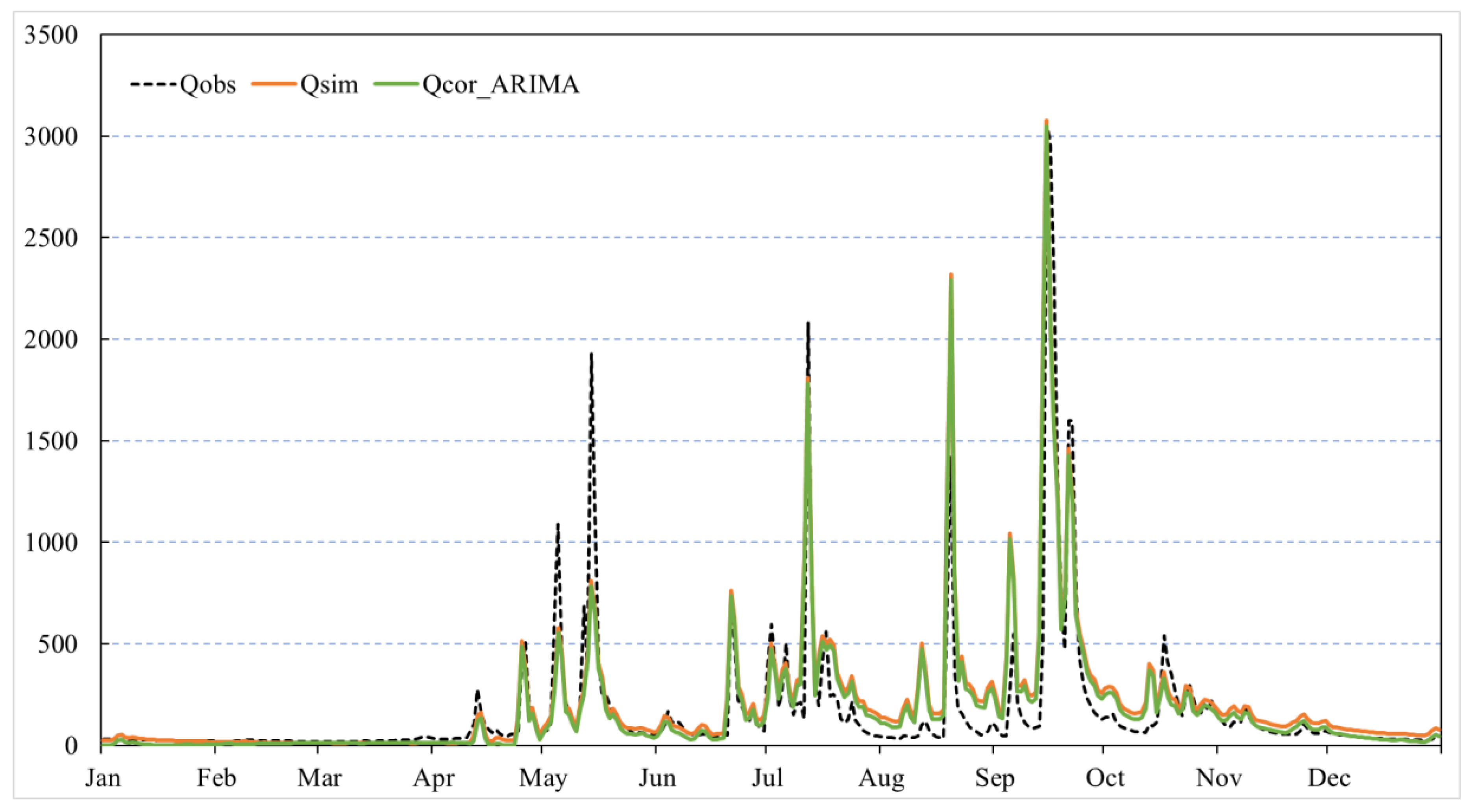
4.1.1. Performance of ARIMA Model
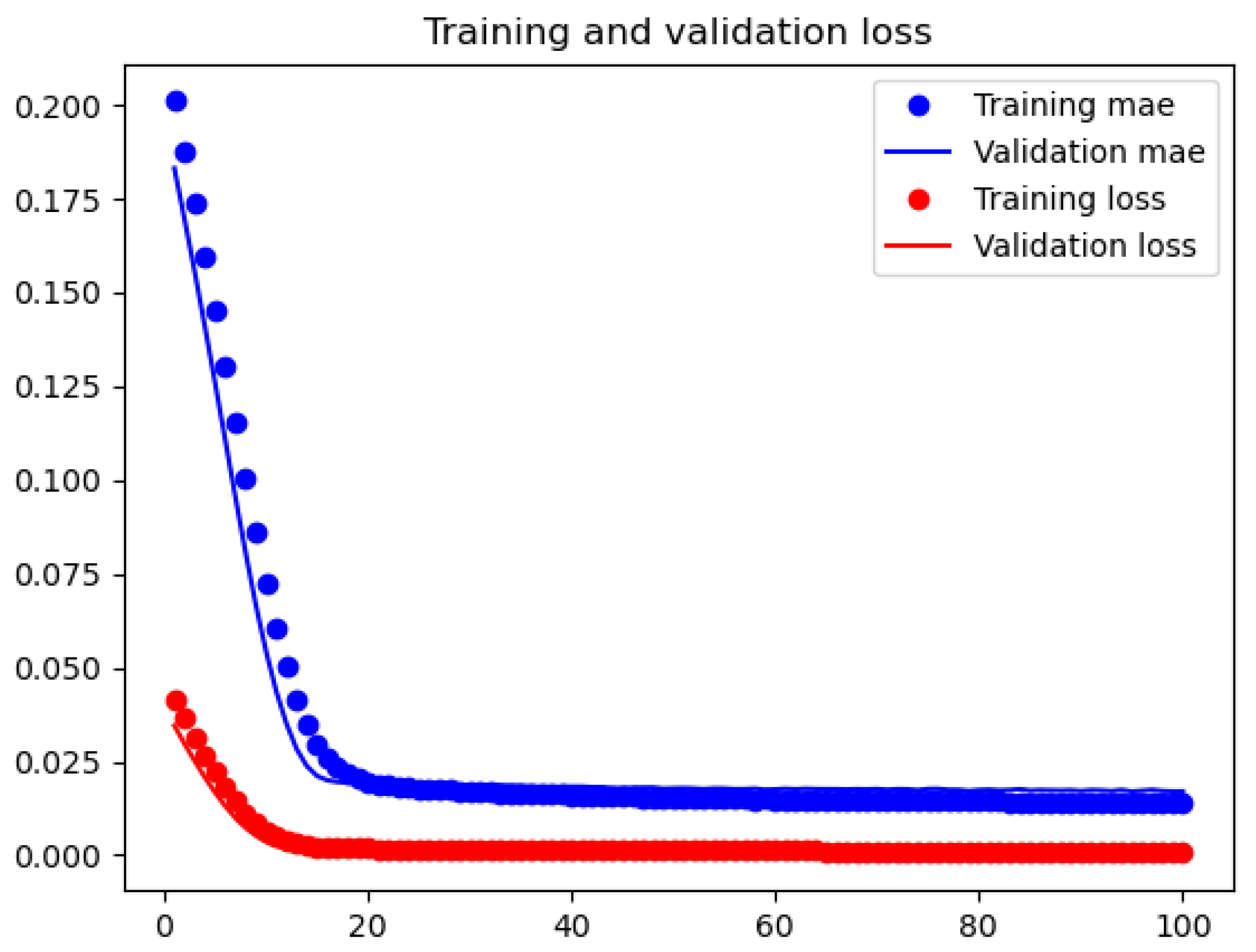
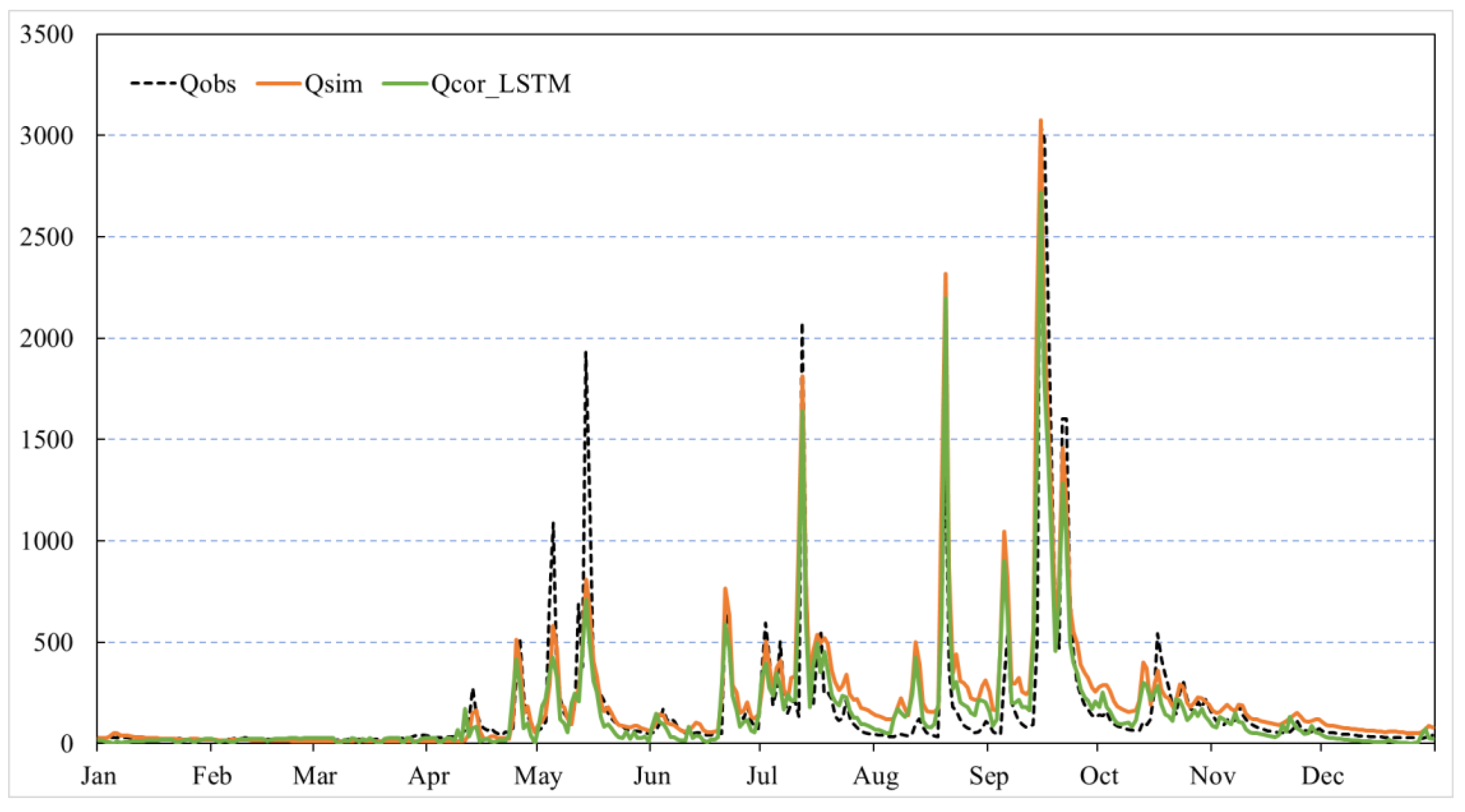
4.1.2. Performance of LSTM Model
4.1.3. Performance of Improved Prophet Model
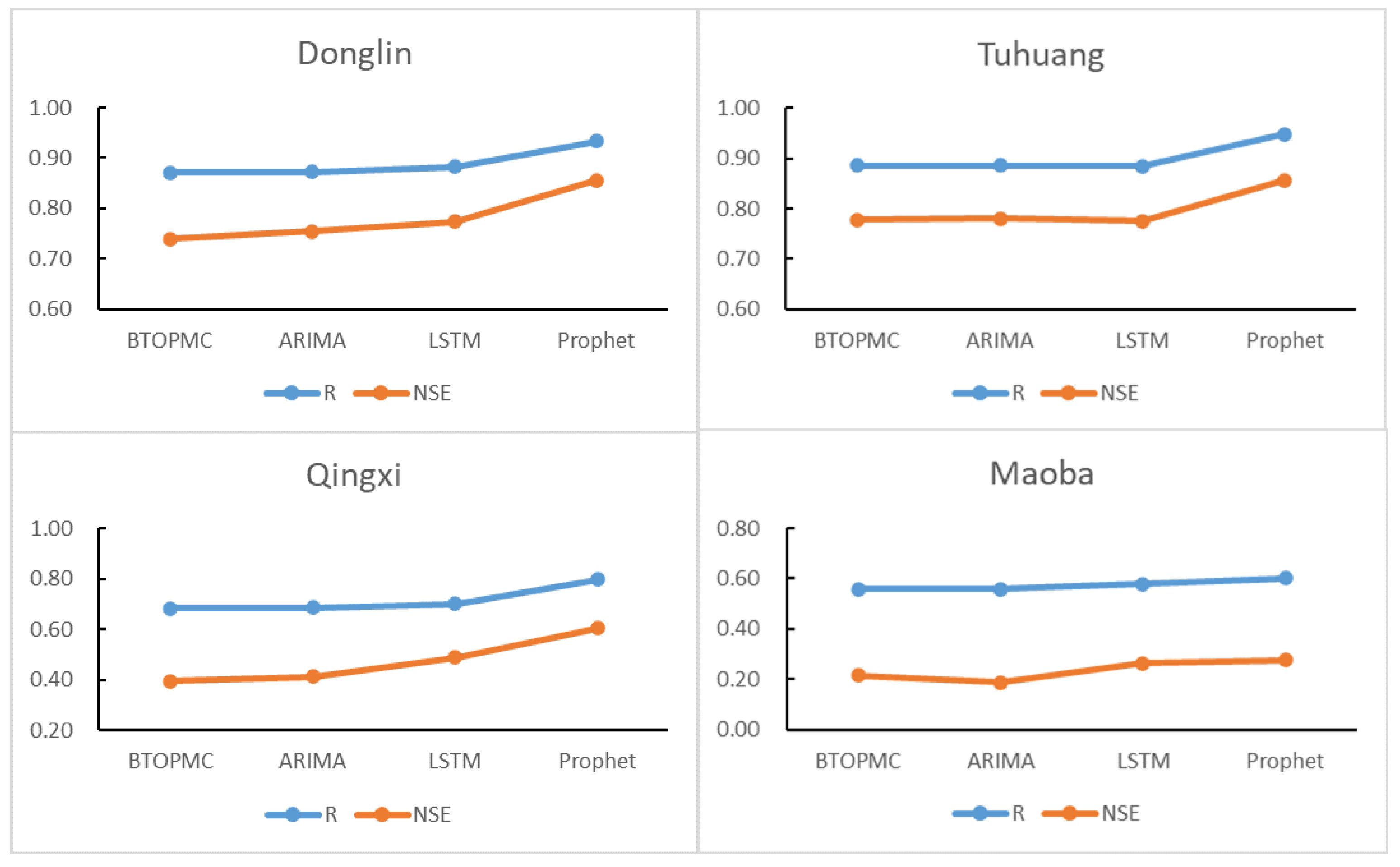
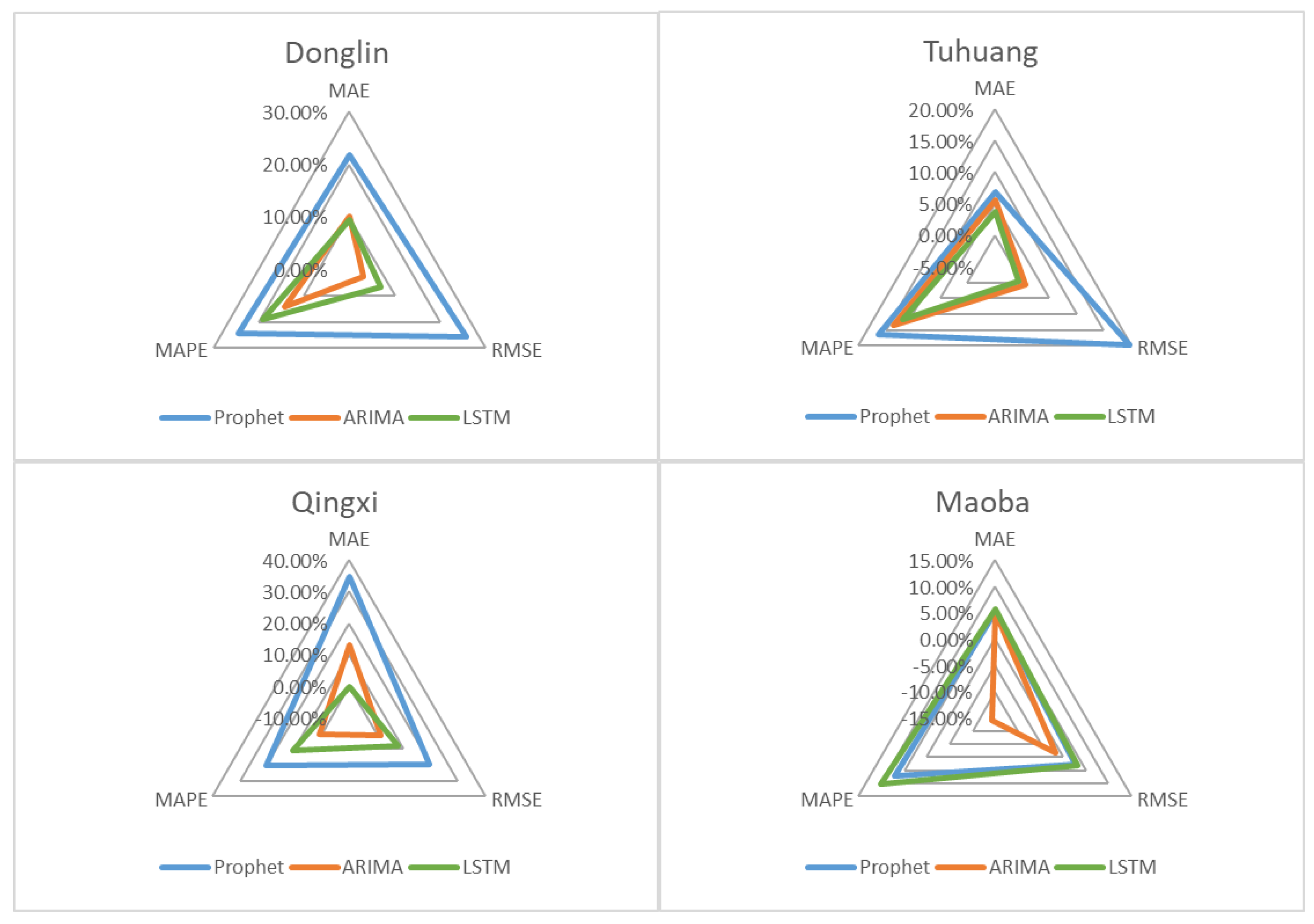
4.2. Comprison between Three Time Series Models
- (1)
- At Donglin and Tuhuang stations, where BTOP simulations are better, MAE, RMSE and MAPE decreased by 6.94%~21.06%, 19.75%~25.74%, and 16.41%~24.49%, respectively, after Prophet modification. At this time, the Prophet model has a good correction effect, but the LSTM and ARIMA models have a poor effect, and the reduction rate of the corresponding error index after correction is far less than that of the Prophet model.
- (2)
- At Qinxi station, where the BTOP simulation is slightly less effective, MAE, RMSE, and MAPE decreased by 34.91%, 19.29% and 20.3%, respectively, after Prophet modification. At this time, the Prophet model is also well modified, and the effects of LSTM and ARIMA models are improved, but the reduction rate of the corresponding error index after modification is still less than half of that of the Prophet model.
- (3)
- At Maoba station, where the BTOP simulation is the least effective, MAE, RMSE and MAPE decreased by 5.15%, 2.61% and 7.05% after Prophet modification. At this time, the modified effect of the Prophet model began to decline, and the error reduction rate after the modification of LSTM and ARIMA models was close to that of the Prophet.
5. Summary and Conclusions
- (1)
- The simulation of the BTOP model in the Zhou River basin is excellent. When the BTOP hydrological model is used for simulation in the study area, the law of error can be followed. We can see that the simulated flow of BTOP is generally slightly higher than the observed flow during the low-flow periods, while the simulated flood peak flow is smaller than the observed flow in high-flow periods.
- (2)
- The integration of the BTOP model and three time series models, Prophet, LSTM, and ARIMA, effectively improved the simulated runoff from the BTOP model. Among them, the prophet model performed best.
- (3)
- The LSTM model has a poor correction effect in high-flow periods due to its lack of scenario prediction. The ARIMA model does not consider seasonal factors and outlier processing and lacks physical analysis of the causes, leading to poor simulation results in both high-flow and low-flow periods.
- (4)
- In this study, the holiday function in the Prophet model is improved to the flow function , which makes the sequence more consistent with the runoff pattern and makes up for the poor effect of the comparison models in the high-flow periods. The improved model can better predict the hydrological time series and greatly improve the runoff simulation accuracy of the hydrological model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhatt, D.; Mall, R.K. Surface Water Resources, Climate Change and Simulation Modeling. Aquat. Procedia 2015, 4, 730–738. [Google Scholar] [CrossRef]
- Croley, T.E.; He, C. Distributed-Parameter Large Basin Runoff Model. I: Model Development. J. Hydrol. Eng. 2005, 10, 173–181. [Google Scholar] [CrossRef]
- Li, D.; Wrzesien, M.L.; Durand, M.; Adam, J.; Lettenmaier, D.P. How much runoff originates as snow in the western United States, and how will that change in the future? Geophys. Res. Lett. 2017, 44, 6163–6172. [Google Scholar] [CrossRef] [Green Version]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Impact of an emergent model vegetation patch on flow adjustment and velocity. In Water Management; Thomas Telford Ltd.: London, UK, 2021; pp. 1–42. [Google Scholar]
- Liu, C.; Shan, Y.; Sun, W.; Yan, C.; Yang, K. An open channel with an emergent vegetation patch: Predicting the longitudinal profiles of velocities based on exponential decay. J. Hydrol. 2019, 582, 124429. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.; Liu, L.; Chen, T.; Liu, X.; Ren, Y.; Zhang, H.; Li, X.; Ao, T. An Approach to Evaluate Non-Point Source Pollution in An Ungauged Basin: A Case Study in Xiao'anxi River Basin, China; IWA Publishing: London, UK, 2020. [Google Scholar]
- Esling, P.; Agon, C. Time-Series Data Mining. ACM Comput. Surv. 2013, 45, 11–12. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970; Volume 3. [Google Scholar]
- Lngkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recogn. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Arıkan, S.M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet-Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, Y.; Liu, D.; Fu, Q.; Li, M. A new method for runoff prediction error correction based on LS-SVM and a 4D copula joint distribution. J. Hydrol. 2021, 598, 126223. [Google Scholar] [CrossRef]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40, 75–88. [Google Scholar] [CrossRef]
- Cheng, C.; Li, Y.; Liu, L. Study on real-time flood prediction in Xijiang River Basin based on ArMA-GARCH Model. In Proceedings of the Chinese Society of Dam Engineering 2021 Annual Conference, Guangzhou, China, 11–12 November 2021; p. 7. [Google Scholar]
- Zhang, H.; Guo, S. Bayesian probabilistic flood forecasting system. Sci. Technol. Eng. 2004, 4, 74–75. [Google Scholar] [CrossRef]
- Jiao, W.; Long, H. Prediction correction of distributed hydrological model based on autoregressive model. J. Water Resour. Water Eng. 2015, 6. [Google Scholar] [CrossRef]
- The Data Set Is Provided by Geospatial Data Cloud Site, Computer Network Information Center, Chinese Academy of Sciences. Available online: http://www.gscloud.cn (accessed on 25 March 2022).
- LP DAAC-MCD12Q1. Available online: https://lpdaac.usgs.gov/products/mcd12q1v006/ (accessed on 25 March 2022).
- FAO Digital Soil Map of the World (DSMW). Available online: http://www.fao.org/land-water/land/land-governance/land-resources-planning-toolbox/category/details/en/c/1026564/ (accessed on 25 March 2022).
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- The Potential Evapotranspiration (EP) from the Climatic Research Unit (CRU) of the School of Environmental Sciences (ENV) at the University of East Anglia (UEA). Available online: http://www.cru.uea.ac.uk/ (accessed on 25 March 2022).
- The Leaf Area Index (LAI) of the National Centers for Environmental Information. Available online: https://www.ncei.noaa.gov/data/avhrr-land-leaf-area-index-and-fapar/access/ (accessed on 25 March 2022).
- Zhu, Y.; Liu, L.; Qin, F.; Zhou, L.; Zhang, X.; Chen, T.; Li, X.; Ao, T. Application of the Regression-Augmented Regionalization Approach for BTOP Model in Ungauged Basins. Water 2021, 13, 2294. [Google Scholar] [CrossRef]
- Gusyev, M.A.; Magome, J.; Kiem, A.; Takeuchi, K. The BTOP Model with Supplementary Tools User Manual; Public Works Research Institute (PWRI): Tsukuba, Japan, 2017. [Google Scholar]
- Takeuchi, K.; Ao, T.; Ishidaira, H. Introduction of block-wise use of TOPMODEL and Muskingum-Cunge method for the hydroenvironmental simulation of a large ungauged basin. Int. Assoc. Sci. Hydrol. Bull. 1999, 44, 633–646. [Google Scholar] [CrossRef]
- Tianqi, A.; Takeuchi, K.; Ishidaira, H.; Yoshitani, J.; Fukami, K. Development and application of a new algorithm for automated pit removal for grid DEMs. Int. Assoc. Sci. Hydrol. Bull. 2003, 48, 985–997. [Google Scholar] [CrossRef]
- Takeuchi, K.; Hapuarachchi, P.; Zhou, M.; Ishidaira, H.; Magome, J. A BTOP model to extend TOPMODEL for distributed hydrological simulation of large basins. Hydrol. Process. 2010, 22, 3236–3251. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, L.; Li, X.; Ting; Ao, T. Screening and Optimizing the Sensitive Parameters of BTOPMC Model Based on UQ-PyL Software: Case Study of a Flood Event in the Fuji River Basin, Japan. J. Hydrol. Eng. 2020, 25, 5020030. [Google Scholar] [CrossRef]
- Zhou, L.; Rasmy, M.; Takeuchi, K.; Koike, T.; Selvarajah, H.; Ao, T. Adequacy of Near Real-Time Satellite Precipitation Products in Driving Flood Discharge Simulation in the Fuji River Basin, Japan. Appl. Sci. 2021, 11, 1087. [Google Scholar] [CrossRef]
- Zhou, L.; Koike, T.; Takeuchi, K.; Rasmy, M.; Onuma, K.; Ito, H.; Selvarajah, H.; Liu, L.; Li, X.; Ao, T. A study on availability of ground observations and its impacts on bias correction of satellite precipitation products and hydrologic simulation efficiency. J. Hydrol. 2022, 610, 127595. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Takeuchi, K.; Zhou, M.; Kiem, A.S.; Georgievski, M.; Magome, J.; Ishidaira, H. Investigation of the Mekong River basin hydrology for 1980–2000 using the YHyM. Hydrol. Process. 2008, 22, 1246–1256. [Google Scholar] [CrossRef]
- Takeuchi, K. Studies on the Mekong River Basin-Modelling of Hydrology and Water Resources. Hydrol. Process. 2008, 22, 1243–1245. [Google Scholar] [CrossRef]
- Liu, L.; Ao, T.; Zhou, L.; Takeuchi, K.; Gusyev, M.; Zhang, X.; Wang, W.; Ren, Y. Comprehensive evaluation of parameter importance and optimization based on the integrated sensitivity analysis system: A case study of the BTOP model in the upper Min River Basin, China. J. Hydrol. 2022, 610, 127819. [Google Scholar] [CrossRef]
- Shrestha, S.; Bastola, S.; Babel, M.S.; Dulal, K.N.; Magome, J.; Hapuarachchi, H.; Kazama, F.; Ishidaira, H.; Takeuchi, K. The assessment of spatial and temporal transferability of a physically based distributed hydrological model parameters in different physiographic regions of Nepal. J. Hydrol. 2007, 347, 153–172. [Google Scholar] [CrossRef]
- Ao, T.; Ishidaira, H.; Takeuchi, K.; Kiem, A.S.; Yoshitari, J.; Fukami, K.; Magome, J. Relating BTOPMC model parameters to physical features of MOPEX basins. J. Hydrol. 2006, 320, 84–102. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optimiz. Theory App. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Bandura, E.; Jadoski, G.S.; Junior, G. Applications of the ARIMA model for time series data analysis. Appl. Res. Agrotechnol. 2019, 12, 145–150. [Google Scholar]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energ. 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Cong, M.; Li, Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using RBFN Based on EEMD Decomposition. DEStech Trans. Eng. Technol. Res. 2017. [Google Scholar] [CrossRef] [Green Version]
- Rizkya, I.; Syahputri, K.; Sari, R.M.; Siregar, I.; Utaminingrum, J. Autoregressive Integrated Moving Average (ARIMA) Model of Forecast Demand in Distribution Centre. IOP Conf. Ser. Mater. Sci. Eng. 2019, 598, 12071. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Essen, B.V.; Awwal, A.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef] [Green Version]
- Duarte, D.; Walshaw, C.; Ramesh, N. A Comparison of Time-Series Predictions for Healthcare Emergency Department Indicators and the Impact of COVID-19. Appl. Sci. 2021, 11, 3561. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2017, 5, e3190v2. [Google Scholar] [CrossRef]
- Aditya Satrio, C.B.; Darmawan, W.; Nadia, B.U.; Hanafiah, N. Time series analysis and forecasting of coronavirus disease in Indonesia using ARIMA model and PROPHET. Procedia Comput. Sci. 2021, 179, 524–532. [Google Scholar] [CrossRef]
- Medina, I.; Montaner, D.; Tárraga, J.; Dopazo, J. Prophet, a web-based tool for class prediction using microarray data. Bioinformatics 2007, 23, 390–391. [Google Scholar] [CrossRef] [Green Version]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max- flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [Green Version]
- Devaraj, J.; Elavarasan, R.M.; Pugazhendhi, R.; Shafiullah, G.M.; Hossain, E. Forecasting of COVID-19 cases using Deep learning models: Is it reliable and practically significant? Results Phys. 2021, 21, 103817. [Google Scholar] [CrossRef]
- Tashman, L.J.; Leach, M.L. Automatic forecasting software: A survey and evaluation. Int. J. Forecast. 1991, 7, 209–230. [Google Scholar] [CrossRef] [Green Version]
- Elliott, G.; Rothenberg, T.J.; Stock, J.H. Efficient Tests for an Autoregressive Unit Root. Econometrica 1996, 64, 813–836. [Google Scholar] [CrossRef] [Green Version]
- Gep, B.; Gm, J. Times Series Analysis—Forecasting and Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Mitic, P. Is a Reputation Time Series White Noise? In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Guilin, China, 30 October–1 November 2017. [Google Scholar]
- Hill, R.J.; Flack, H.D. The use of the Durbin–Watsondstatistic in Rietveld analysis. J. Appl. Crystallogr. 1987, 20, 356–361. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energ. 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Zhang, Q.; Ding, Y.; Zhang, D. Application of a hybrid ARIMA-LSTM model based on the SPEI for drought forecasting. Environ. Sci. Pollut. R. 2021, 29, 4128–4144. [Google Scholar] [CrossRef]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-Driven Forecasting of High-Dimensional Chaotic Systems with Long Short-Term Memory Networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef] [Green Version]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D: Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
- Gusyev, M.A.; Kwak, Y.; Khairul, M.I.; Arifuzzaman, M.B.; Magome, J.; Sawano, H.; Takeuchi, K. Effectiveness of water infrastructure for river flood management: Part 1—Flood Hazard Assessment using hydrological models in Bangladesh. Proc. Int. Assoc. Hydrol. Sci. 2015, 370, 75–81. [Google Scholar] [CrossRef] [Green Version]
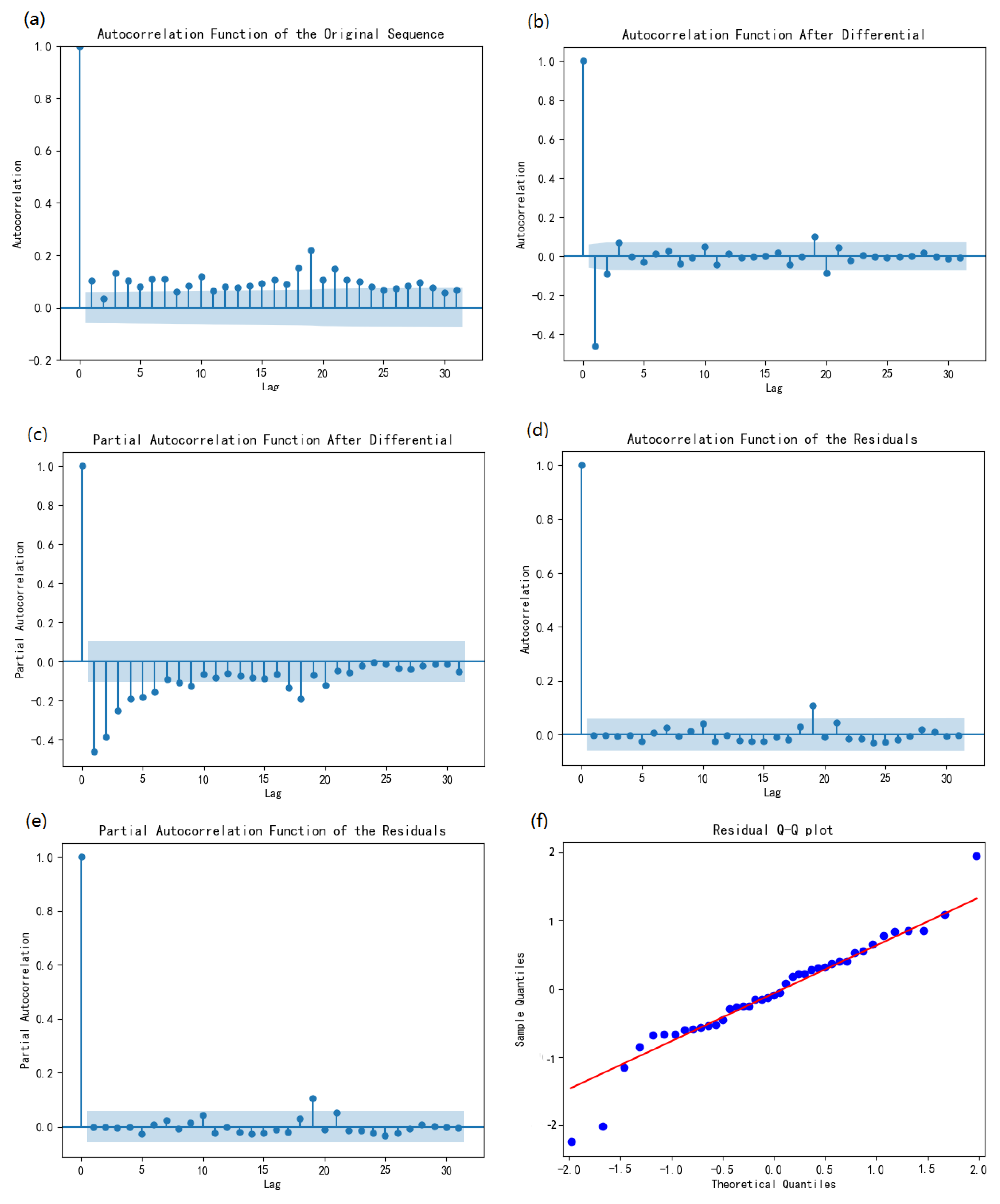
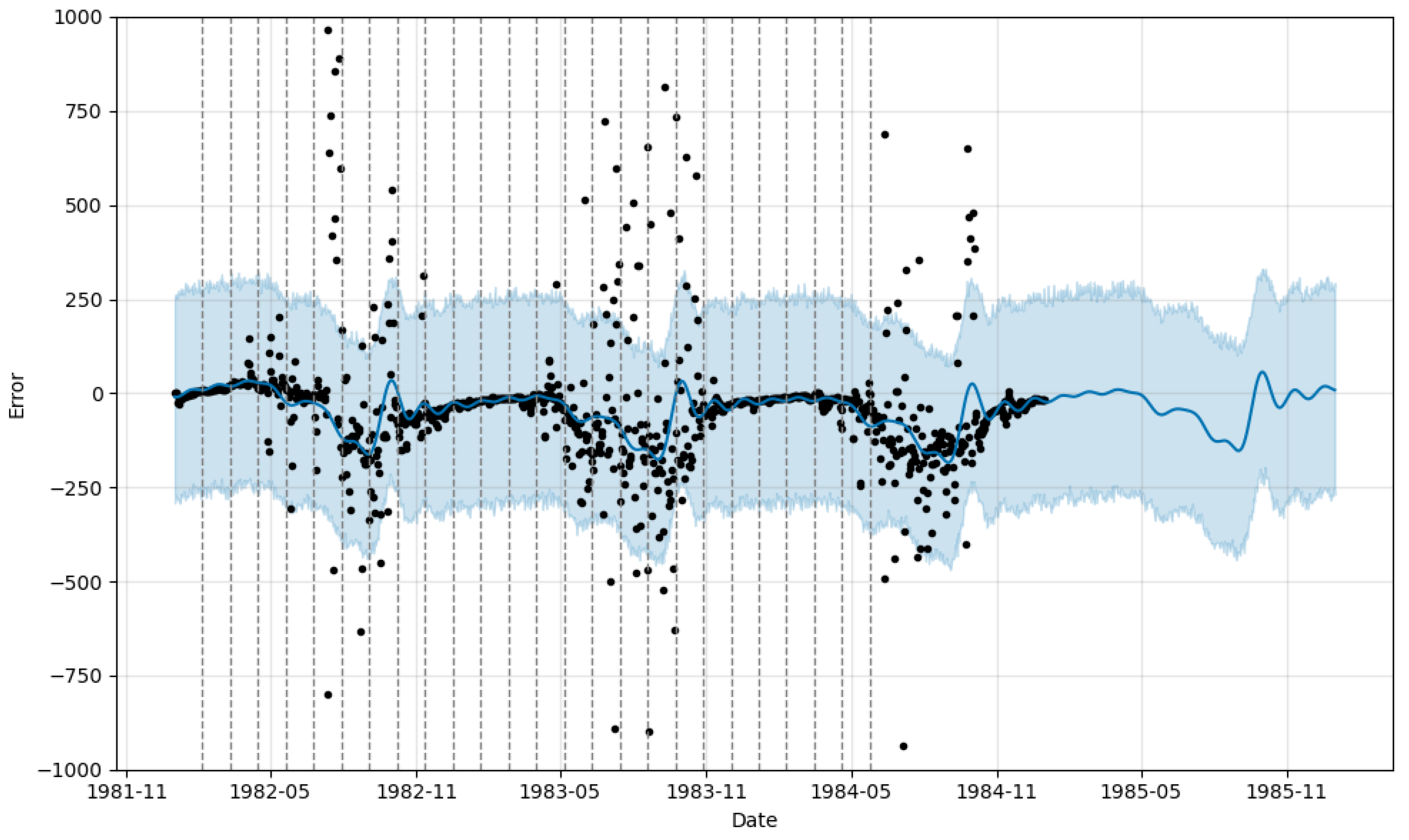
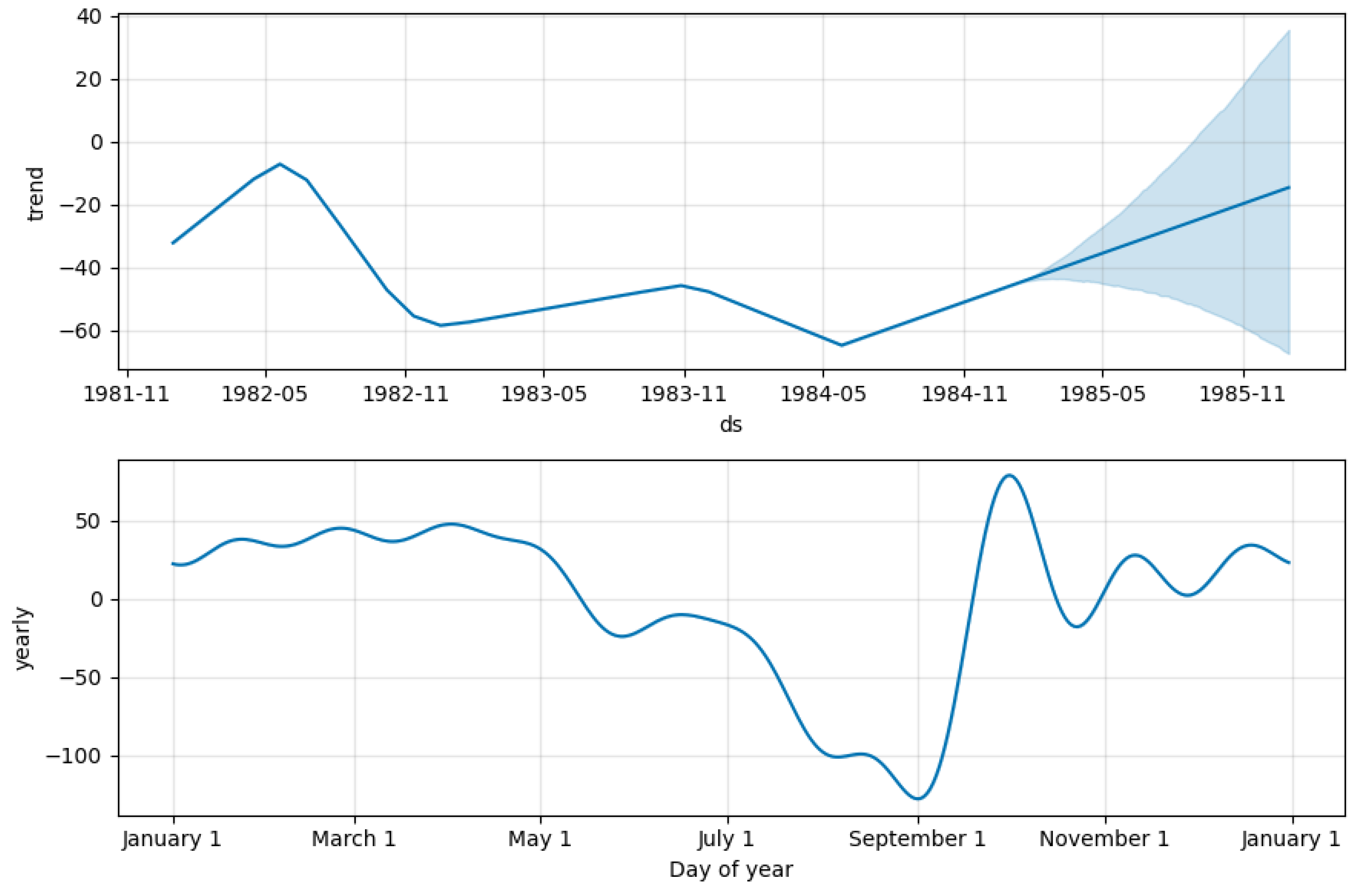

| Parameter Nature | Parameter Name | Value |
|---|---|---|
| Trend parameters | growth | linear |
| changepoints | None | |
| n_changepoints | 25 | |
| changepoint_range | 0.8 | |
| changepoint_prior_scale | 0.5 | |
| Periodic parameters | yearly_seasonality | 10 |
| weekly_seasonality | false | |
| daily_seasonality | false | |
| seasonality_mode | additive | |
| seasonality_prior_scale | 20 | |
| Flow parameters | flow | flow |
| flow_prior_scale | 10 | |
| Other parameters | mcmc_samples | 0 |
| interval_width | 0.8 | |
| uncertainty_samples | 1000 | |
| stan_backend | cmdstanpy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Q.; Zhou, L.; Xiang, X.; Liu, L.; Liu, X.; Li, X.; Ao, T. Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China. Appl. Sci. 2022, 12, 6883. https://doi.org/10.3390/app12146883
Xiao Q, Zhou L, Xiang X, Liu L, Liu X, Li X, Ao T. Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China. Applied Sciences. 2022; 12(14):6883. https://doi.org/10.3390/app12146883
Chicago/Turabian StyleXiao, Qintai, Li Zhou, Xin Xiang, Lingxue Liu, Xing Liu, Xiaodong Li, and Tianqi Ao. 2022. "Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China" Applied Sciences 12, no. 14: 6883. https://doi.org/10.3390/app12146883
APA StyleXiao, Q., Zhou, L., Xiang, X., Liu, L., Liu, X., Li, X., & Ao, T. (2022). Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China. Applied Sciences, 12(14), 6883. https://doi.org/10.3390/app12146883







