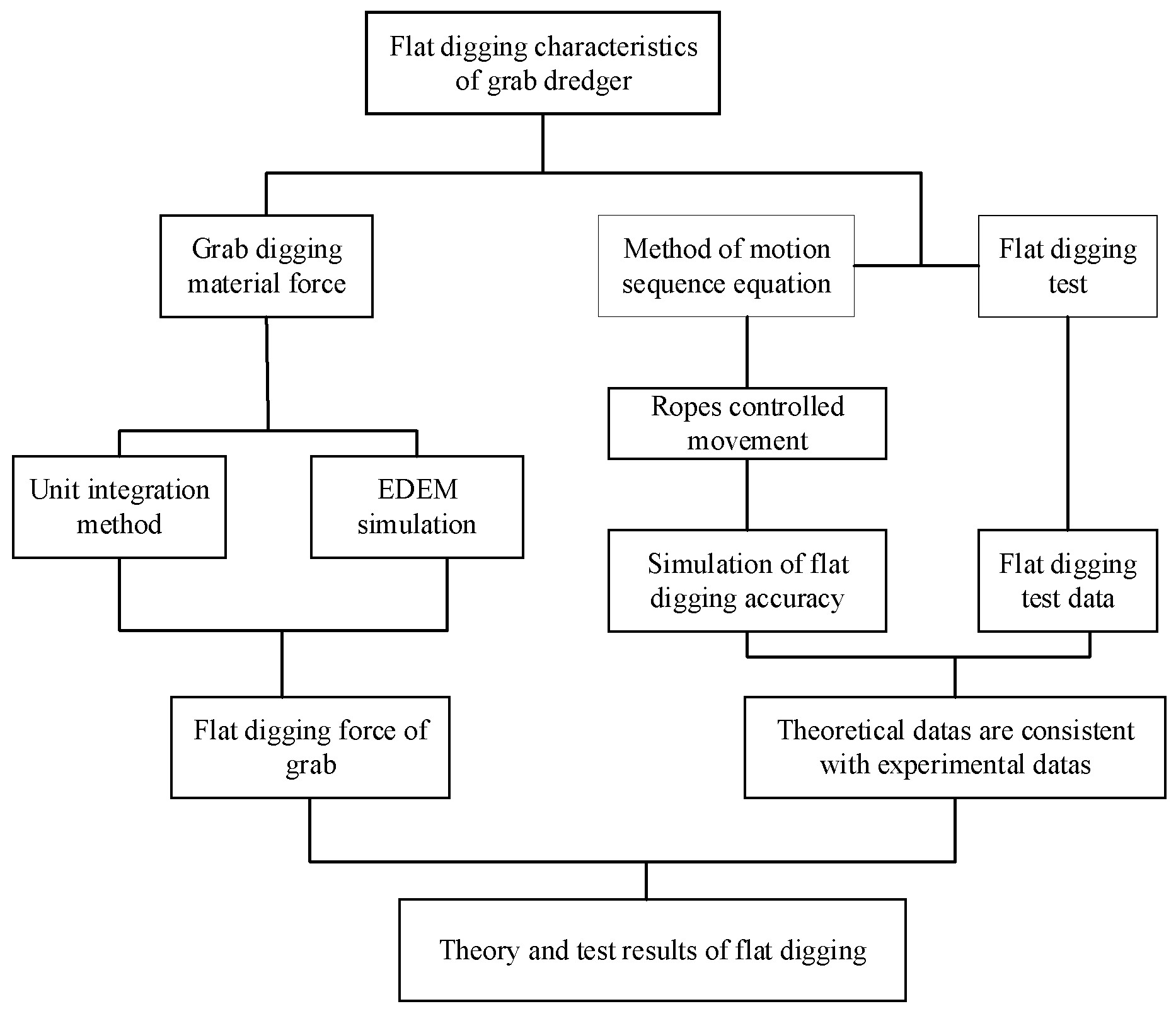
Unit Integration Method Solution and Experimental Research on Mechanism Characteristics for Flat Digging of Grab Dredgers

Abstract

In the process of grab dredger dredging, how to ensure the accuracy of flat digging is a key technical question. The accuracy of flat digging is related to the force of grab digging. However, there are limitations in the traditional method of studying the force of grab digging. In this study, based on the Rankine theory, the unit integration method is proposed to calculate the force process of grab excavation. This method determines the shape and position of the failure surface under the action of active pressure $F_B$ and passive pressure $F_E$ and further obtains a functional expression for the relation between digging force and digging parameters. Through the simulation of flat digging force using the discrete element method (DEM), we obtained results consistent with the calculation results of the unit integration method. In addition, this study sought to control the movement distance of the closing wires and the hoist wires through the equation of motion, to carry out the precision calculations of theoretical data, and experimental research into grab flat digging. By comparing theoretical data and test data, the following conclusion was drawn: the deviation of the theoretical flat digging precision from the test data falls within the allowable range, at 3.15%. This study provides technical support for the flat digging process of the grab dredger.

1. Introduction

“The 21st century is the era of ocean development” has now become a global consensus. For China, aiming at developing the ocean is a far-reaching choice. For the present, it will certainly drive the rapid development of ocean engineering as part of the process of becoming a maritime power. At present, the construction of large-scale marine projects such as the Hong Kong–Zhuhai–Macao Bridge and the subsea tunnel requires large-scale subsea caisson operations, and large-scale marine engineering caisson operations have higher requirements for the flatness of the seabed. Seabed digging operations require large grab dredgers for construction operations [1,2,3]. Therefore, seabed digging and leveling operations are important and challenging issues in current large-scale ocean engineering research.

The basic structure of a grab dredger consists of the lower sheave block, the upper sheave block, the bucket body, the gear segment, the hoist wires, the closing wires, etc. Under the gravity action of the grab, the digging force is generated through the action of the closing wires. This is a process of digging dynamic balance [4,5]. As shown in Figure 1a, the grab digging operation is carried out by the following steps: open the bucket, lower the grab down to the material, apply tension to the closing wires, keep the hoist wires static, gradually close the bucket, and start digging with the grab; load the grab dredger to a certain height, while raising the closing wires and hoist wires to achieve full closure of the bucket; then, move the grab to the release site, release the closing wires, keep the hoist wires static, and release the bucket. The operation just described is discontinuous and cyclic [6,7].

Under normal and flat digging conditions with a grab dredger, the digging curve is different, depending upon the conditions. In the normal digging state, the digging curve is steep, while, in the flat digging state, the digging curve is smooth. In order to achieve the effect of flat digging, it is necessary to control the movement of the closing wires and the hoist wires [8,9,10,11]. When lifting the closing wires, while automatically controlling the hoist wires of the grab, the digging plane formed is flat, as shown in Figure 1b.

In order to achieve automatic flat digging with a grab dredger, the first step lies in improving the structural design of the bucket through the analysis of digging resistance. Over the years, many useful results have been obtained through experimental and theoretical studies of the mechanical mechanisms of grab dredgers, laying a solid foundation for their extensive application.

Miedema, S.A. [12] analyzed and studied a mechanical model of the closing process of the grab dredger during the digging operation and conducted theoretical simulations of—and experimental research on—the digging characteristics of the grab dredger. This is one of the earliest studies of the force characteristics of the grab. Chang Qiren [13] analyzed the translation process of the grab and obtained a calculation method and formula for the digging resistance. Ji Sanyou [14] simulated and calculated the process of grabbing bulk materials and obtained reasonable parameters of grabbing resistance and pushing resistance. Zhang Haining [15] conducted static finite element analysis on—and dynamic numerical simulation of—the mechanical characteristics of the grab dredger; and conducted an experimental study on the grab digging process. An analysis of the above literature shows that, in order to study the mechanical mechanism of the grab digging material, the simulation of—and experimental research into—the grab digging process are both very meaningful.

In the excavation process of the grab, the interactions between the material and the grab device and the interactions between the materials themselves are more complicated. In this study, the research method is different from the traditional research methods. Based on the Rankine theory, this paper proposes the unit integration method to analyze the process of excavating materials. Along with deep digging and fixed depth digging, flat digging is a key function of the grab dredger. Through comparative analysis, we found the variation law of the simulation result curve of the force of the flat digging was basically consistent with the theoretical calculation provided by the unit integration method. Using the dynamic model of flat digging, the theoretical precision of flat digging was obtained. The flat digging test was then carried out, and the test data obtained. We then discovered that the theoretical data of the flat digging characteristics coincided with the test data. This paper therefore completes the theoretical and experimental research on the flat digging of grab dredgers, as shown in Figure 2.

2. Theoretical Analysis and Experimental Details

2.1. Theoretical Model Analysis of Digging

Based on the Rankine theory, this paper proposes the unit integration method to analyze the process of excavating materials. Analysis of the destruction process of the material shows that the front and back directions of the grab form a failure surface. The destruction of the material creates a passive pressure in the front of the grab, and an active pressure in the back of the grab [16,17]. Through the unit integration method, the functional expression of the digging resistance of the grab can be obtained. In Figure 3, the curved surface BC represents the active failure surface, and the curved surfaces BE and BD represent the passive failure surface. In the figure, AB represents the grab bucket, and the digging direction of the grab is from right to left.

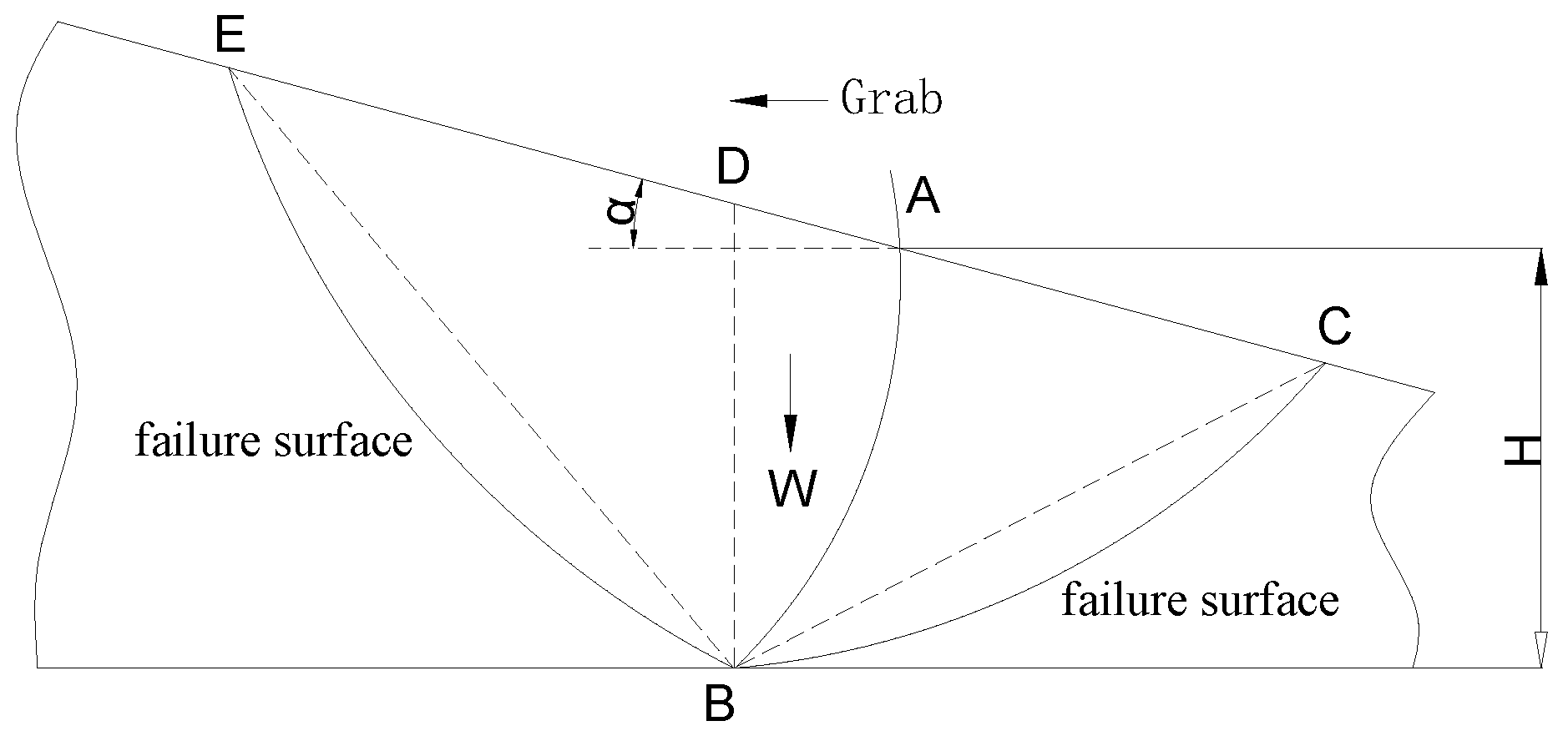
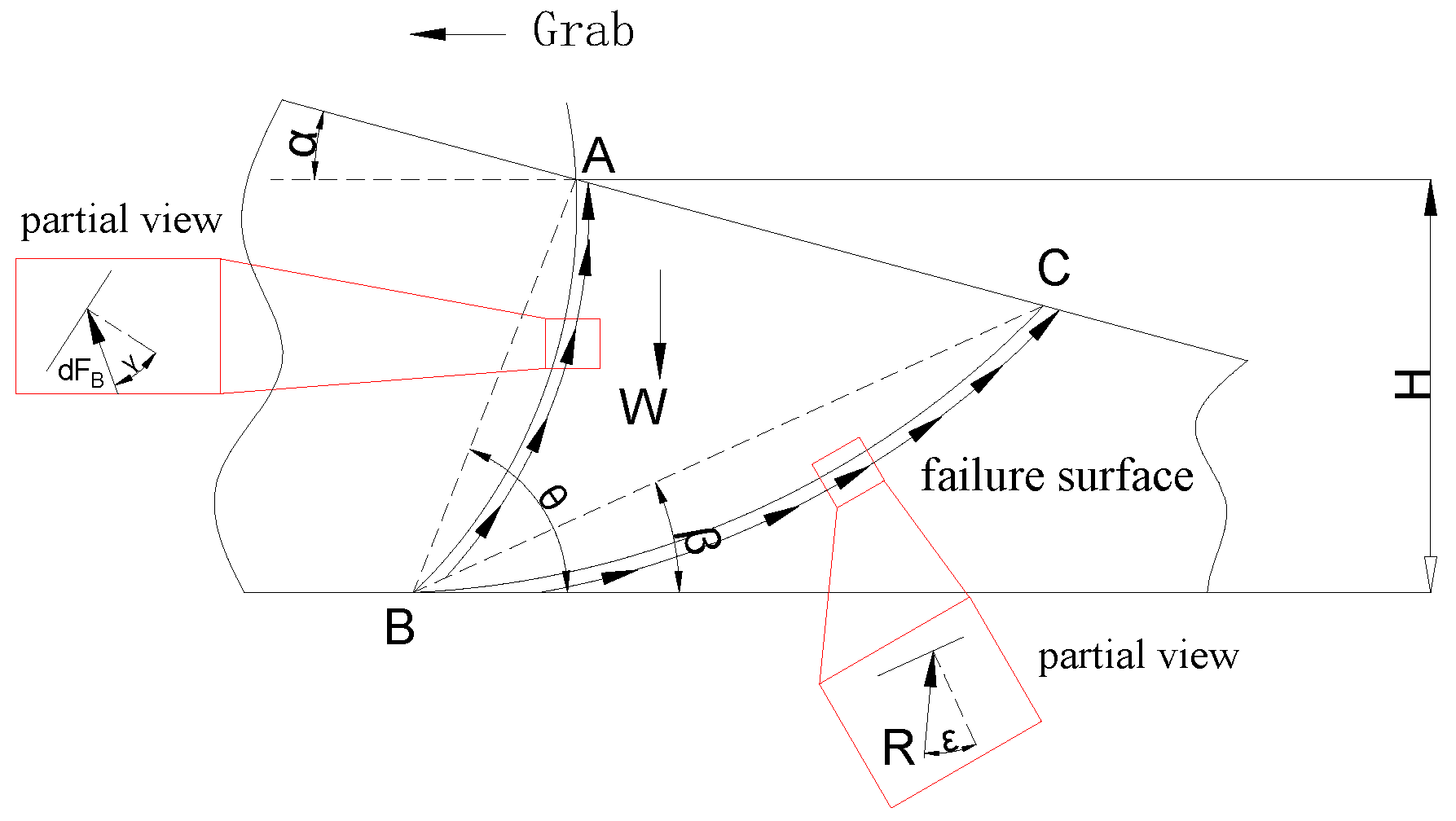
2.1.1. Active Material Pressure and Its Failure Surface

This can be simplified by studying the interaction force between the grab and the material. The schematic diagram of the active pressure and the failure surface of the grab is shown in Figure 4, and the surface BC represents the active failure surface. Analyzing the size of the friction force R between the damaged failure surfaces of the material, we find the friction force is related to the characteristic parameters of the material [18]. The material gravity is calculated according to the calculation in Formula (1). On the back-of-AB surface of the grab bucket, the material generates active pressure, and its calculation is obtained using Formula (2). To analyze the active pressure of the grab, the depth can be calculated using Formula (3).

$$W=\rho b{S}_{ABC}$$

(1)

$$F_B={{\displaystyle \int }}_0^H{p}_B\left(z\right)dz$$

(2)

$$d{F}_B=p_B\left(z\right)dz$$

(3)

where $W$ is the weight of the material boundary body ABC (N), $\rho$ is the material density ($\mathrm{N}/{\mathrm{m}}^3$), $b$ is the grab width (m),$S_{ABC}$ is the area of the material volume ABC (${\mathrm{m}}^2$), $F_B$ is the active pressure resultant value (N), $H$ is the digging depth (m), $z$ represents the integral formal parameters (m), $p_B$ is the pressure value at depth z ($\mathrm{N}/\mathrm{m}$), and $d{F}_B$ is the element of active pressure at depth z of body ABC.

According to the dynamic balance of the material body ABC, the equilibrium state of the material body ABC is calculated using Formula (4). The angle of the active pressure on the horizontal plane can be determined according to Equation (5):

$${\overrightarrow{F}}_B+\overrightarrow{W}+\overrightarrow{R}=0$$

(4)

$$\frac{d{F}_B\left(\beta \right)}{d\beta }=0$$

(5)

where $R$ is the frictional force generated by the soil (N) and $\beta$ is the angle of the active pressure on the horizontal plane (rad).

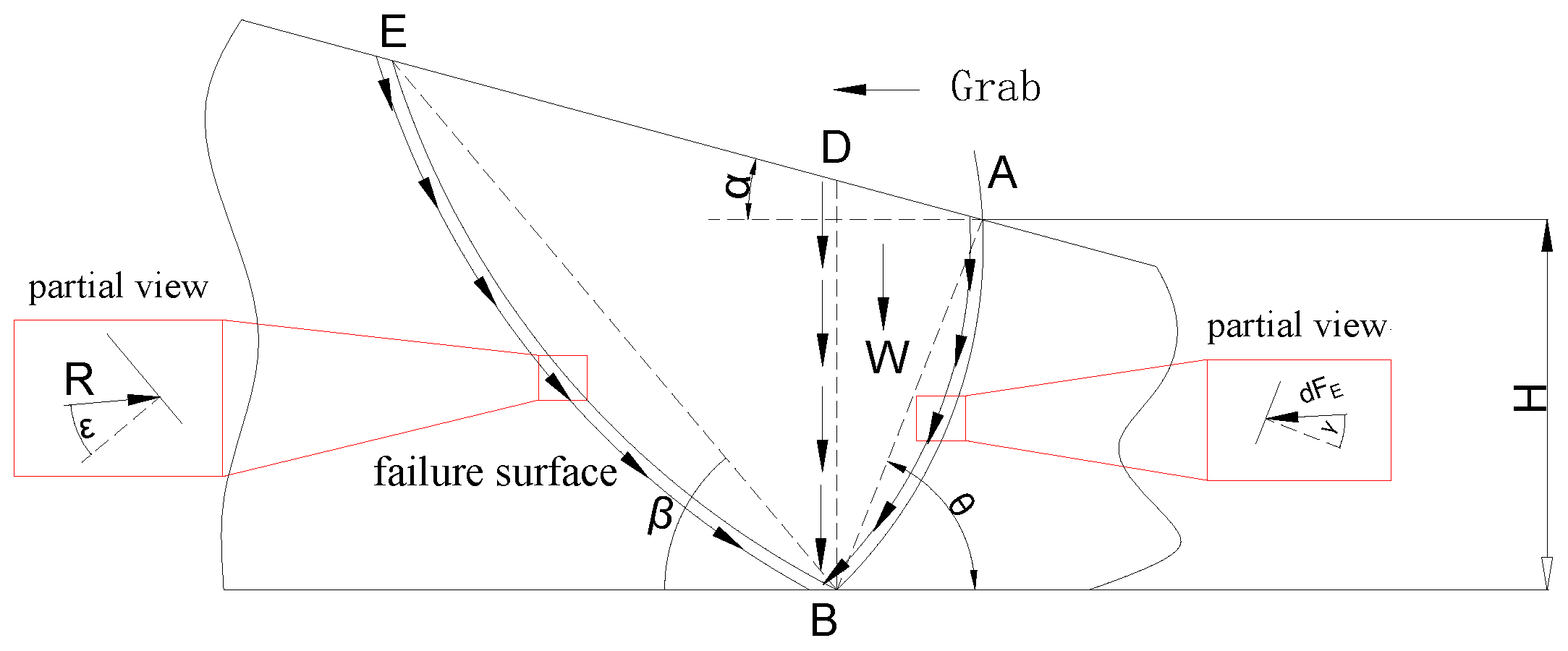
2.1.2. Passive Material Pressure and Its Failure Surface

As observed through comparative analysis of the active pressure of the material, the material in front of the grab generates passive pressure, and the material is destroyed, resulting in a failure surface, as shown in Figure 5. The analysis of the interaction force between the grab and the material shows that the material’s weights $W_{ABD}$, $W_{BED}$ and passive pressure $F_E$ are as calculated in Formula (6):

$$W_{ABD}=\rho b{S}_{ABD}, W_{BED}=\rho b{S}_{BED}, F_E={{\displaystyle \int }}_0^H{p}_E\left(z\right)dz$$

(6)

where $W$ is the weight of body ABE (N), $\rho$ is the material density ($\mathrm{N}/{\mathrm{m}}^3$), $b$ is the grab width (m), $S_{ABD}$ is the area of body ABD ($m^2$), $S_{BED}$ is the area of body BED (${\mathrm{m}}^2$), $F_E$ is the passive resultant value (N), $H$ is the digging depth (m), $z$ represents the integral formal parameters (m), and $p_E$ is the pressure value at depth z ($\mathrm{N}/\mathrm{m}$).

The force balance condition of the material body ABE is:

$${\overrightarrow{F}}_E+{\overrightarrow{W}}_{ABD}+{\overrightarrow{W}}_{BDE}+\overrightarrow{R}=0$$

(7)

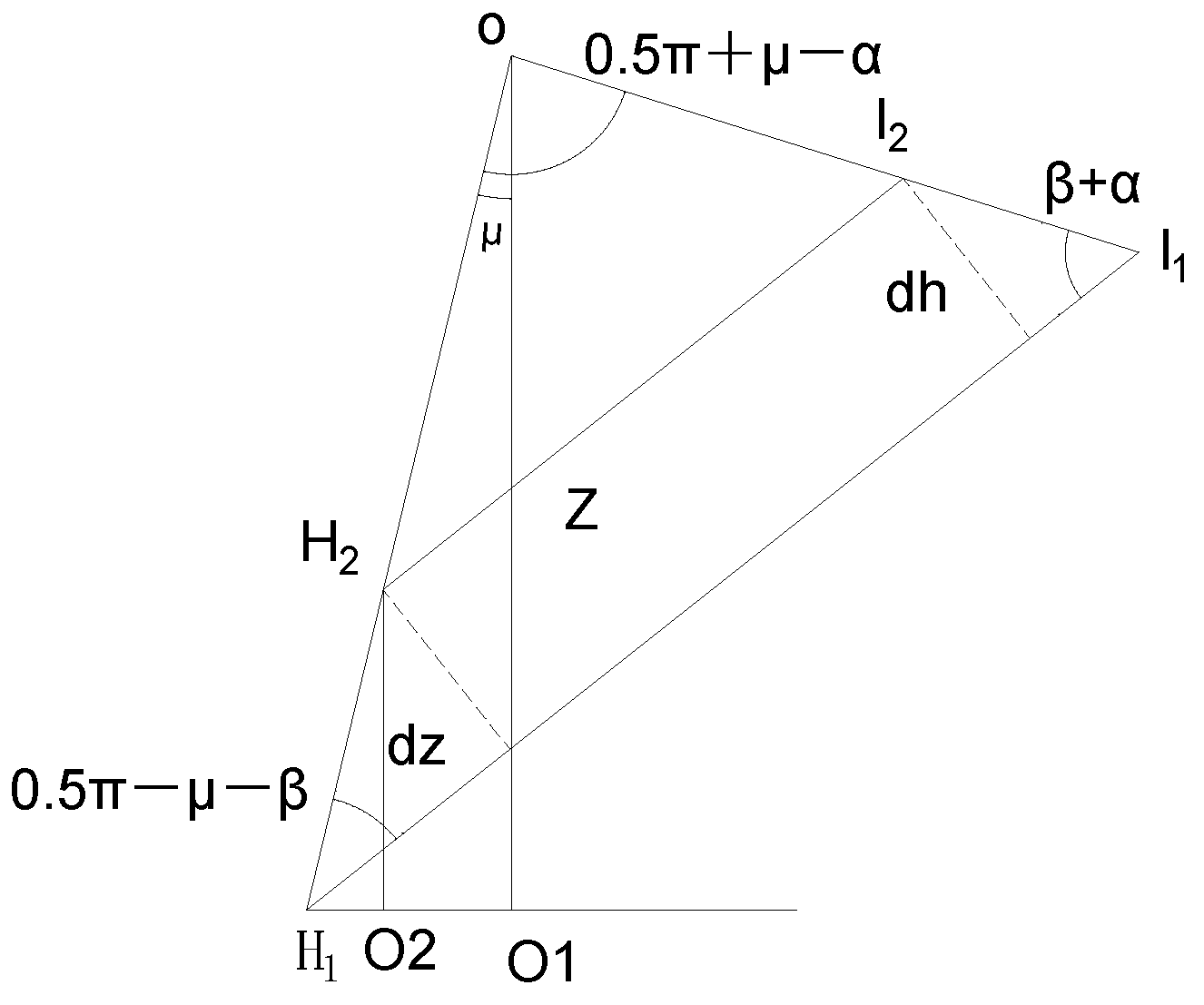
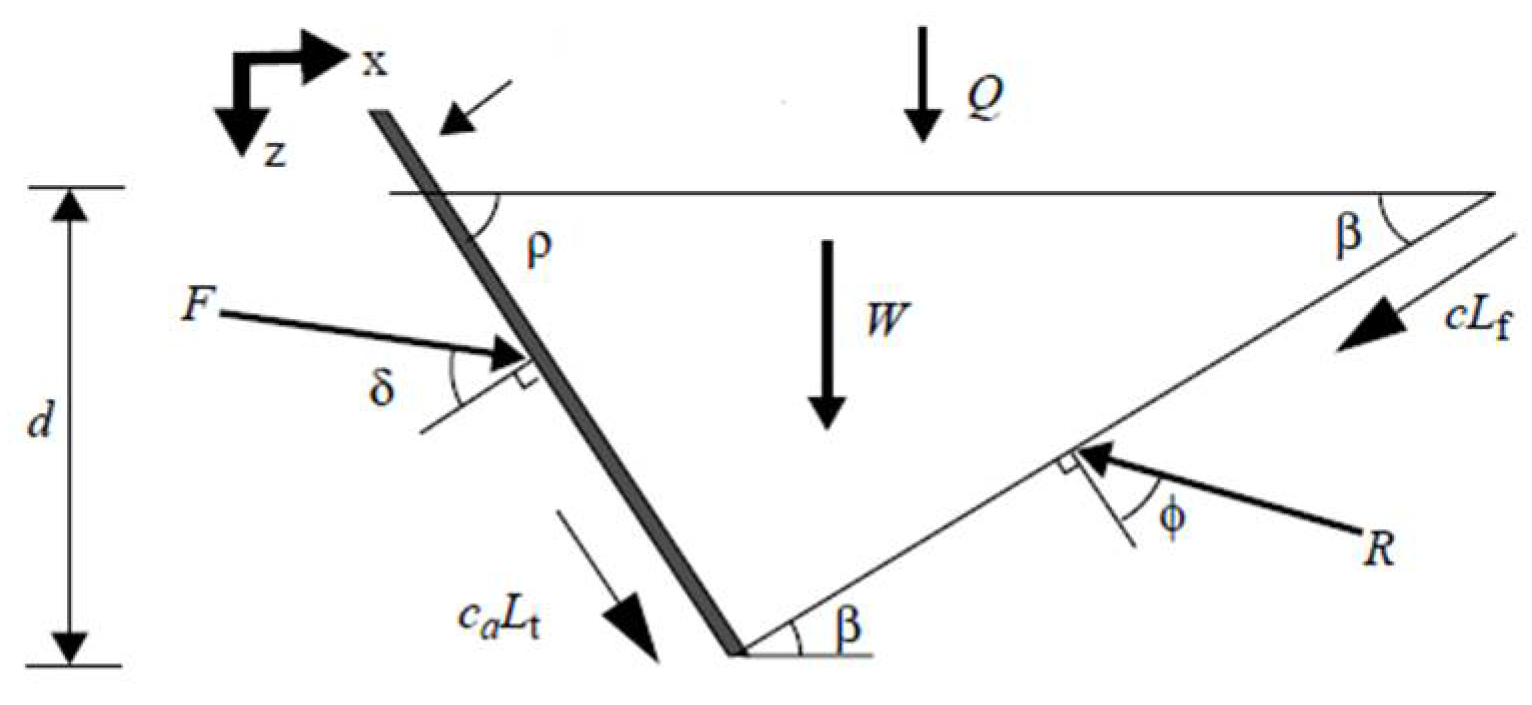
2.1.3. Analysis of Force Based on Unit Integration Method

From the analysis of the force model of the material excavated by the grab, it can be seen that the unit integration method may be used to analyze the equilibrium state of the material bodies ABC and ABD, as shown in Figure 6. The interaction force between the grab and the material can be calculated according to Formula (8):

$$F_D=F_E-F_B={{\displaystyle \int }}_0^H(p_E\left(z\right)-p_B\left(z\right))dz$$

(8)

where $F_D$ is the digging resistance (N), $F_B$ is the active pressure resultant value (N), and $F_E$ is the passive pressure resultant value (N).

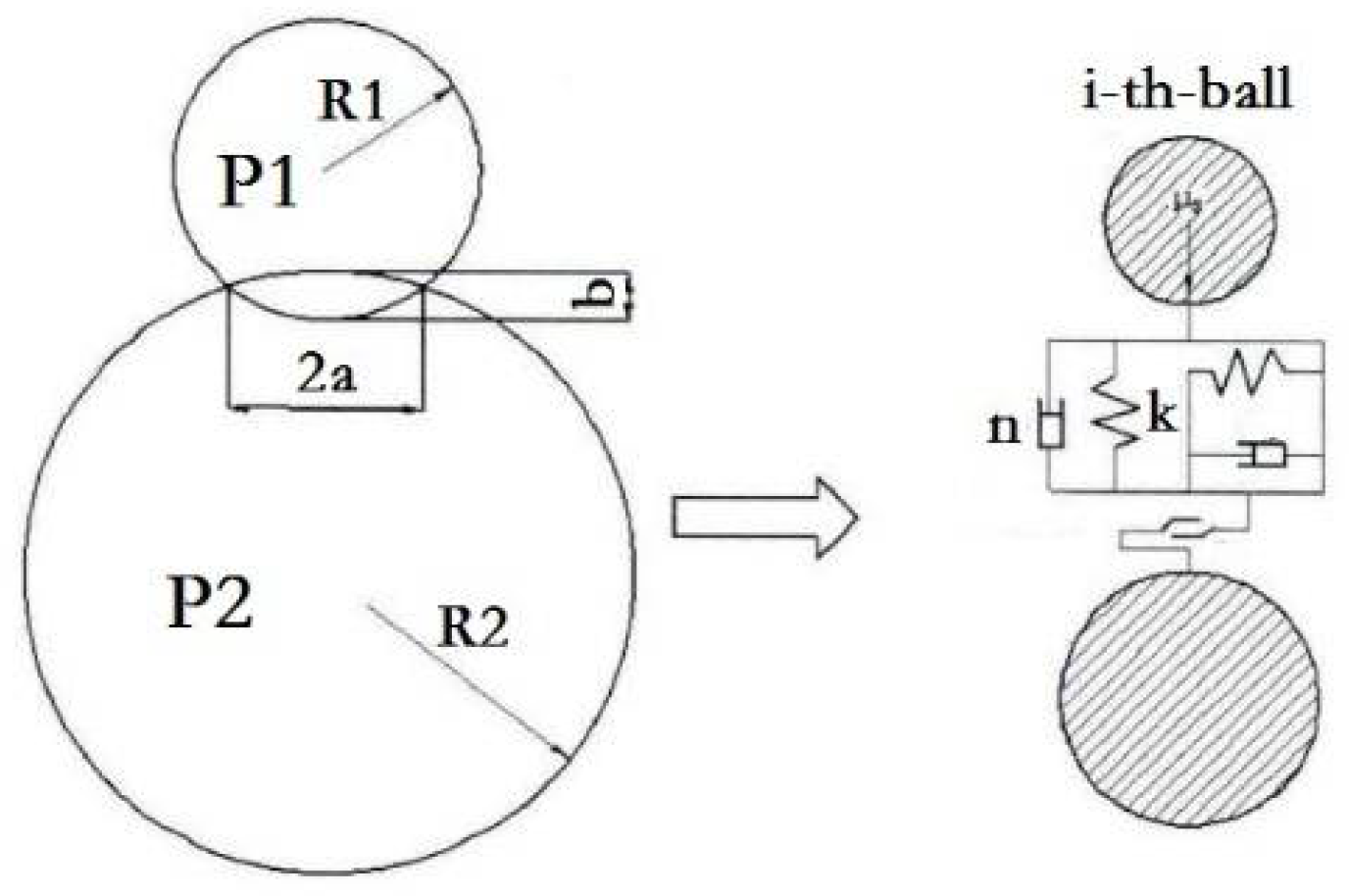
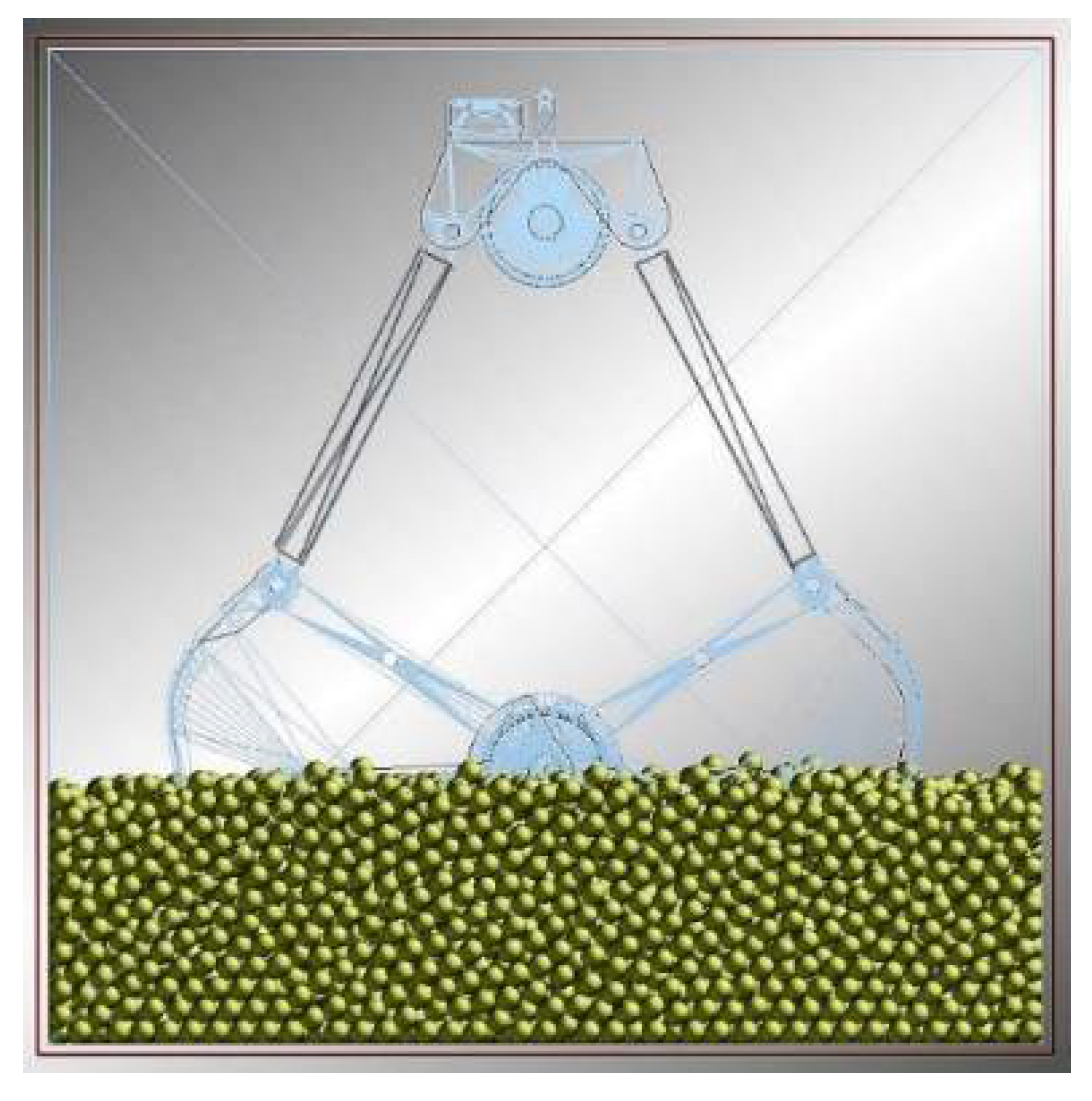
2.2. Mechanical Mechanism of Flat Digging Based on the DEM

2.2.1. Particle Model of the DEM

The analysis object of the DEM is a series of discrete objects, and each unit is a particle. In the DEM, the motion parameters and motion characteristics of each particle are calculated, and a discrete simulation of the material is carried out. In the DEM, the mechanical characteristics of the particles need to be analyzed and specified. Through the vibration equation, the contact between the particles and the force between the particles can be obtained. Figure 7 presents the vibration model of the particle [19,20,21].

In this study, the DEM is used to analyze the contact process of the material particles. Through the output of the particle vibration model, the normal vibration motion equation of the particles can be obtained [22,23]:

$$m_{1,2}{d}^2{u}_n/d{t}^2+c_{n}d{u}_n/dt+K_n{u}_n=F_n$$

(9)

In the same way, the tangential vibration equation of the particle can be obtained:

$$m_{1,2}{d}^2{u}_s/d{t}^2+c_{s}d{u}_s/dt+K_s{u}_s=F_s$$

(10)

$$I_{1,2}{d}^2\theta /d{t}^2+\left(c_{s}d{u}_s/dt+K_s{u}_s\right)s=M$$

(11)

In the above formulae, $m_{1,2}$ are the masses of particles i and j, $I_{1,2}$ are the moments of inertia of the particles, $s$ is the radius of rotation, $u_n$ and $u_s$ are the particle normal and tangential displacements, respectively, $\theta$ is the particle rotation angle, $F_n$ and $F_s$ are the particle normal component and tangential component, respectively, $M$ is the external moment of the particle, $K_n$ and $K_s$ are the particle normal and tangential elastic coefficients, and $c_n$ and $c_s$ are the particle normal and tangential damping coefficients, respectively.

2.2.2. Mechanical Numerical Simulation

For the process of flat digging by the grab, a discrete element mechanical model is constructed. The spherical sand particle is selected as the particle for the transfer process and the simulated spherical sand is generated in the particle factory. The particles produced by the particle factory need a space to be stored, so we create a box area to store particles of the same size as the particle factory setup. The relevant parameters, which are used for DEM simulations, are summarized in

Table 1. DEM parameters used in simulations.

Parameters (Unit)	Value
Sand Poisson ratio	0.5
Sand shear modulus (Pa)	1.0 × 107
Sand density (kg/m3)	2650
Steel Poisson ratio	0.3
Steel shear modulus (Pa)	7 × 1010
Steel density (kg/m3)	7850
Sand–sand restitution coefficient	0.48
Sand–sand static friction coefficient	0.57
Sand–sand rolling friction coefficient	0.07
Sand–steel restitution coefficient	0.45
Sand–steel static friction coefficient	0.58
Sand–steel rolling friction coefficient	0.08
Surface energy (J/m2)	6.5

. The size of the sand model constructed in this section is 3000 mm × 2200 mm × 1200 mm. For the process of flat digging the sand with the grab, the simulated sand is generated in the particle factory. The generation methods of material particles can be static or dynamic. As shown in Figure 8, the static method of generating materials was selected for this simulation.

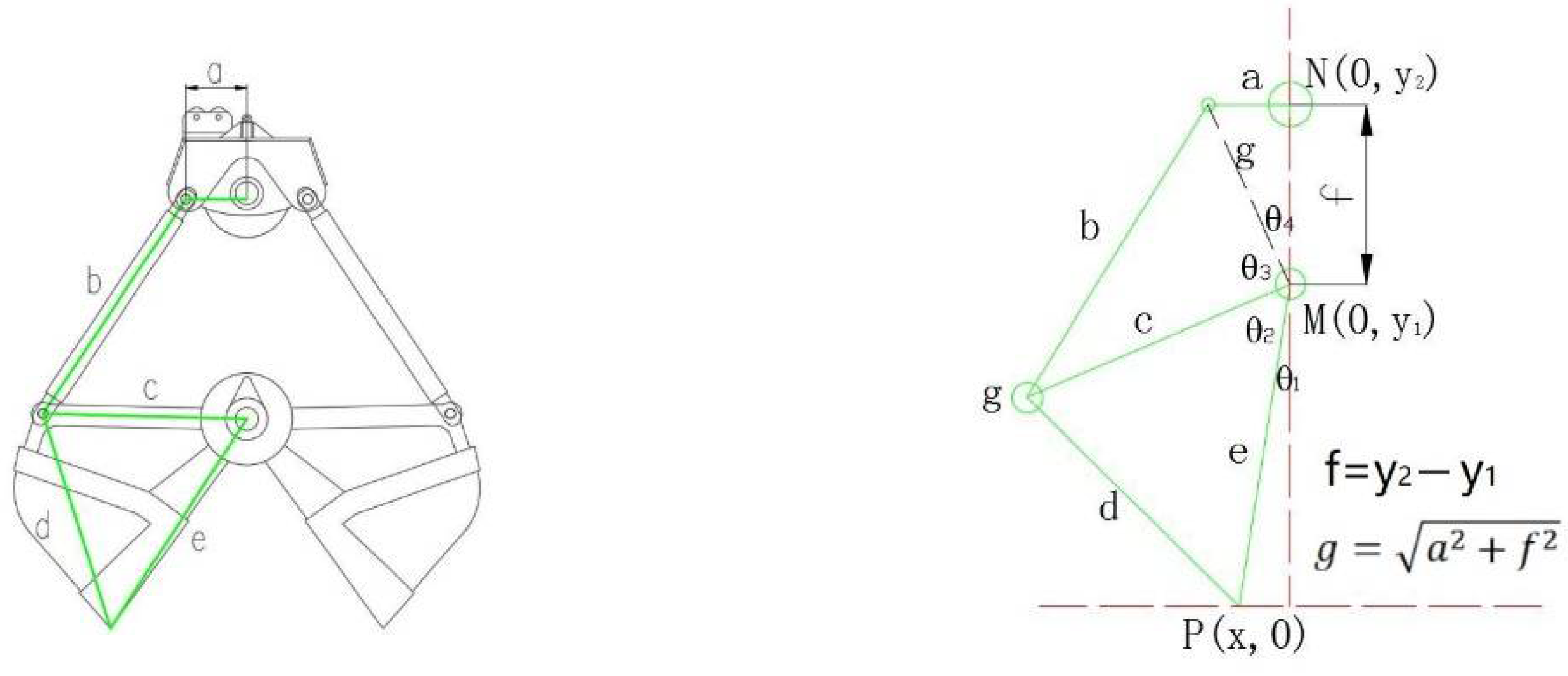
2.3. Theoretical Simulation Analysis of Flat Digging Precision

The flat digging process of the grab is analyzed, and the flat digging movement of the grab is determined by controlling the kinematic relation between the hoist wires and the closing wires. The simplification of the flat digging movement of the grab can convert the movement of the hoist wires and the closing wires to the movement of the lower sheave block and the upper sheave block [24]. In Figure 9, point P is the edge of the grab, which moves in the horizontal direction, and points N and M are the upper and lower beams, respectively, which move in the vertical direction only.

Analyzing the flat digging mathematical model of the grab, Equation (12) can be expressed, where $a$, $b$, $c$, $d$, and $e$ are the main structural dimensions of the grab; ${\theta }_1$, ${\theta }_2$, ${\theta }_3$, and ${\theta }_4$ are the intermediate parameters; and $y_1$ and $y_2$ are the ordinate values of the upper and lower blocks.

$$\{\begin{array}{c}\mathit{cos}{\theta }_1=\frac{y_1}{e}\\ \mathit{cos}{\theta }_2=\frac{c^2+e^2-d^2}{2ce}\\ \mathit{cos}{\theta }_3=\frac{c^2+g^2-b^2}{2cg}\\ \mathit{tan}{\theta }_4=\frac{a}{y_2-y_1}\\ g=\sqrt{a^2+{(y_2-y_1)}^2}\\ {\theta }_1+{\theta }_2+{\theta }_3+{\theta }_4=\pi \end{array}$$

(12)

In the formula above, $a$ is the distance from the upper end of the strut to the center of the upper block, $b$ is the length of the strut, $c$ is the distance from the lower end of the strut to the center of the lower block, $d$ is the distance from the lower end of the strut to the grab tooth end, $e$ is the distance from the grab tooth end to the lower block, and f is the distance between the upper and lower blocks.

2.4. Flat Digging Experiment

The 0.3 m³ grab dredger mainly consists of a hoisting mechanism, a luffing mechanism, a cable hook device, a boom, a frame, a slewing ring, a machine room, a driver room, and an electrical control system. Figure 10 presents a physical diagram of the equipment. When the 0.3 m³ grab dredger is in flat digging operation, the measurement of the flat digging precision can reflect the shape precision characteristics of the grab.

At the test site, the foundation pit was divided into two parts; the left part was filled with dry sand (1.25–1.6 t/m³), and the right with wet soil (1.65–2.0 t/m³). According to actual measurements, the proportion of clay in the dry sand was 1.45 t/m³, and the specific weight of wet sand was 1.86 t/m³.

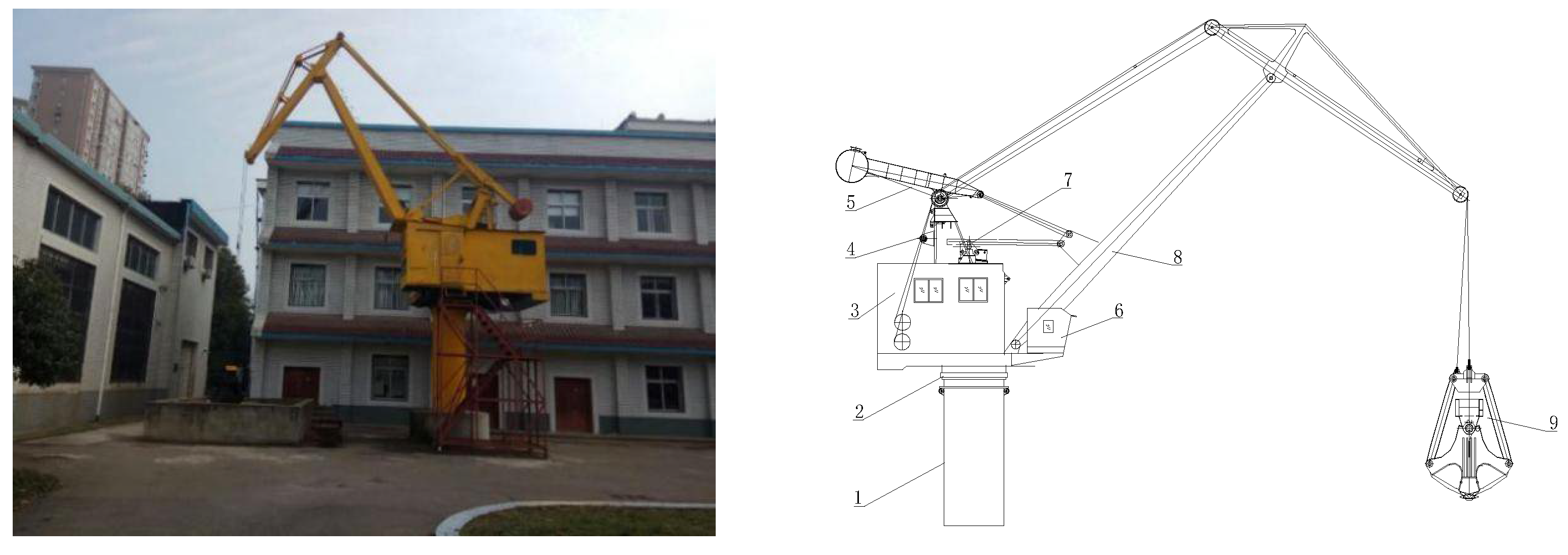
The theoretical flat digging precision can now be verified by the flat digging experiment.

3. Results

3.1. Theoretical Digging Resistance

3.1.1. Active Pressure $F_B$

From the analysis of the force in the process of excavating material using the grab, it can be understood that the force can be further simplified on the basis of the characteristics of forces W, R and $F_B$. In Figure 11, the roles of unit forces for $dW$, $q$ and $d{F}_B$ are presented, where $q-dq$ and $q$ represent the contact forces between the material layers.

The weight $dW$ of the material is determined by the area of the material unit $H_1{I}_1{H}_2{I}_2$ body.

$$dh=\frac{\mathit{cos}(\beta +\mu )}{\mathit{cos}\mu }dz$$

(13)

$$\mu \left(z\right)=\frac{\pi }{2}-\tan \left(\frac{d}{d\eta }H\left(\eta \right){|}_{\eta =z}\right)$$

(14)

where $dh$ is the height of the trapezoid of $H_1{I}_1{H}_2{I}_2$ (m), $\mu$ is the angle between the tangent and the vertical direction of the surface point (rad), $\beta$ is the angle between the failure plane and the horizontal plane (rad), $\eta$ is the grab digging depth (m), and $H\left(\eta \right)$ is a function of the grab geometry parameters (m).

The following section analyzes the calculation of the pressure of the grab for any shape of material, as shown in Figure 12.

The trapezoidal area of the material unit is calculated according to the following formulae:

$$\begin{gathered} \frac{H_1{I}_1}{\mathit{sin}(0.5\pi -\left(\mu +\alpha \right))}=\frac{O{H}_1}{\mathit{sin}\left(\beta +\alpha \right)},O{H}_1=\frac{z}{\mathit{cos}\mu } \\ {H}_1{I}_1=\frac{\mathit{cos}\left(\alpha +\mu \right)}{\mathit{sin}\left(\beta +\alpha \right)\mathit{cos}\mu }z \end{gathered}$$

(15)

$$H_2{I}_2=\frac{\cos \left(\alpha +\mu \right)}{\sin \left(\beta +\alpha \right)\cos \mu }z-\frac{\sin \left(\beta +\mu \right)}{\cos \mu }dz-\frac{\cos \left(\beta +\mu \right)}{\cos \mu \tan \left(\beta +\alpha \right)}dz$$

(16)

$$S_{H_1{I}_1{H}_2{I}_2}=\frac{1}{2}\left(H_1{I}_1+H_2{I}_2\right)dh=\frac{\cos \left(\alpha +\mu \right)\cos \left(\beta +\mu \right)}{\sin \left(\beta +\alpha \right){\cos }^2\mu }zdz$$

(17)

The weight of the material unit body is:

$$dW=\rho b{S}_{H_1{I}_1{H}_2{I}_2}=\frac{\cos \left(\alpha +\mu \right)\cos \left(\beta +\mu \right)}{\sin \left(\beta +\alpha \right){\cos }^2\mu }z\rho bdz$$

(18)

where $dW$ is the material weight (N).

By analyzing the force balance of the trapezoidal material unit body, in the X and Y directions, the balance formula is obtained:

$$\{\begin{array}{l}{\displaystyle \sum F_x=d{F}_B\cos \left(\gamma -\mu \right)+\left(\left(q-dq\right)H_2{I}_2-q{H}_1{I}_1\right)\sin \left(\beta -\epsilon \right)=0}\\ {\displaystyle \sum F_y=d{F}_B\sin \left(\gamma -\mu \right)-\left(\left(q-dq\right)H_2{I}_2-q{H}_1{I}_1\right)\cos \left(\beta -\epsilon \right)-dW=0}\end{array}$$

(19)

where $\gamma$ is the friction angle between grab and material (rad).

Solving the above equation, the formula of active pressure $d{F}_B$ is obtained as follows:

$$d{F}_B=\frac{dW}{\sin \left(\gamma -\mu \right)-\cos \left(\gamma -\mu \right)\cot \left(\beta -\epsilon \right)}$$

(20)

Further analysis of the force can be carried out as follows:

$$d{F}_B=\frac{\cos \left(\alpha +\mu \right)\cos \left(\beta +\mu \right)}{\left(\sin \left(\gamma -\mu \right)-\cos \left(\gamma -\mu \right)\cot \left(\beta -\epsilon \right)\right)\sin \left(\beta +\alpha \right){\cos }^2\mu }z\rho bdz$$

(21)

By dividing the left and right ends of the above equation by dz, we obtain:

$$P_B:=\frac{d{F}_B}{dz}=f_B\left(\beta \right)zb\rho$$

(22)

where $f_B\left(\beta \right)$. is satisfied thus:

$$f_B\left(\beta \right)=\frac{\cos \left(\alpha +\mu \right)\cos \left(\beta +\mu \right)}{\left(\sin \left(\gamma -\mu \right)-\cos \left(\gamma -\mu \right)\cot \left(\beta -\epsilon \right)\right)\sin \left(\beta +\alpha \right){\cos }^2\mu }$$

(23)

It is now necessary to find the extreme value of $f_B\left(\beta \right)$. to determine the sliding surface, and so Formula (23) can be further transformed into:

$$\begin{array}{l}{f}_B\left(\beta \right)=\frac{\cos \left(\alpha +\mu \right)(\cos \mu -\tan \beta \sin \mu )/{\cos }^2\mu }{[\sin (\gamma -\mu -\epsilon )\tan \beta -\cos (\gamma -\mu -\epsilon )]}\\ \times \frac{\tan \beta \cos \epsilon -\sin \epsilon }{\tan \beta \cos \alpha +\sin \alpha }\end{array}$$

(24)

The extreme value of function $f_B\left(\beta \right)$. for $\beta$ can be understood as equivalent to the extreme value of function $f_B\left(tan\beta \right)$ for $tan(\beta )$, so let

$$\frac{d{f}_B\left(\tan \left(\beta \right)\right)}{d\tan \left(\beta \right)}=0$$

(25)

Analysis shows that the equation for $tan(\beta )$ is:

$$\begin{array}{l}[-2\tan \beta \sin \mu \cos \epsilon +\cos (\mu -\epsilon )][\sin (\gamma -\mu -\epsilon )\tan \beta -\cos (\gamma -\mu -\epsilon )]\\ \times (\tan \beta \cos \alpha +\sin \alpha )\\ -[2\tan \beta \sin (\gamma -\mu -\epsilon )\cos \alpha -\cos (\gamma -\mu -\epsilon +\alpha )](\cos \mu -\tan \beta \sin \mu )\\ \times (\cos \epsilon \tan \beta -\sin \epsilon )=0\end{array}$$

(26)

It can be seen from the analysis of the above formula that $\varphi$ is the only solution of Equation (27), and so its expression is:

$$\varphi =f_{\varphi }(\alpha ,\mu ,\gamma ,\epsilon )=\tan \left({\beta }_1*\right)$$

(27)

where ${{\beta }_1}^{*}$ is the angle between the failure plane and the horizontal plane (rad), and so can be expressed thus:

$${{\beta }_1}^{\ast }={\tan }^{-1}\left(\varphi \right)$$

(28)

The expression to obtain $P_B$ is:

$$P_B=\frac{\cos \left(\alpha +\mu \right)(\cos \mu -\varphi \sin \mu )/{\cos }^2\mu }{[\sin (\gamma -\mu -\epsilon )\varphi -\cos (\gamma -\mu -\epsilon )]}\times \frac{\varphi \cos \epsilon -\sin \epsilon }{\varphi \cos \alpha +\sin \alpha }b\rho z$$

(29)

The active pressure coefficient $p_B$ is a function of the excavation depth z, and $F_B$ is expressed in definite integral form as follows:

$$F_B=b\rho {\displaystyle \underset{0}{\overset{H}{\int }}\frac{\cos \left(\alpha +\mu \right)(\cos \mu -\varphi \sin \mu )/{\cos }^2\mu }{[\sin (\gamma -\mu -\epsilon )\varphi -\cos (\gamma -\mu -\epsilon )]}\times \frac{\varphi \cos \epsilon -\sin \epsilon }{\varphi \cos \alpha +\sin \alpha }dz}$$

(30)

where $\varphi =f_{\varphi }(\alpha ,\mu ,\gamma ,\epsilon )=\tan \left({\beta }_1*\right)$.

3.1.2. Passive Pressure $F_E$

Figure 13 is a schematic diagram of the force of the unit body under passive pressure.

We analyze the material pressure calculation of the shape of the trapezoidal unit body, so that:

$$dW=\rho b{S}_{J_1{K}_1{J}_2{K}_2}=\frac{\cos \left(\beta -\mu \right)}{\sin \beta \cos (\mu +\alpha )}(H-z)\rho bdz$$

(31)

Carrying out the force analysis on the trapezoidal unit body $J_1{K}_1{J}_2{K}_2$, the mechanical balance equation of the unit body is obtained as follows:

$$\{\begin{array}{l}{\displaystyle \sum F_X}=d{F}_E\cos \left(\gamma -\beta -\frac{\pi }{2}\right)-\left(\left(q-dq\right)J_2{K}_2-q{J}_1{K}_1\right)\sin \left(\epsilon -\alpha \right)=0\\ {\displaystyle \sum F_y}=d{F}_E\sin \left(\gamma -\beta -\frac{\pi }{2}\right)+\left(\left(q-dq\right)J_2{K}_2-q{J}_1{K}_1\right)\cos \left(\epsilon -\alpha \right)-dW=0\end{array}$$

(32)

where $d{F}_E$ is the passive pressure (N).

Using the same elimination method as the previous section, the unit pressure can now be derived thus:

$$d{F}_E=\frac{\tan (\epsilon -\alpha )}{\tan (\epsilon -\alpha )\cos (\beta -\gamma )-\sin (\beta -\gamma )}\times \frac{\cos (\beta -\mu )}{\sin \beta \cos (\mu +\alpha )}(H-z)\rho bdz$$

(33)

The specific expression for $f_E\left(\beta \right)$ is:

$$f_E\left(\beta \right)=\frac{\tan \left(\epsilon -\alpha \right)\cos \left(\beta -\mu \right)}{\left(\tan \left(\epsilon -\alpha \right)\cos (\beta -\gamma )-\sin (\beta -\gamma )\right)\sin \beta \cos (\mu +\alpha )}$$

(34)

We can now convert $f_E\left(\beta \right)$ further into the following formula:

$$\begin{array}{l}{f}_E\left(\beta \right)=\frac{\tan (\epsilon -\alpha )}{\sin \beta \cos (\mu +\alpha )}\\ \times \frac{\cos \beta \cos \mu +\sin \beta \sin \mu }{\left\{\tan (\epsilon -\alpha )(\cos \beta \cos \gamma +\sin \beta \sin \gamma )-(\sin \beta \cos \gamma -\sin \gamma \cos \beta )\right\}}\end{array}$$

(35)

In order to determine the position of the failure surface under passive pressure, we must find the extreme value of $f_E\left(\beta \right)$,

$$\frac{d{f}_E\left(\beta \right)}{d\beta }=0$$

(36)

The above equation is solved and analyzed, and then simplified as the following formal equation:

$$\begin{array}{l}\cos \mu (\tan (\epsilon -\alpha )\cos (\beta -\gamma )-\sin (\beta -\gamma ))=\\ \sin \beta \cos (\beta -\mu )(\tan (\epsilon -\alpha )\sin (\beta -\gamma )+\cos (\beta -\gamma ))\end{array}$$

(37)

The specific expression is:

$$\omega =\sin \beta =f_{\omega }\left(\alpha ,\mu ,\gamma ,\epsilon \right)$$

(38)

$${{\beta }_2}^{*}={\sin }^{-1}\left(\omega \right)$$

(39)

where ${{\beta }_2}^{*}$ is the angle between the failure surface and the horizontal surface (rad).

The expression to obtain $P_E$ is:

$$\begin{array}{l}{P}_E=\frac{\tan (\epsilon -\alpha )}{\omega \cos (\mu +\alpha )}\\ \times \frac{\sqrt{1-{\omega }^2}\cos \mu +\omega \sin \mu }{\left\{\tan (\epsilon -\alpha )(\sqrt{1-{\omega }^2}\cos \gamma +\omega \sin \gamma )-(\omega \cos \gamma -\sin \gamma \sqrt{1-{\omega }^2})\right\}}\end{array}$$

(40)

It can now be deduced that:

$$\begin{array}{l}{F}_E=b\rho {\displaystyle \underset{0}{\overset{H}{\int }}\frac{\tan (\epsilon -\alpha )}{\omega \cos (\mu +\alpha )}\times \frac{\sqrt{1-{\omega }^2}\cos \mu +\omega \sin \mu }{\left\{\tan (\epsilon -\alpha )(\sqrt{1-{\omega }^2}\cos \gamma +\omega \sin \gamma )-(\omega \cos \gamma -\sin \gamma \sqrt{1-{\omega }^2})\right\}}}\\ (H-z)dz\end{array}$$

(41)

where $\omega =\sin \beta =f_{\omega }(\alpha ,\mu ,\gamma ,\epsilon )$.

3.1.3. Digging Force $F_D$

On the basis of deriving the active and passive pressure resultant forces $F_B$ and $F_E$, the final grab digging force expression in the material excavation process is:

$$\begin{array}{l}{F}_D=F_E-F_B\\ =b\rho {\displaystyle \underset{0}{\overset{H}{\int }}\frac{\tan (\epsilon -\alpha )}{\omega \cos (\mu +\alpha )}\times \frac{\sqrt{1-{\omega }^2}\cos \mu +\omega \sin \mu }{\left\{\tan (\epsilon -\alpha )(\sqrt{1-{\omega }^2}\cos \gamma +\omega \sin \gamma )-(\omega \cos \gamma -\sin \gamma \sqrt{1-{\omega }^2})\right\}}}\\ (H-z)dz\\ -b\rho {\displaystyle \underset{0}{\overset{H}{\int }}\frac{\cos \left(\alpha +\mu \right)(\cos \mu -\varphi \sin \mu )/{\cos }^2\mu }{[\sin (\gamma -\mu -\epsilon )\varphi -\cos (\gamma -\mu -\epsilon )]}\times \frac{\varphi \cos \epsilon -\sin \epsilon }{\varphi \cos \alpha +\sin \alpha }dz}\\ =F_D(\alpha ,\mu ,\gamma ,\epsilon )\end{array}$$

(42)

where $\varphi =\tan {{\beta }_1}^{\ast }=f_{\varphi }(\alpha ,\mu ,\gamma ,\epsilon )$, $\omega =\sin {{\beta }_2}^{\ast }=f_{\omega }(\alpha ,\mu ,\gamma ,\epsilon )$.

The unit integration method is used to analyze and calculate the interaction force between the grab and the material, and a reasonable mathematical expression can be obtained.

In the process of calculating the digging force of the grab, some design dimensions related to the structure of the grab can be directly measured. The main structural dimensions and main parameter expressions related to the calculation are shown in

Table 2. Main characteristic parameters.

Parameters (Unit)	Value
Sand density $\mu$ (kg/m3)	0.5
The angle of internal friction of sand $\gamma$ (°)	30
Friction angle between sand and grab $\epsilon$ (°)	20
Cohesion (Pa)	14,300
Digging angle of grab $\alpha$ (°)	Parameter solution

.

By bringing the above parameters into the calculation, the digging force can now be obtained for flat digging depths of 75 mm and 100 mm, respectively. As shown in Figure 14, the abscissa is the opening ratio of the grab, and the ordinate is the digging force.

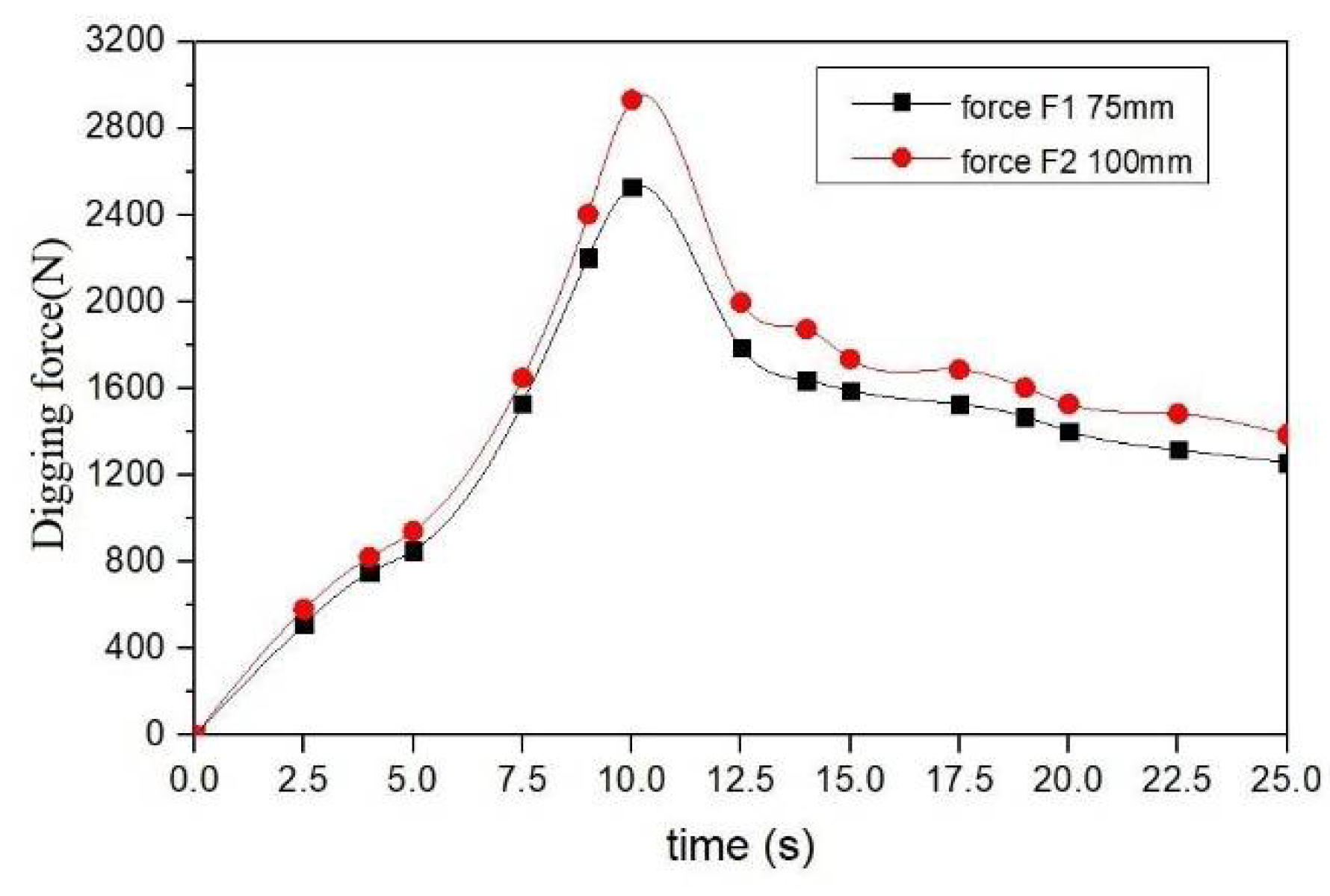
3.2. Simulation of Digging Force Value

In the mechanical model of the grab, the parameters of the grab are set so that the width of the grab edge is 30 mm. Based on the DEM in the simulation software, we inputted the parameter settings of the grab and material, ran the simulation and obtained the corresponding simulation results. As shown in Figure 15, the simulation is comprised of three stages: initialization, digging and completion.

In the process of flat digging by the grab, as the digging depth of the grab continues to increase, the digging resistance increases gradually due to the continuous cutting and pushing of the material by the grab body. Figure 16 illustrates the resistance to the flat digging force at depths of 75 mm and 100 mm, respectively. The simulation results of flat digging match well with the analytical results.

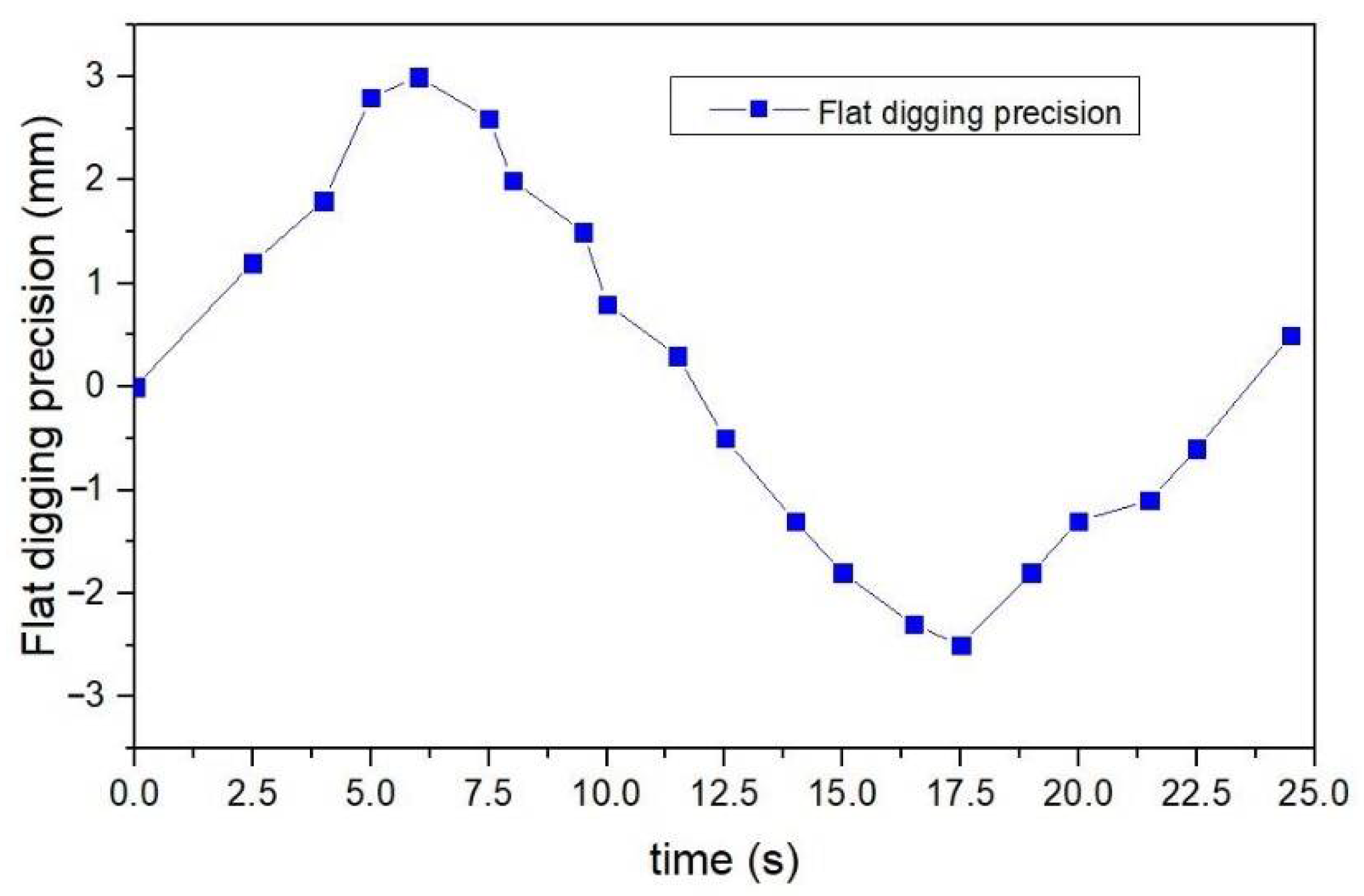
3.3. Flat Digging Precision Value

Based on the analysis in Section 2.3, we take the 0.3 m³ grab as an example. The parameter values of the 0.3 m³ grab are: a = 187 mm; b = 790 mm; c = 655 mm; d = 690 mm; e = 761 mm.

When analyzing the kinematics of the grab, the movement displacement and speed function of the closing wires of the grab are determined as follows (units: mm, mm/s):

$$s_1=\{\begin{array}{c}12.5t^2,0\le t\le 6\\ 450+150\times (t-6),6<t\le 18.5\\ 2775-12.5\times {(24.5-t)}^2,18.5<t\le 24.5\end{array}$$

(43)

$$v_1=\{\begin{array}{c}25t,0\le t\le 6\\ 150, 6<t\le 18.5\\ 25\times \left(24.5 - \mathrm{t}\right),18.5<t\le 24.5\end{array}$$

(44)

By analyzing the kinematics model of grab digging, the above-mentioned data are fitted, and the least square method can be used to obtain the displacement function and speed function for the hoist wires, in units of mm and mm/s, respectively:

$$s_2=2643sin(0.2633t+2.865)+2521sin(0.2635t-0.2123) 0\le t\le 24.5$$

(45)

$$v_2=695.9cos(0.2633t+2.865)+664.3cos(0.2635t-0.2123) 0\le t\le 24.5$$

(46)

It can be seen from Figure 17 that the precision of flat digging can be controlled within ±10 mm, and the leveling precision of the grab meets these requirements.

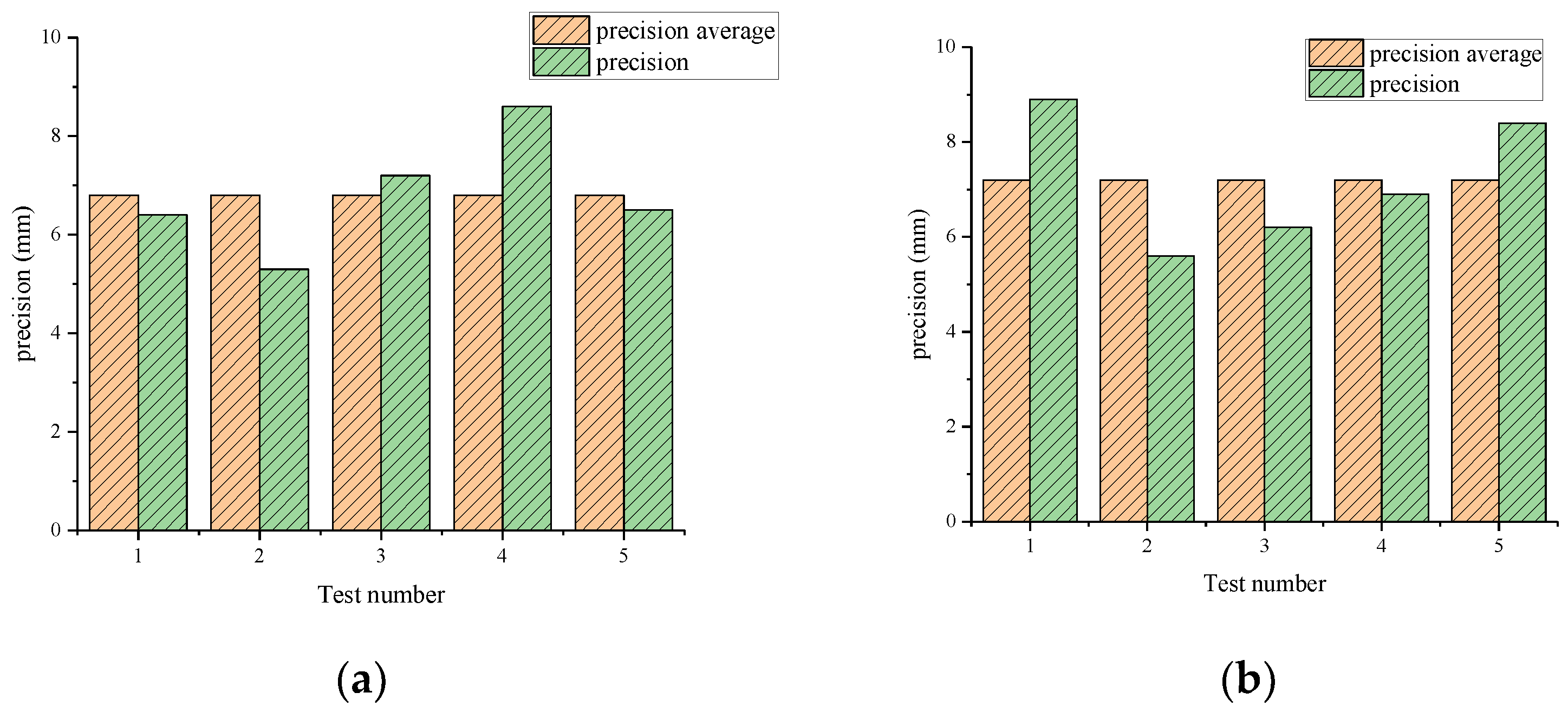
3.4. Flat Digging Experiment Results

In order to further verify the effect of flat digging precision, the experimental results were studied and discussed. Both the dry and wet sands were dug through to verify the precision of the grab dredger in different sands. Figure 18 shows the topography of the bottom of the trench after flat digging.

The digging test aims to measure the precision of digging. In this study, the standard measurement method of the leveling instrument is adopted. This method is widely used in plane measurement and can obtain accurate measurement data, as shown in Figure 19.

As shown in

Table 3. Analysis of grab flat digging precision data.

Test Number	Sand Proportion (t/m3)	Digging Depth (mm)	Flat Digging Precision (mm)	Precision Average (mm)
1	1.45	100	6.4
2	1.45	100	5.3
3	1.45	100	7.2	6.8
4	1.45	100	8.6
5	1.45	100	−6.5
6	1.86	100	8.9
7	1.86	100	5.6
8	1.86	100	−6.2	7.2
9	1.86	100	6.9
10	1.86	100	8.4

, the flat digging in the dry soil (specific gravity: 1.45 t/m³) and in the wet soil (specific gravity: 1.86 t/m³) exhibit similar precision (6.8 mm vs. 7.2 mm) at a depth of 100 mm. Both precision values fall within the expected range for the maximum allowable depth difference at 8.6 mm and 8.9 mm, respectively.

Figure 20 shows the precision data of flat digging.

In the flat digging test of the grab dredger, the grab is placed in a vertical drop and inserted into the sand without an inclination. The precision of flat digging mainly depends on the compensation error and the error caused by the manual selection of measuring points. Comparing the test data of flat digging precision with the theoretical data, it is found that in the flat digging test, the digging precision is still within the controllable range. The transfer of the error depends on the nature of the error and the relationship between the theoretical and the measured results.

We can now identify the basic equation thus:

$$M=f\left(M_x,M_y,M_z\right)$$

(47)

$$dM=\frac{\partial f}{\partial M_x}d{M}_x+\frac{\partial f}{\partial M_y}d{M}_y+\frac{\partial f}{\partial M_z}d{M}_z$$

(48)

The absolute error transfer equation can also be expressed [25,26]:

$$\mathsf{\Delta }M=\left|\frac{\partial f}{\partial M_x}\right|\mathsf{\Delta }{M}_x+\left|\frac{\partial f}{\partial M_y}\right|\mathsf{\Delta }{M}_y+\left|\frac{\partial f}{\partial M_z}\right|\mathsf{\Delta }{M}_z$$

(49)

Compared with the theoretical calculation (5.8 mm), we find the precision of flat digging (6.8 mm) is slightly better than that of the theoretical calculation. We therefore conclude that the precision of flat excavation is basically the same as that of the theoretical calculation, with a calculated error of about 3.15%.

4. Discussion and Conclusions

4.1. Discussion

4.1.1. Characteristics of Unit Integration Method

In this study, the unit integration method was proposed to calculate the excavation force of the grab. Regarding the traditional research on the excavation force of the grab, the excavation mechanics model and excavation force equation given by McKyes [27] are shown in Figure 21.

For the balance state of the excavating tool and the material, the force on the X-axis and the Y-axis is zero, the equation is as follows:

$$\sum F_x=F\sin (\alpha +\delta )+c_{a}L\cos \alpha -R\sin (\beta +\varphi )-c{L}_1\cos \beta =0$$

(50)

$$\sum F_z=-F\cos (\alpha +\delta )+c_{a}L\sin \alpha -R\cos (\beta +\varphi )+c{L}_1\sin \beta +W+Q=0$$

(51)

With further simplification, the equation for the digging force F can be obtained.

$$F=(\gamma g{d}^2{N}_{\gamma }+cd{N}_c+qd{N}_q+c_{a}d{N}_{ca})w$$

(52)

where $\gamma$ is material density; $g$ is the acceleration of gravity; $c$ is the material cohesion; $d$ is the excavation depth; $w$ is the excavation width; $q$ is the load on the material; $c_a$ is the adhesion coefficient; $N_{ca}$ is the influence coefficient of digging force; $N_{\gamma }$ is the density influence coefficient; $N_c$ is the viscosity influence coefficient of the material; $N_q$ is the influence coefficient of the load.

The research reported in this paper suggests that it is reasonable to use the unit integration method to calculate the relationship between the excavation force and the excavation parameters. Compared with the McKyes method, this method has the following advantages:

(1)

The grab has complex structural geometric parameters, and the analysis of the unit body mechanics model avoids the influence of the grab’s geometric parameters. Using the unit integration method, it can be converted into active pressure $F_B$ and passive pressure $F_E$.

(2)

For the characteristic analysis of the interaction force between the grab and the material, the unit body model can consider the friction between the materials. The construction of the mechanical model of the grab excavating material is more consistent with the actual grab excavation mechanical model.

4.1.2. Characteristics of Flat Digging Control

Due to the normal excavation operation of the grab, grooves will be formed at the bottom, as shown in Figure 22.

In contrast with the traditional excavation method, the grab level excavation described in this paper can achieve high flat digging precision. The steps by which such flat digging control is achieved were as follows:

(1) In Formula (12), the size parameters $a$, $b$, $c$, $d$, and $e$ of grab were determined, the kinematic equation established according to the kinematic relationship, and the variable parameters determined; (2) according to the set depth of flat digging, the motion trajectory of the natural excavation stage was calculated; (3) through the control movement of the closing wires and hoist wires, the upper block compensation method was used to carry out flat digging, and the movement trajectory calculated; (4) in this study, the flat digging precision was calculated and the parameters obtained as output. We found that reasonable surface accuracy could be obtained through flat digging grab control.

However, there are several limitations in this research. First, the property parameters of materials in DEM simulation were derived from their engineering characteristic parameters, and their complete accuracy cannot be guaranteed. Material parameters need to be verified by experiments to ensure the accuracy of experimental parameters; second, the material studied in this paper was exclusively sand, and there is a lack of research into other materials. It is necessary to further study the mechanical test of the grab digging material; third, this test was carried out on a land test site. Sea testing of the grab dredger may produce different results. Economic effects, weather factors and seawater flow should all be considered in future studies. The sea test will be completed in our follow-up work, which will further fulfil the research goal set out in this paper.

4.2. Conclusions

(1)

In this paper, in contrast with traditional research on the force of grab excavation, the unit integration method for analyzing the force of the grab excavation material was proposed. During the excavation process of the grab, the force on the grab produced active pressure $F_B$ and passive pressure $F_E$. $F_B$ and $F_E$, as expressed by integral equations, and the material was divided into units. Digging force $F_D$ was obtained by subtracting $F_B$ and $F_E$. Depending upon the characteristics of the material unit, this method can analyze the functional expression between the grab bucket digging force and the digging parameters.

(2)

Based on the DEM theory, the process of excavating materials with a grab was simulated. In the simulation process, reasonable data parameters were set, and the the grab flat digging force obtained. The simulation data shows that the digging force first increases and then decreases. Through comparative analysis, we found that the simulation results of the force of the grab flat digging are basically consistent with the theoretical calculation by the unit integration method, which verifies the correctness of the relevant theoretical models.

(3)

This study sought to control the movement distance of the closing wires and the hoist wires through the equation of motion, to carry out theoretical precision calculations and experimental research into grab flat digging. A flat digging test was carried out on land in fine weather conditions. The flat digging test was carried out on both dry soil and wet soil, and both demonstrated similar precisions (6.8 mm vs. 7.2 mm) at a depth of 100 mm. By comparing theoretical data and test data, the following conclusion is drawn: the deviation of the theoretical flat digging precision from the test data falls within the allowable range, at 3.15%. It is already known that sea tests differ from land tests, but land tests provide a foundation—and can provide supporting data—for future sea tests. Such sea tests will be completed in our follow-up work, which will more realistically reflect the flat digging test.