A State of the Art Review on Sensible and Latent Heat Thermal Energy Storage Processes in Porous Media: Mesoscopic Simulation
Abstract
:1. Introduction
2. Sensible Heat Storage (SHS) Method
2.1. Sensible Heat Storage Materials (SHSMs)
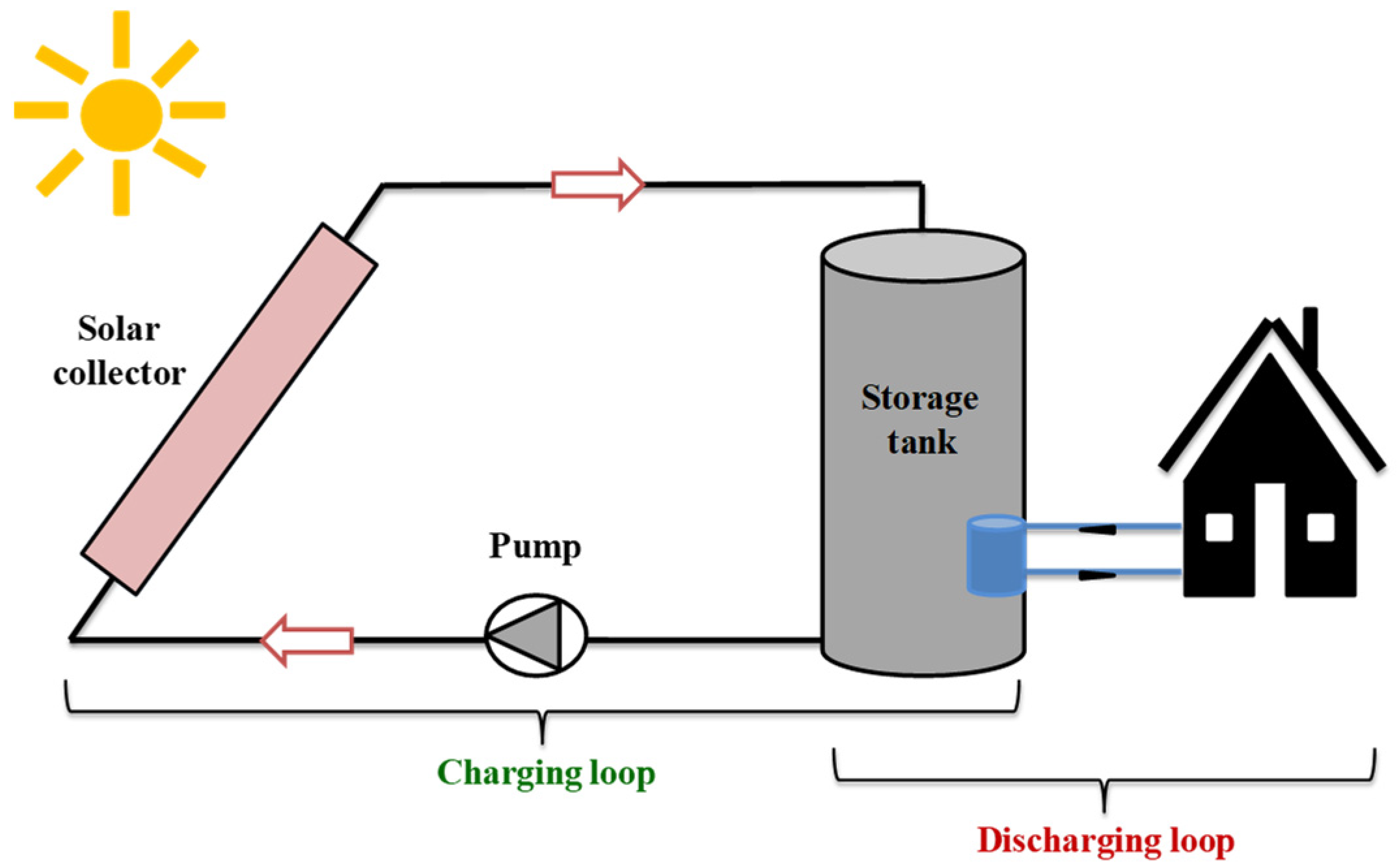
2.2. Sensible Heat Storage in Porous Media
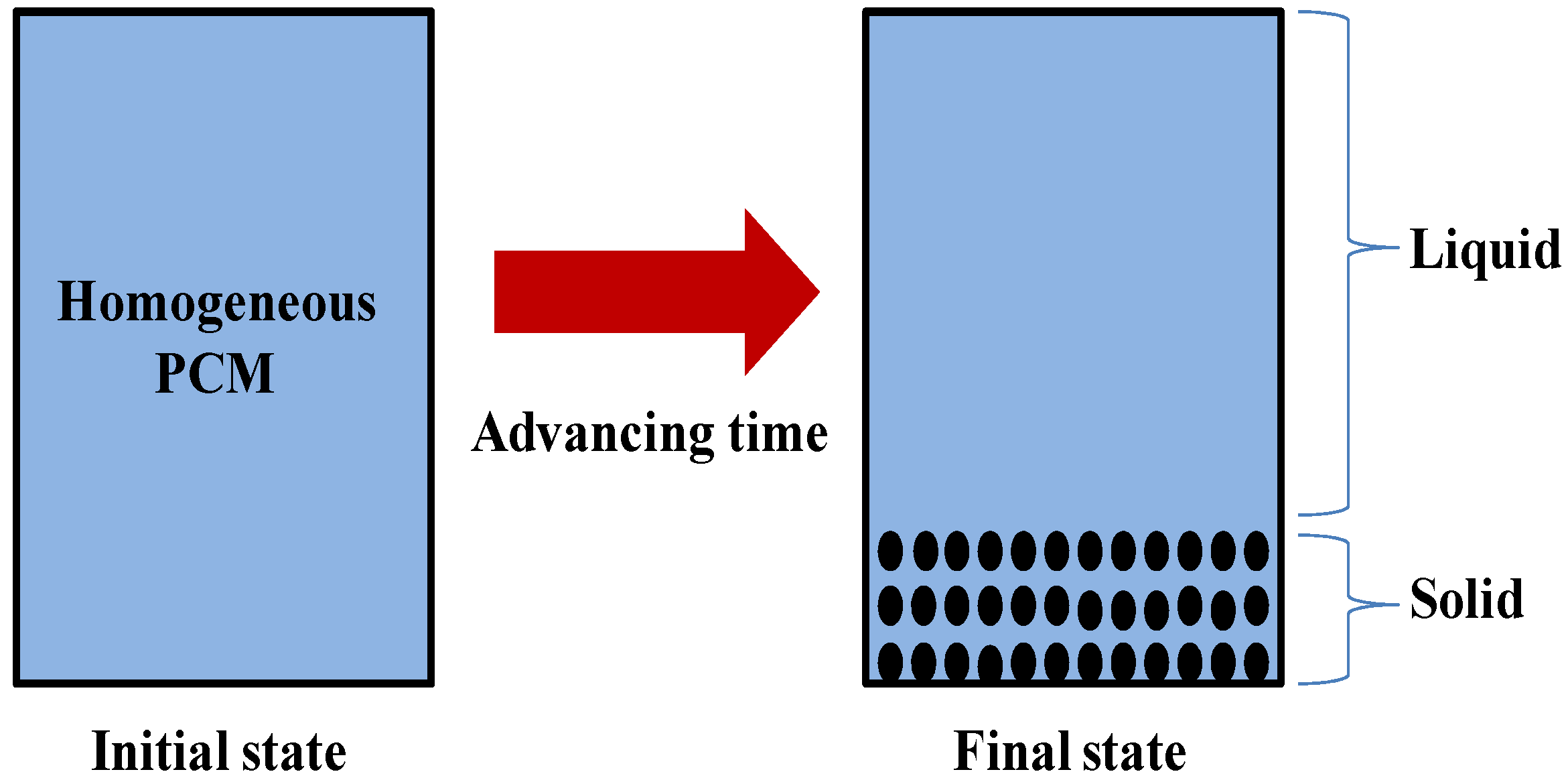
3. Latent Heat Storage (LHS) Method
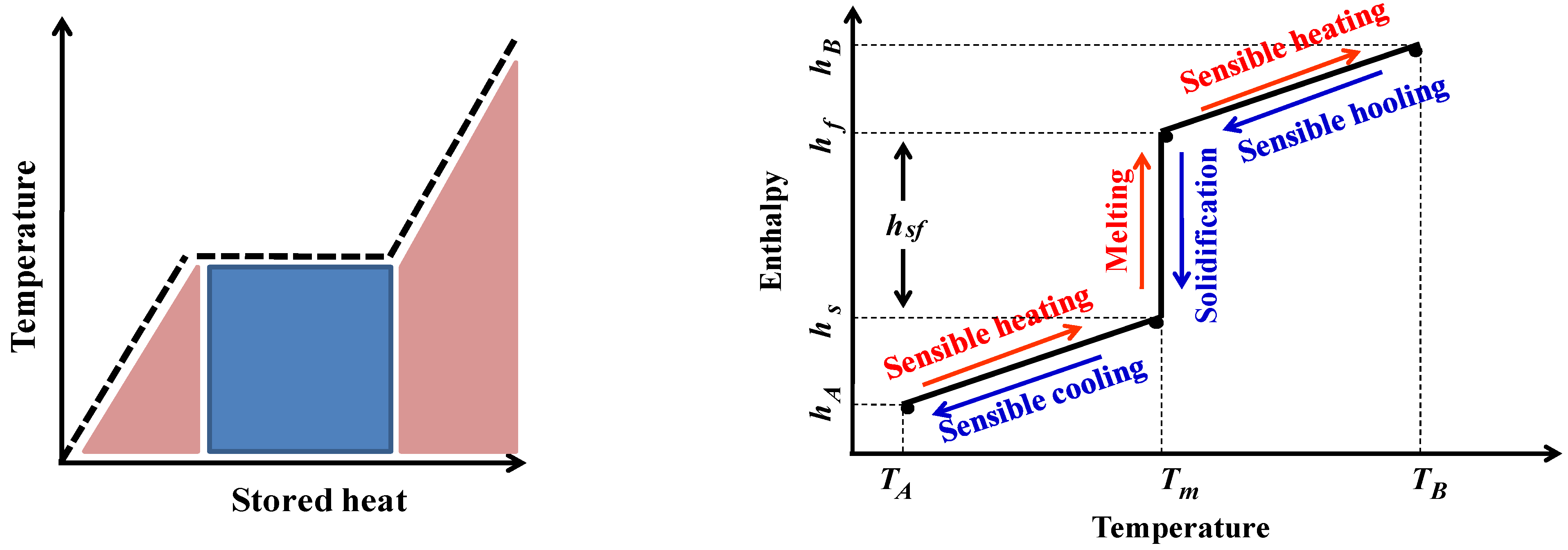
- The phase change enthalpy of PCMs is much higher than the sensible heat;
- LHS materials (PCM) have a storage density that can be five to 14 times greater than that of SHS materials [60];
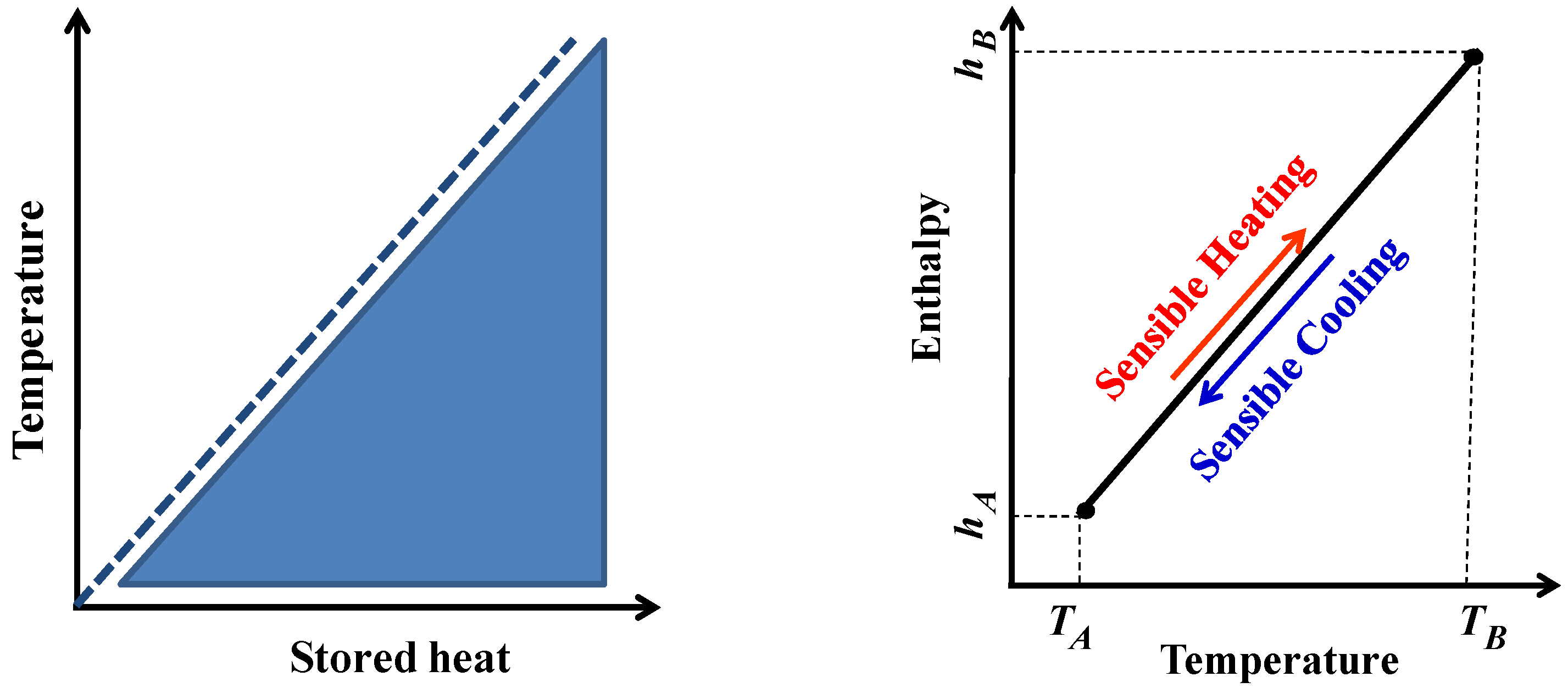
- The LHS method takes place in a quasi-isothermal manner unlike the SHS process where the materials temperature is too high;
- SHS systems using rocks (resp. water) require three times (resp. 1.5 times) more volume than LHS systems using paraffin wax [34];
- Seasonal overheating problems can be avoided in LHS systems due to the involved low mass.
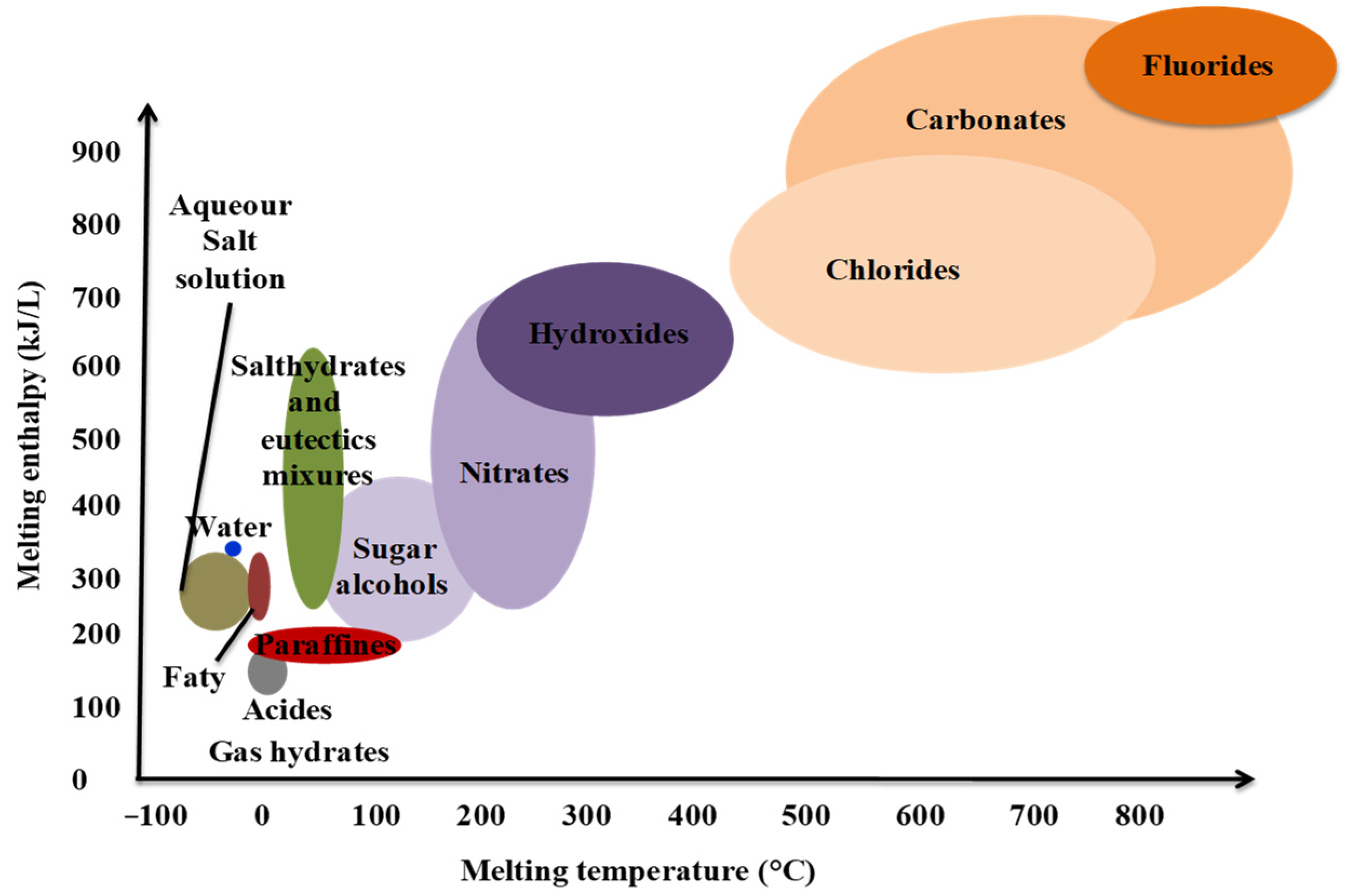
3.1. Latent Heat Storage Materials (LHSMs or PCMs)
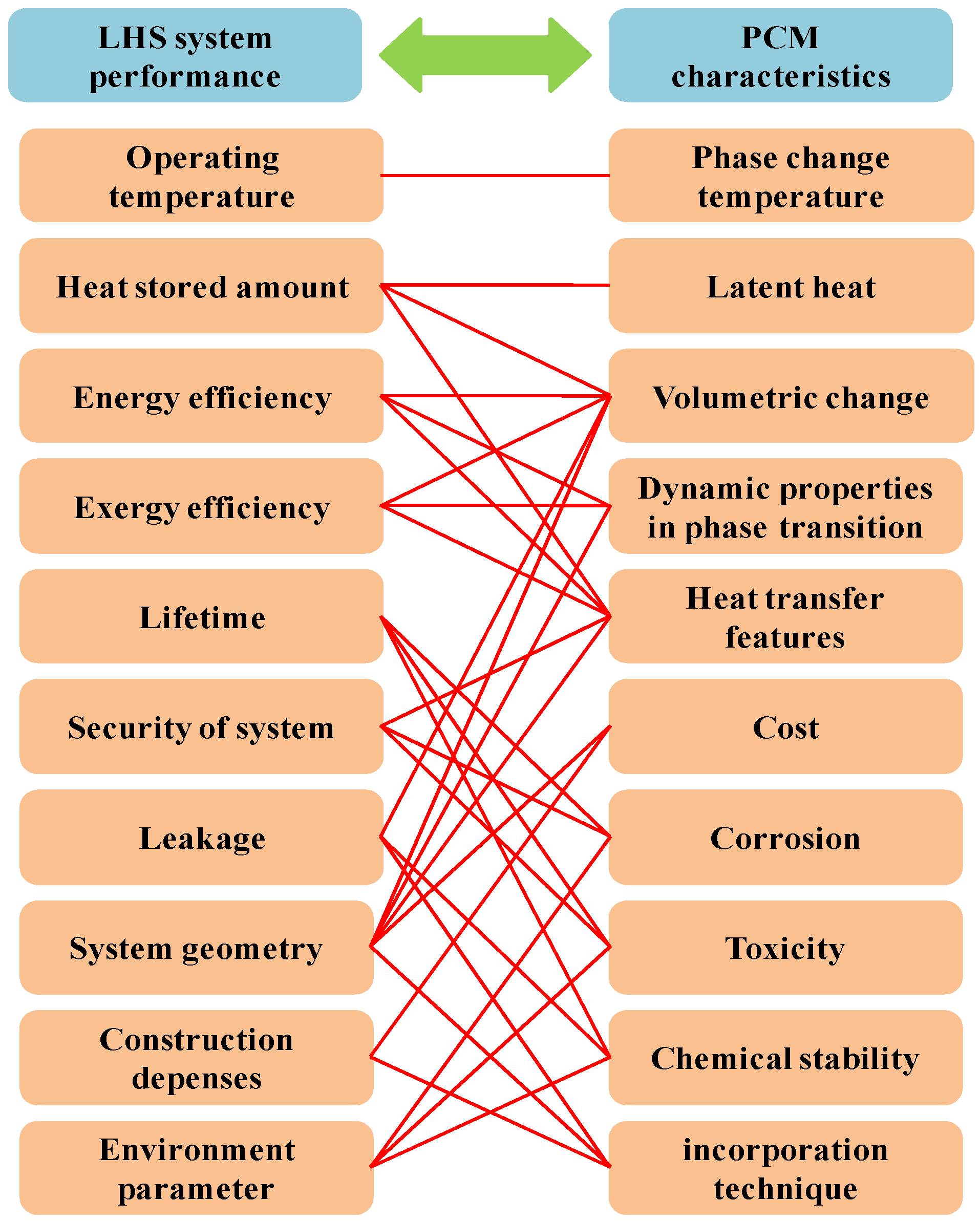
- In terms of thermal properties, the PCM must have a phase change temperature corresponding to the operating temperature of the LHS application. Moreover, it must have a latent heat and a specific heat. PCMs with high thermal conductivity are advocated to facilitate phase transition and interstitial heat transfer;
- Regarding physical properties, PCMs should exhibit large density, small volume changes and low vapor pressure during the phase transition process while respecting the operating temperature range to limit containment issues;
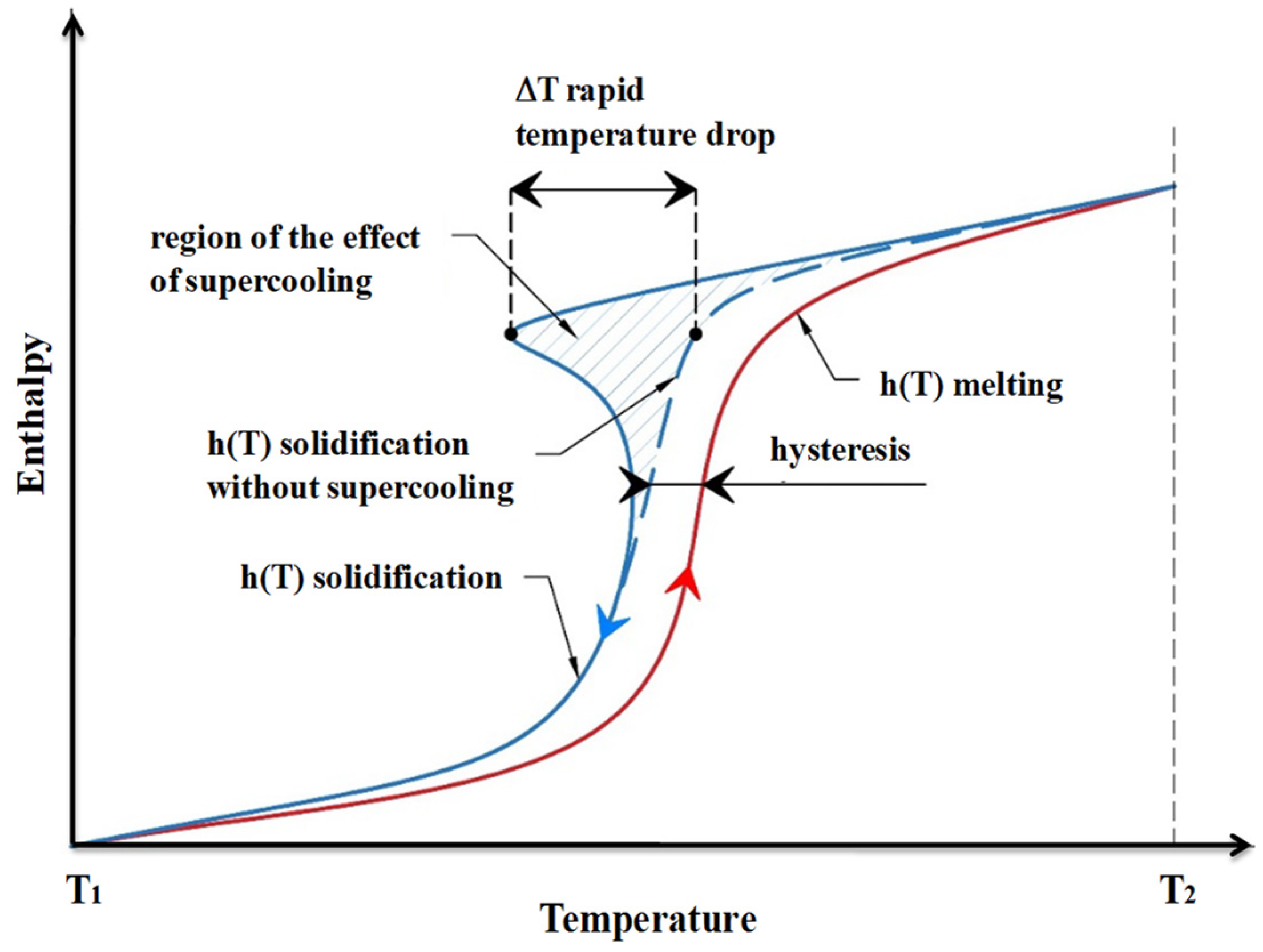
- As for kinetics properties, subcooling and supercooling should be avoided, and a sufficient crystallization rate should be achieved;
- For chemical properties, PCMs should be compatible with the materials in the application. They should retain their chemical stability for long-term cycles (no chemical degradation and breakdown). In addition, the latent heat storage material should be a non-toxic, non-flammable, non-corrosive, and even less explosive substance. Moreover, charging and discharging periods must be fully completed;
- Low-cost PCMs should be preferred in terms of economic properties.
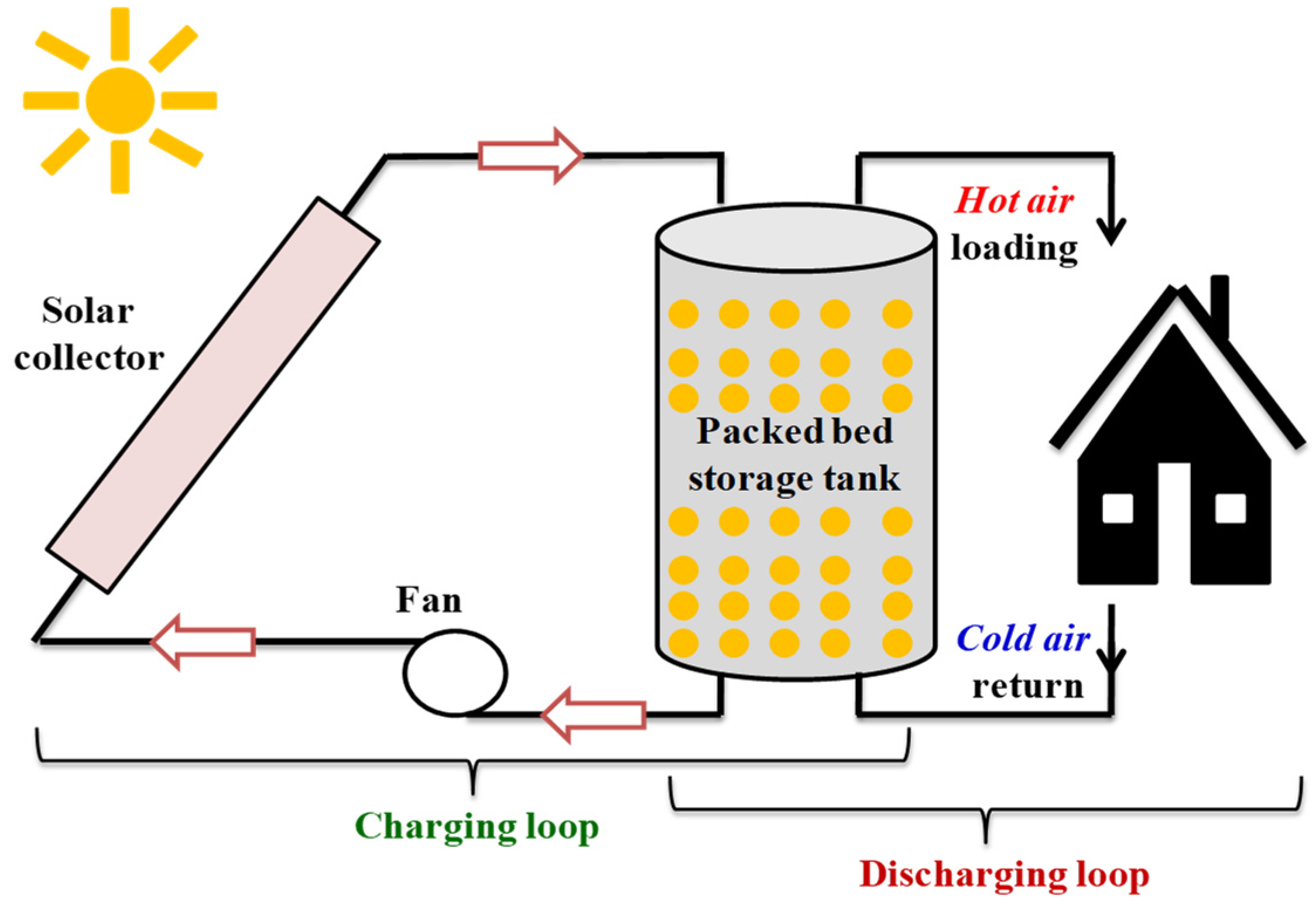
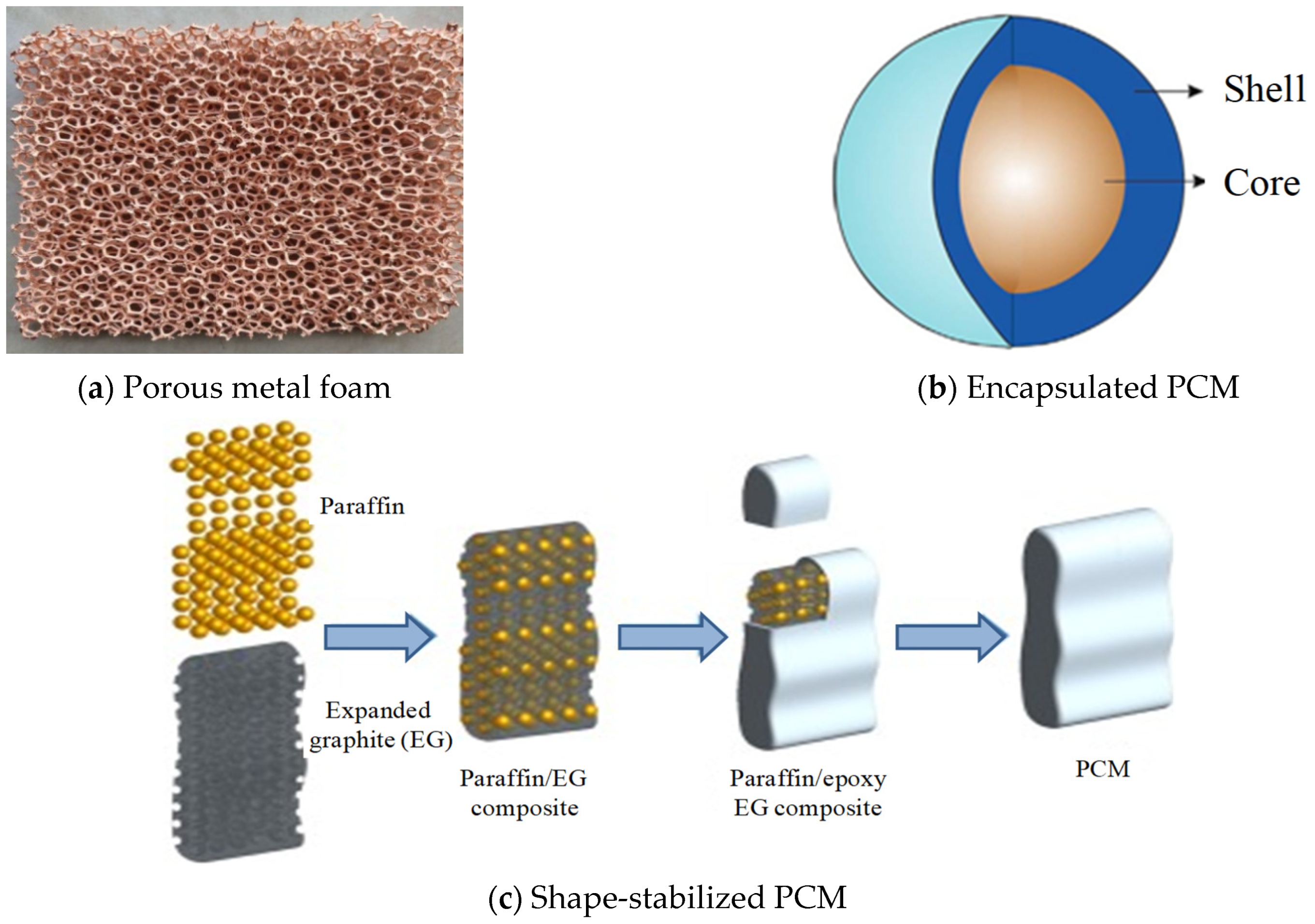
3.2. Latent Heat Storage in Porous Medium
- Manufacture of a composite by associating a PCM and a porous matrix (metal foam or expanded graphite) [106];
4. Latent Heat Storage (LHS) vs. Sensible Heat Storage (SHS)
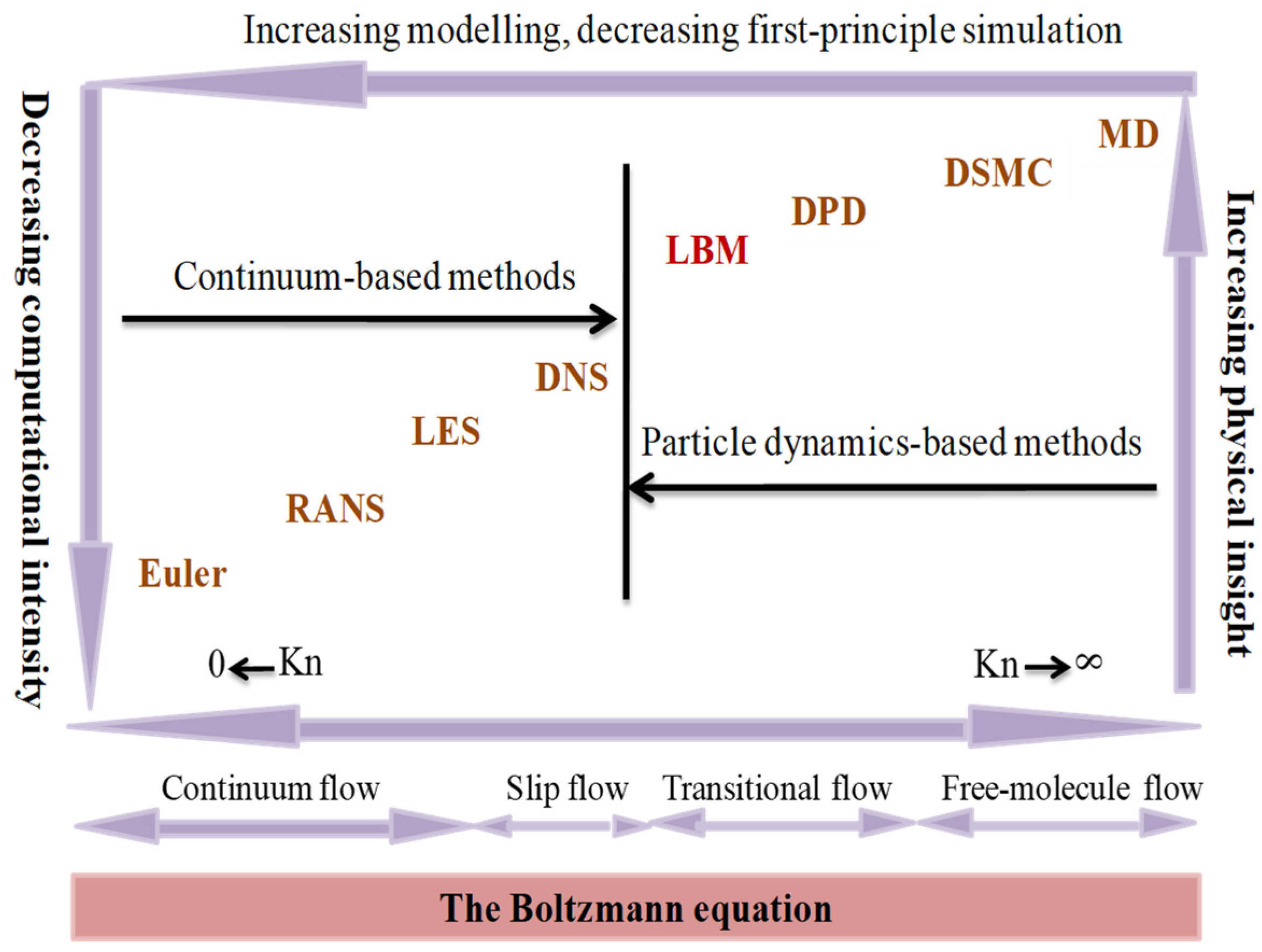
5. Lattice Boltzmann Methods (LBMs)
5.1. Single Relaxation Time (SRT) Collision Model
5.2. Multiple Relaxation Time (MRT) Collision Model
5.3. Two Relaxation Time (TRT) Collision Model
5.4. Application to Fluid Flows by Advection/Diffusion with Phase Change in Porous Media
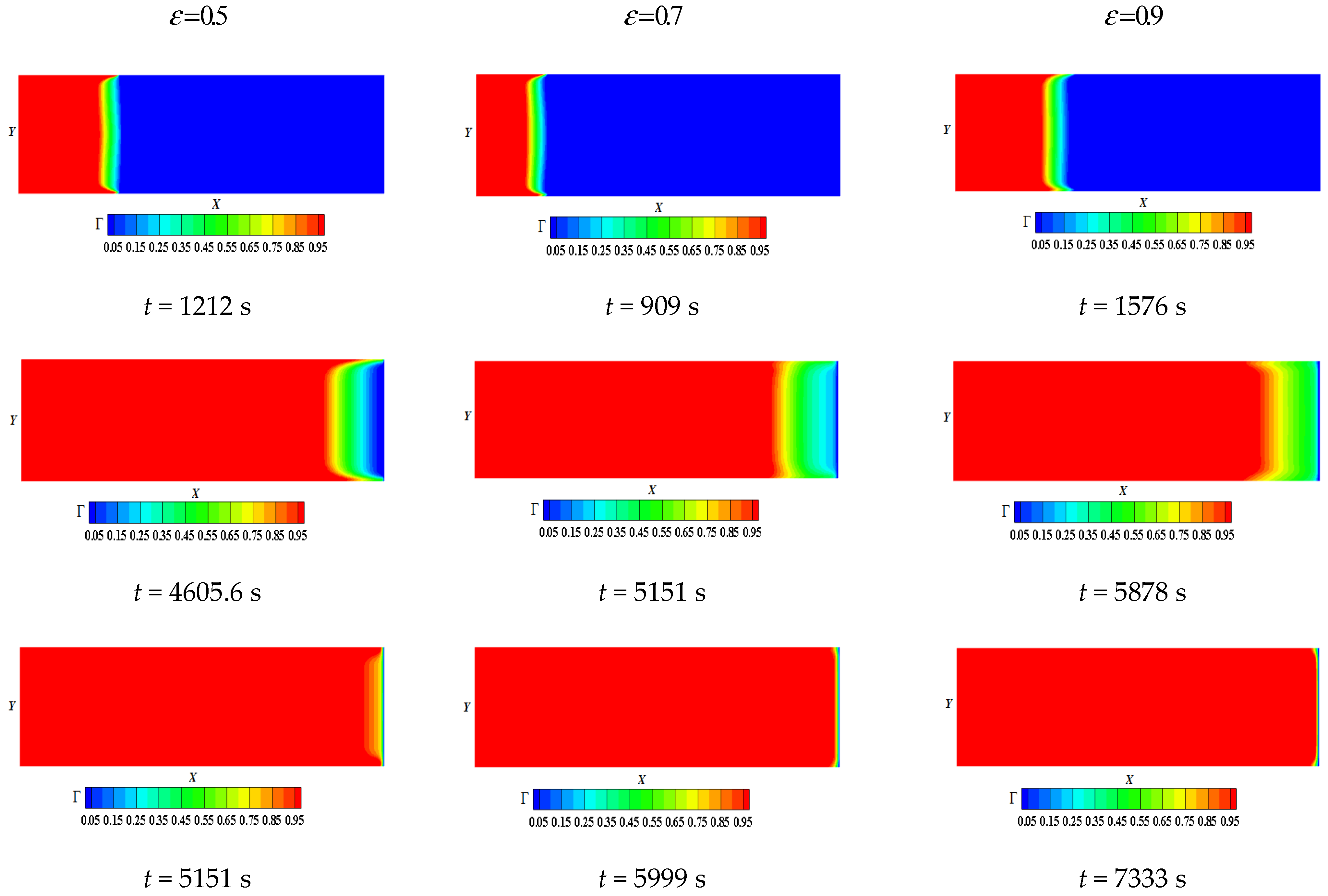
5.4.1. Forced Convection Melting of a PCM in a Latent Heat Thermal Energy System (LHTES)
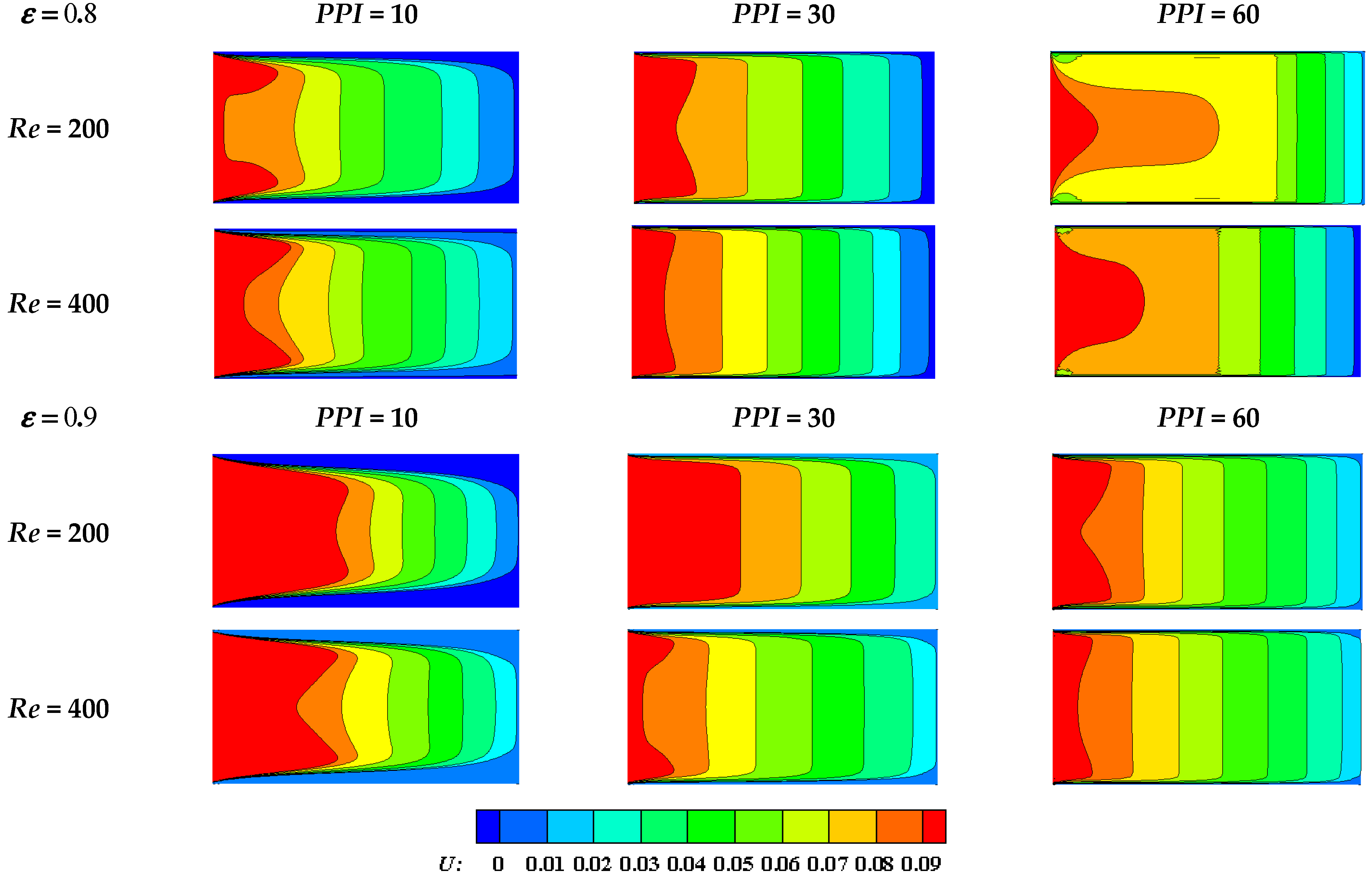
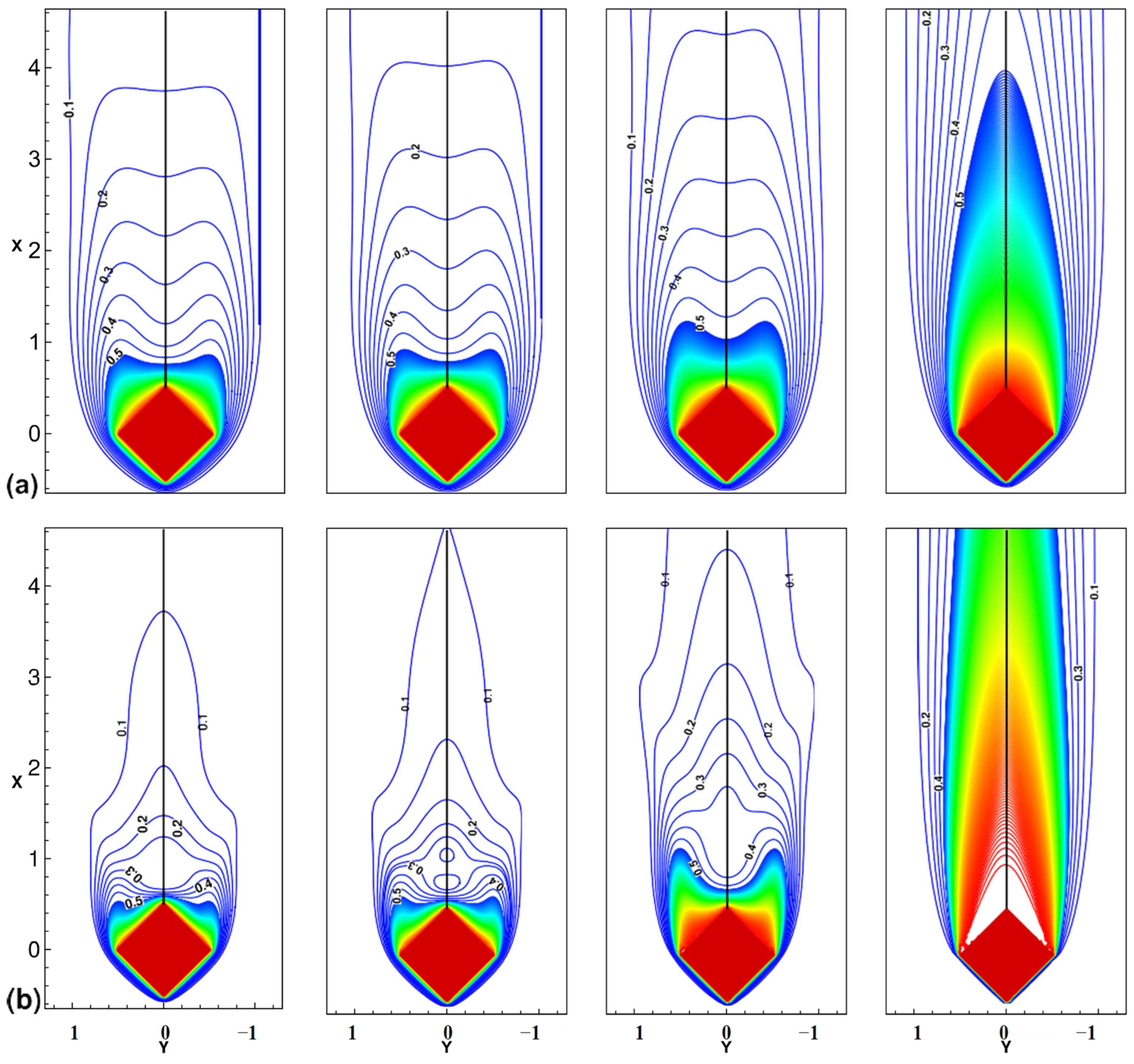
5.4.2. REV-LBM Simulation of Unsteady Flow and Heat Transfer around and through a Confined Diamond-Shaped Porous Block
6. Conclusions
- Through the bibliometric analysis that was carried out on TES methods, it is the LHS category that appeared to be the most relevant technique investigated.
- SHS and LHS systems are most widely used systemsin different applications due to their high availability. However, most TCHS devices are not commercially available, except in a small range of applications, due to their unstable lifetime and high prices.
- The SHS method has been widely used in solar applications where water is the most used material due to its low cost and high specific heat capacity. Note that porosity is one of the main parameters that influences the performance of any SHS system.
- Despite their low thermal conductivity, PCMs can still be integrated into applications using various modes of incorporation, of which the impregnation of PCMs in porous structures appears to be the most relevant solution due to the high thermal conductivity engendered.
- It turns out that PCMs can store an appreciable amount of energy which ismore than that ofSHSMs in a small relative storage volume.
- Using foam metal in thermal energy storage can improve heat transfer rate while shortening charge/discharge periods.
- Decreasing the porosity speeds up the melting phenomenon
- Increasing the PPI can enhance the forced convection heat transfer performance of the liquid PCM.
- Pore-scale and REV-scale LBM approaches showed great potential for thesimulation of phase change phenomenon and sensible storage in a porous medium due to their inherent transienceand robustness to handle complexphysics. They can help to understand the complex interactions between different processes, which are challenging to obtain even for the most advanced experimental techniques. Their combinations with macro/micro/nano scale fabrication techniques will certainly lead to new generation porous media.
- There is no doubt that LB methods will continue to play an increasingly important role in the study of solid-liquid phase change heat transfer in porous LHTES. However, this will certainly have to entail a development of a numerically stable and accurate multi-scale simulation method by combining the REV-scale and pore-scale methods.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Specific interfacial area (m−1) | |
| Biot number, | |
| c | Lattice speed () |
| Specific heat capacity at constant pressure () | |
| Sound speed () | |
| Darcy number, | |
| df | Mean ligament diameter (m) |
| dp | Mean pore diameter (m) |
| Eckert number, | |
| Discrete velocity in direction i | |
| Forchheimer form coefficient | |
| Body force per unit mass () | |
| Discrete body force in direction i () | |
| Distribution function in direction i | |
| g | Gravity |
| Equilibrium distribution function in direction i | |
| Symmetric distribution function | |
| Antisymmetric distribution function | |
| H | Characteristic length scale (m) |
| h | Enthalpy |
| Interfacial heat transfer coefficient () | |
| Porous medium permeability (m2) | |
| Kn | Knudsen number |
| Thermal conductivity ratio, | |
| Latent heat () | |
| M (N) | Transformation relaxation matrix |
| m (n) | Velocity moment |
| meq (neq) | Equilibrium moment |
| Pressure () | |
| Prandtl number, | |
| R | Universal gas constant |
| Ra | Rayleigh number |
| Reynolds number, | |
| Pore Reynolds number, | |
| Heat capacity ratio, | |
| Source terms | |
| Sf(Sg) | Diagonal relaxation matrix |
| Stefan number, | |
| Temperature () | |
| PCM melting temperature () | |
| Dimensionless temperature | |
| Time (s) | |
| Velocity () | |
| Inlet velocity() | |
| Cartesian coordinates () | |
| Greek symbols | |
| Gradient operator | |
| Divergence operator | |
| Thermal diffusivity () | |
| Thermal expansion coefficient () | |
| Media porosity | |
| Pore density (PPI) | |
| Thermal conductivity () | |
| Dynamic fluid viscosity () | |
| PCM melting fraction | |
| Kinematic viscosity () | |
| Density () | |
| Free relaxation time | |
| Single relaxation time | |
| Relaxation rates | |
| Viscous relaxation time | |
| Monitor factor | |
| Collision operator | |
| Weight coefficient in direction i | |
| Superscripts/subscripts | |
| Effective | |
| f | Fluid |
| Direction opposite to i | |
| m | Melting |
| Initial state | |
| Ref | Reference |
| s | Solid |
| Abbreviations | |
| ARM | Adaptive mesh refinement |
| BGK | Bhatnagar–Gross–Krook |
| CFD | Computational fluid dynamics |
| CFL | Courant–Friedrichs–Lewy |
| CNT | Carbon nanotubes |
| DBTE | Discretization of Boltzmann transport equation |
| DSMC | Direct simulation Monte Carlo |
| DNS | Direct numerical simulation |
| DPD | Dissipative particle dissipation |
| EG | Expanded graphite |
| ES | Energy storage |
| EU | European union |
| ESS | Energy storage system |
| FDM | Finite difference method |
| FEM | Finite element methods |
| FVM | Finite volume methods |
| GKM | Gas-kinetic method |
| HPC | Hierarchical porous carbon |
| HPP | Hierarchical porouspolystyrene |
| HTF | heat transfer fluid |
| IRENA | International renewable energy agency |
| LES | Large eddy simulation |
| LBM | Lattice Boltzmann method |
| MD | Molecular dynamics |
| MOF | Metal organic framework |
| MRT | Multiple relaxation time |
| NSCG | Non-uniform staggered Cartesian grid |
| PCM | Phase change material |
| PPI | Pore density (Pore Per Inch) |
| RANS | Reynolds-averaged Navier–Stokes |
| REV | Representative elementary volume |
| TCHS | Thermochemical heat storage |
| TES | Thermal energy storage |
| TRT | Two relaxation time |
| LHTES | Latent heat thermal energy storage |
| LHS | Latent heat storage |
| PCP | Porous coordination polymers |
| SHS | Sensible heat storage |
| SHSM | Sensible heat storage material |
| SRT | Single relaxation time |
| STES | Seasonal thermal energy storage |
| ZEB | Zero energy buildings |
References
- Xu, H.; Wang, N.; Zhang, C.; Qu, Z.; Cao, M. Optimization on the melting performance of triplex-layer PCMs in a horizontal finned shell and tube thermal energy storage unit. Appl. Therm. Eng. 2020, 176, 115409. [Google Scholar] [CrossRef]
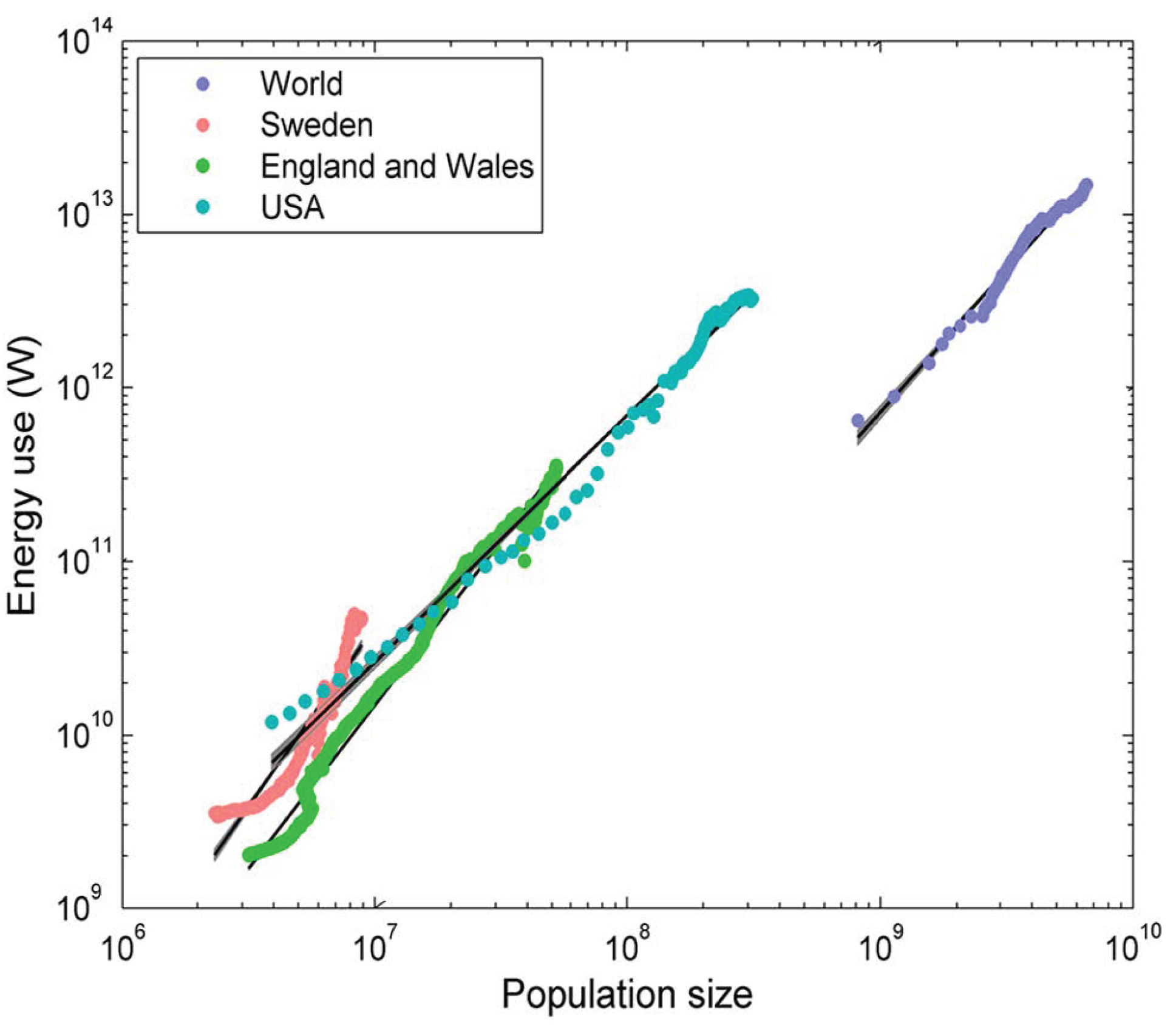
- DeLong, J.P.; Burger, O. Socio-economic instability and the scaling of energy use with population size. PLoS ONE 2015, 10, e0130547. [Google Scholar] [CrossRef] [PubMed]
- Dincer, I.; Ezan, M.A. Heat Storage: A Unique Solution for Energy Systems; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Sarbu, I.; Sebarchievici, C. Solar Heating and Cooling Systems: Fundamentals, Experimentsand Applications; Elsevier: Oxford, UK, 2016. [Google Scholar]
- Cabeza, L.F. Advances in Thermal Energy Storage Systems; Woodhead Publishing Series in Energy; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Stutz, B.; Le Pierres, N.; Kuznik, F.; Johannes, K.; Del Barrio, E.P.; Bédécarrats, J.-P.; Gibout, S.; Marty, P.; Zalewski, L.; Soto, J.; et al. Storage of thermal solar energy. Comptes Rendus Phys. 2017, 18, 401–414. [Google Scholar] [CrossRef]
- Arce, P.; Medrano, M.; Gil, A.; Oró, E.; Cabeza, L.F. Overview of thermal energy storage (TES) potential energy savings and climate change mitigation in Spain and Europe. Appl. Energy 2011, 88, 2764–2774. [Google Scholar] [CrossRef]
- IRENA. Innovation Outlook: Thermal Energy Storage; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- Calderón, A.; Barreneche, C.; Hernández-Valle, K.; Galindo, E.; Segarra, M.; Fernández, A.I. Where is Thermal Energy Storage (TES) research going?—A bibliometric analysis. Sol. Energy 2020, 200, 37–50. [Google Scholar] [CrossRef]
- Ibrahim, H.; Ilinca, A.; Perron, J. Energy storage systems-Characteristics and comparisons. Renew. Sustain. Energy Rev. 2008, 12, 1221–1250. [Google Scholar] [CrossRef]
- Dahash, A.; Ochs, F.; Janetti, M.B.; Streicher, W. Advances in seasonal thermal energy storage for solar district heating applications: A critical review on large-scale hot-water tank and pit thermal energy storage systems. Appl. Energy 2019, 239, 296–315. [Google Scholar] [CrossRef]
- Guo, F.; Yang, X.; Xu, L.; Torrens, I.; Hensen, J. A central solar-industrial waste heat heating system with large scale borehole thermal storage. Procedia Eng. 2017, 205, 1584–1591. [Google Scholar] [CrossRef]
- Persson, J.; Westermark, M. Low-energy buildings and seasonal thermal energy storages from a behavioral economics perspective. Appl. Energy 2013, 112, 975–980. [Google Scholar] [CrossRef]
- Reed, A.L.; Novelli, A.P.; Doran, K.L.; Ge, S.; Lu, N.; McCartney, J.S. Solar district heating with underground thermal energy storage: Pathways to commercial viability in North America. Renew. Energy 2018, 126, 1–13. [Google Scholar] [CrossRef] [Green Version]
- International Renewable Energy Agency (IRENA). The Energy Technology Systems Analysis Program (ETSAP): Technology Brief E17; International Energy Agency (IEA): Paris, France, 2013; Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2013/IRENA-ETSAP-Tech-Brief-E17-Thermal-Energy-Storage.pdf (accessed on 1 January 2013).
- Navarro, L.; de Gracia, A.; Niall, D.; Castell, A.; Browne, M.; McCormack, S.J.; Griffiths, P.; Cabeza, L.F. Thermal energy storage in building integrated thermal systems: A review. Part 2. Integration as passive system. Renew. Energy 2015, 85, 1334–1356. [Google Scholar] [CrossRef] [Green Version]
- Navarro, L.; De Gracia, A.; Niall, D.; Castell, A.; Browne, M.; Mccormack, S.J.; Griffiths, P.; Cabeza, L.F. Thermal energy storage in building integrated thermal systems: A review. Part 1. Active storage systems readable. Renew. Energy 2016, 88, 526–547. [Google Scholar] [CrossRef] [Green Version]
- Lizana, J.; Chacartegui, R.; Barrios-Padura, A.; Valverde, J.M. Advances in thermal energy storage materials and their applications towards zero energy buildings: A critical review. Appl. Energy 2017, 203, 219–239. [Google Scholar] [CrossRef]
- Romdhane, S.B.; Amamou, A.; Khalifa, R.B.; Said, N.M.; Younsi, Z.; Jemni, A. A review on thermal energy storage using phase change materials in passive building applications. J. Build. Eng. 2020, 32, 101563. [Google Scholar] [CrossRef]
- Rathore, P.K.S.; Shukla, S.K. Potential of macroencapsulated PCM for thermal energy storage in buildings: A comprehensive review. Constr. Build. Mater. 2019, 225, 723–744. [Google Scholar] [CrossRef]
- Hauer, A.; Bayern, Z. Storage Technology Issues and Opportunities. In Proceedings of the Strategic and Cross-Cutting Workshop “Energy Storage—Issues and Opportunities”, France, Paris, 15 February 2011. [Google Scholar]
- Borri, E.; Tafone, A.; Zsembinszki, G.; Comodi, G.; Romagnoli, A.; Cabeza, L.F. Recent trends on liquid air energy storage: A bibliometric analysis. Appl. Sci. 2020, 10, 2773. [Google Scholar] [CrossRef]
- Tarragona, J.; de Gracia, A.; Cabeza, L.F. Bibliometric analysis of smart control applications in thermal energy storage systems. A model predictive control approach. J. Energy Storage 2020, 32, 101704. [Google Scholar] [CrossRef]
- Cardenas-Ramírez, C.; Jaramillo, F.; Gomez, M. Systematic review of encapsulation and shape-stabilization of phase change materials. J. Energy Storage 2020, 30, 101495. [Google Scholar] [CrossRef]
- Mustapha, A.N.; Onyeaka, H.; Omoregbe, O.; Ding, Y.; Li, Y. Latent heat thermal energy storage: A bibliometric analysis explicating the paradigm from 2000–2019. J. Energy Storage 2020, 33, 102027. [Google Scholar] [CrossRef]
- Cabeza, L.F.; de Gracia, A.; Zsembinszki, G.; Borri, E. Perspectives on thermal energy storage research. Energy 2021, 231, 120943. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, C.Y.; Markides, C.N.; Wang, H.; Li, W. Medium-and high-temperature latent and thermochemical heat storage using metals and metallic compounds as heat storage media: A technical review. Appl. Energy 2020, 280, 115950. [Google Scholar] [CrossRef]
- De Gracia, A.; Cabeza, L.F. Phase change materials and thermal energy storage for buildings. Energy Build. 2015, 103, 414–419. [Google Scholar] [CrossRef] [Green Version]
- Chandel, S.S.; Agarwal, T. Review of current state of research on energy storage, toxicity, health hazards and commercialization of phase changing materials. Renew. Sustain. Energy Rev. 2017, 67, 581–596. [Google Scholar] [CrossRef]
- Lin, Y.; Alva, G.; Fang, G. Review on thermal performances and applications of thermal energy storage systems with inorganic phase change materials. Energy 2018, 165, 685–708. [Google Scholar] [CrossRef]
- Fernández, A.; Martínez, M.; Segarra, M.; Martorell, I.; Cabeza, L.F. Selection of materials with potential in sensible thermal energy storage. Sol. Energy Mater. Sol. Cells 2010, 94, 1723–1729. [Google Scholar] [CrossRef]
- Kalaiselvam, S.; Parameshwaran, R. Thermal Energy Storage Technologies. In Thermal Energy Storage Technologies for Sustainability: Systems Design, Assessment, and Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 2014; pp. 57–64. [Google Scholar] [CrossRef]
- Ståhl, F. Influence of Thermal Mass on the Heating and Cooling Demands of a Building Unit. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2009. [Google Scholar]
- Tatsidjodoung, P.; Le Pierrès, N.; Luo, L. A review of potential materials for thermal energy storage in building applications. Renew. Sustain. Energy Rev. 2013, 18, 327–349. [Google Scholar] [CrossRef]
- González-Roubaud, E.; Pérez-Osorio, D.; Prieto, C. Review of commercial thermal energy storage in concentrated solar power plants: Steam vs. molten salts. Renew. Sustain. Energy Rev. 2017, 80, 133–148. [Google Scholar] [CrossRef]
- Myers, P.D., Jr.; Goswami, D.Y. Thermal energy storage using chloride salts and their eutectics. Appl. Therm. Eng. 2016, 109, 889–900. [Google Scholar] [CrossRef] [Green Version]
- Elashmawy, M. Improving the performance of a parabolic concentrator solar tracking-tubular solar still (PCST-TSS) using gravel as a sensible heat storage material. Desalination 2020, 47, 114182. [Google Scholar] [CrossRef]
- Koçak, B.; Fernandez, A.I.; Paksoy, H. Review on sensible thermal energy storage for industrial solar applications and sustainability aspects. Sol. Energy 2020, 209, 135–169. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials Selection in Mechanical Design, 3rd ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Ashby, M.F.; Shercliff, H.; Cebon, D. Materials Engineering, Science, Processing and Design, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Ayyappan, S.; Mayilsamy, K.; Sreenarayanan, V.V. Performance improvement studies in a solar greenhouse drier using sensible heat storage materials. Heat Mass Transf. 2016, 52, 459–467. [Google Scholar] [CrossRef]
- Klein, P.; Roos, T.H.; Sheer, T.J. Experimental investigation into a packed bed thermal storage solution for solar gas turbine systems. Energy Procedia 2014, 49, 840–849. [Google Scholar] [CrossRef] [Green Version]
- Almendros-Ibanez, J.A.; Fernandez-Torrijos, M.; Díaz-Heras, M.; Belmonte, J.F.; Sobrino, C.A. Review of solar thermal energy storage in beds of particles: Packed and fluidized beds. Sol. Energy 2018, 192, 193–237. [Google Scholar] [CrossRef]
- Elouali, A.; Kousksou, T.; El Rhafiki, T.; Hamdaoui, S.; Mahdaoui, M.; Allouhi, A.; Zeraouli, Y. Physical models for packed bed: Sensible heat storage systems. J. Energy Storage 2019, 23, 69–78. [Google Scholar] [CrossRef]
- Pelay, U.; Luo, L.; Fan, Y.; Stitou, D.; Rood, M. Thermal energy storage systems for concentrated solar power plants. Renew. Sustain. Energy Rev. 2017, 79, 82–100. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.H. Solar air-heating system with packed-bed energy-storage systems. Renew. Sustain. Energy Rev. 2017, 72, 215–227. [Google Scholar] [CrossRef]
- Gil, A.; Medrano, M.; Martorell, I.; Lázaro, A.; Dolado, P.; Zalba, B.; Cabeza, L.F. State of the art on high temperature thermal energy storage for power generation. Part 1-Concepts, materials and modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar] [CrossRef]
- Mabrouk, R.; Naji, H.; Dhahri, H. Numerical Investigation of Metal Foam Pore Density Effect on Sensible and Latent Heats Storage through an Enthalpy-Based REV-Scale lattice Boltzmann Method. Processes 2021, 9, 1165. [Google Scholar] [CrossRef]
- Amami, B.; Rabhi, R.; Dhahri, H.; Mhimid, A. Numerical thermodynamic analysis of heat storage porous duct under pulsating flow using lattice Boltzmann method. Int. J. Exergy 2017, 22, 376–395. [Google Scholar] [CrossRef]
- Kasaeian, A.; Daneshazarian, R.; Mahian, O.; Kolsi, L.; Chamkha, A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I. Natural convection in a horizontal cylindrical annulus filled with a porous medium saturated by a nanofluid using Tiwari and Das’ nanofluid model. Eur. Phys. J. Plus 2015, 130, 107. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Grosan, T.; Pop, I. Free convection in a square cavity filled with a porous medium saturated by nanofluid using Tiwari and Das’ nanofluid model. Transp. Porous Media 2015, 106, 595–610. [Google Scholar] [CrossRef]
- Amami, B.; Dhahri, H.; Mhimid, A. Viscous dissipation effects on heat transfer, energy storage, and entropy generation for fluid flow in a porous channel submitted to a uniform magnetic field. J. Porous Media 2014, 17, 841–859. [Google Scholar] [CrossRef]
- Heap, M.J.; Xu, T.; Chen, C.F. The influence of porosity and vesicle size on the brittle strength of volcanic rocks and magma. Bull. Volcanol. 2014, 76, 859. [Google Scholar] [CrossRef]
- Dhifaoui, B.; Jabrallah, S.B.; Belghith, A.; Corriou, J.P. Experimental study of the dynamic behaviour of a porous medium submitted to a wall heat flux in view of thermal energy storage by sensible heat. Int. J. Therm. Sci. 2007, 46, 1056–1063. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, C.Y. A review of solar collectors and thermal energy storage in solar thermal applications. Appl. Energy 2013, 104, 538–553. [Google Scholar] [CrossRef] [Green Version]
- Mahlia, T.M.I.; Saktisahdan, T.J.; Jannifar, A.; Hasan, M.H.; Matseelar, H.S.C. A review of available methods and development on energy storage; technology update. Renew. Sustain. Energy Rev. 2014, 33, 532–545. [Google Scholar] [CrossRef]
- Reddy Prasad, D.M.; Senthilkumar, R.; Lakshmanarao, G.; Krishnan, S.; Naveen Prasad, B.S. A critical review on thermal energy storage materials and systems for solar applications. AimsEnergy 2019, 7, 507–526. [Google Scholar] [CrossRef]
- Saffari, M.; De Gracia, A.; Fernández, C.; Cabeza, L.F. Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Appl. Energy 2017, 202, 420–434. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Garg, H.P.; Mullick, S.C.; Bhargava, A.K. Solar Thermal Energy Storage; Reidel Publishing Company: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Pillai, K.K.; Brinkwarth, B.J. The storage of low grade thermal energy using phase change materials. Appl. Energy 1976, 2, 205–216. [Google Scholar] [CrossRef]
- Alva, G.; Lin, Y.; Fang, G. An overview of thermal energy storage systems. Energy 2018, 144, 341–378. [Google Scholar] [CrossRef]
- Hasnain, S.M. Review on sustainable thermal energy storage technologies, Part I: Heat storage materials and techniques. Energy Convers. Manag. 1998, 39, 1127–1138. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Sol. Energy 2010, 84, 1402–1412. [Google Scholar] [CrossRef] [Green Version]
- Dincer, I.; Rosen, M.A. Thermal Energy Storage Systems and Applications; John Wiley & Sons: Chichester, UK, 2002. [Google Scholar]
- Kimura, H.; Kai, J. Mixtures of calcium chloride hexahydrate with some salt hydrates or anhydrous salts as latent heat storage materials. Energy Convers. Manag. 1988, 28, 197–200. [Google Scholar] [CrossRef]
- Abhat, A. Low temperature latent heat thermal energy storage: Heat storage materials. Sol. Energy 1983, 30, 313–332. [Google Scholar] [CrossRef]
- Jegadheeswaran, S.; Pohekar, S.D. Performance enhancement in latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2009, 13, 2225–2244. [Google Scholar] [CrossRef]
- Yehya, A.; Naji, H.; Zalewski, L. Experimental and numerical characterization of an impure phase change material using a thermal lattice Boltzmann method. Appl. Therm. Eng. 2019, 154, 738–750. [Google Scholar] [CrossRef]
- Kant, K.; Biwole, P.H.; Shamseddine, I.; Tlaiji, G.; Pennec, F.; Fardoun, F. Recent advances in thermophysical properties enhancement of phase change materials for thermal energy storage. Sol. Energy Mater. Sol. Cells 2021, 231, 111309. [Google Scholar] [CrossRef]
- Junaid, M.F.; Ur Rehman, Z.; Čekon, M.; Čurpek, J.; Farooq, R.; Cui, H.; Khan, I. Inorganic phase change materials in thermal energy storage: A review on perspectives and technological advances in building applications. Energy Build. 2021, 252, 111443. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Hu, P.; Hu, G. Study on the supercooling degree and nucleation behavior of water-based graphene oxide nanofluids PCM. Int. J. Refrig. 2015, 50, 80–86. [Google Scholar] [CrossRef]
- Nomura, T.; Okinaka, N.; Akiyama, T. Technology of latent heat storage for high temperature application: A review. ISIJ Int. 2010, 50, 1229–1239. [Google Scholar] [CrossRef] [Green Version]
- Khadiran, T.; Hussein, M.Z.; Zainal, Z.; Rusli, R. Advanced energy storage materials for building applications and their thermal performance characterization: A review. Renew. Sustain. Energy Rev. 2016, 57, 916–928. [Google Scholar] [CrossRef]
- Memon, S.A. Phase change materials integrated in building walls: A state of the art review. Renew. Sustain. Energy Rev. 2014, 31, 870–906. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, C.Y.; Tian, Y. Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 2012, 92, 593–605. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Li, W.; Luo, Z.; Wang, K.; Shah, S.P. A critical review on phase change materials (PCM) for sustainable and energy efficient building: Design, characteristic, performance and application. Energy Build. 2022, 260, 111923. [Google Scholar] [CrossRef]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef]
- Zhang, W.; Mazzarello, R.; Wuttig, M.; Ma, E. Designing crystallization in phase change materials for universal memory and neuro-inspired computing. Nat. Rev. Mater. 2019, 4, 150–168. [Google Scholar] [CrossRef]
- Yancheshme, A.A.; Allahdini, A.; Maghsoudi, K.; Jafari, R.; Momen, G. Potential anti-icing applications of encapsulated phase change material-embedded coatings; a review. J. Energy Storage 2020, 31, 101638. [Google Scholar] [CrossRef]
- Rostami, S.; Afrand, M.; Shahsavar, A.; Sheikholeslami, M.; Kalbasi, R.; Aghakhani, S.; Shadlo, M.S.; Oztop, H.F. A review of melting and freezing processes of PCM/nano-PCM and their application in energy storage. Energy 2020, 211, 118698. [Google Scholar] [CrossRef]
- Dieckmann, J. Latent Heat Storage in Concrete; University of Kai Serslautern: Kaiserslautern, Germany, 2006. [Google Scholar]
- Sarbu, I.; Dorca, A. Review on heat transfer analysis in thermal energy storage using latent heat storage systems and phase change materials. Int. J. Energy Res. 2019, 43, 29–64. [Google Scholar] [CrossRef] [Green Version]
- Faraj, K.; Khaled, M.; Faraj, J.; Hachem, F.; Castelain, C. Phase change material thermal energy storage systems for cooling applications in buildings: A review. Renew. Sustain. Energy Rev. 2020, 119, 109579. [Google Scholar] [CrossRef]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Famileh, I.Z.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.D.; De Gracia, A.; Fernández, A.I. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Battisti, A.; Persiani, S.G.; Crespi, M. Review and mapping of parameters for the early stage design of adaptive building technologies through life cycle assessment tools. Energies 2019, 12, 1729. [Google Scholar] [CrossRef] [Green Version]
- Fabiani, C.; Pisello, A.L.; Barbanera, M.; Cabeza, L.F.; Cotana, F. Assessing the potentiality of animal fat based-bio phase change materials (PCM) for building applications: An innovative multipurpose thermal investigation. Energies 2019, 12, 1111. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.; Zou, P.X.; Sanjayan, J.; Ramakrishnan, S. Energy saving performance assessment and lessons learned from the operation of an active phase change materials system in a multi-storey building in Melbourne. Appl. Energy 2019, 238, 1582–1595. [Google Scholar] [CrossRef]
- Arivazhagan, R.; Geetha, N.B.; Sivasamy, P.; Kumaran, P.; Gnanamithra, M.K.; Sankar, S.; Loganathan, G.B.; Arivarasan, A. Review on performance assessment of phase change materials in buildings for thermal management through passive approach. Mater. Today Proc. 2020, 22, 419–431. [Google Scholar] [CrossRef]
- Souayfane, F.; Fardoun, F.; Biwole, P.H. Phase change materials (PCM) for cooling applications in buildings: A review. Energy Build. 2016, 129, 396–431. [Google Scholar] [CrossRef]
- Umair, M.M.; Zhang, Y.; Iqbal, K.; Zhang, S.; Tang, B. Novel strategies and supporting materials applied to shape-stabilize organic phase change materials for thermal energy storage-A review. Appl. Energy 2019, 235, 846–873. [Google Scholar] [CrossRef]
- Kenisarin, M.M. Thermophysical properties of some organic phase change materials for latent heat storage. A review. Sol. Energy 2014, 107, 553–575. [Google Scholar] [CrossRef]
- Zhang, N.; Yuan, Y.; Cao, X.; Du, Y.; Zhang, Z.; Gui, Y. Latent heat thermal energy storage systems with solid–liquid phase change materials: A review. Adv. Eng. Mater. 2018, 20, 1700753. [Google Scholar] [CrossRef]
- Ferrer, G.; Solé, A.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Review on the methodology used in thermal stability characterization of phase change materials. Renew. Sustain. Energy Rev. 2015, 50, 665–685. [Google Scholar] [CrossRef] [Green Version]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Shchukina, E.M.; Graham, M.; Zheng, Z.; Shchukin, D.G. Nanoencapsulation of phase change materials for advanced thermal energy storage systems. Chem. Soc. Rev. 2018, 47, 4156–4175. [Google Scholar] [CrossRef] [Green Version]
- Al Shannaq, R.; Farid, M.M. Microencapsulation of phase change materials (PCMs) for thermal energy storage systems. In Advances in Thermal Energy Storage Systems; Woodhead Publishing: Sawston, UK, 2015; pp. 247–284. [Google Scholar] [CrossRef]
- Liu, C.; Rao, Z.; Zhao, J.; Huo, Y.; Li, Y. Review on nano-encapsulated phase change materials: Preparation, characterization and heat transfer enhancement. Nano Energy 2015, 13, 814–826. [Google Scholar] [CrossRef]
- Liu, L.; Alva, G.; Huang, X.; Fang, G. Preparation, heat transfer and flow properties of microencapsulated phase change materials for thermal energy storage. Renew. Sustain. Energy Rev. 2016, 66, 399–414. [Google Scholar] [CrossRef]
- Weaver, J.A.; Viskanta, R. Freezing of water saturated porous media in a rectangular cavity. Int. Commun. Heat Mass Transf. 1986, 13, 245–252. [Google Scholar] [CrossRef]
- Wang, Z.; Situ, W.; Li, X.; Zhang, G.; Huang, Z.; Yuan, W.; Yang, C.; Yang, C. Novel shape stabilized phase change material based on epoxy matrix with ultrahigh cycle life for thermal energy storage. Appl. Therm. Eng. 2017, 123, 1006–1012. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Preparation and thermal characterization of paraffin/metal foam composite phase change material. Appl. Energy 2013, 112, 1357–1366. [Google Scholar] [CrossRef]
- Huang, X.; Chen, X.; Li, A.; Atinafu, D.; Gao, H.; Dong, W.; Wang, G. Shape-stabilized phase change materials based on porous supports for thermal energy storage applications. Chem. Eng. J. 2019, 356, 641–661. [Google Scholar] [CrossRef]
- Zhang, H.L.; Baeyens, J.; Degrève, J.; Cáceres, G.; Segal, R.; Pitié, F. Latent heat storage with tubular-encapsulated phase change materials (PCMs). Energy 2014, 76, 66–72. [Google Scholar] [CrossRef] [Green Version]
- Ling, Z.; Zhang, Z.; Shi, G.; Fang, X.; Wang, L.; Gao, X.; Fang, Y.; Xu, T.; Wang, S.; Liu, X. Review on thermal management systems using phase change materials for electronic components, Li-ion batteries and photovoltaic modules. Renew. Sustain. Energy Rev. 2014, 31, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Bianco, N.; Busiello, S.; Iasiello, M.; Mauro, G.M. Finned heat sinks with phase change materials and metal foams: Pareto optimization to address cost and operation time. Appl. Therm. Eng. 2021, 197, 117436. [Google Scholar] [CrossRef]
- Khodadadi, J.M.; Fan, L.; Babaei, H. Thermal conductivity enhancement of nanostructure-based colloidal suspensions utilized as phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 24, 418–444. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Şahan, N.; Fois, M.; Paksoy, H. Improving thermal conductivity phase change materials—A study of paraffin nanomagnetite composites. Sol. Energy Mater. Sol. Cells 2015, 137, 61–67. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, X.L.; Wang, T.; Wang, R.Z. A review on phase change cold storage in air-conditioning system: Materials and applications. Renew. Sustain. Energy Rev. 2013, 22, 108–120. [Google Scholar] [CrossRef]
- Feng, D.; Feng, Y.; Qiu, L.; Li, P.; Zang, Y.; Zou, H.; Yu, Z.; Zhang, X. Review on nano-porous composite phase change materials: Fabrication, characterization, enhancement and molecular simulation. Renew. Sustain. Energy Rev. 2019, 109, 578–605. [Google Scholar] [CrossRef]
- Zhang, S.; Feng, D.; Shi, L.; Wang, L.; Jin, Y.; Tian, L.; Yan, Y. A review of phase change heat transfer in shape-stabilized phase change materials (ss-PCMs) based on porous supports for thermal energy storage. Renew. Sustain. Energy Rev. 2021, 135, 110127. [Google Scholar] [CrossRef]
- Gao, H.; Wang, J.; Chen, X.; Wang, G.; Huang, X.; Li, A.; Dong, W. Nanoconfinement effects on thermal properties of nanoporous shape-stabilized composite PCMs: A review. Nano Energy 2018, 53, 769–797. [Google Scholar] [CrossRef]
- Mesalhy, O.; Lafdi, K.; Elgafy, A.; Bowman, K. Numerical study for enhancing the thermal conductivity of phase change material (PCM) storage using high thermal conductivity porous matrix. Energy Convers. Manag. 2005, 46, 847–867. [Google Scholar] [CrossRef]
- Alva, G.; Liu, L.; Huang, X.; Fang, G. Thermal energy storage materials and systems for solar energy applications. Renew. Sustain. Energy Rev. 2017, 68, 693–706. [Google Scholar] [CrossRef]
- Mabrouk, R.; Naji, H.; Dhahri, H.; Hammouda, S.; Younsi, Z. Numerical investigation of porosity effect on a PCM’s thermal performance in a porous rectangular channel via thermal lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2020, 119, 104992. [Google Scholar] [CrossRef]
- Mabrouk, R.; Naji, H.; Dhahri, H.; Younsi, Z. Insight into Foam Pore Effect on Phase Change Process in a Plane Channel under Forced Convection Using the Thermal Lattice Boltzmann Method. Energies 2020, 13, 3979. [Google Scholar] [CrossRef]
- Yang, X.; Wei, P.; Wang, X.; He, Y.L. Gradient design of pore parameters on the melting process in a thermal energy storage unit filled with open-cell metal foam. Appl. Energy 2020, 268, 115019. [Google Scholar] [CrossRef]
- Li, Z.; Shahsavar, A.; Al-Rashed, A.A.; Talebizadehsardari, P. Effect of porous medium and nanoparticles presences in a counter-current triple-tube composite porous/nano-PCM system. Appl. Therm. Eng. 2020, 167, 114777. [Google Scholar] [CrossRef]
- Sardari, P.T.; Mohammed, H.I.; Giddings, D.; Gillott, M.; Grant, D. Numerical study of a multiple-segment metal foam-PCM latent heat storage unit: Effect of porosity, pore density and location of heat source. Energy 2019, 189, 116108. [Google Scholar] [CrossRef]
- Yang, X.; Bai, Q.; Zhang, Q.; Hu, W.; Jin, L.; Yan, J. Thermal and economic analysis of charging and discharging characteristics of composite phase change materials for cold storage. Appl. Energy 2018, 225, 585–599. [Google Scholar] [CrossRef]
- Zhang, P.; Meng, Z.N.; Zhu, H.; Wang, Y.L.; Peng, S.P. Melting heat transfer characteristics of a composite phase change material fabricated by paraffin and metal foam. Appl. Energy 2017, 185, 1971–1983. [Google Scholar] [CrossRef] [Green Version]
- Atal, A.; Wang, Y.; Harsha, M.; Sengupta, S. Effect of porosity of conducting matrix on a phase change energy storage device. Int. J. Heat Mass Transf. 2016, 93, 9–16. [Google Scholar] [CrossRef]
- Mallow, A.; Abdelaziz, O.; Graham, S. Thermal charging performance of enhanced phase change material composites for thermal battery design. Int. J. Therm. Sci. 2018, 127, 19–28. [Google Scholar] [CrossRef]
- Li, W.Q.; Qu, Z.G.; He, Y.L.; Tao, W.Q. Experimental and numerical studies on melting phase change heat transfer in open-cell metallic foams filled with paraffin. Appl. Therm. Eng. 2012, 37, 1–9. [Google Scholar] [CrossRef]
- Allen, M.J.; Bergman, T.L.; Faghri, A.; Sharifi, N. Robust heat transfer enhancement during melting and solidification of a phase change material using a combined heat pipe-metal foam or foil configuration. J. Heat Transf. 2015, 137, 102301. [Google Scholar] [CrossRef]
- Devaux, P.; Farid, M.M. Benefits of PCM underfloor heating with PCM wallboards for space heating in winter. Appl. Energy 2017, 191, 593–602. [Google Scholar] [CrossRef]
- Luo, K.H.; Xia, J.; Monaco, E. Multiscale modeling of multiphase flow with complex interactions. J. Mult. Model. 2009, 1, 125–156. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Yoshino, M.; Matsuda, Y.; Shao, C. Comparison of accuracy and efficiency between the lattice Boltzmann method and the finite difference method in viscous/thermal fluid flows. Int. J. Comput. Fluid Dyn. 2004, 18, 333–345. [Google Scholar] [CrossRef]
- Mishra, S.C.; Lankadasu, A. Transient conduction-radiation heat transfer in participating media using the lattice Boltzmann method and the discrete transfer method. Numer. Heat Transf. Part A Appl. 2005, 47, 935–954. [Google Scholar] [CrossRef]
- Mondal, B.; Mishra, S.C. Application of the lattice Boltzmann method and the discrete ordinates method for solving transient conduction and radiation heat transfer problems. Numer. Heat Transf. Part A Appl. 2007, 52, 757–775. [Google Scholar] [CrossRef]
- Gohari, S.M.I.; Ghadyani, M. Effects of GPU structuring on accelerated schemes of LBM and classical CFD for flow over a flat plate. J. Math. Sys. Sci. 2012, 2, 126–132. [Google Scholar]
- Goodarzi, M.; Safaei, M.R.; Karimipour, A.; Hooman, K.; Dahari, M.; Kazi, S.N.; Sadeghinezhad, E. Comparison of the finite volume and lattice Boltzmann methods for solving natural convection heat transfer problems inside cavities and enclosures. Abstr. Appl. Anal. 2014, 2014, 762184. [Google Scholar] [CrossRef]
- Kerimo, J.; Girimaji, S.S. Boltzmann-BGK approach to simulating weakly compressible 3D turbulence: Comparison between lattice Boltzmann and gas kinetic methods. J. Turbul. 2009, 8, N46. [Google Scholar] [CrossRef]
- Sharma, K.V.; Straka, R.; Tavares, F.W. Lattice Boltzmann methods for industrial applications. Ind. Eng. Chem. Res. 2019, 58, 16205–16234. [Google Scholar] [CrossRef]
- Fakhari, A.; Lee, T. Finite-difference lattice Boltzmann method with a block-structured adaptive-mesh-refinement technique. Phys. Rev. E 2014, 89, 033310. [Google Scholar] [CrossRef]
- Schönherr, M.; Kucher, K.; Geier, M.; Stiebler, M.; Freudiger, S.; Krafczyk, M. Multi-thread implementations of the lattice Boltzmann method on non-uniform grids for CPUs and GPUs. Comput. Math. Appl. 2011, 61, 3730–3743. [Google Scholar] [CrossRef] [Green Version]
- Lagrava, D.; Malaspinas, O.; Latt, J.; Chopard, B. Advances in multi-domain lattice Boltzmann grid refinement. J. Comput. Phys. 2012, 231, 4808–4822. [Google Scholar] [CrossRef] [Green Version]
- Valero-Lara, P.; Jansson, J. A non-uniform Staggered Cartesian grid approach for Lattice-Boltzmann method. Procedia Comput. Sci. 2015, 51, 296–305. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Luo, L.S.; Dembo, M. Some progress in lattice Boltzmann method. Part I. Nonuniform mesh grids. J. Comput. Phys. 1996, 129, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.S.; Liao, W.; Chen, X.; Peng, Y.; Zhang, W. Numerics of the lattice Boltzmann method: Effects of collision models on the lattice Boltzmann simulations. Phys. Rev. E 2011, 83, 056710. [Google Scholar] [CrossRef] [Green Version]
- Le, G.; Zhang, J. Boundary slip from the immersed boundarylattice Boltzmann models. Phys. Rev. E 2009, 79, 026701. [Google Scholar] [CrossRef] [PubMed]
- d’Humières, D. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. A 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Hilpert, M. A multiple-relaxation-time lattice-Boltzmannmodel for bacterial chemotaxis: Effects of initial concentration, diffusion, and hydrodynamic dispersion on traveling bacterial bands. Bull. Math. Biol. 2014, 76, 2449–2475. [Google Scholar] [CrossRef]
- Ginzburg, I. Equilibrium-type and link-type lattice Boltzmann models for generic advection and anisotropic-dispersion equation. Adv. Water Resour. 2005, 28, 1171–1195. [Google Scholar] [CrossRef]
- Ginzburg, I. Generic boundary conditions for lattice Boltzmann models and their application to advection and anisotropic dispersion equations. Adv. Water Resour. 2005, 28, 1196–1216. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.S. Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef]
- Mezrhab, A.; Moussaoui, M.A.; Jami, M.; Naji, H.; Bouzidi, M.H. Double MRT thermal lattice Boltzmann method for simulating convective flows. Phys. Lett. A 2010, 374, 3499–3507. [Google Scholar] [CrossRef]
- Ginzburg, I. Lattice Boltzmann modeling with discontinuous collision components: Hydrodynamic and advection-diffusion equations. J. Stat. Phys. 2007, 126, 157–206. [Google Scholar] [CrossRef]
- Ginzburg, I. Consistent Lattice Boltzmann schemes for the Brinkman model of porous flow and infinite Chapman-Enskog expansion. Phys. Rev. E 2008, 77, 066704. [Google Scholar] [CrossRef]
- Ginzburg, I.; Verhaeghe, F.; d’Humieres, D. Two-relaxation-time lattice Boltzmann scheme: About parametrization, velocity, pressure and mixed boundary conditions. Commun. Comput. Phys. 2008, 3, 427–478. [Google Scholar]
- Ma, Q.; Chen, Z.; Liu, H. Multiple-relaxation-time lattice Boltzmann simulation for flow, mass transfer, and adsorption in porous media. Phys. Rev. E 2017, 96, 013313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef] [Green Version]
- Gao, D.; Chen, Z. Lattice Boltzmann simulation of natural convection dominated melting in a rectangular cavity filled with porous media. Int. J. Therm. Sci. 2011, 50, 493–501. [Google Scholar] [CrossRef]
- Yang, X.; Bai, Q.; Guo, Z.; Niu, Z.; Yang, C.; Jin, L.; Lu, T.J.; Yan, J. Comparison of direct numerical simulation with volume-averaged method on composite phase change materials for thermal energy storage. Appl. Energy 2018, 229, 700–714. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Xu, Z.; Ma, T.; Zhang, H.; Liu, J.; Wang, Q.; Wang, Q. A three-dimensional pore-scale lattice Boltzmann model for investigating the supergravity effects on charging process. Appl. Energy 2019, 254, 113507. [Google Scholar] [CrossRef]
- Ren, Q.; He, Y.-L.; Su, K.-Z.; Chan, C.L. Investigation of the effect of metal foam characteristics on the PCM melting performance in a latent heat thermal energy storage unit by pore-scale lattice Boltzmann modeling. Numer. Heat Transf. A-Appl. 2017, 72, 745–764. [Google Scholar] [CrossRef]
- Li, X.; Ma, T.; Liu, J.; Zhang, H.; Wang, Q. Pore-scale investigation of gravity effects on phase change heat transfer characteristics using lattice Boltzmann method. Appl. Energy 2018, 222, 92–103. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Tucci, C. Numerical Investigation of a Phase Change Material Including Natural Convection Effects. Energies 2021, 14, 348. [Google Scholar] [CrossRef]
- Feng, S.; Shi, M.; Li, Y.; Lu, T.J. Pore-scale and volume-averaged numerical simulations of melting phase change heat transfer in finned metal foam. Int. J. Heat Mass Transf. 2015, 90, 838–847. [Google Scholar] [CrossRef]
- Mabrouk, R.; Dhahri, H.; Naji, H.; Hammouda, S.; Younsi, Z. Lattice Boltzmann simulation of forced convection melting of a composite phase change material with heat dissipation through an open-ended channel. Int. J. Heat Mass Transf. 2020, 153, 119606. [Google Scholar] [CrossRef]
- Vijaybabu, T.R.; Anirudh, K.; Dhinakaran, S. LBM simulation of unsteady flow and heat transfer from a diamond-shaped porous cylinder. Int. J. Heat Mass Transf. 2018, 120, 267–283. [Google Scholar] [CrossRef]


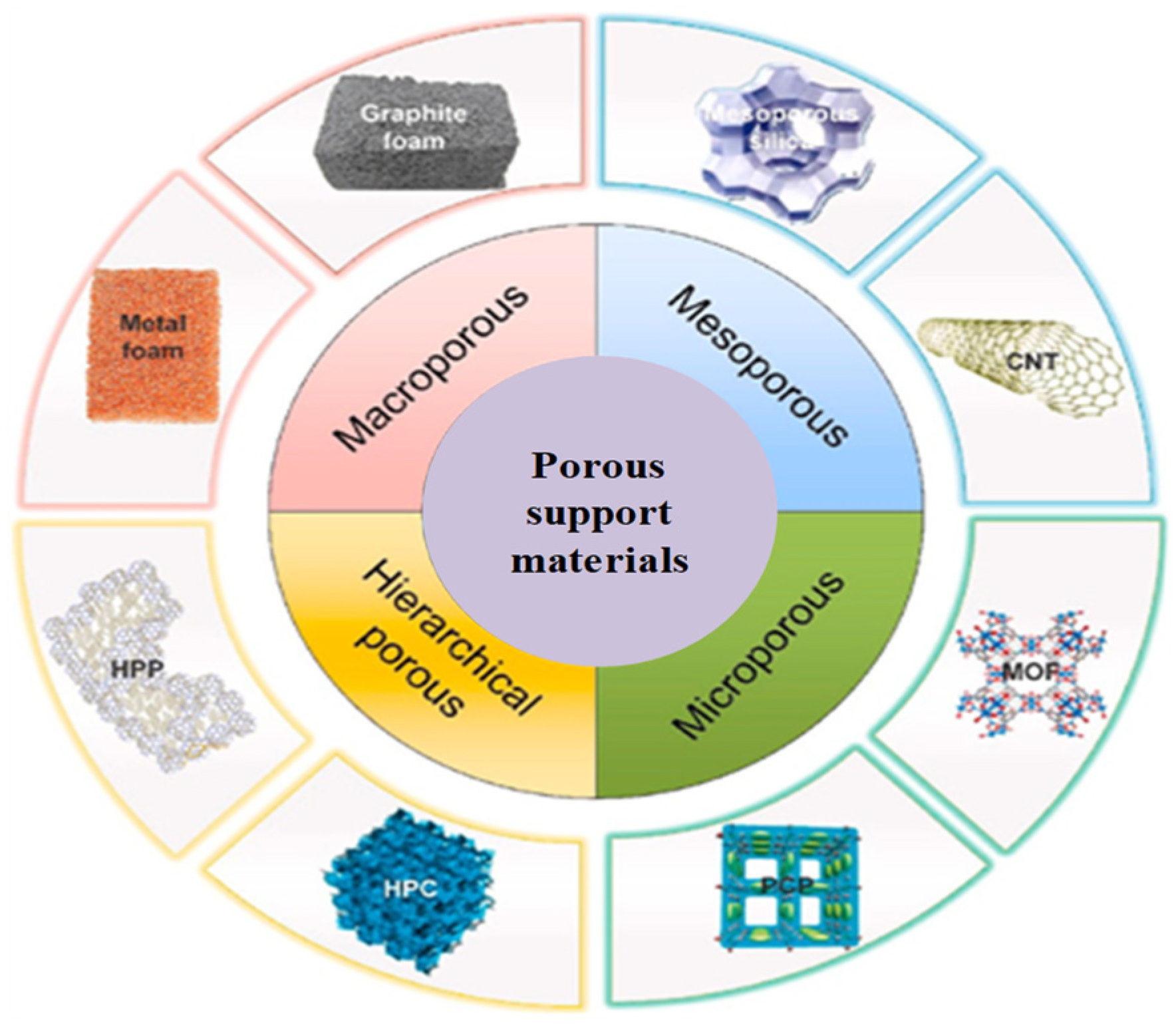


| Energy Storage Methods | ||||
|---|---|---|---|---|
| Thermal | Mechanical | Electromechanical | Electrical | Chemical |
| Sensible thermal | Pumped hydro | Electrochemical capacitors | Capacitors | Hydrogen storage |
| Latent thermal | Compressed air | Batteries | Super capacitors | Synthetic natural gas |
| Thermochemical | Flywheel | Fuel cells | Super conducting magnetic ES (SCMES) | |
| TES Technique | Capacity (kWh/ton) | Power (MW) | Efficiency (%) | Storage Time | Cost (€/kWh) |
|---|---|---|---|---|---|
| Sensible heat | 10–50 | 0.001–10 | 50–90 | d/m | 0.1–10 |
| Latent heat | 50–150 | 0.001–1 | 75–90 | h/m | 10–50 |
| Thermochemical heat | 120–250 | 0.01–1 | 75–100 | h/d | 8–100 |
| SHS Techniques | Classification | |||
|---|---|---|---|---|
| Underground thermal energy storage | Aquifer thermal energy storage | Borehole thermal energy storage | Tank thermal energy storage | Pit thermal energy storage |
| Thermal energy storage in tanks | Vertical (thermocline) | Horizontal | ||
| Thermal energy storage in packed bed | Stationary beds | Fluidized beds | ||
| Thermal energy storage in building structures | ||||
| SHSM | Type | Density (kg·m−3) | Thermal Conductivity (W·m−1·K−1) | Specific Heat (kJ·m−1·K−1) |
|---|---|---|---|---|
| Water (80 °C) | Liquid | 970 | 0.67 | 4.19 |
| Water (40 °C) | Liquid | 990 | 0.63 | 4.19 |
| Water (10 °C) | Liquid | 1000 | 0.6 | 4.19 |
| Oil | Liquid | 880 | 0.14 | 1.88 |
| Ethanol | Liquid | 790 | 0.171 | 2.4 |
| Propanol | Liquid | 800 | 0.161 | 2.5 |
| Butanol | Liquid | 809 | 0.167 | 2.4 |
| Ceramic brick | Solid | 1800 | 0.73 | 0.92 |
| Rock | Solid | 2800–1500 | 3.5–0.85 | 1 |
| Concrete | Solid | 2000 | 1.35 | 1 |
| Wood | Solid | 700–450 | 0.18–0.12 | 1.6 |
| Aluminum | Solid | 2707 | 204 | 0.896 |
| Copper | Solid | 8954 | 385 | 0.383 |
| Granite | Solid | 2640 | 4.0–1.7 | 0.82 |
| Sand and gravel | Solid | 2200–1700 | 2 | 1.18–0.91 |
| Clay or silt | Solid | 1800–1200 | 1.5 | 2.5–1.67 |
| Limestone | Solid | 2600–1600 | 2.3–0.85 | 1 |
| Cement mortar | Solid | 1800 | 1 | 1 |
| Brick | Solid | 1600 | 1.2 | 0.84 |
| Marble | Solid | 2500 | 2 | 0.88 |
| Plastic board | Solid | 1050 | 0.5 | 0.837 |
| Classification | Benefits | Drawbacks |
|---|---|---|
| Organic PCMs | No subcooling No supercooling No phase segregation Large storage capacity High latent heat Recyclable substances Certain renewable substances (fatty acids and alcohols) Available for all temperature range Compatible with other materials | Low thermal conductivity () Flammable Large volume change Certain non-renewable substances |
| Inorganic PCMs | High thermal conductivity High latent heat High storage capacity Small volume change Availability and low cost | Supercooling Corrosion Presentation of chemical instability |
| Eutectics | No segregation High storage density Adjustable phase transition temperature | Lack of test data for certain thermophysical characteristics Same drawbacks of pure organic or inorganic PCMs |
| Operating Principle | Benefits | Materials | Application Domains | |
|---|---|---|---|---|
| SHS | Temperature change (Increase/Decrease) | Inexpensive; Simple operation | Water, rock, concrete, etc. | Concentrated solar power (CSP) Plants or desalination Building heating |
| LHS | Phase change (Solid–Liquid) | Large storage density; Large latent heat; Stable temperature | Paraffins, salt hydrates, metallics, etc. | Solar applications Building heating/cooling Heat pump Thermal control Industrial waste heat storage |
| Heat Storage Density | Storage Period | Heat Transfer Time | Technical Maintenance | |
|---|---|---|---|---|
| SHS | limited | short | uncomplicated | |
| LHS | limited | short | complicate |
| Problem | Method | Ra | Re | Grid Number | Iterations Number | CPU Time (s) |
|---|---|---|---|---|---|---|
| Buoyancy-driven flow | LBM FDM | 710 | - | 50 × 50 | 11,146 8501 | 282 542 |
| LBM FDM | 105 | - | 50 × 50 | 27,352 30,148 | 705 1904 | |
| LBM FDM | 106 | - | 100 × 100 | 58,101 32,029 | 4802 8594 | |
| Lid-driven flow | LBM FDM | - | 100 | 100 × 100 | 10,963 5149 | 886 1131 |
| LBM FDM | - | 400 | 150 × 150 | 30,557 10,848 | 5249 5360 | |
| LBM FDM | - | 1000 | 200 × 200 | 50,853 13,964 | 15,902 12,214 |
| Method | REVScale | PoreScale | ||
|---|---|---|---|---|
| Simulation approach | Volume average simulation (FVM, FEM, LBM). | Direct numerical simulation (LBM, DNS). | ||
| Advantages | Fluent implementation and programming; less computational requirements; large computational domain size. | Reflection of pores’ effect on mechanisms involved; interstitial heat transfer study; no need for empirical models. | ||
| Disadvantages | Less reflection of pores’ transport mechanisms; need for semi-empirical models. | Important computing platform; small computational domain; high computational demands; tedious implementation and programming. | ||
| Computational domain [160,161] |  |  | ||
| Momentum equations [114,118] | (14) | (15) | ||
| Energy equations [114,118] | For liquid phase | For liquid phase | ||
| (16) | (17) | |||
| For solid phase | For solid phase | |||
| (18) | (19) | |||
| Application conditions | Macroporous material | Macro/meso/microporous material | ||
| Flow field [160,162] |  |  | ||
| Thermal field [124,163] |  |  | ||
| Evolution of solid/liquid phase interface [124,163] |  |  | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabrouk, R.; Naji, H.; Benim, A.C.; Dhahri, H. A State of the Art Review on Sensible and Latent Heat Thermal Energy Storage Processes in Porous Media: Mesoscopic Simulation. Appl. Sci. 2022, 12, 6995. https://doi.org/10.3390/app12146995
Mabrouk R, Naji H, Benim AC, Dhahri H. A State of the Art Review on Sensible and Latent Heat Thermal Energy Storage Processes in Porous Media: Mesoscopic Simulation. Applied Sciences. 2022; 12(14):6995. https://doi.org/10.3390/app12146995
Chicago/Turabian StyleMabrouk, Riheb, Hassane Naji, Ali Cemal Benim, and Hacen Dhahri. 2022. "A State of the Art Review on Sensible and Latent Heat Thermal Energy Storage Processes in Porous Media: Mesoscopic Simulation" Applied Sciences 12, no. 14: 6995. https://doi.org/10.3390/app12146995
APA StyleMabrouk, R., Naji, H., Benim, A. C., & Dhahri, H. (2022). A State of the Art Review on Sensible and Latent Heat Thermal Energy Storage Processes in Porous Media: Mesoscopic Simulation. Applied Sciences, 12(14), 6995. https://doi.org/10.3390/app12146995








