Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension
Abstract
:1. Introduction
2. Materials and Methods
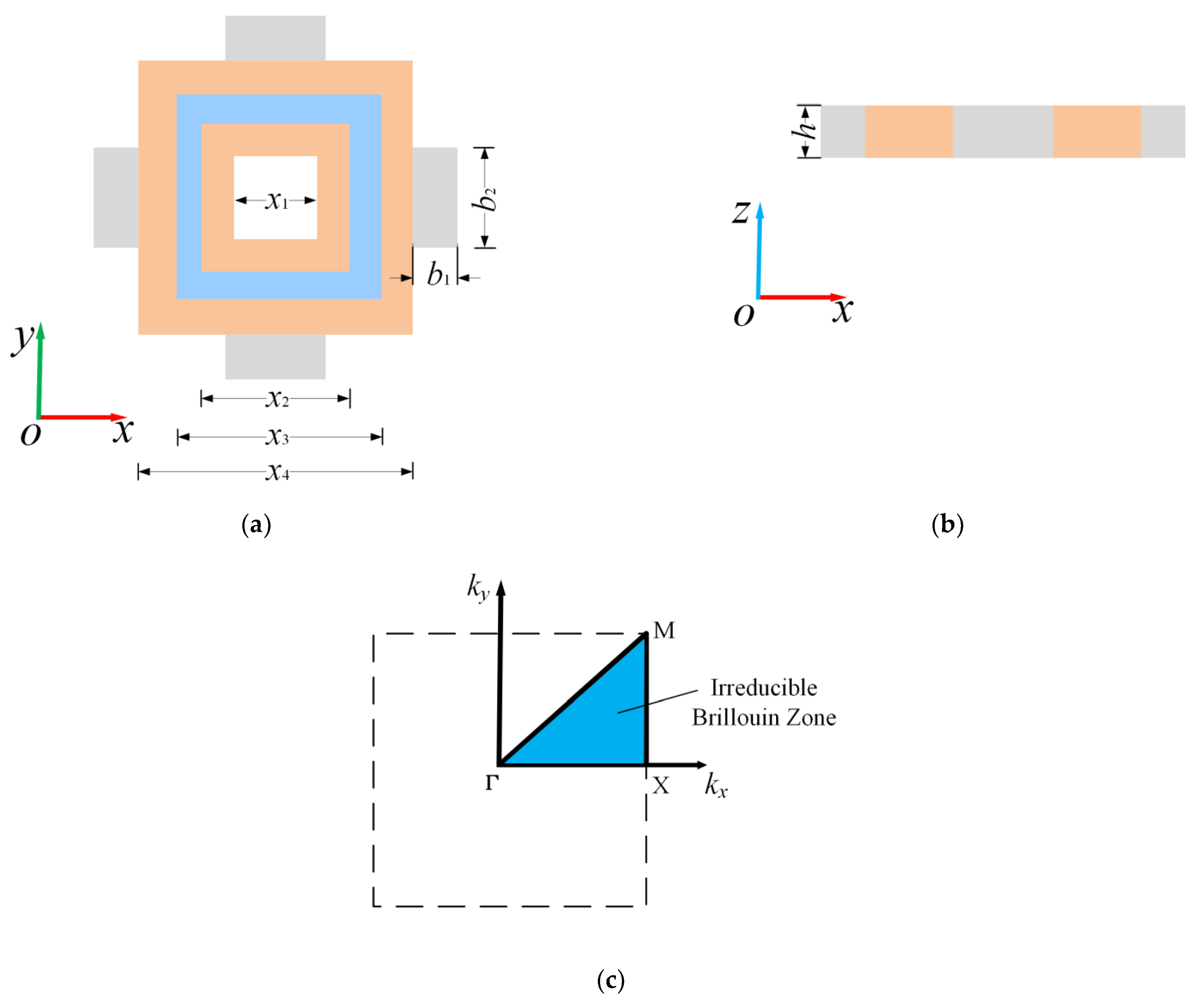
2.1. Model Descriptions
2.2. Analytical Approach
2.2.1. Constitutive Equations
2.2.2. Band Structure Solution
2.2.3. Complex Wavenumber Derivation
2.3. Material and Geometric Parameters
3. Results and Discussion
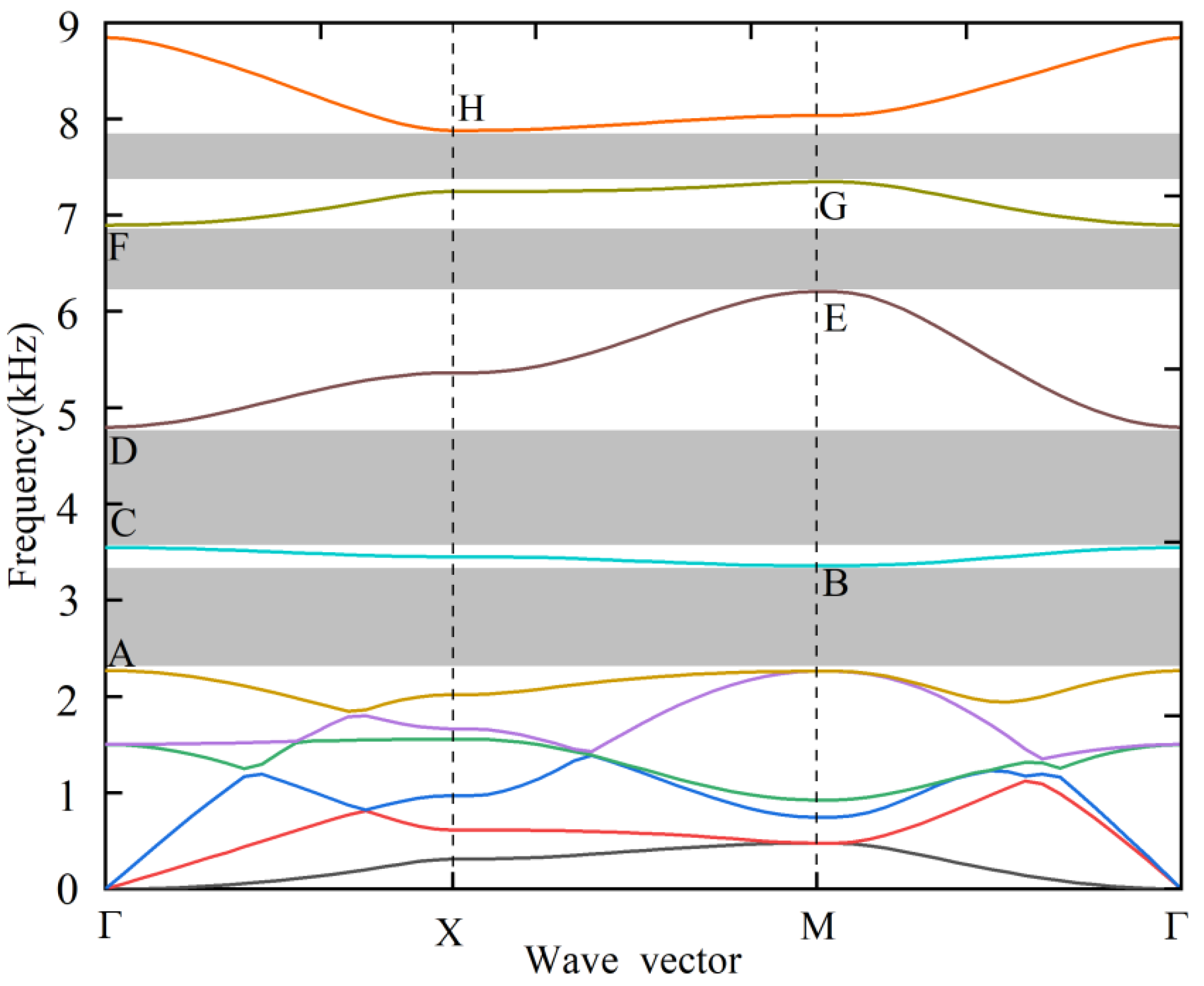
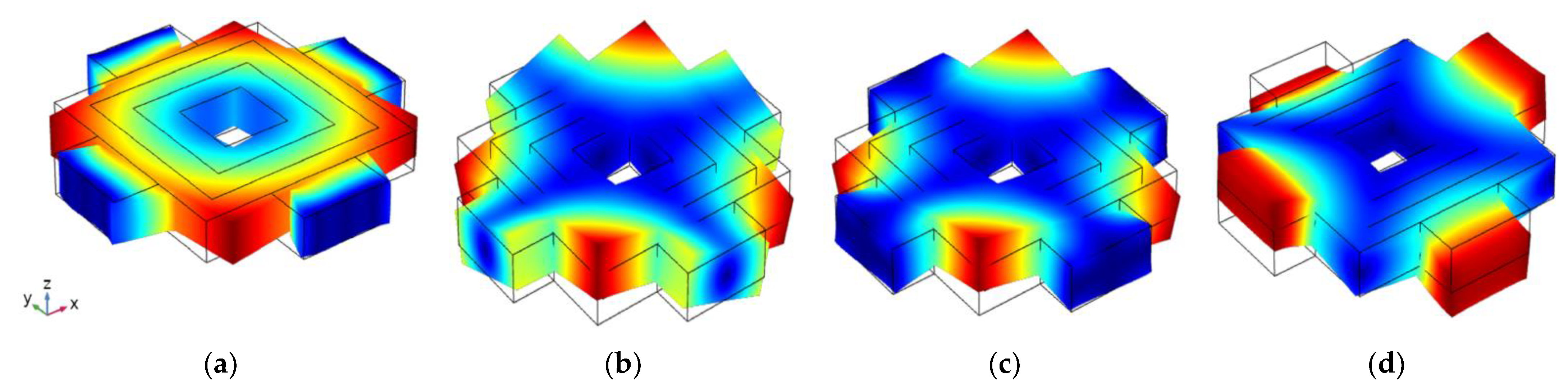
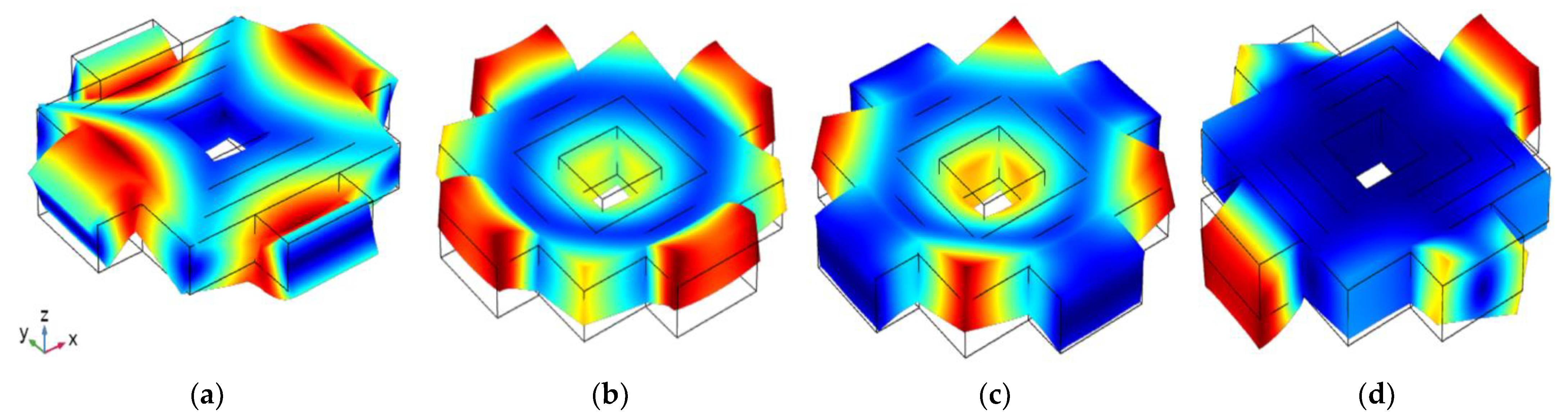
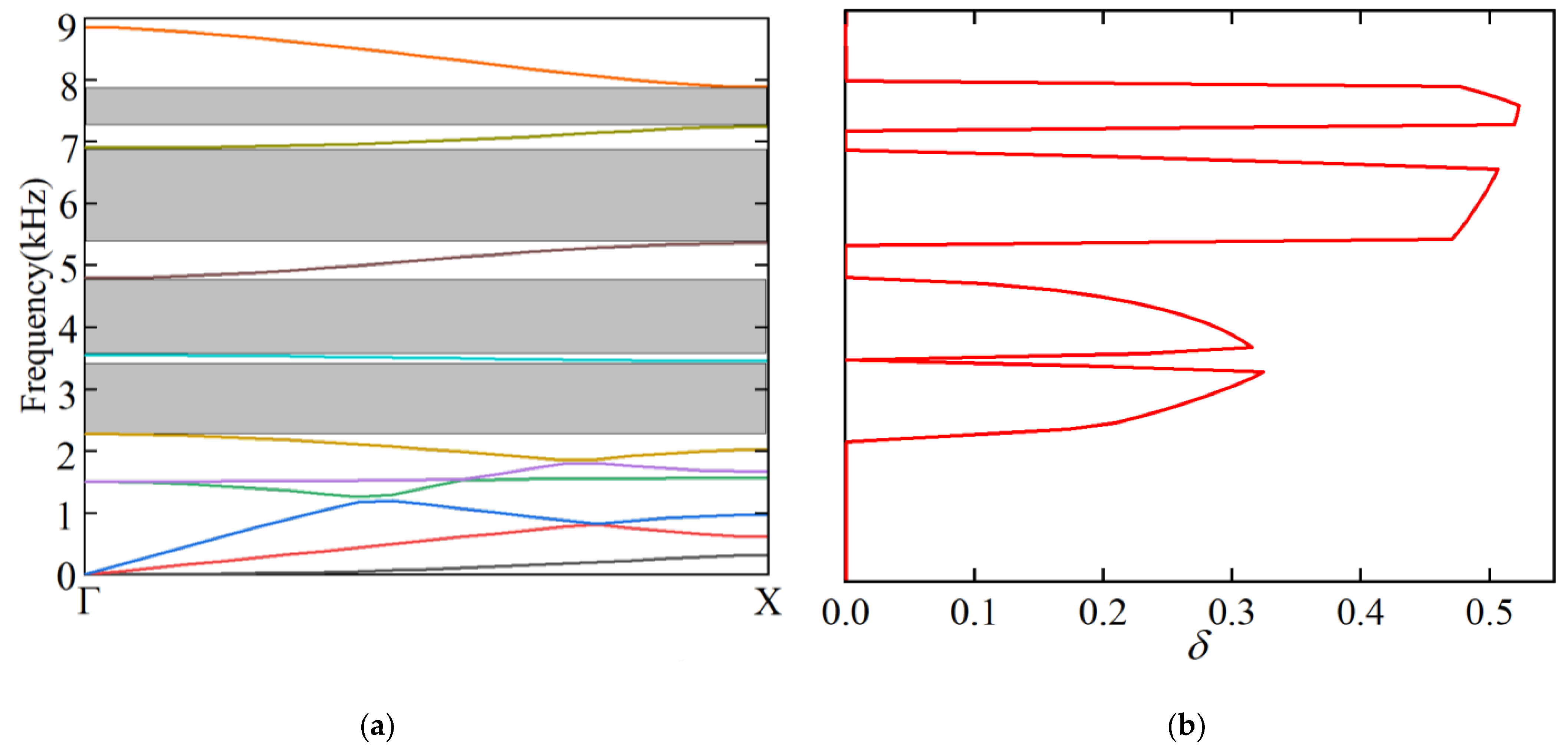
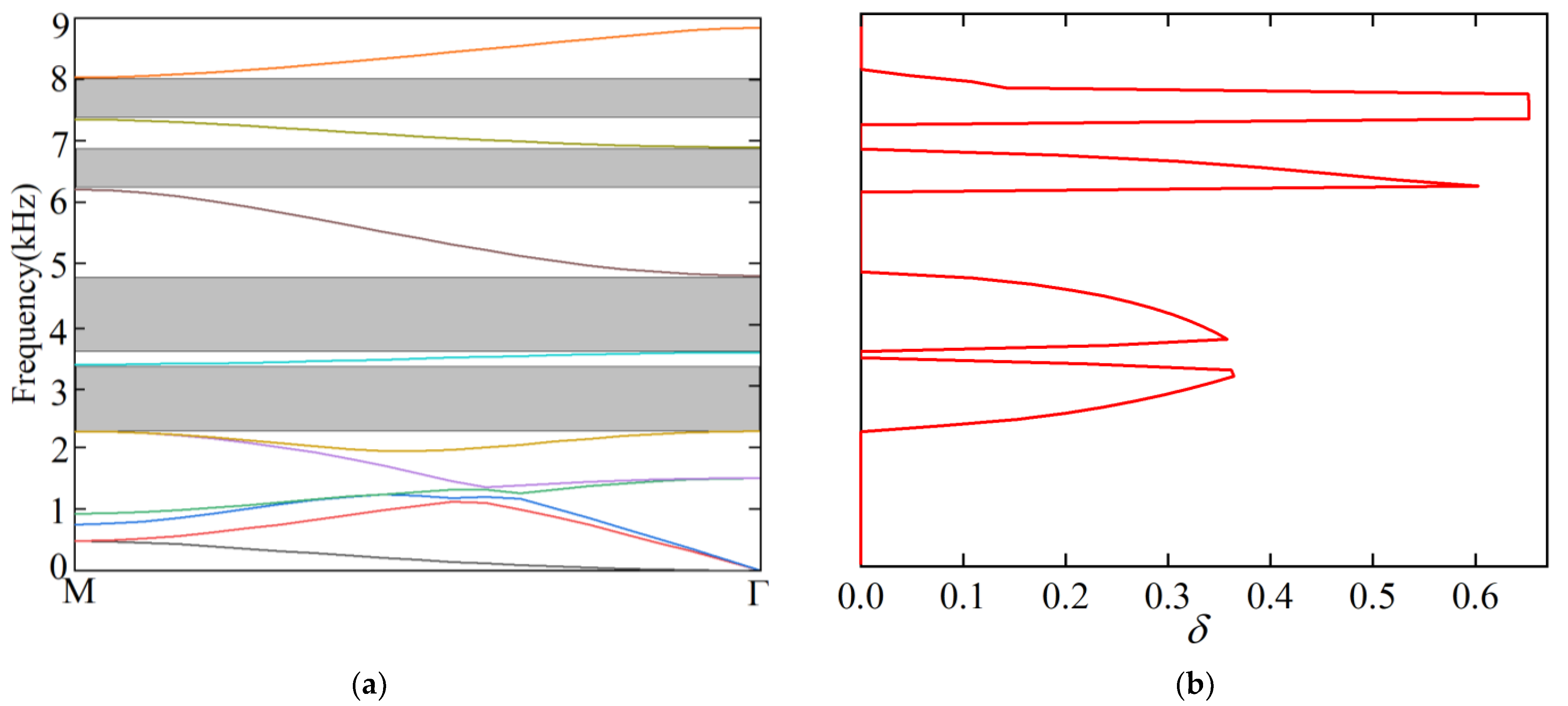
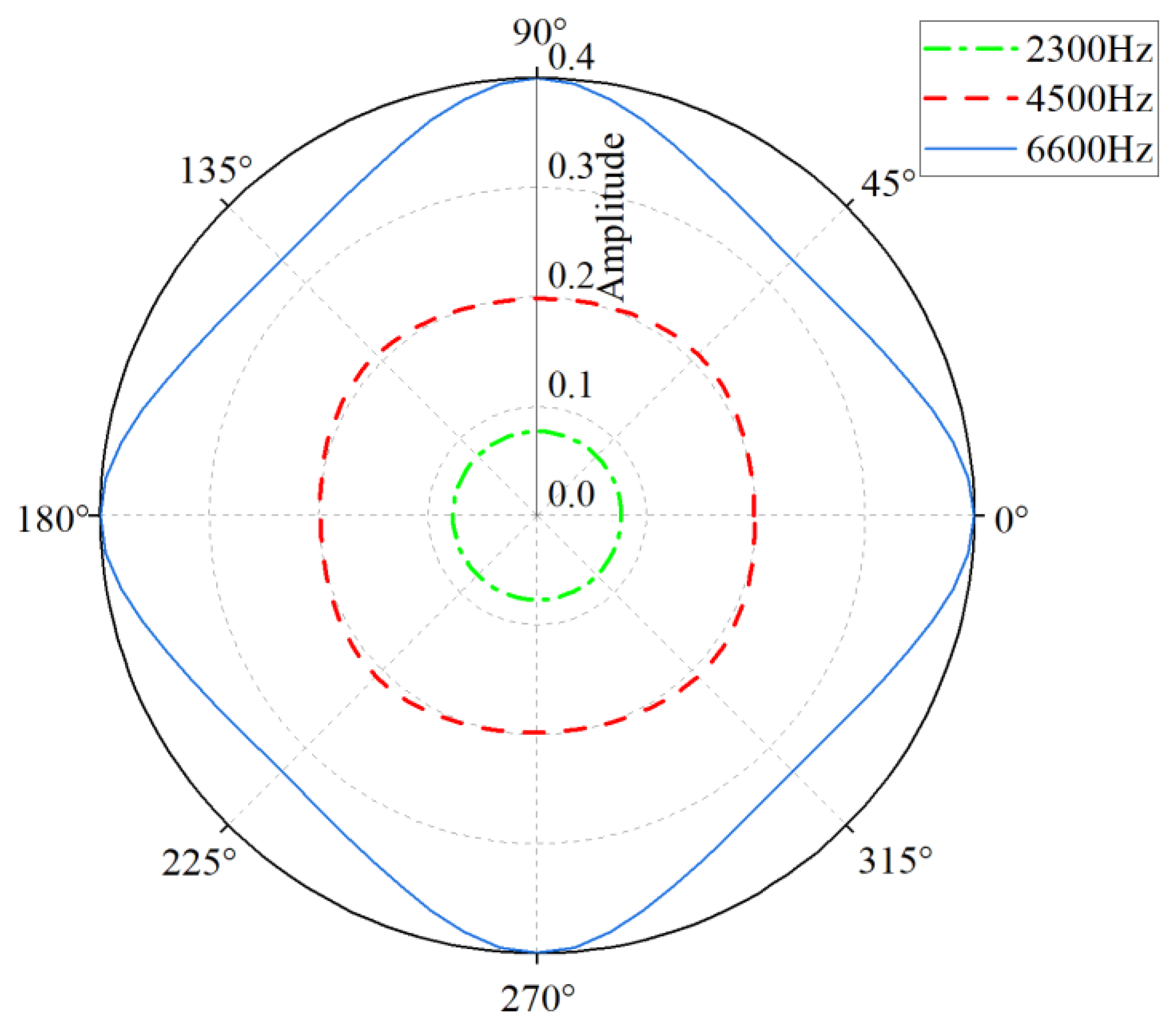
3.1. Band Structure Analysis
3.2. Complex Band Structure
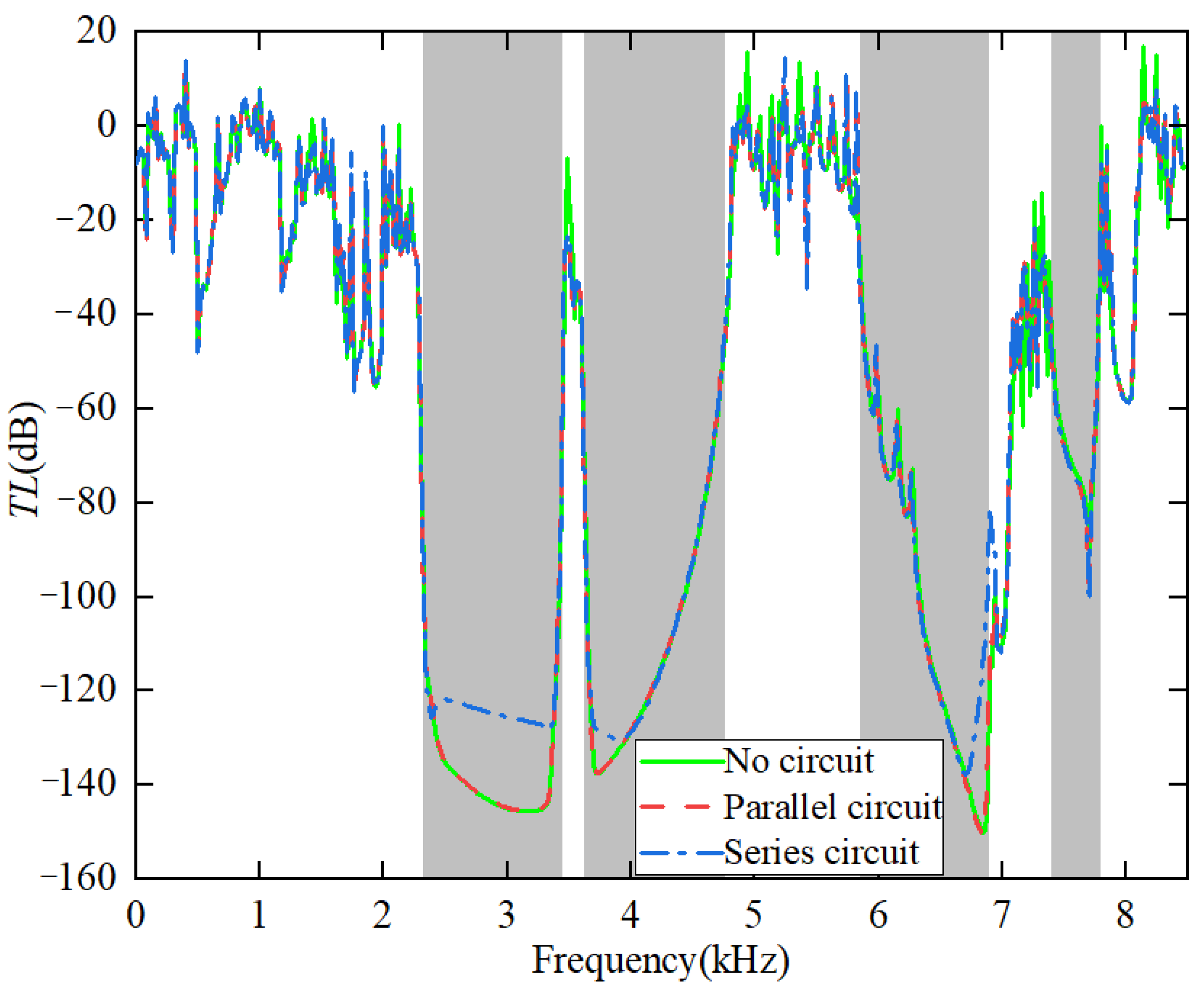
4. Parametric Analysis
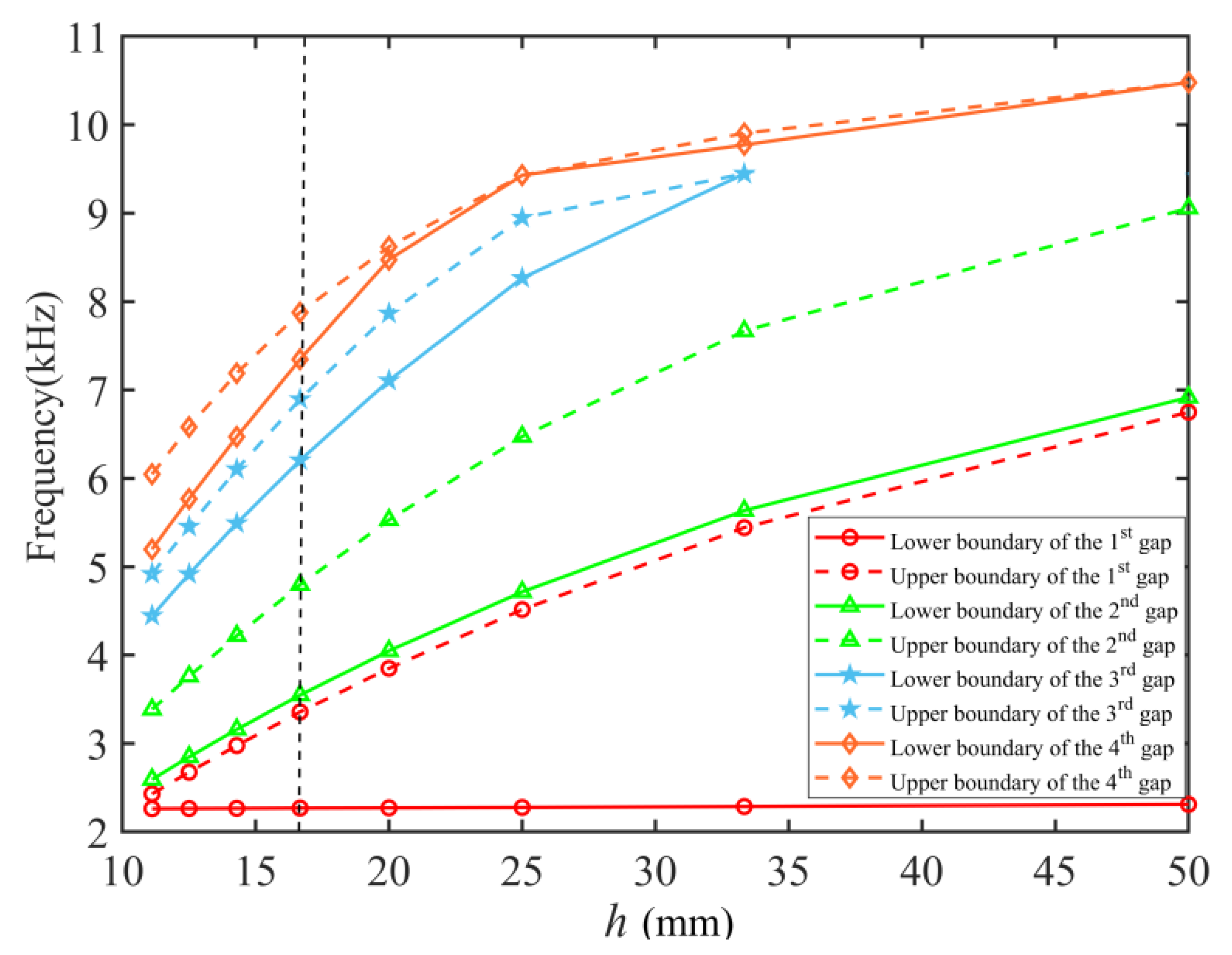
4.1. Effects of the Unit Cell Thickness
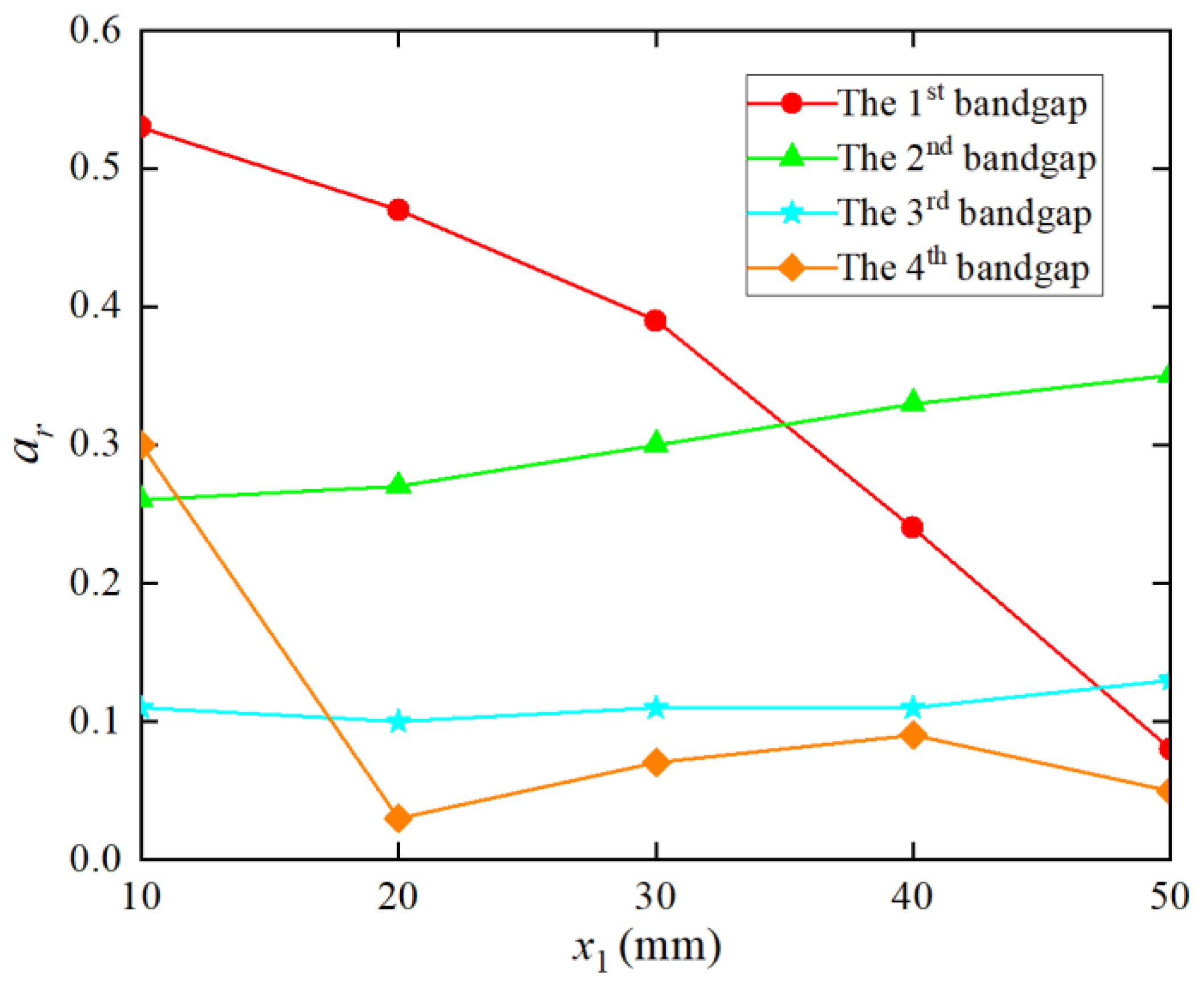
4.2. Effects of the Unit Cell Square Hollow Size
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, J.; Liu, Z.; Qiu, C. Negative Refraction Imaging of Acoustic Waves by a Two-Dimensional Three-Component Phononic Crystal. Phys. Rev. B 2006, 73, 054302. [Google Scholar] [CrossRef]
- Feng, L.; Liu, X.-P.; Chen, Y.-B. Negative Refraction of Acoustic Waves in Two-Dimensional Sonic Crystals. Phys. Rev. B 2005, 72, 033108. [Google Scholar] [CrossRef]
- Sigalas, M.M. Defect States of Acoustic Waves in a Two-Dimensional Lattice of Solid Cylinders. J. Appl. Phys. 1998, 84, 3026–3030. [Google Scholar] [CrossRef]
- Kafesaki, M.; Sigalas, M.M.; García, N. Wave Guides in Two-Dimensional Elastic Wave Band-Gap Materials. Phys. B Condens. Matter 2001, 296, 190–194. [Google Scholar] [CrossRef]
- Wu, F.; Hou, Z.; Liu, Z.; Liu, Y. Point Defect States in Two-Dimensional Phononic Crystals. Phys. Lett. A 2001, 292, 198–202. [Google Scholar] [CrossRef]
- Torres, M.; Montero de Espinosa, F.R.; García-Pablos, D.; García, N. Sonic Band Gaps in Finite Elastic Media: Surface States and Localization Phenomena in Linear and Point Defects. Phys. Rev. Lett. 1999, 82, 3054–3057. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, X.; Liu, Z. Far-Field Imaging of Acoustic Waves by a Two-Dimensional Sonic Crystal. Phys. Rev. B 2005, 71, 054302. [Google Scholar] [CrossRef]
- Gupta, B.C.; Ye, Z. Theoretical Analysis of the Focusing of Acoustic Waves by Two-Dimensional Sonic Crystals. Phys. Rev. E 2003, 67, 036603. [Google Scholar] [CrossRef] [Green Version]
- Cervera, F.; Sanchis, L.; Sánchez-Pérez, J.V.; Martínez-Sala, R.; Rubio, C.; Meseguer, F.; López, C.; Caballero, D.; Sánchez-Dehesa, J. Refractive Acoustic Devices for Airborne Sound. Phys. Rev. Lett. 2001, 88, 023902. [Google Scholar] [CrossRef]
- García-Pablos, D.; Sigalas, M.; Montero de Espinosa, F.R.; Torres, M.; Kafesaki, M.; García, N. Theory and Experiments on Elastic Band Gaps. Phys. Rev. Lett. 2000, 84, 4349–4352. [Google Scholar] [CrossRef] [Green Version]
- Sigalas, M.; Economou, E.N. Band Structure of Elastic Waves in Two Dimensional Systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Liu, Y.; Wu, F. Elastic Wave Band Gaps for Three-Dimensional Phononic Crystals with Two Structural Units. Phys. Lett. A 2003, 313, 455–460. [Google Scholar] [CrossRef]
- Cheng, Y.; Xu, J.Y.; Liu, X.J. Broad Forbidden Bands in Parallel-Coupled Locally Resonant Ultrasonic Metamaterials. Appl. Phys. Lett. 2008, 92, 051913. [Google Scholar] [CrossRef]
- Heckl, M.A. Coupled waves on a periodically supported timoshenko beam. J. Sound Vib. 2002, 252, 849–882. [Google Scholar] [CrossRef]
- Mangaraju, V.; Sonti, V.R. Wave Attenuation in Periodic Three-Layered Beams: Analytical and FEM Study. J. Sound Vib. 2004, 276, 541–570. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Economou, E.N. Elastic and Acoustic Wave Band Structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Berjamin, H.; De Pascalis, R. Acoustoelastic Analysis of Soft Viscoelastic Solids with Application to Pre-Stressed Phononic Crystals. Int. J. Solids Struct. 2022, 241, 111529. [Google Scholar] [CrossRef]
- Lucklum, R.; Mukhin, N.; Djafari Rouhani, B.; Pennec, Y. Phononic Crystal Sensors: A New Class of Resonant Sensors—Chances and Challenges for the Determination of Liquid Properties. Front. Mech. Eng. 2021, 7, 705194. [Google Scholar] [CrossRef]
- Miao, L.; Li, C.; Lei, L.; Fang, H.; Liang, X. A New Periodic Structure Composite Material with Quasi-Phononic Crystals. Phys. Lett. A 2020, 384, 126594. [Google Scholar] [CrossRef]
- Thorp, O.; Ruzzene, M.; Baz, A. Attenuation and Localization of Wave Propagation in Rods with Periodic Shunted Piezoelectric Patches. Smart Mater. Struct. 2001, 10, 979–989. [Google Scholar] [CrossRef]
- Kim, Y.; Baz, A.M. Active Control of a Two-Dimensional Periodic Structure. In Proceedings of the Smart Structures and Materials 2004: Damping and Isolation, San Diego, CA, USA, 29 July 2004; Volume 5386, pp. 329–339. [Google Scholar]
- Hsu, J.-C. Switchable Frequency Gaps in Piezoelectric Phononic Crystal Slabs. Jpn. J. Appl. Phys. 2012, 51, 07GA04. [Google Scholar] [CrossRef]
- Ruzzene, M.; Baz, A. Active Control of Wave Propagation in Periodic Fluid-Loaded Shells. Smart Mater. Struct. 2001, 10, 893–906. [Google Scholar] [CrossRef]
- Gripp, J.A.B.; Rade, D.A. Vibration and Noise Control Using Shunted Piezoelectric Transducers: A Review. Mech. Syst. Signal Processing 2018, 112, 359–383. [Google Scholar] [CrossRef]
- Gozum, M.M.; Aghakhani, A.; Basdogan, I. An Investigation of the Electromechanical Coupling and Broadband Shunt Damping in Composite Plates with Integrated Piezo-Patches. J. Intell. Mater. Syst. Struct. 2019, 30, 3008–3024. [Google Scholar] [CrossRef]
- Ren, T.; Liu, C.; Li, F.; Zhang, C. Active Tuning of the Vibration Band Gap Characteristics of Periodic Laminated Composite Metamaterial Beams. J. Intell. Mater. Syst. Struct. 2020, 31, 843–859. [Google Scholar] [CrossRef]
- Liu, P.; Zuo, S.; Wu, X.; Sun, L.; Zhang, Q. Study on the Vibration Attenuation Property of One Finite and Hybrid Piezoelectric Phononic Crystal Beam. Eur. J. Mech. A/Solids 2020, 84, 104017. [Google Scholar] [CrossRef]
- Zhou, W.; Muhammad; Chen, W.; Chen, Z.; Lim, C.W. Actively Controllable Flexural Wave Band Gaps in Beam-Type Acoustic Metamaterials with Shunted Piezoelectric Patches. Eur. J. Mech. A/Solids 2019, 77, 103807. [Google Scholar] [CrossRef]
- Espo, M.; Abolbashari, M.H.; Hosseini, S.M. Band Structure Analysis of Wave Propagation in Piezoelectric Nano-Metamaterials as Periodic Nano-Beams Considering the Small Scale and Surface Effects. Acta Mech. 2020, 231, 2877–2893. [Google Scholar] [CrossRef]
- Qureshi, E.M.; Shen, X.; Chen, J. Piezoelectric Shunt Damping by Synchronized Switching on Negative Capacitance and Adaptive Voltage Sources. Int. J. Aeronaut. Space Sci. 2014, 15, 396–411. [Google Scholar] [CrossRef] [Green Version]
- Bacigalupo, A.; De Bellis, M.L.; Misseroni, D. Design of Tunable Acoustic Metamaterials with Periodic Piezoelectric Microstructure. Extrem. Mech. Lett. 2020, 40, 100977. [Google Scholar] [CrossRef]
- Zhang, H. Study on Sound Insulation Properties of Piezoelectric Shunt Acoustic Metamaterial. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2016. [Google Scholar]
- Petyt, M. Introduction to Finite Element Vibration Analysis. J. Sound Vib. 2010, 242, 103–124. [Google Scholar] [CrossRef]
- Dieulesaint, E. Elastic Waves in Solids I. Springer Berl. 2000, 4, 673–684. [Google Scholar] [CrossRef]
- Narisetti, R.K.; Ruzzene, M.; Leamy, M.J. A Perturbation Approach for Analyzing Dispersion and Group Velocities in Two-Dimensional Nonlinear Periodic Lattices. J. Vib. Acoust. 2011, 133, 061020. [Google Scholar] [CrossRef]
- Scarpa, F.L.; Ruzzene, M.; Soranna, F. Wave Beaming Effects in Bidimensional Cellular Structures. In Proceedings of the Smart Structures and Materials 2002: Damping and Isolation, San Diego, CA, USA, 18–20 March 2002; Volume 4697, pp. 63–77. [Google Scholar]
- Li, J.; Yang, P.; Ma, Q.; Xia, M. Complex Band Structure and Attenuation Performance of a Viscoelastic Phononic Crystal with Finite Out-of-Plane Extension. Acta Mech. 2021, 232, 2933–2954. [Google Scholar] [CrossRef]
- Bonhomme, J.; Oudich, M.; Segura Chavez, P.A.; Bellaredj, M.L.F.; Bryche, J.-F.; Beyssen, D.; Charette, P.G.; Sarry, F. Numerical Characterization of Love Waves Dispersion in Viscoelastic Guiding-Layer under Viscous Fluid. J. Appl. Phys. 2020, 128, 154502. [Google Scholar] [CrossRef]



| Material Parameters | Piezoelectric Material | Elastic Materials | |
|---|---|---|---|
| PZT-5H | Iron | Epoxy | |
| (kg/m3) | 7500 | 7870 | 1200 |
| Em (Pa) | - | 200 × 109 | 2.8 × 109 |
| υ | - | 0.29 | 0.39 |
| C11 (GPa) | 127.205 | - | - |
| C12 (GPa) | 80.212 | - | - |
| C13 (GPa) | 84.670 | - | - |
| C22 (GPa) | 127.205 | - | - |
| C23 (GPa) | 84.670 | - | - |
| C33 (GPa) | 117.436 | - | - |
| C44 (GPa) | 22.989 | - | - |
| C55 (GPa) | 22.989 | - | - |
| C66 (GPa) | 23.474 | - | - |
| e15 (C/m2) | 17.035 | - | - |
| e24 (C/m2) | 17.035 | - | - |
| e31 (C/m2) | −6.623 | - | - |
| e32 (C/m2) | −6.623 | - | - |
| e33 (C/m2) | 23.240 | - | - |
| ε11 (F/m) | 1.509 × 10−8 | - | - |
| ε22 (F/m) | 1.509 × 10−8 | - | - |
| ε33 (F/m) | 1.269 × 10−8 | - | - |
| Parameters | Descriptions | Value |
|---|---|---|
| b1 (mm) | The width of the convex structures | 20 |
| b2 (mm) | The length of the convex structures | 40 |
| x1 (mm) | The side length of the square hollow | 30 |
| x2 (mm) | The side length of the internal hard material | 56 |
| x3 (mm) | The side length of the piezoelectric material | 80 |
| x4 (mm) | The side length of the outer hard material | 100 |
| h (mm) | The thickness of the phononic crystal | 16.67 |
| x1 (mm) | 1st Gap | 2nd Gap | 3rd Gap | 4th Gap |
|---|---|---|---|---|
| 10 | [2260.10, 3886.33] | [4066.74, 5283.68] | [6775.12, 7554.94] | [11091.72, 15008.91] |
| 20 | [2261.77, 3667.03] | [3850.89, 5077.89] | [6522.89, 7234.90] | [7686.61, 7947.03] |
| 30 | [2268.89, 3356.36] | [3547.67, 4795.41] | [6204.55, 6894.88] | [7345.23, 7877.57] |
| 40 | [2345.95, 2992.60] | [3196.86, 4456.71] | [5852.81, 6560.45] | [7046.26, 7718.97] |
| 50 | [2457.48, 2649.43] | [2870.53, 4077.25] | [5465.80, 6213.06] | [8238.10, 8676.57] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Z.; Li, J.; Li, S.; Ma, Q. Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension. Appl. Sci. 2022, 12, 7021. https://doi.org/10.3390/app12147021
Miao Z, Li J, Li S, Ma Q. Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension. Applied Sciences. 2022; 12(14):7021. https://doi.org/10.3390/app12147021
Chicago/Turabian StyleMiao, Zhongjian, Jingru Li, Sheng Li, and Qingfen Ma. 2022. "Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension" Applied Sciences 12, no. 14: 7021. https://doi.org/10.3390/app12147021
APA StyleMiao, Z., Li, J., Li, S., & Ma, Q. (2022). Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension. Applied Sciences, 12(14), 7021. https://doi.org/10.3390/app12147021





