Research on a Wi-Fi RSSI Calibration Algorithm Based on WOA-BPNN for Indoor Positioning
Abstract
:1. Introduction
- (1)
- Firstly, we propose a Wi-Fi RSSI calibration algorithm based on a whale optimisation algorithm (WOA)-BPNN and use the WOA to find the optimal initial weights and thresholds of the BPNN model. The proposed algorithm has a simple process and few parameters to adjust. Secondly, to speed up the establishment and optimisation of the calibration algorithm and upgrade the updating and iterating speed, we propose a nonlinear convergence factor a to simulate the shrinking behaviour of the surrounding prey of the whales and obtain an improved WOA-BPNN calibration algorithm. The convergence factor a changes dynamically only with the current iterations t and effectively prevents the algorithm from falling into the local optimum. We use the calibration algorithm to calibrate the Wi-Fi RSSI data received by the different mobile terminals at the same position to make the Wi-Fi RSSI consistent. Finally, by changing the hidden layer structure of the BPNN model, we compare the performance of different BPNN models on the calibration results.
- (2)
- Focusing on the problem of the low positioning accuracy of location fingerprint indoor positioning algorithms based on the Wi-Fi RSSI, we propose a region-adaptive weighted KNN (WKNN) positioning algorithm based on hierarchical clustering. Firstly, we employ the BWP index to evaluate the clustering results and find the optimal number of clustering regions, which can help narrow the online matching positioning range and improve the positioning speed. Secondly, this algorithm adaptively determines the K fingerprint data in the fingerprint database of its attribution area, which is similar to the RSSI values received by the mobile terminals at a real-time position, then uses the WKNN algorithm to calculate the final position results comprehensively.
2. Methods and Algorithms
2.1. Methods
2.1.1. BPNN
2.1.2. WOA
2.1.3. Agglomerative Hierarchical Clustering Method
2.2. Algorithms
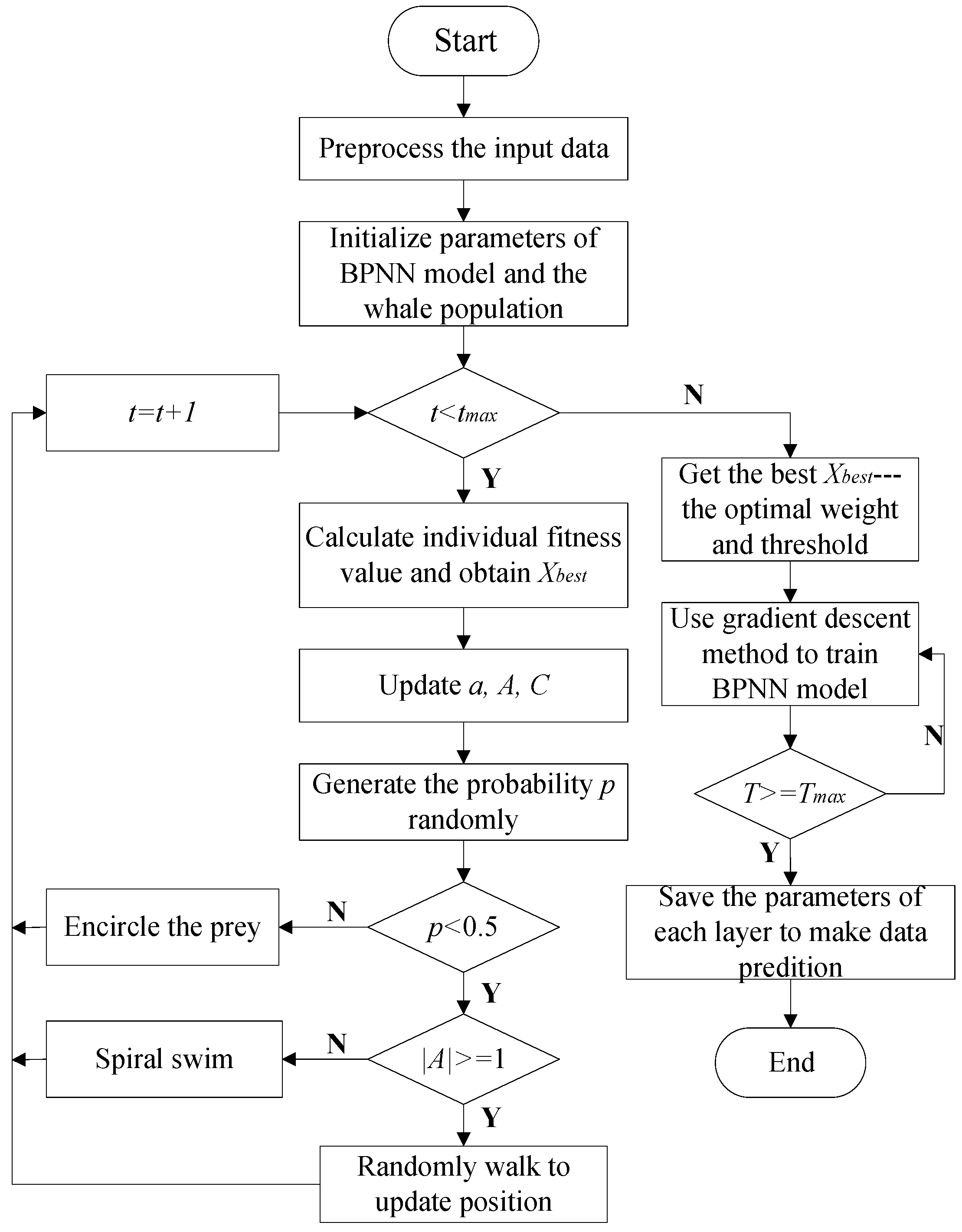
2.2.1. Calibration Algorithm Based on WOA-BPNN
- (1)
- A New Convergence Factor
- (2)
- WOA-BPNN Calibration Algorithm Steps
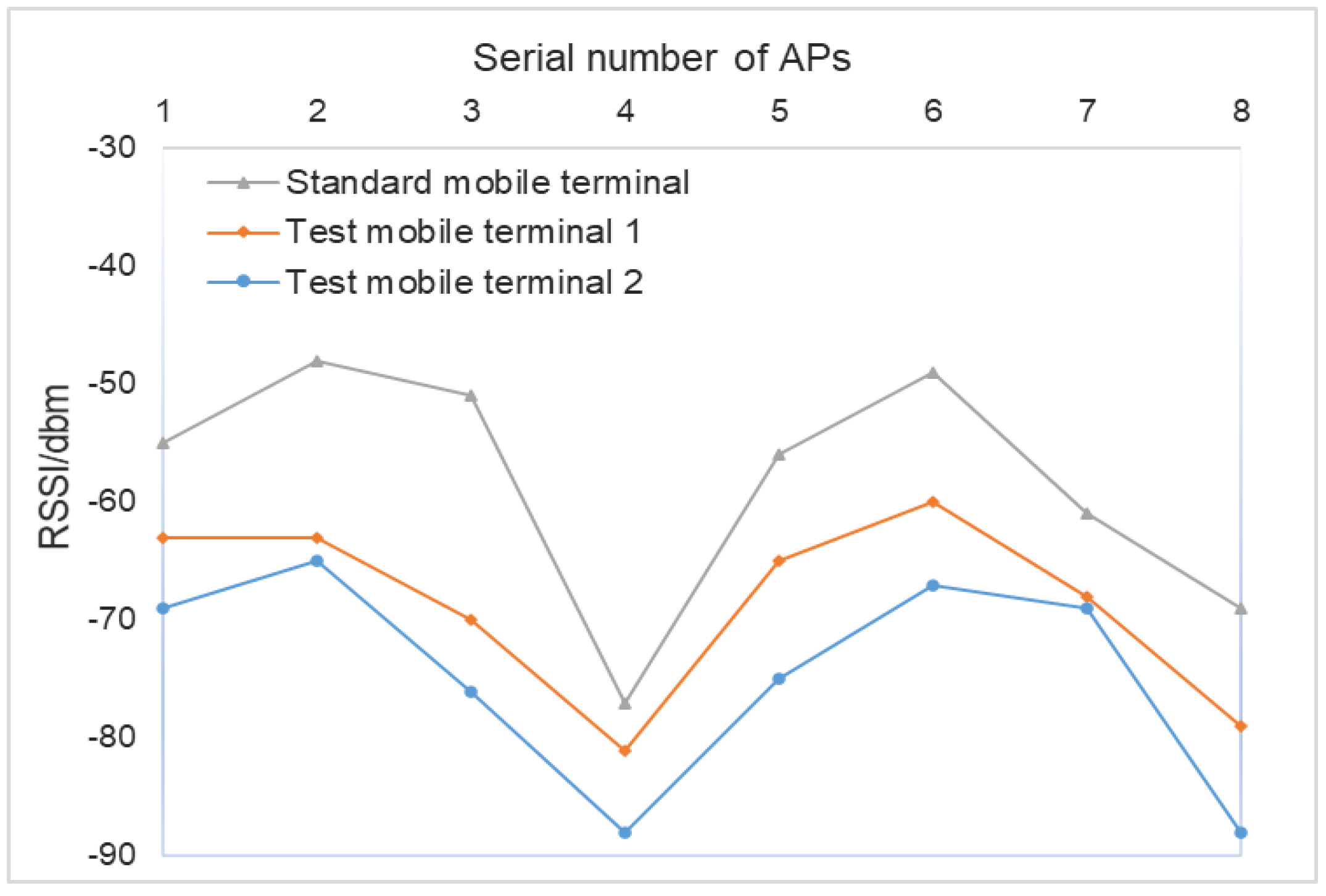
- Step 1: Randomly select several acquisition points in the room and use a standard mobile terminal and test mobile terminal to collect the RSSI values of all APs at all acquisition points. To reduce the noise impact of personnel disturbance and same frequency interference during the RSSI propagation, process the received multiple RSSI values of the same AP via mean filtering. Take the average RSSI values of each AP collected from all acquisition points by the standard mobile terminal as the initial standard sampling data and take the average RSSI values of all the corresponding APs of the test mobile terminal at the corresponding acquisition points as the test sampling data. In addition, take the test sampling data as the real input value of the WOA-BPNN calibration model and take the initial standard sampling data as the real output value of the WOA-BPNN calibration model.
- Step 2: Initialise the weight and threshold of each layer randomly to build the BPNN, which also means initialising the whale group position . Next, set the size of the whale population N, the current number of iterations of the whale population , the maximum number of iterations of the whale population , the current number of iterations of the BPNN model , and the maximum number of iterations of the BPNN model .
- Step 3: When the current number of iterations of the whale population t is less than the maximum iteration number of the whale population, according to the fitness function formula, as Equation (2), calculate the fitness value of each whale, obtain the position of the optimal fitness value, and then find the best fitness and the corresponding optimal whale position .where is the real value of the ith RSSI, is the predicted value of the ith RSSI and is the number of samples.
- Step 4: To speed up the establishment and optimisation of the calibration algorithm and upgrade the updating and iterating speed, use the proposed nonlinear convergence factor a to simulate the shrinking behaviour of the surrounding prey of the whales. The convergence factor a changes dynamically only with the current iteration times t and effectively prevents the algorithm from falling into the local optimum. The formula of the nonlinear convergence factor a is shown as Equation (1). Update the whale position parameters A and C. The formulas are shown in Equations (3) and (4).where r is a random value of [0, 1].
- Step 5: Randomly generate probability p and judge whether it is less than 0.5. If , then update the position by shrinking and surrounding, as shown in Equation (5).where t is current number of iterations of the whale population, is the optimal whale position, is the current whale position and and are the whale position parameters obtained in Step 4, else if , then select the swimming mode according to the value of |A|: when , the whales will choose to update their position by swimming in a circular motion, as shown in Equation (6).where indicates the distance between the whale and the optimal position, is a constant that defines the logarithmic spiral shape and is a random value in [–1, 1]; when , the whales choose to swim randomly according to Equation (7):where is the randomly selected position of a whale.
- Step 6: The current number of iterations of the whale population t increases automatically, and the optimal position is updated according to Step 2. When the maximum number of iterations of the whale population is reached, it outputs , which represents the optimal weight and threshold as the optimal initial parameters of the BPNN model.
- Step 7: The BPNN performs forward propagation, processing data through the connection weight between the neuron i and the neuron j and threshold of the neuron j. Obtain the predicted output value using the nonlinear sigmoid activation function, as shown in Equations (8) and (9), as follows:where is the connection weight between the neuron and the neuron , , and are the threshold, input value and output value of the neuron , respectively, and is the input value of the neuron and is the number of samples.
- Step 8: With the forward propagation process, we obtain the predicted value of the output layer neuron. According to the error between the predicted output value and the real output value, obtain the loss function of the current iteration number , as shown in Equation (10); the error is propagated back to the upper layer of neurons to obtain the error in this layer, and then passes layer by layer until the top hidden layer is reached. Update and adjust the connection weights and thresholds based on the gradient descent method, as shown in Equations (11) and (12), as follows:where is the real output value of the output layer neuron j, is the predicted output value of the output layer neuron j, is the number of samples, is the updated weight between the neuron i and the neuron j, is the updated threshold of the neuron j, and is the learning rate, if is too large, the convergence will be fast but easy to fall into the local optimum, if the value is too small, the convergence will be slow but close to the global optimum.
- Step 9: After repeated learning and training, when the current number of iterations of the BPNN model T reaches the maximum number of iterations of the BPNN model Tmax, select the BPNN model with the smallest loss function as the final calibration model, and save the parameters of the current WOA-BPNN calibration model and corresponding mobile terminal model.
- Step 10: Repeat Step 1 to Step 8 for multiple mobile terminals, then establish the calibration model database.
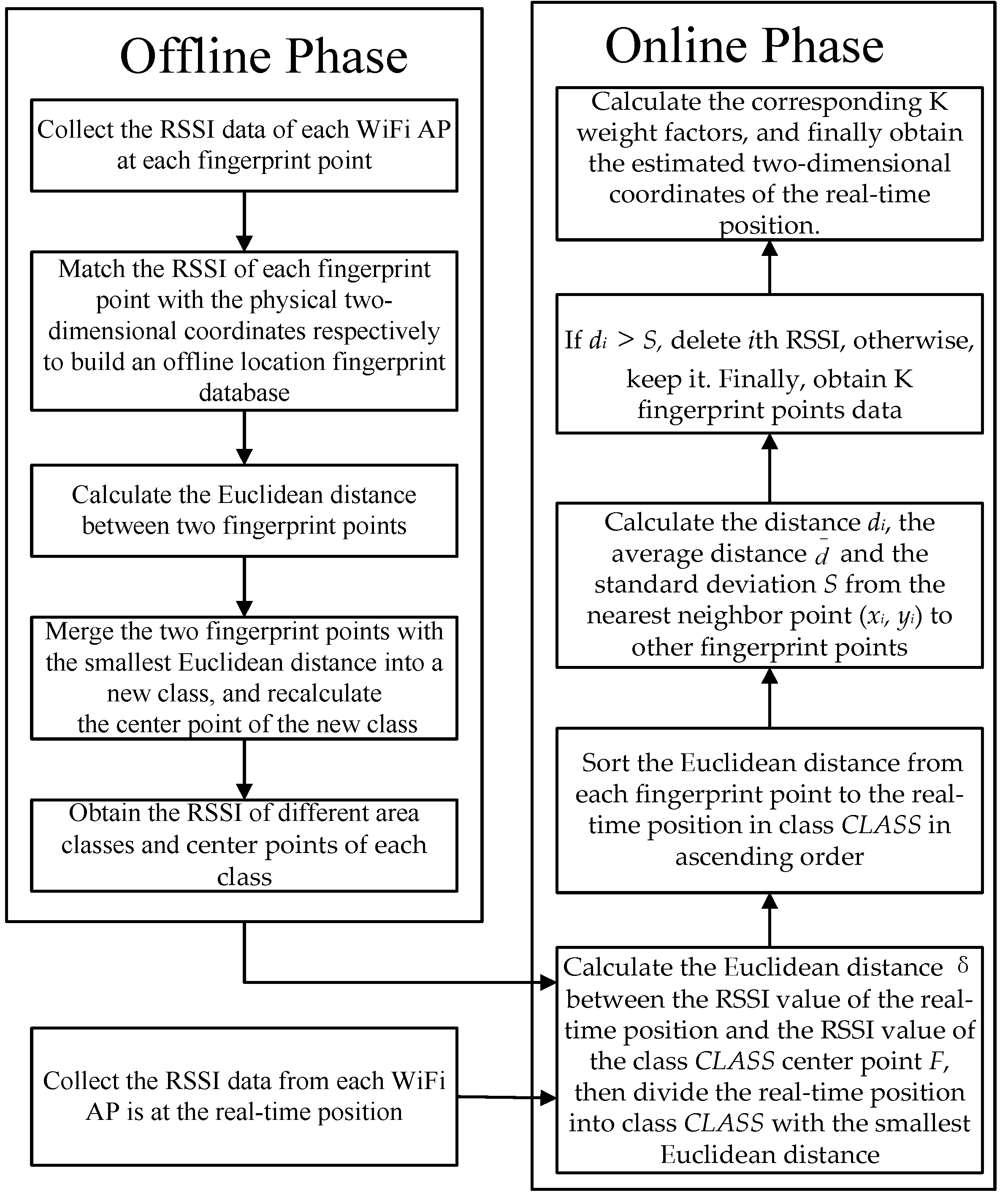
2.2.2. Region-Adaptive WKNN Algorithm Based on Hierarchical Clustering
- Step 1: In the offline phase, a mobile terminal collects the average RSSI data of each Wi-Fi AP at each fingerprint point, match the RSSI of each fingerprint point with the physical two-dimensional coordinates to build an offline location fingerprint database.
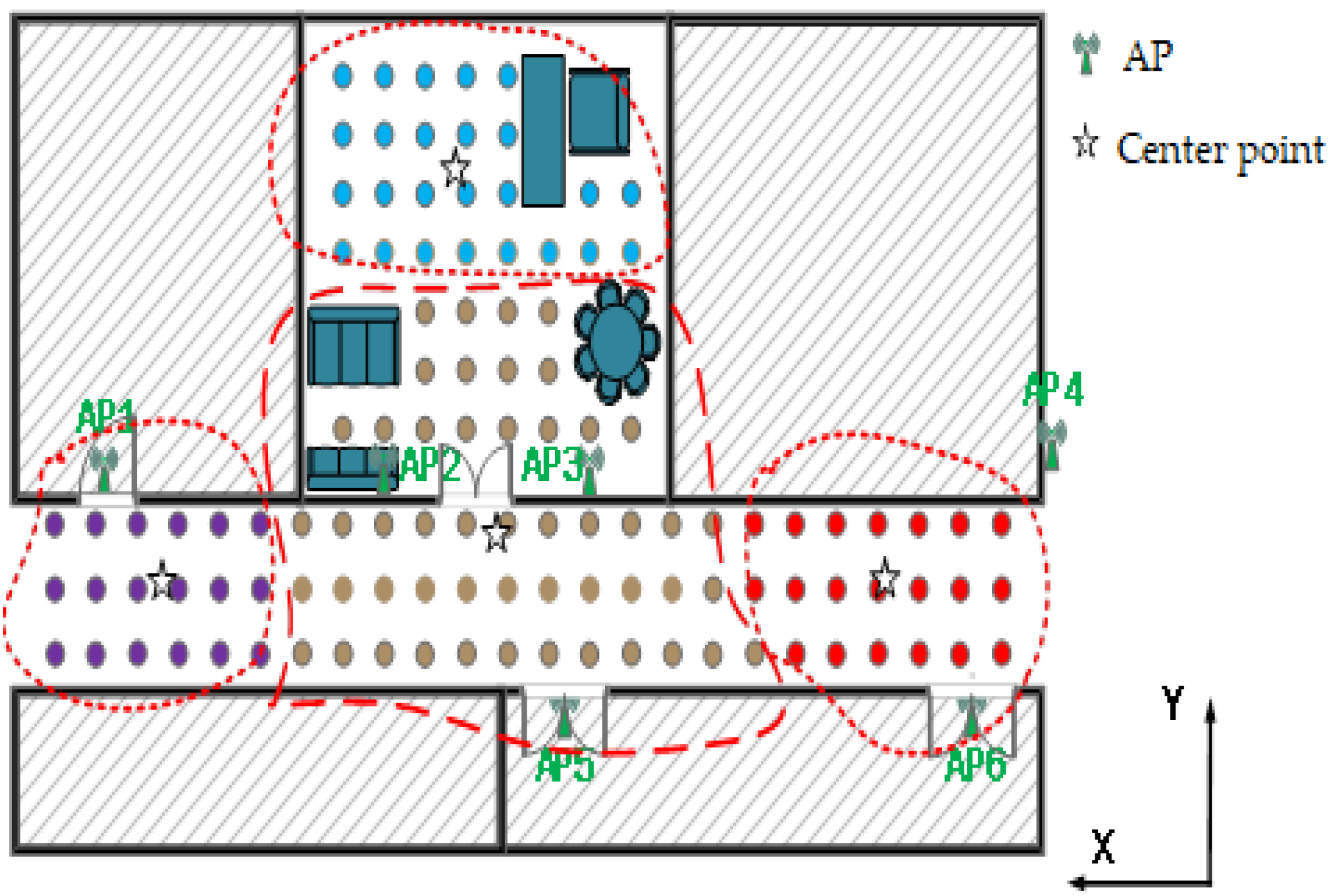
- Step 2: Calculate the Euclidean distance between two fingerprint points, then merge the two fingerprint points with the smallest Euclidean distance into a new class and recalculate the centre point of the new class. Finally, obtain the RSSI of different area classes and centre points of each class.
- Step 3: In the online phase, the mobile terminal collects RSSI values from each Wi-Fi AP at a real-time position to form a set of RSSI data. Calculate the Euclidean distance D between the RSSI value of the real-time position and the RSSI value of the class CLASS centre point F in turn, as shown in Equation (13), then divide the real-time position into the class CLASS with the smallest Euclidean distance.where rssij is RSSI value of the jth Wi-Fi AP collected from the real-time position, RSSIFj is the RSSI value of the jth Wi-Fi AP of the CLASS centre point F of class, and n is the number of Wi-Fi APs.
- Step 4: Sort the Euclidean distance from each fingerprint point to the real-time position in class CLASS in ascending order. Find the corresponding two-dimensional coordinates (x1, y1) of the fingerprint points, calculate the distance , the average distance and the standard deviation from the nearest neighbour point to the other fingerprint points, as shown in Equations (14)–(16).
- Step 5: Filter the fingerprint points in class C further. When , delete the ith RSSI, otherwise, when , keep the ith RSSI. Finally, obtain K fingerprint points data, n is the number of Wi-Fi AP.
- Step 6: According to the Euclidean distance of the remaining K fingerprint points, calculate the corresponding weight factor and obtain the estimated two-dimensional coordinates of the real-time position.
3. Experiments and Results
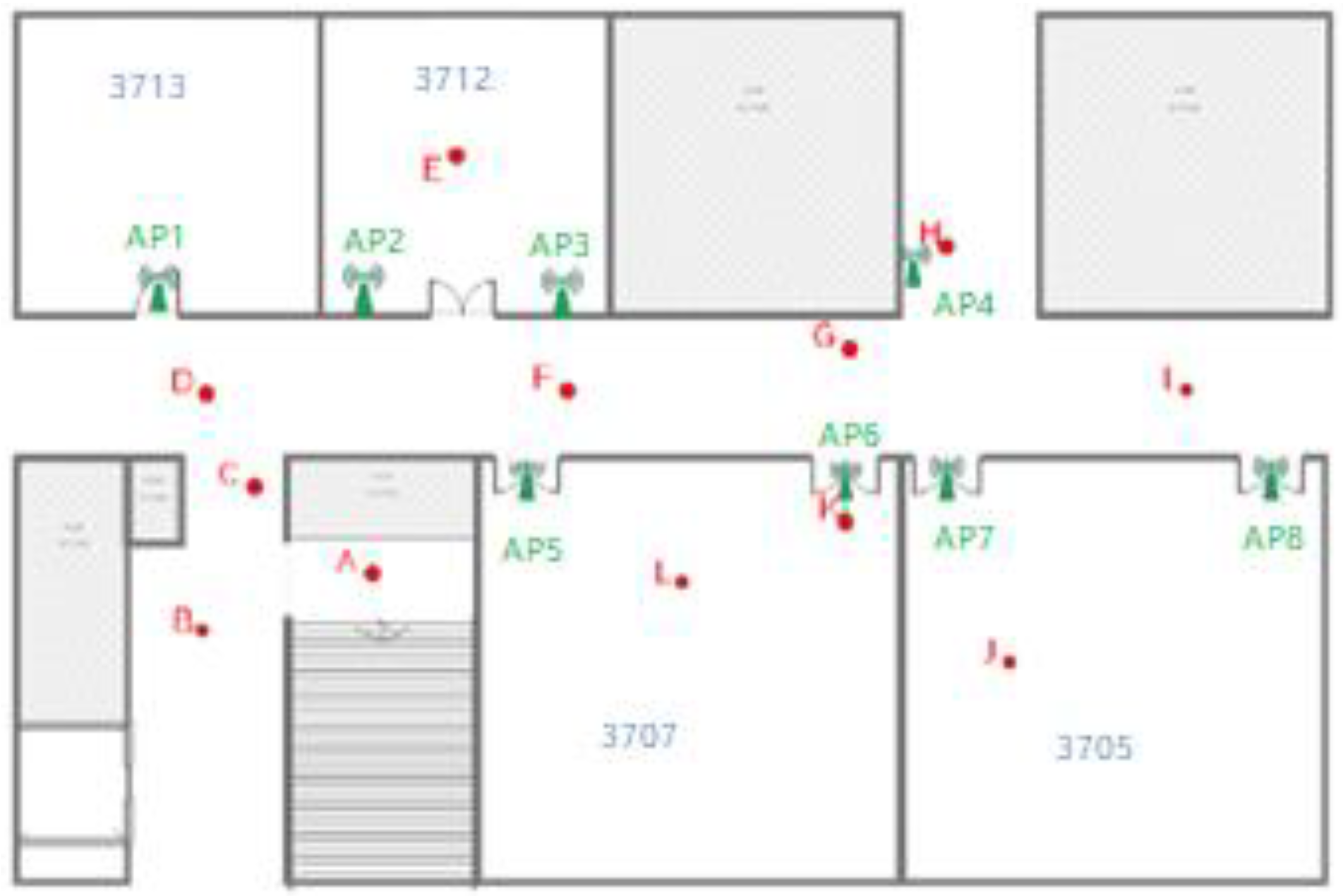
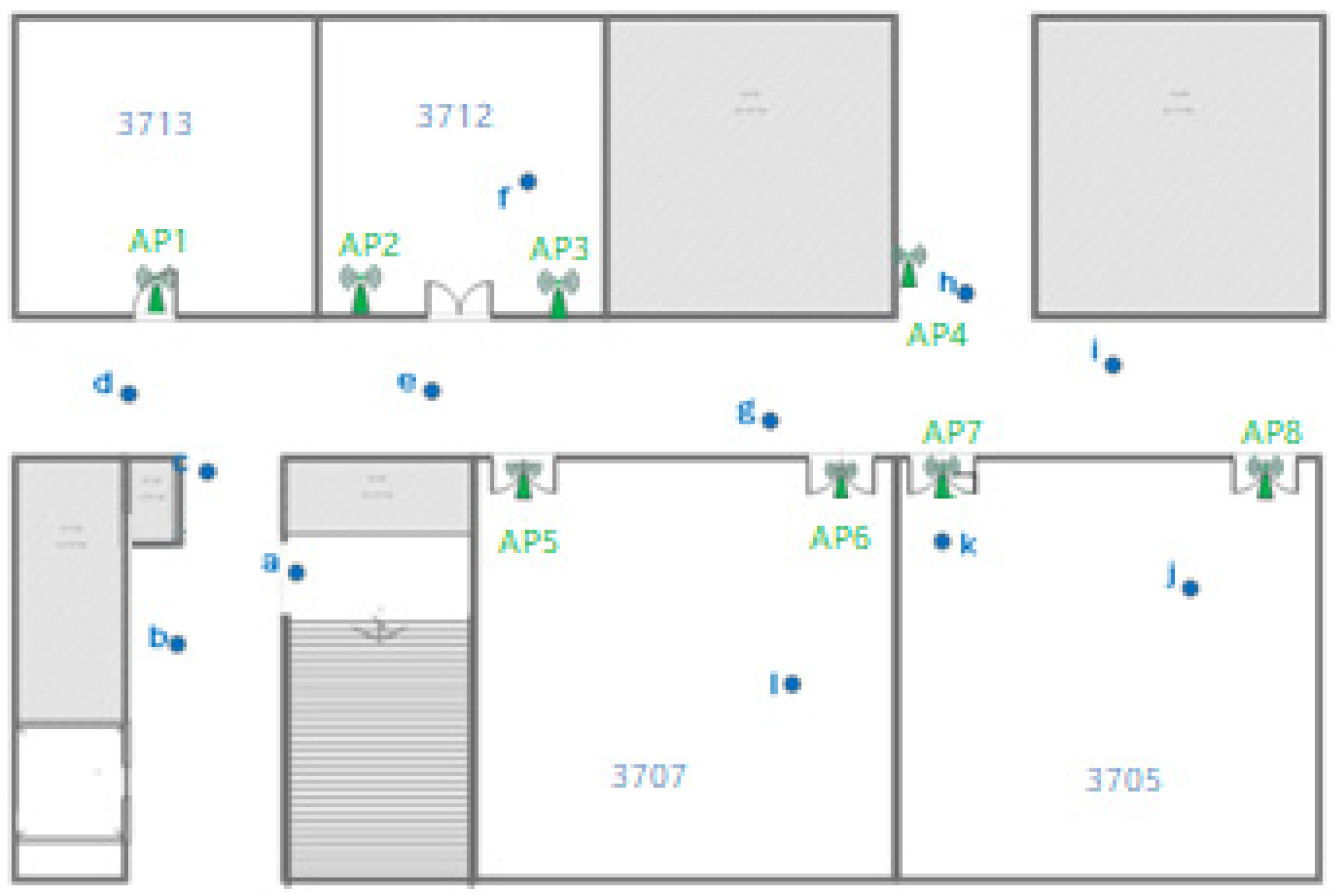
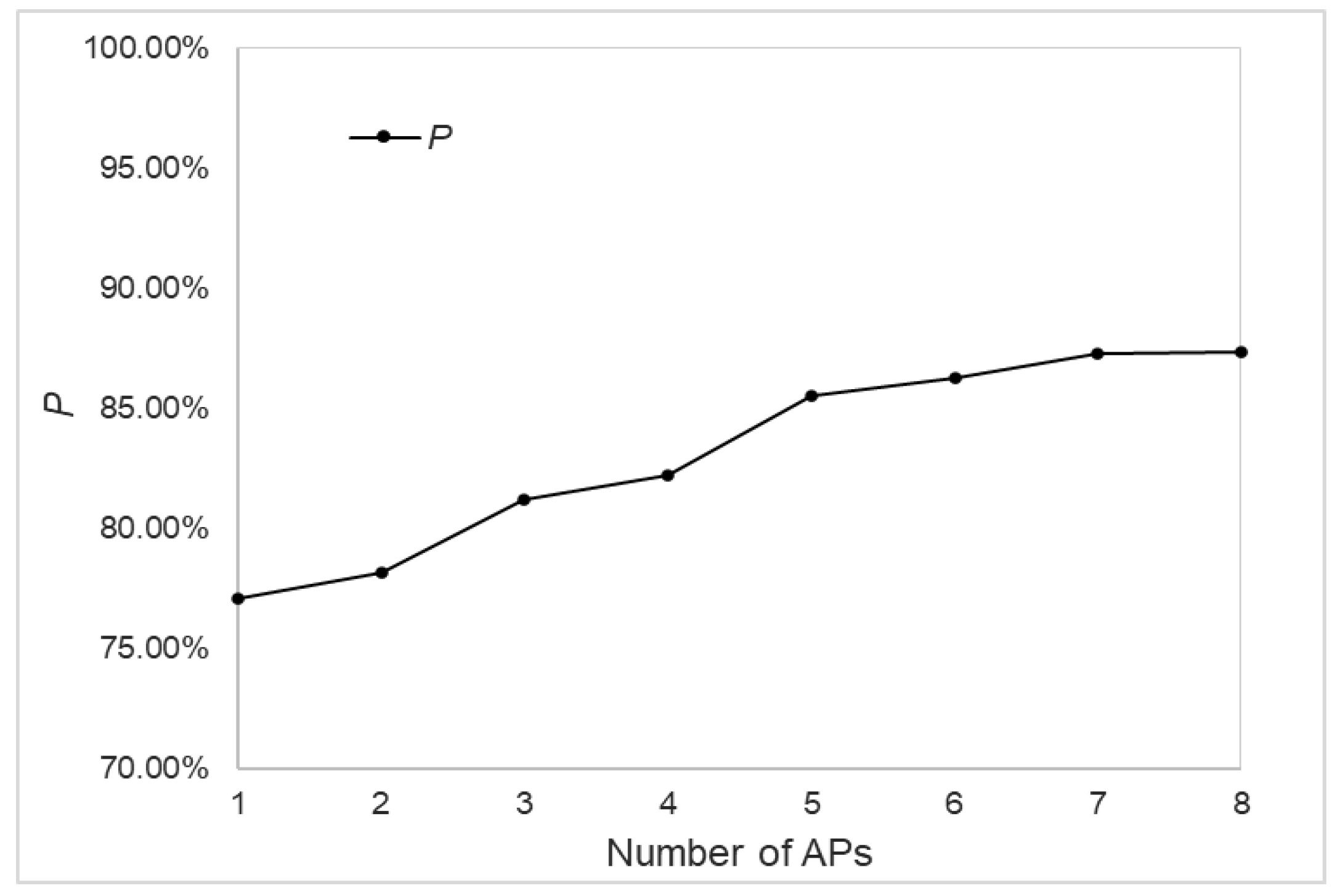
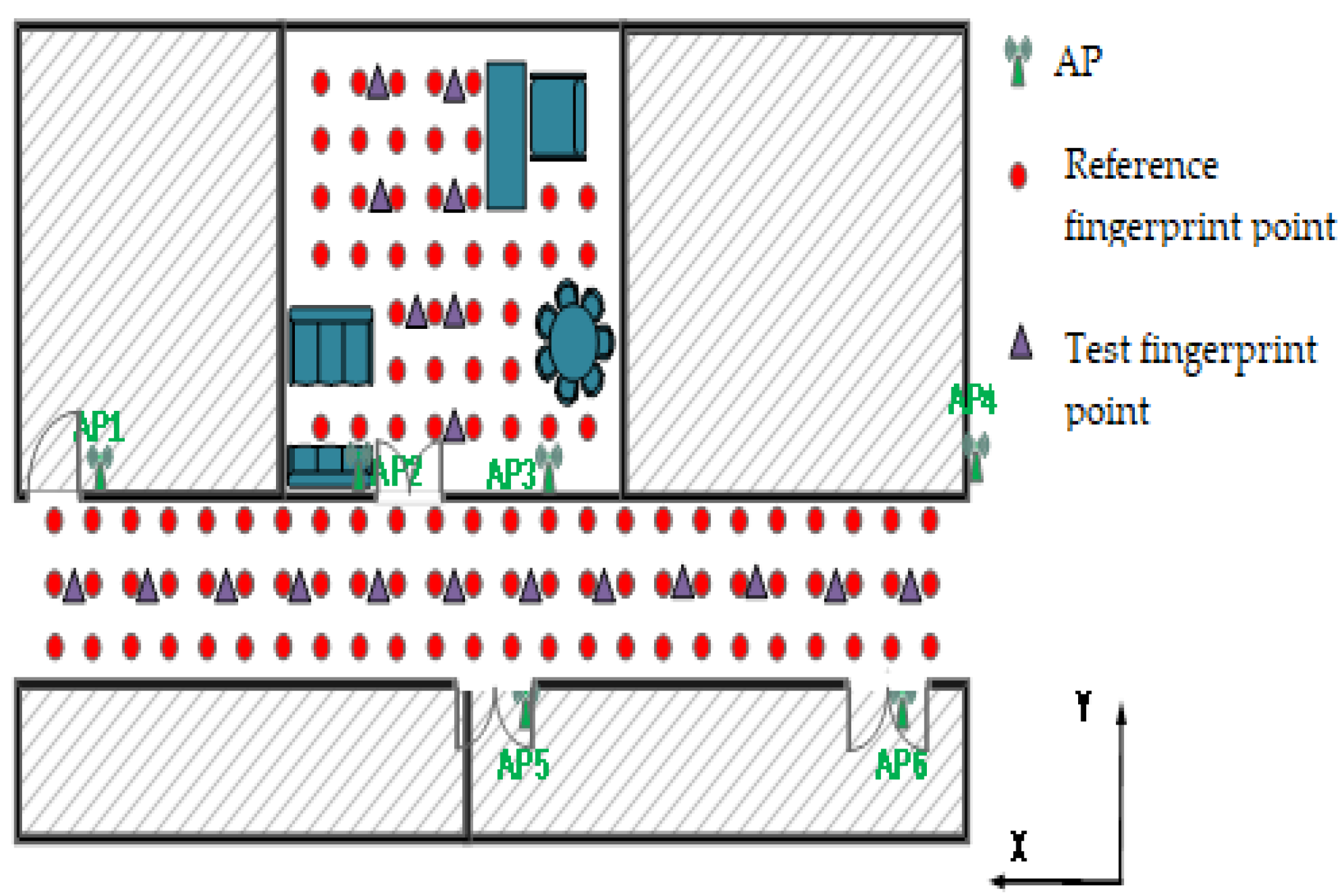
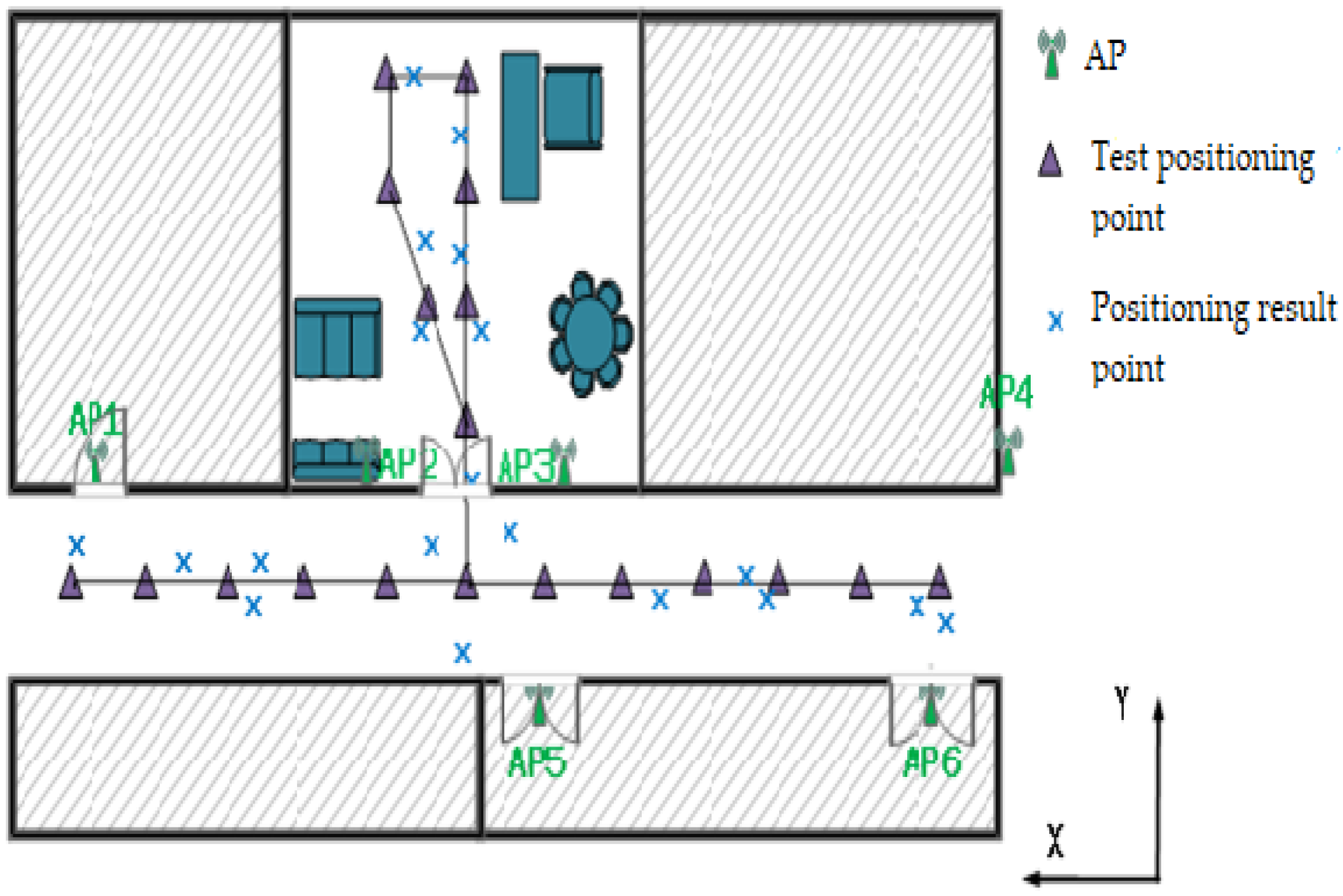
3.1. Wi-Fi AP Number Setting
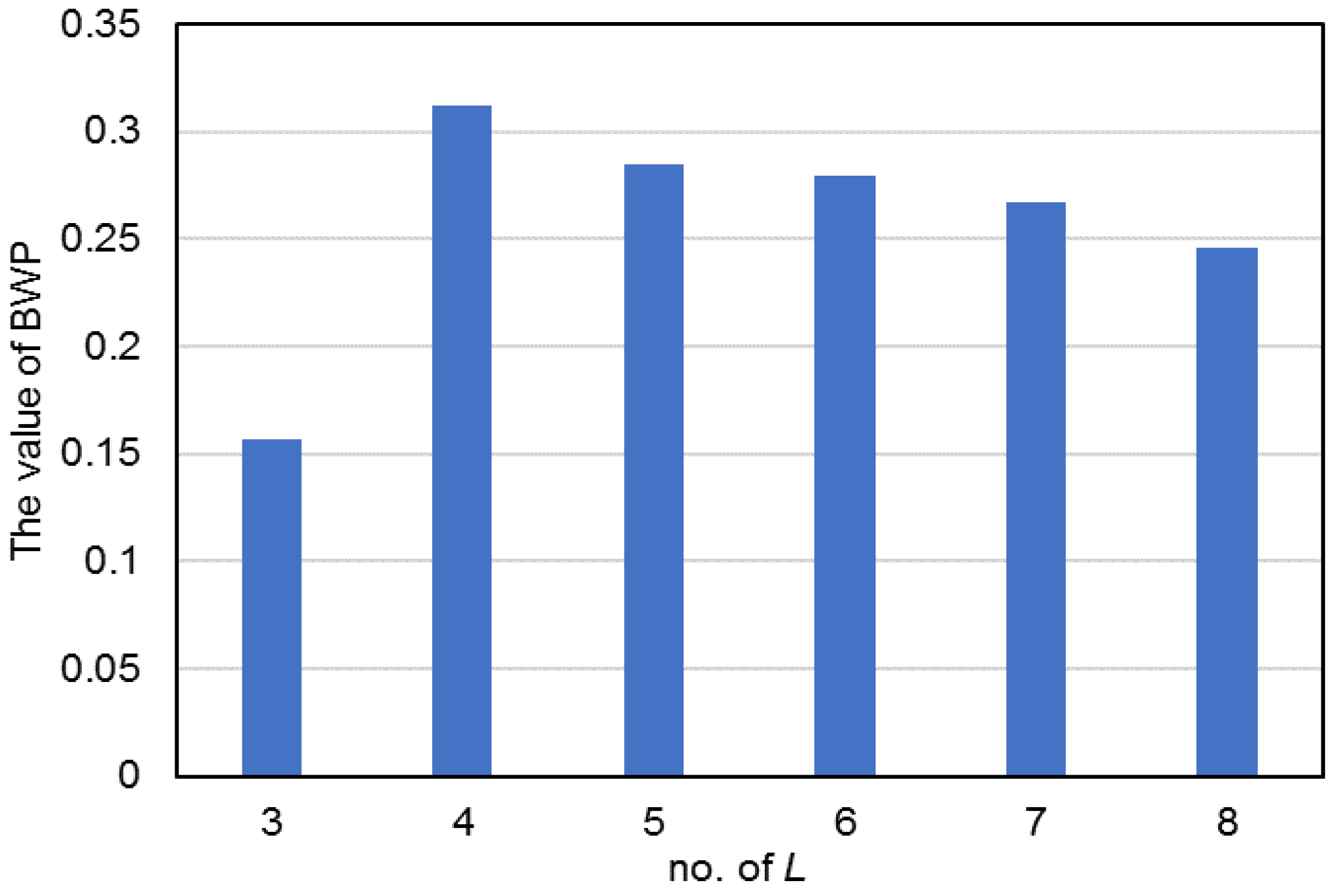
3.2. Region Division Result
3.3. Hidden Layer Structure Setting
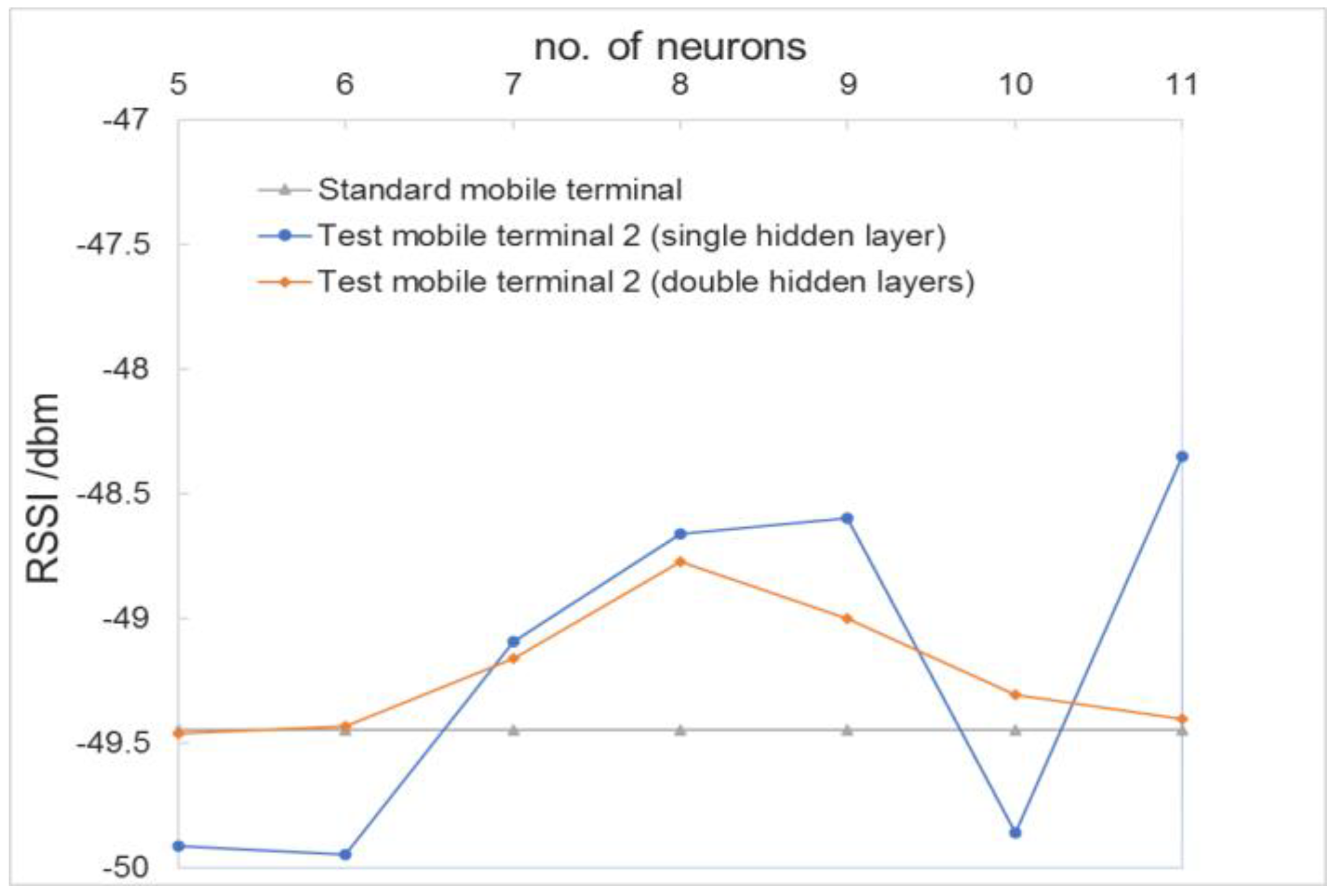
3.3.1. Influence of Hidden Layer Structure on Average RSSI Value
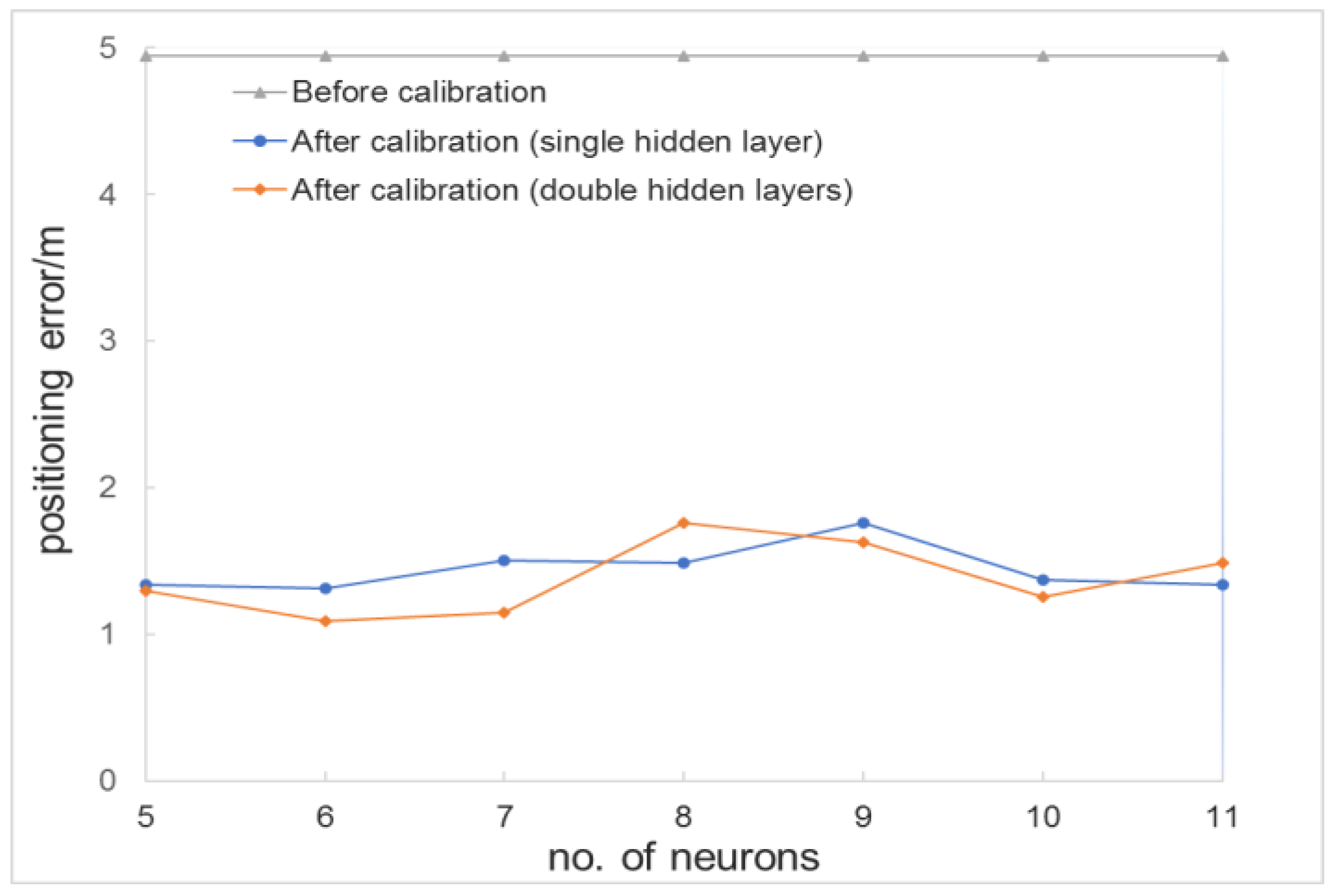
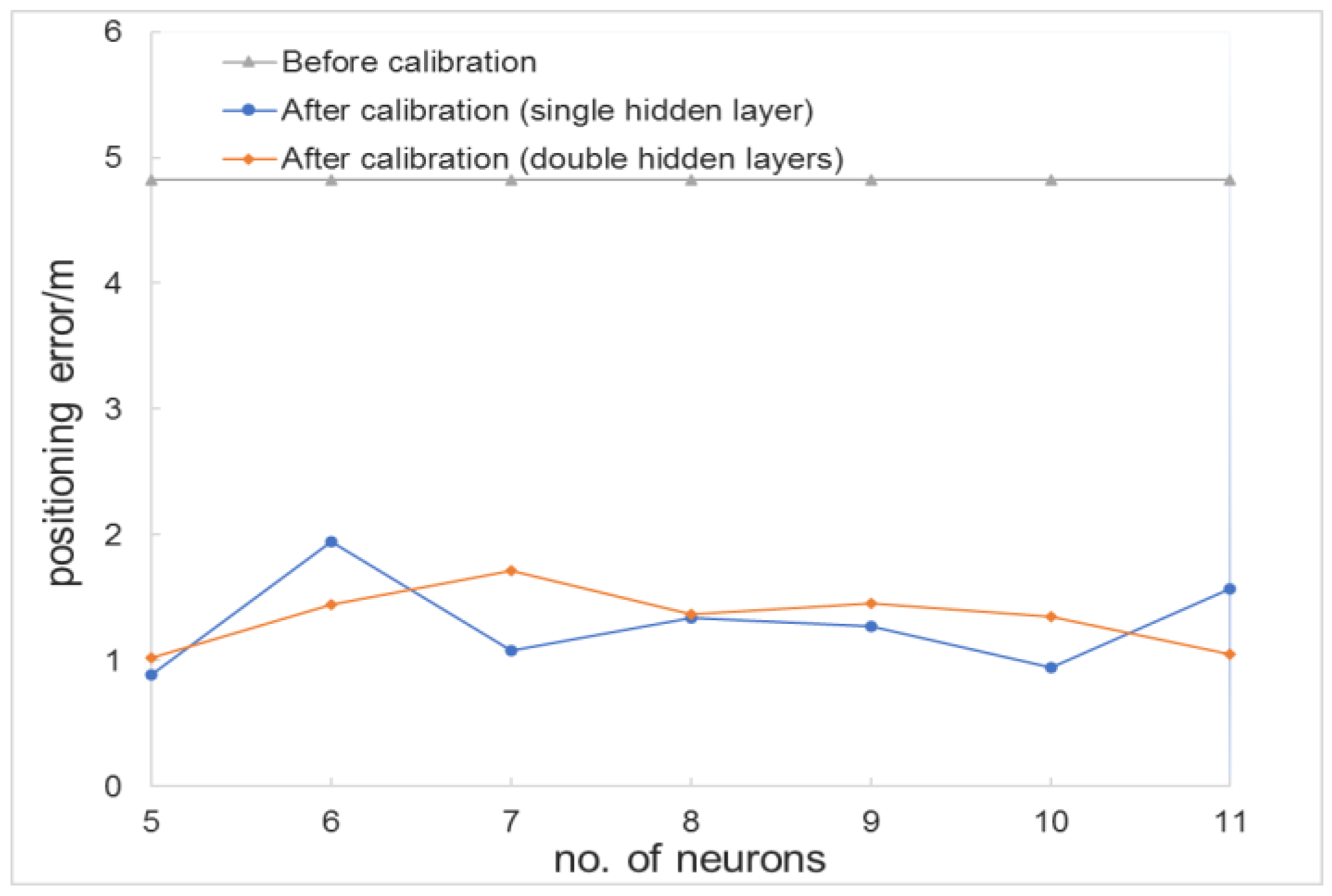
3.3.2. Influence of Hidden Layer Structure on Average Positioning Error
3.4. Trajectory Positioning Points
4. Discussion
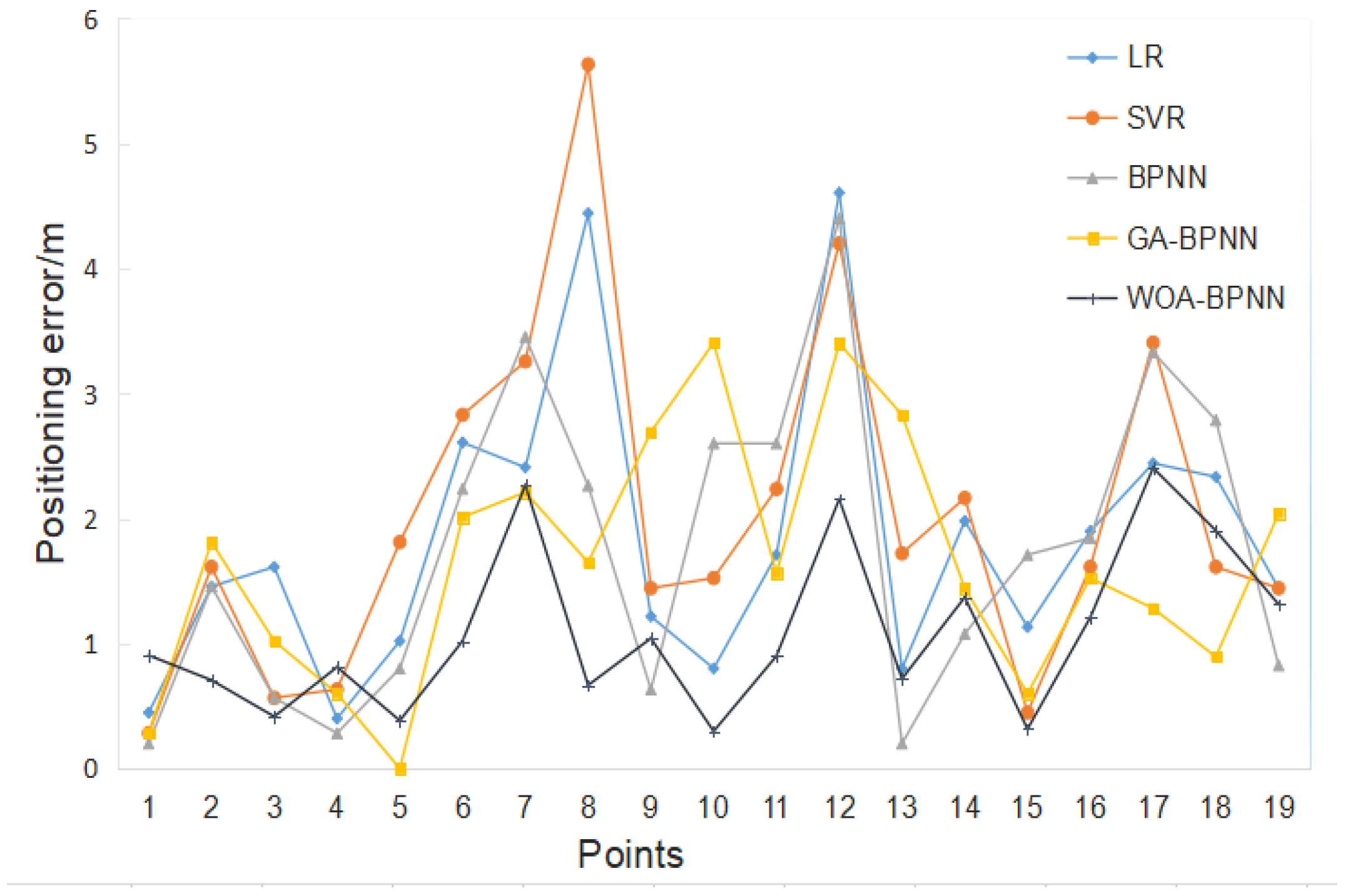
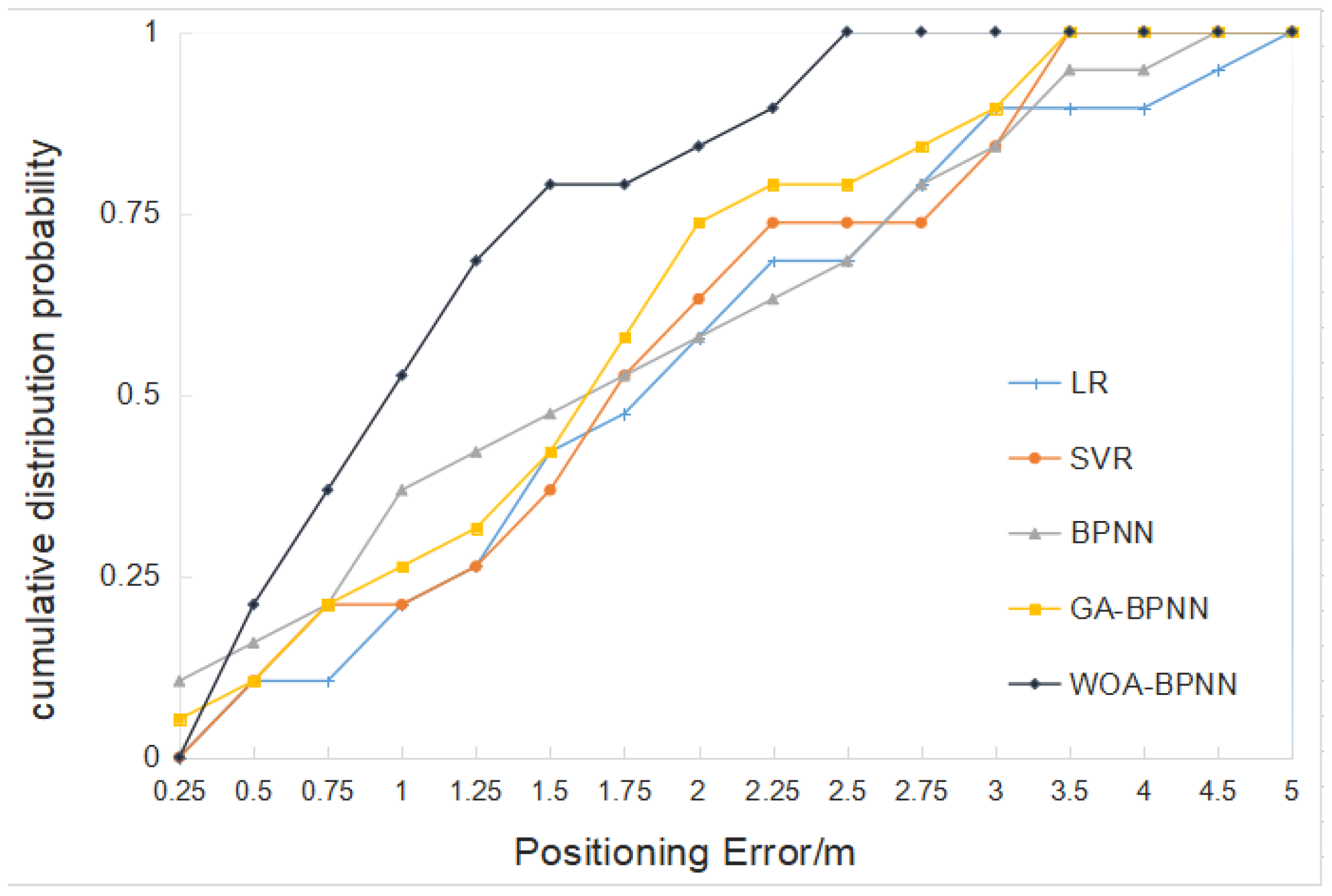
4.1. Comparison with Other Positioning Algorithms
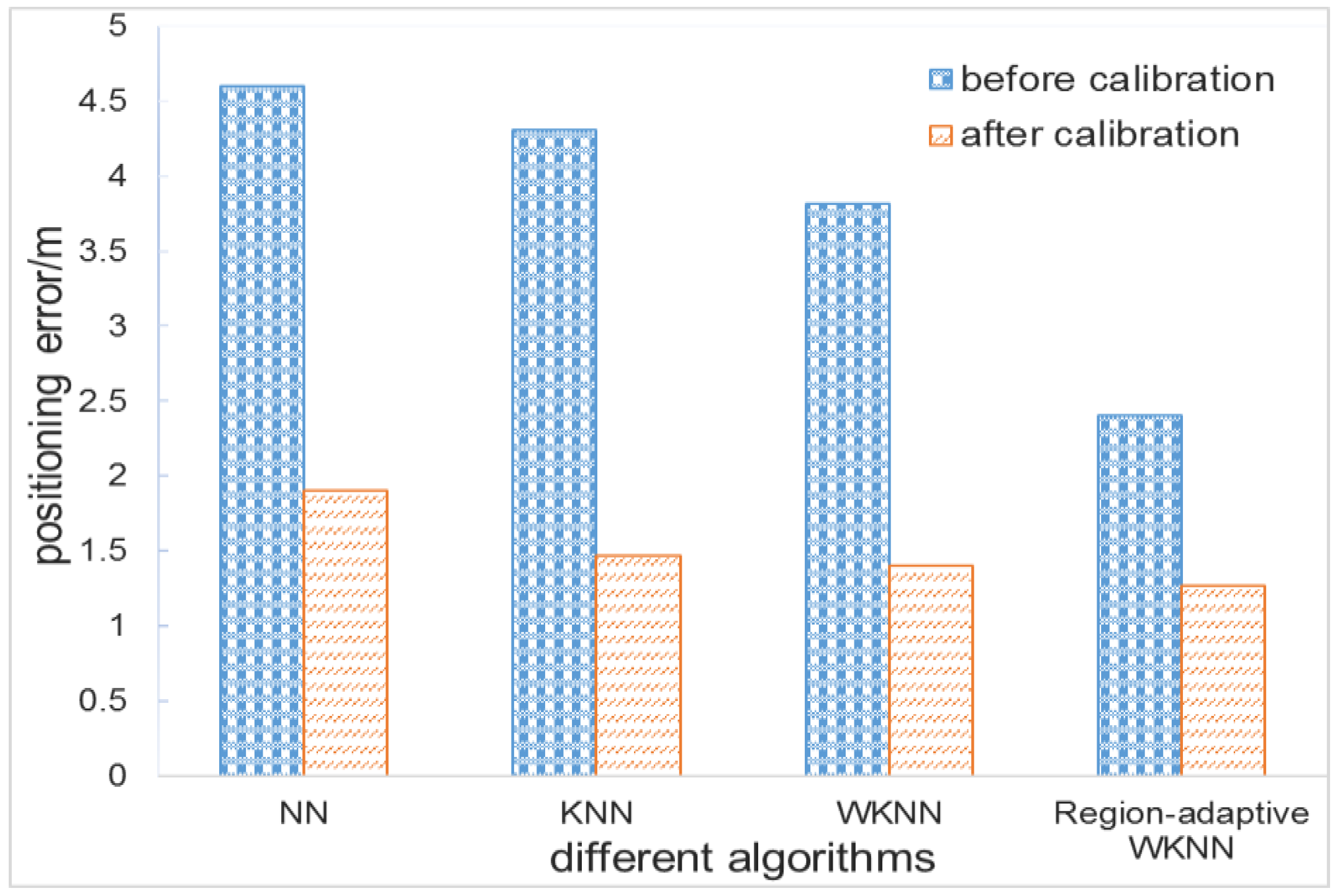
4.2. Comparison with Other Calibration Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Meaning |
| a | convergence factor |
| t | the current number of iterations of the whale population |
| tmax | the maximum number of iterations of the whale population |
| the initial weight | |
| the initial threshold | |
| the whale group position | |
| N | the size of whale population |
| T | the current number of iterations of the BPNN model |
| Tmax | the maximum number of iterations of the BPNN model |
| the fitness function | |
| the number of samples | |
| yi | the real value of the ith RSSI |
| y | the predicted value of the ith RSSI |
| A | one of the whale position parameters |
| C | one of the whale position parameters |
| r | a random value of [0, 1] |
| p | a random probability |
| the current whale position | |
| the optimal whale position | |
| the position of the whale at the next moment | |
| the distance between the current position and the optimal position | |
| b | a constant, which defines the logarithmic spiral shape |
| l | a random value in [–1, 1] |
| the randomly selected position of a whale | |
| the optimal weight and threshold of the BPNN model | |
| the connection weight between the neuron i and the neuron j | |
| the threshold of the neuron j | |
| the input value of the neuron j | |
| the output value of the neuron j | |
| the input value of the neuron i | |
| the loss function of the current iteration number | |
| the real output value of the output layer neuron j | |
| the predicted output value of the output layer neuron j | |
| the updated weight between the neuron i and the neuron j | |
| the updated threshold of the neuron j | |
| the learning rate between 0–1 | |
| D | the Euclidean distance between the RSSI of the real-time position and the RSSI of the class centre point F |
| rssij | the RSSI value of the jth Wi-Fi AP collected in real-time position |
| RSSImj | the RSSI value of the jth Wi-Fi AP of the centre point m of class |
| n | the number of Wi-Fi APs |
| (x1, y1) | the corresponding two-dimensional coordinates of the fingerprint points |
| di | the distance from the nearest neighbor point to other fingerprint points |
| the average distance from the nearest neighbor point to other fingerprint points | |
| S | the standard deviation from the nearest neighbor point to other fingerprint points |
| p | the error reduction ratio |
| the error between RSSI value of the test mobile terminal and that of the standard mobile terminal before calibration | |
| the error between the RSSI value of the test mobile terminal after calibration and that of the standard mobile terminal | |
| the number of error reduction after calibration in the test data | |
| Z | the total number of test data sets, which is proportional to the number of APs |
| L | the number of clusters |
| the number of neurons in the hidden layer | |
| the number of neurons in the input layer | |
| the number of neurons in the output layer | |
| a constant between 1–10 |
References
- Machaj, J.; Brida, P.; Piché, R. Rank based fingerprinting algorithm for indoor positioning. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–6. [Google Scholar]
- Li, Z.; Liu, J.; Yang, F.; Niu, X.; Li, L.; Wang, Z.; Chen, R. A Bayesian Density Model Based Radio Signal Fingerprinting Positioning Method for Enhanced Usability. Sensors 2018, 18, 4063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, S.; Chan, S.; Lei, Y. SLAC: Calibration-Free Pedometer-Fingerprint Fusion for Indoor Localization. IEEE Trans. Mob. Comput. 2018, 17, 1176–1189. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Q.; Xu, J.; Hu, J.; Song, T. An Indoor RFID Location Algorithm Based on Support Vector Regression and Particle Swarm Optimisation. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar]
- Song, B.; Yu, M.; He, X. An Indoor Location WIFI Calibration Method Based on BP Neural Network. J. Navig. Position. 2019, 7, 43–47. [Google Scholar]
- Yu, Z.; Lu, X.; Tao, X. RSSI Ranging Algorithm Based on GA-BP Neural Network Model. J. Navig. Position. 2020, 8, 63–68. [Google Scholar]
- Ferreira, D.; Souza, R.; Carvalho, C. QA-kNN: Indoor Localization Based on Quartile Analysis and the kNN Classifier for Wireless Networks. Sensors 2020, 20, 4714. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Hua, X.; Li, Q.; Qiu, W.; Peng, X. Improved Clustering Algorithm of Neighboring Reference Points Based on KNN for Indoor Localization. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–4. [Google Scholar]
- Zhao, H.; Huang, B.; Jia, B. Applying kriging interpolation for WiFi fingerprinting based indoor positioning systems. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Li, J.; Gao, X.; Hu, Z.; Wang, H.; Cao, T.; Yu, L. Indoor Localization Method Based on Regional Division with IFCM. Electronics 2019, 8, 559. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Guo, S.; Wu, Y.; Yang, Y. A Novel Radio Map Construction Method to Reduce Collection Effort for Indoor Localization. Measurement 2016, 94, 423–431. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Selami, Y.; Lv, N.; Tao, W.; Yang, H.; Zhao, H. Optimizing laser triangulation displacement sensor of 3D positioning and posture using COA Based BPNN. Sens. Rev. 2020, 40, 112–120. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Z.; Qin, X.; Geng, H.; Gao, Z. An Extended Kalman Filter and Back Propagation Neural Network Algorithm Positioning Method Based on Anti-lock Brake Sensor and Global Navigation Satellite System Information. Sensors 2018, 18, 2753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xing, S.; Zhang, H.; Liang, X.; Gulliver, A. A 60 GHz impulse radio positioning algorithm based on a BP neural network. In Proceedings of the 2017 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Victoria, BC, Canada, 21–23 August 2017; pp. 1–5. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimisation Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Shaun, C.; Cedric, L. The Structure of Dark Matter Haloes in Hierarchical Clustering Models. Mon. Not. R. Astron. Soc. 1995, 281, 716–736. [Google Scholar]
- Long, W.; Jiao, J.; Liang, X.; Tang, M. An Exploration-enhanced Grey Wolf Optimiser to Solve High-dimensional Numerical Optimisatin. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]
- Wang, W.; Tang, R.; Li, C.; Liu, P.; Luo, L. A BP Neural Network Model Optimised by Mind Evolutionary Algorithm for Predicting the Ocean Wave Heights. Ocean Eng. 2018, 162, 98–107. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Z.; Zhang, C.; Dong, F.; Wei, P. Numerical Investigation of the Dynamic Responses of Long-Span Bridges with Consideration of the Random Traffic Flow Based on the Intelligent ACO-BPNN Model. IEEE Access 2018, 6, 28520–28529. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Mirjalili, S. A Hyper-heuristic for Improving the Initial Population of Whale Optimisation Algorithm. Knowl. Based Syst. 2019, 172, 42–63. [Google Scholar] [CrossRef]
- Lei, Y.; Yan, C.; Renu, S.; Belay, A. A modified WKNN indoor Wi-Fi localization method with differential coordinates. In Proceedings of the 2017 International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1822–1824. [Google Scholar]
- Zhou, S.; Xu, Z.; Tang, X. Method for Determining the Optimal Cluster Number of K-means Algorithm. J. Comput. Appl. 2010, 30, 1995–1998. [Google Scholar]




| Algorithms | LR | SVR | BPNN | GA-BPNN | WOA-BPNN | ||
|---|---|---|---|---|---|---|---|
| Indicator | |||||||
| Mobile Terminal | |||||||
| Test mobile terminal 1 | positioning error(one sigma) | 1.71 | 1.81 | 1.84 | 1.65 | 1.02 | |
| positioning error (two sigma) | 4.44 | 3.26 | 3.45 | 3.40 | 2.27 | ||
| Test mobile terminal 2 | positioning error (one sigma) | 2.24 | 2.21 | 2.34 | 2.00 | 1.32 | |
| positioning error (two sigma) | 3.49 | 3.41 | 3.29 | 2.61 | 2.72 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Yao, S.; Wu, X.; Chen, L. Research on a Wi-Fi RSSI Calibration Algorithm Based on WOA-BPNN for Indoor Positioning. Appl. Sci. 2022, 12, 7151. https://doi.org/10.3390/app12147151
Yu M, Yao S, Wu X, Chen L. Research on a Wi-Fi RSSI Calibration Algorithm Based on WOA-BPNN for Indoor Positioning. Applied Sciences. 2022; 12(14):7151. https://doi.org/10.3390/app12147151
Chicago/Turabian StyleYu, Min, Shuyin Yao, Xuan Wu, and Liang Chen. 2022. "Research on a Wi-Fi RSSI Calibration Algorithm Based on WOA-BPNN for Indoor Positioning" Applied Sciences 12, no. 14: 7151. https://doi.org/10.3390/app12147151
APA StyleYu, M., Yao, S., Wu, X., & Chen, L. (2022). Research on a Wi-Fi RSSI Calibration Algorithm Based on WOA-BPNN for Indoor Positioning. Applied Sciences, 12(14), 7151. https://doi.org/10.3390/app12147151






