Optimal Design of Fluid Flow and Heat Transfer in Pipe Jackets Having Bow Cross-Sections
Abstract
:1. Introduction
2. Numerical Simulation
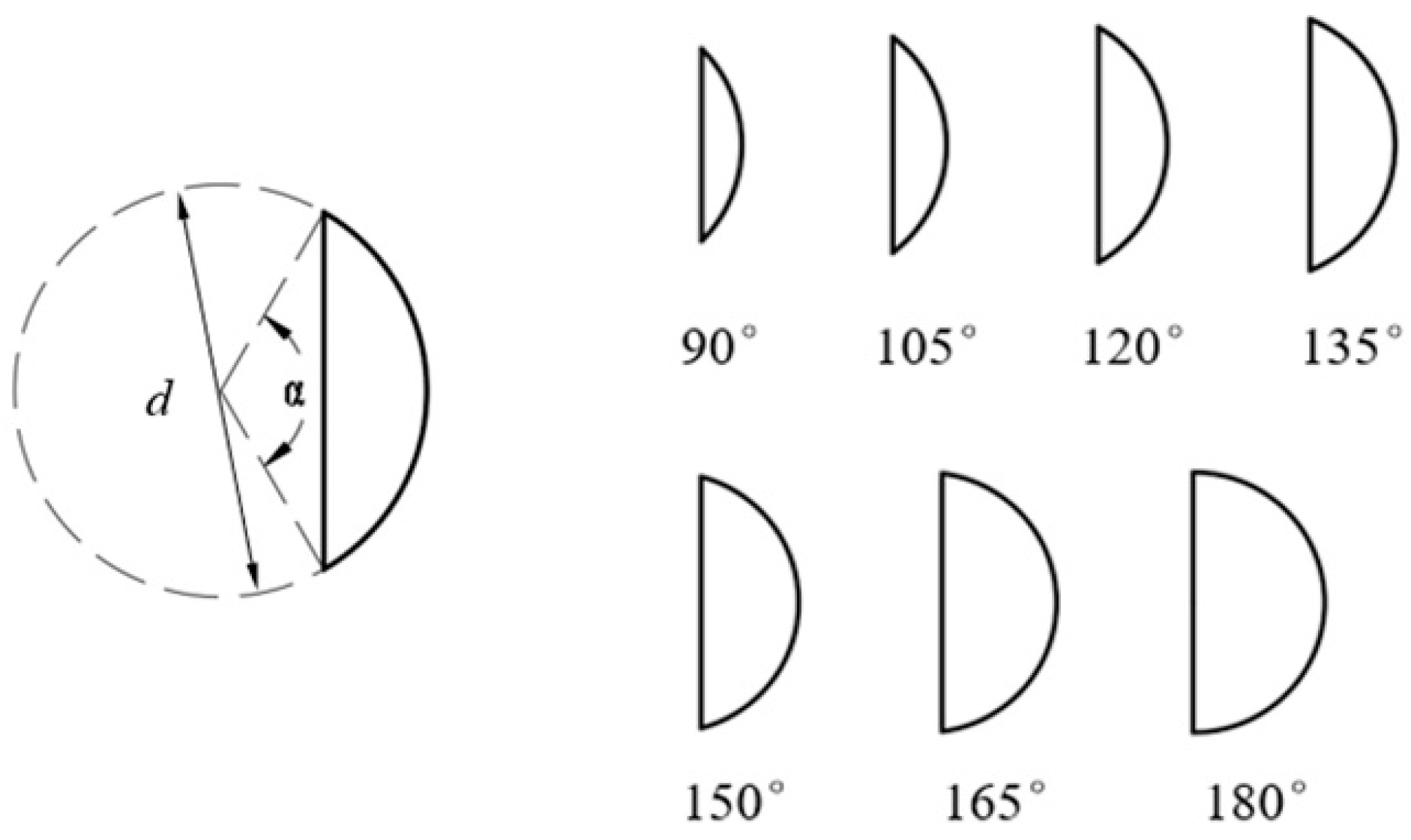
2.1. Geometrical Model
2.2. Governing Equations and Boundary Conditions
2.3. Data Reduction
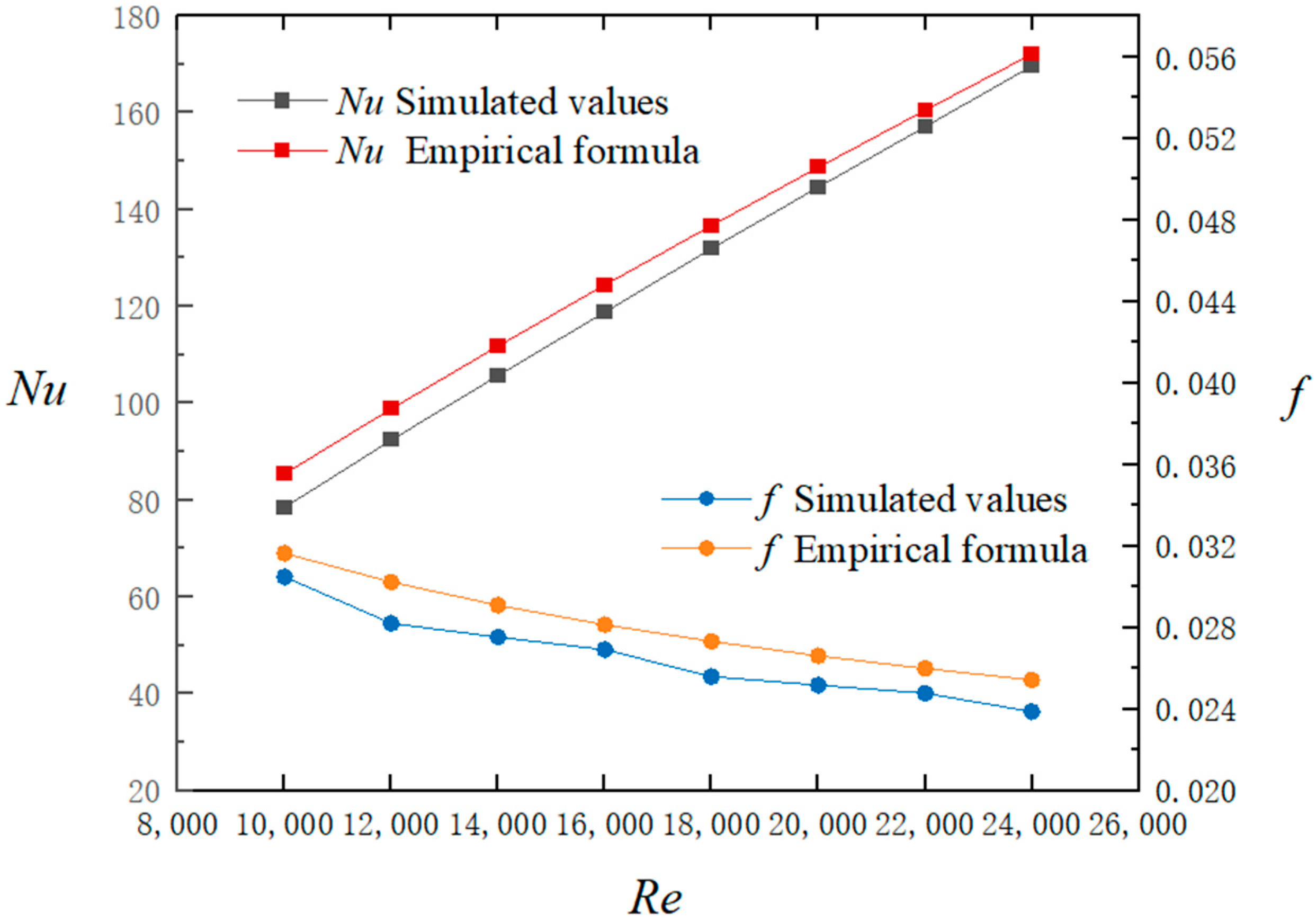
2.4. Mesh and Simulation Verification
3. Results and Discussion
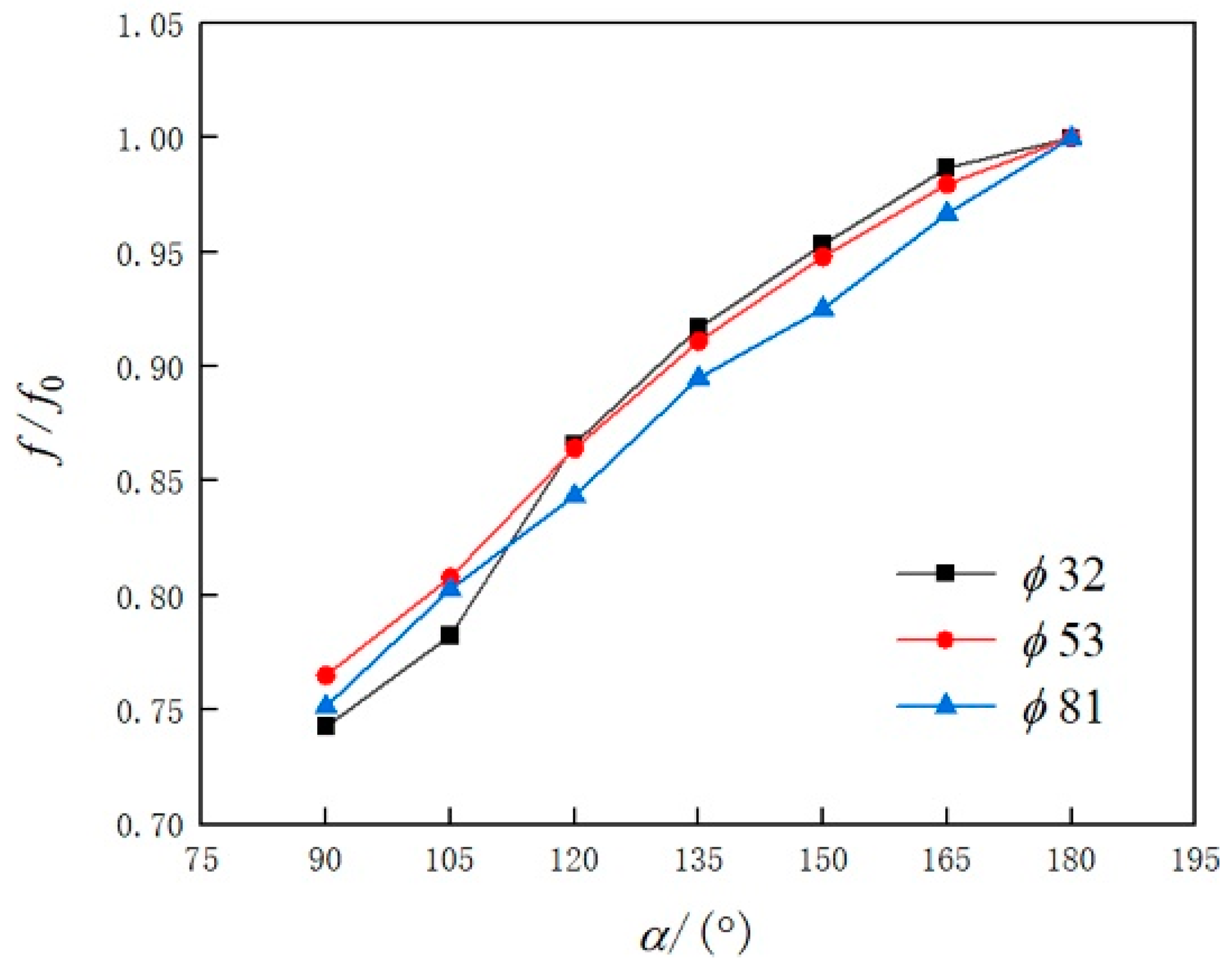
3.1. Optimal Design of Pipe Cross-Sections
3.2. Modification of Nu and f Correlation Formulas for Bow Cross-Section Pipes
4. Conclusions
- (1)
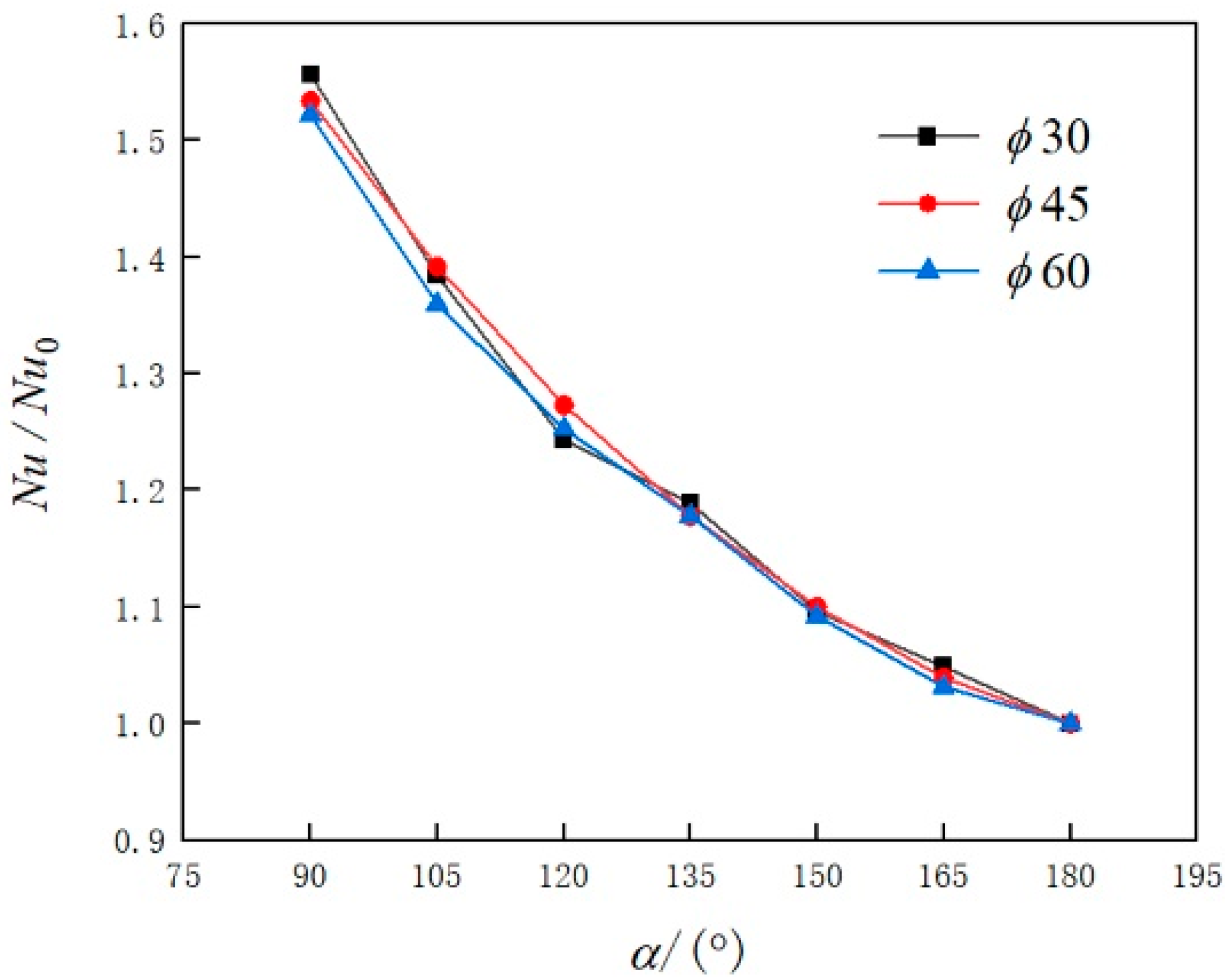
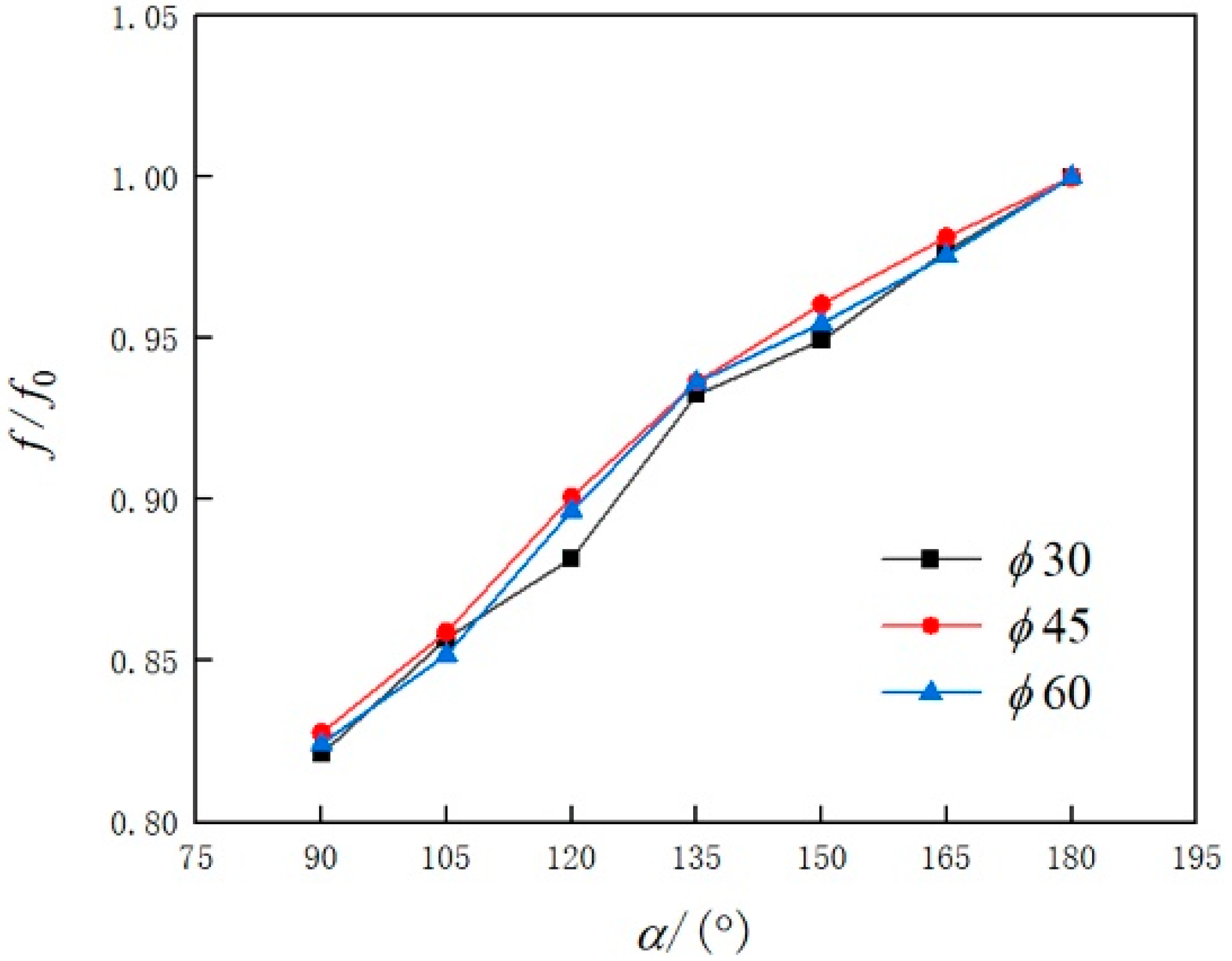
- For a given volume flow rate, by decreasing the central angle α of the bow cross-sections in the range of 90–180°, Re and Nu for both straight pipes and helical pipes increase, meaning that the bow cross-sections can enhance heat transfer in the pipes. However, at the same time, the flow resistance will also increase.
- (2)
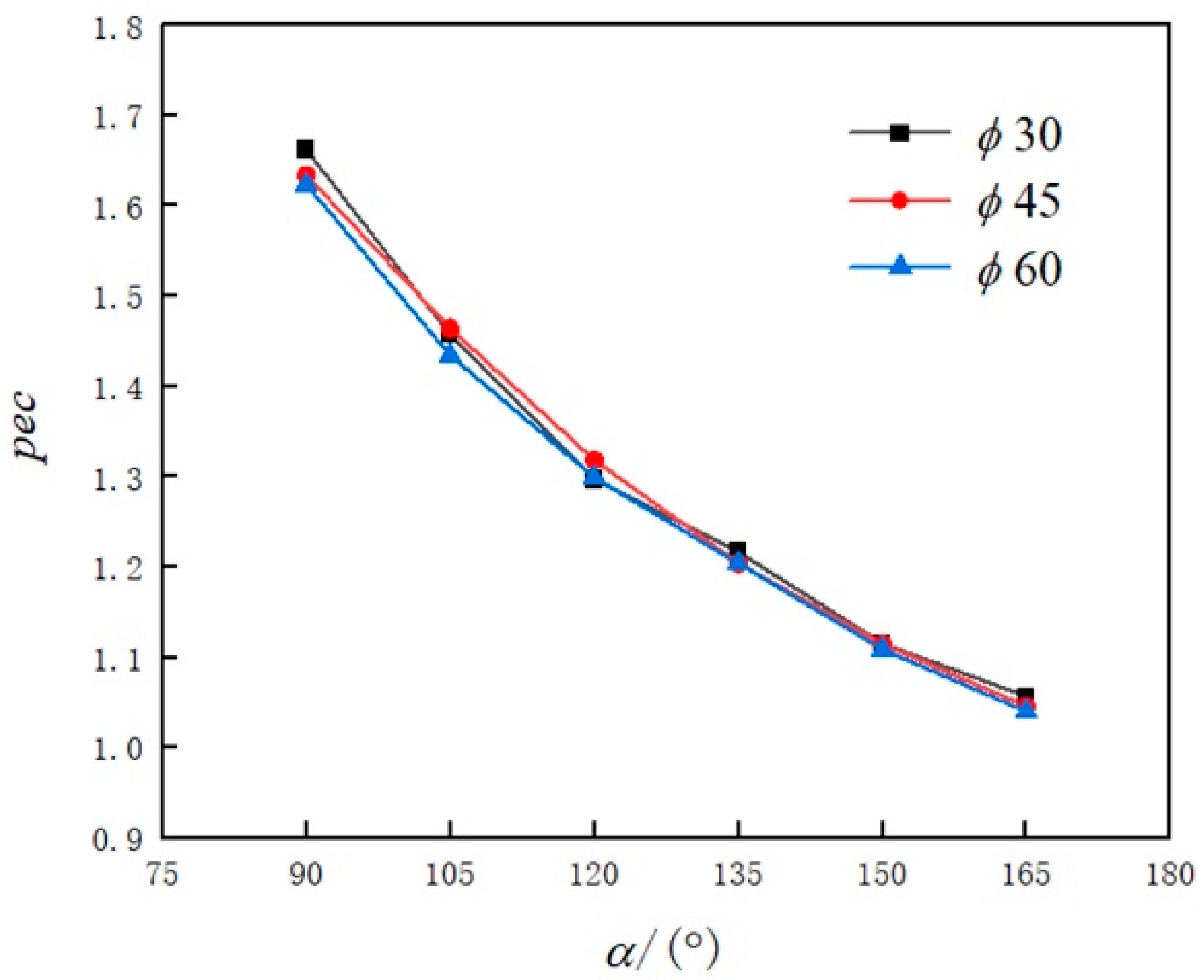
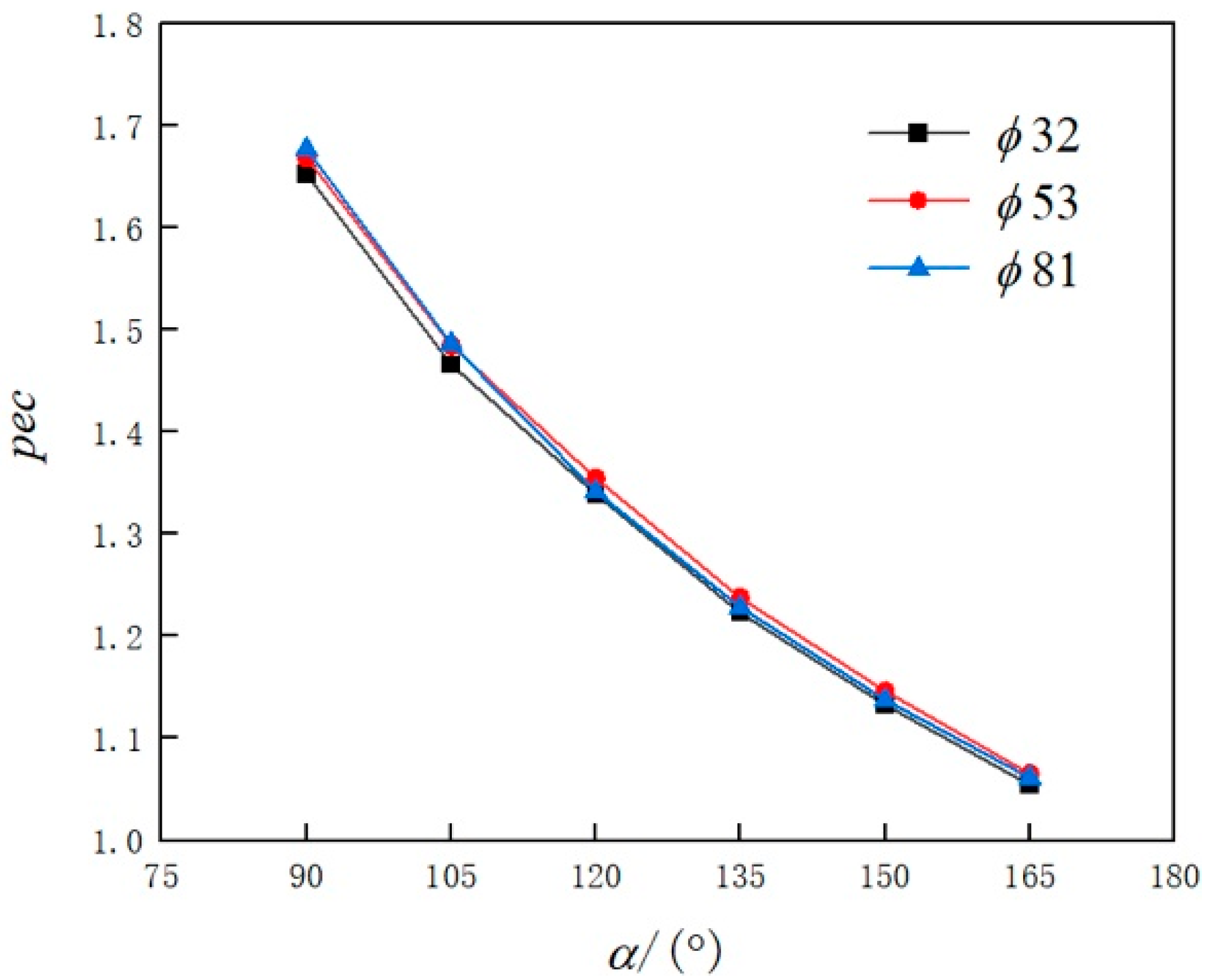
- Compared with half-pipes with the central angle α being 180°, the comprehensive performance evaluation factor pec for both straight pipes and helical pipes having bow cross-sections is greater than 1, meaning that bow cross-sectional pipes have better comprehensive heat transfer performance. Specifically, for the helical pipes, when α is 90°, the pec can reach 1.68 times that with α being 180°.
- (3)
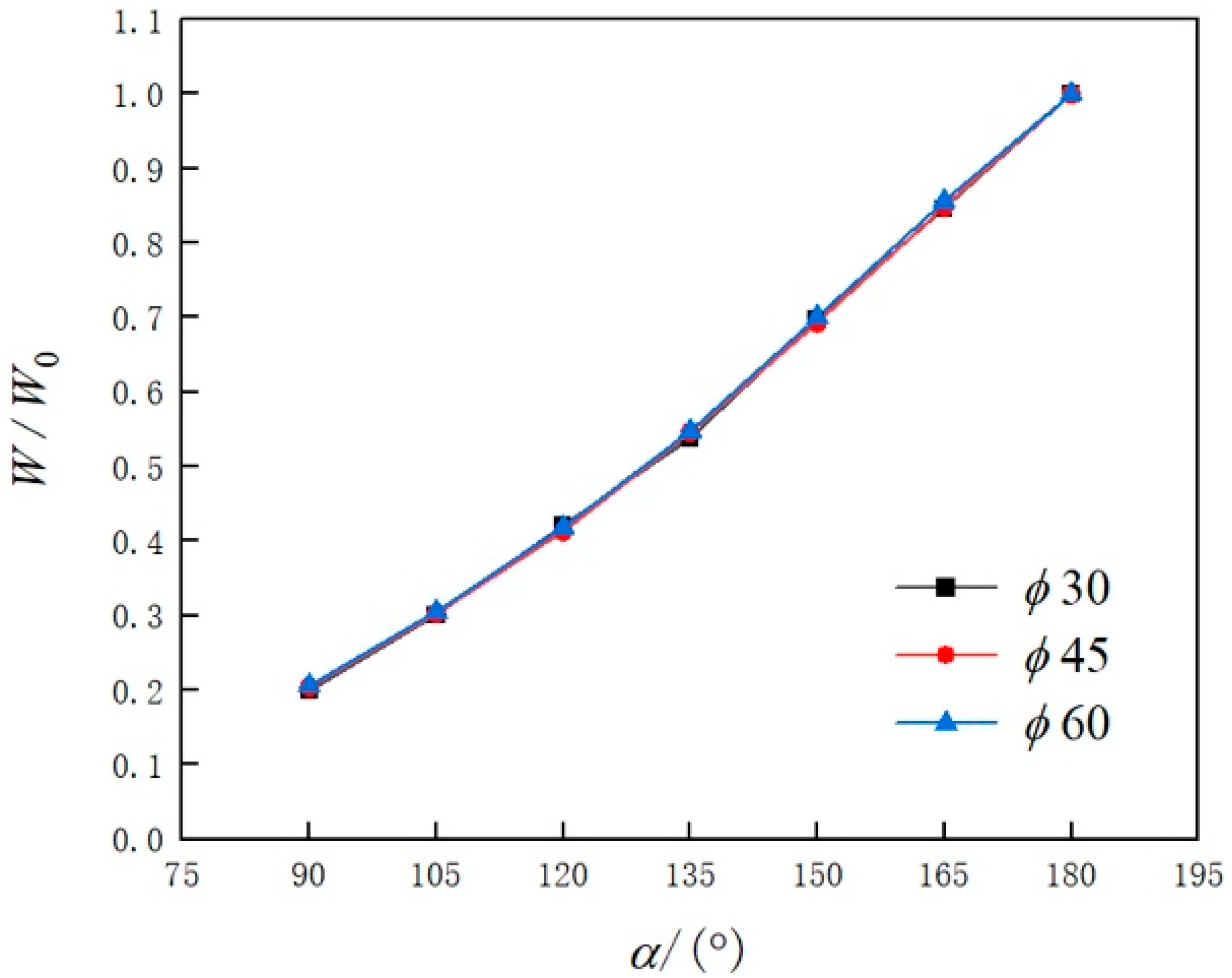
- Compared with the half-pipe with α equal to 180°, less weight of the bow cross-sectional pipe is needed for transferring the same amount of heat. For the helical pipe having a bow cross-section with α being 90°, the weight of the pipe can be reduced by about 80%, a significant saving of the material or the manufacturing cost;
- (4)
- Correlation formulas for Nu and f of the whole straight pipe and the helical pipe were modified to include the influence of the central angle α of the bow cross-sections. With relative errors of less than 10%, the modified formulas can be applied in engineering to construct jackets with bow cross-sectional pipes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gai, C.; Zheng, X.; Wang, C.; Zhou, N.; Xiao, J. Finite element stress analysis of vessel with half-pipe jacket. J. Wuhan Inst. Technol. 2011, 33, 77–80. [Google Scholar]
- Deng, X. The Development and Application of the Spiral Semicircle Double-Layered Reactor. Press. Vessel. Technol. 2001, 18, 45–47. [Google Scholar]
- Chu, X.; Laurien, E. Flow stratification of supercritical CO2 in a heated horizontal pipe. J. Supercrit. Fluids 2016, 116, 172–189. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, L.; Wang, Y. A numerical study on heat transfer enhancement and flow structure in enhanced pipe with cross ellipsoidal dimples. Int. J. Heat Mass Transf. 2018, 125, 434–444. [Google Scholar] [CrossRef]
- Dhotre, M.T.; Murthy, Z.V.P.; Jayakumar, N.S. Modeling & dynamic studies of heat transfer cooling of liquid in half-coil jackets. Chem. Eng. J. 2006, 118, 183–188. [Google Scholar] [CrossRef]
- Subramanian, J.N.; Mjalli, F.S. The dynamics of liquid cooling in half-coil jackets. Chem. Prod. Process Model. 2008, 3, 1264. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Zhan, H.; Wang, C. Fluid flow and heat transfer characteristic of outer and inner half coil jackets. Chin. J. Chem. Eng. 2011, 19, 253–261. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Zhang, L.; Kou, L. Comparison of fluid flow and heat transfer behavior in outer and inner half coil jackets and field synergy analysis. Appl. Therm. Eng. 2011, 31, 3078–3083. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, Y.; Wang, W. Numerical research on flow and heat transfer in helically coiled pipes with different cross-sections. Comput. Appl. Chem. 2016, 33, 1261–1266. [Google Scholar] [CrossRef]
- Wang, C.; Liu, S.; Wu, J.; Li, Y. Laminar flow and heat transfer characteristics in jackets of triangular flow channels. Chin. J. Chem. Eng. 2013, 21, 1224–1231. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Wu, J. Effect of Varying Pitch and Overlap Scale on Enhanced Heat Transfer of Half-coil Jackets. The Chin. J. Process Eng. 2017, 17, 697–703. [Google Scholar] [CrossRef]
- Li, Y.; Lan, L.; Wu, J. Fluid Flow and Heat Transfer Characteristic in the Half-Pipe Coiled Jacket with Arch Cross Section. Contemp. Chem. Ind. 2012, 41, 1291–1294. [Google Scholar] [CrossRef]
- Wang, L.; Liao, X.; Li, H. Evaluation of flow and heat transfer performance of spiral coil jacket with different cross sections. J. Phys. Conf. Ser. 2022, 2235, 012036. [Google Scholar] [CrossRef]
- Wei, L.; Xiao, X.; Hao, W. The Design and Manufacture of Half Pipe Jacket. China Chem. Ind. Equip. 2017, 19, 45–48. [Google Scholar]
- Xu, X.; Wu, Y.; Liu, C.; Wang, K.; Ye, J. Numerical study of cooling heat transfer of supercritical carbon dioxide in a horizontal helically coiled pipe. Acta Phys. Sin. 2015, 64, 258–264. [Google Scholar] [CrossRef]
- Yang, M.; Li, G.; Liao, F.; Li, J.; Zhou, X. Numerical study of characteristic influence on heat transfer of supercritical CO2 in helically coiled pipe with non-circular cross section. Int. J. Heat Mass Transf. 2021, 176, 121511. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, D.; Xiang, S.; Han, Y.; Peng, X. Numerical investigation of heat transfer and pressure drop in helically coiled pipe with spherical corrugation. Int. J. Heat Mass Transf. 2017, 113, 332–341. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Huang, F.L.; Chen, C.G.; Chai, C.J. Principles of Chemical Engineering; Tianjin University Press: Tianjin, China, 1999; pp. 336–342. [Google Scholar]
- Itō, H. Friction Factors for Turbulent Flow in Curved Pipes. J. Basic Eng. 1959, 81, 123–132. [Google Scholar] [CrossRef]
- Lin, C.X.; Ebadian, M.A. Developing turbulent convective heat transfer in helical pipes. Int. J. Heat Mass Transf. 1997, 40, 3861–3873. [Google Scholar] [CrossRef]
- Cioncolini, A.; Santini, L. An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 2006, 30, 367–380. [Google Scholar] [CrossRef]
- Błasiak, P.; Pietrowicz, S. An experimental study on the heat transfer performance in a batch scraped surface heat exchanger under a turbulent flow regime. Int. J. Heat Mass Transf. 2017, 107, 379–390. [Google Scholar] [CrossRef]
- Błasiak, P.; Pietrowicz, S. Towards a better understanding of 2D thermal-flow processes in a scraped surface heat exchanger. Int. J. Heat Mass Transf. 2016, 98, 240–256. [Google Scholar] [CrossRef]
- Błasiak, P.; Pietrowicz, S. A numerical study on heat transfer enhancement via mechanical aids. Int. J. Heat Mass Transf. 2019, 140, 203–215. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Cp | 4182 J·(kg·K)−1 |
| μ | 0.001003 Pa·s |
| ρ | 998.2 kg·m−3 |
| λ | 0.6 W (m·K)−1 |
| Mesh Number | Nu | Error (%) | f | Error (%) |
|---|---|---|---|---|
| 929,583 | 168.52 | 0.38 | 0.0237 | −1.66 |
| 1,920,556 | 168.36 | 0.29 | 0.0239 | −0.83 |
| 3,945,627 | 167.88 | 0 | 0.0241 | 0 |
| Mesh Number | Nu | Error (%) | f | Error (%) |
|---|---|---|---|---|
| 1,164,672 | 84.502 | −0.75 | 0.00720 | −2.04 |
| 2,326,812 | 84.846 | −0.34 | 0.00726 | −1.22 |
| 4,628,355 | 85.138 | 0 | 0.00735 | 0 |
| α (°) | Re | d (mm) | Nu (Simulation) | Nu with Equation (11) | Relative Error (%) | f (Simulation) | f with Equation (12) | Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| 100 | 18,000 | 45 | 120.43 | 117.83 | −2.16% | 0.02288 | 0.02285 | −0.12% |
| 155 | 22,000 | 40 | 151.86 | 148.07 | −2.49% | 0.02326 | 0.02336 | 0.44% |
| 90 | 22,000 | 60 | 141.22 | 136.11 | −3.76% | 0.02155 | 0.02136 | −0.89% |
| 120 | 16,000 | 60 | 112.72 | 110.31 | −2.19% | 0.02464 | 0.02425 | −1.58% |
| 95 | 23,000 | 55 | 148.04 | 142.22 | −3.93% | 0.02159 | 0.02131 | −1.3% |
| 145 | 12,000 | 50 | 90.23 | 90.24 | 0.005% | 0.02695 | 0.02689 | −0.21% |
| 140 | 17,000 | 32 | 117.92 | 118.59 | 0.57% | 0.02401 | 0.02451 | 2.08% |
| 135 | 14,000 | 35 | 99.27 | 100.96 | 1.70% | 0.02527 | 0.02557 | 1.21% |
| 170 | 15,000 | 30 | 108.02 | 110.57 | 2.36% | 0.02519 | 0.02611 | 3.64% |
| 180 | 24,000 | 53 | 164.12 | 162.47 | −1.00% | 0.02285 | 0.02343 | 2.53% |
| α (°) | Re | d (mm) | Dc (mm) | Nu (Simulation) | Nu with Equation (13) | Relative Error (%) | f (Simulation) | f with Equation (15) | Relative Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 22,000 | 70 | 900 | 137.13 | 139.28 | 1.57% | 0.0055 | 0.00563 | 2.36% |
| 90 | 16,000 | 32 | 450 | 104.13 | 104.47 | 0.32% | 0.00596 | 0.0059 | −1.03% |
| 150 | 23,000 | 32 | 1000 | 147.79 | 137.41 | −7.02% | 0.00587 | 0.00581 | −1.03% |
| 140 | 17,000 | 40 | 600 | 113.89 | 112.97 | −0.81% | 0.00636 | 0.00634 | −0.42% |
| 95 | 13,000 | 65 | 700 | 86.43 | 90.3 | 4.48% | 0.00613 | 0.00633 | 3.28% |
| 110 | 19,000 | 55 | 950 | 121.78 | 120.24 | −1.27% | 0.00576 | 0.0058 | 0.80% |
| 120 | 24,000 | 81 | 450 | 153.33 | 165.34 | 7.83% | 0.00619 | 0.00629 | 1.67% |
| 160 | 24,000 | 81 | 1000 | 155.38 | 155.98 | 0.38% | 0.00637 | 0.0063 | −1.10% |
| 180 | 12,000 | 50 | 680 | 84.52 | 86.46 | 2.30% | 0.00732 | 0.00739 | 0.83% |
| 170 | 20,000 | 45 | 800 | 132.23 | 129.39 | −2.15% | 0.00644 | 0.00639 | −0.69% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Yin, X.; Li, H.; Qian, C.; Wu, Z. Optimal Design of Fluid Flow and Heat Transfer in Pipe Jackets Having Bow Cross-Sections. Appl. Sci. 2022, 12, 7179. https://doi.org/10.3390/app12147179
Li W, Yin X, Li H, Qian C, Wu Z. Optimal Design of Fluid Flow and Heat Transfer in Pipe Jackets Having Bow Cross-Sections. Applied Sciences. 2022; 12(14):7179. https://doi.org/10.3390/app12147179
Chicago/Turabian StyleLi, Weicong, Xia Yin, Huifang Li, Caifu Qian, and Zhiwei Wu. 2022. "Optimal Design of Fluid Flow and Heat Transfer in Pipe Jackets Having Bow Cross-Sections" Applied Sciences 12, no. 14: 7179. https://doi.org/10.3390/app12147179





