Comparative Study on the Synthesis of Path-Generating Four-Bar Linkages Using Metaheuristic Optimization Algorithms
Abstract
:1. Introduction
- (1)
- Swarm intelligence-based algorithms:
- (2)
- Evolutionary-based algorithms:
- (3)
- Path-based synthesis methods:
- (4)
- Other optimization methods:
2. Position Analysis of the Planar Four-Bar Linkage
3. Optimization Methods
3.1. Particle Swarm Optimization and Hybrid Particle Swarm Optimization Methods
- (1)
- The use of the linear inertia weight (ω) proposed by Shi et al., that is, multiply the original velocity by an inertia weight to linearly change the original velocity to increase the search ability of particles. This increases the versatility of PSO in the search and is closer to the optimal solution. The improved velocity formula is:
- (2)
- The use of a constriction factor (K) to improve the PSO algorithm. This can effectively control the stability and trajectory of the particle search process without limiting the maximum speed of the particle movement. The updated formula for the new velocity of an individual in the HPSO method combines the merits of the methods proposed by Shi et al. [96] and Clerc [97], and can be expressed as follows:
- (3)
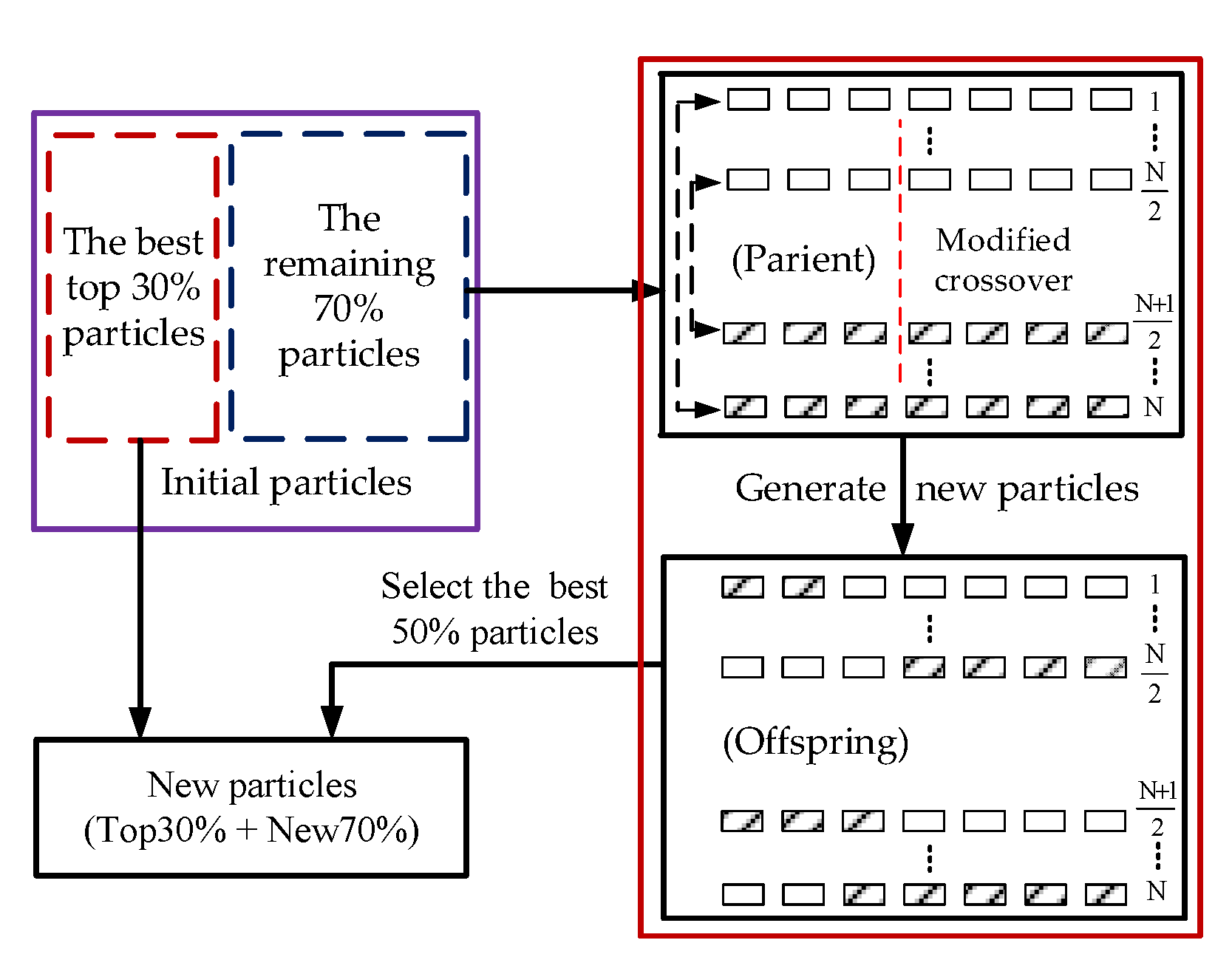
- The crossover of the two modified operations of GA and the incorporation of the top 30% selection rule into the algorithm.
3.2. Differential Evolution Algorithm
3.2.1. Mutation
3.2.2. Crossover
3.2.3. Selection
3.3. Linearly Ensemble of Parameters and Mutation Strategies in Differential Evolution
- (1)
- DE/rand/1Exhibits stronger exploration capabilities, and it is faster, robust and is one of the most widely used mutation strategies in the DE literature.
- (2)
- DE/best/2Utilizes two difference vectors, and it is more robust than a strategy that utilizes one difference vector
- (3)
- DE/current-to-rand/1Takes advantage of its rotation-invariant characteristics, and does not require a crossover operation.
4. Optimization of Path Generating Four-Bar Linkage
4.1. Objective Function and Constraint Conditions
4.2. Parameters of Optimization Methods
4.3. Five Problems of the Dimensional Synthesis of the Path-Generating Four-Bar Linkages
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Payvandy, P.; Sbrahimi, S. Optimization of the thread take-up lever mechanism in lockstitch sewing machine using the imperialistic competitive algorithm. J. Text. Polym. 2015, 3, 12–19. [Google Scholar]
- Felezi, M.E.; Vahabi, S.; Nariman-zadeh, N. Pareto optimal design of reconfigurable rice seedling transplanting mechanisms using multi-objective genetic algorithm. Neural Comput. Appl. 2016, 27, 1907–1916. [Google Scholar] [CrossRef]
- Ji, Z.M.; Manna, Y. Synthesis of a pattern generation mechanism for gait rehabilitation. ASME J. Med. Devices 2008, 2, 031004. [Google Scholar] [CrossRef]
- Singh, R.; Chaudhary, H.; Singh, A.K. A novel gait-based synthesis procedure for the design of 4-bar exoskeleton with natural trajectories. J. Orthop. Transl. 2018, 12, 6–15. [Google Scholar] [CrossRef]
- Jin, S.; Kim, J.; Bae, J.; Seo, T.; Kim, J. Design, modeling and optimization of an underwater manipulator with four-bar mechanism and compliant linkage. J. Mech. Sci. Technol. 2016, 30, 4337–4343. [Google Scholar] [CrossRef]
- Pertuz, S.A.; Llanos, C.H.; Muñoz, D.M. Development of a robotic hand using bioinspired optimization for mechanical and control design: UnB-Hand. IEEE Access 2021, 9, 61010–61023. [Google Scholar] [CrossRef]
- Sandor, G.N.; Erdman, A.G. Advanced Mechanism Design: Analysis and Synthesis; Prentice-Hall Book Company: Englewood Cliffs, NJ, USA, 1984; Volume 2. [Google Scholar]
- Fox, R.L.; Gupta, K.C. Optimization technology as applied to mechanism design. ASME J. Eng. Ind. 1973, 95, 657–663. [Google Scholar] [CrossRef]
- Root, R.R.; Ragsdell, K.M. A survey of optimization methods applied to the design of mechanisms. ASME J. Eng. Ind. 1976, 98, 1036–1041. [Google Scholar] [CrossRef]
- Lee, W.T.; Russell, K. Developments in quantitative dimensional synthesis (1970–2018): Four-bar path and function generation. Inverse Probl. Sci. Eng. 2018, 26, 1280–1304. [Google Scholar] [CrossRef]
- Jensen, P.W. Synthesis of four-bar linkages with a coupler point passing through 12 points. Mech. Mach. Theory 1984, 19, 149–156. [Google Scholar] [CrossRef]
- Tsai, L.W.; Lu, J.J. Coupler-point-curve synthesis using homotopy methods. ASME J. Mech. Des. 1990, 112, 384–389. [Google Scholar] [CrossRef]
- Subbian, T.; Flugrad, D.R., Jr. Four-bar path generation synthesis by a continuation method. ASME J. Mech. Des. 1991, 113, 63–69. [Google Scholar] [CrossRef]
- Wampler, C.W.; Morgan, A.P.; Sommese, A.J. Complete solution of the nine-point path synthesis problem for four-bar linkages. ASME J. Mech. Des. 1992, 114, 153–159. [Google Scholar] [CrossRef]
- Angeles, J.; Alivizators, A.; Akhras, R. An unconstrained nonlinear least-square method of optimization of RRRR planar path generators. Mech. Mach. Theory 1988, 23, 343–353. [Google Scholar] [CrossRef]
- Bakthavachalam, N.; Kimbrell, J.T. Optimum synthesis of path-generating four-bar mechanisms. ASME J. Eng. Ind. 1975, 97, 314–321. [Google Scholar] [CrossRef]
- Mariappan, J.; Krishnamurty, S. A generalized exact gradient method for mechanism synthesis. Mech. Mach. Theory 1996, 31, 413–421. [Google Scholar] [CrossRef]
- Sancibrain, R.; Viadero, F.; Garcia, P.; Fernandez, A. Gradient-based optimization of path synthesis problems in planar mechanisms. Mech. Mach. Theory 2004, 39, 839–856. [Google Scholar] [CrossRef]
- Sancibrian, R.; García, P.; Viadero, F. A general procedure based on exact gradient determination in dimensional synthesis of planar mechanisms. Mech. Mach. Theory 2006, 41, 212–229. [Google Scholar] [CrossRef]
- Hernández, A.; Muñoyerro, A.; Urízar, M.; Amezua, E. Comprehensive approach for the dimensional synthesis of a four-bar linkage based on path assessment and reformulating the error function. Mech. Mach. Theory 2021, 156, 140126. [Google Scholar] [CrossRef]
- Smaili, A.; Diab, N. Optimum synthesis of mechanism using tabu-gradient search algorithms. ASME J. Mech. Des. 2005, 127, 917–923. [Google Scholar] [CrossRef]
- Smaili, A.; Diab, N. Optimum synthesis of hybrid-task mechanisms using ant-gradient search method. Mech. Mach. Theory 2007, 42, 115–130. [Google Scholar] [CrossRef]
- Smaili, A.; Diab, N. A new approach to shape optimization for closed path synthesis of planar mechanisms. ASME J. Mech. Des. 2007, 129, 941–948. [Google Scholar] [CrossRef]
- Diab, N.; Smaili, A. Optimum exact/approximated point synthesis of planar mechanisms. Mech. Mach. Theory 2008, 43, 1610–1624. [Google Scholar] [CrossRef]
- De Bustos, I.F.; Urkullu, G.; Marina, V.G.; Ansola, R. Optimization of planar mechanisms by using a minimum distance function. Mech. Mach. Theory 2019, 138, 149–168. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via L´evy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Gandomi, A.H.; Alavi, H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, WA, USA, 1975. [Google Scholar]
- Storn, R.; Price, K. Differential evolution- a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Kang, Y.H.; Lee, C.T. The synthesis of four-bar linkages for path generation using hybrid particle swarm optimization. In Proceedings of the First IFToMM Asian Conference on Mechanism and Machine Science, Taipei, Taiwan, 21–25 October 2010; pp. 1–8. [Google Scholar]
- Bulatovic, R.R.; Miodragovic, C.; Boskovic, M.S. Modified krill herd (MKH) algorithm and its application in dimensional synthesis of a four-bar linkage. Mech. Mach. Theory 2016, 95, 1–21. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hsiao, K.M. Cuckoo search and teaching-learning-based optimization for optimum synthesis of path-generating four-bar mechanisms. J. Chin. Inst. Eng. 2017, 40, 6–74. [Google Scholar] [CrossRef]
- Sadeghi, S.M.; Bakhshinezhad, N.; Fathi, A.; Daniali, H.M. An optimal defect-free of four-bar mechanisms using constrained APT-FPSO algorithm. J. Comput. Robot. 2019, 12, 39–48. [Google Scholar]
- Mo, X.; Ge, W.; Zhao, D.; Shen, Y. Path and function synthesis of multi-bar mechanisms using beetle antennae search algorithm. Filomat 2020, 34, 5215–5233. [Google Scholar] [CrossRef]
- Connor, A.M.; Douglas, S.; Gilmartin, M. The kinematic synthesis of path generating mechanisms using genetic algorithms. In Proceedings of the 10th International Conference on Applications of Artificial Intelligence in Engineering, Udine, Italy, 4–6 July 1995; pp. 237–244. [Google Scholar]
- Kunjur, A.; Krishnamurty, S. Genetic algorithms in mechanism synthesis. J. Appl. Mech. Robot. 1997, 4, 18–24. [Google Scholar]
- Zhou, H.; Cheung, E.H.M. Optimal synthesis of crank-rocker linkages for path generation using the orientation structural error of the fixed link. Mech. Mach. Theory 2001, 36, 973–982. [Google Scholar] [CrossRef]
- Cabrera, J.A.; Simon, A.; Prado, M. Optimal synthesis of mechanisms with genetic algorithms. Mech. Mach. Theory 2002, 37, 1165–1177. [Google Scholar] [CrossRef] [Green Version]
- Shiakolas, P.S.; Koladiya, D.; Keberle, J. On the optimum synthesis of four-bar linkage using differential envolution and the geometric centroid of precision positions. Inv. Probl. Eng. 2002, 10, 485–502. [Google Scholar] [CrossRef]
- Laribi, M.A.; Mlika, A.; Romdhane, L.; Zegloul, S. A combined genetic algorithm-fuzzy logic method (GA-FL) in mechanism synthesis. Mech. Mach. Theory 2004, 39, 717–735. [Google Scholar] [CrossRef]
- Nariman-Zadeh, N.; Felezi, M.; Jamali, A.; Ganji, M. Pareto optimal synthesis of four-bar mechanisms for path generation. Mech. Mach. Theory 2009, 44, 180–191. [Google Scholar] [CrossRef]
- Bulatović, R.R.; Dordević, S.R. On the optimal synthesis of a four-bar linkage using differential evolution and method of variable controlled deviations. Mech. Mach. Theory 2009, 44, 235–246. [Google Scholar] [CrossRef]
- Acharyya, S.K.; Mandal, M. Performance of EAs for four-bar linkage synthesis. Mech. Mach. Theory 2009, 44, 1784–1794. [Google Scholar] [CrossRef]
- Lin, W.Y. A GA-DE hybrid evolutionary algorithm for path synthesis of four-bar linkage. Mech. Mach. Theory 2010, 45, 1096–1107. [Google Scholar] [CrossRef]
- Cabrera, J.A.; Ortiz, A.; Nadal, F.; Castillo, J.J. An evolutionary algorithm for path synthesis of mechanisms. Mech. Mach. Theory 2011, 46, 127–141. [Google Scholar] [CrossRef]
- Peñuñuri, F.; Peón-Escalante, R.; Villanueva, C.; Pech-Oy, D. Synthesis of mechanisms for single and hybrid tasks using differential evolution. Mech. Mach. Theory 2011, 46, 1135–1349. [Google Scholar]
- Khorshidi, M.; Soheilypour, M.; Peyro, M.; Atai, A.; Panahi, M.S. Optimal design of four-bar mechanisms using hybrid multi-objective GA with adaptive local search. Mech. Mach. Theory 2011, 46, 1453–1465. [Google Scholar] [CrossRef]
- Matekar, S.B.; Gogate, G.R. Optimum synthesis of path generating four-bar mechanisms using differential evolution and a modified error function. Mech. Mach. Theory 2012, 52, 58–179. [Google Scholar] [CrossRef]
- Badduri, J.; Srivatsan, R.A.; Kumar, G.S.; Bandyopadhyay, S. Coupler-curve synthesis of a planar four-bar mechanism using NSGA-II. In Simulated Evolution and Learning; Lecture Notes on Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7673, pp. 460–469. [Google Scholar]
- Ortiz, A.; Cabrera, J.A.; Nadal, F.; Bonilla, A. Dimensional synthesis of mechanisms using differential evolution with auto-adaptive control parameters. Mech. Mach. Theory 2013, 64, 210–229. [Google Scholar] [CrossRef]
- Lin, W.Y. Optimization of scale-rotation-translation synthesis after shape synthesis for path generation of planar mechanisms. J. Chin. Inst. Eng. 2014, 37, 497–505. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Payvandy, P. Efficiency constrained synthesis of path generating four-bar mechanisms based on the heuristic optimization algorithms. Mech. Mach. Theory 2015, 85, 189–204. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hsiao, K.M. More effective optimum synthesis of path generating four-bar mechanisms. J. Multidiscip. Eng. Sci. Technol. 2015, 2, 905–913. [Google Scholar]
- Hernandez-Ocana, B.; Pozos-Parra, M.D.P.; Mezura-Montes, E.; Portilla-Flores, E.A.; Vega-Alvarado, E.; Calva-Yanez, M.B. Two-swin operators in the modified bacterial foraging algorithm for the optimal synthesis of four-bar mechanisms. Comput. Intell. Neurosci. 2016, 2016, 4525294. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Four-bar linkage path generation through self-adaptive population size teaching-learning based optimization. Knowl. Based Syst. 2017, 35, 180–191. [Google Scholar] [CrossRef]
- Mohamed, N.; Bilel, N.; Zouhaier, A.; Lotfi, R. Multi-objective design optimisation of four-bar mechanisms using a hybrid ICA-GA algorithm. Intern. J. Reason.-Based Intell. Syst. 2017, 9, 43–51. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hsiao, K.M. A new differential evolution algorithm with a combined mutation strategy for optimum synthesis of path-generating four-bar mechanisms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2690–2705. [Google Scholar] [CrossRef]
- Kafash, S.H.; Nahvi, A. Optimal synthesis of four-bar path generator linkages using circular proximity function. Mech. Mach. Theory 2017, 115, 18–34. [Google Scholar] [CrossRef]
- Singh, R.; Chaudhary, H.; Singh, A.K. Defect-free optimal synthesis of crank-rocker linkage using nature-inspired optimization algorithms. Mech. Mach. Theory 2017, 116, 105–122. [Google Scholar] [CrossRef]
- Buskiewicz, J. Reduced number of design parameters in optimal path synthesis with timing of four-bar linkage. J. Theor. Appl. Mech. 2018, 56, 43–55. [Google Scholar] [CrossRef] [Green Version]
- Sleesongsom, S.; Bureerat, S. Optimal synthesis of four-bar linkage path generation through evolutionary computation with a novel constraint handing technique. Comput. Intell. Neurosci. 2018, 2018, 5462563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sabaapour, M.Z.; Yoon, J.W. A novel method for optimal path synthesis of mechanisms based on tracking control of shadow robot. Mech. Mach. Theory 2019, 131, 218–233. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, Q.J.; Zhang, Y.M.; Song, J.C.; Shi, J. Hybrid Lagrange interpolation differential evolution algorithm for path synthesis. Mech. Mach. Theory 2019, 134, 512–540. [Google Scholar] [CrossRef]
- Huang, Q.J.; Zhang, K.; Song, J.C.; Zhang, Y.M.; Shi, J. Adaptive differential evolution with a Lagrange interpolation argument algorithm. Inf. Sci. 2019, 472, 180–202. [Google Scholar] [CrossRef]
- Romero, N.N.; Campos, A.; Martins, D.; Vieira, R.S. A new approach for the optimal synthesis of four-bar path generator linkages. SN Appl. Sci. 2019, 1, 1504. [Google Scholar] [CrossRef] [Green Version]
- Sancibrian, R.; Sedano, A.; Sarabia, E.G.; Blanco, J.M. Hybridizing differential evolution algorithm and local search optimization for dimensional synthesis of linkages. Mech. Mach. Theory 2019, 140, 389–412. [Google Scholar] [CrossRef]
- Flores-Pulido, L.; Portilla-Flores, E.A.; Santiago-Valentin, E.; Veta-Alvarado, E.; Yanez, M.B.C.; Nino-Suarez, P.A. A comparative study of improved harmony search algorithm in four bar mechanisms. IEEE Access 2020, 8, 148757–148778. [Google Scholar] [CrossRef]
- Zarkandi, S. A novel optimization-based method to find multiple solutions for path synthesis of planar four-bar and slider-crank mechanisms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5385–5405. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, J.H.; Zhang, Y.M.; Huang, Q.J. Optimization method for linear constraint problems. J. Comput. Sci. 2021, 51, 101315. [Google Scholar] [CrossRef]
- Bureerat, S.; Sleesongsom, S. Constraint handling technique for four-bar linkage path generation using self-adaptive teaching-learning-based optimization with a diversity archive. Eng. Optim. 2021, 53, 513–530. [Google Scholar] [CrossRef]
- Sardashti, A.; Daniali, H.M.; Varedi-Koulaei, S.M. Geometrical similarity error function-innovative adaptive algorithm methodology in path generation synthesis of the four-bar mechanism using metaheuristic algorithms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1550–1570. [Google Scholar] [CrossRef]
- Valencia-Segura, L.E.; Villarreal-Cervantes, M.G.; Corona-Ramirez, L.G.; Cuenca-Jimenez, F.; Castro-Medina, A.R. Optimal synthesis of four-bar mechanism by using relative angle method: A comparative performance study. IEEE Access 2021, 9, 132990–133010. [Google Scholar] [CrossRef]
- Huang, Q.J.; Yu, Y.H.; Zhang, K.; Li, S.Q.; Lu, H.B. Optimal synthesis of mechanisms using repellency evolutionary algorithm. Knowl.-Based Syst. 2022, 239, 107928. [Google Scholar] [CrossRef]
- Sy, N.V.; Lieu, Q.X.; Nguyen, X.M.; Nguyen, T.T.N. A new study on optimization of four-bar mechanisms based on a hybrid-combined differential evolution and Jaya algorithm. Symmetry 2022, 14, 381. [Google Scholar]
- Yao, X.Y.; Wang, X.D.; Sun, W.; Kong, J.Y.; Lin, Z.K. Optimal synthesis of four-bar linkages for path generation using the individual repairing method. Mech. Sci. 2022, 13, 79–87. [Google Scholar] [CrossRef]
- McGarva, J.R. Rapid search and selection of path generation mechanisms from a library. Mech. Mach. Theory 1994, 29, 223–235. [Google Scholar] [CrossRef]
- Ullah, I.; Kota, S. Optimal Synthesis of mechanism for path generation using Fourier descriptors and global search methods. ASME J. Mech. Des. 1997, 119, 504–510. [Google Scholar] [CrossRef]
- Vasiliu, A.; Yannou, B. Dimensional synthesis of planar mechanisms using neural networks: Application to path generator linkages. Mech. Mach. Theory 2001, 36, 299–310. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xiao, R. Optimal synthesis of mechanisms for path generation using refined numerical representation based model and AIS based searching method. ASME J. Mech. Des. 2005, 127, 688–691. [Google Scholar] [CrossRef]
- Starosta, R. Application of genetic algorithm and Fourier coefficients (GA-FC) in mechanism synthesis. J. Theor. Appl. Mech. 2008, 46, 395–411. [Google Scholar]
- Galán-Marín, G.; Alonso, F.J.; Del Castillo, J.M. Shape optimization for path synthesis of crank-rocker mechanisms using a wavelet-based neural network. Mech. Mach. Theory 2009, 44, 1132–1143. [Google Scholar] [CrossRef]
- Buskiewicz, J.; Starosta, R.; Walczak, T. On the application of curve curvature in path synthesis. Mech. Mach. Theory 2009, 44, 1223–1239. [Google Scholar] [CrossRef]
- Khan, N.; Ullah, I.; Al-Grafi, M. Dimensional synthesis of mechanical linkages using artificial neural networks and Fourier descriptors. Mech. Sci. 2015, 6, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Liu, W.; Chu, J. Dimensional synthesis of open path generator of four-bar mechanisms using the Haar wavelet. ASME J. Mech. Des. 2015, 137, 082303. [Google Scholar] [CrossRef]
- Lin, X.Y.; Chen, P. A parameterization-invariant Fourier approach to planar linkage synthesis for path generation. Math. Probl. Eng. 2017, 2017, 8458149. [Google Scholar]
- Sharma, S.; Purwar, A.; Ge, Q.J. An optimal parametrization scheme for path generation using Fourier descriptors for four-bar mechanism synthesis. ASME J. Comput. Inf. Sci. Eng. 2019, 19, 014501. [Google Scholar] [CrossRef]
- Kim, J.-W.; Seo, T.; Kim, J. A new design methodology for four-bar linkage mechanisms based on derivations of coupler curve. Mech. Mach. Theory 2016, 100, 138–154. [Google Scholar] [CrossRef]
- Kim, J.-W.; Jeong, S.M.; Kim, J.; Seo, T.W. Numerical hybrid Taguchi-random coordinate search algorithm for path synthesis. Mech. Mach. Theory 2016, 102, 203–216. [Google Scholar] [CrossRef]
- Li, X.G.; Wei, S.M.; Liao, Q.H.; Zhang, Y. A novel analytical method for the four-bar path generation synthesis based on Fourier series. Mech. Mach. Theory 2020, 144, 103671. [Google Scholar] [CrossRef]
- Ahmadi, B.; Nariman-Zadeh, N.; Jamali, A. A Stackelberg game theoretic multi-objective synthesis of four-bar mechanisms. Struct. Multidiscipl. Optim. 2019, 60, 699–710. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ahmadi, B.; Chegini, S.N. Multi-objective reliability-based optimal synthesis of path generating four-bar mechanisms: A cooperative game theoretic approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2298–2311. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
- Shi, Y.H.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE 1998 International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1951–1957. [Google Scholar]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Yan, H.S.; Wu, L.I.; Hwang, W.M.; Wu, Y.C.; Lan, C.C. Modern Mechanisms; Dong-Hua Book Company: Taiwan, China, 2021. (In Chinese) [Google Scholar]






















| Optimization Method | PSO | HPSO | DE-gr | EPSDE | L-EPSDE |
|---|---|---|---|---|---|
| Number of particles or population (NP) | 100 | 100 | 100 | 100 | 100 |
| Number of iterations (Nitmax) | 1000 | 1000 | 1000 | 1000 | 1000 |
| Minimum group (NPmin) | -- | -- | -- | -- | 5 |
| Crossover method | -- | Single point- uniform | Multi-point | Multi-point | Multi-point |
| Crossover rate (Cr) | -- | -- | 0.618 | 0.1~0.9 | 0.1~0.9 |
| Mutation method | -- | -- | DE/best/1 | DE/best/2 DE/rand/1 DE/current-to-rand/1 | DE/best/2 DE/rand/1 DE/current-to-rand/1 |
| Mutation factor (F) | -- | -- | 0.382 | 0.4~0.9 | 0.4~0.9 |
| Selection method | -- | -- | Competition law | Competition law | Competition law |
| Learning factor () | 2.05 | 2.05 | -- | -- | -- |
| Inertia weight () | 0~1 | 0~1 | -- | -- | -- |
| Case 1: 5 Target Points, Non-Aligned Point Curve | Case 2: 18 Target Points, Irregular Closed Curve | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Median | Mean | SD | Best | Worst | Median | Mean | SD | |
| PSO | 1.16E−05 | 1.92E−03 | 4.21E−05 | 1.12E−04 | 2.83E−04 | 1.92E−02 | 2.53E+00 | 4.67E−02 | 2.43E−01 | 6.33E−01 |
| HPSO | 8.01E−06 | 6.37E−05 | 4.21E−05 | 3.95E−05 | 1.32E−05 | 1.09E−02 | 8.43E−01 | 4.64E−02 | 1.03E−01 | 1.50E−01 |
| DE-gr | 7.42E−07 | 2.36E−05 | 7.42E−07 | 2.36E−06 | 2.35E−05 | 1.09E−02 | 2.53E+00 | 4.53E−02 | 2.32E−01 | 5.93E−01 |
| EPSDE | 7.42E−07 | 7.42E−07 | 7.42E−07 | 7.42E−07 | 9.64E−20 | 9.91E−03 | 2.60E−01 | 1.14E−01 | 1.18E−01 | 5.88E−02 |
| L-EPSDE | 7.42E−07 | 7.42E−07 | 7.42E−07 | 7.42E−07 | 1.08E−19 | 9.91E−03 | 4.53E−01 | 4.53E−02 | 7.77E−02 | 8.08E−02 |
| Case 3:6 target points, semi-circular arc curve | Case 4:6 target points, straight-line segment curve | |||||||||
| Best | Worst | Median | Mean | SD | Best | Worst | Median | Mean | SD | |
| PSO | 3.26E+00 | 1.91E+02 | 7.55E+00 | 1.21E+01 | 2.16E+01 | 5.74E−03 | 1.68E+01 | 2.99E+00 | 4.00E+00 | 3.38E+00 |
| HPSO | 2.95E+00 | 1.40E+02 | 8.27E+00 | 1.55E+01 | 1.89E+01 | 4.54E−03 | 1.43E+01 | 6.32E+00 | 6.12E+00 | 3.09E+00 |
| DE-gr | 2.58E+00 | 7.16E+01 | 4.67E+00 | 1.02E+01 | 1.62E+01 | 2.32E−04 | 2.50E+01 | 2.36E+00 | 3.53E+00 | 4.10E+00 |
| EPSDE | 2.58E+00 | 1.37E+01 | 2.58E+00 | 3.47E+00 | 1.90E+00 | 2.59E−04 | 8.84E+00 | 1.00E−01 | 1.17E+00 | 2.43E+00 |
| L-EPSDE | 2.58E+00 | 7.16E+01 | 2.58E+00 | 2.91E+00 | 5.26E+00 | 4.71E−04 | 7.12E+00 | 1.09E−01 | 3.24E−01 | 8.15E−01 |
| Case 5:10 target points, elliptical path curve | ||||||||||
| Best | Worst | Median | Mean | SD | ||||||
| PSO | 2.30E−01 | 3.44E+02 | 9.59E+01 | 1.21E+02 | 9.81E+01 | |||||
| HPSO | 5.42E−03 | 2.92E+02 | 1.71E+01 | 4.96E+02 | 7.35E+01 | |||||
| DE-gr | 8.00E−03 | 3.73E+02 | 4.37E+01 | 7.51E+01 | 8.42E+01 | |||||
| EPSDE | 1.83E−02 | 2.77E+02 | 4.15E+01 | 6.47E+01 | 7.13E+01 | |||||
| L-EPSDE | 7.02E−03 | 1.89E+02 | 5.44E+00 | 1.31E+01 | 1.85E+01 | |||||
| GA-KK [39] | Exact Grad. [41] | GA-CSP [41] | MUMSA [48] | IOAS-at [53] | HLIDE [66] | BAS [37] | ODSRA + CP [75] | REA [76] | HCDJ [77] | EPSDE This Work | L-EPSDE This Work | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Np | 100 | -- | 50 | 50 | 25 | 100 | -- | 50 | -- | 50 | 100 | 100 |
| NF | 5000 | 39 | 5000 | 5000 | 5000 | 3900 | 10,000 | 5000 | 3900 | 5000 | 100,000 | 100,000 |
| (mm) | 3.50964 | 2.85813 | 3.06304 | 3.77327 | 2.80361 | 3.670110 | 3.713526 | 3.6537 | 1.996566 | 4.293081 | 3.66973 | 3.66973 |
| (mm) | 1.85791 | 1.99965 | 1.99596 | 2.00000 | 1.99226 | 1.99781 | 1.997874 | 1.9977 | 3.901976 | 1.997832 | 1.99781 | 1.99781 |
| (mm) | 4.72584 | 3.06518 | 3.30582 | 4.11697 | 3.30461 | 3.99675 | 4.046953 | 3.9780 | 2.679281 | 4.73741 | 3.99632 | 3.99632 |
| (mm) | 3.51872 | 2.46329 | 2.52471 | 2.74616 | 2.47412 | 2.70500 | 2.719239 | 2.7000 | 1.669044 | 2.94173 | 2.70489 | 2.70489 |
| (mm) | 1.95754 | 1.71710 | 1.64516 | 1.67849 | 1.64413 | 1.67206 | 1.67414 | 1.6677 | 1.684562 | 1.70741 | 1.67205 | 1.67205 |
| (mm) | 1.55890 | 1.63089 | 1.70896 | 1.67098 | 1.71454 | 1.68011 | 1.67796 | 1.6844 | 0.0000009 | 1.64417 | 1.68013 | 1.68013 |
| Error | 9.54E−04 | 6.80E−05 | 1.83E−06 | 1.77E−06 | 4.27E−06 | 7.42E−07 | 7.467E−07 | 7.67E−07 | 8.64E−07 | 1.924E−06 | 7.42E−07 | 7.42E−07 |
| (a) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GA-KK [39] | Exact Grad. [41] | GA-CSP [41] | Tabu- Grad. [21] | Ant- Grad. [22] | GA-FC [83] | GA-DE [54] | MUMSA [48] | IOAS-at [53] | DE-SRT [56] | MKH [34] | L-EPSDE This Work | |
| Np | 100 | -- | 100 | -- | -- | 100 | 100 | 50 | 50 | 200 | -- | 100 |
| NF | 5000 | 240 | 5000 | 550 | 479 | 20,000 | 5000 | 5000 | 5000 | 200,000 | 25,000 | 100,000 |
| (mm) | 1.87966 | 2.85452 | 3.05788 | 10.2629 | 4.1928 | 1.01 | 49.9592 | 4.45377 | 4.0404 | 1.05393 | 1.00429 | 1.05875 |
| (mm) | 0.27485 | 0.36355 | 0.23780 | 0.3297 | 0.3333 | 0.28 | 0.21861 | 0.29706 | 0.2452 | 0.42388 | 0.4218 | 0.42557 |
| (mm) | 1.18025 | 2.91374 | 4.82895 | 0.5012 | 0.5202 | 0.36 | 42.4842 | 3.91301 | 6.3829 | 0.91425 | 0.87821 | 0.94469 |
| (mm) | 2.13821 | 0.49374 | 2.05646 | 10.191 | 4.0224 | 0.98 | 32.7470 | 0.84937 | 2.6205 | 0.59892 | 0.58013 | 0.57794 |
| (mm) | −0.83359 | 1.03122 | 0.76704 | 0.100 | −0.2183 | −0.1407 | −47.9660 | −2.06734 | 1.1391 | 0.37060 | 0.35907 | 0.38873 |
| (mm) | −0.37877 | 1.71747 | 1.85083 | 0.3805 | −0.3040 | −0.3314 | 15.3586 | 1.66106 | 1.8661 | 0.39934 | 0.38081 | 0.39467 |
| (mm) | 1.13206 | 0.95928 | 1.77681 | 0.5856 | 0.5616 | 0.074 | 44.1750 | −1.30924 | 1.8918 | 0.26765 | 0.26886 | 0.26244 |
| (mm) | 0.66343 | −1.19645 | −0.64199 | 0.7346 | 0.7409 | 0.191 | −23.9643 | 2.80696 | −0.7613 | 0.15465 | 0.17715 | 0.14396 |
| (rad.) | 4.35422 | 0.76398 | 1.00217 | 2.9719 | −2.9283 | −2.4433 | 5.37543 | 2.73874 | 1.1877 | 0.28482 | 0.29249 | 0.33656 |
| (rad.) | 2.55863 | 0.51172 | 0.22619 | −2.4483 | 3.4519 | -- | 1.88551 | 4.85354 | 0.0000 | 0.8916 | 0.88595 | 0.83767 |
| Error | 4.30E−02 | 1.68E−02 | 3.37E−02 | 1.37E−02 | 1.09E−02 | 3.78E−02 | 4.61E−02 | 1.96E−02 | 3.49E−02 | 9.03E−03 | 9.11E−03 | 9.91E−03 |
| (b) | ||||||||||||
| CMDE [60] | CS [35] | DE [63] | ADELI [67] | Multi- Start [65] | Game [93] | BAS [37] | Anal-FC [92] | GSA [71] | ODSRA + CP [75] | HCDJ [77] | L-EPSDE This Work | |
| Np | 200 | 200 | 50 | -- | -- | -- | 40 | -- | -- | 400 | 50 | 100 |
| NF | 2000,000 | 400,001 | 500,000 | -- | -- | -- | 200,000 | -- | 100,000 | 400,000 | 5000 | 100,000 |
| (mm) | 1.05395 | 1.05394 | 1.5395 | 1.15326 | 1.40 0 063 | 11.968126 | 1.054180 | 1.1309 | 0.9695 | 1.0587 | 49.80089 | 1.05875 |
| (mm) | 0.42387 | 0.42388 | 0.4102 | 0.23181 | 0.402133 | 0.478725 | 0.423871 | 0.4326 | 0.4246 | 0.42567 | 0.28817 | 0.42557 |
| (mm) | 0.91425 | 0.91425 | 1.2166 | 44.54400 | 1.362497 | 8.469510 | 0.914564 | 0.9709 | 0.8209 | 0.9447 | 48.47614 | 0.94469 |
| (mm) | 0.59890 | 0.59892 | 1.1230 | 44.55035 | 0.540046 | 8.469510 | 0.598871 | 0.5934 | 0.5955 | 0.5779 | 1.63364 | 0.57794 |
| (mm) | 0.37060 | 0.37060 | 0.5279 | 0.70441 | 0.547398 | 4.432594 | 0.3707 | 0.3765 | 0.3325 | 0.3887 | −23.41281 | 0.38873 |
| (mm) | 0.39935 | 0.39935 | 0.5822 | 1.10756 | 0.677040 | 0.762830 | 0.3995 | 0.4086 | 0.3487 | 0.3947 | 7.66449 | 0.39467 |
| (mm) | 0.26766 | 0.26766 | 0.3630 | 1.29094 | 0.399159 | 1.833678 | 0.267700 | 0.2409 | 0.2560 | 0.2624 | −14.83615 | 0.26244 |
| (mm) | 0.15465 | 0.15465 | −0.0874 | −0.10367 | −0.170030 | 4.912576 | 0.154427 | 0.1429 | 0.2214 | 0.1440 | 20.14022 | 0.14396 |
| (rad.) | 0.28483 | 0.28482 | 0.1110 | 6.22254 | 0.529247 | 3.402143 | 0.285040 | 0.2878 | 0.2371 | 0.3366 | 2.52861 | 0.33656 |
| (rad.) | 0.89155 | 0.89156 | 0.8721 | 1.189290 | -- | 3.937901 | 1.176411 | 0.8622 | 1.1692 | 0.8377 | 5.06442 | 0.83767 |
| Error | 9.03E−03 | 9.03E−03 | 1.86E−02 | 2.778E−02 | 8.971E−02 | 1.21E−02 | 9.03E−03 | 1.195E−02 | 4.6E−03 | 9.91E−03 | 1.608E−02 | 9.91E−03 |
| DE [46] | GA-DE [47] | MUMSA [48] | IOAS-at [53] | ICA [55] | HTRCA [91] | DE [63] | HLIDE [66] | BAS [37] | REA [76] | HCDJ [77] | L-EPSDE This Work | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Np | 100 | 100 | 100 | 50 | -- | -- | 80 | 100 | 40 | -- | 50 | 100 |
| NF | 1000 | 100,000 | 100,000 | 100,000 | -- | -- | 800,000 | 50,000 | 120,000 | 90, 000 | 50,000 | 100,000 |
| (mm) | 50.00000 | 50.00000 | 50.00000 | 49.96897 | 50.00000 | 49.46 | 43.30492 | 50.00000 | 47.23450 | 49.999992 | 49.999980 | 50.00000 |
| (mm) | 5.00000 | 5.00000 | 5.00000 | 4.78566 | 5.00000 | 5.504 | 11.1149 | 5.00000 | 8.84740 | 5.000002 | 1.348432 | 5.00000 |
| (mm) | 5.90535 | 6.97009 | 7.03105 | 6.49103 | 7.08248 | 8.015 | 42.6226 | 7.03091 | 25.04747 | 7.031010 | 1.348451 | 7.03105 |
| (mm) | 50.00000 | 48.1993 | 48.13418 | 48.39394 | 48.05733 | 47.165 | 11.9381 | 48.13432 | 50.00000 | 48.134251 | 50.000000 | 48.13418 |
| (mm) | 18.81931 | 17.045 | 16.97669 | 16.44478 | 16.4264 | 17.9 | 51.9215 | 16.9770 | 42.02840 | 16.976890 | 11.384434 | 16.97669 |
| (mm) | 0.00000 | 12.638 | 12.95214 | 11.98809 | 13.7111 | 15.3 | −7.1475 | 12.95115 | −27.08529 | 12.952033 | 4.442436 | 12.95214 |
| (mm) | 14.37377 | 12.2377 | 12.19749 | 12.04659 | 11.88034 | 12.0 | −43.3598 | 12.19769 | 16.55312 | 12.197689 | 10.194752 | 12.19749 |
| (mm) | −12.44430 | −15.8332 | −15.99820 | −14.7749 | −16.08766 | −18.7 | −0.0067 | −15.9978 | −48.14738 | −15.99843 | −3.694134 | −15.9982 |
| (rad.) | 0.463633 | 0.05085 | 0.04282 | 0.03868 | 6.28319 | 6.2832 | 6.2819 | 0.04286 | 0.82260 | 0.042844 | 6.215880 | 0.04282 |
| Error | 5.52 | 2.58286 | 2.58035 | 2.491 | 2.5998 | 3.571 | 2.10037 | 2.58036 | 0.78637 | 2.58036 | 1.216212 | 2.58036 |
| (a) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GA-CSP [41] | DE [46] | GA-DE [47] | MUMSA [48] | IOAS-at [53] | ICA [55] | MKH [34] | HTRCA [91] | DE-gr This Work | L-EPSDE This Work | |
| Np | 100 | 100 | 100 | 100 | 50 | -- | 25 | -- | 100 | 100 |
| NF | 100,000 | 100,000 | 100,000 | 100,000 | 100,000 | -- | 25,000 | -- | 200,000 | 200,000 |
| (mm) | 39.46629 | 35.02074 | 33.5959 | 31.78826 | 54.71582 | 60.0000 | 34.36458 | 18.42 | 44.9998 | 58.94653 |
| (mm) | 8.56291 | 6.40420 | 5.02972 | 8.20465 | 18.73099 | 17.51102 | 7.97728 | 35.14 | 16.2478 | 10.35726 |
| (mm) | 19.09486 | 31.60722 | 11.1847 | 24.93213 | 31.22310 | 60.0000 | 26.95316 | 56.42 | 34.5751 | 35.62035 |
| (mm) | 47.83886 | 50.59949 | 28.0878 | 31.38593 | 42.22374 | 33.2268 | 32.28634 | 49.99 | 36.5490 | 34.77291 |
| (mm) | 13.38556 | 20.80324 | −24.1755 | 34.19372 | −27.2984 | −28.6280 | 36.96182 | 55.08 | −1.8620 | 24.58724 |
| (mm) | 12.21961 | 41.54364 | 5.51479 | 14.41567 | 31.65051 | −52.7299 | 19.66793 | −59.52 | 41.7710 | 35.03822 |
| (mm) | 29.72255 | 60.00000 | 39.7799 | −6.36652 | 43.07086 | 60.0000 | −11.09434 | −25.92 | 45.5386 | 43.14491 |
| (mm) | 23.45454 | 18.07791 | 24.7195 | 56.83676 | 27.41706 | −1.45505 | 58.82813 | 42.12 | 18.1837 | −2.77085 |
| (rad.) | 6.20163 | 0.00000 | 5.45884 | 4.01596 | 5.97746 | 0.93032 | 4.02771 | 5.9313 | 0.1859 | 0.64073 |
| (rad.) | 6.11937 | 6.28319 | 0.524005 | 1.36655 | 6.42411 | 5.54638 | 1.50348 | 2.34740 | −0.1661 | 4.93899 |
| (rad.) | 0.19304 | 0.26494 | 0.853145 | 2.33077 | 6.53496 | 5.70544 | 2.38566 | 2.58490 | −0.0325 | 5.74501 |
| (rad.) | 0.44083 | 0.50038 | 1.16505 | 2.87104 | 0.36230 | 5.85061 | 2.91751 | 2.84754 | 0.0933 | 6.11814 |
| (rad.) | 0.68467 | 0.73532 | 1.49253 | 3.39459 | 0.46906 | 5.99041 | 3.42257 | 3.11772 | 0.2174 | 0.17071 |
| (rad.) | 0.958335 | 0.99653 | 1.87456 | 3.97096 | 0.57765 | 6.13185 | 3.96923 | 3.37658 | 0.3449 | 0.54382 |
| (rad.) | 1.35533 | 1.33355 | 2.44206 | 4.96349 | 0.69047 | 6.28318 | 5.18616 | 3.61158 | 0.4812 | 1.27020 |
| Error | 2.62 E−02 | 1.23E−01 | 7.37E−04 | 2.06E−04 | 2.37E−04 | 2.0E−03 | 2.37E−05 | 5.6E−03 | 2.32E−04 | 4.71E−04 |
| (b) | ||||||||||
| SAP-TLBO [58] | TLBO [62] | HLIDE [66] | ImHS [70] | GSEF-IAA[74] | ODSRA + CP [75] | RBDO-MCS [94] | HCDJ [77] | DE-gr This Work | L-EPSDE This Work | |
| Np | 100 | 150 | 100 | -- | -- | 100 | -- | 100 | 100 | 100 |
| NF | -- | 82,500 | 100,000 | -- | 25,000 | 100,000 | -- | 100,000 | 200,000 | 200,000 |
| (mm) | 59.9864 | 60.0000 | 9.50437 | 49.334 | 30.3659 | 24.7256 | 55.7371 | 14.20137 | 44.9998 | 58.94653 |
| (mm) | 52.6078 | 14.6488 | 5.32006 | 12.095 | 10.1183 | 12.6722 | 9.3933 | 8.01431 | 16.2478 | 10.35726 |
| (mm) | 56.7209 | 47.6577 | 50.79235 | 35.234 | 41.018 | 29.4207 | 41.8429 | 16.30992 | 34.5751 | 35.62035 |
| (mm) | 59.3396 | 59.9128 | 52.45868 | 38.446 | 43.0375 | 34.5590 | 41.8429 | 12.25387 | 36.5490 | 34.77291 |
| (mm) | 53.0988 | 66.7653 | 17.28743 | 26.466 | −25.8055 | 58.6473 | 42.3130 | 27.79772 | −1.8620 | 24.58724 |
| (mm) | −56.6734 | −63.5825 | −31.80356 | 0.75083 | 33.9840 | 0.1583 | 37.7486 | 11.30541 | 41.7710 | 35.03822 |
| (mm) | −39.3209 | −55.5544 | −10.87584 | 47.33 | −12.548 | −24.7229 | 59.1841 | −2.30953 | 45.5386 | 43.14491 |
| (mm) | 59.9851 | 1.8752 | 36.94543 | 0.5213 | 29.0686 | 1.3009 | −7.3972 | 45.69508 | 18.1837 | −2.77085 |
| (rad.) | 3.6177 | 4.4871 | 5.53592 | -- | –3.4795 | 1.7411 | 7.0812 | 4.51724 | 0.1859 | 0.64073 |
| (rad.) | 2.9048 | 3.5408 | 1.92725 | -- | 3.43788 | 2.8192 | -- | 6.25324 | −0.1661 | 4.93899 |
| (rad.) | 2.9995 | 3.9269 | 2.50525 | -- | 3.2624 | 3.1006 | -- | 2.40390 | −0.0325 | 5.74501 |
| (rad.) | 3.0942 | 4.2133 | 3.08097 | -- | 3.10181 | 3.3863 | -- | 2.93624 | 0.0933 | 6.11814 |
| (rad.) | 3.1890 | 4.4653 | 3.66536 | -- | 2.9464 | 3.6770 | -- | 3.49056 | 0.2174 | 0.17071 |
| (rad.) | 3.2837 | 4.7052 | 4.24372 | -- | 2.78698 | 3.9769 | -- | 4.06508 | 0.3449 | 0.54382 |
| (rad.) | 3.3784 | 4.9469 | 4.82479 | -- | 2.61095 | 4.2996 | -- | 5.20950 | 0.4812 | 1.27020 |
| Error | 8.82E−04 | 1.48E−01 | 5.18E−07 | 8.76E−03 | 7.95E−04 | 8.66E−06 | 6.0E−04 | 8.84E−29 | 2.32E−04 | 4.71E−04 |
| DE [46] | GA-DE [47] | MUMSA [48] | IOAS-at [53] | DE-SRT [56] | HTRCA [91] | CMDE [60] | TLBO [64] | HLIDE [66] | GSA [71] | REA [76] | HPSO This Work | L-EPSDE This Work | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Np | 100 | 100 | 100 | 50 | 100 | -- | 100 | 500 | 50 | -- | -- | 100 | 100 |
| NF | 100,000 | 100,000 | 100,000 | 100,000 | 100,000 | -- | 100,000 | 50,000 | 100,000 | 100,000 | 100,000 | 100,000 | 100,000 |
| (mm) | 54.36089 | 80.0000 | 79.51607 | 65.42877 | 79.9985 | 54.857 | 80.00000 | 42.0053 | 80.00000 | 63.0882 | 79.99431 | 66.14036 | 79.98736 |
| (mm) | 8.68335 | 8.24689 | 9.72397 | 8.01639 | 8.72535 | 9.725 | 8.04566 | 8.0876 | 8.203235 | 9.5896 | 8.117863 | 8.02857 | 8.72534 |
| (mm) | 34.31863 | 45.8968 | 45.84252 | 47.22166 | 51.8801 | 49.925 | 50.81902 | 28.2600 | 52.34788 | 39.7516 | 51.10882 | 37.27658 | 40.04208 |
| (mm) | 79.99617 | 58.5404 | 51.43285 | 44.13656 | 43.3619 | 23.375 | 42.20801 | 24.1099 | 41.17572 | 34.4096 | 42.17296 | 38.55923 | 59.08385 |
| (mm) | 0.00019 | −6.40389 | 8.21392 | −11.5709 | −6.63658 | 7.840 | −10.6370 | −4.4860 | −10.9879 | 6.5766 | −10.9301 | −6.61025 | −4.38869 |
| (mm) | 1.46525 | −9.12264 | −2.95396 | −1.90491 | 8.2734 | −4.320 | −2.29109 | −4.7935 | 1.97982 | 2.3035 | −0.00687 | −3.30141 | 7.55335 |
| (mm) | 10.95440 | 6.52409 | 2.02111 | 10.63541 | 15.9712 | 1.440 | 8.49481 | 11.1765 | 6.74348 | 3.9094 | 7.575251 | 3.68216 | 14.92300 |
| (mm) | 11.07453 | 20.5220 | 13.21659 | −1.67548 | 18.5445 | 12.160 | −0.75797 | 3.5870 | −0.60110 | 7.0455 | −0.61085 | 9.42430 | 16.98752 |
| (rad.) | 2.12965 | 0.136532 | 5.59694 | 3.86733 | 1.34791 | 6.1135 | 3.88921 | 2.73892 | 4.12317 | 0.6061 | 4.009837 | 2.63731 | 1.22009 |
| (rad.) | 6.28319 | 6.05991 | 0.63769 | 2.41993 | 5.04915 | 0.14828 | 2.44944 | 6.26862 | 2.24025 | 0.0480 | 2.344066 | 2.65557 | 5.17437 |
| (rad.) | 0.61673 | 0.488453 | 1.32553 | 3.10927 | 5.73644 | 0.82561 | 3.15397 | 0.66488 | 2.95502 | 0.07579 | 3.054448 | 3.35029 | 5.86615 |
| (rad.) | 1.31025 | 1.17805 | 2.00803 | 3.81295 | 0.13974 | 1.52053 | 3.83711 | 1.33889 | 3.64900 | 1.4689 | 3.742718 | 4.01064 | 0.27374 |
| (rad.) | 2.19357 | 1.88339 | 2.69557 | 4.50644 | 0.832578 | 2.23681 | 4.52017 | 2.01652 | 4.33396 | 2.1897 | 4.426518 | 4.69612 | 0.96047 |
| (rad.) | 2.91717 | 2.59806 | 3.38458 | 5.18114 | 1.53611 | 2.90660 | 5.20480 | 2.70122 | 5.01670 | 2.9098 | 5.109552 | 5.38508 | 1.66772 |
| (rad.) | 3.49075 | 3.28585 | 4.08294 | 5.88342 | 2.24424 | 3.56508 | 5.89854 | 3.42419 | 5.70450 | 3.6268 | 5.799614 | 6.08002 | 2.37867 |
| (rad.) | 4.13202 | 3.96674 | 4.79845 | 0.29626 | 2.96272 | 4.29519 | 0.316204 | 4.13519 | 0.11548 | 4.2894 | 0.214054 | 0.5060 | 3.08000 |
| (rad.) | 4.92208 | 4.65966 | 5.51171 | 0.99115 | 3.66871 | 5.02152 | 1.023356 | 4.84542 | 0.81571 | 4.9616 | 0.917886 | 1.22339 | 3.79256 |
| (rad.) | 5.69537 | 5.35231 | 6.21279 | 1.70779 | 4.36455 | 5.71896 | 1.73899 | 5.57812 | 1.52796 | 5.6481 | 1.631829 | 1.94338 | 4.49363 |
| (rad.) | 6.28297 | 6.06263 | 0.63719 | 2.41887 | 5.04915 | 0.14283 | 2.44944 | 6.26817 | 2.24025 | 0.0481 | 2.344052 | 2.65573 | 5.174236 |
| Error | 1.952326 | 3.12E−02 | 4.70E−03 | 1.91E−02 | 4.56E−04 | 1.65E−01 | 4.02E−04 | 1.92E−02 | 5.77E−04 | 2.88E−03 | 4.17E−04 | 5.42E−03 | 7.02E−03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.-H.; Lin, J.-W.; You, W.-C. Comparative Study on the Synthesis of Path-Generating Four-Bar Linkages Using Metaheuristic Optimization Algorithms. Appl. Sci. 2022, 12, 7368. https://doi.org/10.3390/app12157368
Kang Y-H, Lin J-W, You W-C. Comparative Study on the Synthesis of Path-Generating Four-Bar Linkages Using Metaheuristic Optimization Algorithms. Applied Sciences. 2022; 12(15):7368. https://doi.org/10.3390/app12157368
Chicago/Turabian StyleKang, Yaw-Hong, Jau-Wen Lin, and Wei-Chen You. 2022. "Comparative Study on the Synthesis of Path-Generating Four-Bar Linkages Using Metaheuristic Optimization Algorithms" Applied Sciences 12, no. 15: 7368. https://doi.org/10.3390/app12157368







