Featured Application
The onset, offset, and transition detector algorithm that this paper is proposing can be used in singing assessment, note extraction, score following, automatic signing to score transcription, and singing to score alignment, but it is not limited to them.
Abstract
This paper introduces a new method for detecting onsets, offsets, and transitions of the notes in real-time solo singing performances. It identifies the onsets and offsets by finding the transitions from one note to another by considering trajectory changes in the fundamental frequencies. The accuracy of our approach is compared with eight well-known algorithms. It was tested with two datasets that contained 130 files of singing. The total duration of the datasets was more than seven hours and had more than 41,000 onset annotations. The analysis metrics used include the Average, the F-Measure Score, and ANOVA. The proposed algorithm was observed to determine onsets and offsets more accurately than the other algorithms. Additionally, unlike the other algorithms, the proposed algorithm can detect the transitions between notes.
1. Introduction
One of the fundamental processes of analyzing audio signals is finding the start and endpoint of the notes, which are called the onset and the offset, respectively. Onset and offset are not exact points/times that are universally agreed as the starting and ending of a note but exist within an acceptable range [1,2,3,4].
Several applications need the results of onset/offset detection, such as tempo and pitch estimation, beat tracking, score following, automatic music transcription, and analysis of recorded music. Real-time music applications demand almost instantaneous results, i.e., real-time onset detection for systems such as the interactive music systems explained in Müller-Rakow [5] and Malloch [6], or for music transcriptions as discussed by Kroher and Díaz-Báñez [7]. Therefore, it is vital to minimize the time delay between the onset or offset and their detection in real-time environments.
Over the years, many research contributions have been made for onset detection, but most work offline. If the onset detection function has been appropriately created, then onsets events will give rise to well-localized recognizable features, e.g., a peak, in the detection function [8]. Several common approaches for detecting onsets, such as spectral difference, phase deviation, wavelet regularity modulus, negative log-likelihood, and high-frequency content, are well explained in the Bello et al. [8] study and then compared by Collins [9]. Moreover, Dixon [10] has proposed multiple future enhancements for some of these methods.
In addition, Lacoste and Eck [11] propose an offline music onset detection algorithm using single and combined versions of Artificial Neural Networks (ANN) trained with different hyperparameters, and Eyben et al. [12] employ a Recurrent Neural Network (RNN) based on Mel spectrograms. Furthermore, after pre-processing with a time-variant filter, a method using Hidden Markov Models (HMMs) was proposed by Degara et al. [13] for offline onset detection. Schlüter and Böck [14] refined the model proposed by Eyben et al. [12] and trained Convolutional Neural Networks (CNNs) with mini-batch gradient descent (this splits the training dataset into small batches) to reduce model error, and the input to their model was two log Mel-spectrograms. Their approach outperformed other traditional methods and required less additional processing. However, the peak-picking approaches used for CNN and RNN-based methods rely on future information (not probabilistic) to detect an event; thus, they cannot work for real-time music onset detection.
Some of the studies are mainly focused on detecting onsets from singing signals. For instance, the singing onset detection method of Toh et al. [15] is based on audio features such as Mel Frequency Cepstral Coefficients, Linear Predictive Cepstrum Coefficients, pitch stability zero-crossing rate, and signal periodicity. First, the extracted audio features are classified into onset and non-onset frames using Gaussian Mixture Models (GMM). After GMM scoring, the feature evaluation is preceded by a dual detection function (feature level and decision level fusion) for higher accuracy in selecting the most optimal features. This method resulted in an 86.5% precision, 83.9% recall, and an F-measure of 85.2%. The recall shows the proportion of real positive cases that are correctly predicted positive. Precision implies the fraction of predicted positive cases that are correctly real positives. In binary classification, the F-measure calculates a test’s accuracy. It is calculated from the precision and recall of the test. The F-measure is the harmonic mean of the precision and the recall. The value of an F-measure is between 0 and 1. The highest value specifies perfect precision and recall, while the lowest shows whether the precision or the recall is zero [16]. However, despite the high F-measure score, it was still possible that their result could contain bias because of the dataset they used. The training and test set come from a tiny dataset comprising 18 singing recordings from four singers with 1127 onsets.
In the study conducted by Gong and Serra [17], a deep learning model was trained for musical onset detection in solo singing, and the authors discussed how their algorithm could lead to improve live onset detection models. They used two datasets, one of which contains more than 25,000 onsets, mostly complex mixtures or solo instrumental excerpts, and only three excerpts are of a solo singing voice, and the other dataset is a subset of a solo Jingju singing voice that contains 100 recordings. They employed seven deep learning-based architectures.
In the Gong and Serra [17] study, it was preferred to use the score-informed method if the musical score information was available. Score-informed approaches evaluate the data with the assistance of musical scores. Based on the results, score-informed HMM outperformed peak picking for all of the architectures used in this experiment [17]. The reported F-measure for the combination of the peak picking method and a no-dense neural network architecture was 73.88%, with a p-value of 0.002. For the score-informed HMM method, a nine-layer CNN architecture worked best, giving an F-measure of 80.90% and a p-value of 0.001. Learning strategies for inter-dataset knowledge transfer were also studied, but due to different musical patterns, the authors claimed that when the musical patterns from the two datasets used to train their model were different, the onset prediction was not accurate.
Despite these studies, onset detection of a musical note remains a challenge, primarily for the singing voice. Chang and Lee [18] explain several reasons for this, including inconsistency of articulation, singer-dependent tonal quality, and gradual variation in onset envelopes over time. In other words, the time-varying spectral envelope and the inconsistency of vocal tracks may produce fake maxima (i.e., peaks) in an onset detection function that can lower the precision rate for onset detection. Therefore, detecting onsets from the singing voice is still an active area of study because of waveform unpredictability and the occurrence of many noisy segments. Moreover, most methods are only suitable for recorded singing and are designed to work offline.
According to the previously published results, most existing approaches do not work well for soft onsets, including singing music. A soft onset has a long attack duration or vague envelope shape that becomes a challenge to the peak-picking procedure. The underlying reason for these issues is that the singing voice is classified as a pitched non-percussive (PNP) instrument, and PNP instruments still present a challenge for onset detection [9]. The nature of the singing voice adds further complexity due to its natural inconsistency with respect to pitch and time dynamics. Unlike some instruments, where their timbre is usually consistent throughout a note, the singing voice inherently can produce more variations of formant structures (for articulation); sometimes, it may even variate within the duration of a single note [19]. While most onset detection algorithms are based on detecting spectral changes, they can fail to differentiate such variations in a singing voice because of singing features such as vibration and soft onset.
Relevant challenges for onset detection in solo singing voices were identified in a report from the Music Information Retrieval Evaluation eXchange 2012 (MIREX 2012). According to this report, the best-performing detection method gives an F-measure of only 55.9% [4], which even becomes lower for solo sustained strings with an average F-measure of 52.8%. In addition, training datasets for dynamically changing patterns in a singing voice is still a challenge [17,20].
One of the missing parts of most of the onset detection algorithms is considering the actual singing style features. In the Mayor et al. [21] study, it is shown that one of the crucial features that should be taken into account in onset detection is the transition from a note to another note where there is no intervening silence, i.e., legato singing [21]. The transition means a singer will take a while to reach the target note. If the time for the transiting is not incorporated, the onset detector cannot find the correct times for onset and offset events. These transitions are categorized as a soft onset.
This paper aims to introduce a new onset detection algorithm incorporating more knowledge about the singing features for a more accurate onset estimation. Although the result of this study is based on an offline F0 estimator algorithm, the proposed algorithm can work in a real-time environment if fundamental frequencies can be estimated correctly.
2. Materials and Methods
This section explains the details of the approach taken to develop our algorithm. It first describes the datasets used, then explains the algorithm thoroughly, followed by the structure of the evaluation procedure.
2.1. Datasets
Two onset-annotated vocal datasets, Erkomaishvili [2] and SVNote1 [4,18], are used for this study. The following paragraphs provide a summary description of these different musical datasets.
2.1.1. Erkomaishvili Dataset
This dataset includes 100 monophonic audio files of traditional Georgian vocal music performed by a professional singer, Artem Erkomaishvili. Each audio file contains the fundamental frequencies, segment annotation, onset annotations, and sheet music in XML. Moreover, it contains more than seven hours of music with 40,135 onset annotations. The annotations were estimated manually except for the fundamental frequencies, whose calculation was semi-automated. Moreover, in this dataset, the points for onset and offset in successive notes were deemed to coincide, i.e., the offset of the previous note is the onset of the new note. Since the files were recorded in 1966, the audio files have poor quality. In addition, the recordings are of natural melodic singing rather than only some scales or arpeggios. Therefore, it is a challenging dataset for automatic annotation algorithms.
2.1.2. Note-Level Singing Voice Dataset (SVNote1)
This dataset included 30 audio files sung by seven men and three women. Each of the singers recorded three popular pieces of music (1—“soft kitty, warm kitty, little ball of fur”, 2—“school bell”, and 3—“Twinkle, twinkle little star”). They are, in total, around 16 min of music with 1440 onset annotations. In addition, three people annotated the onsets of each audio file separately, which means that three sets of annotations are provided for each audio file. The three annotators’ average is considered to be the ground truth for this study.
2.2. State of-the-Art Onset Detection Algorithms
To evaluate our proposed algorithm’s efficiency and accuracy, eight different onset detection algorithms were selected against which to compare the accuracy of the proposed algorithm. The implemented versions of the algorithms in Python were used. The algorithms were taken from implementations across four different Python libraries, namely Librosa [22,23], Madmom [24], Aubio [25], and Essentia [26]. The explanations of the algorithms are provided in the following by categorizing them based on the Python libraries.
2.2.1. Librosa
Librosa is a well-known library for sound analysis and feature extraction [23]. It has three different methods to estimate onsets. The first method (referred to as “LibRaw” in this paper) locates the note onsets based on peaks in the onset strength envelope. The onset strength envelope is calculated by finding the spectral flux, which is the difference in power spectrum between two consecutive frames, applying a threshold, and returning a one-dimensional array representing the change in spectral energy for each frame. Then, based on the onset strength, it peaks where the energy is a minimum based on the heuristic described by Boeck et al. [27]. Another two methods rely on backtracking from the nearest preceding minimum energy point [28]. The second method (called “LibBt”) works by backtracking using the onset strength profile, while the third method (named “LibBtRMS”) depends on backtracking with the Root Mean Square (RMS) or amplitude value. All these three methods are offline; they have not been designed to work in real time.
2.2.2. Madmom
This Python library provides two real-time onset detection methods [24,29]. The first approach (called “MadmomCNN” in this article) uses a Convolutional Neural Network model [14] trained on 26,000 annotated onsets. The model was trained to predict percussive and harmonic onsets with a frame rate of 100 per second. Next, the spectral onset processor method detects the onsets from a logarithmically scaled audio signal representation based on the spectral magnitude and phase, which is referred to using the name “MadmomSF” in this paper.
2.2.3. Aubio
This real-time library uses a window size of 2048 frequency samples to detect onsets [30]. In addition, Aubio sets a threshold value to mark quiet regions. Finally, it constructs a function based on successive spectral frames with a window size of 2048 and a hop-size of 1024, meaning the frame duration was approximately 23.22 ms for a 44,100 Hz sample rate. The dynamic thresholding and peak selections return the onset frames.
2.2.4. Essentia
This offline onset tracking method was used with its default values for the window and hop sizes, 1024 and 512, respectively, for a Hann window [26]. Therefore, the duration of each frame was roughly 11.61 ms. There are two approaches to this library. The first method, Essentia Onset HFC (EssHFC), uses a high-frequency content detection function [31]. The high frequency is calculated by multiplying the magnitude of each frame position (frequency) with the summation of the magnitudes of the spectral frame. The discrete spectrum of N unique points is formulated in Equation (1).
The second method, Essentia Onset Complex (EssCplx), uses a complex domain spectral difference function to identify significant changes in magnitude and phase [32]. This algorithm tries to identify significant energy changes on note onsets or the deviation of phase values within the phase spectrum caused due to pitch changes.
Finally, it should be mentioned that all these algorithms/libraries calculate only onsets and do not compute offsets or identify transitions.
2.3. The Methods for Evaluation
The accuracy of the proposed algorithm is evaluated by running the algorithms presented in Section 2.2 and the proposed algorithm on the datasets mentioned in Section 2.1. Then, the F-measure scores were calculated by the mir_eval Python library [33], and the results were ordered so that they could be compared with each other. As mentioned above, the onset points are not exact times but a range of acceptable times. Therefore, to calculate F-measure scores, each of the estimated onsets’ points should be compared with a range of points around the ground truth points. Thus, six different window sizes (10, 50, 100, 150, 200, and 250 ms) were considered to calculate the F-measure scores. Furthermore, the F-measure scores’ average, variance, and ANOVA were calculated to better understand the results.
3. The Proposed Algorithm
This algorithm is based on our observations following investigations that involved many singing pitch contours. From many of the plotted pitch contours, it was noticed that there is a noticeable trajectory change in the fundamental frequency when moving from one note to another. Therefore, the proposed algorithm is focused on evaluating the changes on a pitch contour to identify those meaningful changes that will signify onsets, offsets, and transitions.
The pitch contour is selected because it is a robust indicator of onset compared to other features. For example, Rabiner and Sambur [34] looked to find significant changes in the sound energy contour to find the start and the end of an isolated utterance. Their approach is based on short-time energy and zero-crossing rate. However, although in the case of a silence existing between notes, as considered by Rabiner and Sambur [34], a noticeable change in amplitude contour is easy to see, it is difficult to rely on the amplitude contour as a feature when analyzing legato singing, as unpredictable variation occurs in the movement from one note to the next. In contrast, the fundamental frequency track is either erratic before the onset and then quickly becomes stable or moves smoothly from one value to the next in the case of legato singing, even when the consecutive notes are in the same pitch frequency. Thus, the proposed algorithm can be explained as seven main steps to find the onsets, offsets, and transitions, as shown in Figure 1. The steps are explained in the subsequent paragraphs.
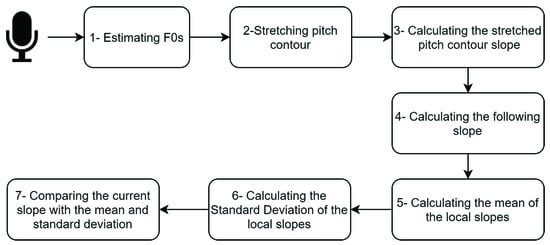
Figure 1.
The main steps to find onsets in the proposed algorithm.
3.1. Estimating F0s
Since the algorithm is based on the fundamental frequencies, the F0s must be estimated correctly. However, as mentioned in [35,36,37], the current real-time pitch detection algorithms are unreliable when applied to singing phrases. Therefore, according to the study by Faghih and Timoney [35], a more reliable offline algorithm, pYin [38], was employed to avoid a compounding effect in this analysis if any real-time pitch detector algorithm would be used. Thus, it was possible to evaluate the accuracy of the onset algorithm without any adverse effects caused by the pitch detection algorithms. A Python library, Librosa [22], was used for pYin.
The main difference between the real-time and offline algorithms is the amount of data they need for the calculation. Therefore, real-time algorithms are only based on the previous data points and/or a few later data points meaning that only a short buffer delay is required. On the other hand, offline algorithms require a long buffer delay to have sufficient data to perform their calculations. Using the pYin algorithm does not mean the proposed algorithm needs a long buffer delay to obtain a large amount of data, but the algorithm can work with a very short buffer delay, as explained below.
3.2. Stretching Pitch Contour
Since humans’ vocal pitch range is wide, generally from 77 to 900 Hz [39], calculating significant changes occurring on pitch contour has some difficulty. For example, the slope of the line when moving from the note to the note is much less than when it moves from the note to the note . Therefore, to counteract any adverse effect of this wide pitch frequency range on the slopes, the F0s are stretched to be on the almost same pitch frequency range.
Figure 2 plots two estimated pitch contours (panels a and b) and the stretched version of them (panels c and d, respectively). As depicted in Figure 2, although (a) and (b) are in different pitch frequency ranges, after stretching, the slopes between notes in both (c) and (d) are almost similar.
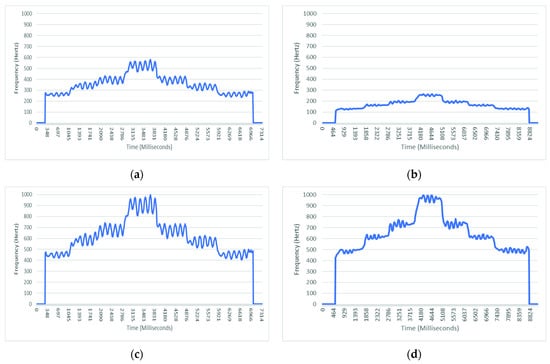
Figure 2.
The effect of stretching on pitch contour’s slopes. (c,d) are the stretched pitch contours of (a,b), respectively.
The following formulas, Equations (2) and (3), are used to implement the stretch.
where the variable holds the maximum F0 estimated until index , and the constant value holds the maximum possible F0. Since the maximum pitch frequencies of the singers in both datasets mentioned above are less than 1000 Hz, for this study, 1000 Hz is considered as the In Equation (2), if the current F0, , is more than the variable, Equation (3) should be run for all the F0 from index to index .
3.3. Calculating the Stretched Pitch Contour Slopes
To find the significant changes in F0s, the slopes between points in the pitch contour are needed. Figure 3 illustrates the process of calculating the slopes: in the left-hand panel, (a), the estimated pitch contour is plotted; the graph in the middle panel, (b), shows a stretched pitch contour of the contour in panel (a) as discussed in Section 3.2, while that the right-hand panel, (c), depicts the slopes between the F0s of the stretched pitch contour. It is computed by differentiating the contour. The vertical red lines in Figure 3 show the possible offset points, and the vertical green lines are the possible onset points.
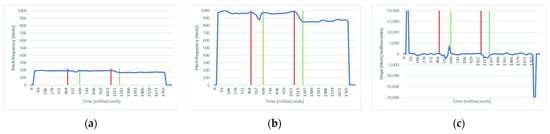
Figure 3.
Analyzing the pitch contour. (a) The original pitch contour of three notes, the first two notes are the same, and the third one is lower than the previous notes, (b) the stretched estimated values for the fundamental frequencies in (a), and (c) the slope of the pitch contour computed using differentiation. The red lines show the possible points for offsets, and the green lines are possible onsets.
3.4. Calculating the Summation of Slopes in the following Line
In singing, transitions can be observed as the singer moves from one note to another. An example of this is outlined between the two pairs of orange-colored lines in Figure 4.
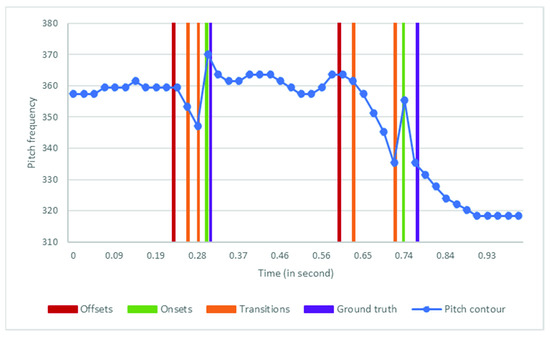
Figure 4.
Points’ statuses on a pitch contour. There are three notes: F4, F4, and E4, in order, sung by a professional female singer. The average pitch frequencies of the notes are 359, 362, and 323 Hertz, respectively.
In this step, the summation of the following points’ slopes is calculated to find the transitions at each point. In other words, as far as the direction of the line (upward, downward, or straight) in the stretched pitch contour remains the same, the slopes between every two consecutive points would be added to each other. The algorithm is depicted in Figure 5, where is the current point in this figure.
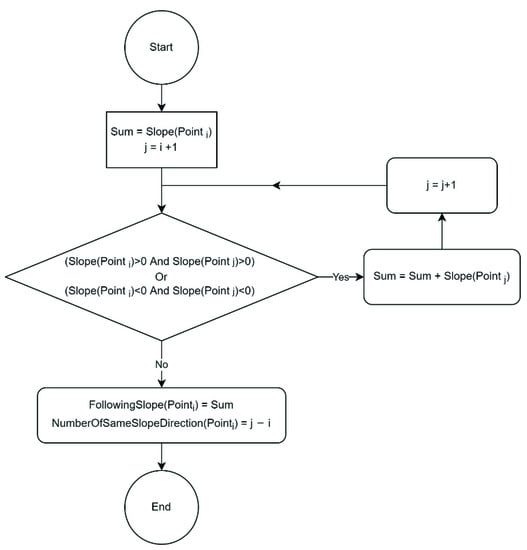
Figure 5.
Calculating the summation of the following slopes of the differentiated contour.
The algorithm commences by computing the cumulative sum of the consecutive points in the slope representation. In other words, their amplitudes, the values on the y-axis in Figure 3c, are summed. According to the evaluation of several manually annotated onsets, offsets, and transitions, it is observed that there is a sharp upward or downward movement between two consecutive notes in a pitch contour. Therefore, a heuristic function implemented using decision logic is applied to assess how much change happens after each new point. In addition, it is found how many consecutive points have the same sign as the current point’s slope: that is, how many of the successive values are heading in the same direction. The function denotes this in Figure 5, which is named .
Therefore, the algorithm, at this point, detects when the slope changes sign.
3.5. Calculating the Mean of the Local Slopes
In this step, the mean of the local slopes needs to be calculated. This mean is always accounted for by considering some of the previous points until the current point, as shown in Equation (4).
where is the size of the window. The value of is important to produce a mean that can show the mean of the fluctuations in a note. If is too big, it may include some old-time fluctuations that make an incorrectly local mean. In contrast, if is too small, there would not be enough fluctuations to calculate the correct local mean. The should be selected based on the singing technique, duration, and intervals. In this study, the selected values of were chosen to be 230 ms for the Erkomaishvili dataset and 46 ms for the SVNote1 dataset. These selections for were made according to a trial-and-error method of adjusting the value to have the best result for one of the files of each dataset.
As shown in Figure 6, although the median duration of the notes in both datasets is almost similar, roughly 0.42 s, the duration of most of the notes in the Erkomaishvili dataset is longer than the median. In contrast, the duration of the notes in the SVNote1 dataset is distributed approximately uniformly below and above the average. Therefore, the variance of notes’ duration in the Erkomaishvili dataset is greater than in the SVNote1 dataset. In addition, the variance of the intervals between notes in the Erkomaishvili dataset is smaller than in the SVNote1 dataset. Thus, two different values for each dataset were selected.
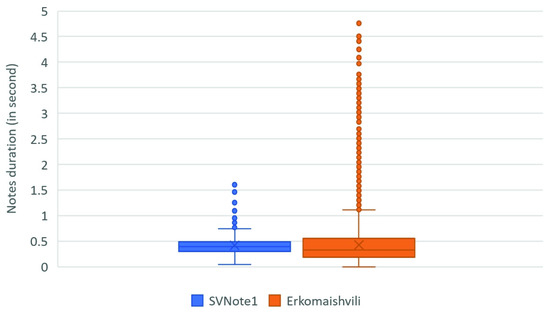
Figure 6.
Box and whisker of the estimated notes’ duration in the SVNote1 and the Erkomaishvili datasets.
3.6. Calculating the Standard Deviation of the Local Slopes
To define a trajectory change in the fundamental frequencies, the sample standard deviation of the local slopes is calculated as shown in Equation (5).
The same window size ( value) as for calculating the mean was used for estimating the standard deviation.
3.7. Comparing the Current Slope with the Mean and Standard Deviation
In this step, all the required information is prepared to determine if a significant change has occurred in the fundamental frequency trajectory.
Each of the points in the pitch contour can have only one of the following statuses:
- A.
- Onset: this means the point is an onset.
- B.
- Offset: this means the point is an offset.
- C.
- StartTransition: this means a transition will follow, and this point is the start of the transition.
- D.
- EndTransition: this means it is the end of the transition.
- E.
- None: this means this point is neither an event’s start nor the end.
These statuses are illustrated in the diagram in Figure 4. The red and green lines show offset and onset events respectively, while the orange lines denote a transition from a note to the following note, i.e., the points between an offset and its subsequent onset.
Figure 7 illustrates the algorithm for finding each point’s status. This algorithm works based on the values calculated by the algorithm illustrated in Figure 5. This algorithm is run iteratively on each of the estimated pitch values.
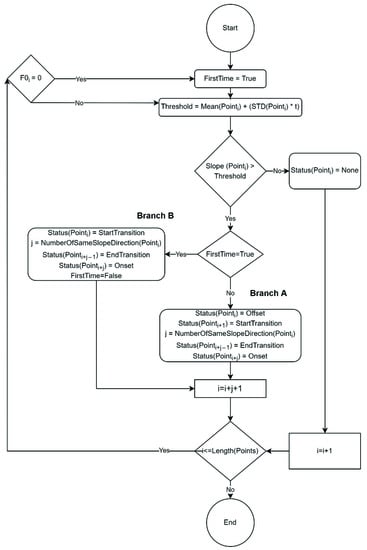
Figure 7.
The algorithm for finding a significant change to find onset, offset, and transition.
First, a for the local pitch contour’s slope must be calculated. This is completed by adding the mean of the local slopes at to the product of the standard deviation of the local slopes at P and coefficients. The is a user-specified value that indicates which range of frequencies, based on their variation from the mean, should be considered as belonging to the same note. The value t does not define a fixed variation from the mean but is derived based on the singer’s techniques. For instance, when the singer uses vibrato, the variation is higher than singing in an unmodulated tone. This study selected a threshold of 5 for the Erkomaishvili dataset and 2 for the SVNote1 dataset.
Second, if the slope at is bigger than the , it means that a trajectory change has happened. This significant change should be an , , or . If it is the first trajectory change after a silence (see Branch B in Figure 7), it is a movement to reach an ; otherwise (see Branch A in Figure 7), the current point is an . Based on each of these situations, Onset, Offset, StartTransition, and EndTransition statuses will be marked. The start and end of transitions are consecutively after and before an Offset and an Onset, respectively. In other words, the start and end of transitions are one point apart from the Offset and Onset points.
When the algorithm finds a trajectory change at , all the events between and will be labeled; thus, the following point that needs to be checked is . Therefore, there is a jump with a size of at the end of the algorithm to set the value for the next iteration.
In the beginning, the variable is set to true, and when a rest is reached (when equals zero), a value will be assigned to this variable.
A full implementation of the algorithm has been released to provide all the details at https://github.com/BehnamFaghihMusicTech/Onset-Detection, accessed on 15 July 2022.
4. Results and Discussion
This section provides the results and the details of the procedure for evaluating the proposed algorithm. It should be mentioned that the accuracy of the real-time proposed algorithm is compared against a set of real-time and offline algorithms. The delay of the proposed algorithms in calculating each event depends on its parameters, as mentioned in Section 3. Delays of 230 and 46 ms are used for the Erkomaishvili and SVNote1 datasets, respectively.
Since the other onset detection algorithms mentioned in Section 2.2 only estimate onsets but not offsets and transitions, only onsets need to be extracted to evaluate and compare the proposed algorithm with them. Therefore, two types of onset times were considered: (1) First, there are only those points in the pitch contour labeled as an onset. The green line illustrates these in Figure 8, and (2) the middle point between the start time of the transition and onset, illustrated by the pink lines in Figure 8, is considered as the new onset point. The reason for considering the second type is to align with the approach used for ground truth datasets’ because this one does not consider that transitions occurs between notes. Therefore, they would probably select a point between the red and green lines in Figure 8 as the onset. Therefore, considering the middle point should result in just a minor deviation from the ground truths.
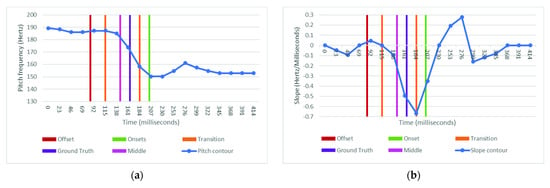
Figure 8.
An example illustrates the position of the onset point in the Erkomaishvili dataset (ground truth) compared to the onset, offset, and transition points indicated by the proposed algorithm. Panel (a) shows the pitch frequencies, and panel (b) depicts the slope contour according to panel (a).
Generally, as shown in Figure 8, a range of points between the offset and the start of the following note could be selected as an onset. Therefore, the algorithms were compared with different window sizes of 10, 50, 100, 150, 200, and 250 ms for calculating the F-measure. Table 1 and Table 2 display F-measures computed across all the algorithms in the six window sizes. A larger window size for F-measure shows more similarity, since an enormous difference between the ground truth and the estimated onset would be accepted in this case. However, as seen in Table 1 and Table 2, after applying the window size of 150 ms, the speed of improvement in F-measure values decreases. In addition, a window size of more than 250 cannot be meaningful, since it accepts more than a 250 ms difference between the ground truth and the estimated onset, which is too long. These tables provide the similarity between the ground truth’s onsets times and the estimated onsets times by each algorithm. As mentioned above, two onset point selections are considered regarding the proposed algorithm. The rows titled “Pro Algorithm 1” in Table 1 and Table 2 consider the green line in Figure 8 as the onset, while the rows titled “Pro Algorithm 2” select the middle point, which is the pink line in Figure 8.

Table 1.
The average of the F-measures of all the algorithms on the Erkomaishvili dataset based on six window sizes, from 10 to 250 ms.

Table 2.
The average of the F-measures of all the algorithms on the SVNote1 dataset based on six window sizes, from 10 to 250 ms.
All the algorithms show better results on the SVNote1 dataset than the Erkomaishvili dataset. One of the possible reasons for the better result could be the better audio quality of the SVNote1 dataset. In addition, there is a speaking introduction at the beginning of each audio file that is not included in their annotations. Nevertheless, since all the algorithms are working on the same audio files, they all have the same faulty sound, which will not affect the comparison.
As the result of the comparison, our proposed algorithm finds more correct onsets compared to the other algorithms when the window size is equal to or greater than 150 ms, as shown in the rows for Pro Algorithm 1 in Table 1 and Table 2. The bold numbers in these two tables highlight the performance of the best algorithm.
Selecting the average of the onset and the start of the transition as the onset leads to an increase in the accuracy of the proposed algorithm by 3.4% on average for the Erkomaishvili dataset. However, the opposite is the case for the SVNote1 dataset, in which the accuracy of the onset identification decreased by 3.8%. The reason for these opposing results is that the annotator of the Erkomaishvili dataset considered onsets more closely to the middle, as depicted in Figure 8. However, the SVNote1 dataset’s annotators mostly considered onsets after the proposed algorithm’s onset point, as shown in Figure 4. Both approaches can be interpreted as correct, since the onset point is not universally agreed in a pitch contour, as mentioned above, but it is deemed to be valid over a range of points.
To check the meaningfulness of the averages of the F-measure values of each onset detection algorithm, the p-values for ANOVA were calculated for all the F-measure values calculated for every single file. The ANOVA’s p-values for both Table 1 and Table 2 were less than 0.0001, which means a significant difference between the accuracy of all evaluated algorithms.
As another result, the average and the standard deviation of the duration of the transitions are shown in Table 3. This table also provides the minimum (average minus standard deviation) and the maximum (average plus standard deviation) typical duration for the transitions. Therefore, the average transitions’ duration in the datasets is almost the same. Overall, based on the results, the minimum and maximum duration of the transitions were approximately 16 and 98 ms. Therefore, since the proposed algorithm is based on the trajectory changes in a pitch contour and the transitions show these significant changes, the minimum delay required to find the onset, offset, and the transition is 16 ms and the maximum of 98 ms. However, most events should be found correctly, with the average transition duration being around 57 ms. This delay would be acceptable for most real-time music information retrieval applications. For example, Henkel and Widner’s real-time score-following system [40] requires a delay of around 56 ms.

Table 3.
The average, standard deviation, the minimum, and the maximum typical duration of transitions in both the datasets and overall.
Since the proposed algorithm is based on the changes in a pitch contour, when the intervals between notes are bigger, and there are fewer soft onsets, the algorithm can estimate onsets more accurately.
The accuracy of the proposed algorithm may be improved by considering more spectrogram channels, i.e., including other related frequency components from the spectrogram and not only the fundamental frequencies. In this way, a more comprehensive formula weighted together with the measurements for each channel could improve the overall measure. Therefore, a new series of numbers will be generated to find the onsets, offsets, and transitions from the trajectory changes in the new contour. In this approach, the adverse effect of the incorrect F0 estimation may be reduced, especially in a real-time environment.
Moreover, the accuracy of the proposed algorithm can be improved by incorporating a function tracking significant changes in the magnitudes of each spectral channel that are also associated with the onset.
Another possible approach instead of using the starting pitch explained in Section 3.2 is to scale down all F0s to one specific octave and then use a log frequency axis. This approach may help in regularizing the slopes and making them comparable.
In addition, the algorithm is based on two parameters, window size (as explained in Section 3.5) and the proportion of the standard deviation to calculate the thresholds, as discussed in Section 3.7. By evaluating the algorithm on other larger datasets such as VocalSet [41], these parameters could be fixed to be a constant value that is generally applicable to all singers or could be determined by a formula and therefore be adaptive to the nature of the style of input singing.
Furthermore, the algorithm’s efficiency and accuracy could be evaluated on notes performed by musical instruments to see if it is also applicable in that domain.
Lastly, making the algorithm more computationally efficient requires a smaller buffer size to work faster in real-time environments.
5. Conclusions
This paper has proposed a new algorithm for detecting onsets, offsets, and the transitions between notes in singing. The algorithm can work in both offline and real-time environments. In the case of real-time, a 57-millisecond delay is needed to have adequate information for calculating the events. Compared to other well-known algorithms, the algorithm shows an improvement of between 2% and 36%, especially when the window size for calculating the F-measure is equal to or greater than 150 ms.
Author Contributions
Conceptualization, B.F.; methodology, B.F. and S.C.; software, B.F.; validation, B.F.; formal analysis, B.F.; investigation, B.F. and S.C.; resources, B.F. and S.C.; data curation, B.F. and S.C.; writing—original draft preparation, B.F., A.Y., S.C.; writing—review and editing, B.F., J.T., A.Y., S.C.; visualization, B.F.; supervision, J.T.; project administration, B.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the relevant files to this study, such as an implementation of the proposed algorithm and the dataset generated by all the algorithms mentioned in this paper, are available online at https://github.com/BehnamFaghihMusicTech/Onset-Detection, accessed on 15 July 2022.
Acknowledgments
Thanks to Maynooth University and the Higher Education Authority in the Department of Further and Higher Education, Research, Innovation and Science in Ireland for their support.
Conflicts of Interest
The authors declare no conflict of interest. In addition, the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Bittner, R.M.; Pasalo, K.; Bosch, J.J.; Meseguer-Brocal, G.; Rubinstein, D. Vocadito: A Dataset of Solo Vocals with F0, Note, and Lyric Annotations. In Proceedings of the International Society for Music Information Retrieval, Virtual, 7–12 November 2021. [Google Scholar]
- Rosenzweig, S.; Scherbaum, F.; Shugliashvili, D.; Arifi-Müller, V.; Müller, M. Erkomaishvili Dataset: A Curated Corpus of Traditional Georgian Vocal Music for Computational Musicology. Trans. Int. Soc. Music Inf. Retr. 2020, 3, 31–41. [Google Scholar] [CrossRef]
- Choi, S.; Kim, W.; Park, S.; Yong, S.; Nam, J. Children’s Song Dataset for Singing Voice Research Soonbeom. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Virtual, 11–16 October 2020. [Google Scholar]
- Hoon, H.; Dooyong, S.; Kyogu, L. Note Onset Detection Based on Harmonic Cepstrum Regularity. In Proceedings of the 2013 IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, USA, 15–19 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Müller-Rakow, A.; Flechtner, R. Designing Interactive Music Systems with and for People with Dementia. Des. J. 2017, 20, S2207–S2214. [Google Scholar] [CrossRef][Green Version]
- Malloch, J.; Garcia, J.; Wanderley, M.M.; Mackay, W.E.; Beaudouin-Lafon, M.; Huot, S. A Design Workbench for Interactive Music Systems. In New Directions in Music and Human-Computer Interaction; Holland, S., Mudd, T., Wilkie-McKenna, K., McPherson, A., Wanderley, M.M., Eds.; Springer: Cham, Switzerland, 2019; pp. 23–40. [Google Scholar]
- Kroher, N.; Díaz-Báñez, J.-M. Modelling Melodic Variation and Extracting Melodic Templates from Flamenco Singing Performances. J. Math. Music 2019, 13, 150–170. [Google Scholar] [CrossRef]
- Bello, J.P.; Daudet, L.; Abdallah, S.; Duxbury, C.; Davies, M.; Sandler, M.B. A Tutorial on Onset Detection in Music Signals. IEEE Trans. Speech Audio Process. 2005, 13, 1035–1047. [Google Scholar] [CrossRef]
- Collins, N. A Comparison of Sound Onset Detection Algorithms with Emphasis on Psychoacoustically Motivated Detection Functions. In Proceedings of the Audio Engineering Society Convention 118, Barcelona, Spain, 28–31 May 2005; Audio Engineering Society: New York, NY, USA, 2005. [Google Scholar]
- Dixon, S. Onset Detection Revisited. In Proceedings of the 9th International Conference on Digital Audio Effects, Montréal, QC, Canada, 18–20 September 2017; Citeseer: Princeton, NJ, USA, 2006; Volume 120, pp. 133–137. [Google Scholar]
- Lacoste, A.; Eck, D. A Supervised Classification Algorithm for Note Onset Detection. EURASIP J. Adv. Signal Process. 2006, 2007, 43745. [Google Scholar] [CrossRef]
- Eyben, F.; Böck, S.; Schuller, B.; Graves, A. Universal Onset Detection with Bidirectional Long-Short Term Memory Neural Networks. In Proceedings of the 11th International Society for Music Information Retrieval Conference, ISMIR, Utrecht, The Netherlands, 9–13 August 2010; pp. 589–594. [Google Scholar]
- Degara, N.; Davies, M.E.P.; Pena, A.; Plumbley, M.D. Onset Event Decoding Exploiting the Rhythmic Structure of Polyphonic Music. IEEE J. Sel. Top. Signal Process. 2011, 5, 1228–1239. [Google Scholar] [CrossRef]
- Schluter, J.; Bock, S. Improved Musical Onset Detection with Convolutional Neural Networks. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 6979–6983. [Google Scholar]
- Toh, C.C.; Zhang, B.; Wang, Y. Multiple-Feature Fusion Based Onset Detection for Solo Singing Voice. In Proceedings of the ISMIR 2008—International Conference on Music Information Retrieval, Philadelphia, PA, USA, 14–18 September 2008; pp. 515–520. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness and Correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Gong, R.; Serra, X. Towards an Efficient Deep Learning Model for Musical Onset Detection. arXiv 2018, arXiv:1806.06773v1. [Google Scholar]
- Chang, S.; Lee, K. A Pairwise Approach to Simultaneous Onset/Offset Detection for Singing Voice Using Correntropy. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 629–633. [Google Scholar]
- Lindblom, B.; Sundberg, J. The Human Voice in Speech and Singing. In Springer Handbook of Acoustics; Springer: New York, NY, USA, 2007; pp. 669–712. [Google Scholar]
- Schindler, A.; Lidy, T.; Böck, S. Deep Learning for MIR Tutorial. arXiv 2020, arXiv:2001.05266. [Google Scholar]
- Mayor, O.; Bonada, J.; Loscos, A. The Singing Tutor: Expression Categorization and Segmentation of the Singing Voice. In Proceedings of the AES 121st Convention, San Francisco, CA, USA, 5–8 October 2006. [Google Scholar]
- McFee, B.; Lostanlen, V.; Metsai, A.; McVicar, M.; Balke, S.; Thomé, C.; Raffel, C.; Zalkow, F.; Malek, A.; Dana; et al. Librosa/Librosa: 0.8.0. 2020. Available online: https://librosa.org/doc/latest/index.html (accessed on 1 June 2021).
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.; McVicar, M.; Battenberg, E.; Nieto, O. Librosa: Audio and Music Signal Analysis in Python. In Proceedings of the 14th Python in Science Conference (SciPy 2015), Austin, TX, USA, 6–12 July 2015; pp. 18–24. [Google Scholar] [CrossRef]
- Böck, S.; Korzeniowski, F.; Schlüter, J.; Krebs, F.; Widmer, G. Madmom: A New Python Audio and Music Signal Processing Library. In Proceedings of the Proceedings of the 24th ACM International Conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 1174–1178. [Google Scholar]
- Aubio. Available online: https://aubio.org/ (accessed on 1 June 2021).
- Bogdanov, D.; Wack, N.; Gómez, E.; Gulati, S.; Herrera, P.; Mayor, O.; Roma, G.; Salamon, J.; Zapata, J.; Serra, X. Essentia: An Audio Analysis Library for Music Information Retrieval. In Proceedings of the Proceedings of the 14th International Society for Music Information Retrieval Conference, ISMIR 2013. Curitiba, Brazil, 4–8 November 2013; pp. 493–498. [Google Scholar]
- Sebastian, B.; Krebs, F.; Schedl, M. Evaluating the Online Capabilities of Onset Detection Methods. In Proceedings of the 13th International Society for Music Information Retrieval Conference (ISMIR), Porto, Portugal, 8–12 October 2012; pp. 49–54. [Google Scholar]
- Jehan, T. Creating Music by Listening. Ph.D. Thesis, Media Arts and Sciences Department, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Böck, S.; Arzt, A.; Krebs, F.; Schedl, M. Online Real-Time Onset Detection with Recurrent Neural Networks. In Proceedings of the 15th International Conference on Digital Audio Effects (DAFx-12), York, UK, 17–21 September 2012; pp. 15–18. [Google Scholar]
- Brossier, P.M. Fast Onset Detection Using Aubio (Brossier), Mirex 2005; Citeseer: Princeton, NJ, USA, 2005. [Google Scholar]
- MasJri, P.; Bateman, A. Improved Modelling of Attack Transients in Music Analysis-Resynthesis. In Proceedings of the 1996 International Computer Music Conference, ICMC 1996, Hong Kong, China, 19–24 August 1996; pp. 100–103. [Google Scholar]
- Bello, J.P.; Duxbury, C.; Davies, M.; Sandler, M. On the Use of Phase and Energy for Musical Onset Detection in the Complex Domain. IEEE Signal Process. Lett. 2004, 11, 553–556. [Google Scholar] [CrossRef]
- Raffel, C.; McFee, B.; Humphrey, E.J.; Salamon, J.; Nieto, O.; Liang, D.; Ellis, D.P.W. Mir_eval: A Transparent Implementation of Common MIR Metrics. In Proceedings of the Proceedings of the 15th International Society for Music Information Retrieval Conference, ISMIR 2014. Taipei, Taiwan, 27–31 October 2014; pp. 367–372. [Google Scholar]
- Rabiner, L.R.; Sambur, M.R. An Algorithm for Determining the Endpoints of Isolated Utterances. Bell Syst. Tech. J. 1975, 54, 297–315. [Google Scholar] [CrossRef]
- Faghih, B.; Timoney, J. An Investigation into Several Pitch Detection Algorithms for Singing Phrases Analysis. In Proceedings of the 2019 30th Irish Signals and Systems Conference (ISSC), Maynooth, Ireland, 17–18 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Faghih, B.; Timoney, J. Smart-Median: A New Real-Time Algorithm for Smoothing Singing Pitch Contours. Appl. Sci. 2022, 12, 7026. [Google Scholar] [CrossRef]
- Faghih, B.; Timoney, J. Real-Time Monophonic Singing Pitch Detection. Preprint 2022. [Google Scholar] [CrossRef]
- Mauch, M.; Dixon, S. PYIN: A Fundamental Frequency Estimator Using Probabilistic Threshold Distributions. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 659–663. [Google Scholar] [CrossRef]
- Heylen, L.; Wuyts, F.L.; Mertens, F.; De Bodt, M.; Van de Heyning, P.H. Normative Voice Range Profiles of Male and Female Professional Voice Users. J. Voice 2002, 16, 1–7. [Google Scholar] [CrossRef]
- Henkel, F.; Widmer, G. Real-Time Music Following in Score Sheet Images via Multi-Resolution Prediction. Front. Comput. Sci. 2021, 3, 718340. [Google Scholar] [CrossRef]
- Wilkins, J.; Seetharaman, P.; Wahl, A.; Pardo, B. VocalSet: A Singing Voice Dataset. In Proceedings of the 19th International Society for Music Information Retrieval Conference, Paris, France, 23–27 September 2018; pp. 468–472. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).