Systematic Methods to Increase the Lifetime of Mechanical Products Such as Refrigerators by Employing Parametric Accelerated Life Testing
Abstract
:1. Introduction
2. Parametric ALT for Mechanical Product
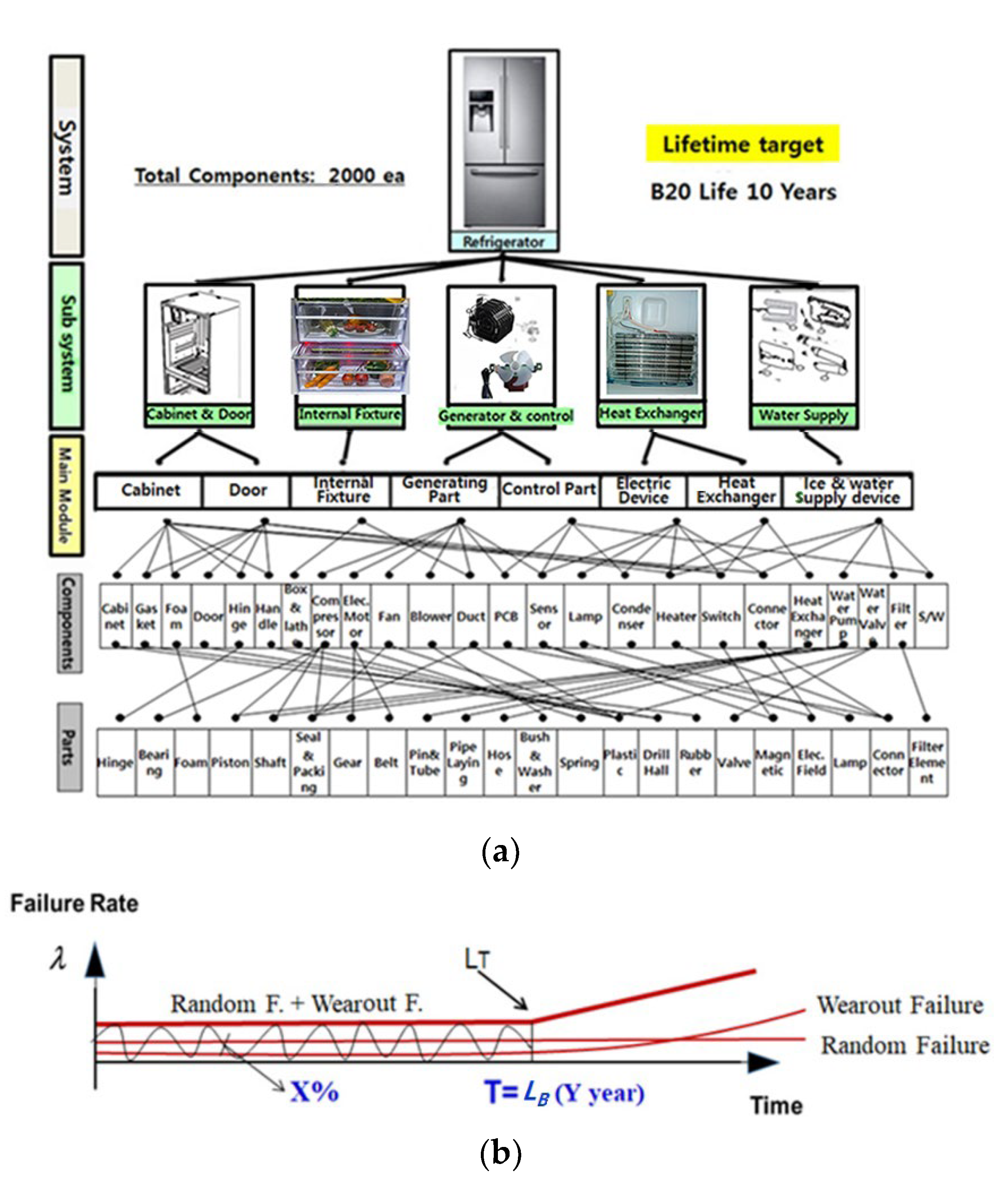
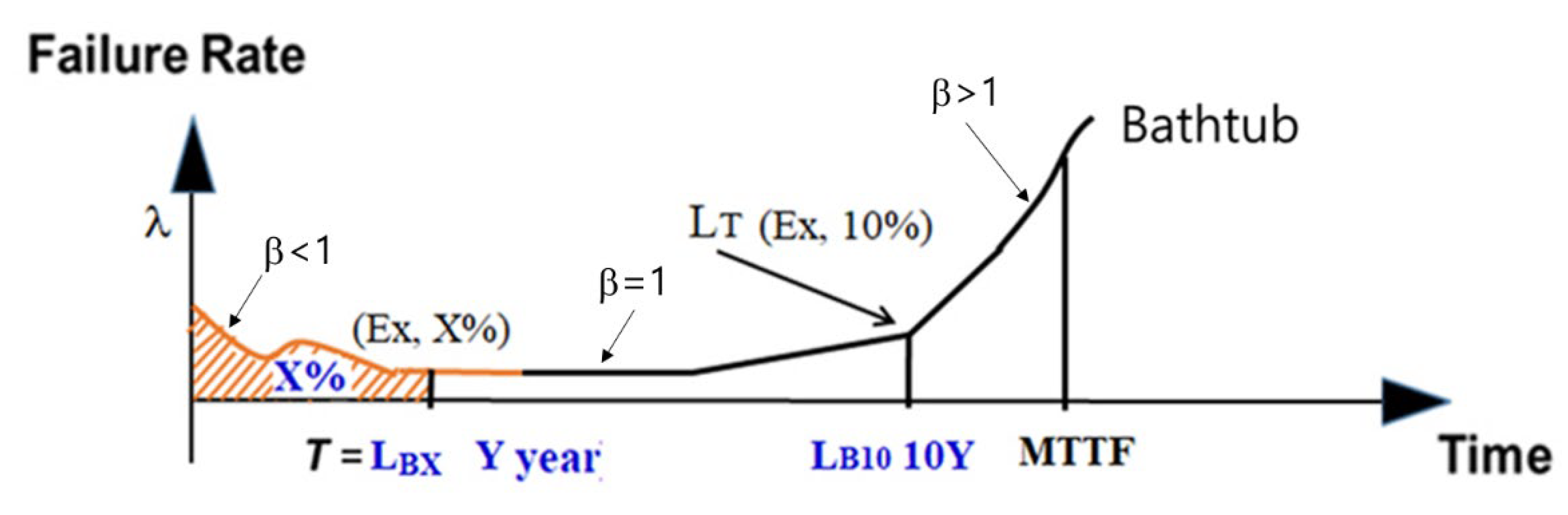
2.1. BX Lifetime in a Product
2.2. Positioning a Total Parametric ALT Procedure
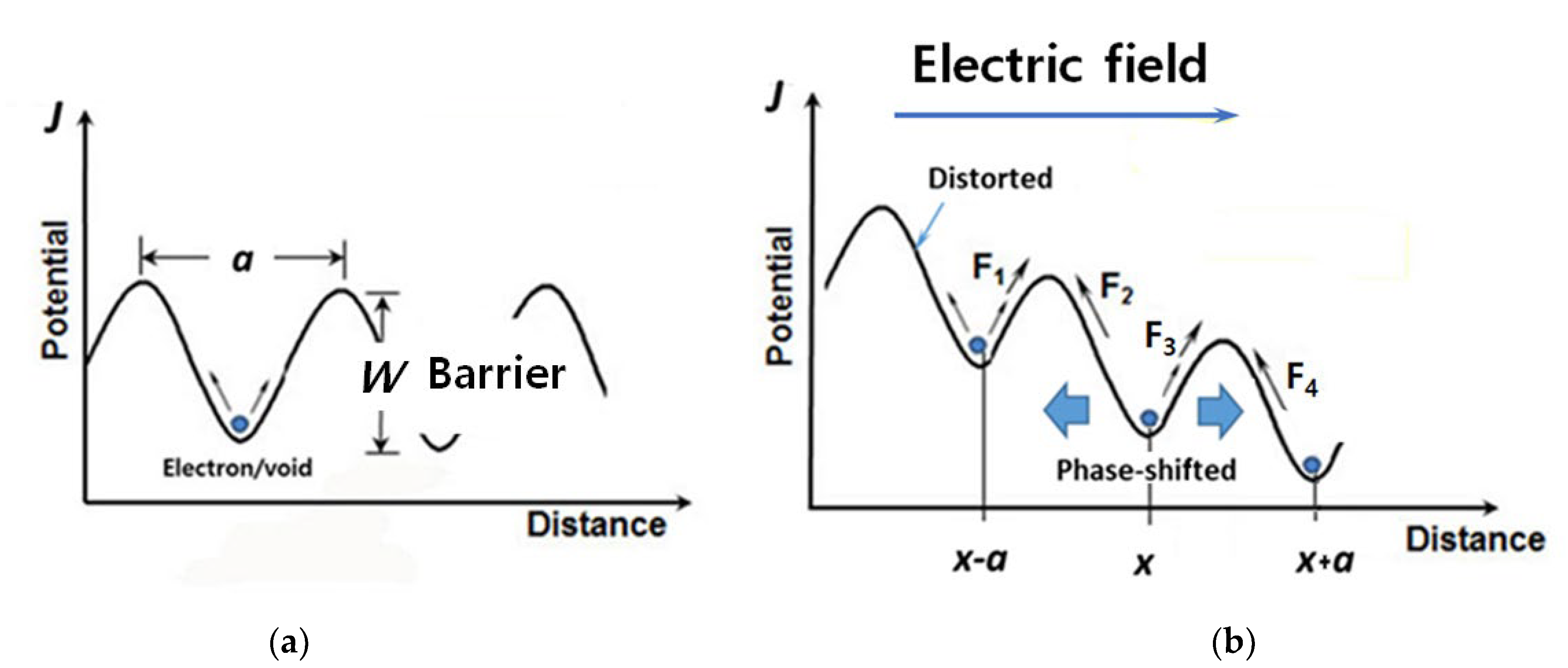
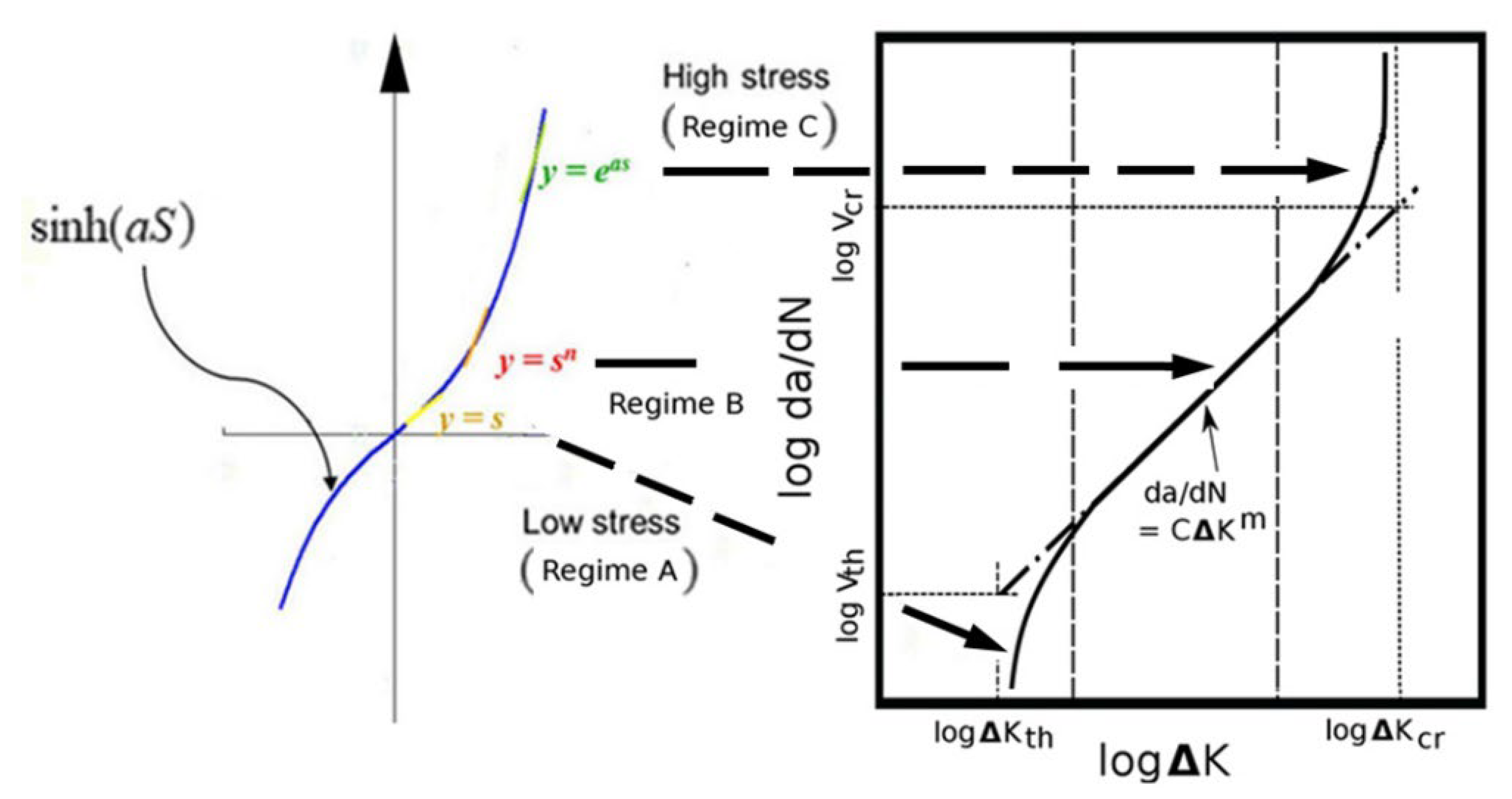
2.3. (Generalized) Failure Model and Sample Size Formulation
- at the beginning has some linear effect;
- has what is formed as a middle effect;
- in the end is high.
2.4. Case Study—Lifetime of a Localized Ice-Maker including Auger Motor with Gear System in a Domestic Refrigerator
3. Results and Discussion
4. Summary and Conclusions
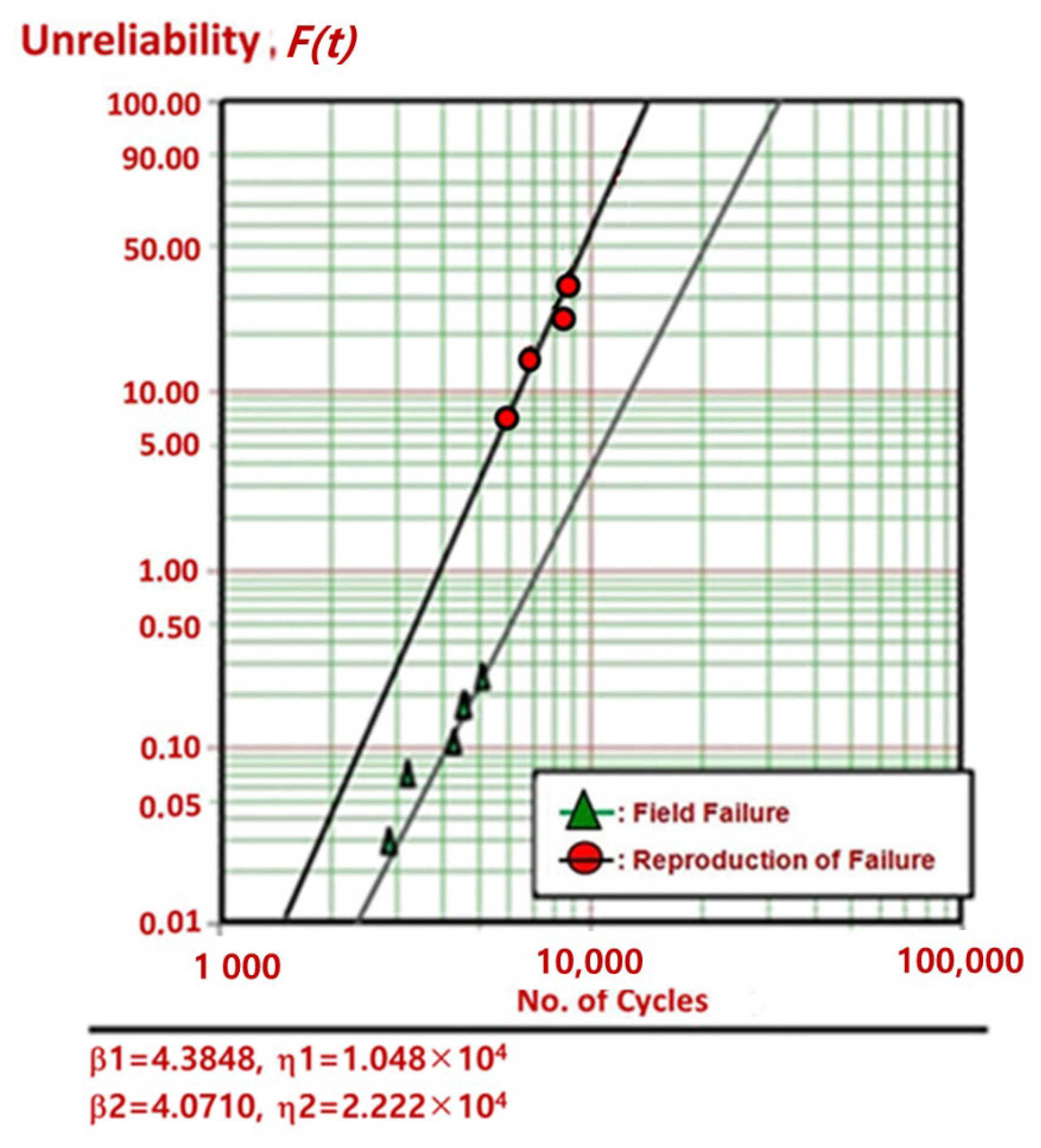
- In the first ALT, the auger motor (n = 10) made stopped near 6000 cycles, 6900 cycles, 8500 cycles, and 8700 cycles when applied for impact torque 1.47 kN-cm. After disassembling four problematic samples, we found that the teeth of gear system in the auger motor fractured. The gear material in a refrigerator ice-maker was modified from cast iron (carbon, 3 wt% and silicon, 2 wt%) to a sinter-hardened powder metallurgy nickel steel.
- In the second ALT, we discovered the fractured helix made of polycarbonates (PC) at 9900 cycles and 12,000 cycles because the ice-maker system did not have enough fatigue strength for repeated impact stress in the freezer section. As an alternation, a strengthened rib on the side and front of the helix was added.
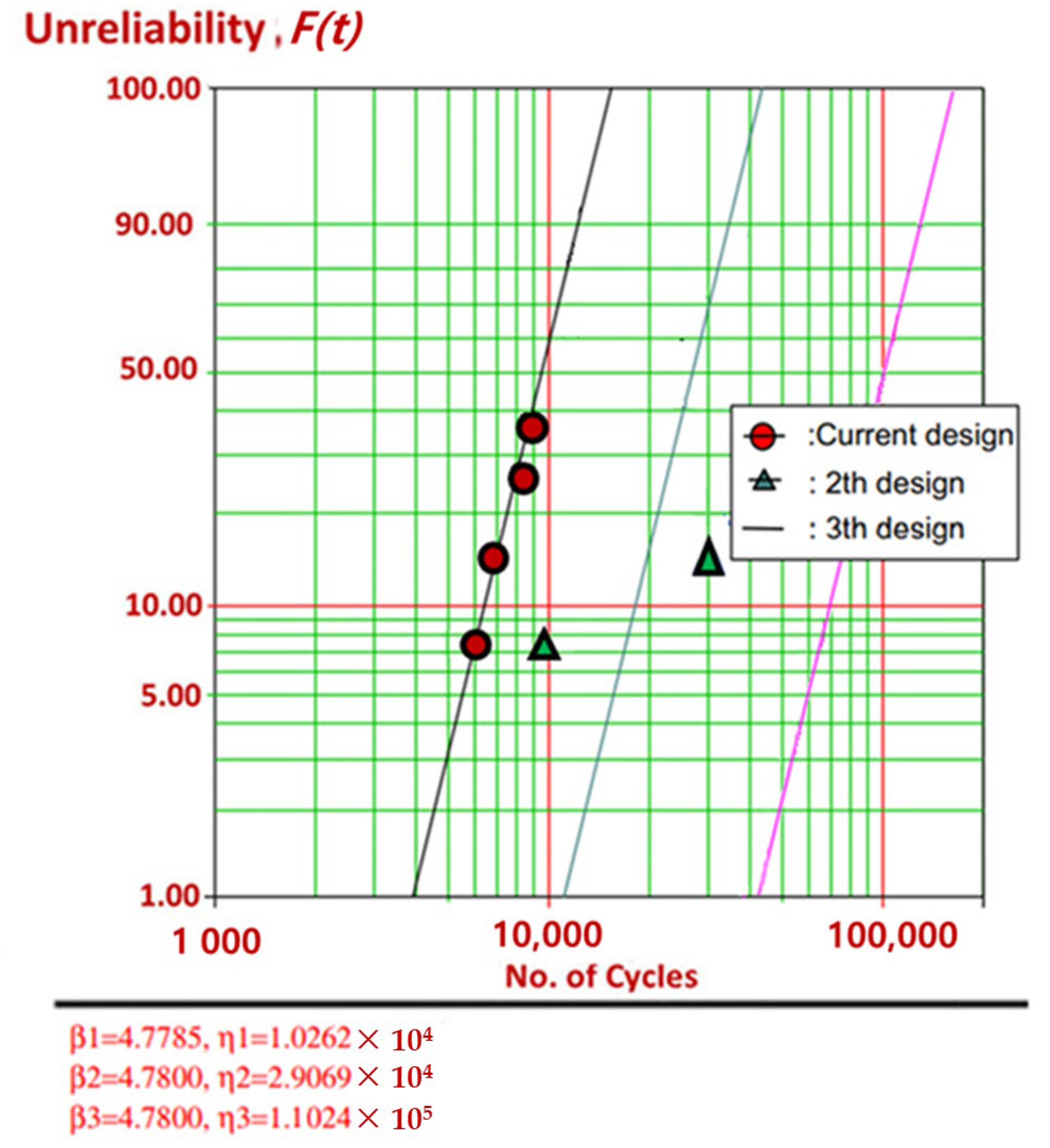
- During the third ALT, no issues were discovered. The ice-maker including an auger motor might fulfil the life target—B1 life 10 years. By examining problematical market products and conducting parametric ALTs with design alternations, it could enhance the lifetime of an auger motor including a gear system in a refrigerator ice-maker.
- By understanding the design issues returned for field products, we might perform parametric ALTs with design alternations. After reproducing the field failures, we could alter them. Eventually, we estimated if the product fulfilled the life objectives. In the meantime, we used the (generalized) time-to-failure model and sample size formulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BX | Time that is a cumulated failure rate of X%: durability index |
| Ea | Activation energy, eV |
| e | Effort |
| eb | Counter-electromotive force |
| ef | Field voltage, V |
| f | Flow |
| Fc | Ice crushing force, kN |
| F(t) | Unreliability |
| h | Testing time (or cycles) |
| h* | Non-dimensional testing cycles, |
| if | Field current, A |
| J | Momentum of inertia, kg m2 |
| k | Boltzmann’s numerical quantity, 8.62 × 10−5 eV/deg |
| LB | Target BX life and x = 0.01 X, on the circumstances that x ≤ 0.2 |
| m | Gear ratio |
| MGY | Gyrator in causal forms for basic 2-ports and 3-ports |
| n | Number of test samples |
| Q | Level of energy absorbed or released during the reaction. For the semiconductor, whole number of dopants per unit area |
| R | Proportion for minimum stress to maximum stress in stress cycle, σmin/σmax |
| r | Unsuccessful numbers |
| r | Coefficient of gyrator |
| S | Stress |
| T | Temperature, K |
| ti | Test time for each sample |
| TF | Time to failure |
| TL | Ice-crushing torque in bucket, kN cm |
| X | Cumulated failure rate, % |
| x | x = 0.01 X, on condition that x ≤ 0.2. |
| Greek symbols | |
| ξ | Electrical field applied |
| η | Characteristic life |
| λ | Cumulative damage quantity in Palmgren–Miner’s rule |
| χ2 | Chi-square distribution |
| α | Confidence level |
| ω | Angular velocity in ice bucket, rad/s |
| Superscripts | |
| β | Shape parameter in Weibull distribution |
| n | Stress dependence, |
| Subscripts | |
| 0 | Usual stress conditions |
| 1 | Elevated stress conditions |
Appendix A. Deriving Sample Size Formulation
References
- Bigg, G.; Billings, S. The iceberg risk in the Titanic year of 1912: Was it exceptional? Significance 2014, 11, 6–10. [Google Scholar] [CrossRef]
- ISO 1328-2:2020; Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 2: Definitions and Allowable Values of Double Flank Radial Composite Deviations: General Procedures. ISO: Geneva, Switzerland, 2020.
- ISO 17804:2020; Founding—Ausferritic Spheroidal Graphite Cast Irons—Classification Cylindrical Gears. ISO: Geneva, Switzerland, 2020.
- AGMA 939-A07; Austempered Ductile Iron for Gears. AGMA Information Sheet: Alexandria, VA, USA, 2018.
- DVB Bank SE Aviation Research (AR). An Overview of Commercial Jet Aircraft 2013; DVB Bank SE Aviation Research (AR): Schiphol, The Netherlands, 2014; p. 20. [Google Scholar]
- Woo, S.; Pecht, M.; O’Neal, D. Reliability design and case study of the domestic compressor subjected to repetitive internal stresses. Reliab. Eng. Syst. Saf. 2019, 193, 106604. [Google Scholar] [CrossRef]
- Duga, J.J.; Fisher, W.H.; Buxaum, R.W.; Rosenfield, A.R.; Buhr, A.R.; Honton, E.J.; McMillan, S.C. The Economic Effects of Fracture in the United States; Final Report; Available as NBS Special Publication 647-2; Battelle Laboratories: Columbus, OH, USA, 1982. [Google Scholar]
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Elsayed, E.A. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hahn, G.J.; Meeker, W.Q. How to Plan an Accelerated Life Test (E-Book); ASQ Quality Press: Milwaukee, WI, USA, 2004. [Google Scholar]
- Moura, E.C. How to Determine Sample Size and Estimate Failure Rate in Life Testing; ASQ Quality Press: Milwaukee, WI, USA, 2004. [Google Scholar]
- McPherson, J. Reliability Physics and Engineering: Time-to-Failure Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R Soc. Lond. A 1921, 221, 163–198. [Google Scholar]
- Wang, Y.; He, Z. Experimental and Statistical Study of the Fracture Mechanism of Sn96.5Ag3Cu0.5 Solder Joints via Ball Shear Test. Materials 2022, 15, 2455. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.L. Fracture Mechanics—Fundamentals and Applications, 3rd ed.; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- ASTM E606/E606M; Standard Test Method for Strain-Controlled Fatigue Testing. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM E399; Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM E647; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM E739-10; Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data. ASTM International: West Conshohocken, PA, USA, 2015.
- Elishakoff, I. Stepan Prokofievich Timoshenko and America. ZAMM—J. Appl. Math. Mech. 2019, 99, e201800338. [Google Scholar] [CrossRef]
- David, J.G. Introduction to Quantum Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Cemal, B. Introduction to Unified Mechanics Theory with Applications, 1st ed.; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Weingart, R.G.; Stephen, P. Timoshenko: Father of Engineering Mechanics in the U.S. Structure Magazine, 1 August 2007. [Google Scholar]
- Reddy, J.N. An Introduction to the Finite Element Method, 4th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- Dyniewicz, B.; Bajkowski, J.M.; Bajer, C.I. Effective Viscoplastic-Softening Model Suitable for Brain Impact Modelling. Materials 2022, 15, 2270. [Google Scholar] [CrossRef] [PubMed]
- Vijaya Kumar, S.D.; Karuppanan, S.; Ovinis, M. Artificial Neural Network-Based Failure Pressure Prediction of API 5L X80 Pipeline with Circumferentially Aligned Interacting Corrosion Defects Subjected to Combined Loadings. Materials 2022, 15, 2259. [Google Scholar] [CrossRef] [PubMed]
- Vega, M.A.; Todd, M.D. A variational Bayesian neural network for structural health monitoring and cost-informed decision-making in miter gates. Struct. Health Monit. 2022, 21, 4–18. [Google Scholar] [CrossRef]
- IEEE Standard Glossary of Software Engineering Terminology. IEEE STD 610.12-1990. Standards Coordinating Committee of the Computer Society of IEEE. (REAFFIRMED SEPTEMBER 2002). Available online: https://ieeexplore.ieee.org/document/159342 (accessed on 31 December 2020).
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley and Son: Hoboken, NJ, USA, 2011; p. 683. [Google Scholar]
- Grove, A. Physics and Technology of Semiconductor Device, 1st ed.; Wiley International Edition: New York, NY, USA, 1967; p. 37. [Google Scholar]
- Minges, M.L. Electronic Materials Handbook; ASM International: Cleveland, OH, USA, 1989; Volume 1, p. 888. [Google Scholar]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems, 6th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Woo, S.; O’Neal, D.L. Reliability design and case study of mechanical system like a hinge kit system in refrigerator subjected to repetitive stresses. Eng. Fail. Anal. 2019, 99, 319–329. [Google Scholar] [CrossRef]
- Wasserman, G. Reliability Verification, Testing, and Analysis in Engineering Design; Marcel Dekker: New York, NY, USA, 2003; p. 228. [Google Scholar]
- Tang, L.C. Multiple-steps step-stress accelerated life tests: A model and its spreadsheet analysis. Int. J. Mater. Prod. Technol. 2004, 21, 423–434. [Google Scholar] [CrossRef]
- William, E.L.; David, M.; Christoper, N.M.; Stephen, W.B.; Richard, J.F.; Timothy, F.; Thomas, A.S.; Frank, W.G. Mechanical Properties of Structural Steels; NIST NCSTAR 1-3D; NIST: Gaithersburg, MD, USA, 2005.


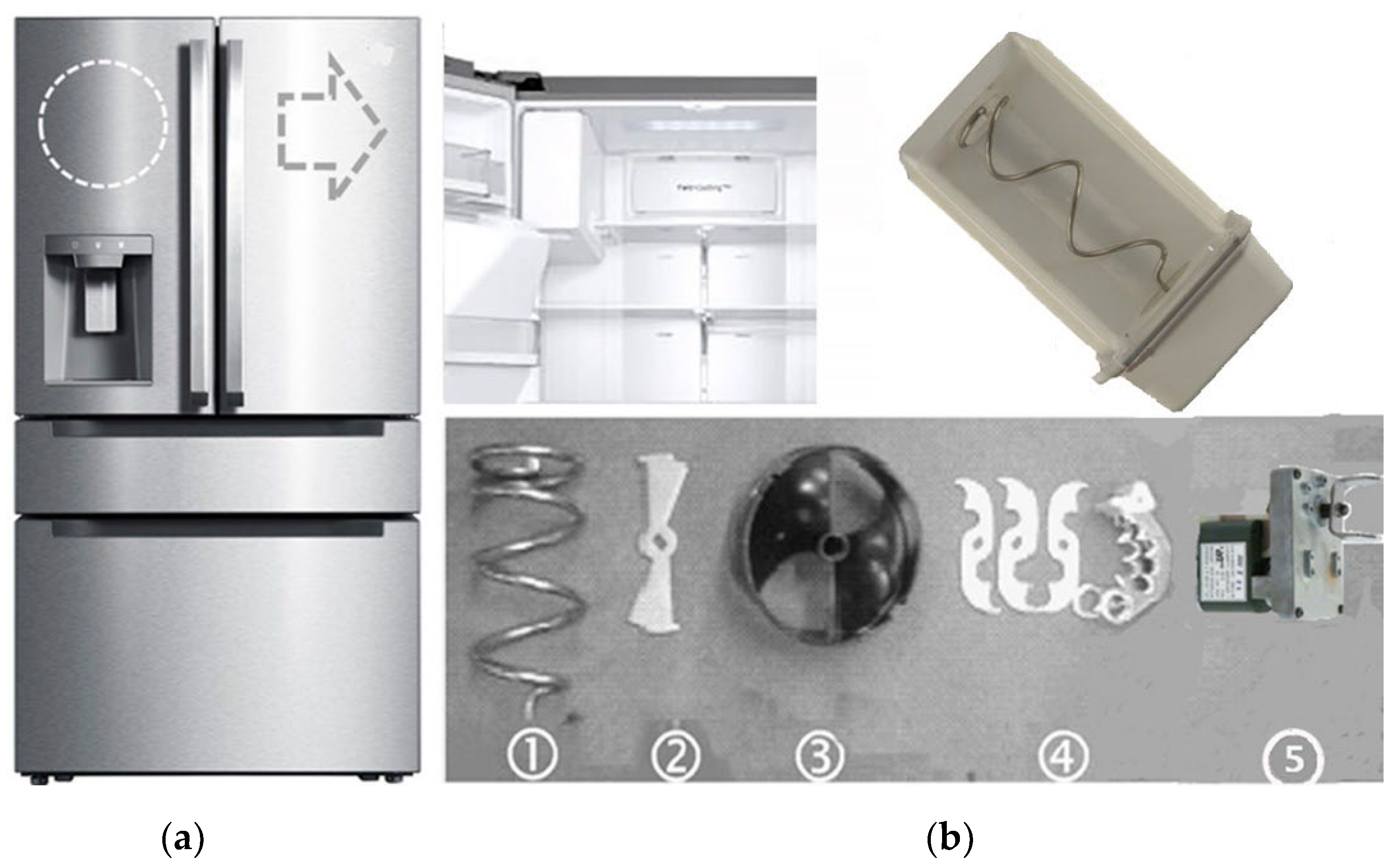







| Modules | Field Data | Expected Reliability | Intended Reliability | |||||
|---|---|---|---|---|---|---|---|---|
| Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | |||
| A | 0.30 | 3.3 | The same | ×1 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| B | 0.35 | 2.9 | The same | ×1 | 0.35 | 2.9 | 0.10 | 10(BX = 1.0) |
| C | 0.24 | 4.2 | New | ×5 | 1.20 | 0.83 | 0.10 | 10(BX = 1.0) |
| D | 0.15 | 6.7 | Adjusted | ×2 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| E | 0.31 | 3.2 | Adjusted | ×2 | 0.62 | 1.61 | 0.10 | 10(BX = 1.0) |
| Others (F/G/H) | 0.50 | 10.0 | The same | ×1 | 0.50 | 10.0 | 0.50 | 10(BX = 5.0) |
| System | 1.9 | 2.9 | 3.27 | 0.83 | 1.00 | 10(BX = 10) | ||
| System Feature | Power, e(t) × f(t) | Effort, e(t) | Flow, f(t) |
|---|---|---|---|
| Translation | F × V | Force, F(t) | Velocity, V(t) |
| Rotation | Τ × ω | Torque, τ(t) | Angular velocity, ω(t) |
| Pump, compressor | ∆P × Q | Pressure difference, ∆P(t) | Volume flow rate, Q(t) |
| Electric | V × i | Voltage, V(t) | Current, i(t) |
| Magnetic | em × φ | Magneto-motive force, em(t) | Magnetic flux, φ(t) |
| Parametric ALT | 1st ALT | 2nd ALT | 3rd ALT |
|---|---|---|---|
| Draft Design | Final Design | ||
| Over the course of 42,000 cycles, the gear system has no problems | 6000 cycles: 1/10 fracture 6900 cycles: 1/10 fracture 8500 cycles: 1/10 fracture 8700 cycles: 1/10 fracture (Failed gear samples) | 9900 cycles: 1/10 fracture 12,000 cycles: 1/10 fracture (Failed helix samples) | 42,000 cycles: 10/10 OK |
| Structure |  |  | |
| Action plans | C1: material: from cast iron to a sinter-hardened powder steel | C2: added reinforced rib on side and front of helix |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, S.; O’Neal, D.L.; Hassen, Y.M. Systematic Methods to Increase the Lifetime of Mechanical Products Such as Refrigerators by Employing Parametric Accelerated Life Testing. Appl. Sci. 2022, 12, 7484. https://doi.org/10.3390/app12157484
Woo S, O’Neal DL, Hassen YM. Systematic Methods to Increase the Lifetime of Mechanical Products Such as Refrigerators by Employing Parametric Accelerated Life Testing. Applied Sciences. 2022; 12(15):7484. https://doi.org/10.3390/app12157484
Chicago/Turabian StyleWoo, Seongwoo, Dennis L. O’Neal, and Yimer Mohammed Hassen. 2022. "Systematic Methods to Increase the Lifetime of Mechanical Products Such as Refrigerators by Employing Parametric Accelerated Life Testing" Applied Sciences 12, no. 15: 7484. https://doi.org/10.3390/app12157484
APA StyleWoo, S., O’Neal, D. L., & Hassen, Y. M. (2022). Systematic Methods to Increase the Lifetime of Mechanical Products Such as Refrigerators by Employing Parametric Accelerated Life Testing. Applied Sciences, 12(15), 7484. https://doi.org/10.3390/app12157484







