Assessment of the Perspective Ratios in Rail Crossings as an Important Evaluation Factor of Rail Crossings

Abstract

It is currently necessary to solve several bottlenecks in railway infrastructure. This is important because it is needed to improve railway infrastructure to be faster, safer and of high quality. Rail crossings on railway lines are also a significant bottleneck. There are still many rail crossings and a high number of accidents in many countries of the European Union. The issue of rail crossings must be addressed because many rail crossings reduce the flow of road and railway traffic. However, it is about the safety of transportation, as several serious and fatal traffic accidents have happened at rail crossings. Many times, the perspective ratios of the rail crossings are a significant problem and the main cause of traffic accidents. Therefore, it is important to propose a certain methodological procedure for the assessment of the perspective ratios in rail crossings. The main contribution goal is to briefly describe the development of the rail crossings number according to security devices and analyze the factors influencing the rail crossing potential and restrictive elements factors of the rail crossings as a matter of priority. Great emphasis is placed on the perspective ratios as a key safety factor. The heuristic procedure of the perspective ratios determination is presented within the proposals. Subsequently, there are analyzed the perspective ratios at the selected rail crossing with the light protection device and to assess whether these ratios are safe for the given crossing in the event of the light protection device failure. The rail crossing in the Czech Republic has been selected as a representative on railway line no. 196 from České Budějovice to Horní Dvořiště in the empirical part of the research. The rail crossing has been analyzed in terms of its characteristics and parameters and has been assessed as complying with legal regulations.

1. Introduction

Rail transport occupies a significant position in Europe, offering the diversity of the infrastructure network. It provides a cheap, long-term sustainable and especially ecological way of transporting passengers and goods practically over various long distances. Railways often become the main artery for the flow of freight and passenger traffic at the national and international levels with gradual electrification, modernization, and construction. However, within international transport, railways become less flexible, and carriers have to overcome operational problems in the form of national interlocking systems for individual national railway infrastructure managers.

From the viewpoint of safety on the railway network, the most dangerous place is a rail crossing for the railway track and road (railway-crossing or level-crossing) as practically the only place of direct physical contact between otherwise relatively isolated transport modes. This is also documented by accident statistics. Promoting the reduction in unsecured railways is one of the national priorities of national governments and the European Union [1].

From a safety point of view, level crossings (LCs) are critical points in the safe conduct of rail and road traffic. Due to the different characteristics of rail and road vehicles (size, speed, stopping distance, maneuvering capabilities, etc.) level crossings are often places with frequent accidents and in most cases result in human fatalities and big material damages, even though, all of them are secured with an appropriate level of technical protection. Accident statistics have shown that the main cause for all accidents (more than 95%) is the human factor of road users (drivers, cyclists and pedestrians) who did not follow and obey traffic safety regulations at level crossings. These ideas and outputs are mentioned in the study [2]. Safety measures for preventing or diminishing rail crossing accidents are presented and proposed in the study. The mentioned study is very important because it serves as an inspiration for the further development of the rail crossing issue. It offers a certain point of view on the safety assessment of railway crossings and creates space for the creation of new methodological procedures. Very useful professional and scientific information, including practical applications related to perspective ratios, are contained in the publications [3]. It is a very instructive and beneficial publication for this research because the aim of this article is to analyze the perspective ratios at selected railway crossings with the traffic light securing device and to assess whether these ratios are safe for passage in the case of the traffic light securing device failure or in the case of non-compliance with the determined rules by the driver.

The Railway Infrastructure Manager in the Slovak Republic (ŽSR) adopts measures that, to a certain extent, eliminate accidents at rail crossings. Reversing the accidents trend at rail crossings is the result of a reduction in the number of rail crossings, as well as a targeted effort by the Transport Ministries of individual countries to take measures to eliminate the possible train collision with a road motor vehicle. The approved Crossing Security Enhancement Project set priorities in this area and categorized measures to eliminate cross-border accidents. It is primarily a legislative definition of the issue. For example, it can be a clear and transparent definition of public authorities’ rights and obligations in matters relating to the establishment, cancellation and management of rail crossings, the management and maintenance of road markings on roads and so on. It should also be appropriate to implement the principle that the costs of constructing and extending the rail crossing, as well as securing it, are borne by the person in whose interest it is established. For quick orientation of accident participants and rescue services within the Integrated Rescue System 112, it is also necessary to introduce a unique rail crossing number assigned to each rail to identify the rail crossing immediately.

However, from the scientific point of view in the field of transport processes in railway transport, it is necessary to look for other scientific and professional solutions to increase safety at rail crossings. Therefore, this contribution based on the available statistics and literature reviews deals with the assessment of the perspective ratios as an important part of the potential evaluation of the rail crossings and tries to find suitable solutions. The research also includes a practical application [4].

There are many interesting and useful publications, studies and contributions that deal with the issue of rail transport and especially railway infrastructure. Railway infrastructure can be examined from several angles. There are lots of facts that need to be constantly observed and analyzed and subsequently developed in order to make some progress in this area as well.

Many areas are also necessary to address and explore in the rail crossing issues. Several famous foreign authors have dealt with this topic in the recent past. For example, the study [5] compares accidents at passive and active railway rail crossings and both immediate and background risk factors are considered. In this study, passive railway rail crossings have no warning devices, although there might be a static warning sign. Active rail crossings are equipped with automatic devices warning road users of approaching trains. The paper [6] describes the basic design principles for the rail crossings where rail vehicles reach speeds up to 200 km/h, as well as the review of the necessary measures to increase the safety level. Another paper [7] focuses on the results of studies that cover irregularities occurring on rail crossings and pedestrian crossings.

Very interesting outputs are in the article [8], which described the methods to reduce the time waiting for public transport and vehicles before the railway rail crossing. One of the proposed methods is the optimization of the rail crossing algorithm. A useful and quality publication [9] presents a methodological development proposed for railway rail crossing safety systems which is applied in the South Australia region. Rail crossing safety performance is also a very important factor. The most significant publication on the topic is the paper [10] where data envelopment analysis was performed on the accident data occurring on five types of rail crossings in Turkey and measurement of safety performances of rail crossings in Turkey was provided.

Further, study [11] examines relationships among attitudes toward traffic rules, impulsiveness, and behavioral intentions at rail crossings. Specific professional and scientific ideas and outputs are mentioned in the publication [12]. Although it is not a new contribution, the mathematical principles proposed in it are still very beneficial because the rail crossing density estimation method is proposed.

Accidents at rail crossings are a very important but unpopular topic. The development of accidents at rail crossings is closely followed by the phenomenon in the Slovak Republic. When reconstructing railway corridors to 160 km/h, rail crossings are canceled, leading to a reduction in their number. This issue is addressed in detail in the publication [13]. The aim of the paper is to propose actions to reduce the number of occurrences of these accidents on road and railway transport system crossings based on the analysis of incidents at rail crossings in the example of the Slovak Republic. There are analyses of the development of rail crossing accidents between 2000 and 2021 in Slovakia in the paper. A special graph was also created showing a trend exponential curve for rail crossing development and for the number of accidents, as shown in Figure 1.

Other publications that address similar issues and offer interesting ideas and modern progressive solutions, including an analysis of the various factors related to rail crossings are, for example, contributions [14,15,16]. There are also many scientific methods of optimization that can be used in transport processes and railway transport rationalization and optimization. For example, the employment of the Monte Carlo optimization method is described in the article [17]. This method can be used to optimize the railway infrastructure and its capacity. The railway infrastructure improvement is also necessary in order to improve the transport service of the area. Public passenger transport rationalization and timetabling are mentioned in the publications [18,19]. This issue is seamlessly followed by other outputs related to rail transport operations [20] and other infrastructure measures [21], as well as economic measures [22].

Last but not least, it is necessary to mention the publications [23,24,25,26,27,28,29], which also serve as inspiration in achieving the stated goal and the proposed methodology.

All this information shows that several scientists and experts have dealt with the issue of rail crossings. However, the factors influencing the potential of the rail crossing and the factors influencing the restrictive elements of the rail crossing have not yet been specified. The methodology of the perspective ratios of the rail crossing determination has also not been proposed. Therefore, this paper focuses on this part of the research in the field of rail crossings.

2. Materials and Methods

The second chapter consists of the current status analysis, describing several materials (publications, studies, theses at all) that have been studied and from which is drawn inspiration in the research. The used methods are also described.

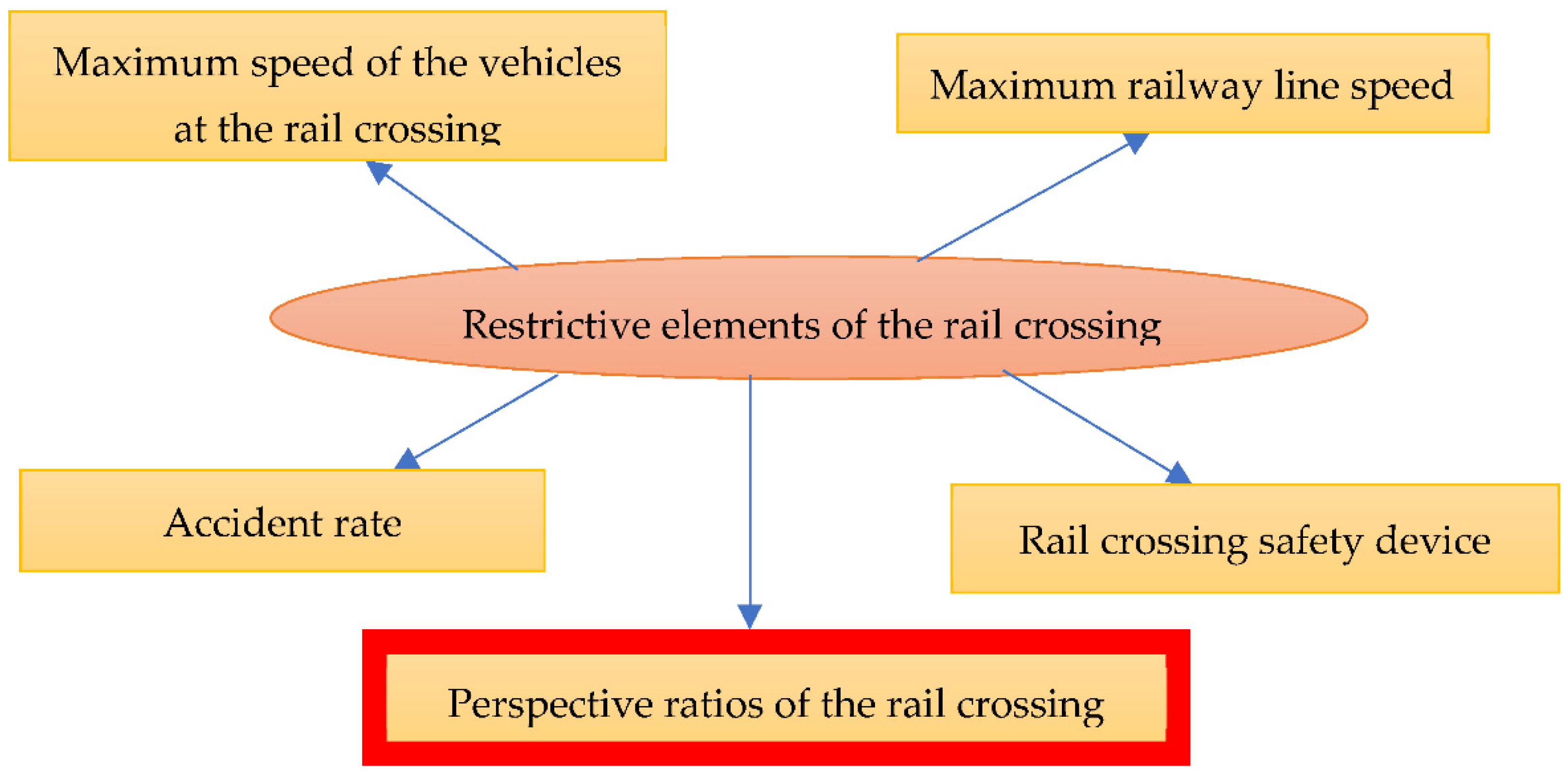
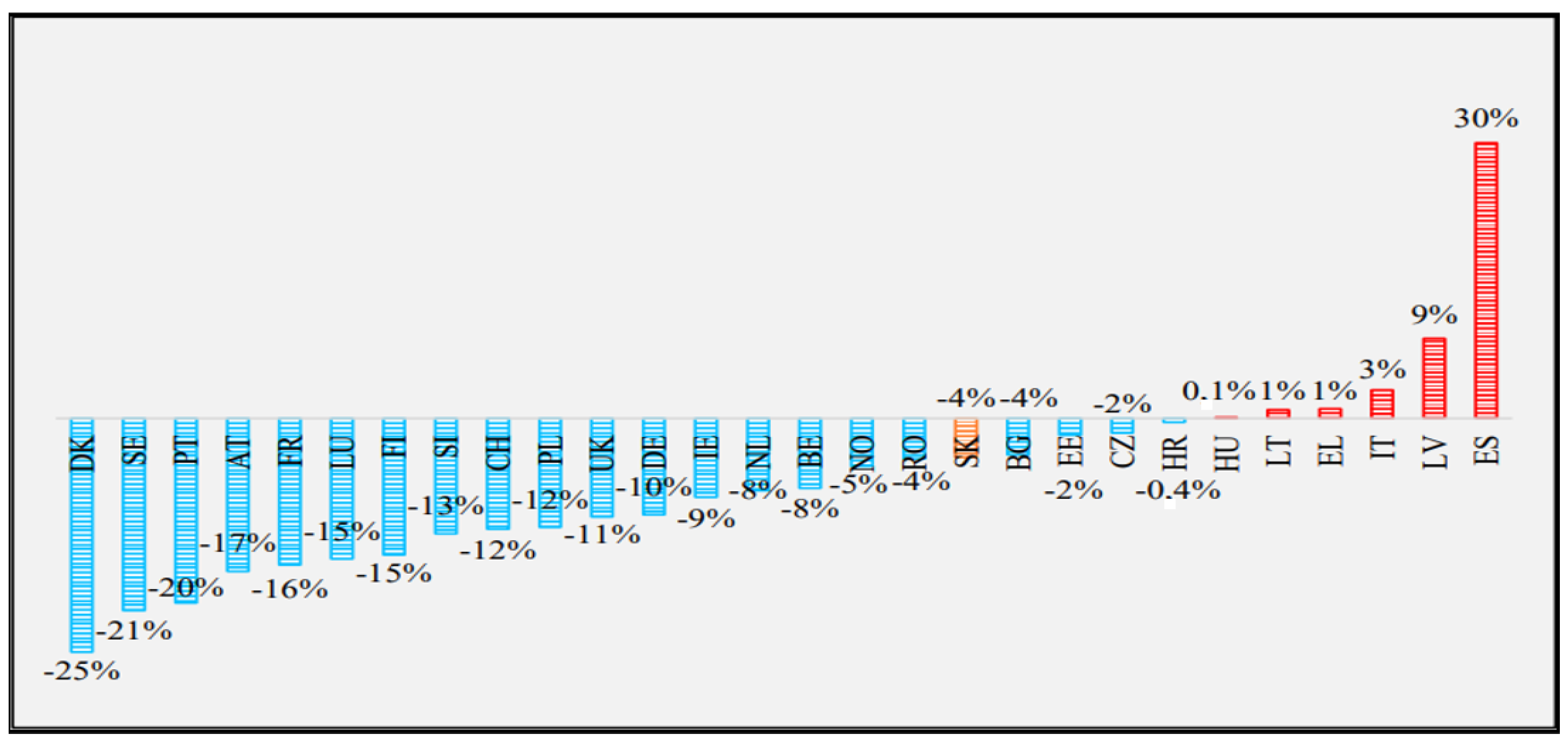
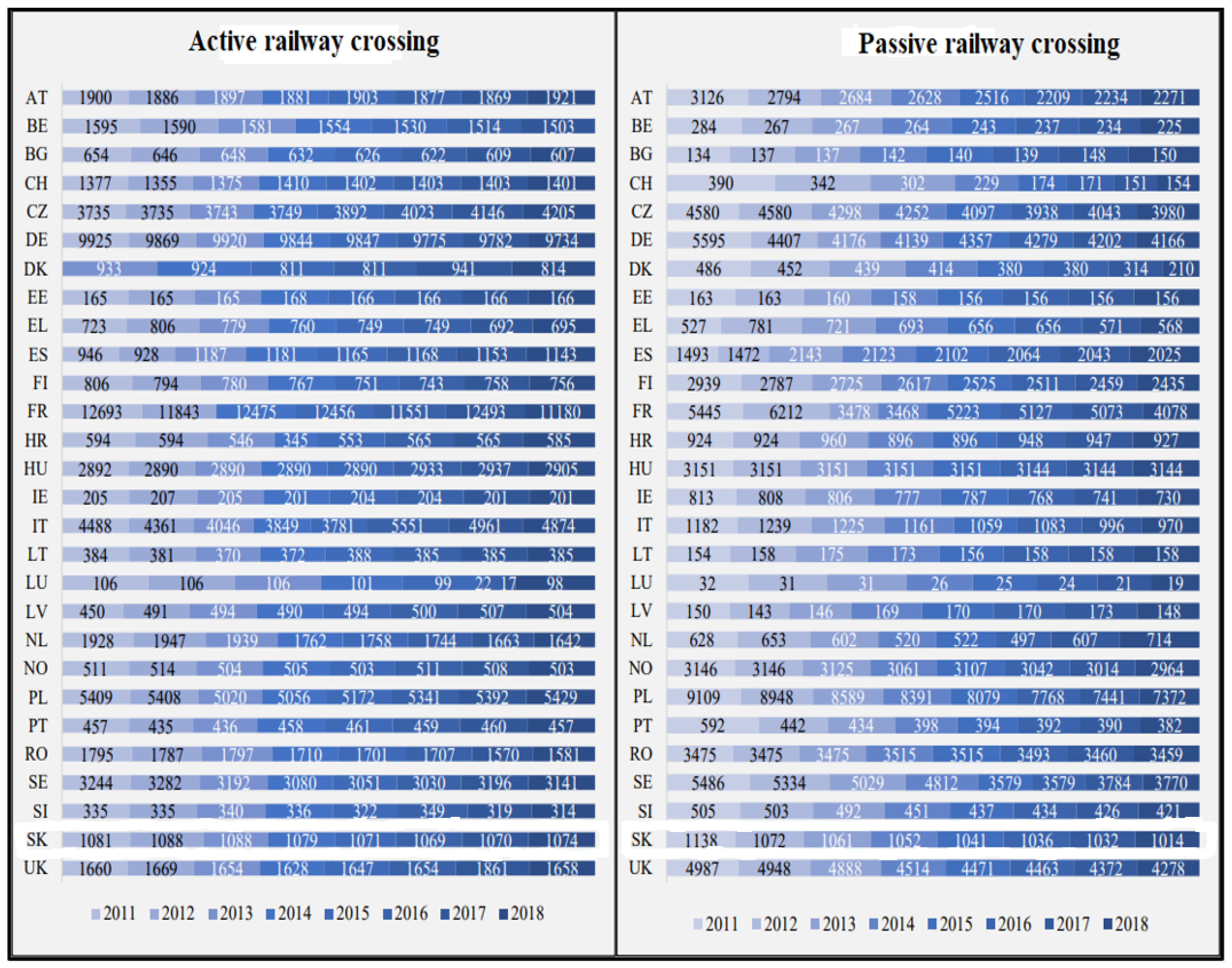
2.1. Current Status of the Issue

The analysis of the current situation is focused on the analysis and characteristics of rail crossings, in particular in European countries. It is very important to point out current trends and statistics.

According to the European Railway Agency (ERA), there were 114,580 rail crossings in 28 European countries, of which, 47% were unsecured in 2015. Since 2010 number, passive crossings have decreased by 4% per year, at this rate, their amount will decrease by 2030 by half at the most. Within the EU, there are, on average, 5 km per track and 5 rail crossings, but this value varies considerably between countries. Sweden, Austria, the Czech Republic and Hungary have a high density of crossings per kilometer of tracks (up to 75 per 100 km). Conversely, Bulgaria and Spain can be classified as countries with the lowest density of rail crossings (25 per 100 km) [30].

In general, the number of rail crossings has decreased in recent years in most “ERA countries”. The largest percentage decrease in the observed period was recorded in Denmark (25%) followed by Sweden (down 21%) and Portugal (down 20%). The number of rail crossings decreased the least in the Czech Republic (only by 2%) and Croatia (decrease of 0.4%). There was also the opposite trend-the number of rail crossings increased in six countries (Spain, Lithuania, Italy, Greece, Hungary, Latvia). The information on the percentage change in the number of rail crossings in ERA countries between 2011 and 2021 is shown in Figure 2 [30].

The development of the number of passive and active rail crossings in ERA countries in absolute terms is mentioned in Figure 3. These statistics show that the country with the highest number of rail crossings is France, and the country with the lowest number of rail crossings is Luxembourg.

Regarding the analysis of the number of rail crossings in particular ERA countries, the density of rail crossings is also a very important indicator. There has been a trend in the past to build many rail crossings, especially on regional railway lines in most countries [30].

The Czech Republic is one of the EU countries with the highest number of rail crossings. This is also given by the fact that the Czech Republic has a railway network with the most density in the EU.

Table 1. Rail crossing numbers according to the types in the Czech Republic [31].

Rail Crossing Type	Amount
Total Number of Rail Crossing	7734
Rail crossing secured only by a warning cross	3486
Crossing secured by a rail crossing security device	4248
Crossing secured by the traffic lights	3974
Barrier rail crossing	1611
Barrier-free rail crossing	2363
Crossing secured by a mechanical rail crossing safety device	265
Rail crossing operated remotely	47
Rail crossing operated locally	218
Rail crossing operated in combination	0

contains exact actual data of the rail crossings current number on the Czech Republic railway network including specification of type [31].

This fact causes the choice of the Czech railway network for the case study on the selected rail crossing [31].

2.2. Methods

There were several significant scientific methods used in the proposal part of this research. The most advantageous was the use of expert methods that are based on expert estimates in this case. Their essence is to obtain information from certain experts based on certain specific procedures and algorithms. The mentioned methods can be procedural, universal or structural. Within the solved research problem, which is the subject of the mentioned contribution, the most advantageous was to use the following methods [32]:

• Brainstorming method—it is known as a creative method used to solve various problems using the generation of progressive ideas and thoughts; the result should be an original and unique solution to a specific problem, which also represents the proposals and outputs listed in the chapter [33];
• mind mapping method—the method develops the brainstorming method, through which the logic of the researched problem, context and priorities are developed [33];
• panel expert method—it is a forecasting method that, based on the input data, provides a vision or recommendations for future options and needs related to the analyzed transport topic; the method involves about 15–20 experts who work on a certain problem for a certain period of time (3–18 months), the basis is the elaboration of final outputs on the basis of joint compromises and joint scientific and professional research [33];
• the system approach method—it is a method that emphasizes the overall picture and the interrelationships and connections between the individual components of the whole, it can be called the science of management, decision-making or the science of systems thinking [33];
• the heuristic method—the method offers and discovers new ways of solving problems and inventing certain new contexts; it is a scientific activity based on a “discovery” procedure, which usually starts with a general proposal or some rough estimate, which is gradually refined; this method represents an intersection between empirical and exact methods [34];
• FMEA (Failure mode and effect analysis) method—it belongs to the basic group analytical methods used in the quality management process, management reliability, and security; it is one of the basic methods used in semi-quantitative risk analysis, applying not only to production processes and products but also services, financial, social and other processes [35];
• SFMEA—(System Failure Mode Effects Analysis)-analyzes systems and subsystems at an early (conceptual) stage and focuses on interactions between systems and system elements [35].

These methods were used mainly in the creation of the factors described in Figure 4 and Figure 5 and also in the creation of the methodological procedure described in Figure 6. The most important is to use the correct synergistic effect of these methods.

The specific methods used in the main part of the research (within the particular parts of the proposed heuristic procedure of the rail crossing perspective ratios) are mainly physical methods. These are methods deriving from classical mechanics, which are based on Newton’s laws of motion. They are derived from the basic equation of motion. Subsequently, the particular formulas are applied in the research of the perspective ration calculation [36].

3. Results

The assessment of rail crossings depends on two areas, based on an assessment of the potential of the rail crossing and on the limiting elements of the rail crossing. Based on the input data from the previous chapter, factors were set that will be used to monitor the rail crossing potential, what factors affect the crossing potential in the future and what are the limiting elements that limit the crossing. The more restrictive elements there are, the more the rail crossing attractiveness decreases due to the cancellation of the rail crossing without the possibility of replacement or without prioritizing modernization.

There are four factors of the rail crossing potential proposed, which are shown in Figure 4.

Figure 4. Factors of rail crossing potential.

Figure 4. Factors of rail crossing potential.

There are five main factors of the restrictive elements of the rail crossing proposed and they are shown in Figure 5.

Figure 5. Restrictive elements of rail crossing.

Figure 5. Restrictive elements of rail crossing.

3.1. Methodical Procedure Proposal

However, in order to create a high-quality and unique methodology for the assessment of the rail crossings, it is necessary to analyze in detail and subsequently evaluate all the mentioned factors. For the purposes of this research, we focused on the factor “perspective ratios of the rail crossing” only. This factor can be considered one of the most important and significant, as it is often a decisive factor in rail crossing accidents. The mentioned ideas and outputs are based on publications [3,37] and studies [2]. Brainstorming methods, mind mapping methods and panel expert methods were mostly used in the creation of these factors. The main principles of FMEA and SFMEA methods were also used in the process.

The proposed procedure is also based on this intersection with some steps using exact methods or exact problem-solving procedures. The heuristic method and the system approach method are mostly used. The above procedure contains four theoretical partial “calculation” steps. The last step is a practical application. The proposed procedure is shown in Figure 6.

Figure 6. Methodical procedure of the perspective ratios determination.

Figure 6. Methodical procedure of the perspective ratios determination.

The specific description of particular item calculations is mentioned in the following subchapters. These subchapters contain several equations that were primarily derived and explained in the paper [3].

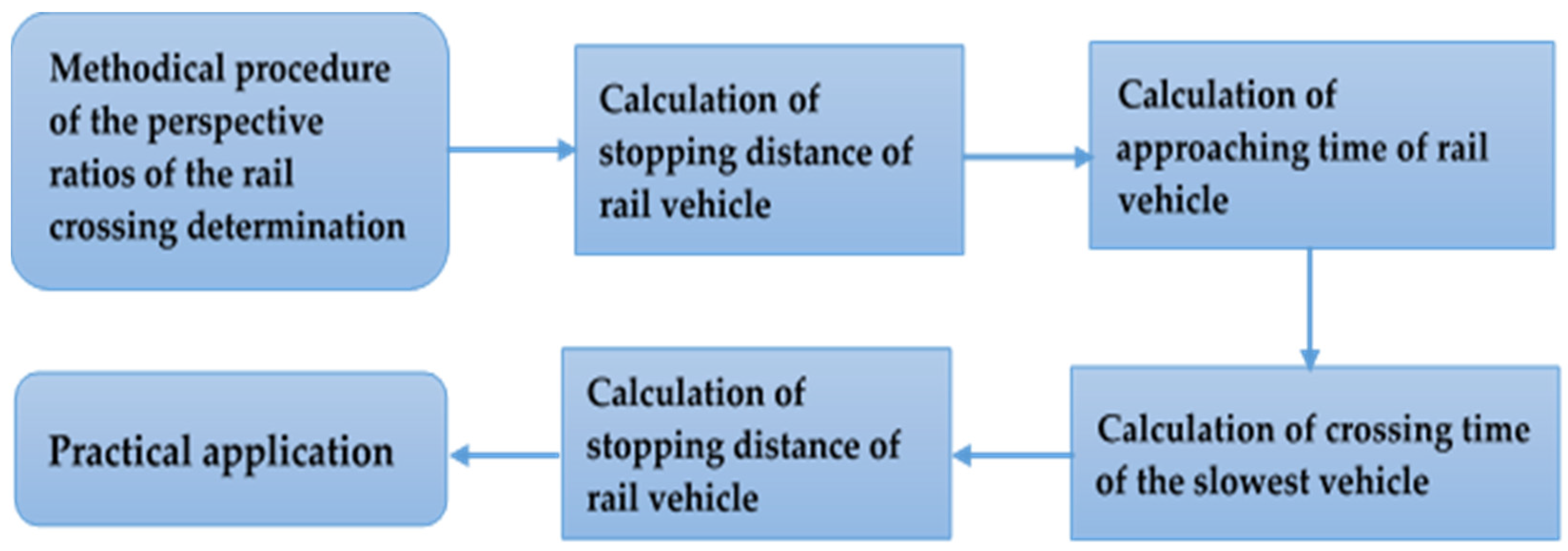
3.1.1. The Calculation of Stopping Distance of Rail Vehicle

The stopping distance of the rail vehicle can be calculated by using the following formula:

$$S=s_r · s_b · s_z\left[\mathrm{m}\right]$$

(1)

where:

• S—stopping distance of rail vehicle [m];
• s_r—travel distance of rail vehicle within the train driver’s reaction time [m];
• s_b—travel distance of rail vehicle within the rise time of braking effect [m];
• s_z—travel distance of rail vehicle from the rise time of braking effect to the point of stopping the vehicle [m].

It is necessary to calculate the following to fit the 1st equation. Acceleration of rail vehicle on the rise of braking effect (a_z) and afterwards (a_b)

$${\mathrm{a}}_{\mathrm{z}}=\mathrm{g} \ast \mathrm{\mu }[\mathrm{m}.{\mathrm{s}}^{-2}]$$

(2)

where:

• g—gravitational acceleration [m.s⁻²];
• µ—coefficient of usable adhesion [-].

Speed of rail vehicle after the rise of braking effect (v_z).

$$v_z=v_p-a_b · t_b[\mathrm{m}.{\mathrm{s}}^{-1}]$$

(3)

where:

• v_p—initial speed of rail vehicle [m.s⁻¹];
• a_b—acceleration of rail vehicle after the rise of braking effect [m.s⁻²];
• t_b—time of the rise of braking system [s].

Time from the point of rise of braking effect to the point of stopping the vehicle (t_z)

$$t_z=\frac{v_z-v_0}{a_z}\left[\mathrm{s}\right]$$

(4)

where:

• v_z—speed of rail vehicle after the rise of braking effect [m.s⁻¹];
• a_z—acceleration of rail vehicle on the rise of braking effect [m.s⁻²].

Calculation of individual distances:

$$S_r=v_p · t_r\left[\mathrm{m}\right]$$

(5)

$$S_b=v_p · t_b-\frac{1}{2} · a_b · t_b^2\left[\mathrm{m}\right]$$

(6)

$$S_z=v_z · t_z-\frac{1}{2} · a_z · t_z^2\left[\mathrm{m}\right]$$

(7)

where:

• t_r—train driver’s reaction time;
• t_z—time from the rise of braking effect to the point of stopping the vehicle.

After completing the default equation to calculate the stopping distance of the rail vehicle we obtain the following relation:

$$S=v_p · t_p+v_p · t_p-\frac{1}{2} · a_b · t_b^2+v_z · t_z-\frac{1}{2} · a_z · t_z^2\left[\mathrm{m}\right]$$

(8)

Possibility of avoiding the collision of vehicles by personal vehicle drivers

From this point of view, it is essential that the perspective ratios are sufficient to allow the slowest vehicle to safely pass through the crossing before the rail vehicle approaches at the line speed. Therefore, it is important to determine the approaching speed of the rail vehicle to the crossing on the condition that we take into account the viewing distance of the crossing and the speed at which the slowest personal vehicle crosses the railway crossing [38].

3.1.2. Calculation of Approaching Time of Rail Vehicle

Approaching time of rail vehicle can be calculated according to the formula:

$${\mathrm{T}}_{\mathrm{ž}}=\frac{s_r}{v_t}\left[\mathrm{s}\right]$$

(9)

where:

• s_r—viewing distance of the slowest vehicle;
• v_t—line speed.

3.1.3. Calculation of Crossing Time of the Slowest Vehicle

Crossing time of the slowest vehicle can be calculated according to the formula:

$${\mathrm{T}}_{\mathrm{s}}=\frac{s_p}{v_{nv}}\left[\mathrm{s}\right]$$

(10)

where:

• s_p—distance from the warning device to the external edge of the danger zone of crossing [m];
• v_nv—speed of the slowest vehicle [m.s⁻¹].

3.1.4. Calculation of Stopping Distance of Rail Vehicle

The calculation of stopping distance is based on the procedure according to Equation (1). For illustration, the input data are shown in

Table 2. Input values.

μ–Dry Surface	μ–Wet Surface	μ–Slippery Surface	g (m.s−2)	tr (s)	tb (s)	vp (m.s−1)
0.15	0.10	0.05	9.81	2	0.5	100

and there is a calculation introduced for the case of rail vehicles with a speed of 100 km/h on a dry track surface in

Table 3. Calculations.

az (m.s−2)	ab (m.s−2)	vz (m.s−1)	tz (s)	Sr (m)	Sb (m)	Sz (m)	S (m)
1.47	0.74	27.41	18.63	55.56	13.80	255.32	324.68

.

The distances for the purpose of stopping the rail vehicle at various speeds and with various coefficients of usable adhesion are given in

Table 4. Stopping distances of rail vehicles.

Speed of the Rail Vehicle		Surface Adhesion
km/h	m/s	Dry	Wet	Slippery
		0.15	0.10	0.05
10	2.78	8.83	10.16	14.12
20	5.56	22.97	28.24	44.01
30	8.34	42.35	54.19	89.65
40	11.12	66.99	88.01	151.05
50	13.89	96.76	129.56	227.91
60	16.67	131.89	179.11	320.76
80	22.23	217.89	301.86	553.75

.

The distances for stopping at 80 km/h speed are suggested in Table 4 which means that it is the line speeds at rail crossings that cover the topic of the research. It mainly concerns the maximum speeds available to rail vehicles at rail crossings and the maximum distance required for stopping. The other figures suggest speeds based on standard ČSN(EN) 63 73 80 that determine perspective ratios for the slowest vehicle [39].

3.2. Practical Application of the Methodology at Rail Crossing P5567

The mentioned methodological procedure must be practically applied to a specific rail crossing. A rail crossing P5567 in the southern part of the Czech Republic on the České Budějovice–Horní Dvořište railway line was chosen for both objective and subjective reasons. Crossing no. P5567 is a rail crossing equipped with a security device with lights and without railway barriers. It is situated on the 95th km of railway line no. 196 from České Budějovice to Horní Dvořiště. As well as the previous rail crossing, it is located between Velešín město railway stop and Velešín railway station. The rail crossing consists of the crossing of a single-track line with Road No. III/15536. The rail crossing is shown in Figure 7. The basic figures for rail crossings are in

Table 5. Rail Crossing No. P5567–basic figures.

Rail Crossing Number	P5567
Line No.	196
Line kilometer	95
Number of line tracks	1
Type of rail crossing	Light CSE without railway barriers
Number of collisions	0
Road type	3rd class road
Surface of the crossing track	Rubber panels

[40].

Approaching the crossing in the direction of Skřidla, drivers are informed about the arrival at the crossing by the A31a signal board and A30a “rail crossing without barriers” road sign, which informs drivers about the type of the rail crossing. Drivers can thereby see the rail crossing from this distance. The A31b signal board is located 160 m away from the crossing and the A31c signal board is 80 m away from the crossing, the distance from which drivers can clearly see the crossing. In the direction of Velešín, drivers are informed about the approaching crossing by the A31a signal board and the A30 “rail crossing without barriers” road sign, which also informs drivers about the type of rail crossing. A31b and A31c signal boards follow upon further approaching. Figure 7 also shows that neither from 80 m can a driver clearly see the rail crossing. As a matter of fact, a safe view of the warning sign is not possible as far as 33 m. For that reason, the warning sign is located not only on the right but also on the left side of the road [3,41].

Table 6. Basic parameters of Crossing No. P5567.

Line Speed	80 km/h
Length of crossing	4.2 m
Width of crossing	5.3 m
Warning signs distance–Skřidla direction	4.9 m
Warning sign distance–Velešín direction	4.8 m
Distance from the warning sign to a further border of the dangerous zone–Skřidla direction	6.6 m
Distance from the warning sign to a further border of the dangerous zone–Velešín direction	6.5 m

shows that the line speed of rail vehicles at the rail crossing point is determined to be 80 km/h. The width of the rail crossing and the distance of warning signs is highlighted green in the table in order to comply with the statutory requirements. Requirements for other parameters are not clearly set by the law. The possibility of avoiding collisions by the car driver can be assessed in regard to perspective ratios and figures in Table 4, which determine the stopping distance of the rail vehicle at different speeds and the condition of the rail surface. Comparing figures from the table and specific perspective ratios, we can identify whether the car driver is able to stop the rail vehicle before the crossing [3].

3.2.1. Possibilities of Avoiding Collisions in the Direction of Horní Dvořiště

Possibilities of avoiding collisions by the car driver of the rail vehicle are suggested in

Table 7. Possibilities of avoiding collisions at crossing P5967 in the direction of Horní Dvořiště.

Speed of the Rail Vehicle km.h−1	Surface Adhesion
	Dry	Wet	Slippery
	0.15	0.10	0.05
	Stopping of the Rail Vehicle
10	Yes	Yes	Yes
20	Yes	Yes	Yes
30	Yes	Yes	Yes
40	Yes	Yes	Yes
50	Yes	Yes	Yes
60	Yes	Yes	Yes
80	Yes	No	Yes

.

Table 7 suggests if the rail vehicle is moving at 80 km/h of the maximum line speed, the car driver would not be able to stop it before the rail crossing on time in case of a slippery rail surface. In other cases, the car driver would be able to stop the rail vehicle before the rail crossing on time.

3.2.2. Possibilities of Avoiding Collisions in the Direction of České Budějovice

Possibilities of avoiding collisions by the car driver of the rail vehicle are suggested in

Table 8. Possibilities of avoiding collisions at crossing P5967 in the direction of České Budějovice.

Speed of the Rail Vehicle km.h−1	Surface Adhesion
	Dry	Wet	Slippery
	0.15	0.10	0.05
	Stopping of the Rail Vehicle
10	Yes	Yes	Yes
20	Yes	Yes	Yes
30	Yes	Yes	Yes
40	Yes	Yes	Yes
50	Yes	Yes	Yes
60	Yes	Yes	Yes
80	Yes	Yes	No

according to the line rail vehicle speed.

Table 8 indicates that neither in the opposite direction to České Budějovice would the car driver be able to stop the rail vehicle moving at 80 km/h of the maximum line speed only in the case of a slippery rail surface. In other cases, the car driver would be able to stop the rail vehicle before the rail crossing on time [3].

3.2.3. Possibility of Avoiding Collisions by the Passenger Vehicle Driver at Crossing P5567

The possibility of avoiding collisions by the driver of a passenger vehicle can be again assessed in regard to the time for the approach of the rail vehicle and the crossing time of the slowest vehicle. Calculated values regarding the methodology are shown in the table. The assessment of the possibility of avoiding collisions by the driver of the road vehicle is suggested in

Table 9. Security of perspective ratios for drivers of road vehicles at crossing P5569.

Direction of the Vehicle	Direction of the View	Sr [m]	Ts [s]	Tz [s]	Security of PerSpective Distance
Velešín	Horní Dvořiště	56 m	4.680 s	2.52 s	No
	České Budějovice	34 m		1.53 s	No
Skřidla	Horní Dvořiště	373 m	4.752 s	16.785 s	Yes
	České Budějovice	71 m		3.198 s	No

.

Table 8 suggests that the distance of perspective ratios is quite insufficient except in one case. This exception indicates the situation when the driver of the road vehicle is moving in the direction of Skřidla and the rail vehicle is reaching the rail crossing from Horní Dvořiště. Thanks to the sufficient perspective ratios, the driver of the road vehicle can either safely cross the rail crossing or wait in case of an approaching rail vehicle and thereby avoid the collision. In that respect, other perspective ratios are wholly insufficient and thus the driver can be in danger of collision even if he did not notice an approaching rail vehicle upon his arrival at the rail crossing [3].

4. Discussion

The contribution was primarily focused on the perspective ratios determination on the rail crossings. The basic goal is primarily to increase safety and reduce accidents at rail crossings at this potentially dangerous point. However, achieving increased safety and quality also depends on other important factors. The possibility of avoiding a collision of vehicles at the rail crossing by the train driver depends on the early observation of the obstacle on the rail crossing and the stopping of the rail vehicle before this obstacle. Whether the train driver can stop the vehicle in time depends mainly on the driver’s perspective ratios and the braking distance of the rail vehicle. In terms of the rail crossings, the train driver’s perspective ratios are determined by the length of his or her clear view of the rail crossing. These ratios are not precisely specified, but the line speed can be adjusted with respect to these ratios at the crossing point). The stopping distance of the rail vehicle is the distance that the rail vehicle covers from the moment when the obstacle is noticed at the rail crossing until the vehicle stops [42].

The length of this distance is significantly influenced by the low coefficient of usable adhesion on the braking of rail vehicle, which is due to the low rolling resistance during the movement of the steel wheel on the rail. The adhesion coefficient values of rail vehicles may vary from 0.05 to 0.15 depending on the condition of the track surface. The fundamental influence on adhesion value is the speed of the vehicle and the contact surfaces of the wheel and rail. Apart from usable adhesion, the stopping distance depends on the starting speed of the rail vehicle, gravity acceleration, train driver reaction time, and rise time of braking effect.

The level of securing a rail crossing is within the competence of ŽSR, but it also falls within the competence of state administration and traffic police. The increase in the security level shall be assessed according to local conditions, the road and rail transport frequency, whether it is a major or minor road, a major or minor line, sighting conditions, and the occurrence of rail crossing accidents are also taken into account.

Several interesting facts were identified in this research. For example, when analyzing the possibility of avoiding a collision by the engine (car) driver, it was found out that even undisturbed perspective ratios do not have to be sufficient to prevent a collision of the rail vehicle with an obstacle at the rail crossing at high line speeds and the low coefficient of useful adhesion. In such cases, the distance needed for stopping the vehicle is too long for the car driver to be able to identify the obstacle at the crossing and start braking. The lower the line speed is and the higher the coefficient of the useful adhesion is, the more influential perspective ratios are on possibly avoiding a collision by the car driver at the rail crossing. However, considering high speeds and low coefficient of useful adhesion, perspective ratios still play a very important role. The sooner the car driver identifies the obstacle, the lower the speed of the vehicle will be and thereby the consequences of the collision will be less fatal.

Based on the above information, it can be stated that there are several ways to increase safety at rail crossings by improving the visibility conditions and perspective ratios. Based on the above information, it can be concluded that there are several ways to increase safety at rail crossings by improving visibility conditions. This paper presents a scientific way of solving this problem, which consists of the design of a methodological (heuristic) procedure, using certain scientific methods. Within this procedure, individual steps are defined, which are based on standard physical and mathematical methods. The article offers one possible way to solve this problem, but it is not the only possible way. The benefit of the article for the readers is to get to know new scientific procedures and outputs in the field of transport process science. The practical application of this methodology is also a very important and useful output [43].

5. Conclusions

The paper analyzes the current state of rail crossings and the trend of their number in Europe. The main goal of the contribution was to analyze the factors influencing the rail crossing potential and restrictive elements factors of the rail crossings. Significant emphasis is placed on the perspective ratios as a key safety factor. The heuristic procedure of the perspective ratios determination was presented within the proposals. Subsequently, the perspective ratios at the selected rail crossing were analyzed.

All the above facts and outputs are the subject of further research and more detailed development of this issue. They will certainly be the subject of further scientific and research work by the authors. This issue is relevant and actually due to the high frequency of traffic accidents at rail crossings, and it must be further developed in the future. It will be necessary, especially in the context of the ever-increasing share of road transport in the transport market and the increasing speed of individual transport flows. It will require a comprehensive solution to meet the requirements of quality, ecology, economy, fluidity and especially safety transport system. Only by coordinating the steps taken by the railway operators, the infrastructure managers, the police force, and the relevant state authorities can overall improvements in the development of safety at rail crossings be achieved.