Study on Share Rate of Support Structure for Super-Large Span Twin Tunnels with Small Interval

Abstract

Super-large span twin tunnels, which can relieve traffic burden and improve the efficiency of roads, have been rapidly popularized in urban construction. Hence, it is very important to master the share rate of support structure in this sort of tunnel correctly. In this paper, some field monitoring and numerical simulation work has been carried out in such a tunnel in Daling, China. The content of field monitoring consisted of the vault settlement, stress of the concrete, and the sum pressure. Firstly, the calculation formula of rock pressure in this kind of tunnel had been deduced, which was based on the theoretical sliding failure mode. Then, the calculated rock pressure was applied to the load structure model step by step with 10% intervals (10%, 20%, …). By comparing the monitoring and the simulation results on vault settlement, the share rate of the primary support was ensured to be 40%. Similarly, by comparing the result on safety factors, the share rate of the secondary lining was obtained (40%). The remained load was born mainly by the surrounding rock itself and the advanced support. Finally, the reliability of the results were verified by the sum pressure. This paper can provide reference for the effective design of support structure in super-large span twin tunnels.

1. Introduction

Recently, with the proceeding of urbanization, the demand from traffic is surging. As a result, the need for improving the capacity of the transportation system, specifically the cross section of tunnels in cities, is getting larger to contain four or more lanes [1]. The tunnels with large-span cross section, however, are usually oblate with a small rise-span ratio, which is challenging to design them in a safe and reliable way. At the same time, on the limitation of land resources and route optimization, twin tunnels with small intervals are becoming more usual at the portals, whose mechanical behaviour is much more complicated than ordinary tunnels.

There are many studies on large-span tunnels and ordinary twin tunnels, respectively. In terms of large-span tunnels, Feng Jimeng [2] evaluated the different installation timing of initial ground support for large-span tunnel in hard rock. Hou Fujin [3] and others [4,5,6,7] studied the excavation (drill and blast) and construction of large-span tunnels and mechanical characteristics of primary support. Li Shucai [8] used hydro-mechanics to research the influence of groundwater on the surrounding rock of large-span tunnels.

As for the ordinary, Chortis, F. [9] quantifies the interaction effect and preliminarily estimates the main support requirements of twin tunnels based on the stress state of a single tunnel, and provided nomographs for preliminary assessments of the optimum spacing between twin tunnels. Vinod and others [10,11] also studied the influence of shape and interval on twin tunnels and sandwiched rock. Boon Chiaweng [12] researched the mechanics performance of a twin arch tunnel under different rock covers. Golshani and others [13,14,15] found a method for selection of optimum distance between tunnel tunnels under different conditions. He Chao and others [15] studied the vibration of twin tunnels and found that certain factors (such as the soil and the interval) can affect it. Khabbaz and others [16,17,18,19,20] researched and monitored the twin tunnels under different conditions. Bai Bing and others [21,22,23,24,25,26,27,28] have studied the interaction between the law of rock and soil and structural characteristics of constructions. Besides, Li Pengfei and others [29,30,31] studied the surrounding rock pressure of deep twin tunnels. And Zhong Zuliang and others [32,33,34] researched the rock pressure of shallow-buried twin tunnels.

Nonetheless, for large-span twin tunnels there are few studies regarding it. Cui S. [35] analysed the mechanical mechanism of highway tunnels with large span and small spacing during the construction and found that large-span twin tunnels were hard to construct, depending on the excavation area, the thickness, and the attributes of the sandwiched rock and the terrain.

The engineering of super large-span twin tunnels, which can contain eight lanes or more, is not usual at home and abroad. Although the total load of surrounding rock is almost explicit nowadays, its distribution law of surrounding rock pressure as well as the share rate of every part of the retaining structure has not yet been considered clearly. However, designs of primary support and secondary lining are respective, so finding out each part’s specific share rate of load is logical for design and construction of actual engineering project. Therefore, in this paper, based on the theory of stratigraphic sliding failure mode and the outcome of monitoring and measurement in the Daling tunnel (twin tunnels, four lanes in each hole), the distribution law of surrounding rock pressure and the share rates of advance support, primary support, and secondary lining are studied. Eventually, by comparing and analyzing the theory and practical results, the correctness of the research method is ensured, which can provide reference for the design and optimization of the retaining structure of super large-span twin tunnels, especially 8-lane (or more) twin tunnels in cities.

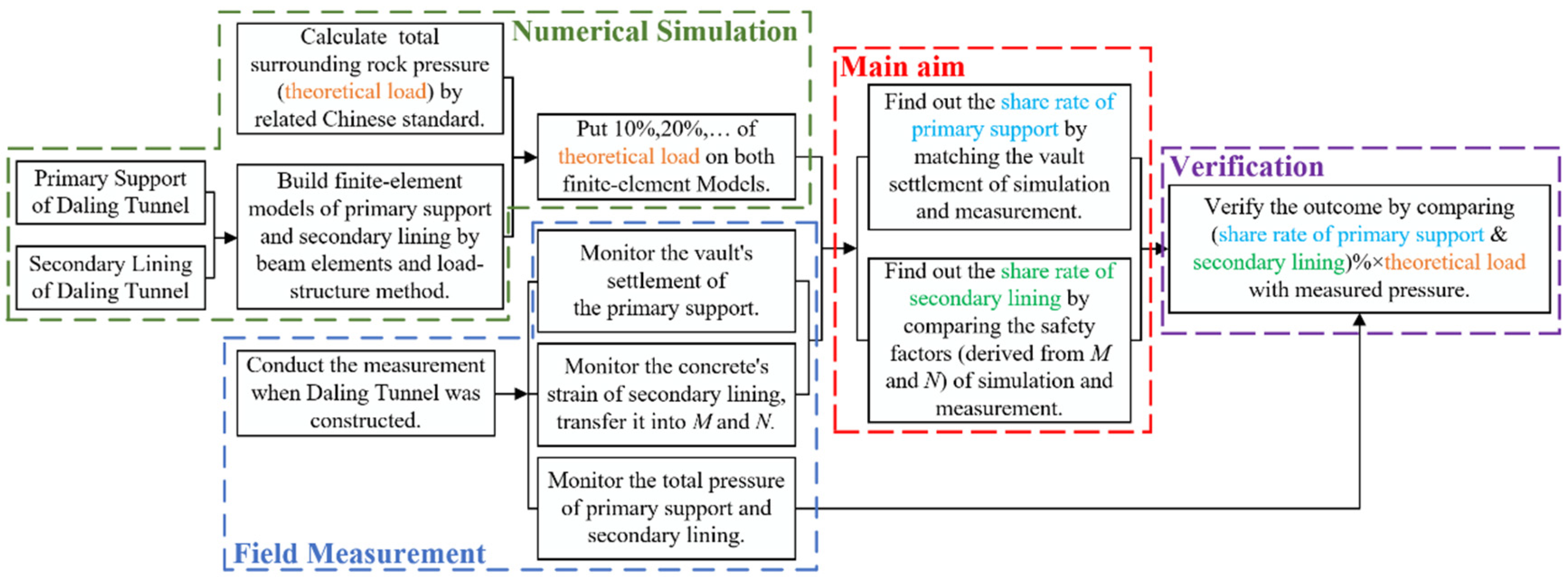
2. Methodology

The aim of this research is to find the share rate of the support structure for twin tunnels with super-large span, especially the primary support and the secondary lining. Therefore, the outcomes of numerical simulation and field measurement are compared and the conclusion is verified. In this paper, Daling Tunnel in Jinan City was simulated and monitored for achieving the goals. The whole process is shown in Figure 1.

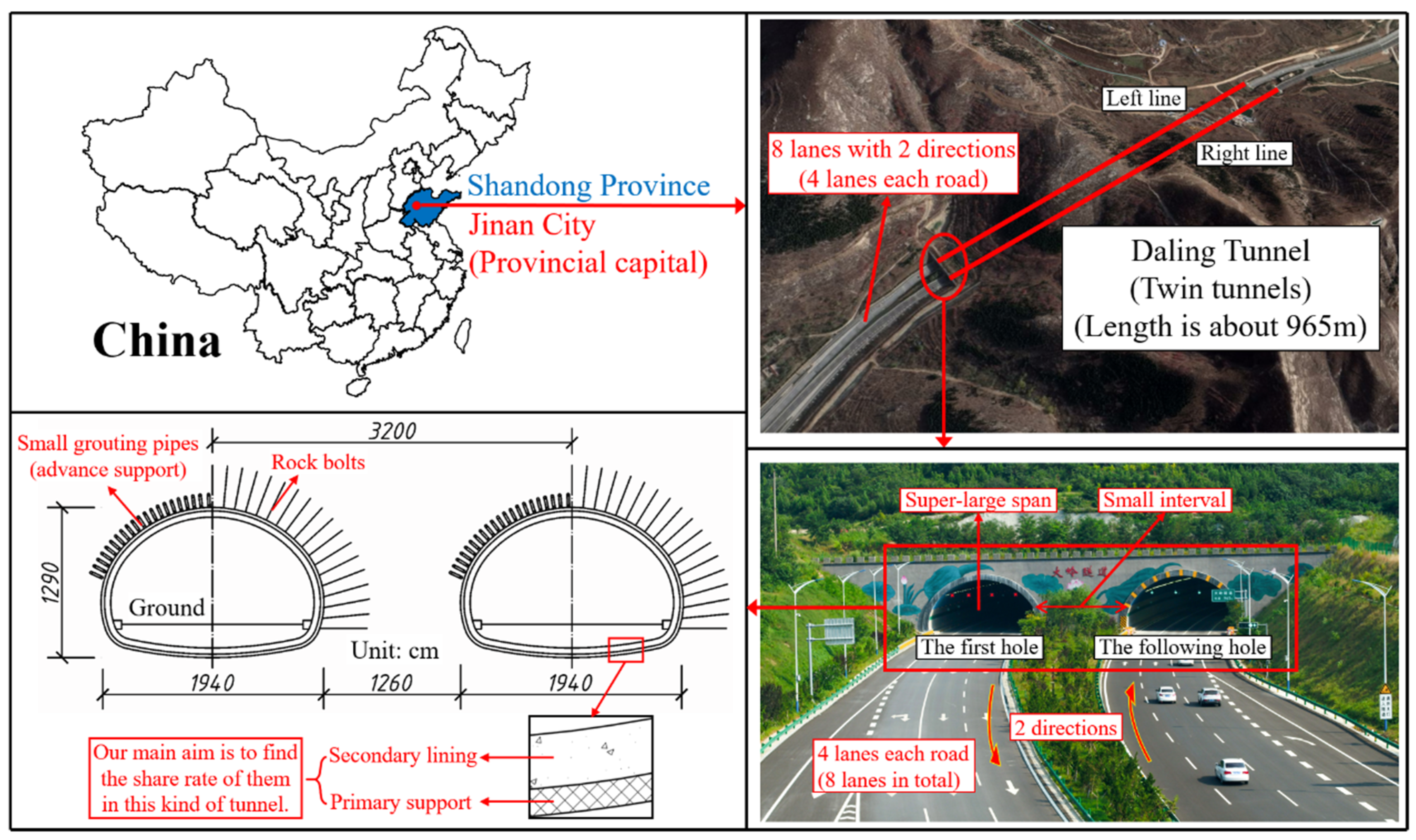
2.1. Daling Tunnel

Daling Tunnel, located in the southeast of Jinan City, is a twin tunnel with a super-large span cross section, which was monitored in this research. This twin tunnel contains 8 lanes (4 lanes each) with a design speed of 80 km/h, which has great capacity in transportation. The height of the twin tunnel is 12.9 m and the span is 19.4 m. Additionally, the net distance between the twin tunnel is 12.6 m.

Daling Tunnel was excavated by the drill-blast method and supported by the composite lining, which consisted of primary support and secondary support. Furthermore, the whole construction process of this tunnel adhered to the principles of NATM. In terms of the composite lining, the primary support included C25 shotcrete, welded-wire fabric reinforcement, steel arches, and hollow rock bolts (used for grouting and reinforcing). The secondary lining is made mainly of the cast-in-place reinforced concrete (C30). Furthermore, the advance support mainly consists of supporting sheds and small grouting pipes. The information of Daling Tunnel is shown in Figure 2.

The cross section of Daling Tunnel we measured and monitored is Level-V surrounding rock [1], which is partly soft and cracked. The related physical parameters are shown in

Table 1. The related parameters of Daling Tunnel.

Parameter	Value
Unit weight, $\gamma$ (kN/m3)	20
Simplified internal friction angle, ${\phi }_c$	45°
Real internal friction angle, $\phi$	22°
Friction angle of the sliding plane, $\theta$	13.2° ($0.6\times \phi$)
Span, B (m)	19.4
Height, Hl (m)	12.9
Net interval, D (m)	12.6
Buried depth, H (m)	20

.

2.2. Theoretical Load

Firstly, we need to assume that the load’s distribution of the super-large span twin tunnels is similar to the normal tunnel, which can be calculated referring to the standard [1]. Then, via the initial formulas of related Chinese standard and various deductions, the total surrounding rock pressure (theoretical load) of the twin tunnels was assured. The details of the calculation and deduction are shown in Section 3.

Next, all the parameters were put into the formulas in Section 3, and the results are shown in Figure 3. In Figure 3, the surrounding rock pressure of the first hole (the hole excavated firstly) and the following hole (the hole excavated later) was symmetric. For this reason, in the following, the analysis will focus on the first hole, while the following hole will be skipped.

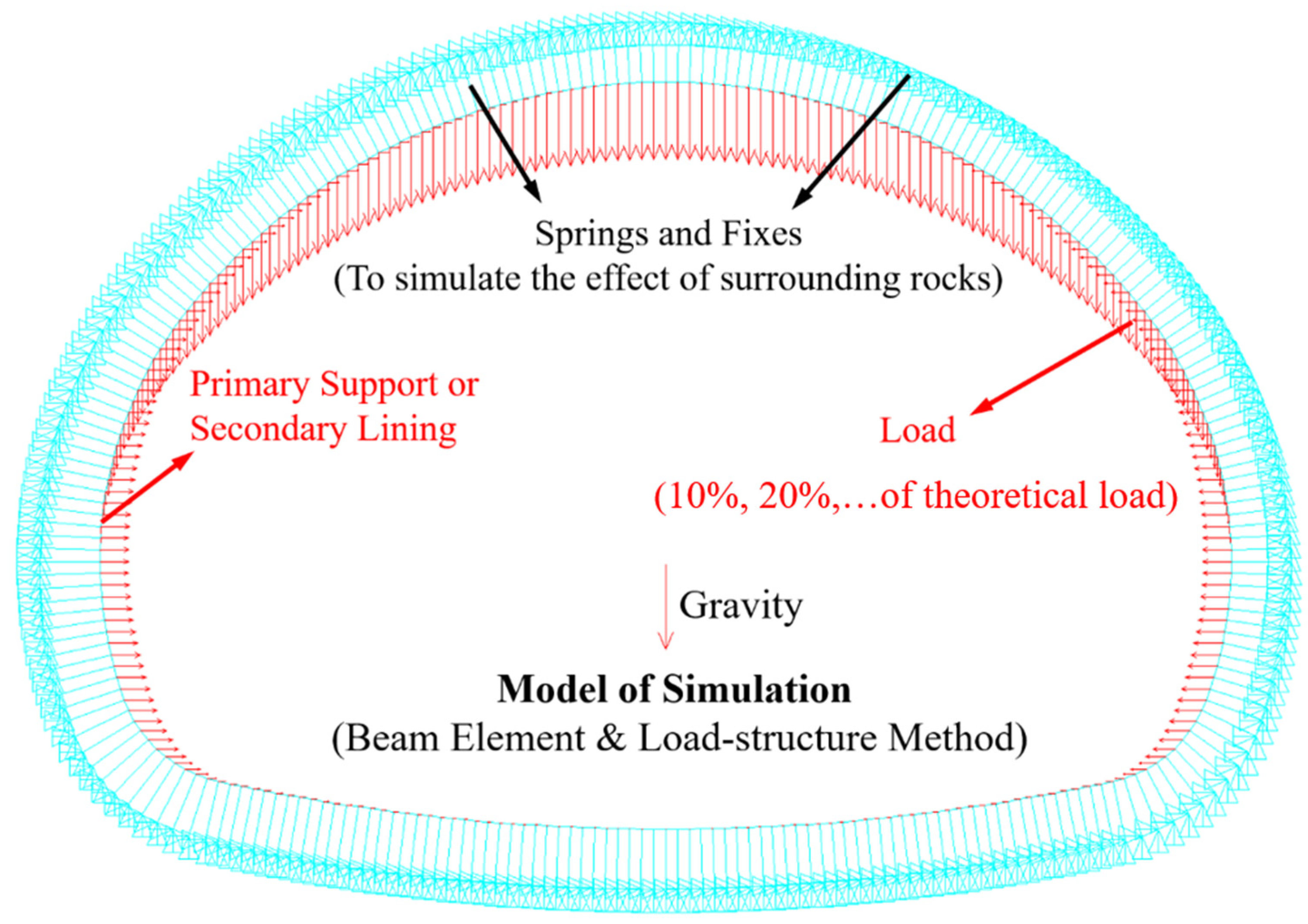
2.3. Finite-Element Model

In this paper, to find out the share rates of support structure, numerical simulation was used for matching the results of field measurement. ANSYS, a powerful finite-element software, was used to build simulation models of primary-support and secondary-lining models of Daling Tunnel, which were both built by beam elements (Beam 3). This is a kind of 2-D element, which has 3-degrees of freedom on each node and can endure axial tension or compression. The parameters of primary support and secondary lining are shown in

Table 2. The parameters of primary support and secondary lining.

Part	Young’s Model /GPa	Poisson’s Ratio	Unit Weight /kN/m3	Thickness /m
Primary Support	25.3	0.2	25	0.3
Secondary Lining	28	0.2	25	0.7

.

As for the boundary conditions, the springs were built by link elements (Link 10) and used to simulate the effect of the surrounding rock. Link 10 is a kind of 3-D two-node element, which has 3-degrees of freedom on each node. Considering the mechanics characteristics of the surrounding rock, these springs were set to only be compressed. Furthermore, the bases of springs were completely fixed. According to the parameters of surrounding rocks in Table 1, the length and elastic module of springs are 0.2 m and 200 MPa, respectively.

In terms of load, the form and direction of load is the same as the theoretical load (shown in Figure 3). Furthermore, the value of load is a portion (10%, 20%, …) of the theoretical load. Moreover, the gravity is 9.8 m/s² downward and applied to all elements. The model is shown in Figure 4; (Since the models of the primary support and secondary lining are similar, only one model is shown as an example.)

2.4. Field Measurement

In this research, three items were monitored in the first hole of Daling Tunnel. The arrangement of measure points is shown in Figure 5. In Figure 5, the rock bolts are omitted.

(1)

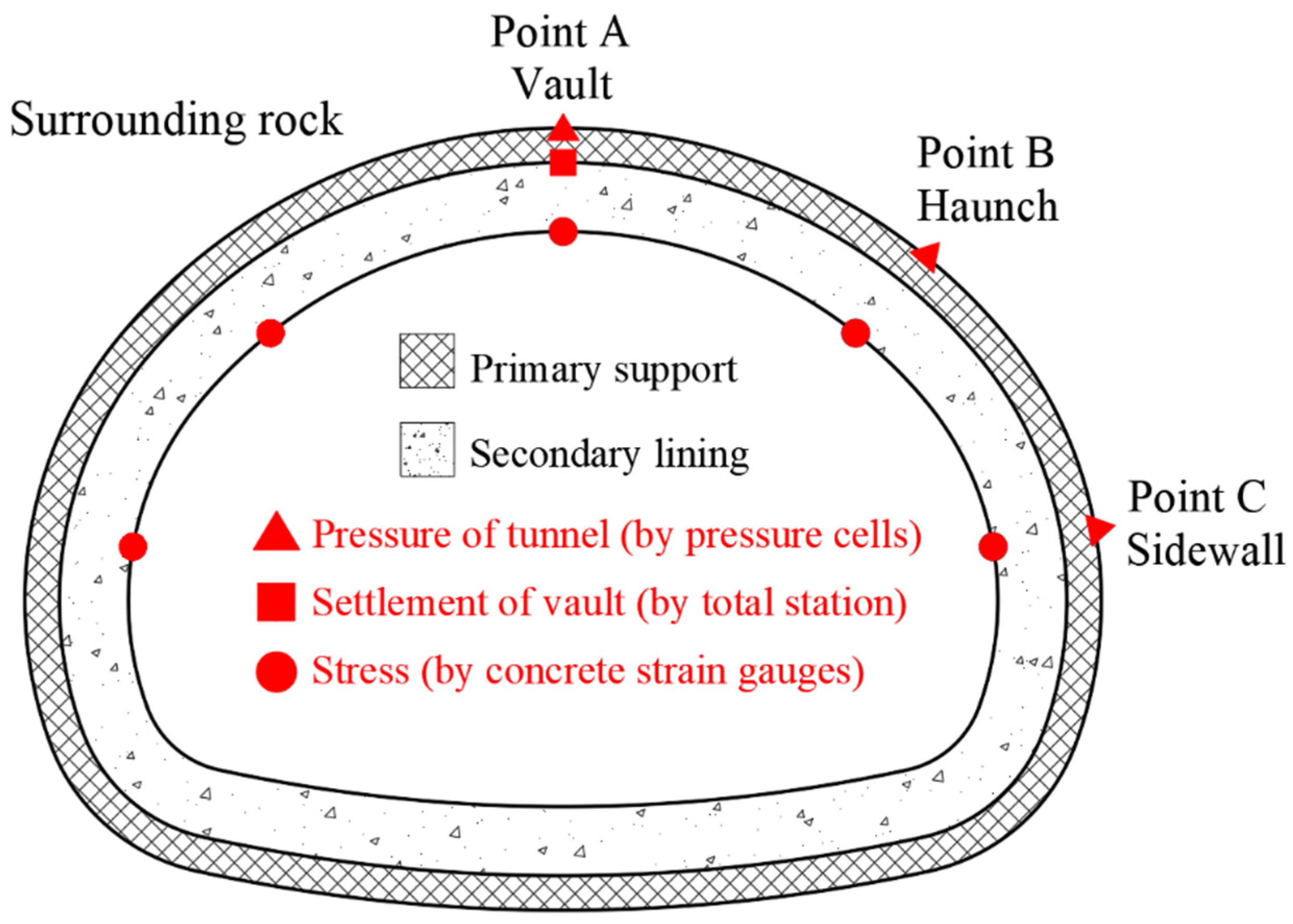
Settlement of the vault of primary support was measured by total stations and steel rulers to find out the share rate of primary support.

(2)

Stress of the secondary lining (derived from the strain) was measured by concrete strain gauges. The gauges were put on both sides of the secondary lining at each point. This is for finding out the share rate of secondary lining. The arrangement of concrete strains is shown in Figure 6.

(3)

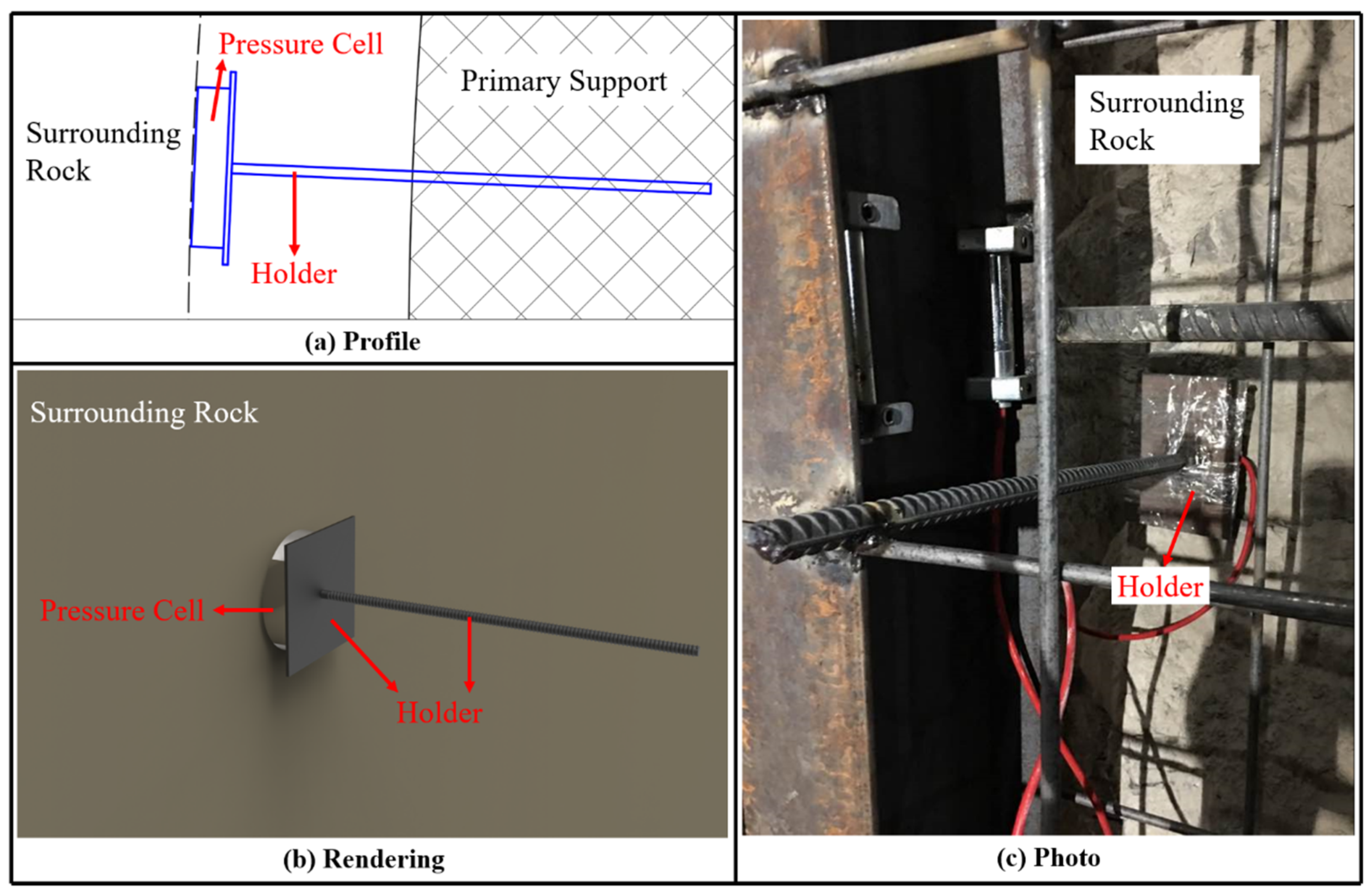
Total pressure of the primary support and secondary lining was measured by pressure cells arranged at the points A, B, and C at the outside of the primary support. This is for comparison and verification. The arrangement of pressure cells is shown in Figure 7.

3. Theoretical Calculation of Surrounding Rock Pressure

3.1. Failure Mode and Assumptions

In Chinese standard [1], the method of calculating surrounding rock pressure of normal tunnels (usually including two or three lanes) is given. This method can be generalized to super-large span twin tunnels (four lanes each hole, wider than a normal tunnel). The failure mode, necessary assumptions, and theoretical method are introduced below.

The theoretical sliding failure mode of the surrounding rock of the twin tunnels is shown in Figure 8. W₁, W₂, and W₃ are the gravity of the rock mass A’C’E’ (ACE), IKOM, and I’KOM’, respectively. T₁ and T₂ are the frictional force caused by the soil on both sides of the tunnel to resist the settlement of the vault. Furthermore, ${\phi }_c$ is the simplified internal friction angle of the surrounding rock. According to the Chinese standard, ${\phi }_c$ is usually greater than the real internal friction angle ($\phi$). When using ${\phi }_c$, it is valid regardless of the cohesion force). $\theta$ is determined by referring to the Chinese standard. Here are some explanation and hypotheses for this sliding failure mode:

(1)

Suppose that the ground was horizontal, the rock mass was homogenous, and isotropic and the twin tunnel was symmetry and parallel. Moreover, excavation of left and right holes is sequent and full section.

(2)

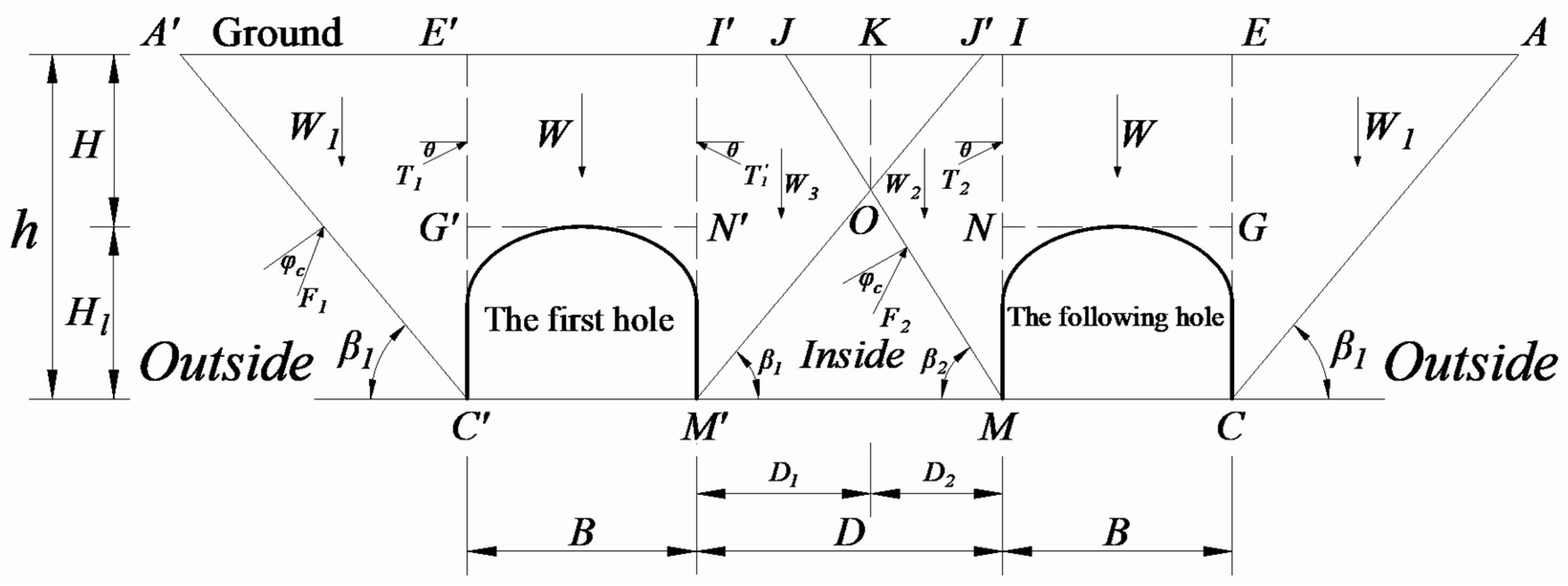
The excavation of the first hole is similar to an ordinary single-hole tunnel. It means that the fracture planes on both sides of the first hole, which are shown as A’C’ and M’J’ in Figure 8, are two inclined straight planes, and at an angle of ${\beta }_1$ to the horizon. In addition, the pressure inside and outside (shown in Figure 8) is symmetric.

(3)

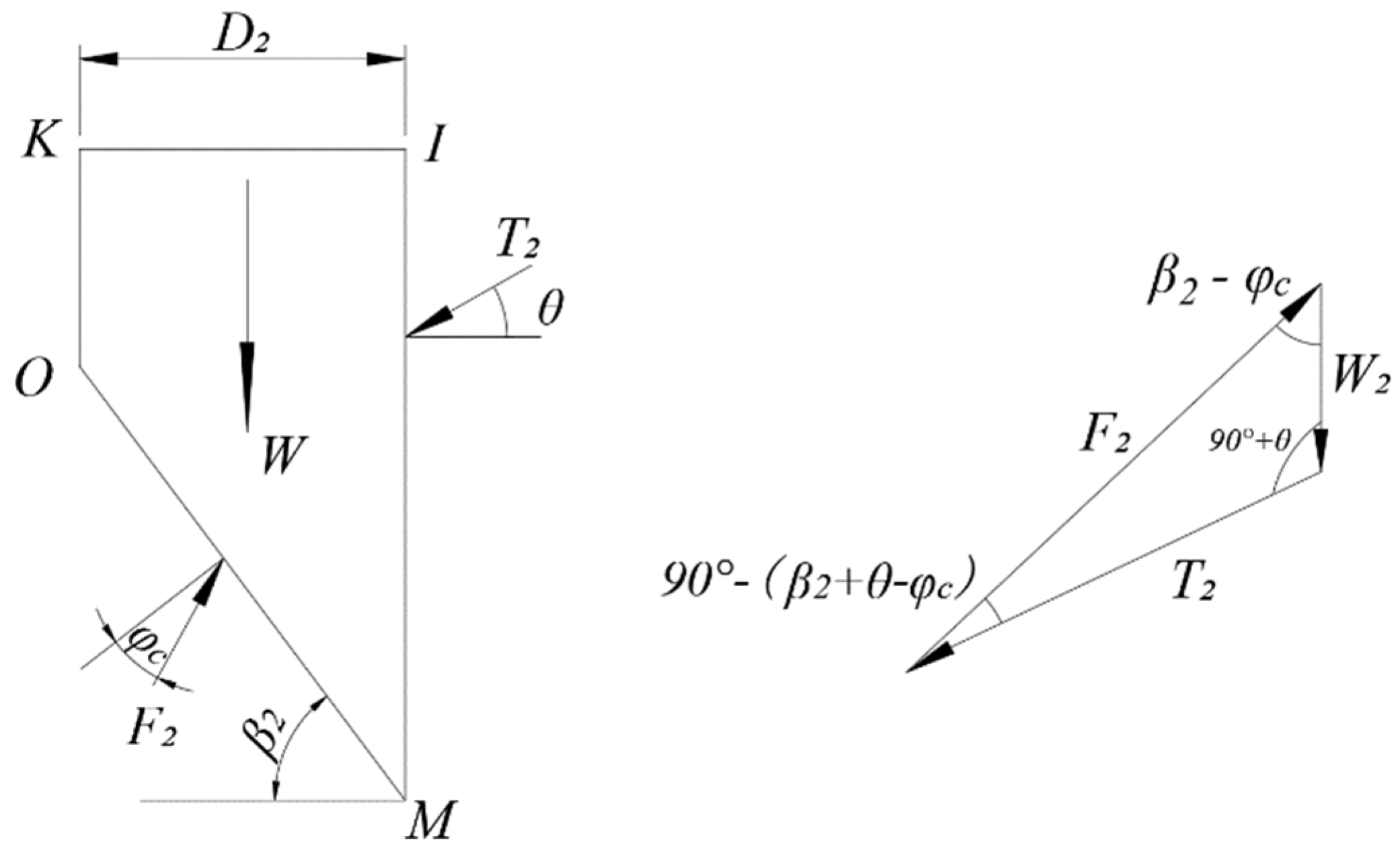
When the following hole is excavated, the fracture plane at the outside of the hole (AC) is at angle ${\beta }_1$ to the horizon, while at the inside of the hole the angle of the fracture plane (MO) is assumed as ${\beta }_2$. Focus on the triangle OJJ’, when the following hole is excavated, it is inclined to slide down along the plane JM. However, since the excavation of the first hole has induced a relative slippage at the plane OJ’ and undermines the cohesion force along the plane OJ’, usually the triangle OJJ’ will not slide and fracture along the plane JO. Instead, the tensile fracture plane will be formed in the triangle OJJ’, which is assumed as a vertical plane (OK). In summary, the fracture plane at the inside of the following hole is assumed as KOM.

(4)

According to the sliding trend of the triangle OJJ’ caused by the sequent excavation of the twin tunnel, and based on the theory of soil mechanics, the interactive force (N) in normal direction at the fracture plane OK must be less than the earth pressure at-rest. For safety, let N equal 0.

3.2. Calculation of Theoretical Load

(1) Surrounding rock pressure of the first hole

Assume that the left hole is the first hole and excavated firstly. Since it is the same as an excavation of a single hole, the formula in the Chinese standard can be adopted to calculate the vertical pressure and the lateral pressure on the outside of the first hole. It is shown as follows:

The formula for calculating the lateral-pressure coefficient (${\lambda }_1$) is:

$${\lambda }_1=\frac{\tan {\beta }_1-\tan {\phi }_c}{\tan {\beta }_1\left[1+\tan {\beta }_1\left(\tan {\phi }_c-\tan \theta \right)+\tan {\phi }_c\tan \theta \right]}$$

(1)

$\tan {\beta }_1$ can be inferred from $\tan {\phi }_c$ and $\tan \theta$:

$$\tan {\beta }_1=\tan {\phi }_c+\sqrt{\frac{\left({\tan }^2{\phi }_c+1\right)\tan {\phi }_c}{\tan {\phi }_c-\tan \theta }}$$

(2)

The lateral pressure of the first hole ($e_i$) is:

$$e_i={\lambda }_1\gamma h_i$$

(3)

where $h_i$ represents the depth of the calculation position and $\gamma$ means the unit weight of the rock.

Hence when the first hole is excavated solely, the vertical pressure on the vault of the hole (q) is:

$$q=\frac{Q}{B}=\gamma H(1-\frac{H}{B}{\lambda }_1\tan \theta )$$

(4)

where B is the span of the hole, Q is the total vertical load on the hole and H is the depth of the vault of the hole.

(2) Surrounding rock pressure of the following hole

When it comes to the right hole (the following hole), the lateral pressure outside of the following hole is the same as the first hole. For calculating the lateral pressure inside of the following hole, a force analysis is carried out on the rock mass IKOM, as shown in Figure 9.

According to the basic mechanics and assumptions above, the force $T_2$ can be solved as:

$$T_2=\frac{\sin \left({\beta }_2-{\phi }_c\right)W_2}{\sin \left[{90}^{°}-\left({\beta }_2+\theta -{\phi }_c\right)\right]}$$

(5)

where $W_2$ denotes the weight of the rock mass IKOM:

$$W_2=\frac{1}{2}\gamma D_2(2h-D_2\tan {\beta }_2)$$

(6)

Seeing that the interval between the twin tunnels (D) is generally small enough, let $D_2=D/2$, approximately. With the Equation (6), the Equation (5) can be transformed into:

$$T_2=\frac{1}{2}\gamma h^2\frac{{\lambda }_2}{\cos \theta }$$

(7)

In the Equation (7), ${\lambda }_2$ is defined as the inside lateral-pressure coefficient of the following hole:

$${\lambda }_2=\frac{\frac{D}{h}\left(1-\frac{D}{4h}\tan {\beta }_2\right)\left(\tan {\beta }_2-\tan {\phi }_c\right)}{1+\tan {\beta }_2\left(\tan {\phi }_c-\tan \theta \right)+\tan {\phi }_c\tan \theta }$$

(8)

To make $T_2$ maximum, let $\frac{\mathrm{d}{\lambda }_2}{\mathrm{d}(\tan {\beta }_2)}=0$, therefore

$$\tan {\beta }_2=\sqrt{\frac{{\tan }^2{\phi }_c+1}{\tan {\phi }_c-\tan \theta }\left[\frac{1}{\tan \left({\phi }_c-\theta \right)}+\frac{4h}{D}\right]}-\frac{1}{\tan \left({\phi }_c-\theta \right)}$$

(9)

Then, the lateral pressure of the following hole ($e_2$) is:

$$e_{2i}={\lambda }_2\gamma h_i$$

(10)

It is mentioned above that q is defined as the vertical pressure on the vault, whereas the vertical pressure on the vault actually varies from inside to outside. Suppose that the vertical pressure was changing linearly inside and outside of the hole (define the vertical pressure outside is $q_1$ and the other is $q_2$, $q_1$, and $q_2$ can be expressed as:

$$q_1=\gamma H\left(1-\frac{H}{B}{\lambda }_1\tan \theta \right)$$

(11)

$$q_2=\gamma H\left(1-\frac{H}{B}{\lambda }_2\tan \theta \right)$$

(12)

When the following hole is being excavated, the lateral pressure on the outside of the first hole can be regarded as a static value, approximately. Then, for calculating the lateral pressure on the inside of the first hole, a force analysis is carried out on the rock mass I’KOM’. As well as $T_2$ (Equation (5)), T₂′ can be solved as:

$${T_2}^{\prime }=\frac{1}{2}\gamma h^2\frac{{{\lambda }_2}^{\prime }}{\cos \theta }$$

(13)

Similarly, ${{\lambda }_2}^{\prime }$ is defined as the lateral-pressure coefficient on the inside of the first hole when the following hole is being excavated:

$${{\lambda }_2}^{\prime }=\frac{\frac{D}{h}\left(1-\frac{D}{4h}\tan {\beta }_1\right)\left(\tan {\beta }_1-\tan {\phi }_c\right)}{1+\tan {\beta }_1\left(\tan {\phi }_c-\tan \theta \right)+\tan {\phi }_c\tan \theta }$$

(14)

$q_1,{q_2}^{\prime }$ are defined as the vertical pressure on the outside and inside of the first hole, respectively. They can be written in the form:

$$q_1=\gamma H\left(1-\frac{H}{B}{\lambda }_1\tan \theta \right)$$

(15)

$${q_2}^{\prime }=\gamma H\left(1-\frac{H}{B}{{\lambda }_2}^{\prime }\tan \theta \right)$$

(16)

Thus, the theoretical formulas for calculating the vertical pressure and lateral pressure of twin tunnels are deduced completely. Next, put all the parameters of Daling Tunnel into Equations (1)–(16), the total surrounding rock pressure (theoretical load) was gained, as shown in Figure 3.

4. Results and Discussion

Generally, the surrounding rock pressure can be mainly divided into three parts: The first part of it is relaxing or transferring to the advance support and the surrounding rock before constructing the primary support. The second and third parts are supported by the primary support (share rate of the primary support) and the secondary lining (share rate of the secondary lining), respectively. By the result of simulation, calculation, and monitoring the share rate of these three parts can be identified.

4.1. Share Rate of the Primary Support

10%, 20%, 30%, 40% … of the theoretical loads were put on the model gradually to match the measured displacement. When proportion of the theoretical load is 10%, 20%, 30%, 40%, etc., the vault settlement of the simulation model is 7.31 mm, 12.56 mm, 17.8 mm, 23.1 mm, respectively, which indicates that the vault settlement is growing as the load proportion is rising. Meanwhile, the measured vault settlement is shown in Figure 10a, which stabilized at 20.3 mm finally. In view of the lagging of the installation of the measuring device [36], the vault settlement of the model under 40% of the theoretical load (shown in Figure 10b) in accordance with the result of measurement. Consequently, share rate of the primary support is 40%.

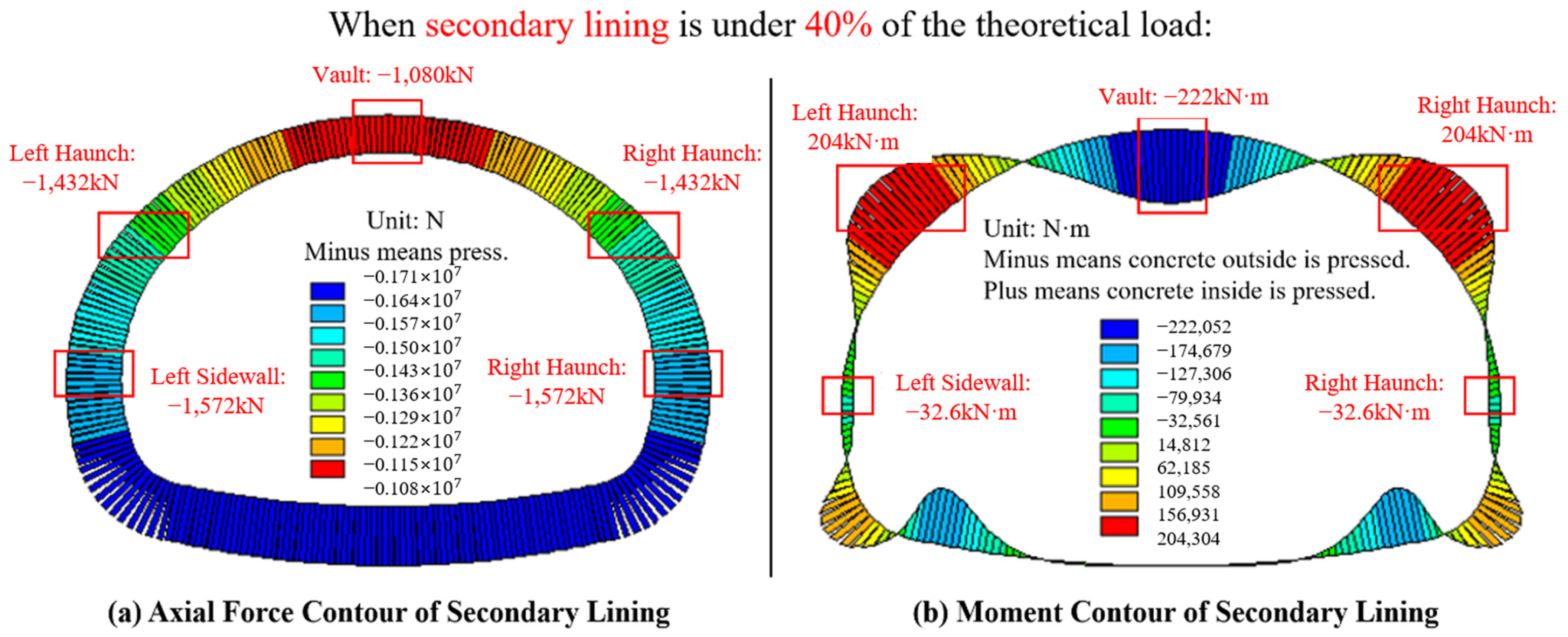
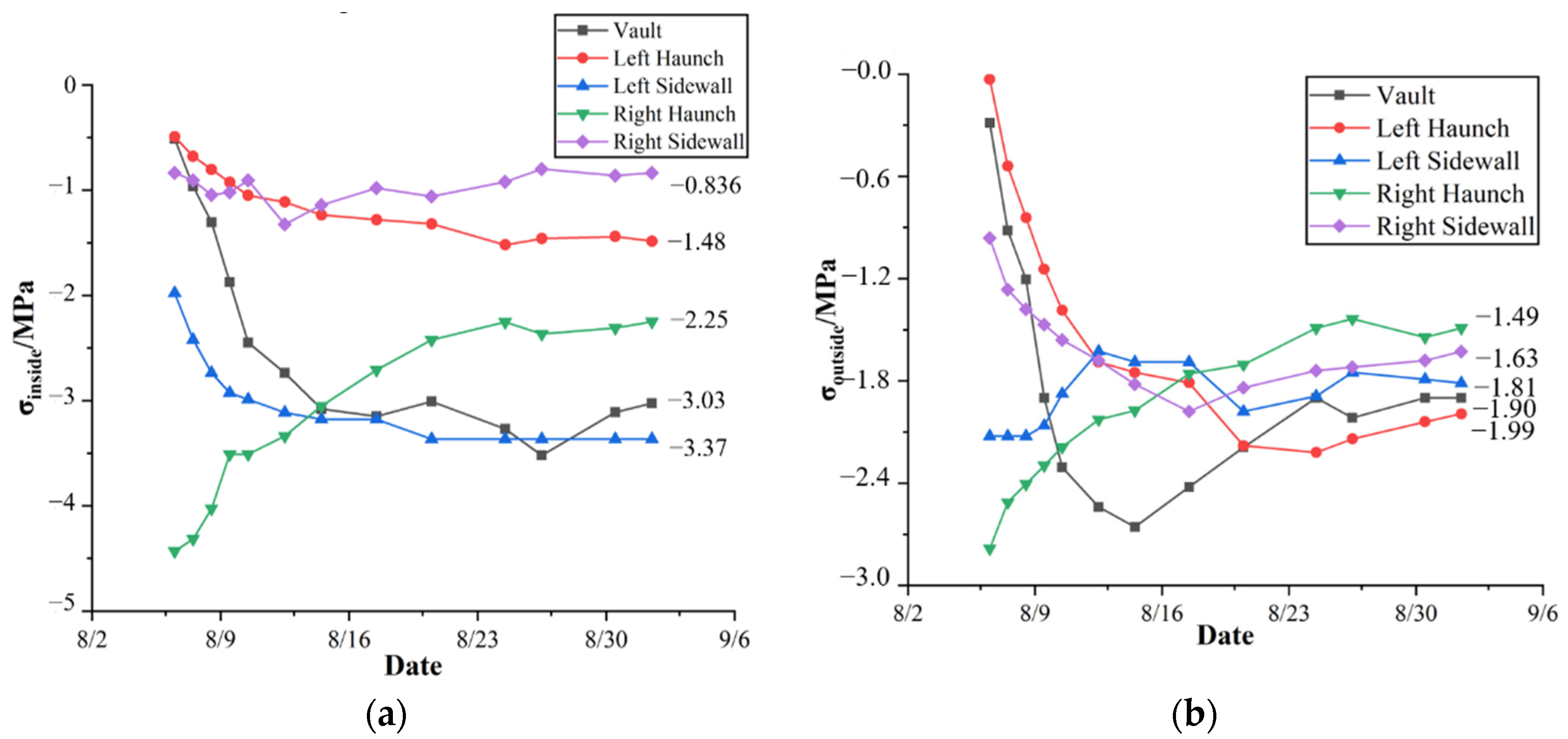
4.2. Share Rate of the Secondary Lining

Further, to find the share rate of the secondary lining, the internal forces of the simulation model were compared with the actual structure. It was found that after stepwise loading, when the load ratio was 40%, internal forces of the simulation model were in good agreement with the practical measurement. Internal forces (axial force and moment) of the simulation model under 40% of the theoretical load is shown in Figure 11a,b.

The measured concrete stress of the inside and outside secondary lining is shown in Figure 12.

According to the theory of mechanics of materials, the actual internal forces can be obtained by the measured stress with the formulas below:

$$N=A\times ({\sigma }_{\mathrm{inside}}+{\sigma }_{\mathrm{outside}})$$

(17)

$$M=\frac{I\times ({\sigma }_{\mathrm{inside}}-{\sigma }_{\mathrm{outside}})}{y}$$

(18)

where A (m²) is the area of the cross section, I (m⁴) is the moment of inertia of the section, y (m) is the distance between the neutral axis, and the edge, ${\sigma }_{\mathrm{inside}}$ (MPa) is the stress of the concrete at the side of the inner section and ${\sigma }_{\mathrm{outside}}$ (MPa) is the stress of the concrete at the side of surrounding rock.

Internal force was gained after putting the related parameters and stress into the formulas. Then, according to the Chinese standard [1] based on the internal force and the capacity of the concrete structure the safety factors were calculated. It is shown in

Table 3. The internal forces and safety factors of the secondary lining.

Item	Position	Axis Force /kN	Moment /kN·m	Eccentricity /mm	Attribute	Safety Factor
Simulation	Vault	−1080	−222	493	All is small eccentricity	9.47
	Left haunch	−1432	204	430		8.19
	Left sidewall	−1572	−32.6	308		10.41
	Right haunch	−1432	204	430		8.19
	Right sidewall	−1572	−32.6	308		10.41
Measurement	Vault	−1723	−53	318		7.85
	Left haunch	−1216	24	307		11.54
	Left sidewall	−781	71	378		14.0
	Right haunch	−1348	−36	314		10.17
	Right sidewall	−862	38	332		15.00

and Figure 13.

$$(\mathit{Safety}\mathit{factor}=\frac{capacity\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}concrete\hspace{0.17em}structure}{stress\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}structure})$$

According to Table 3 and Figure 13, the safety factor of the simulation model is slightly different from the measurement. Generally, the safety factor of the simulation model is about 25% smaller than the measurement. This phenomenon is mainly because the efficiency of the rebar in the secondary lining is not considered during the calculation. Therefore, it is feasible to believe that the share rate of the secondary lining is 40%.

4.3. Total Pressure for Verification

The pressure cells were arranged at the points A, B, and C (in Figure 5) outside of the primary support. They can measure the total pressure of the primary support and the secondary lining. Here, the result of pressure cells is compared with 40% + 40% = 80% of the theoretical load, and it is shown in Figure 14.

It can be seen from the Figure 14a that the pressures at point A, B, and C were surging rapidly after the excavation, then they stabilized in approximately one month. Furthermore, the pressure at vault (Point A) was the largest, haunch (Point B) was the second and sidewall (Point C) was the smallest.

4.4. Discussion

According to the content of Section 4.1 and Section 4.2, the share rate of the primary support and the secondary lining are both reckoned to be 40%. The other 20% of the surrounding rock pressure is taken by multiple factors (mainly the advance support and the surrounding rock itself).

In other words, the aggregated rock pressure borne by primary support and secondary lining is 80% (of the theoretical load). Combined with the content of Section 4.3, the comparison of the calculation and the measurement is shown in

Table 4. Comparison of the calculation and measurement.

Measured Point	Theoretical Load /kPa	80% of the Theoretical Load /kPa	Measured Pressure /kPa	Deviation /%
A	286.90	229.56	180.94	21.18
B	211.63	169.30	142.68	15.73
C	98.40	78.72	65.36	16.97

and Figure 14.

From Table 4, measured pressure, which the rock pressure that the primary support and secondary lining exactly bear, is less than 80% of the theoretical load according to the measurement. The main reason for this deviation is that before the installation of the pressure cells and the construction of the primary support, part of the rock pressure was relaxed and cannot be measured. Usually, this part of the rock pressure was supported by the surrounding rock mass itself. So, in consideration of safety, the conclusion that total share rate of the primary support and the secondary lining is 80% is valid for design. The correctness of theoretical calculation of surrounding rock pressure is also verified by Table 4 and Figure 14 as the deviation is acceptable.

In summary, based on the analysis above, the share rates of the primary support and the secondary lining are both 40% in Daling Tunnel (the super-large span twin tunnel), and other 20% of pressure is mainly born by the advance support and the surrounding rock itself. Although the results of theoretical calculation and the measurement do not match perfectly, the overall deviation is small enough, which basically meets the requirements of design and application in engineering.

Meanwhile, during the whole process, there are several assumptions and limitation, for example:

(1)

The influence of the construction’s sequence of the first hole and following hole was not considered in this research, and the way of excavation was assumed as full section excavation.

(2)

This paper supposed that the stratum was consistent and the surrounding rock mass was ideal.

(3)

The surface of earth was presumed to be horizontal, and so on.

These assumptions and limitation are supposed to be concerned when the conclusion is applied to the practical projects. In addition, the share rate is affected by the strength and stiffness of the composite lining as well as the method and time of excavation and construction. Thus, the share rate of the twin tunnels with super-large span in various conditions still needs to be researched systematically.

5. Conclusions

Based on the theory of stratigraphic slip failure mode and comparison of the simulation and the measurement, the share rate of twin tunnels with super-large span and small interval are studied in this paper. Furthermore, the analysis was verified and supplemented by the outcome of monitoring and measuring. Finally, the conclusions are drawn as follows:

(1)

The formulas of calculating surrounding rock pressure of normal tunnels (usually including two or three lanes) in Chinese standard could be applied to the super-large span twin tunnels (including four or more lanes). The method was verified by field measurement.

(2)

The method of researching the share rate of the primary support and the secondary lining of the tunnel was proposed. The result demonstrates that the share rate of the primary support and the secondary lining of Daling Tunnel are both 40%. Usually for twin tunnels with super-large span in cities, not only the primary support but also the secondary lining should be strong enough to ensure the design is safe and reliable. In addition, this conclusion is conservative when compared to the measurement, which is practical for application in engineering.

(3)

The result of the theoretical calculation and numerical simulation was compared with the measurement to evaluate the research methodology and achievements. These two results match properly, which verify the correctness of this study. Hence the conclusions and the method of this research can make some reference to the design, construction, and maintenance of super-large span twin tunnels.

Since this research is specific for twin tunnels with four lanes (each hole) in cities, this paper can make great contributions to urbanization, infrastructure construction, and even standards drafting. Moreover, this research is more focused on the first hole and does not consider the influence of construction sequence. Therefore, the conclusions drawn in this paper are more appropriate for the first hole.