Experimental-Numerical Investigation of a Steel Pipe Repaired with a Composite Sleeve
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Test
- measuring the defect;
- improving the pipe surface finish (SA 2 ½);
- cleaning the spool with acetone;
- applying dry composite on the pipe and marking the edge of the sleeve;
- removing the composite sleeve and attaching the starter pad;
- increasing the pipe surface temperature to achieve the number of activators;
- mixing filler and the related activator;
- mixing adhesive and the related activator;
- applying the filler on the defect and the starter pad edge;
- applying adhesive to the entire pipe between the marked lines;
- removing the backing of the starter pad and applying the composite sleeve from the starter pad;
- applying the adhesive on each layer of composite and wrapping the eight layers of the composite sleeve;
- securing the cinch bar strap to the dual lock and applying a steady pressure (of 110–140 Pa);
- wrapping filament tape around the composite sleeve.
2.2. Numerical Simulations
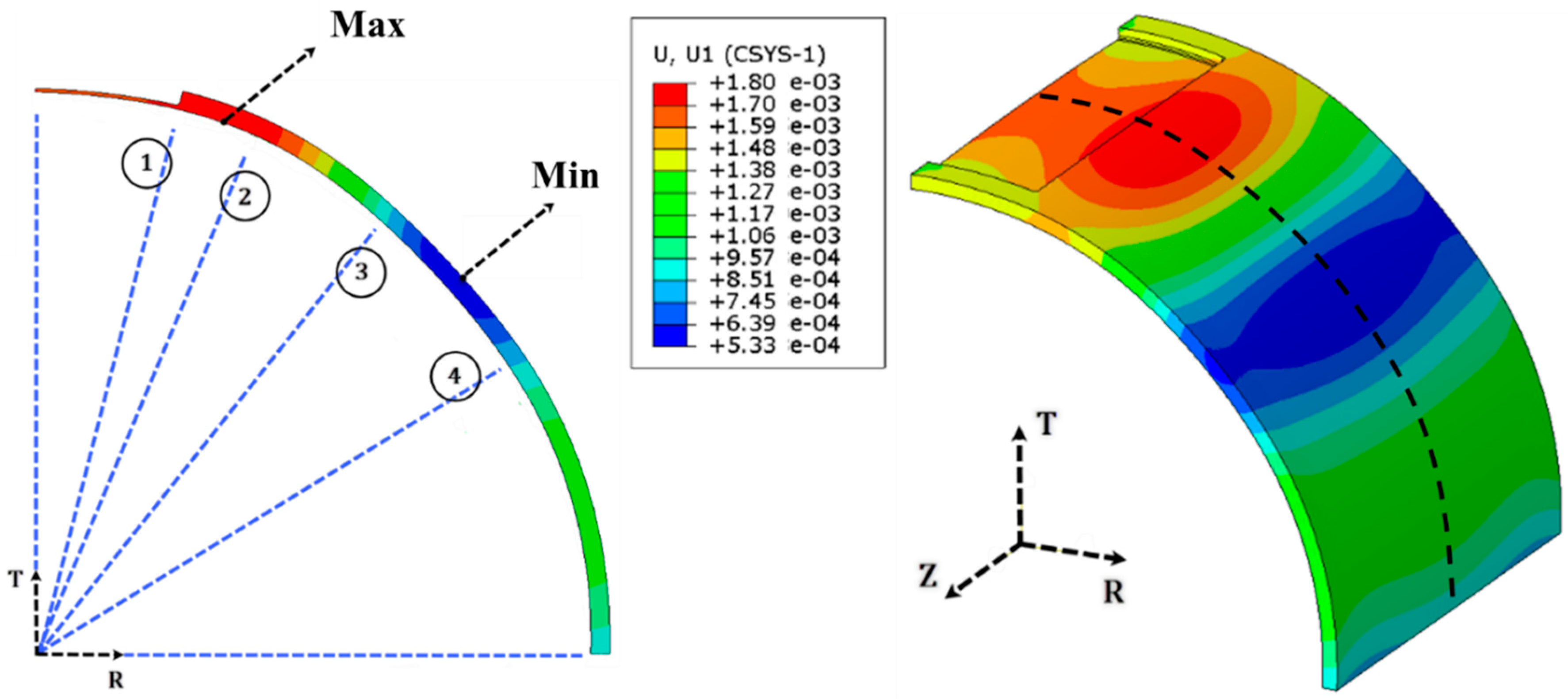
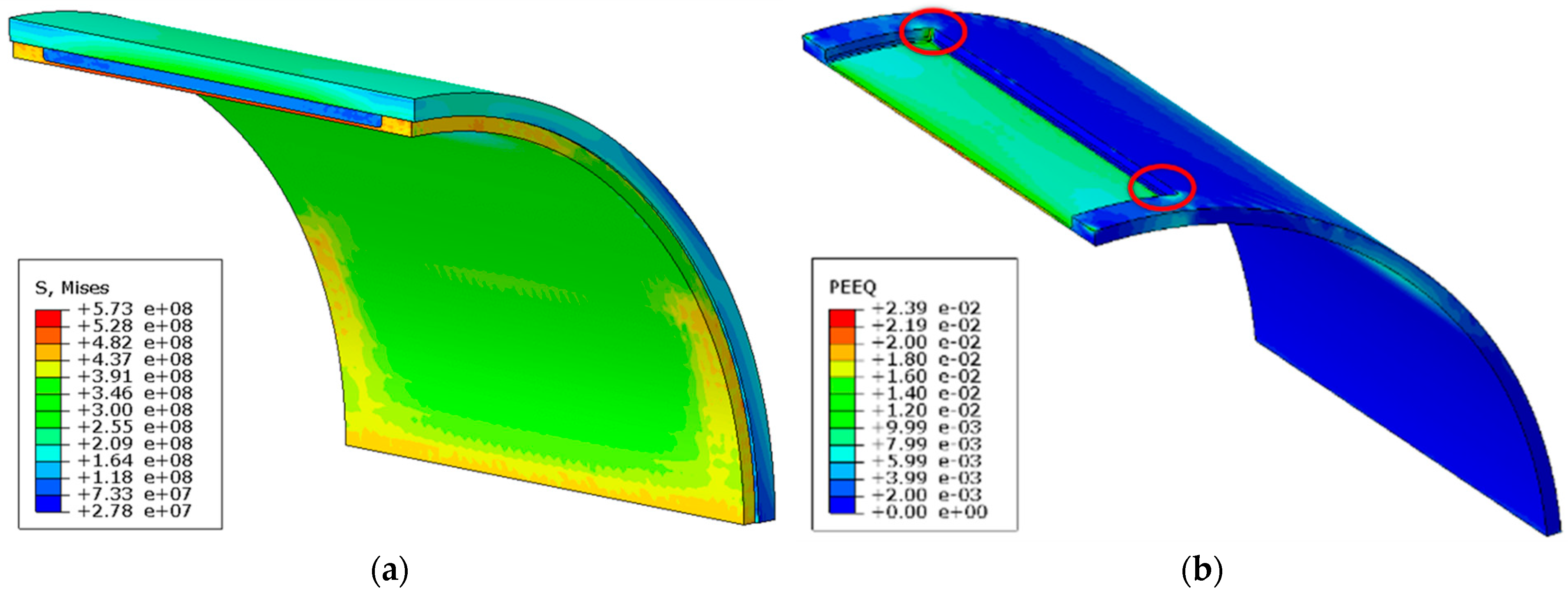
3. Results and Discussion
4. Conclusions
- inspections of pipelines are scheduled to detect potential damages or defects, but their complete understanding must be provided upfront in order to be effective during quick maintenance actions. The understanding of the stress-strain distributions in the surroundings of the damaged and repaired area proposed here provide useful data for engineers on such advanced repairing techniques.
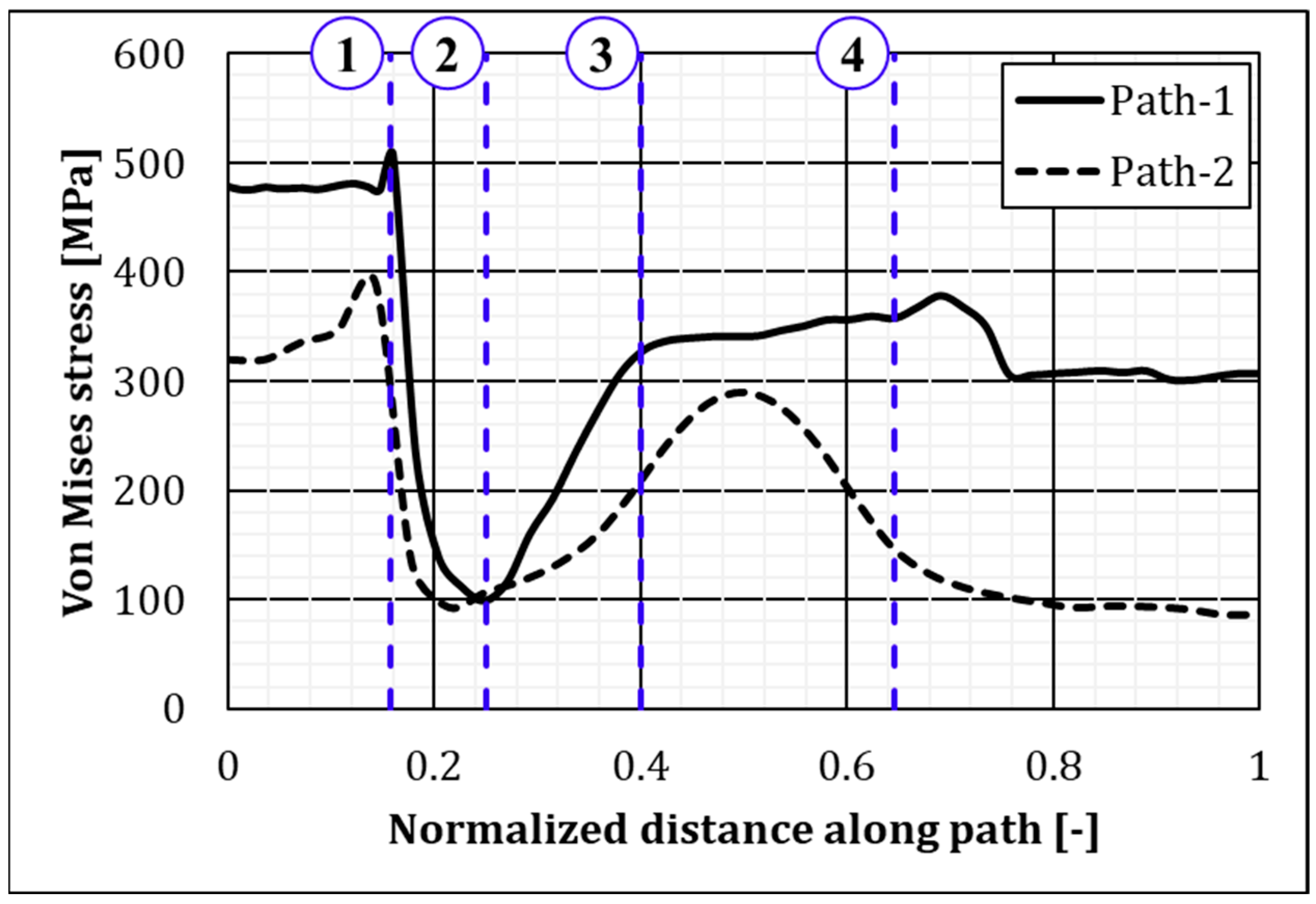
- a plastic hinge is generated by the internal pressure in the composite repaired section of the pipe. Few explanations of such phenomenon are currently available in similar studies, whereas an accurate description of the mechanical behaviour of the plastic hinge on the repaired pipe was here provided.
- the values of the highest stresses in the damaged part and in the healthy part are nearly 3% different from each other. This result indicates that repairing has almost eliminated both the noteworthy thickness reduction of 80% and the related stress concentration in the pipe body.
Author Contributions
Funding
Conflicts of Interest
References
- Pridmore, A.B.; Ojdrovic, R.P. Trenchless Repair of Concrete Pipelines Using Fiber-Reinforced Polymer Composites. In Rehabilitation of Pipelines Using Fiber-Reinforced Polymer (FRP) Composites; Woodhead Publishing: Sawston, UK, 2015; pp. 17–38. ISBN 978-0-85709-684-5. [Google Scholar]
- Witek, M. An assessment of the effect of steel pipeline wall losses on the maximum allowable operating pressure of a gas pipeline. J. Pipeline Eng. 2014, 13, 37–47. [Google Scholar]
- Witek, M.; Szalega, M. EMAT technology applied to high pressure gas pipelines diagnostic, SIGMA NOT Publishing House. Gaz Woda Tech. Sanit. 2015, 11, 387–392. (In Polish) [Google Scholar]
- Shamsuddoha, M.; Manalo, A.; Aravinthan, T.; Islam, M.M.; Djukic, L. Failure analysis and design of grouted fibre-composite repair system for corroded steel pipes. Eng. Fail. Anal. 2020, 119, 104979. [Google Scholar] [CrossRef]
- Köpple, M.F.; Lauterbach, S.; Wagner, W. Composite repair of through-wall defects in pipework—Analytical and numerical models with respect to ISO/TS 24817. Compos. Struct. 2012, 95, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Sahraoui, Y.; Khelif, R.; Chateauneuf, A. Maintenance planning under imperfect inspections of corroded pipelines. Int. J. Press. Vessel. Pip. 2013, 104, 76–82. [Google Scholar] [CrossRef]
- Saeed, N.; Ronagh, H.; Virk, A. Composite repair of pipelines, considering the effect of live pressure—Analytical and numerical models with respect to ISO/TS 24817 and ASME PCC-2. Compos. Part B 2014, 58, 605–610. [Google Scholar] [CrossRef]
- Shamsuddoha, M.; Islam, M.; Aravinthan, T.; Manalo, A.; Lau, K.-T. Effectiveness of using fibre-reinforced polymer composites for underwater steel pipeline repairs. Compos. Struct. 2013, 100, 40–54. [Google Scholar] [CrossRef]
- Alexander, C. The Role of Composite Repair Technology in Rehabilitating Piping and Pipelines. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference (PVP 2014), Anaheim, CA, USA, 20–24 July 2014. [Google Scholar] [CrossRef]
- Chan, P.H.; Tshai, K.Y.; Johnson, M.; Choo, H.L.; Li, S.; Zakaria, K. Burst strength of carbon fibre reinforced polyethylene strip pipeline repair system—A numerical and experimental approach. J. Compos. Mater. 2014, 49, 749–756. [Google Scholar] [CrossRef]
- Shamsuddoha, M.; Islam, M.M.; Aravinthan, T.; Manalo, A.; Djukic, L.P. Effect of hygrothermal conditioning on the mechanical and thermal properties of epoxy grouts for offshore pipeline rehabilitation. AIMS Mater. Sci. 2016, 3, 832–850. [Google Scholar] [CrossRef]
- Sepe, R.; Bollino, F.; Caiazzo, F.; Berto, F. Stress corrosion cracking behavior of welding joint of high strength steel. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012055. [Google Scholar] [CrossRef]
- Kiefner, J.F.; Duffy, A.R. A Study of Two Methods for Repairing Defects in Line Pipe; AGA Cat. No. L22275; American Gas Association: Washington, DC, USA, 1975. [Google Scholar]
- Kiefner, J.F.; Whitacre, G.R. Further Studies of Two Methods for Repairing Defects in Line Pipe; AGA Cat No. L22279; American Gas Association: Washington, DC, USA, 1978. [Google Scholar]
- Mazurkiewicz, Ł.; Małachowski, J.; Tomaszewski, M.; Baranowski, P.; Yukhymets, P. Performance of steel pipe reinforced with composite sleave. Compos. Struct. 2018, 183, 199–211. [Google Scholar] [CrossRef]
- Lim, K.S.; Azraai, S.N.A.; Yahaya, N.; Noor, N.M.; Zardastib, L.; Kim, J.H.J. Behaviour of steel pipelines with composite repairs analyzed using experimental and numerical approaches. Thin-Walled Struct. 2019, 139, 321–333. [Google Scholar] [CrossRef]
- Alexander, C. Overview and recent advances in application of composite materials for repair of transmission pipelines: Evaluation of test results and ongoing research. In Proceedings of the Evaluation and Rehabilitation of Pipelines Conference, Pittsburgh, PA, USA, 21–22 October 2009. [Google Scholar]
- Alexander, C.; Bedoya, J. Repair of dents subjected to cyclic pressure service using composite materials. In Proceedings of the 8th International Pipeline Conference IPC2010, Calgary, AB, Canada, 27 September–1 October 2010. [Google Scholar]
- Bruce, W.A. Comparison of fiber-reinforced polymer wrapping versus steel sleeves for repair of pipelines. In Rehabilitation of Pipelines Using Fiber-Reinforced Polymer (FRP) Composites; Karbhari, V.M., Ed.; Woodhead Publishing: Sawston, UK, 2015. [Google Scholar] [CrossRef]
- Deaton, L. Fiber wrapped steel pipes for high-pressure pipelines. In Rehabilitation of Pipelines Using Fiber-Reinforced Polymer (FRP) Composites; Karbhari, V.M., Ed.; Woodhead Publishing: Sawston, UK, 2015. [Google Scholar] [CrossRef]
- Da Costa-Mattos, H.S.; Reis, J.M.L.; Sampaio, R.F.; Perrut, V.A. An alternative methodology to repair localized corrosion damage in metallic pipelines with epoxy resins. Mater. Des. 2009, 30, 3581–3591. [Google Scholar] [CrossRef]
- Mazurkiewicz, Ł.; Małachowski, J.; Damaziak, K.; Tomaszewski, M. Evaluation of the response of fibre reinforced composite repair of steel pipeline subjected to puncture from excavator tooth. Compos. Struct. 2018, 202, 1126–1135. [Google Scholar] [CrossRef]
- Mazurkiewicz, L.; Tomaszewski, M.; Malachowski, J.; Sybilski, K.; Chebakov, M.; Witek, M.; Yukhymets, P.; Dmitrienko, R. Experimental and numerical study of steel pipe with part-wall defect reinforced with fibre glass sleeve. Int. J. Press. Vessel. Pip. 2017, 149, 108–119. [Google Scholar] [CrossRef]
- Sadrabadi, S.A.; Rahimi, G.; Citarella, R.; Karami, J.S.; Sepe, R.; Esposito, R. Analytical solutions for yield onset achievement in FGM thick walled cylindrical tubes undergoing thermomechanical loads. Compos. Part B Eng. 2017, 116, 211–223. [Google Scholar] [CrossRef]
- Sadrabadi, S.A.; Rahimi, G.H. Yield Onset of Thermo-Mechanical Loading of FGM Thick Walled Cylindrical Pressure Vessels. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 1317–1321. [Google Scholar]
- Mehditabar, A.; Sadrabadi, S.A.; Sepe, R.; Armentani, E.; Walker, J.; Citarella, R.; Sadrabadi, S.A. Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram. Appl. Sci. 2020, 10, 2936. [Google Scholar] [CrossRef]
- Mehditabar, A.; Rahimi, G.H.; Sadrabadi, S.A. Three-dimensional magneto-thermo-elastic analysis of functionally graded cylindrical shell. Appl. Math. Mech. 2017, 38, 479–494. [Google Scholar] [CrossRef]
- Junior, M.M.; Reis, J.M.L.; da Costa Mattos, H.S. Polymer-based composite repair system for severely corroded circumferential welds in steel pipes. Eng. Fail. Anal. 2017, 81, 135–144. [Google Scholar] [CrossRef]
- Mehditabar, A.; Sadrabadi, S.A.; Walker, J. Thermal buckling analysis of a functionally graded microshell based on higher-order shear deformation and modified couple stress theories. Mech. Based Des. Struct. Mach. 2021, 1–19. [Google Scholar] [CrossRef]
- Ansari Sadrabadi, S.; Rahimi, G.H. Elasto-Plastic Behavior Analysis and Yield Onset in FG Cylindrical Tubes under Mechanical and Thermal Loads. Modares Mech. Eng. 2016, 16, 159–166. [Google Scholar]
- Ansari Sadrabadi, S.; Nayebi, A.; Rahimi, G. Behavior of Fgm Spherical Vessels under Internal Pressure and Temperature Difference. J. Mech. Eng. Amirkabir. 2016, 47, 43–50. [Google Scholar]
- Nayebi, A.; Sadrabadi, S.A. FGM elastoplastic analysis under thermomechanical loading. Int. J. Press. Vessel. Pip. 2013, 111–112, 12–20. [Google Scholar] [CrossRef]
- Moustabchir, H.; Azari, Z.; Hariri, S.; Dmytrakh, I. Experimental and numerical study of stress-strain state of pressurized cylindrical shells with external defects. Eng. Fail. Anal. 2010, 17, 506–514. [Google Scholar] [CrossRef]
- Li, X.; Bai, Y.; Su, C.; Li, M. Effect of interaction between corrosion defects on failure pressure of thin wall steel pipeline. Int. J. Press. Vessel. Pip. 2016, 138, 8–18. [Google Scholar] [CrossRef]
- Khalajestani, M.K.; Bahaari, M.R. Investigation of pressurized elbows containing interacting corrosion defects. Int. J. Press. Vessel. Pip. 2014, 123–124, 77–85. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, Y. Reliability and failure pressure prediction of various grades of pipeline steel in the presence of corrosion defects and pre-strain. Int. J. Press. Vessel. Pip. 2012, 89, 75–84. [Google Scholar] [CrossRef]
- Meriem-Benziane, M.; Abdul-Wahab, S.A.; Zahloul, H.; Babaziane, B.; Hadj-Meliani, M.; Pluvinage, G. Finite element analysis of the integrity of an API X65 pipeline with a longitudinal crack repaired with single- and double-bonded composites. Compos. Part B Eng. 2015, 77, 431–439. [Google Scholar] [CrossRef]
- Giannella, V.; Perrella, M.; Citarella, R. Efficient FEM-DBEM coupled approach for crack propagation simulations. Theor. Appl. Fract. Mech. 2017, 91, 76–85. [Google Scholar] [CrossRef]
- Giannella, V.; Fellinger, J.; Perrella, M.; Citarella, R. Fatigue life assessment in lateral support element of a magnet for nuclear fusion experiment “Wendelstein 7-X”. Eng. Fract. Mech. 2017, 178, 243–257. [Google Scholar] [CrossRef] [Green Version]
- Giannella, V.; Citarella, R.; Fellinger, J.; Esposito, R. LCF assessment on heat shield components of nuclear fusion experiment “Wendelstein 7-X” by critical plane criteria. Procedia Struct. Integr. 2018, 8, 318–331. [Google Scholar] [CrossRef]
- Dassault Systemes. ABAQUS User’s and Theory Manuals; Version 6.14; HKS Inc.: Villepinte, France, 2014. [Google Scholar]
- Citarella, R.; Giannella, V.; Vivo, E.; Mazzeo, M. FEM-DBEM approach for crack propagation in a low pressure aeroengine turbine vane segment. Theor. Appl. Fract. Mech. 2016, 86, 143–152. [Google Scholar] [CrossRef]
- Giannella, V.; Vivo, E.; Mazzeo, M.; Citarella, R. FEM-DBEM approach to simulate crack propagation in a turbine vane segment undergoing a fatigue load spectrum. Procedia Struct. Integr. 2018, 12, 479–491. [Google Scholar] [CrossRef]
- Citarella, R.G.; Cricrì, G.; Armentani, E. Multiple Crack Propagation with Dual Boundary Element Method in Stiffened and Reinforced Full Scale Aeronautic Panels. Key Eng. Mater. 2013, 560, 129–155. [Google Scholar] [CrossRef]
- Giannella, V. Stochastic approach to fatigue crack-growth simulation for a railway axle under input data variability. Int. J. Fatigue 2020, 144, 106044. [Google Scholar] [CrossRef]
- Shlyannikov, V.; Yarullin, R.; Yakovlev, M.; Giannella, V.; Citarella, R. Mixed-mode crack growth simulation in aviation engine compressor disk. Eng. Fract. Mech. 2021, 246, 107617. [Google Scholar] [CrossRef]
- Giannella, V.; Sepe, R.; Borrelli, A.; De Michele, G.; Armentani, E. Numerical investigation on the fracture failure of a railway axle. Eng. Fail. Anal. 2021, 129, 105680. [Google Scholar] [CrossRef]



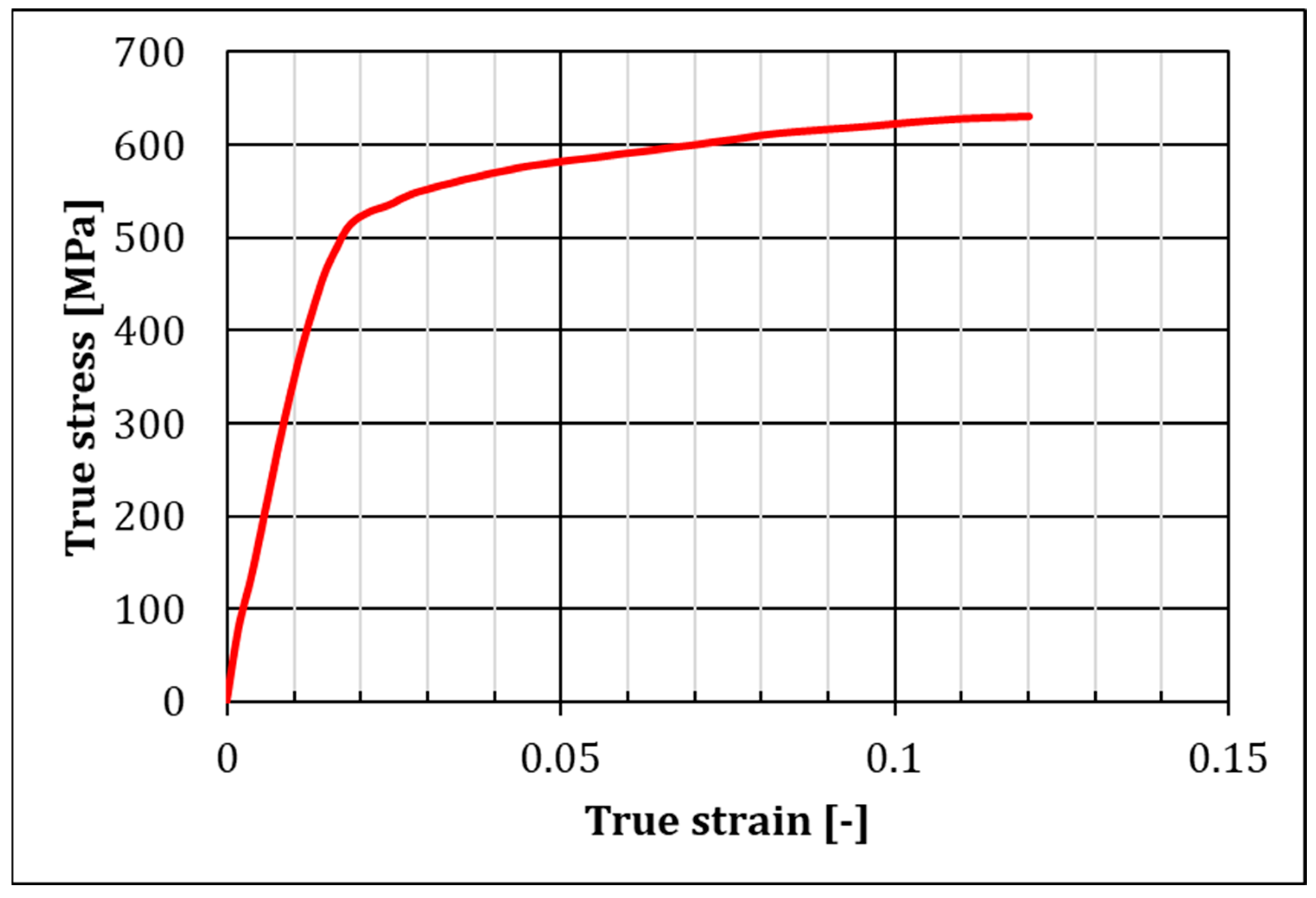
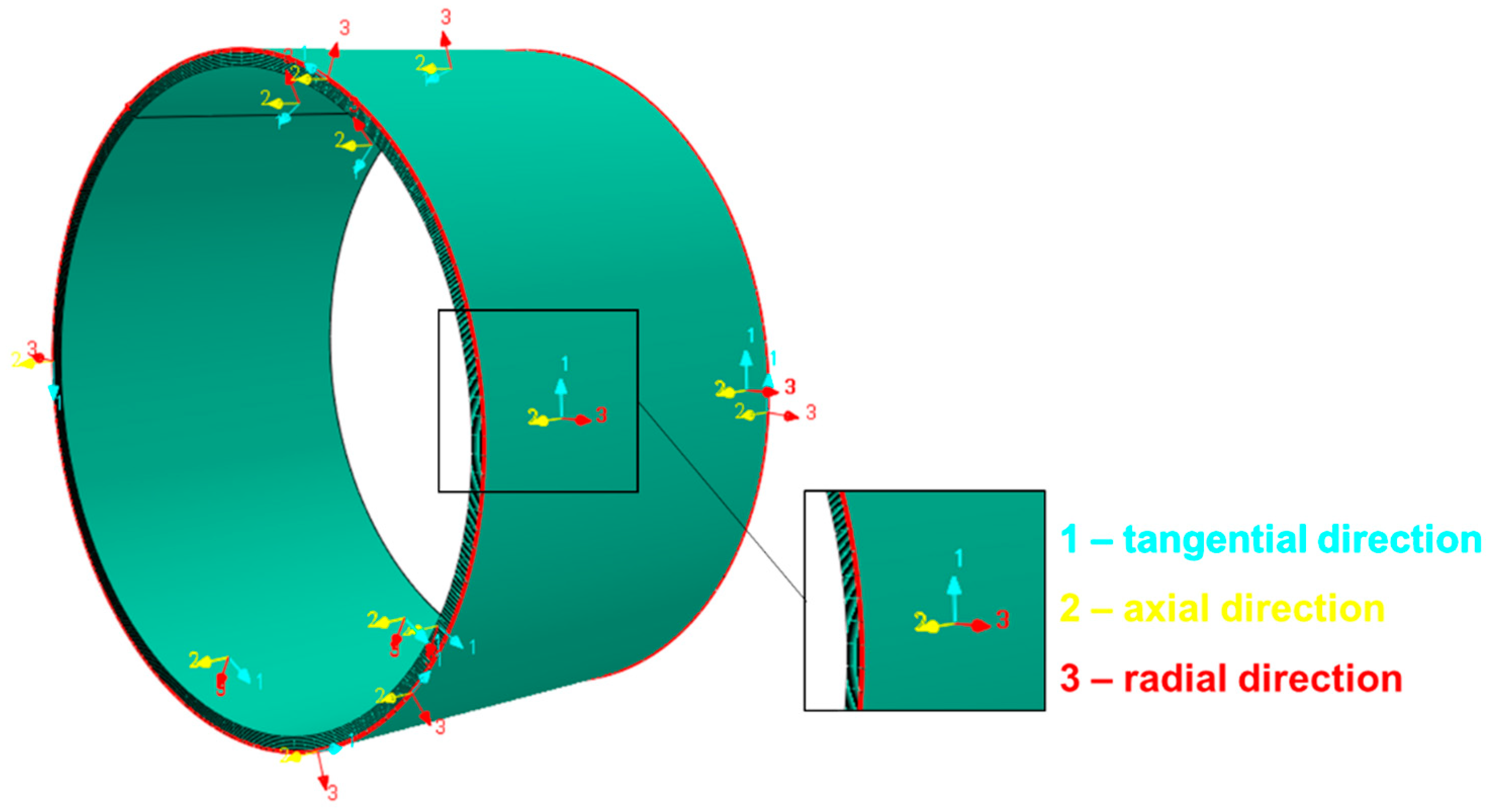
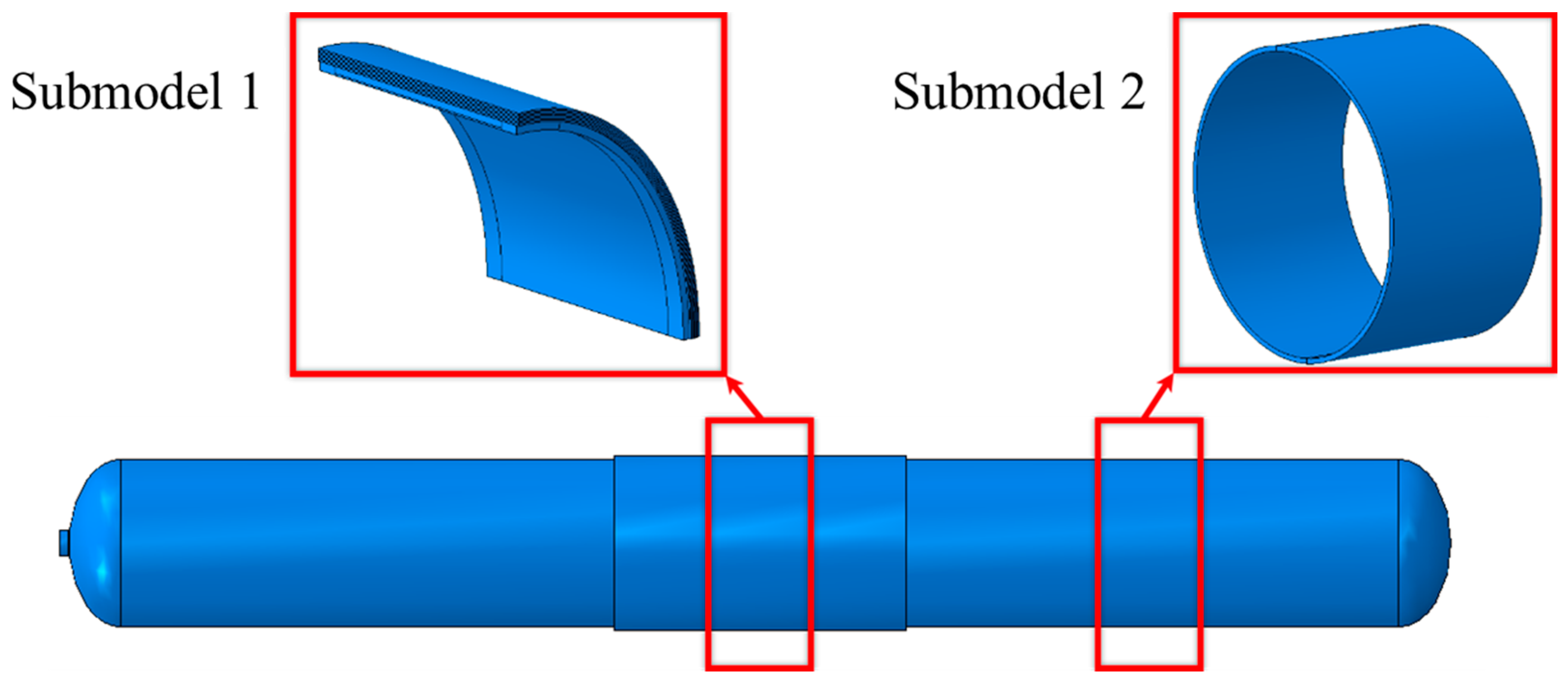








| Young’s Modulus | Poisson’s Ratio | Yield Strength | Tensile Strength |
|---|---|---|---|
| 207 GPa | 0.3 | 300 MPa | 630 MPa |
| Mass density | 1925 |
| Young’s modulus | 41.225 GPa |
| Young’s moduli | 11.542 GPa |
| shear moduli | 3.509 GPa |
| shear moduli | 4.674 GPa |
| Poisson’s ratios | 0.243 |
| Poisson’s ratio | 0.235 |
| Young’s Modulus | Poisson’s Ratio |
|---|---|
| 10 GPa | 0.34 |
| Global model | 11,568 quadratic hexahedral elements, type: C3D20 |
| Submodel 1 (SM1) | 23,934 quadratic tetrahedral elements type: C3D10M; 4480 quadratic hexahedral elements, type: C3D20. |
| Submodel 2 (SM2) | 10,800 quadratic hexahedral elements, type: C3D20. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansari Sadrabadi, S.; Dadashi, A.; Yuan, S.; Giannella, V.; Citarella, R. Experimental-Numerical Investigation of a Steel Pipe Repaired with a Composite Sleeve. Appl. Sci. 2022, 12, 7536. https://doi.org/10.3390/app12157536
Ansari Sadrabadi S, Dadashi A, Yuan S, Giannella V, Citarella R. Experimental-Numerical Investigation of a Steel Pipe Repaired with a Composite Sleeve. Applied Sciences. 2022; 12(15):7536. https://doi.org/10.3390/app12157536
Chicago/Turabian StyleAnsari Sadrabadi, Saeid, Amin Dadashi, Sichen Yuan, Venanzio Giannella, and Roberto Citarella. 2022. "Experimental-Numerical Investigation of a Steel Pipe Repaired with a Composite Sleeve" Applied Sciences 12, no. 15: 7536. https://doi.org/10.3390/app12157536
APA StyleAnsari Sadrabadi, S., Dadashi, A., Yuan, S., Giannella, V., & Citarella, R. (2022). Experimental-Numerical Investigation of a Steel Pipe Repaired with a Composite Sleeve. Applied Sciences, 12(15), 7536. https://doi.org/10.3390/app12157536









